Introduction
Nuclear data (including the cross-sections of all types of reaction channels, differential cross-sections, and double-differential cross-sections) of nucleon-induced 6,7Li reactions are important for various applications, such as the compact accelerator-driven neutron source and the International Fusion Materials Irradiation Facility (IFMIF), as introduced in Refs. [1-7]. A lithium-glass scintillator with natural lithium is used as a small-angle neutron scattering spectrometer (SANS) for material research at the China Spallation Neutron Source (CSNS) to satisfy both the neutron detection efficiency and gamma elimination requirements [8]. 7Li enrichment and 6Li inventory are important influencing factors in molten salt fast reactors (MSFRs) [9]. In recent years, lithium has received considerable attention in astrophysics because it can lead to a better understanding of the evolution and formation of the universe. The standard big-bang nucleosynthesis (BBN) theory overestimates the primordial 7Li abundance by a factor of approximately three to four, that is, the cosmological lithium problem [10]. The reaction 6Li(p, γ) 7Be plays an important role in the consumption of 6Li and the formation of 7Be, and 7Be will eventually decay into 7Li at the end of big-bang nucleosynthesis [11]. In an atmosphere of approximately 1% of giant stars, there exists an anomalous elevation in lithium abundance, directly contradicting the expectations calculated by conventional stellar evolution models. An extremely Li-rich giant (possibly newly enriched) and a rigorous investigation of its evolutionary stage are definitely important [12]. Furthermore, an in-depth study of the nucleon- 6,7Li reaction will enhance our understanding of 1p-shell light nuclear reactions[13-15].
Although 6Li and 7Li differ by only one neutron, they exhibit significant differences. The natural abundance of 6Li is only 7.5%, whereas that of 7Li is as high as 92.5%. The energy levels of 6Li and 7Li are different both in terms of their energy values and widths. Additionally, every energy level of the 6Li nucleus has a spin with an even multiple of 1/2, whereas the spin of the 7Li nucleus is an odd multiple of 1/2 [16]. 6Li is easily captured by neutrons, producing 7Li and high-energy gamma rays, whereas 7Li is more likely to undergo α decay. Moreover, the capture cross-section of 6Li is smaller than that of 7Li in the thermal neutron energy range, making 6Li a common material for slow neutron shielding in certain nuclear applications. Differences in the energy level diagrams of 6Li and 7Li can lead to variations in their decay properties and the particles emitted from the individual levels [1-6]. Therefore, the results of the n+6, 7Li reactions are significantly different, as shown both experimentally and theoretically [1, 2, 7]. In our previous studies, we successfully predicted the double-differential cross-sections of the charged particles for the p+7Li reaction using the statistical theory of light nucleus reaction (STLN) model [15]. On this basis, an ENDF-6-formatted file of the double-differential cross-section was obtained. File-6 (file of the double-differential cross-section), one of the important files of the nuclear reaction database, is recommended when the energy and angular distributions of the emitted particles must be coupled, when it is important to provide a concurrent description of neutron scattering and particle emission, when so many reaction channels are open that it is difficult to provide separate reactions, or when accurate distributions of the charged particle or residual nucleus are required for particle transport, heat deposition, or radiation damage calculations [17]. However, there are still no publications describing the double-differential cross-sections of outgoing particles for the p+6Li reaction.
Quantitatively describing all the physical quantities is challenging because of the limited availability of comprehensive experimental data for the p+6Li reaction. For the p+6Li reaction, there are only a small number of experimental partial cross-sections of the (p, γ), (p, el), and (p, 3He) channels [18-20]. Furthermore, numerous elastic scattering angular distributions have been measured at various incident energies [21, 20]. Fortunately, the double-differential cross-sections of the outgoing proton, deuteron, and mixture of 3He and α for the p+6Li reaction were measured in 1989 and 1991 [23, 22]. This makes it possible to validate the theoretical calculations. The evaluated partial cross-sections of (p, el), (p, 3He) and (p, x) are available in nuclear reaction databases such as ENDF/B-VIII.0 [24] and JENDL-5 [25]. However, the double-differential cross-sections of the outgoing neutron and charged particles were not included in these databases because the effects of the secondary particle emission processes between the discrete levels and cluster separations in light nuclear reactions have not been considered. In ENDF/B-VIII.0, the cross-sections of (p, el), (p, 3He), and (p, x) were derived from the R-matrix analysis [24, 26], while in JENDL-5, multichannel R-matrix fitting was used to evaluate the experimental data in the incident proton energy range from 10 keV to 3 MeV. The CCONE code [25] was employed to calculate the differential cross-sections of the emitted particles in the incident proton energy range from 3 to 200 MeV. Subsequently, proton-induced reactions on 6,7Li were also calculated using the CDCC method in 2013 [5], but the double-differential cross-sections of the outgoing proton, deuteron, and triton were not provided. A possible reason for this is that the sequential secondary particle emission processes were not considered in the CDCC model [6].
This study provides an in-depth analysis of the p+6Li reaction based on the STLN model with energy, angular momentum, and parity conservations. The Coulomb barriers of both the incident and exit channels are considered for different charged particles. Taking an impure target as an example, the influence of contamination is described in terms of the kinetic energy. The double-differential cross-sections of the total outgoing proton, deuteron, and the mixture of 3He and α are calculated by analyzing the reaction channels at different incident energies. The calculated results at Ep = 14 MeV agree well with the available experimental data.
Section 2 briefly introduces the theoretical model used in this study. The reaction channels of the p+6Li reaction below 20 MeV are analyzed in detail in Sect. 3. Section 4 provides a comparison between the calculated results and the experimental data, along with the corresponding analysis. A summary is provided in the final section.
Theoretical descriptions
Theoretical Frame
Based on the unified Hauser–Feshbach and exciton model [27], which can describe the particle emission processes between the discrete energy levels with energy, angular momentum, and parity conservations, a statistical theory of light nucleus reaction (STLN) is developed to describe the mechanism of the nucleon-induced light nucleus reaction [14, 13]. A considerable amount of experimental data, with a focus on double-differential cross-sections (such as the neutron-induced reactions on 6Li [1], 7Li [2], 9Be [28, 29], 10B [30], 11B [31], 12C [32, 27, 33], 14N [34], 16O [35, 36], and 19F [37] as well as the proton-induced reactions on 7Li [15] and 9Be [14, 38]), has been reproduced very well.
The cross-sections of the first emitted particles from the compound nucleus to the discrete energy levels of the first residual nuclei can be expressed as
The cross-section of the second outgoing particle from the discrete energy levels of the first residual nucleus to the discrete energy levels of the second residual nucleus can be expressed as
For the simultaneous emission process, for example,
Based on the isotropic energy spectra assumption in the CMS for the three-body breakup reaction, that is, the spectra for all azimuth angles are identical, the double-differential cross-section of b1 particle in the CMS can be expressed as
εC and
Coulomb Barrier
Owing to the effect of the Coulomb barrier [42, 43], the kinetic energy of the first outgoing charged particle
Therefore, the incident energy Ep must satisfy the following equation for open reaction channels:
Particle Identification
To conveniently describe the expression of the A(a, b)B reaction, some quantities are defined as follows: A, B, a, and b are the target nucleus, residual nucleus, incident particle, and emitted particle, respectively. The target nucleus A is fixed in the LS, so the kinetic energy and momentum are 0, respectively. The reaction value Q is thus expressed as follows:
From Eqs. (16) and (17), the kinetic energy of the first emitted particle b in the LS can be expressed as
Analysis of the reaction channels
For the proton-induced 6Li reaction, reaction channels theoretically exist at an incident energy
Considering the energy, angular momentum, and parity conservations in the particle emission processes, the reaction channels for the first particle emission are as follows:
For the first particle emission channel 6Li(p, n)6Be*, the first residual nucleus 6Be* that reaches the first energy level can still emit a proton with the second residual nucleus 5Li*. Furthermore, the second residual nucleus 5Li* can emit a proton and alpha through the direct two-body breakup process, thus contributing to the (p, n2pα) reaction channel.
For the first particle emission channel 6Li(p, p)6Li*, the second excited energy level (
For the first particle emission channel, 6Li(p, d)5Li*, the reaction process 5Li* → p + α occurs as mentioned above, so this reaction channel belongs to the (p, dpα) reaction channel in the final state. For the first outgoing 3He from the compound nucleus to the ground state of the first residual nucleus α, this process only contributes to the (p, 3He) α reaction channel.
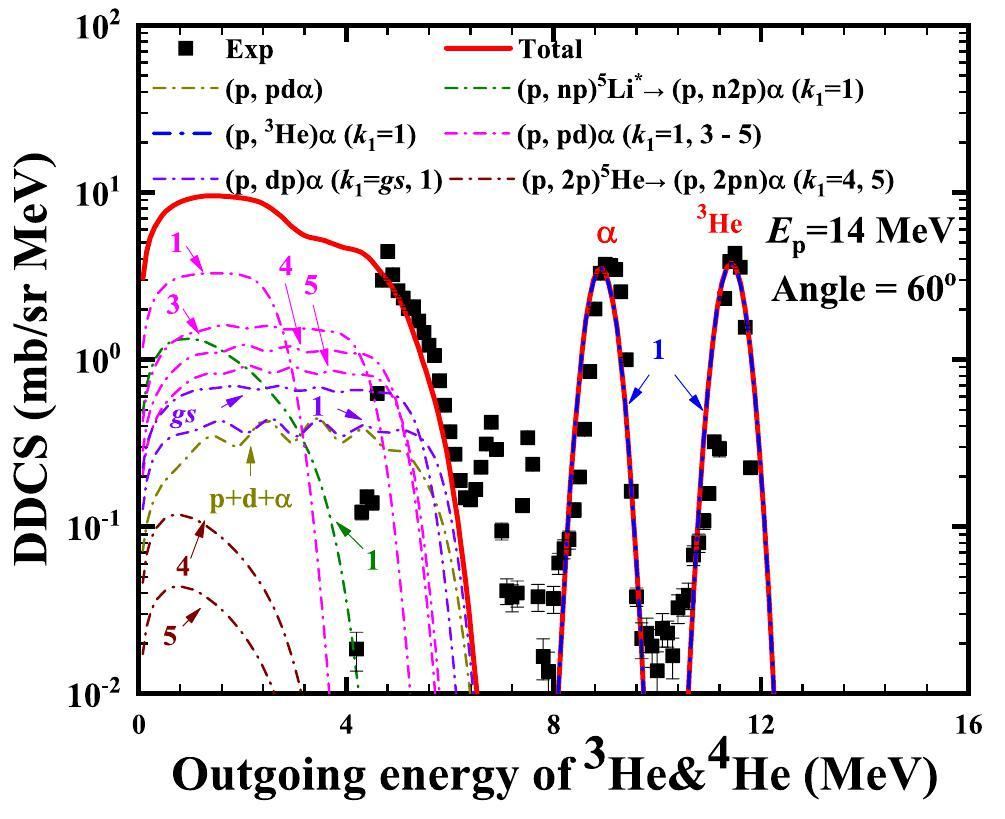
According to the analyses of the reaction channels discussed above, the total spectra can be determined by adding all the partial spectra of the same outgoing particle obtained from every reaction channel. The contributions to the double-differential cross-sections of the total emitted protons are from elastic scattering, inelastic scattering, direct three-body breakup, and the (p,n2pα) and (p,pdα) reaction channels. The contributions to the double-differential cross-sections of the total emitted deuterons are from (p, d)5Li*, (p, pdα), and the direct three-body breakup process 7Be* → p + d + α. The contributions to the double-differential cross-sections of the total emitted alpha are only from (p,3He)α, (p, n2pα), (p, pdα), and the direct three-body breakup process 7Be* → p + d + α. The contribution to the double-differential cross-section of the total emitted 3He is only from the (p, 3He)α reaction channel. It is worth mentioning that the experimental double-differential cross-sections are a mixture of 3He and α because of the difficulties encountered in the measurement [22].
In conclusion, for the proton-induced 6Li reaction, reaction channels finally exist at an incident energy
Calculated results
The experimental double-differential cross-sections of light charged particles (proton, deuteron, 3He, and α) for the p+6Li reaction were measured in Refs. [23, 22]. Based on the STLN model, a PLUNF code for the p+6Li reaction is developed to calculate the double-differential cross-sections of the outgoing nucleon and light composite charged particles. Comparisons are performed between the calculations and measurements of the double-differential cross-sections for the total outgoing proton, deuteron, 3He, and alpha particles for the p+6Li reaction.
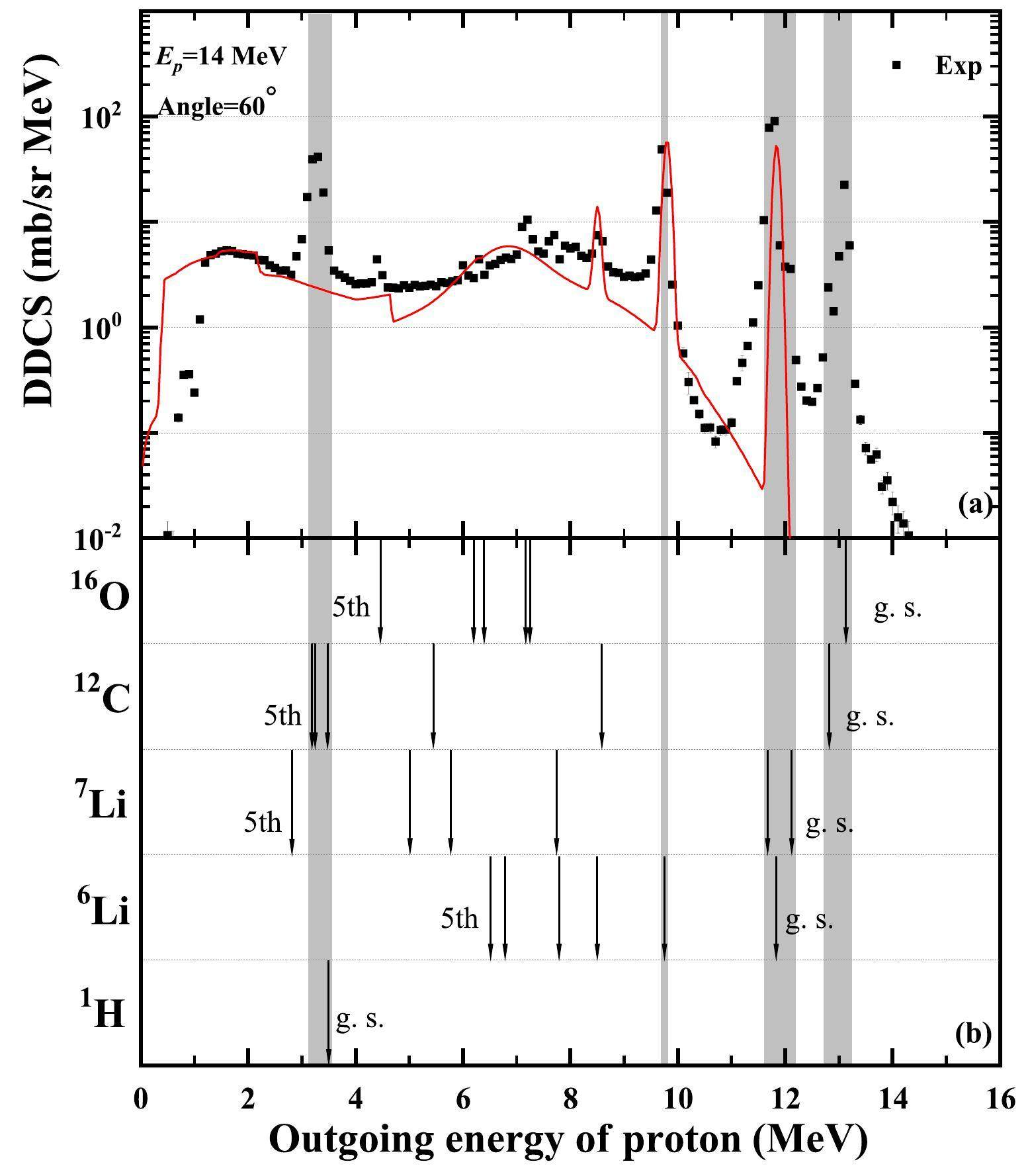
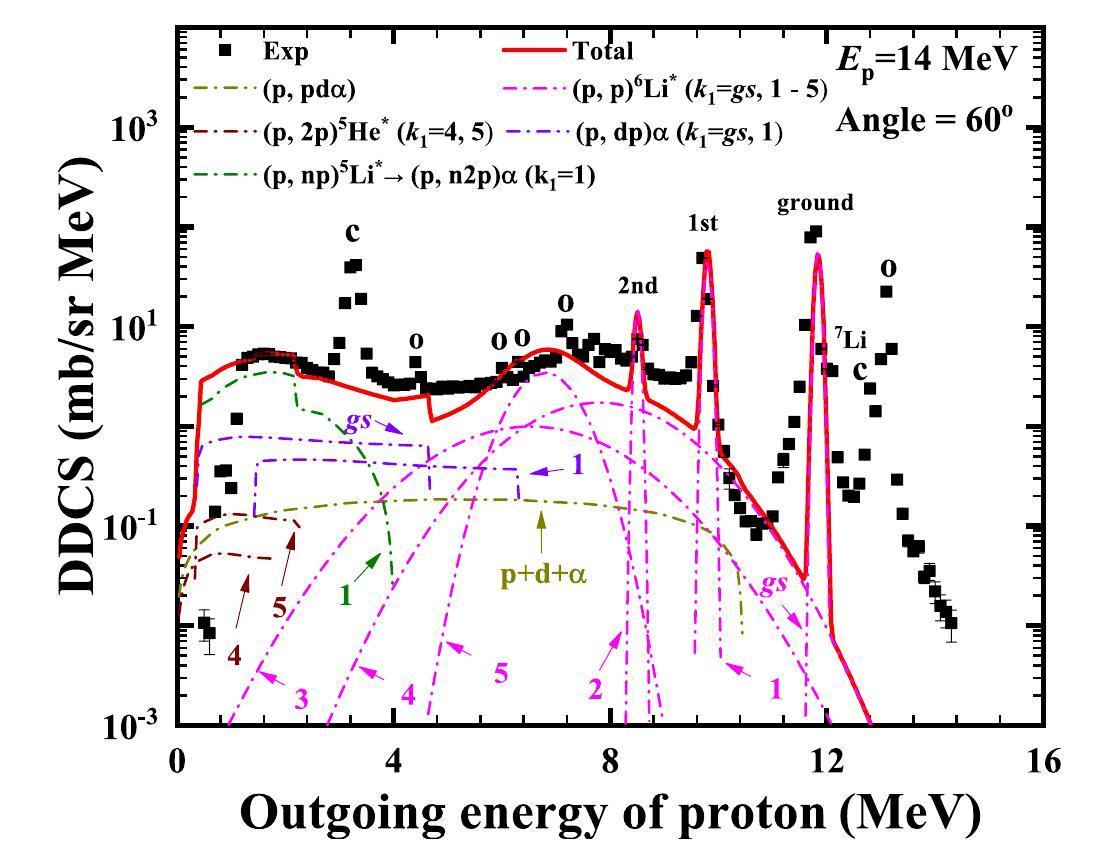
Because the target is contaminated by 1H, 7Li, 12C, and 16O, there are additional contributions to the double-differential cross-sections. Using Eq. (18), the kinetic energies of the outgoing proton and its residual nuclei from the ground state to the fifth energy level of the pure 6Li and contaminants are identified. For example, for the double-differential cross-sections of the outgoing proton at an angle of 60° at Ep=14 MeV in the LS, as shown in Fig. 2 (a), the black narrow bands in the below panel (b) represent the contributions of the outgoing proton from the discrete levels (only illustrated from ground state to the fifth energy level, as marked) of targets 6Li and contaminants (including 1H, 7Li, 12C, and 16O). From Fig. 2, one can see that the contributions to the first abrupt peak on the right-hand side are the elastic scattering of protons with 12C and 16O. The contributions to the second peak on the right-hand side are the elastic scattering of protons with 6Li and 7Li, and the first inelastic scattering of 7Li. The contribution to the third peak on the right-hand side is the pure inelastic scattering of protons with the first excited energy level of 6Li. The contributions to the first peak on the left-hand side are the elastic scattering of protons with 1H, the inelastic scattering of protons from the third to the fifth excited energy level of 12C, and the fifth excited energy level of 7Li. The levels of 7Li exhibit clear differences in their contributions to the double-differential cross-section of the outgoing protons compared with those of 6Li.
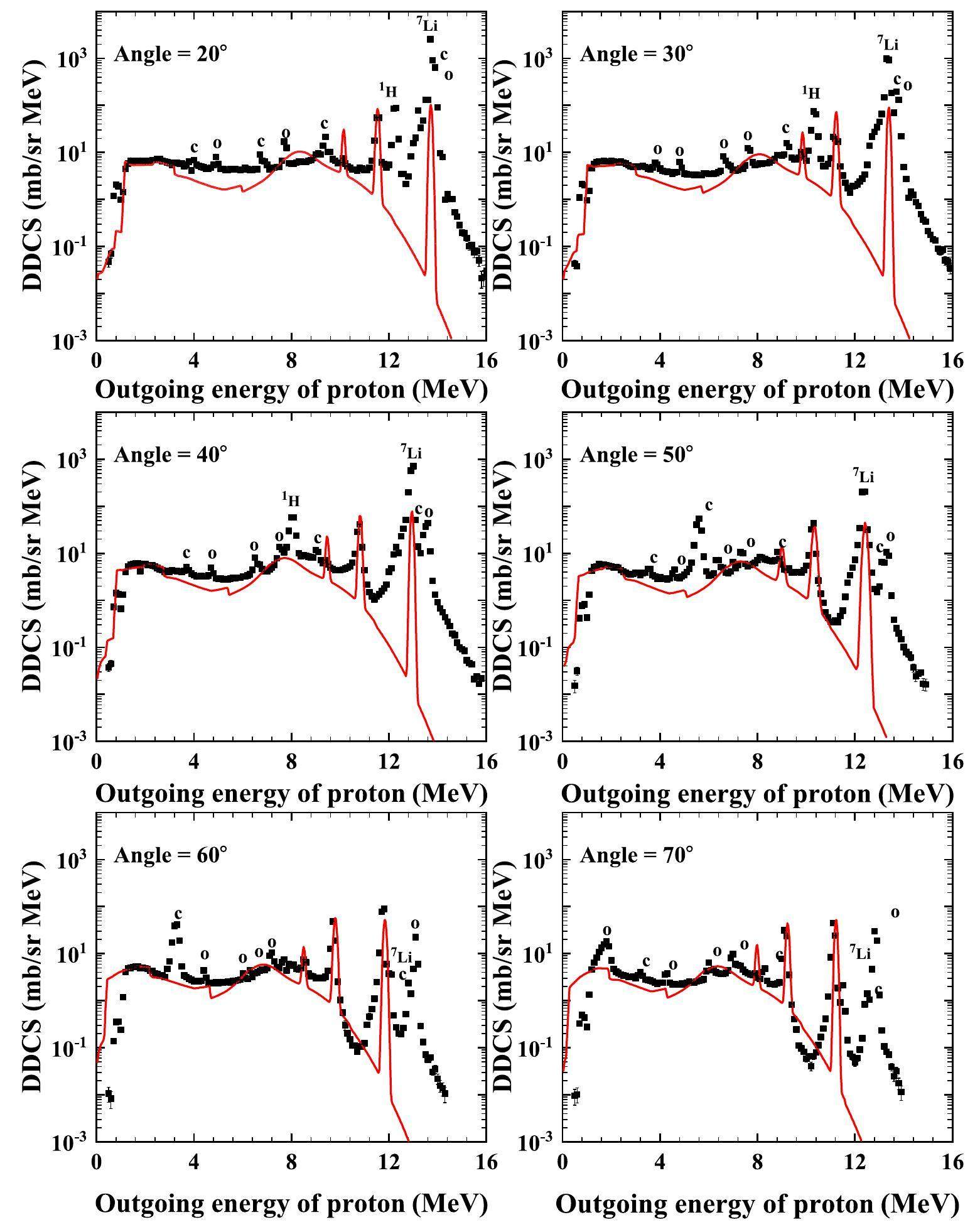
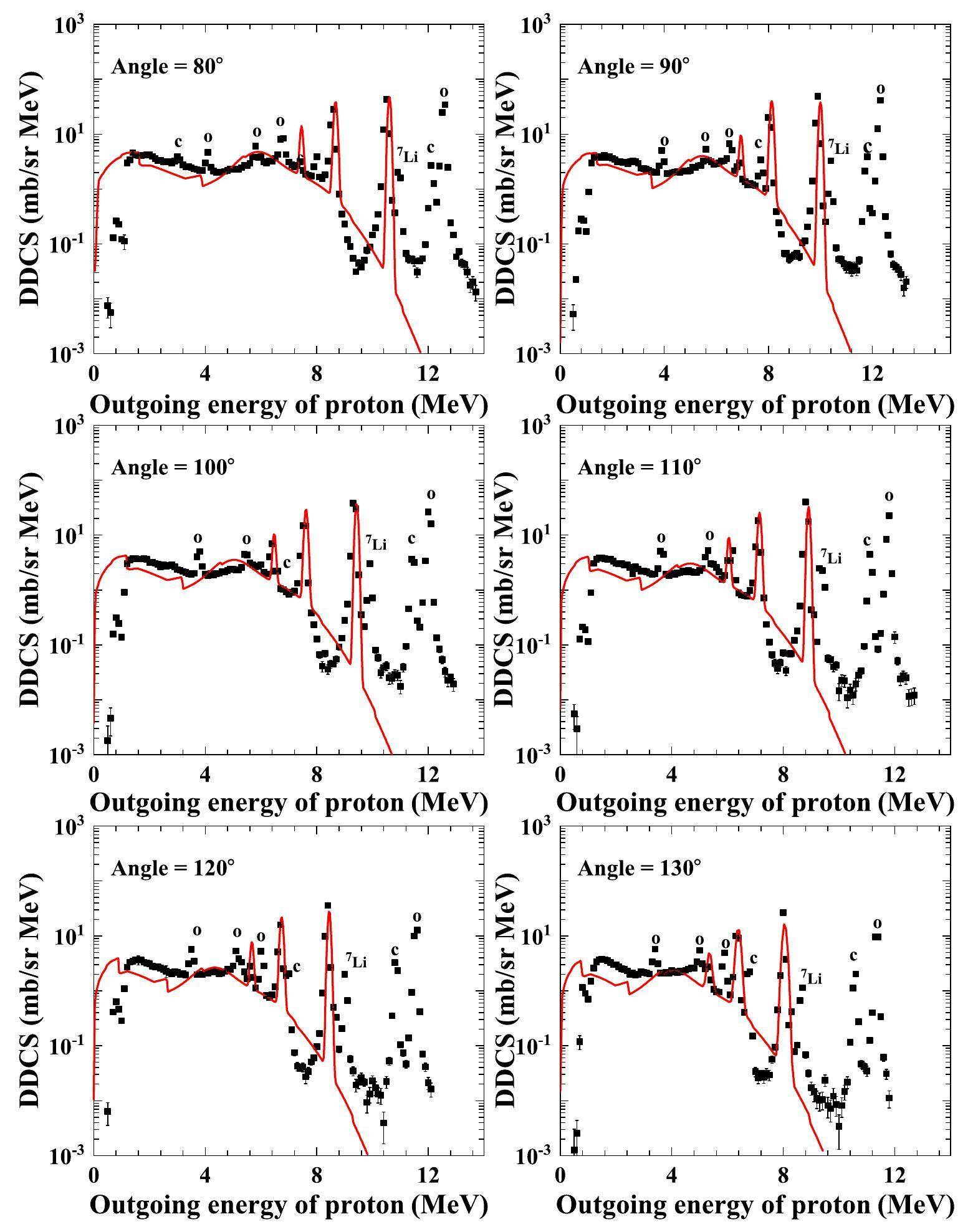
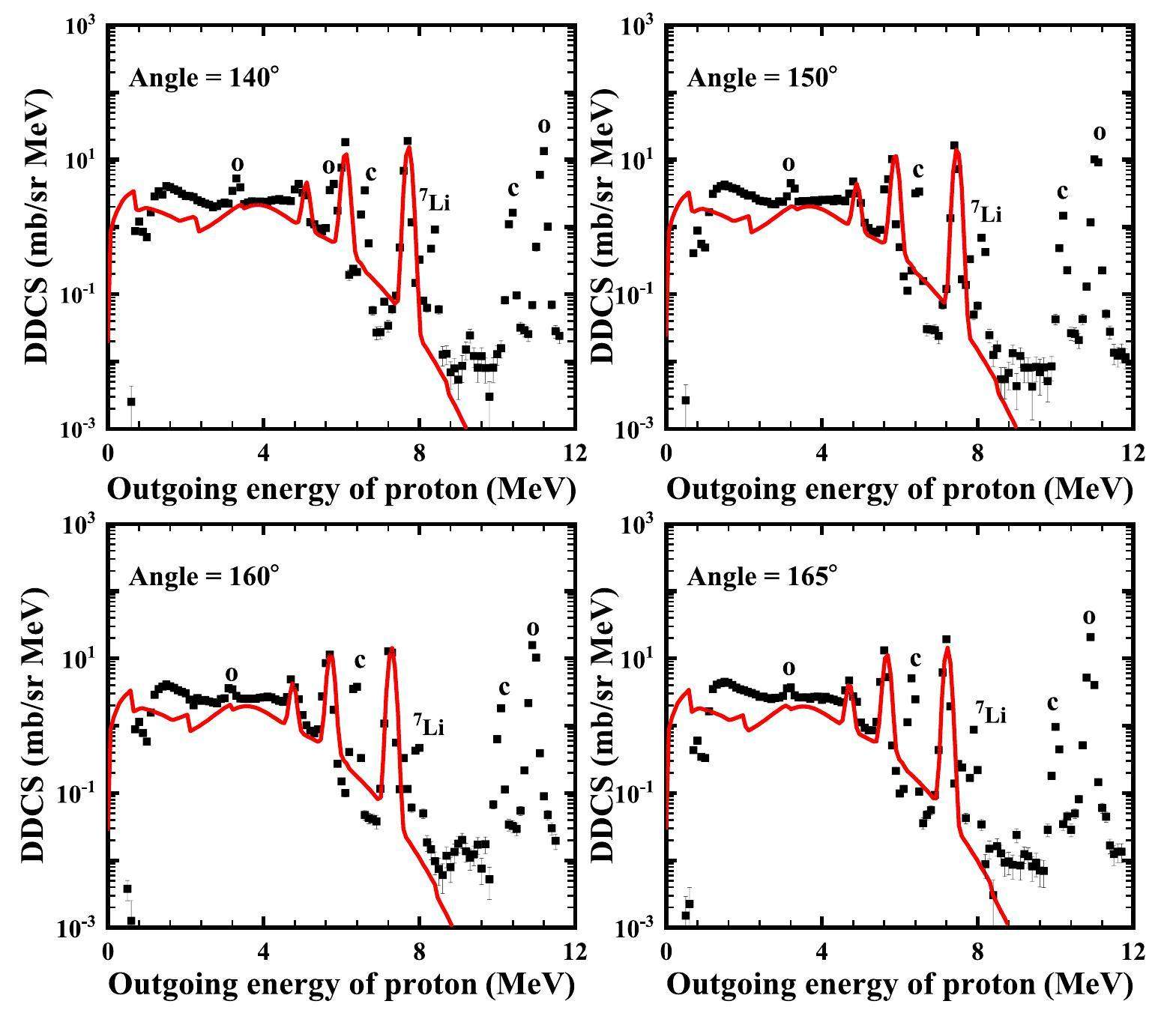
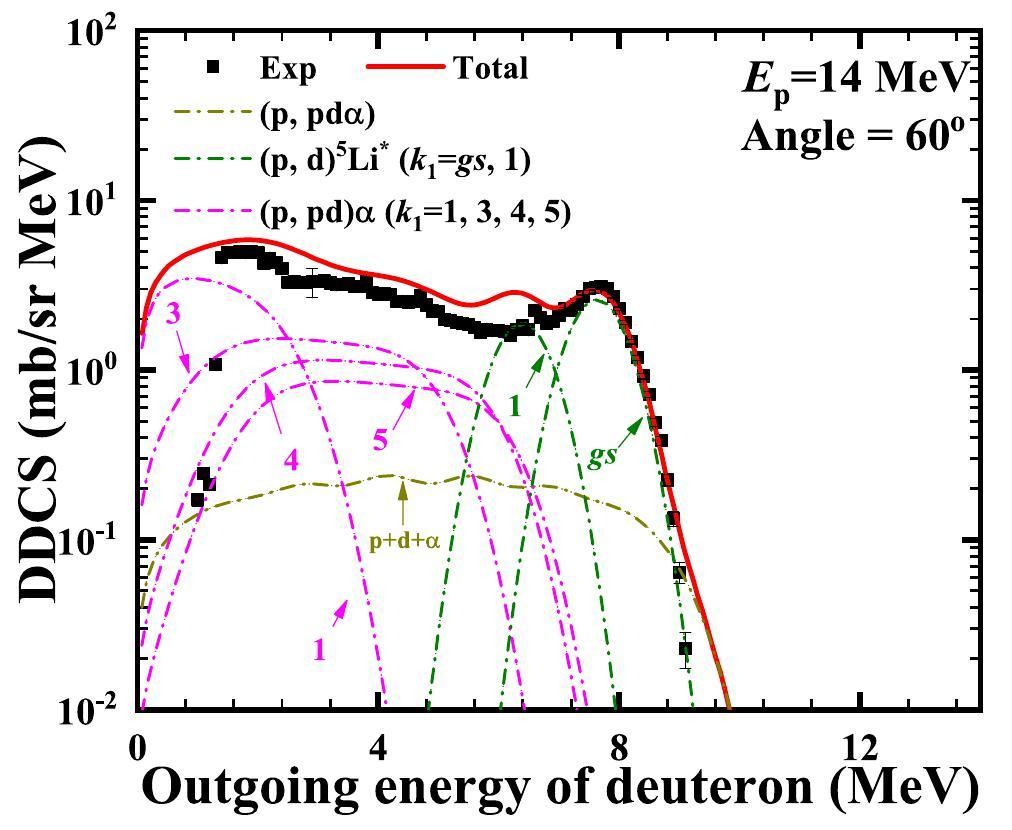
Comparisons of the calculated double-differential cross-sections of the total outgoing proton with the measured data are shown in Figs. 3, 4 and 5 at an incident proton energy of 14 MeV for outgoing angles of 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°, 100°, 110°, 120°, 130°, 140°, 150°, 160°, and 165°. The black points represent the experimental data obtained from Ref. [23], and the red solid lines denote the calculated total double-differential cross-sections of the outgoing proton. One can see that the calculated results agree well with the measurements, except for some peaks contaminated by elastic and inelastic scattering from 1H, 7Li, 12C, and 16O, as reported in Ref. [23]. Taking the calculated double-differential cross-sections of the outgoing proton with 60° at Ep =14 MeV as an example, the partial spectra are shown in Fig. 6. The yellow dash-dotted line denotes the partial spectra of the proton emitted from a direct three-body breakup through
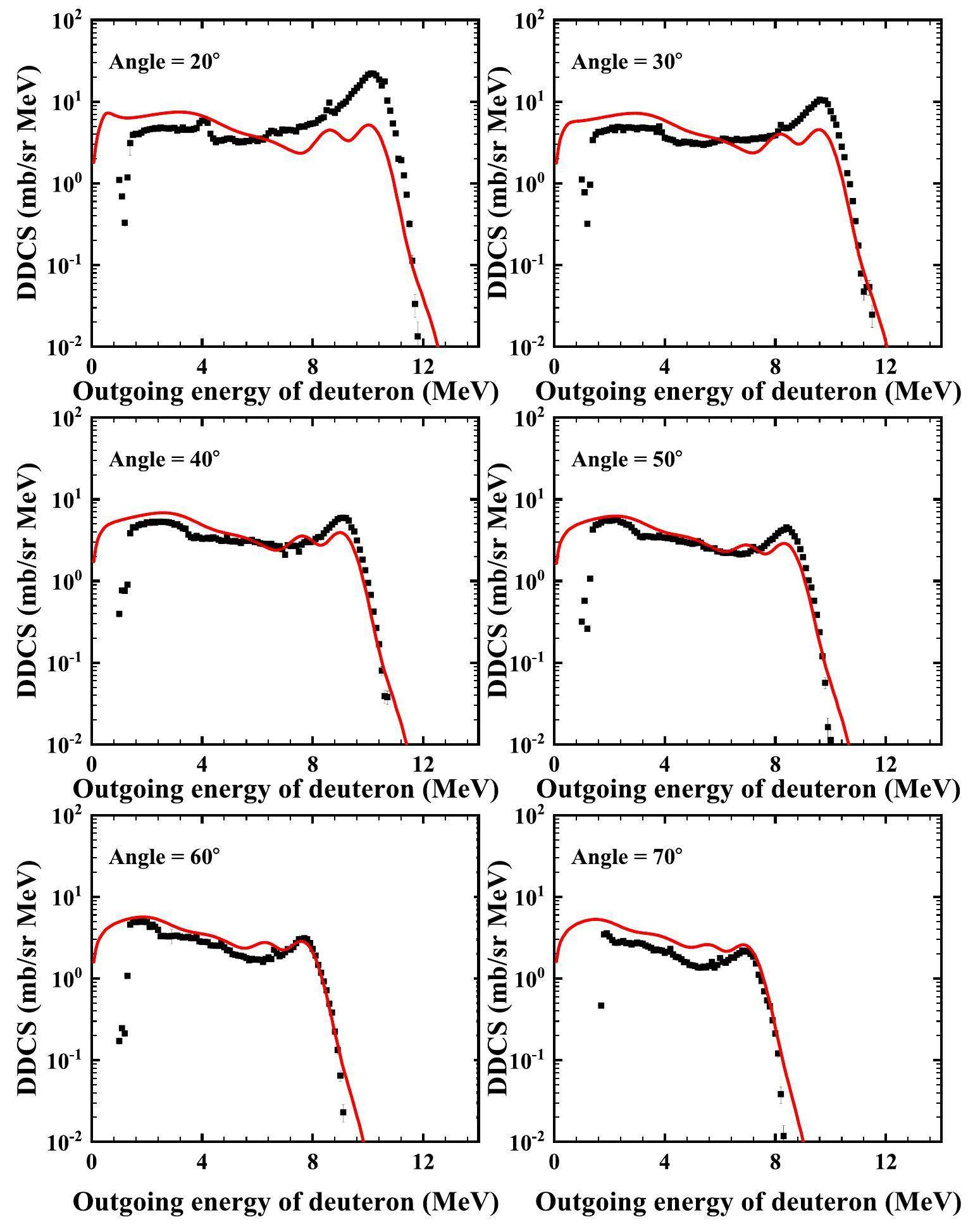
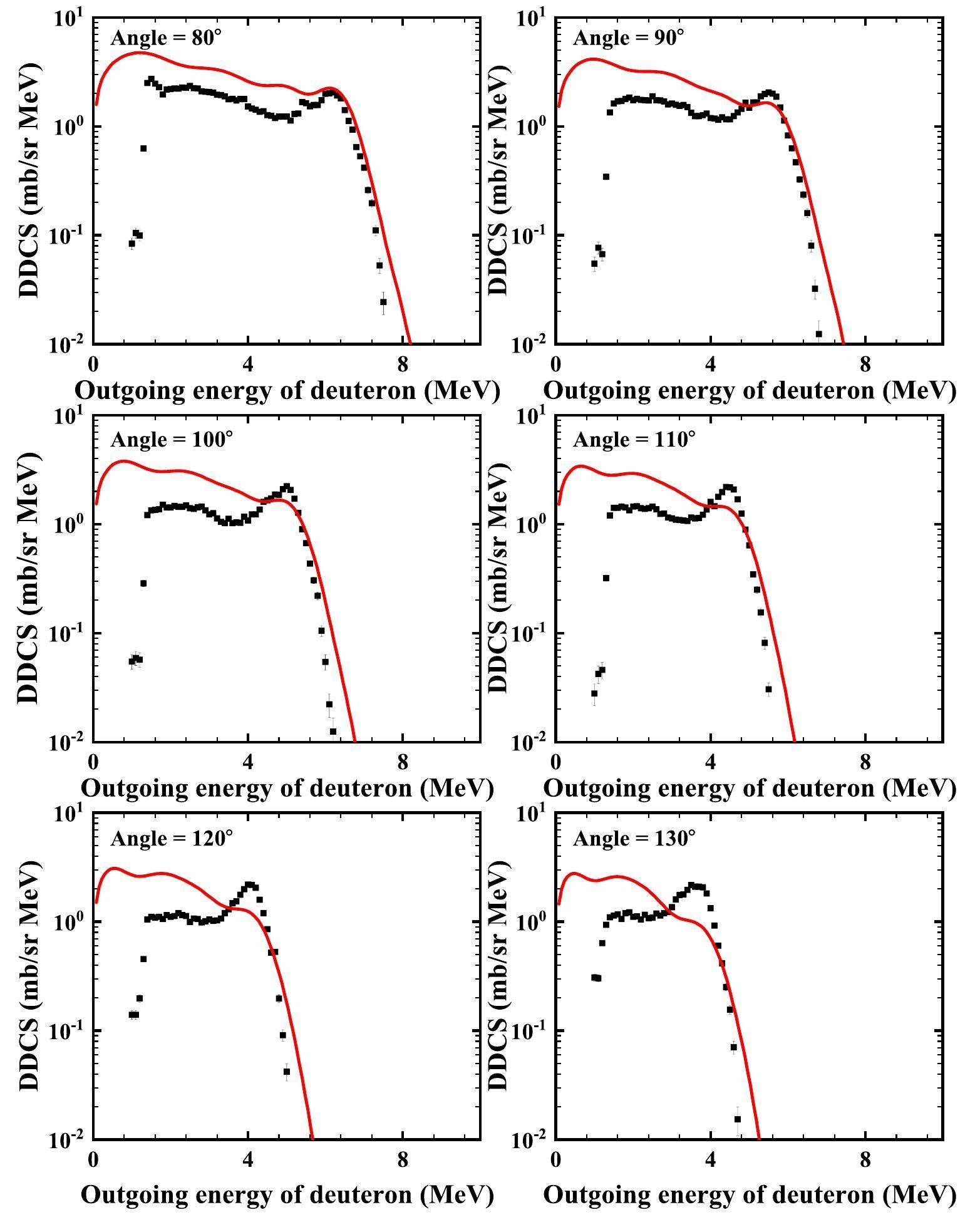
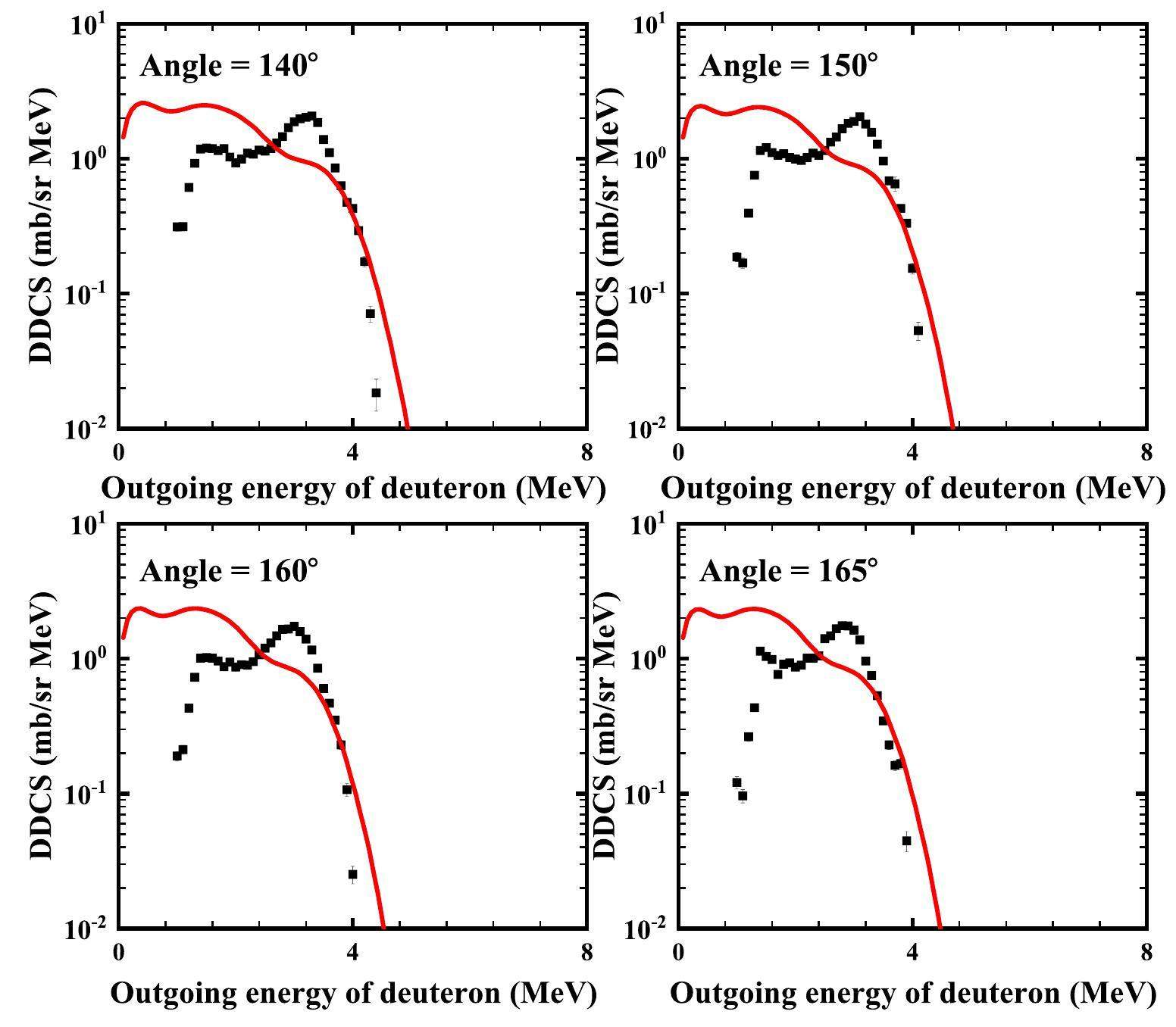
The calculated double-differential cross-sections of the total outgoing deuteron for the p+6Li reaction at 14 MeV are compared with the experimental data obtained at angles of 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°, 100°, 110°, 120°, 130°, 140°, 150°, 160° and 165°, as shown in Figs. 7, 8, 9, and 10. The black points represent the experimental data obtained from Ref. [22], and the red solid lines denote the calculated total double-differential cross-sections of the outgoing deuteron. Figure 10 shows the partial double-differential cross-sections of the outgoing deuteron with an angle of 60° at Ep = 14 MeV in the LS. The yellow dash-dotted line denotes the partial spectra of the emitted deuteron from a direct three-body breakup through
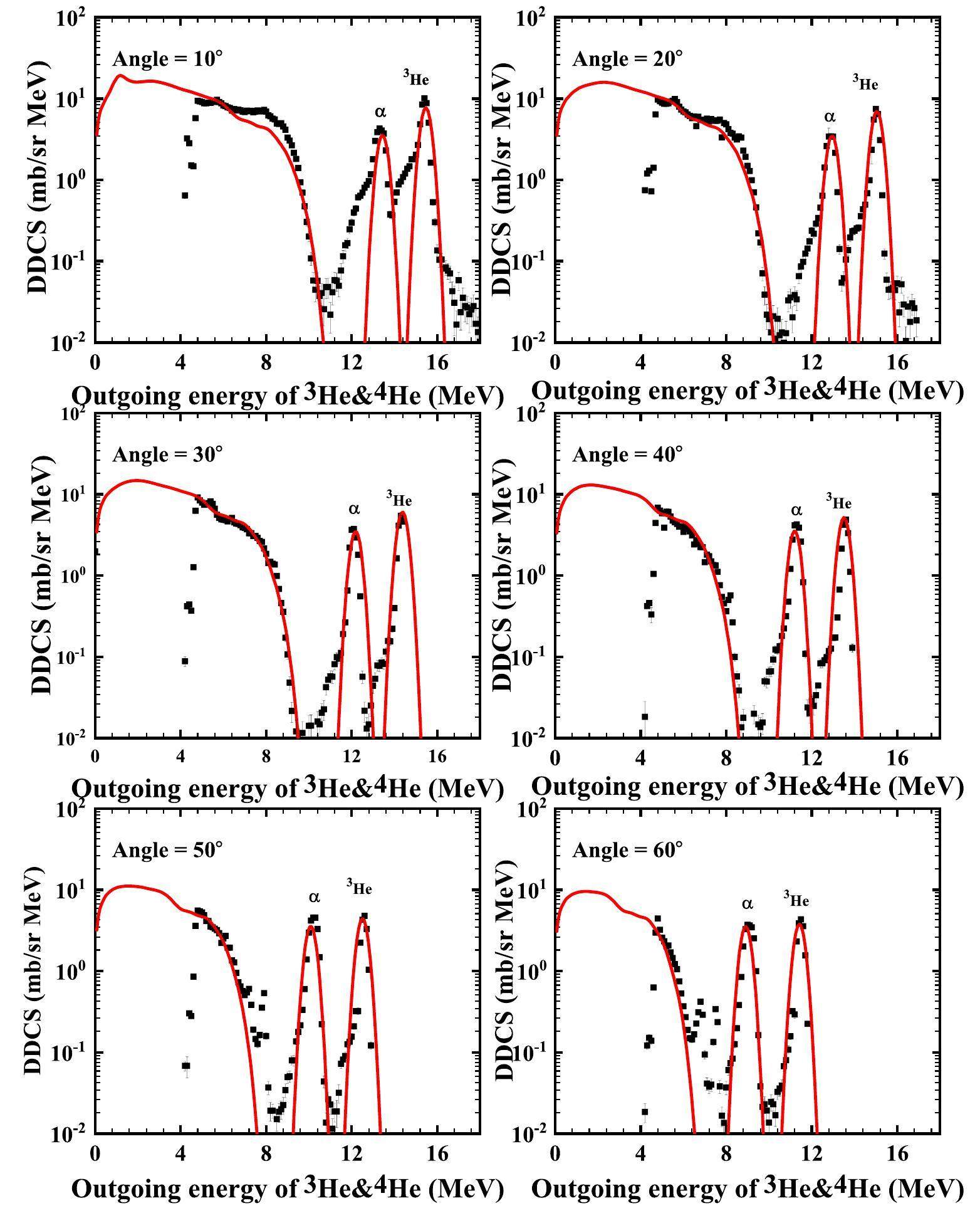
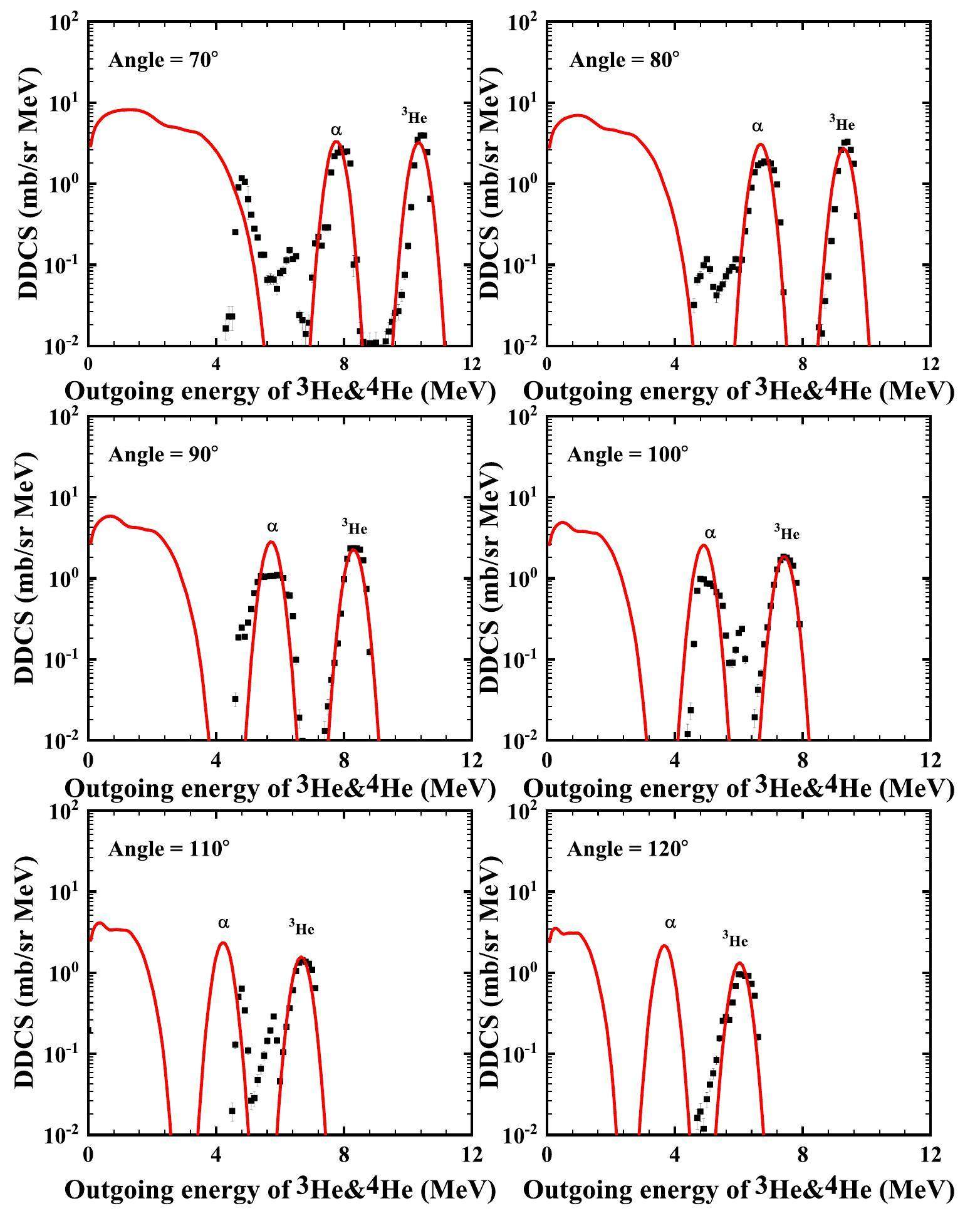
The calculated double-differential cross-sections of the total outgoing 3He and α for the p+6Li reaction at 14 MeV are compared with the experimental data obtained at angles of 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°, 90°, 100°, 110°, and 120°, as shown in Figs. 11, 12. The black points represent the experimental data obtained from Ref. [22], and the red solid lines denote the calculated total double-differential cross-sections. The calculated results agree well with the measurements. From Fig. 13, one can see that the yellow dash-dotted line denotes the partial spectra of the emitted α from the direct three-body breakup process through
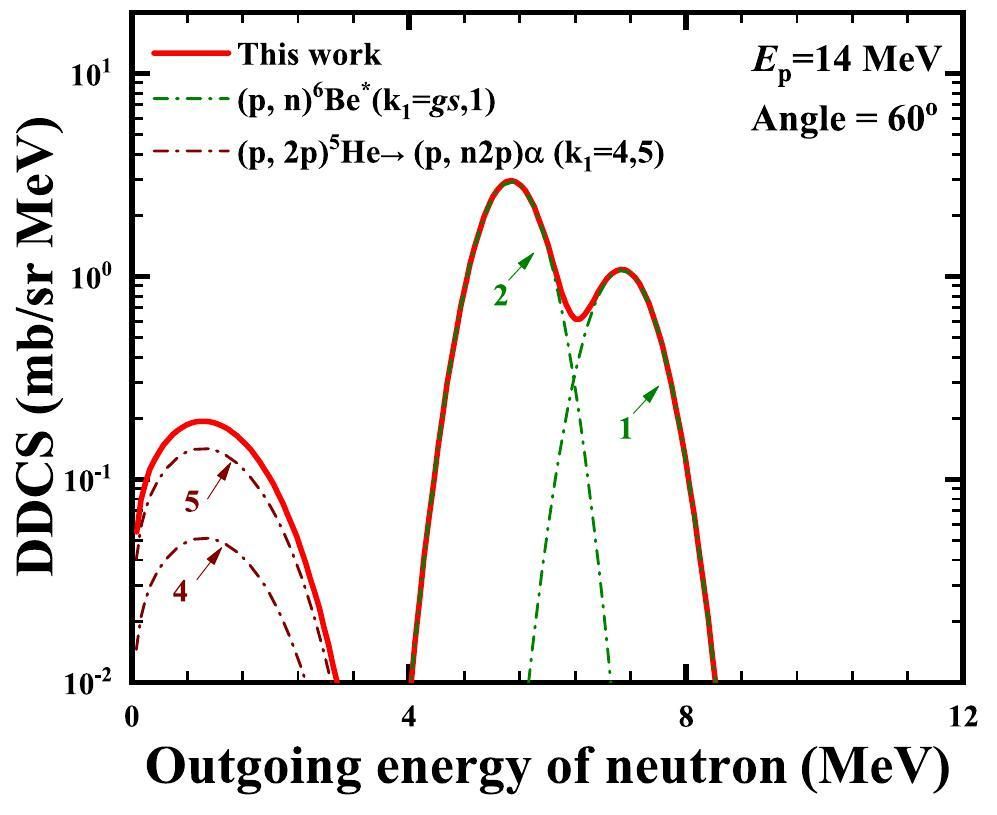
As an example, Fig. 14 shows the predicted total and partial spectra of the outgoing neutron for the p+6Li reaction at 14 MeV at an angle of 60°. The red line shows the total double-differential cross-sections of the outgoing neutron. The green dash-dotted lines denote the partial spectra of the first outgoing neutron from the compound nucleus to the ground state and the first excited energy level of the first residual nucleus, 6Be*. The brown dash-dotted lines denote the contribution of the reaction (p, 2p)5He → (p, n2p)α from the fourth and fifth excited energy levels of 5He* to the ground state of α.
However, the threshold energies of composite charged particles, such as deuteron and triton (except 3He and alpha for the p+6Li reaction), are usually higher than those of the protons for both the target and contaminants. Furthermore, the Coulomb barriers of these outgoing composite charged particles are higher than those of the protons; therefore, the impact of the contaminants is greatly reduced. These factors hinder the accurate measurement of these composite charged particles, particularly at larger outgoing angles. Thus, it is reasonable to assume that the theoretical calculations are slightly higher than those of the measurements for large outgoing angles.
Summary
The STLN model [39, 47, 48] is improved to calculate the double-differential cross-sections of outgoing neutrons, protons, deuterons, 3He, and alpha particles for the p+6Li reaction. The emission processes between discrete energy levels with energy, angular momentum, and parity conservations are strictly considered. The results show that the pre-equilibrium emission process is the dominant reaction mechanism for 1p-shell light nucleus reactions and that the calculated double-differential cross-sections are sensitive to the energy, spin, and parity of the discrete levels for both the target and residual nuclei. Recoiling effects are also considered owing to the light mass of the 1p-shell nuclei. A PLUNF code is developed based on the STLN model to obtain an ENDF-6-formatted file of the double-differential cross-sections of the nucleon and light composite charged particles for the p+6Li reaction. The calculated results agree well with existing measurements of outgoing protons, deuterons, 3He, and alpha particles.
Model calculation of n + 6Li reactions below 20 MeV
. Commun. Theor. Phys. 36, 437 (2001). https://doi.org/10.1088/0253-6102/36/4/437Calculation of double-differential cross sections of n + 7Li reactions below 20 MeV
. Commun. Theor. Phys. 37, 465 (2002). https://doi.org/10.1088/0253-6102/37/4/465Systematic description of the 6Li(n, n’)6Li*→d + α reactions with the microscopic coupled-channels method Phys
. Rev. C 83, 064611 (2011). https://doi.org/10.1103//PhysRevC.83.064611Analysis of 7Li(n, n’)7Li* reactions using the continuum-discretized coupled-channels method
. Phys. Rev. C 86, 064604 (2012). https://doi.org/10.1103/PhysRevC.86.064604Systematic analysis of nucleon scattering from 6, 7Li with the continuum discretized coupled channels method
. Phys. Rev. C 87, 024610 (2013). https://doi.org/10.1103/physrevc.87.024610Analysis of nucleon and triton emissions from nucleon-7Li collisions below 20 MeV
. Phys. Rev. C 99, 034602 (2019). https://doi.org/10.1103/physrevc.99.034602Measurement of the differential cross sections and angle-integrated cross sections of the 6Li(n, t)4He reaction from 1.0 eV to 3.0 MeV at the CSNS Back-n white neutron source
. Chin. Phys. C 44, 014003 (2020). https://doi.org/10.1088/1674-1137/44/1/014003Compact lithium-glass neutron beam monitor for SANS at CSNS
. Nucl. Sci. Tech. 29, 127 (2018). https://doi.org/10.1007/s41365-017-0250-7Influence of 7Li enrichment on Th–U fuel breeding for an Improved Molten Salt Fast Reactor (IMSFR)
. Nucl. Sci. Tech. 28, 97 (2017). https://doi.org/10.1007/s41365-018-0468-zCosmological lithium problem
. Chinese Science Bulletin 65, 4047 (2020). https://doi.org/10.1360/TB-2020-09516Li(n,γ)7Be reaction rate based on new data from the Laboratory for Underground Nuclear Astrophysics
. Phys. Rev. C 105, 065806 (2022).The nature of the lithium enrichment in the most Li-rich giant star
. Nature Astronomy 2 10 (2018). https://doi.org/10.1038/s41550-018-0544-7Statistical theory of light-nucleus reactions and application to the 9Be(p, xn) reaction
. Phys. Rev. C 93, 014609 (2016).https://doi.org/10.1103/PhysRevC.93.014609Theoretical analysis of double-differential cross sections of proton, deuteron, and triton emission in the p + 7Li reaction at 14 MeV
. Phys. Rev. C 101, 034616 (2020). https://doi.org/10.1103/PhysRevC.101.034616Energy levels of light nuclei A = 5, 6, 7
. Nucl. Phys. A 708, 3-163(2002). https://doi.org/10.1016/S0375-9474(02)00597-3A drop in the 6Li(p, γ) reaction at low energies
. Phys. Lett. B 725, 287-291 (2013). https://doi.org/10.1016/j.physletb.2013.07.044Cross-section requirements for charged-particle fusion reactors: The 6Li(p, 3He)α reaction
. Nucl. Sci. Eng. 55, 267-272 (1974). https://doi.org/10.13182/nse74-a23453Elastic scattering of polarized protons by 6Li: (I)
. Optical-model analysis. Nucl. Phys. A 496, 189-204 (1989). https://doi.org/10.1016/0375-9474(89)90171-1Elastic scattering of protons by 6Li
. Phys. Rev. 132, 1963. https://doi.org/10.1103/PhysRev.132.2607Prlarized proton scatter on lithium isotopes at 14 MeV
. JEARI-M 89-167 (1989).https://www-nds.iaea.org/publications/indc/indc-jpn-0130.pdfEvaluation of the neutron data standards
. Nucl. Data Sheets 148, 143-188 (2018).https://doi.org/10.1016/j.nds.2018.02.002Extension of a nuclear reaction calculation code CCONE toward higher incident energies – multiple preequilibrium emission, and spectrum in laboratory system
. J. Nucl. Sci. Technol. 50, 409-418 (2013). https://doi.org/10.1080/00223131.2013.7731688Be nuclear data evaluation
. AIP Conf. Proc. 769, 390-393 (2005).https://doi.org/10.1063/1.1945030Model calculation of n + 12C reactions from 4.8 to 20 MeV
. Nucl. Sci. Eng. 133, 218-234 (1999). https://doi.org/10.13182/NSE98-100Predicted levels of 9Be based on a theoretical analysis of neutron double-differential cross sections at En = 14.1 and 18 MeV
. Phys. Rev. C 80, 064612 (2009).https://doi.org/10.1103/PhysRevC.80.064612Theoretical analysis of neutron double-differential cross sections of n + 9Be reactions
. Commun. Theor. Phys. 54, 129 (2010). https://doi.org/10.1088/0253-6102/54/1/25Theoretical analysis of neutron double-differential cross section of n + 10B at 14.2 MeV
. Commun. Theor. Phys. 39, 433 (2003). https://doi.org/10.1088/0253-6102/39/4/433Theoretical analysis of neutron double-differential cross section of n + 11B at 14.2 MeV
. Commun. Theor. Phys. 39, 83 (2003). https://doi.org/10.1088/0253-6102/39/1/83New calculation method of neutron kerma coefficients for carbon and oxygen below 30 MeV
. Phys. Rev. C 78, 054610 (2008). https://doi.org/10.1103/PhysRevC.78.054610Analysis of neutron double-differential cross sections for n + 12C reaction below 30 MeV
. Commun. Theor. Phys. 48, 534 (2007).https://doi.org/10.1088/0253-6102/48/3/02Analysis of neutron double-differential cross section of n + 14N at 14.2 MeV
. Commun. Theor. Phys. 44, 128 (2005).https://doi.org/10.1088/6102/44/1/128Theoretical analysis of the neutron double differential cross section of n + 16O at En = 14.1 MeV
. Commun. Theor. Phys. 35, 579 (2001).https://doi.org/10.1088/0253-6102/35/5/579Further analysis of neutron double-differential cross section of n + 16O at 14.1 MeV and 18 MeV
. Commun. Theor. Phys. 44, 701 (2005).https://doi.org/10.1088/6102/44/4/701Theoretical analysis of neutron double-differential cross section of n + 19F at 14.2 MeV
. Commun. Theor. Phys. 47, 102 (2007).https://doi.org/10.1088/0253-6102/47/1/020New integral formula for obtaining analytical Legendre expansion coefficients and its applications to light-nucleus reactions
. Phys. Rev. C 92, 061601(R) (2015). https://doi.org/10.1103/PhysRevC.92.061601A unified Hauser-Feshbach and exciton model for calculating double-differential cross sections of neutron-induced reactions below 20 MeV
. Nucl. Sci. Eng. 114, 55 (1993). https://doi.org/10.13182/NSE93-3Kinematic relations in reactions of the form A + B→C+D+E
. Nuclear Instruments and Methods. 37 240-248 (1965). https://doi.org/10.1016/0029-554X(65)90368-XHeavy-ion scattering and reactions near the Coulomb barrier and “threshold anomalies”
. Physics Reports (Review Section of Physics Letters) 199. No.3, 147-190. North-Holland (1991).https://doi.org/10.1016/0370-1573(91)90066-UInfluence of nuclear forces on the Coulomb barrier in heavy-ion reactions
. Phys. Rev. C 2, 6 (1970). https://doi.org/10.1103/PhysRevC.2.2448Table of experimental nuclear ground state charge radii: An update
. At. Data and Nucl. Data Tables 99, 69-95 (2013). https://doi.org/10.1016/j.adt.2011.12.006Energy levels of light nuclei A = 4
. Nucl. Phys. A 541, 1 (1992).https://doi.org/10.1016/0375-9474(92)90635-WEnergy levels of light nuclei A = 8, 9, 10
. Nucl. Phys. A 745, 155 (2004).https://doi.org/10.1016/j.nuclphysa.2004.09.059Statistical theory of light nucleus reactions with 1p-shell light nuclei
, EPJ Web of Conferences 146, 12026 (2017).https://doi.org/10.1051/epjconf/201714612026Double-differential cross section of 5He emission
. Commun. Theor. Phys. 43, 299 (2005).https://doi.org/10.1088/0253-6102/43/2/020The authors declare that they have no competing interests.


