Introduction

In recent years, the shortage of medical radioisotopes has been repeatedly highlighted[1, 2], and the gap between the supply and demand of medical radioisotopes has become increasingly prominent. Currently, the global production of medical radioisotopes is concentrated in a few large research reactors with a global supply strategy. These include the National Research Universal Reactor in Canada, High Flux Reactor in the Netherlands, High Flux Isotope Reactor in the United States, and Missouri University Research Reactor in the United States. However, the specific activity of the medical radioisotopes produced by reactors is low, and the aging reactors built in the 1950s and the 1960s are being decommissioned. Therefore, a new methods for producing medical radioisotopes with higher specific activity are urgently required[3].

Photonuclear reactions have attracted considerable attention worldwide because of their good selectivity, relatively single reaction products, and high specific activity of the radioisotopes produced by photonuclear transmutation. The reports of the Nuclear Science Advisory Committee-Isotope Subcommittee in 2009 and 2015 concluded that the study of radioisotope production methods based on accelerators was essential and the photonuclear transmutation method based on an electron linear accelerator was a unique source of radioisotopes [4, 5]. Recently, the Nuclear Science Advisory Committee described this approach as one of the most compelling and influential opportunities for producing medical radioisotopes with high specific activity.

Two methods for photonuclear transmutation exist. One method uses an electron accelerator to generate bremsstrahlung to drive photonuclear transmutation [6]. The second method is based on photonuclear transmutation driven directly by the next generation of quasi-monochromatic gamma sources [7]. However, regardless of the approach, the greatest uncertainty arises from the cross section of the photonuclear reaction. For most known medical radioisotopes that can be produced, as well as innovative medical radioisotopes with significant potential applications, the scarcity of data on the reaction cross section of photonuclear reactions severely limits the study and development of medical radioisotopes produced by photonuclear reactions and the evaluation of photonuclear transmutation efficiency and selection of target nuclear reaction paths. In the electron-accelerator-driven scheme, the photonuclear reaction cross section determines the selection of the highest energy of the electron accelerator, which affects the maximum yield of the target isotope and specific activity of the product. Furthermore, the photonuclear reaction cross section affects the energy selection of the quasi-monochromatic gamma source and the assessment of the specific activity of the product. Therefore, measuring the photonuclear reaction cross section for medical radioisotopes of interest is highly significant.

High-precision measurements of the reaction cross section can be performed by offline measurements with shielding devices, which reduce interference from the surrounding environment gamma, neutron, and cosmic rays and improve the signal-to-noise ratio, even when the characteristic gamma intensity branching ratio is small. In our simulation, a quasi-monochromatic gamma beam was used to activate the target material, and the characteristic gamma rays of radioisotopes produced by photonuclear reactions were measured with an offline measuring device to detect the types and quantities of target nuclides generated in the reactive target. Finally, the reaction cross sections of photonuclear reactions (γ, n), (γ, p), and (γ, γ’) were obtained. A shielding gamma-ray spectrometer was used to obtain high-precision reaction cross sectional measurements. Based on the quasi-monochromatic gamma beam of the Shanghai Laser Electron Gamma Source (SLEGS) [8, 9], the entire process of medical radioisotopes production, decay, and measurement was simulated using the GEANT4 toolkit [11-12]. Finally, the feasibility of medical radioisotopes of interest is discussed. This study is of guiding significance for measuring reaction cross sections of medical radioisotopes produced by photonuclear reactions.

Measurement method

The parameters for the candidate medical radioisotopes produced by the (γ,n) and (γ,p) reactions are listed in Table 1 [13-15]. The theoretical reaction cross section data in the energy region are obtained from the TENDL-2021 database. Most photonuclear reaction cross sections for medical radioisotopes of interest in the giant dipole resonance energy region do not have experimental data and require further accurate measurements through experiments.

Generally, two methods are used to measure the reaction cross section of the (γ, n), (γ, p), and (γ, γ’) reactions that generate target nuclei: the first directly measures the neutron, proton, and γ’ products generated by the reaction online, while the second performs offline measurements of the characteristic gamma rays of the target nucleus produced by the online activation. However, natural targets typically contain multiple isotopes, making it impossible to distinguish which isotope the neutrons, protons, and γ products detected by online measurements originated from. Furthermore, achieving 100% purity is difficult even with enriched isotopic targets, and accurate measurements of reaction cross sections with high-purity isotopic targets are expensive. The measurement of small reaction cross sections is difficult owing to the background from bremsstrahlung radiation in the gamma beam and natural background from the environment.

Compared to direct online measurements, offline measurements completely separate the activity measurement of radionuclides from the photonuclear excitation process and effectively avoid interference from low-energy neutrons, X/γ rays of various energies, and the positron pair spectrum caused by online irradiation [16-18]. Moreover, medical radioisotopes typically have long half-lives and emit gamma rays during decay, making offline decay measurements well-suited. However, most medical radioisotopes possess relatively small photonuclear reaction cross sections. Typically, the characteristic peaks of the γ spectrum of photonuclear activation products in the irradiated target material measured offline are submerged in the environmental background. Thus, the detection limit depends on the background level.

Low-background gamma-ray spectroscopy with germanium (Ge) detectors has become a fundamental tool for identifying and measuring the activity of radionuclides in samples, determining the emission probabilities of radioactive decay, and conducting low-level counts [19].

Table 2 presents a survey of reported low-background systems. All the systems possess an integrated background of ≤ 0.12 c/s/100cm³Ge [20-25]. Additionally, if only passive material shielding is considered, the integrated background can reach a level below 2 c/s under better conditions. Therefore, a low-background gamma-ray spectrometer for offline measurements of medical radioisotopes has been proposed, which reduces the background, achieves high-precision measurements of reaction cross sections, reduces the irradiation time, and saves valuable beam time.

The target nuclei produced by online irradiation can be identified by their characteristic gamma energies and half-lives. N₀ is the number of target nuclei obtained at the end of irradiation, and N is the integral count of the gamma full-energy peak. $N=N_0{I}_{\gamma }{ϵ}_{\gamma }{C}_{k\gamma }{e}^{-\lambda t_{\text{d}}}\left(1-e^{-\lambda t_{\text{m}}}\right)\mathrm{,}$ (1) where Iγ is the gamma decay intensity obtained from the NNDC database, ϵγ is the detection efficiency of HPGe, which can be calibrated using a gamma standard source with known intensity; Ckγ = e^-(μ/ρ)ρx is the penetration factor of gamma-ray of target nuclear decay; μ/ρ is the mass attenuation coefficient(cm²/g); ρx is the mass thickness of the target(g/cm²); λ is the decay constant of the target nucleus; t_d is the time interval between the end of irradiation and the start of measurement; and t_m is the time of offline measurement. As a general activation measurement [26], $N_0=\sigma (E)N_{\text{t}}Q{C}_{\text{kbeam}}{e}^{-{\lambda }_i}{\displaystyle {\int }_0^{t_{\text{i}}}}\phi \left(t\right)e^{\lambda t}\text{d}t\mathrm{,}$ (2) where σ(E) is the energy dependent reaction cross section; ϕ is the integrated gamma-ray flux intensity; N_t is the surface density of the target nucleus (atoms/cm²); Q is the abundance of the target isotope in the target; C_kbeam is the penetration factor of the incident gamma beam in the target; φ(t) is the γ beam intensity as a function of time; and ti is the irradiation duration. If φ(t) is approximated as a constant, then $N_0=\frac{\sigma (E)\varphi N_{t}Q{C}_{\text{kbeam}}\left(1-e^{-\lambda t_{\text{i}}}\right)}{\lambda }\mathrm{.}$ (3) where ϕ is the integrated gamma-ray flux; Because N₀ can be measured from N using Eq. (1), the reaction cross section can be obtained from Eq. (2). The gamma flux from the real measurement of SLEGS was found to be stable because of the stable electron beam intensity of the SSRF storage ring and the laser beam used for Compton scattering. A specific form of the beam intensity φ(t) was required to perform the simulation. A constant beam-intensity approximation was used to study the feasibility of cross-sectional measurements based on realistic beam-intensity measurements. After determining the measurement method for the photonuclear reaction cross section, shielding gamma spectrometer was constructed using GEANT4 and the feasibility of the method was assessed by simulating the entire process of photonuclear reactions for producing medical radioisotopes and offline measurements.

Simulation modeling

GEANT4 is a Monte Carlo simulation toolkit, which is widely used in particle physics, astrophysics, nuclear physics, medical physics, radiation protection, and other fields [12]. GEANT4 enables accurate numerical simulations of interactions between matter and particles, including particle transport, energy deposition, electromagnetic interactions, and nuclear reactions. It also supports extensions in various aspects, such as particle type, geometry, material properties, detector type, and computer operating systems. The main advantages of GEANT4 are its high reproducibility and reliability. Based on GEANT4, we developed a program for simulating medical radioisotopes production, decay, and measurement and performed full-scale simulations.

3.1

Medical radioisotopes production

A laser Compton scattering (LCS) light source is a new X-ray or Gamma-ray source based on the interaction of a relativistic electron beam with laser photons. It is characterized by high energy, short wavelength, fast pulses, and high peak brightness, and has become an important option for advanced international light source technology [27]. SLEGS) produces gamma rays in the energy range of 0.4–20 MeV, thereby covering the energy range from the nuclear structure to giant resonance (keV to MeV) in nuclear physics research. The gamma ray flux integrated over the entire spectrum can reach 10⁵–10⁷ phs/s and is continuously adjustable. Collimation technology can be used to achieve an energy spread greater than 5% [8, 28]. Therefore, in our simulation, we used a gamma beam with an intensity and energy spread of 10⁷ phs/s and of 5%, respectively, to activate the Ti target and produce the target medical radioisotopes, ⁴⁷Sc, via the ⁴⁸Ti(γ,p)⁴⁷Sc reaction for further analysis.

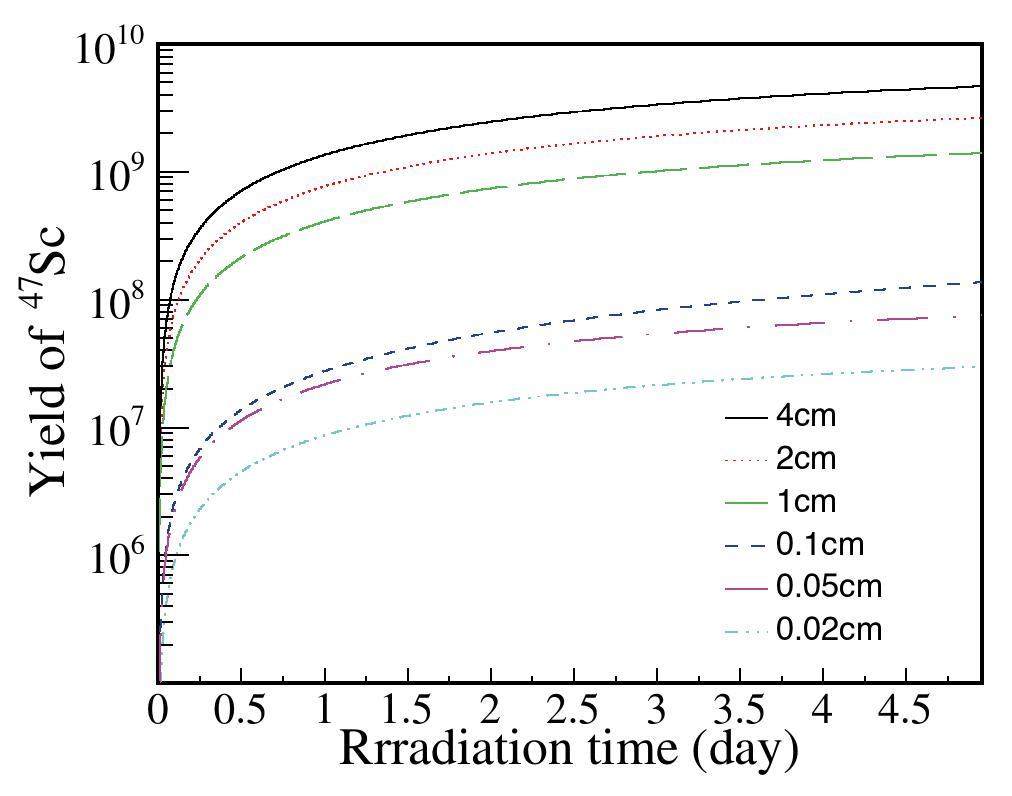
Figure 1 shows that within the first half day of irradiation, the yield of ⁴⁷Sc increases rapidly, and after the irradiation time exceeds half a day, the yield gradually approaches a saturation value of one. The choice of the target thickness was related to the penetration factor of the incident gamma beam in the target(Ckbeam). As the thickness of the target increased, the photons needed to penetrate a longer distance through the target material, resulting in a decreased photon count. Simultaneously, multiple scattering inside the target produced a broader distribution of photon energies. In addition, the choice of the target thickness was also related to the penetration factor of the gamma rays produced by the target nucleus decay (Ckγ). The gamma rays produced by the decay of the target nucleus attenuated with increasing thickness of the target, and the integral count of the gamma full-energy peak decreased, which affected the measurement.

Fig. 1Full-screen View

Variation of the yield of ⁴⁷Sc with irradiation time for targets of different thicknesses

3.2

Low-background gamma-ray spectrometer

The significant effect of the background radiation on the measured energy spectrum results in unreliable analytical results. Background radiation primarily originates from three sources: natural environmental radiation from the laboratory environment, radioactive background from the detection components and shielding materials, and cosmic ray contributions. Low-background gamma-ray spectrometers must be shielded against background radiation to achieve high-precision reaction cross section measurements of medical radioisotopes.

Many low-background gamma-ray spectrometers have been constructed domestically and internationally. Moreover, countries such as China, France, the United States, and Japan have established underground laboratories at different depths to facilitate research in low-background measurement fields. Representative devices abroad include those of the same type established by Miley at thePacific Naval Laboratory in 1991 [20], Byun at the Korea Atomic Energy Research Institute in 2001 [21], Semkow et al. in the United States in 2002 [19], and Heusser et al. in Germany [23, 24]. Such devices have also been built in laboratories in China, including the China Institute of Atomic Energy [22], Institute of High Energy Physics of the Chinese Academy of Sciences, and Third Institute of Oceanography of the State Oceanic Administration [25].

Based on existing low-background gamma-ray spectrometers, a shielding gamma-ray spectrometer was designed using GEANT4 simulations to achieve a shielding effect. The shielding structure is illustrated in Fig. 2 [29].

Fig. 2Full-screen View

Low-background gamma-ray spectroscopy with shielding structure: 1. HPGe detector, 2. sample to be measured, 3. plastic holder, 4. the copper liner (2 mm-thick), 5. inner lead (50 mm-thick), 6. cadmium absorber (3 mm-thick), 7. borated polyethylene (100 mm-thick), 8. plastic scintillator (50 mm-thick), 9 outer lead (100 mm-thick)

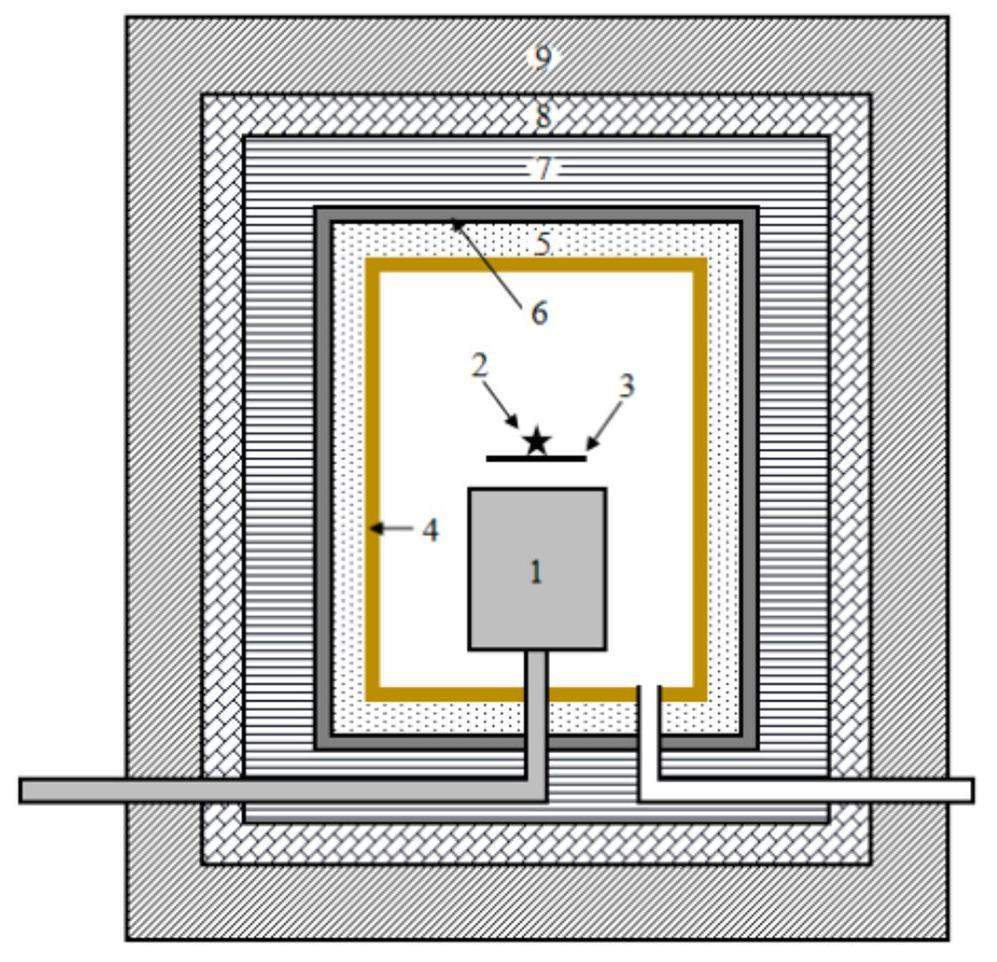
Using a high-purity germanium detector for a low-background gamma spectrometer requires careful consideration of shielding from various backgrounds. The gamma ray intensity decreases drastically as the atomic number of the material increases because materials with higher atomic numbers possess larger gamma attenuation factors than those with lower atomic numbers [30, 31]. Common high-Z materials include lead, oxygen-free copper, and steel; however, iron is easily contaminated with ⁶⁰Co during smelting, and copper has a large thermal neutron capture reaction cross section. Considering factors such as the price, atomic number, and mechanical properties, lead is the best choice for gamma shielding materials.

Cosmic rays in the environment produce secondary particles, such as photons, neutrons, and electrons, when they undergo muon capture in materials with large atomic numbers, such as lead [32-36]. Therefore, the second layer of the shielding device considers neutron shielding. Neutrons must undergo deceleration and absorption. Water, paraffin, and polyethylene are widely used as slowing down materials [37]. Plastic scintillators or polyethylene can be used as a second layer to slow down fast neutrons.

The third layer is used to absorb thermal neutrons. ¹⁰B is an excellent absorber of thermal neutrons and B₄C has a B/C ratio of 0.7828, resulting in a very large neutron capture reaction cross section. Thus, it can effectively absorb decelerated neutrons. Additionally, cadmium has a large absorption reaction cross section for thermal neutrons. Therefore, boron-containing polyethylene can be used to slow down and absorb neutrons, whereas cadmium can be used to absorb thermal neutrons [38]. However, cadmium atoms emit gamma rays with an energy of 2.3 MeV after capturing neutrons. Therefore, a low-background lead must shield this portion of the gamma rays.

Finally, other low-Z materials, such as organic glass or copper, can be added to the inner lining to shield against impurities, such as ²¹⁰Pb, its daughter nucleus ²¹⁰Bi in lead, and the characteristic X-rays of lead [39]. The shielding structure was determined through simulations to select appropriate shielding materials and optimize their thicknesses. The final shield structure from the outside to the inside was determined to be: 100 mm thick lead, 50 mm thick plastic scintillation, 100 mm thick borated polyethylene, 3 mm thick cadmium, 50 mm thick lead, and 2 mm thick oxygen-free copper, which was consistent with the low-background gamma spectrometer designed by Hu et al. [25].

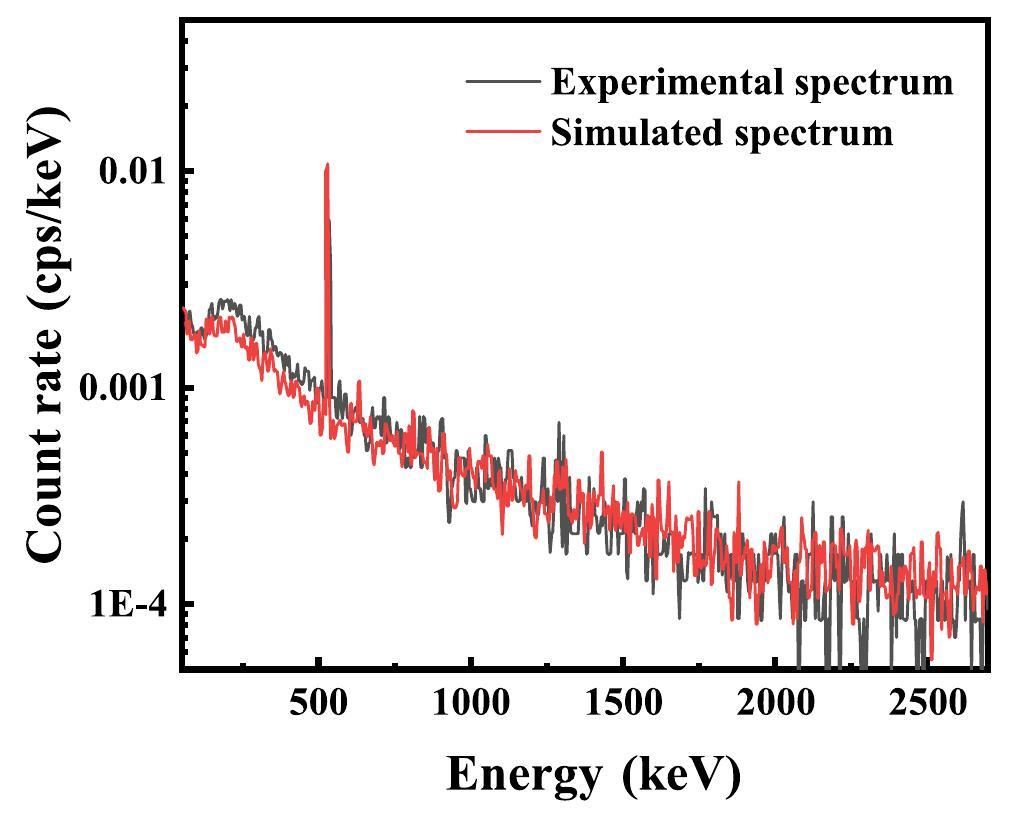
In Fig. 3, a comparison of the simulated HPGe energy deposition spectrum with the results obtained by Hu et al., reveals a similar trend, and the count rate of the 511 keV peak in the spectrum possesses the same order of magnitude (approximately 8×10^-3 cps). It is essential to note that because of the shielding configuration employed, specifically the incorporation of an inner lead layer in our shielding system, the 478 keV peak is obscured and consequently, not evident in Fig. 3. In the low-energy range, the count rate of the experimental spectrum exceeds that of the simulated spectrum owing to the differences in the background and radioactivity of the shielding material and detector. Thus, the reliability of the simulations was verified.

Fig. 3Full-screen View

Comparison between the simulated and experimental spectra

3.3

Medical radioisotopes decay and measurement

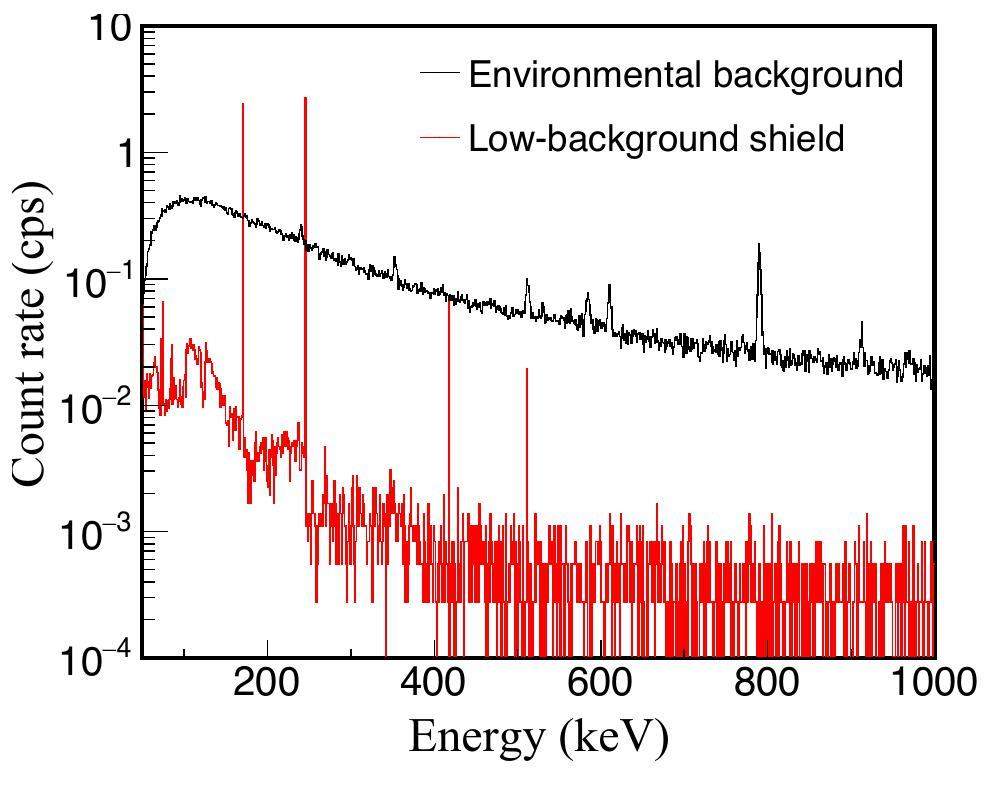
Based on the passive-shielding conditions shown in Fig. 2, the total integral background count rate in the energy range of 100∼2700 keV obtained by the simulation is 0.22 c/s/100cm³Ge, whereas under the better condition of using only lead shielding, the total integral background count rate in the energy range of 100∼2700 keV may reach 1 cps [25, 40, 41]. To reduce simulation complexity, we used lead shielding only in the following simulation. Based on the spectrometer constructed in the GEANT4 simulation program, the number of target nuclei ⁴⁷Sc produced was considered as the input for offline decay measurement simulation when the offline measurements lasted for only 1 h and only lead shielding was used.

In Fig. 4, we present the spectra obtained by simulations under different conditions(Shanghai electron laser gamma source laboratory environment background, low background shielding device, and neglecting the environmental background). After background subtraction, the integral count rate of the gamma full-energy peak from the decay of ⁴⁷Sc is 0.16 c/s at Eγ= 159 keV. When measured in the environmental background, the gamma full-energy peak of ⁴⁷Sc is completely submerged in the background. Low-background shielding effectively reduced the lower limit of detection was, and the integral count of the gamma full-energy peak of the characteristic peak was identifiable.

Fig. 4Full-screen View

Simulated spectra of ⁴⁷Sc under different conditions

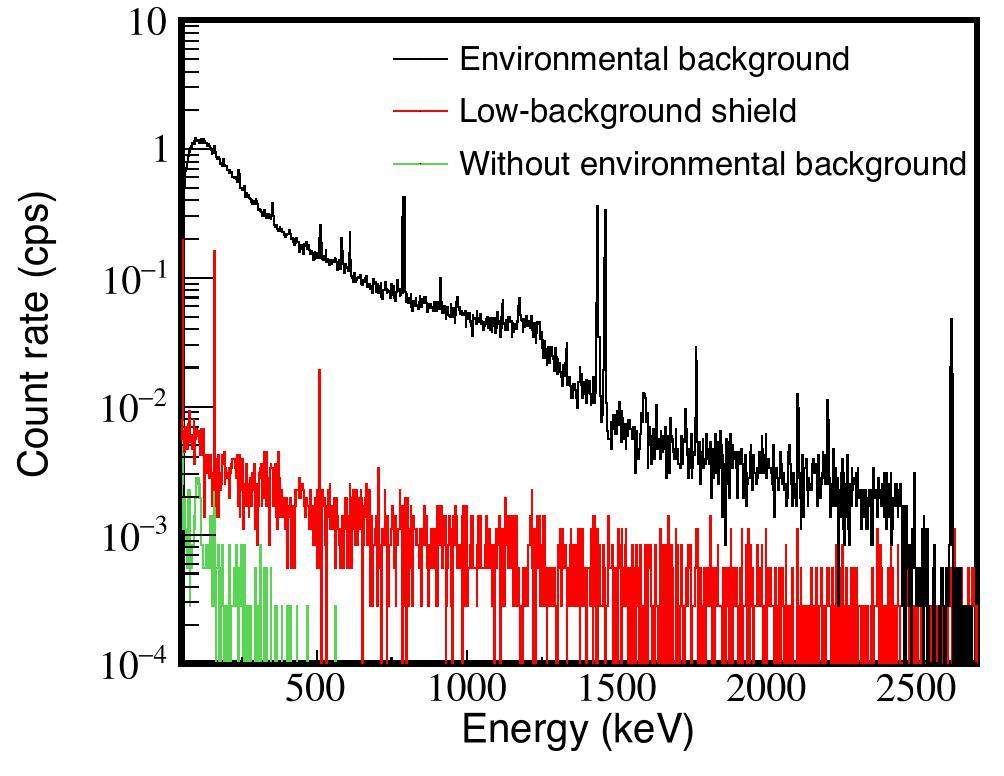
Therefore, the cross sections for medical radioisotopes produced by photonuclear reactions were efficiently measured by reducing the background. In addition, factors such as the irradiation time, measurement time, and beam intensity affected cross section measurements. In the next section, we discuss the detection lower limit through computational simulations.

Feasibility of measurement

Our simulation program includes five control parameters: irradiation time, measurement time, time interval between the end of the irradiation and the beginning of the measurement, thickness of the target, and beam intensity. Considering the influence of the background in a real environment, the background was considered as the sixth control parameter. Based on SLEGS, the gamma beam intensity factor can be set to 10⁷ phs/s [8].

First, we considered the background factor. According to Eq. (1), N is the integral count of the gamma full-energy peak when the background is neglected. However, the detector measures the integral count of the gamma full-energy peak produced by the decay of the target nucleus in combination with the background. Therefore, we obtained the following relationship: $N=C-C_0\mathrm{,}$ (4) where, C and C₀ denote the integral count of the gamma full-energy peak produced by the decay of the target nucleus measured by the detector and the background count in the low-background detection system (considering only lead shielding), respectively. For realistic measurements, the relative statistical error of the counts was set to 10%. According to the error propagation formula, the relative statistical error is expressed by Eq. (5) $\upsilon =\frac{\sqrt{C+C_0}}{C-C_0}\mathrm{.}$ (5) Subsequently, the target thickness was considered. According to Eqs. (1) and (2), the thickness of the target mainly affects the attenuation coefficient and area density. We constructed a function f(x) that varies with the thickness of the target, as shown in Eq. (6) as follows: $\begin{array}{c}f\left(x\right)=N_{\text{t}}{C}_{\text{k}\gamma }{C}_{\text{kbeam}}\\ =\frac{N_{\text{A}}\rho x{e}^{-\left(\mu /\rho \right)\rho x}{e}^{-\left({\mu }^{\prime }/\rho \right)\rho x}}{M},\end{array}$ (6) where $N_{\text{t}}=\frac{N_{\text{A}}\rho x}{M}$, N_A is the Avogadro constant; M is the molar mass; ρx is the mass thickness of the target; μ is the attenuation coefficient of the photon beam incident on the target during online activation; and μ’ is the attenuation coefficient of de-excitation gamma escaping the target in offline measurements. Using ⁶⁹Ga(γ,n)⁶⁸Ga as an example, the relationship between f(x) and x is as shown in Fig. 5.

Fig. 5Full-screen View

Dependence of the equivalent surface density on the target thickness for ⁶⁹Ga(γ,n)⁶⁸Ga

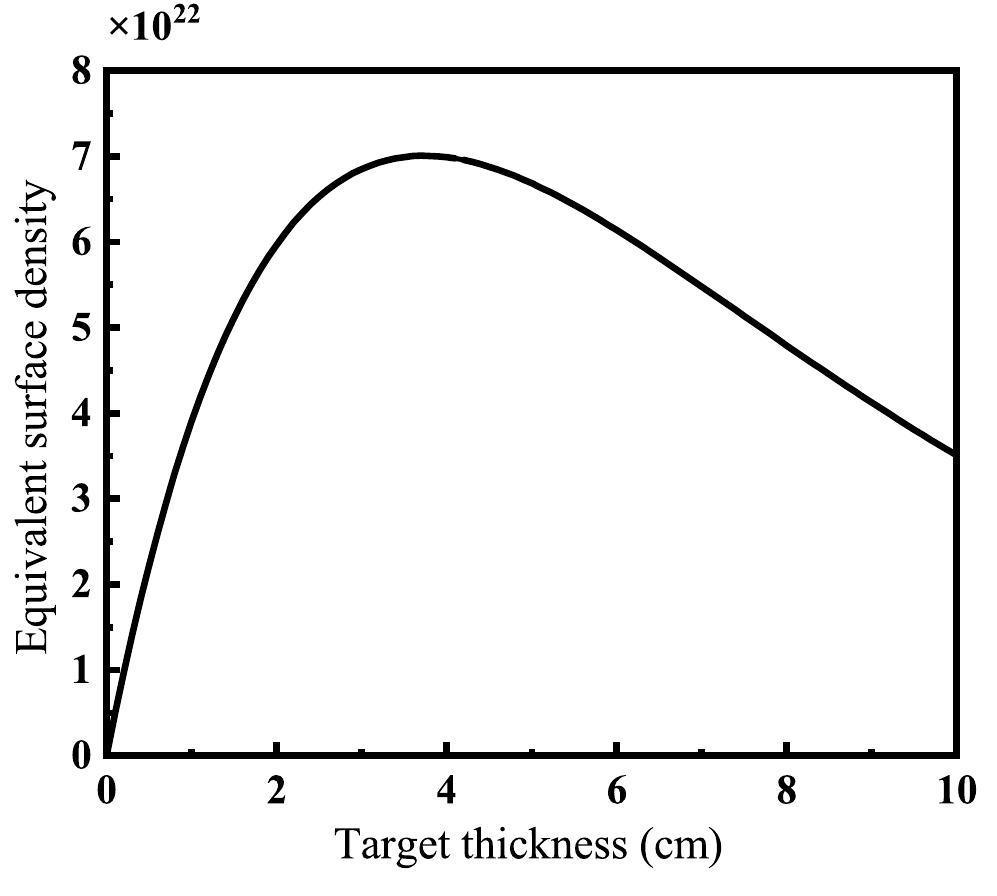
According to Fig. 5, the function f(x) has a maximum value. Rewriting Eqs. (1) and (2) as functions of f(x), as shown in Eq. (7), we obtain: $N=\frac{\sigma \left(E\right)\varphi Q{I}_{\gamma }{ϵ}_{\gamma }{e}^{-\lambda t_{\text{d}}}\left(1-e^{-\lambda t_{\text{m}}}\right)\left(1-e^{-\lambda t_i}\right)f\left(x\right)}{\lambda }\mathrm{,}$ (7) where f(x) is proportional to N. The maximum integral count N can be determined using f(x) when the other conditions are fixed. In realistic measurements, the thickness of the target nucleus affects the count rate of the characteristic gamma owing to the inevitable attenuation of the gamma incident on the target nucleus and the self-absorption of the target nucleus during deexcitation. Therefore, the thickness must be determined based on practical considerations among other factors. For thicknesses ranging from zero to the optimal value, f(x) increased monotonically with x. Based on this property, the detection limit can be determined by combining time factors.

The time factors include the irradiation time t_i, measurement time t_m, and time interval from the end of irradiation to the beginning of measurement t_d. Here, t_d was uniformly set to 5 min, and the relationship between t_i and t_m was determined from Eq. (7). In other words, when the other conditions were fixed, one quantity increased whereas the other decreased. One can define A = t_it_m. Considering the decay of the target nucleus, t_m is limited to 900–3600 s, and t_i is limited to within 24 h in a realistic case.

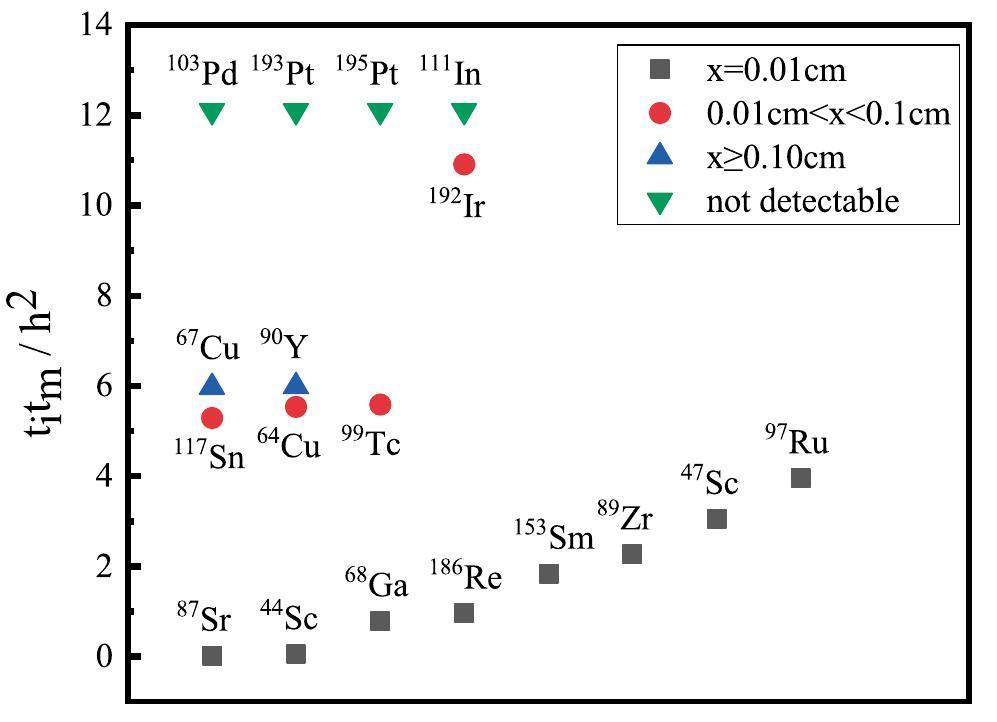
Three limiting factors: x, t_m, and t_i were considered. When x had a minimum value of 0.01 cm, offline measurements were used to measure the cross section of medical radioisotopes generated by photonuclear reactions with a 0.01 cm thick target if the simulated values of t_m and t_i were within their respective limits (i.e., t_m was between 900-3600 s and t_i was within 24 h). Measurements were easier for smaller values of A because less time was required for irradiation and measurement. If t_m and t_i were outside their respective limits when x was set to 0.01 cm, the measurement of medical radioisotopes generated by photonuclear reactions was not feasible at this thickness. The detection limit was determined by gradually increasing the thickness in steps of 0.01 cm, and the difficulty in detection was indicated by the values of x and A.

Some medical radioisotopes of interest were selected, and the simulation was performed using the aforementioned method; the results are shown in Fig. 6. When x = 0.01 cm, ⁸⁷Sr, ⁴⁴Sc, ⁶⁸Ga, ¹⁸⁶Re, ¹⁵³Sm, ⁸⁹Zr, ⁴⁷Sc, and ⁹⁷Ru can be used to measure the production reaction cross section. Smaller values of A indicate shorter irradiation and measurement times. However, ⁴⁵Ti, ¹⁰³Pd, ¹⁹³Pt, ¹⁹⁵Pt, and ¹¹¹In could not be measured within an irradiation time of 24 h and a detection time of 3600 s, even with the optimal thickness.

Fig. 6Full-screen View

Feasibility of reaction cross section measurement for some medical radioisotopes, where t_m, t_i, and h represent the time of offline measurement, irradiation duration, and unit of time in hour, respectively

Several methods can be used to enhance the measurement of reaction cross sections for these medical radioisotopes, such as transferring to stack targets, switching to enriched isotopic targets, increasing the intensity of the gamma beam, and using low-background gamma-ray spectrometers with better shielding.

The characteristic gamma decay can be reduced by stacking several targets together to form a stacked target. Compared to other methods, its implementation is easy. Taking ¹¹²Sn(γ,p)¹¹¹In as an example, natural and stack targets were used for the simulation. The thicknesses of the natural and stack targets were assigned the same value (1 mm) to allow easy comparison of the results. Thus, the natural target was 1 mm thick, and the stack target was divided into five pieces, each with a thickness of 0.2 mm. The results of the comparison are presented in Fig. 7.

Fig. 7Full-screen View

Comparison of the count rates of the natural and stack targets(¹¹²Sn(γ,p)¹¹¹In)

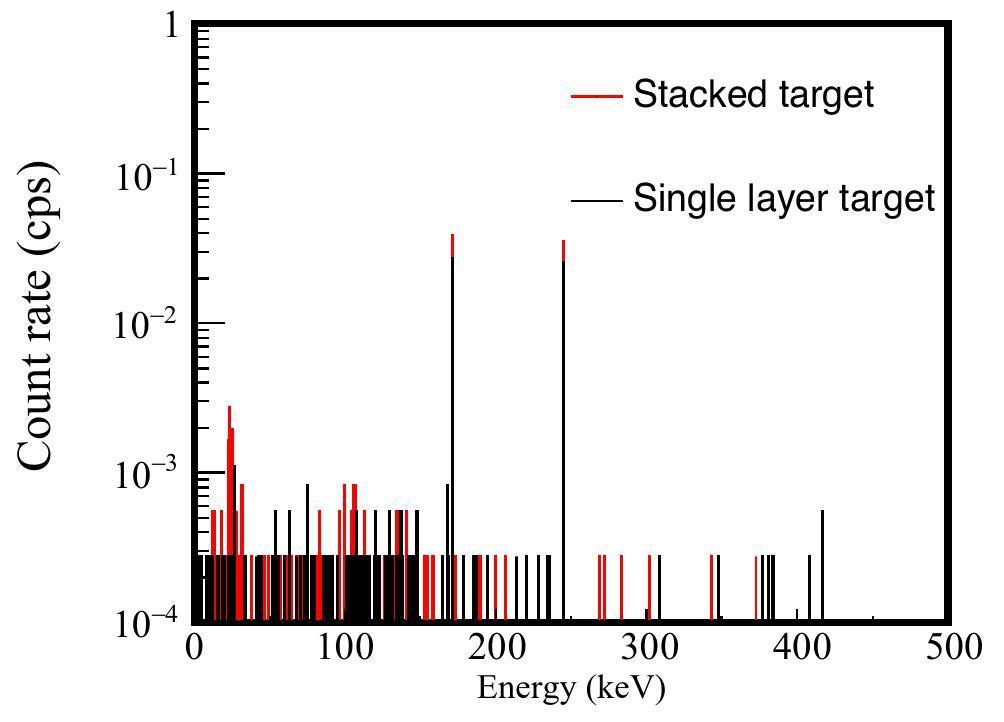
For the characteristic gamma Eγ=171.29 keV, the count rate of the full-energy peak measured using the natural targets was 0.027 c/s whereas the count rate measured using the stack targets was significantly higher than that of the natural targets at 0.039 c/s. However, the low abundance of ¹¹²Sn in the Sn target resulted in a low yield of ¹¹¹In. During the actual measurement, the existence of the background resulted in relative errorυ exceeding 10%, even with the use of a stack target. Therefore, for cross section measurements of ¹¹²Sn(γ,p)¹¹¹In, enriched isotopic targets can be used to improve feasibility. With 100% isotopic targets, the count rate at Eγ=171.29 keV can be increased to 2.409 c/s, and the characteristic gamma full-energy peak can be detected under a low background shield, as shown in Fig. 8.

Fig. 8Full-screen View

Decay spectra of ¹¹¹In under environmental background and low background shield with enriched isotope target

Conclusion

Available data on gamma transmutation cross sections for medical radioisotopes are scarce. Measurements of photonuclear reaction cross sections are useful for filling the gaps in data from gamma transmutation experiments, reducing large data errors, and resolving divergences between various theoretical calculations and data. In this study, the generation, decay, and measurement of medical radioisotopes were simulated using GEANT4 combined with a shielding gamma-ray spectrometer. Low background shielding improved the signal-to-noise ratio, facilitated high-precision measurements, reduced the valuable beam time. Based on SLEGS, the feasibility of specific medical radioisotope reaction cross section measurements was presented. SLEGS, the only available gamma facility in China capable of providing intermediate-and high-energy, high-intensity, quasi-monochromatic, energy continuously adjustable gamma beams, is expected to provide an important platform for studying photonuclear reaction cross sections for medical radioisotopes of interest.