Introduction

Nuclear data measurements are important in multiple fields, including fission physics, fast reactors, accelerator-driven systems for the transmutation of nuclear waste, and global security. The prompt fission neutron spectrum (PFNS) is a key nuclear data quantity of particular interest and has traditionally played a crucial role in understanding and modeling fission processes. In the context of PFNS, the concept “prompt” refers to emission times much less than 1 ns before the onset of a delayed β decay. However, experimental data relating to PFNS are rather scarce and show discrepancies in the low- and high-energy parts [1, 2]. This is partly attributed to the small fission cross sections and low neutron yield at the high-energy side of the Maxwell distribution and the large background from incident neutrons and neutrons from sources other than fission.

Several problems regarding nuclear fission remain to be investigated, including the properties of transitional states around the fission barrier, redistribution of excitation energy between the fission fragments, and the mechanism of evolution to the scission point. Particularly, scission neutrons, which are emitted during the transition from nuclear equilibrium to the scission point, can reveal information on fission dynamics. From an experimental perspective, distinguishing scission neutrons from neutrons emitted by fission fragments is impossible. This problem can only be resolved by comparing the observed PFNSs with those obtained from theoretical calculations. Various theoretical models have been developed for calculating the PFNS, including neutron evaporation models [3, 4], the Scale Method [5], and the Los Alamos Model [7, 6]. These models, which are intrinsically phenomenological and tuned to experimental data, have been widely used to predict and calculate PFNS for present and past evaluations. Currently, more complex and computationally intensive models such as those in Refs. [2, 8, 9] have tracked the decay paths of fission fragments and considered many more observable fission quantities in the modeling process. Analog Hauser-Festival calculations [10] and statistical approaches [11] have also been developed. A recent study revealed that the yield branch of scission neutrons varies between experiments (see Ref. [12]), which is a manifestation of discrepancies in PFNS studies. Thus, reliable experimental data, a good understanding of the discrepancies, and realistic uncertainty estimates are required to guide the evaluation and development of reasonable model predictions.

To determine the time at which fission occurs, fission fragments are conventionally deposited in a gas volume inside fission chambers. These chambers have high efficiency for detecting fission fragments, but they suffer from a limited mass of fission material because of the necessity of allowing fission fragments to escape from the sample [13, 14]. To increase the sample mass that can be used for PFNS measurements, prompt fission γ rays are utilized as the time reference, making the deposition of fission fragments in the sample acceptable. This γ tagging method considers any γ event as the fission start time for spontaneous fission [15], whereas for neutron-induced fission, multiple γ tagging is implemented because the incident neutron beam is accompanied by an intense γ background [16, 17]. At the Lawrence Livermore National Laboratory (LLNL), a parallel-plate avalanche counter (PPAC) was developed for PFNS measurements [18]. The incident neutron energy was calculated from the neutron time-of-flight (TOF) deduced from the difference between the reference timing signal provided by the neutron source and the signal fired by fission fragments on PPAC. The energy spectra of prompt fission neutrons were determined by the time difference between the fission fragment signal and the constant fraction discrimination (CFD) signal from a neutron detector. The use of PPAC is beneficial because its bias voltage is optimizable to improve the signal-to-noise ratio and discriminate α-decay background and fission fragments. In addition, it has a temporal resolution of ∼ 1 ns, which matches that of a liquid scintillation detector, thereby improving the neutron energy resolution. A PPAC with a similar principle and structure was designed and manufactured at the China Institute of Atomic Energy (CIAE), where multiple sample cells were introduced to increase the total sample mass that could be utilized for the PFNS measurement, as described in the next section.

Organic scintillators produce light via both prompt and delayed fluorescence, the decay times of which are typically a couple of nanoseconds and hundreds of nanoseconds, respectively. The majority of the fluorescent light yield is produced by prompt decay, whereas the amount of light in the delayed component often varies as a function of the type of particle, exciting the scintillation material [13]. This difference, known as pulse shape discrimination (PSD), can distinguish between different types of particles. Neutron interactions in organic scintillators produce protons through elastic scattering. These protons have a short range and generate a high concentration of triplet states, which decay by delayed fluorescence. Alternatively, γ-ray interactions in organic scintillators mainly produce scattered electrons. Electrons have a longer range than protons and generate a lower concentration of triplet states (electrons are more likely to produce excited singlet states that decay by prompt fluorescence) [19]. The significant difference in the pulse shape of the signal resulting from the ratio of prompt to delayed fluorescence produced by different types of radiation makes PSD a popular method for high-energy neutron detection in environments comprising γ rays. A high neutron detection efficiency and fast timing features are also required for neutron background characterization. Liquid scintillation detectors have been successfully implemented for nuclear data measurement [20-24] because of their excellent time resolution characteristics, neutron/γ PSD ability, and neutron detection efficiency, making them particularly suitable for fast neutron and γ-ray energy spectrum measurements when γ rays and neutrons coexist. In this study, a fast neutron detector array comprising 48 liquid scintillator detectors was developed. The array was intended to measure the PFNS of actinide nuclei, such as ²³⁵U/²³⁸U, from 1-15 MeV induced by neutrons at different energies. In addition, it can be utilized to select neutron channels for in-beam γ spectroscopy [25] or analyze the energy spectrum and angular distribution of prompt fission γ in neutron-induced reactions. The implementation of multiple detectors greatly increases the detection efficiency and is beneficial for the clarification of the discrepancies in the literature.

The remainder of this paper is organized as follows. Section 2 describes the experiment, including the liquid scintillators, PPAC, and targets. Section 3 describes the test results of the performance of the liquid scintillator. Section 4 provides the details of the Geant4 simulation of the proposed neutron detection array. A pilot measurement of the ²⁵²Cf spontaneous fission source is presented in Sect. 5, and a summary is provided in Sect. 6.

Experimental configuration and data acquisition system

2.1

The liquid scintillator

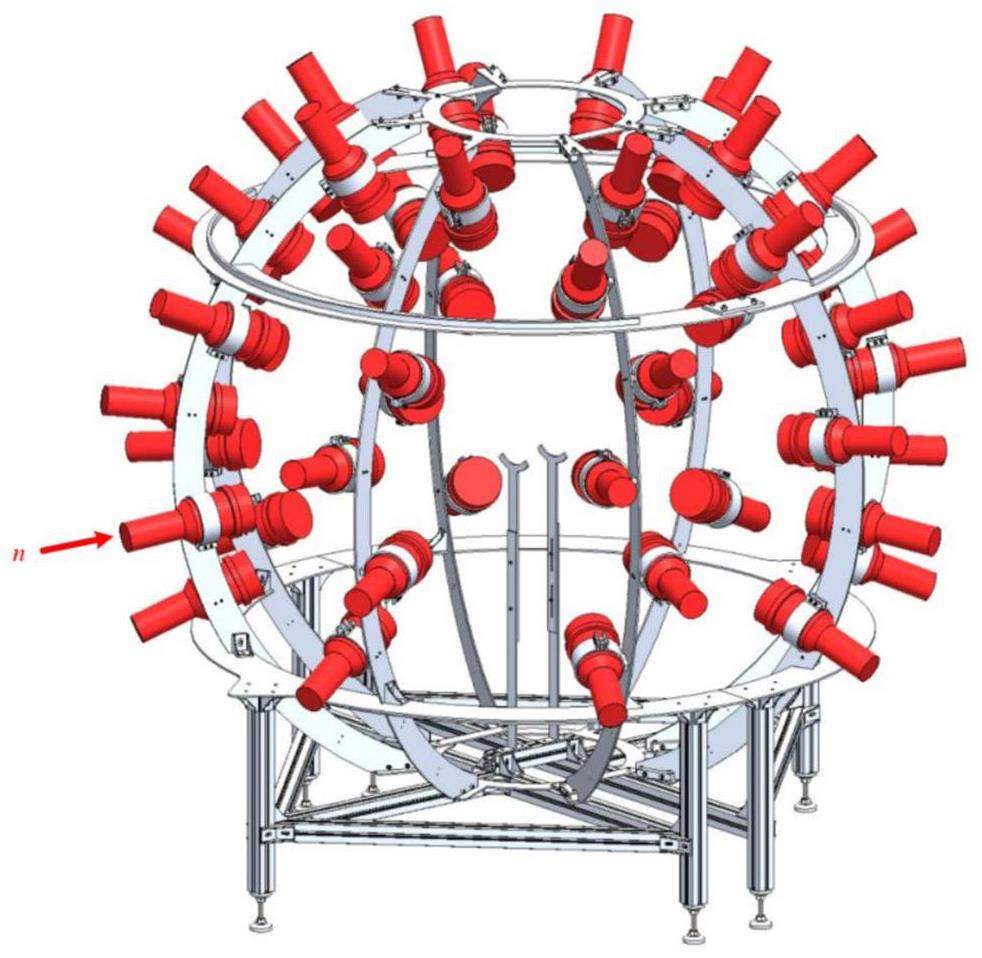
The specific parameters of the liquid scintillator are presented in Table 1. The sensitive volume of the liquid scintillator was Ø12.7 cm×5 cm, coupled with a 5-inch ET9823B photomultiplier tube (PMT). The PMT was powered by the EHS F020n module from iSeg [26] and the negative bias voltage was adjusted such that the measured energy for each detector ranged from 0 keVee to 6000 keVee. The housing material of the detector was aluminum. A schematic of the liquid scintillator detector array is shown in Fig. 1, consisting of eight columns, each with six detectors. The azimuthal angles between two adjacent columns were equal.

Table 1Full-screen View

Properties of the liquid scintillator

Properties	Parameter
Light Output (% Anthracene)	78
Decay Time, Short Component (ns)	3.2
Specific Gravity	0.874
No. of H Atoms (cm-3)	4.82×1022
No. of C Atoms (cm-3)	3.98×1022
No. of Electrons (cm-3)	2.27×1023

Show more

Fig. 1Full-screen View

(Color online) Schematic of the array of 48 liquid scintillator detectors

2.2

The PPAC

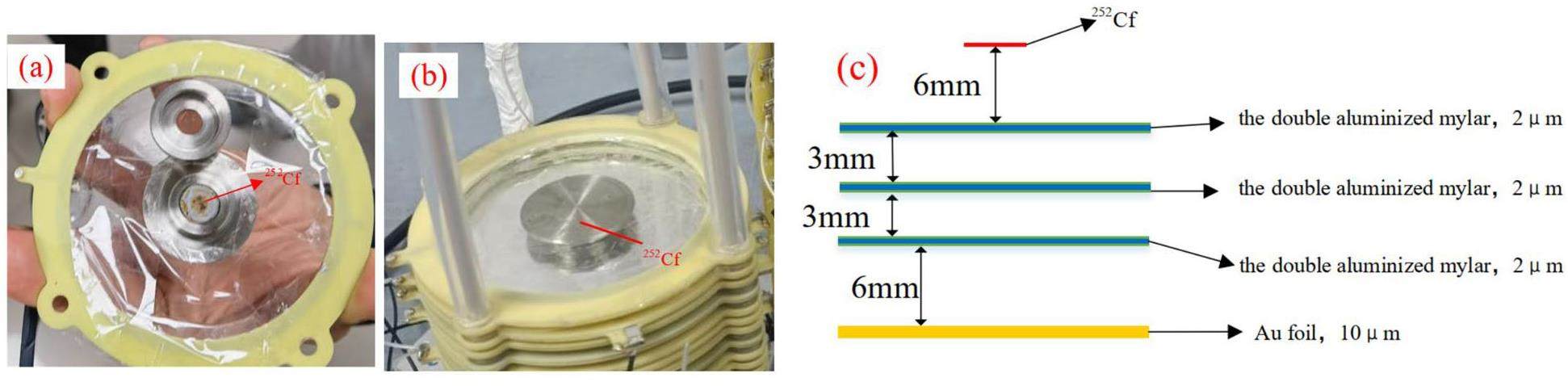
A PPAC was developed to measure the PFNS detailed in other publications [27]; only its main features are described here. The structure of PPAC is shown in Fig. 2, which has a maximum of 10 sample cells, each consisting of a target and aluminized Mylar on both sides. The aluminized Mylar was grounded, and the target was connected to a positive or negative high voltage. A gold foil with a thickness of 10m was used to prevent the impact of fission fragments from different cells. Each ²³⁵U target weighed approximately 5 mg to avoid stopping the fission fragments. During the experiment, the PPAC was filled with continuously flowing perfluoropropane gas at 750±50 Pa and used to measure neutron-induced fission events. The PPAC was made of aluminum and had an incident window with a diameter of 60 mm at each end. The incident window was made of Kapton film with a thickness of 25 μm. The bias voltage was 520 V. The detection of a fission fragment in a PPAC cell provides a starting signal for the TOF measurement of the outgoing fission neutrons. The structure of PPAC in the ²⁵²Cf test shown in Fig. 3 is simplified compared with the ²³⁵U experiment in Fig. 2, which is described in detail in Section 5.

Fig. 2Full-screen View

(Color online) (a) Schematic, (b) internal structure, (c) detailed structure, and (d) circuit diagram of the PPAC used in the ²³⁵U experiment

Fig. 3Full-screen View

(Color online) Neutron detection efficiency calibration using ²⁵²Cf. (a) The ²⁵²Cf source, which undergoes approximately 2400 fissions per second. (b) The internal and (c) detailed structure of the PPAC

2.3

Digital data acquisition system

The data acquisition system adopted was the GDDAQ [29, 30], developed by Peking University. It is easy to use without requiring special technical expertise and has been widely used in multiple nuclear physics experiments [31-36]. The GDDAQ used in this study comprised four 16-channel Pixie-16 500 MSPS 12 bit modules. PPAC signals were connected to module 0, and all liquid scintillators were connected to modules 1–3.

The incoming signals of liquid scintillators and the PPAC were digitized and a digital CFD filter, a fast and a slow trapezoidal filter were applied. The CFD, implemented in a signal processing field-programmable gate array (FPGA), provided a time signal related to the occurrence of the event. The CFD algorithm was unique for 500 MHz when compared to the one implemented in the 100 MHz and 250 MHz Pixie-16 modules since the Analog-to-Digital Converter (ADC) data arriving into the FPGA was initially slowed down by a ratio of 1:5 and the FPGA then utilized the weighing method to locate the CFD trigger point between two adjacent 2 ns ADC samples. The CFD algorithm is as follows [37]. $\begin{array}{l}\text{CFD}(k)=w\left({\displaystyle \sum _{i=k}^{k+L}}a(i)-{\displaystyle \sum _{i=k-B}^{k-B+L}}a(i)\right)\\ -\left({\displaystyle \sum _{i=k-D}^{k-D+L}}a(i)-{\displaystyle \sum _{i=k-D-B}^{k-D-B+L}}a(i)\right)\end{array}$ (1) where $a[i]$ is the ADC trace data, k is the index representing the ADC tick (2 ns). In the 500 MHz Pixie-16 modules, the FPGA did not have sufficient resources to build sums for the five ADC samples in parallel with the variable delays. Therefore, the parameters w, B, D and L were set to w = 1, B = 5, D = 5 and L = 1 to achieve the best performance. The zero-crossing points in Eq. (1) were extracted to obtain the reference start signal for TOF.

The FPGA digitally implemented pulse registration, triggering, discrimination, pile-up detection, and a trapezoidal energy filter. The waveforms of each event could be customized by user-defined functions, such as the trigger threshold value, filter rise time, and flat-top time. The Digital Signal Processor (DSP) processed validated signals on an event-by-event basis, and non-validated events were eliminated with zero dead time. The DSP read the energy filter resulting from the FPGA, computed the pulse height, and performed other tasks such as constant fraction discrimination timing. It communicated with the host computer via an interface through a direct memory access (DMA) channel. A more thorough and detailed description can be found in Ref. [38]. The DSPs onboard the memory allowed it to expand and store the spectra.

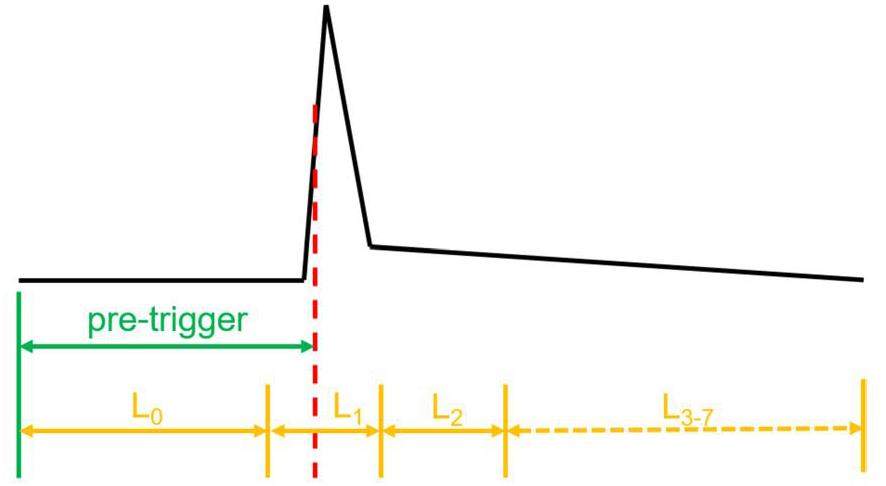
PSD was applied to the ADC traces of liquid scintillator to identify neutrons and γ-rays. Since PSD based on offline-recorded waveforms was limited by loadings and memory, the eight Charge-to-Digital Converter (QDC) sums of the Pixie-16 modules were utilized to perform PSD analysis online. The recording of QDC sums started at the pre-trigger trace, which preceded the trigger point. Subsequently, the eight QDC sums were computed individually without overlapping and ended when all eight intervals had passed. As shown in Fig. 4, at least three of the eight sums are required to obtain the short and long sums of the PSD, which can be expressed as $Q_{\text{short}}=Q_1-Q_0\frac{L_1}{L_0},$ (2) $Q_{\text{long}}=\left(Q_1+Q_2\right)-Q_0\frac{L_1+L_2}{L_0},$ (3) where Qi is the charge integral of the QDC and Li is the length of the ith integral section. The intervals of the remaining five sums were set to the minimum value to minimize the dead time.

Fig. 4Full-screen View

(Color online) A schematic view of the QDC sum

Performance Test

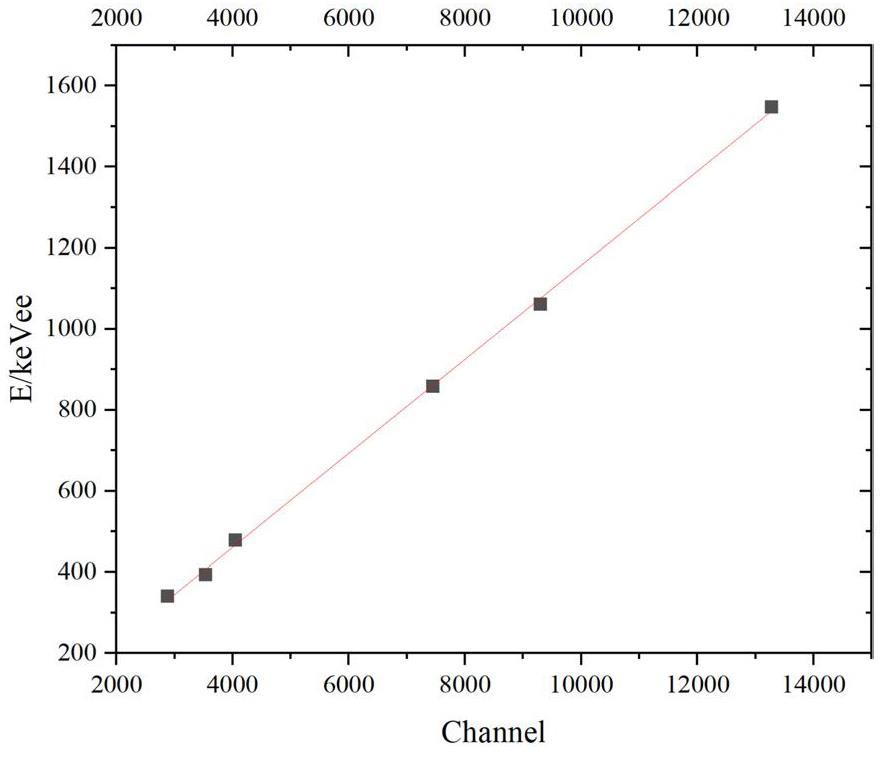
The liquid scintillation detector was energy-calibrated using radioactive sources. The entire energy range was divided into 65,536 channels, and the Compton edge of the ¹³⁷Cs radioactive source was adjusted to 4000 ± 200 channels by tuning the high voltage of the liquid scintillation detector. Energy calibration was then performed using the ²²Na and ²⁰⁷Bi radioactive sources; the resulting energy calibration curve of the liquid scintillation detector is shown in Fig. 5. The fast-time feature of the liquid scintillation detector was clearly demonstrated with a time resolution of 1.16 ns (Full width at half maximum, FWHM) and a 200 keVee threshold in the ²⁰⁷Bi source test, with two liquid scintillation detectors placed 20 cm away from the source. The time difference distribution is shown in Fig. 6. Additionally, the time resolution of PPAC was obtained as 1.08 ns (FWHM) by analyzing the time difference between the PPAC and liquid scintillation detector.

Fig. 5Full-screen View

(Color online) The linearity of the energy calibration of the liquid scintillation detector

Fig. 6Full-screen View

(Color online) The time difference spectrum of two liquid scintillation detectors with 200 keVee threshold in the ²⁰⁷Bi test

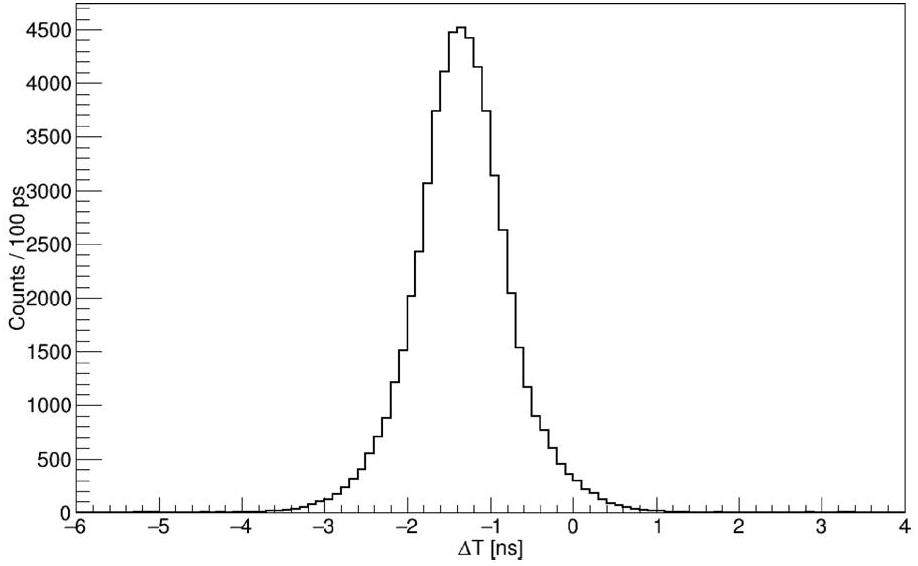
All the detectors in the liquid scintillator array are expected to have identical neutron detection efficiencies for precise measurement of the angular distribution in future ²³⁵U/²³⁸U experiments. The consistency of each liquid scintillation detector was tested in pairs using a ²³⁸Pu–¹³C neutron source. During the test, the ²³⁸Pu-¹³C neutron source is placed in the middle of the two liquid scintillation detectors on a three-dimensional (3D)-printed mold, as shown in Fig. 7a. The relative positions of the liquid scintillation detector and the ²³⁸Pu-¹³C neutron source were fixed, with a measurement time of 10 h.

Fig. 7Full-screen View

(Color online) (a) The efficiency consistency test using ²³⁸Pu-¹³C neutron source. (b) An example of pulse shape discrimination

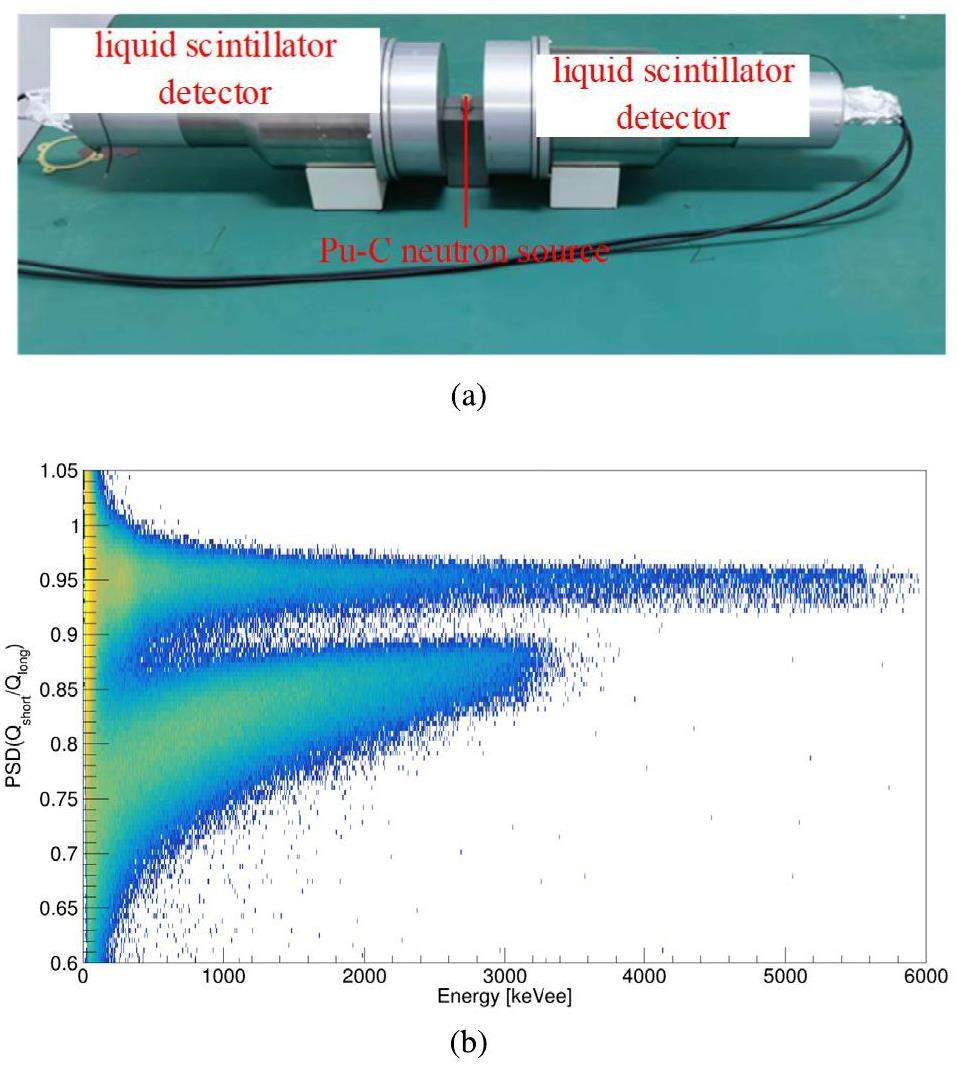
As mentioned in the previous section, the PSD techniques used to distinguish between pulses from neutrons and γ rays rely on differences in the generated pulse shapes. The pulses generated by neutrons have a longer tail than those generated by γ rays because the neutron pulses originate from triplet state interactions (delayed fluorescence), and the pulses produced by γ rays result from a singlet state de-excitation (prompt fluorescence). Therefore, the difference in the ratio of the charge in the fast component to the total charge in the pulse (PSD value) from the two sources can be calculated and used to discern the type of incident particles. The PSD value of the neutron pulses should be lower than that of the γ-ray pulses for the same deposited total charge. By performing PSD on the measured data (Fig. 7b, the number of neutrons and γ events detected by the liquid scintillator detectors were obtained and normalized to the average values according to the counts detected by the entire array. The results of the consistency test showed that the fluctuations in the neutron and γ event counts detected by almost all detectors were within 5%, which satisfied the experimental requirements.

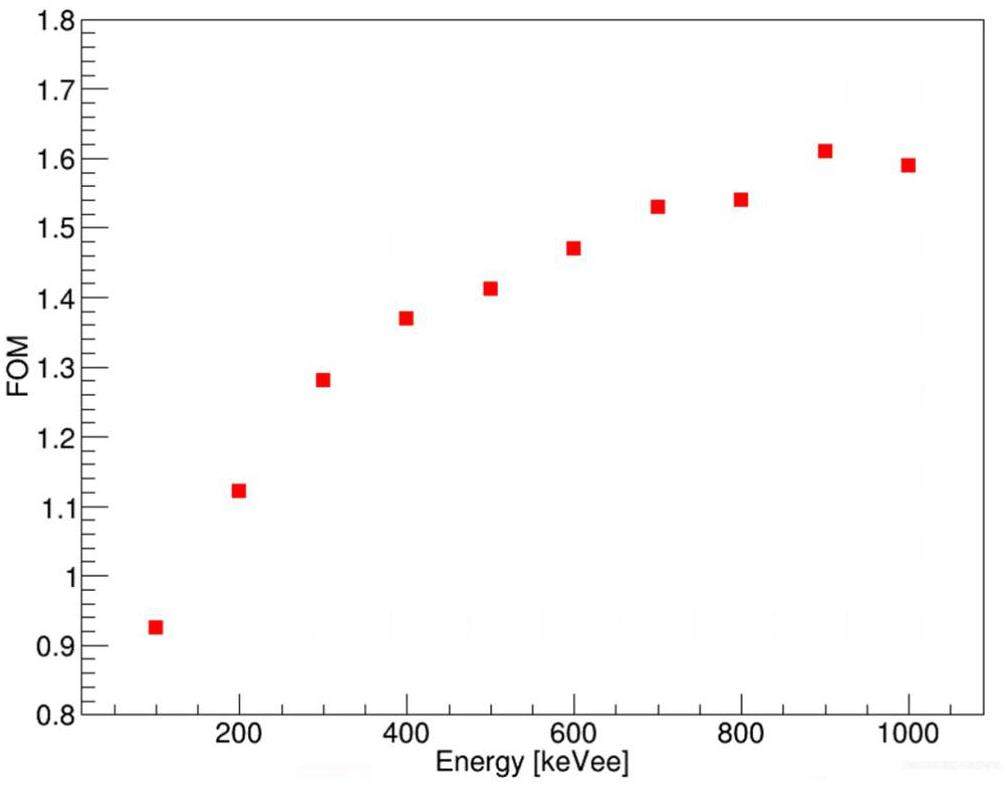
The separation between the neutron and γ-ray signals can be quantified and used to determine the performance metrics. A standard figure of merit (FOM) has been identified for fast neutron detectors and is used to establish their ability to discriminate between pulses generated by γ rays and neutrons. The FOM is calculated from the histogram of the PSD value versus the peak height data after performing PSD to identify the neutron and γ-ray pulses and is defined as follows (note that this definition assumes that the pulse distributions are Gaussian): $\text{FOM}=\frac{S}{{\delta }_{\text{neutron}}+{\delta }_{\text{gamma}}}$ (4) where S is the distance between the γ-ray and neutron peaks, and δ is the FWHM of the peaks. The FOM values at different energies are shown in Fig. 8 where the corresponding value at the 200 keVee threshold is 1.12, which satisfies the requirement for neutron-γ discrimination.

Fig. 8Full-screen View

(Color online) The FOM of the liquid scintillation detector at different deposited energy regions within the range of E ± 30 keVee

Geant4 Simulation

Precise PFNS measurement requires the counts of scattered neutrons whose energy spectra deviate from those of the primary prompt fission neutrons to be discarded. Multiple-neutron scattering has been demonstrated to significantly influence the detected low-energy neutron spectrum [39]. The primary consequence is that the PFNS must be extracted from the measured neutron spectrum using a deconvolution procedure or other methods that fully account for multiple-neutron scattering. In addition, multiple scattered γ-rays invade the fast neutron region in the TOF spectrum, forming a smooth background and overestimating the neutron yield. Therefore, a Monte Carlo simulation is required to assist the experimental data analysis.

The model of the liquid scintillator detectors, as well as its aluminum casing and support, was first constructed using SolidWorks software. To import such complex geometries into the Geant4 simulation program [40], the CADMesh method [41] was chosen to enable the Geant4 program to read ASCII STL files. Advantageously, the CADMesh method can be easily used to handle complex 3D shapes and curved surfaces, such as detector arrays comprising numerous intricate or irregular geometric elements. A geometric simulation and typical subassemblies are shown in Fig. 9. All the PMTs were ignored in the simulation. A cement wall surrounding the array was constructed due to its significant effect on neutron scattering. The horizontal distance from the array to the wall was approximately 4 m, whereas the distance from the ceiling was 6 m.

Fig. 9Full-screen View

(Color online) Typical construction of the liquid scintillator array in Geant4

Two types of primary sources were implemented in the simulation: a neutron source and a γ source. The neutron energy was subject to a Maxwell distribution, whereas the energy spectrum of γ ray was adopted from Ref. [42]. Both the neutrons and γ rays were isotropically emitted at a 4π solid angle.

Selecting an appropriate physical model is crucial for Geant4 simulations. We considered neutron elastic scattering, inelastic scattering, fission, and capture processes using G4NeutronHPElastic, G4NeutronHPinelastic, G4NeutronHPFission, and G4NeutronHPCapture models. The interaction between γ rays and charged particles and materials has been well described by G4EmStandardPhysics. The deposited energy can be traced at each step of the particle transportation using the embedded algorithms of Geant4. The particles were designed to be transported via the functions of the action class in each step until they were absorbed in certain volumes or escaped preset cutoff areas. During the simulation, each particle was labeled with a generation number. The information associated with the particles was transferred via a user-set customized function to the TrackingAction class for further processing.

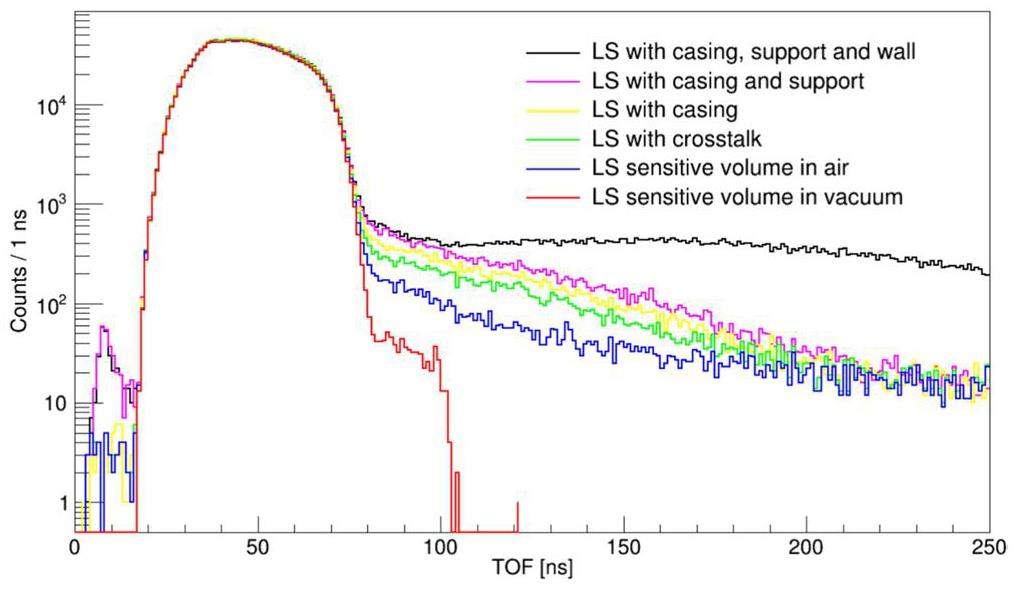
The neutron scattering contributions for each component at the 200 keVee threshold are listed in Table 2. The major contribution was attributed to the cement wall around the array, followed by the liquid scintillation material and its appurtenances. The simulated neutron spectra, including multiple scattering under different conditions, are shown in Fig. 10. When the neutron flight time was greater than 100 ns, the counts were mainly contributed by the neutrons scattered by the environment. Because the effectively measured energy of the fission neutrons ranged from 1 MeV to 10 MeV for the liquid scintillator (the corresponding flight time ranged from 22.9 ns to 72.3 ns), the scattered neutrons had no significant effect on the parts of interest of the PFNS. Figure 11 compares the growth of the simulated neutron count yield after considering only the detector crosstalk and all components in Table 2, indicating that the contributions from the environment are comparable to those from the crosstalk between the liquid scintillation detectors.

Fig. 10Full-screen View

(Color online) Simulation results using Geant4 under different conditions

Fig. 11Full-screen View

(Color online) Growth of simulated neutron-count yield after considering the detector crosstalk (blue) and the detector crosstalk + casing + support + wall (black) with respect to liquid scintillator in air

²⁵²Cf test results

The neutron fission spectrum of ²⁵²Cf is often regarded as the standard energy spectrum because it has been extensively studied experimentally and theoretically [28]. The branching ratio of the ²⁵²Cf spontaneous fission was 3.09%, the average number of neutrons emitted per spontaneous fission was 3.756, and the neutron yield was 2.31× 10¹² s^-1·g^-1. The relative efficiency of the liquid scintillation detector was calibrated using a ²⁵²Cf radioactive source, which underwent approximately 2400 fissions/s at the time of measurement. Most fissions were from ²⁵²Cf, with small contributions from ²⁵⁰Cf(sf) (0.2%) and ²⁴⁸Cm(sf) (6×10^-5%). The different decay rates resulted in an increasing fraction of ²⁵⁰Cf and ²⁴⁸Cm relative to ²⁵²Cf. However, the fission contributions from ²⁵⁰Cf(sf) and ²⁴⁸Cm(sf) were negligible and thus ignored in further analyses. The structure of the PPAC in the ²⁵²Cf test was simplified compared to that in the ²³⁵U experiment. As shown in Fig. 3, the ²⁵²Cf radioactive source is placed inside the PPAC, and the generated fission fragments pass through the aluminized Mylar, ionizing the perfluoropropane gas between the Mylar to produce a starting signal.

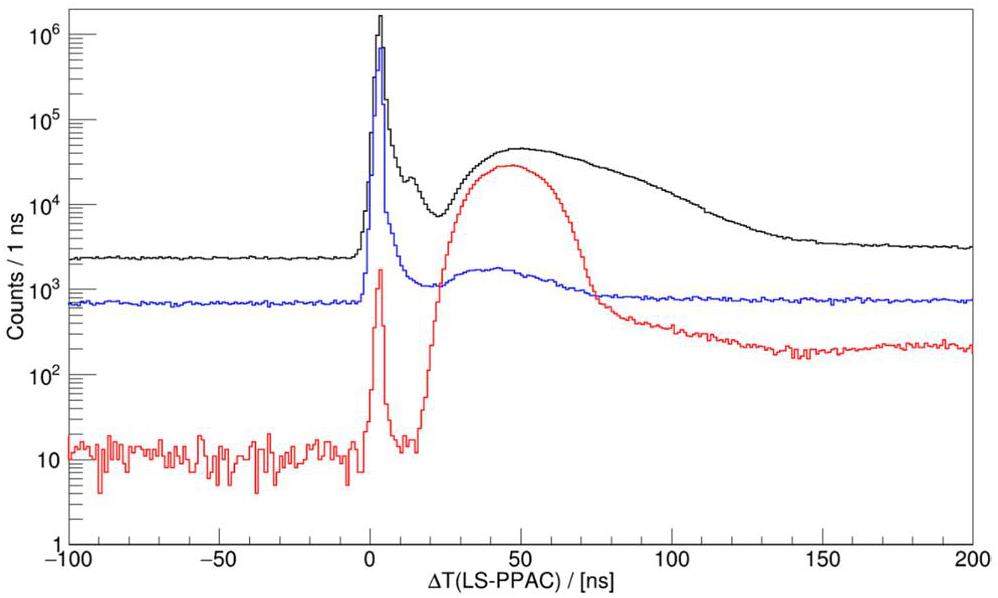
The measurement data for the ²⁵²Cf source were collected for approximately 290 h. The liquid scintillation detectors were placed on the detector array support, and the PPAC was placed at the center of the array, 1 m from the detector surface. Each detector was characterized as both a neutron and γ detector in the analysis, with signals passing through a PSD gate separated and treated accordingly in the subsequent analysis steps. The discrimination threshold was set to 200 keVee, which corresponded to a neutron energy of 1 MeV. Figures 12a and b show the TOF spectra of the liquid scintillator signals before and after PSD, respectively. The PSD greatly suppresses the contamination from γ rays, whereas there are still some γ events that survive the PSD cuts appearing at 3.3 ns, corresponding to the TOF of light propagating a distance of 1 m. The TOF spectra (Fig. 13 shows the discrimination of neutrons and γ rays by PSD.

Fig. 12Full-screen View

(Color online) TOF spectrum of fission neutrons (a) before and (b) after PSD, where signals near 0 ns are the gamma events that survive the PSD cuts

Fig. 13Full-screen View

(Color online) TOF spectrum measured in ²⁵²Cf test (black), where neutrons (red) and γ rays (blue) are identified by PSD

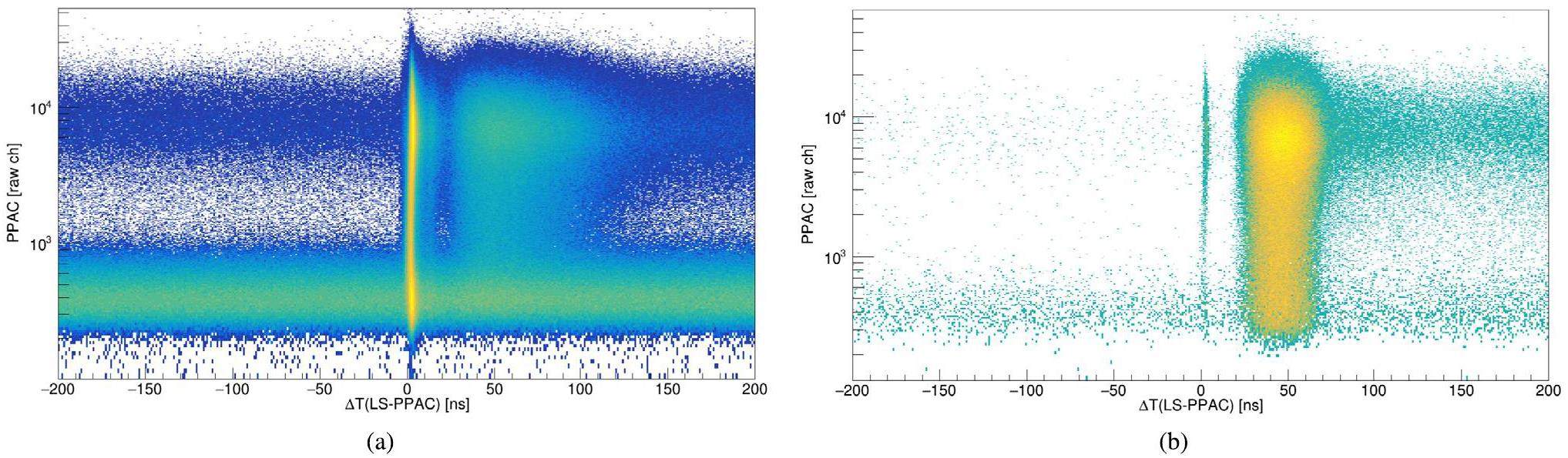
α particles were emitted from ²⁵²Cf simultaneously with spontaneous fission, which generated indistinguishable signals in PPAC. These α events produce spurious coincidences with the neutron events detected in the liquid scintillator detectors because they do not correlate with fission fragments. As shown in the energy spectrum of PPAC (Fig. 14, α particles are typically detected at low-pulse integrals and fissions at higher integrals. Therefore, fission events in PPAC targets have a minor overlap with spontaneous α detection in the pulse integral space. Although no clear separation exists between α and fission detection integrals, a cut is introduced into the PPAC integral spectrum to eliminate as many α particles as possible while retaining most of the detected fission signals, as shown in Fig. 14.

Fig. 14Full-screen View

(Color online) A PPAC pulse height spectrum before (black) and after (red) coincidences with the signals of the liquid scintillator detectors. A dashed green line is placed on the pulse height spectrum. For comparison, the black histogram is scaled down to the red histogram

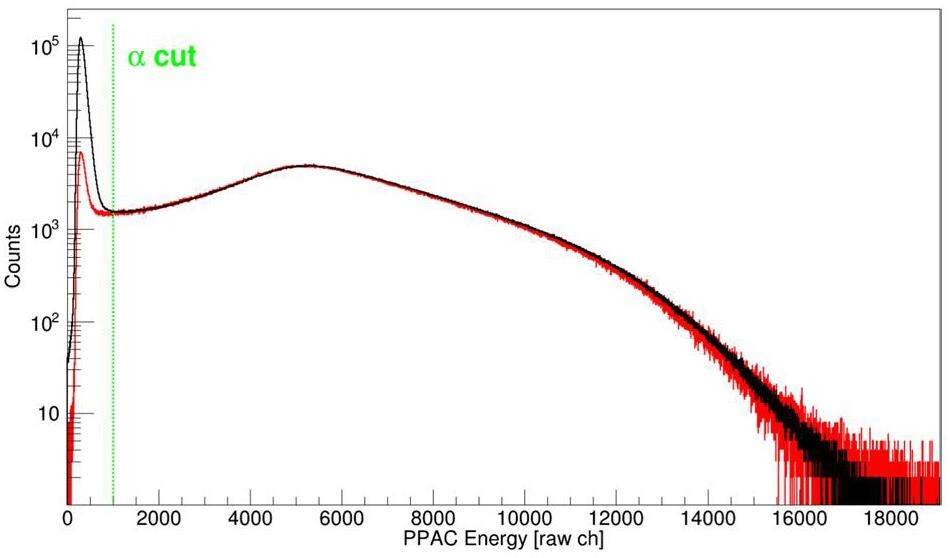
The random coincidence background measurement must be subtracted to obtain accurate PFNS. It is mainly generated by random coincidences between the PPAC and liquid scintillator signals, i.e., between fission neutrons and α signals, fission neutrons and fission signals that do not produce neutrons, or fission events and non-fission neutron signals. In Fig. 13, the counts in the negative time region are random coincidence backgrounds, and the backgrounds in the positive time region should be symmetrical and can be subtracted accordingly to obtain a clean fission neutron spectrum. Notably, the data obtained after cutting, as shown in Fig. 14, inevitably includes a portion of the detected α-particles. Nevertheless, since these are random detections, not in true coincidence with fission neutrons, they can be easily removed using the random coincidence background technique.

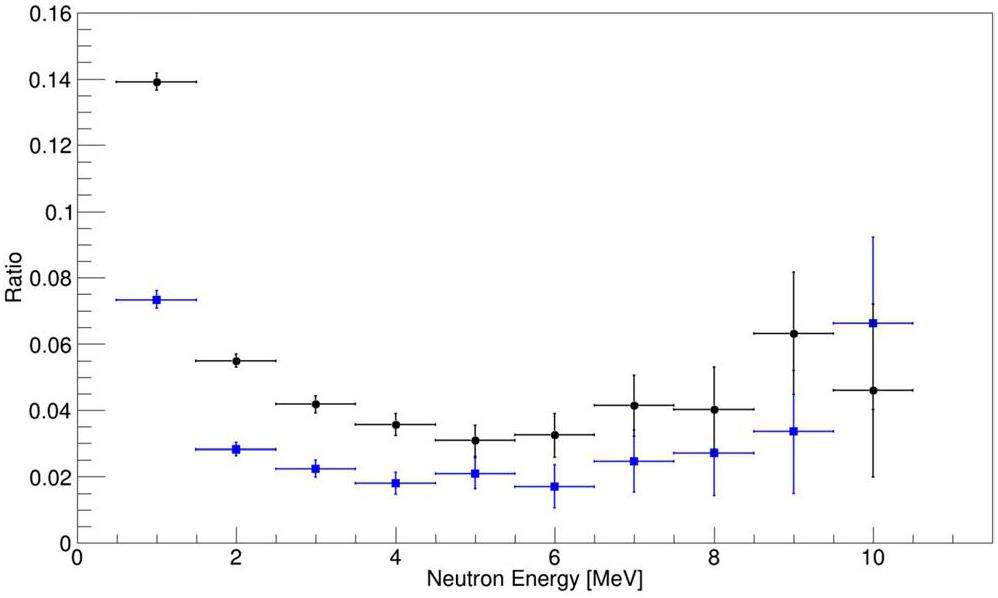
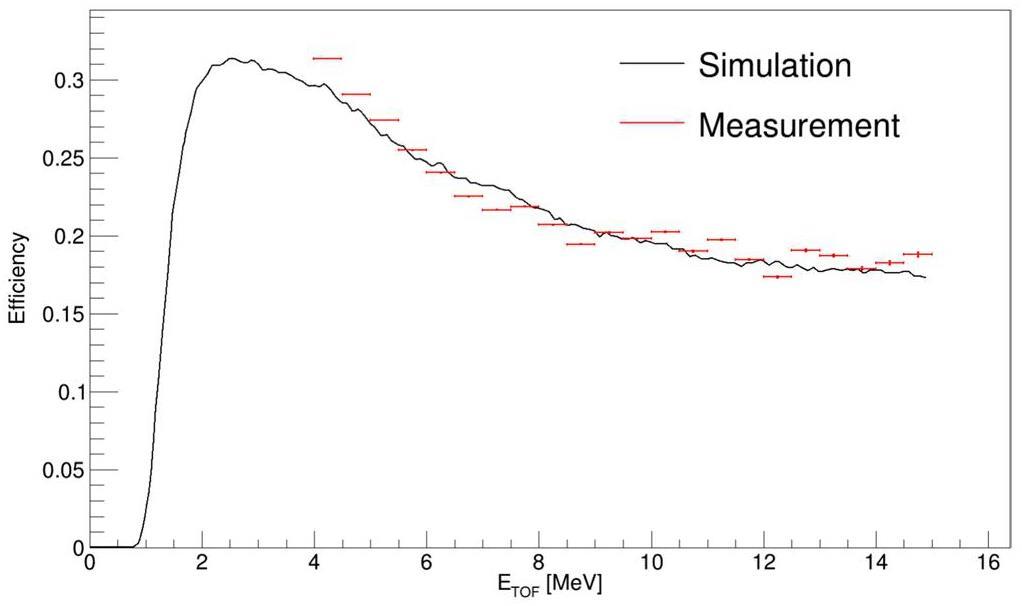
The efficiency of the detection array with 48 scintillation detectors after data reduction is shown in Fig. 15. The neutron yield detected at energies below 4 MeV was significantly affected by the support and wall, which could not be perfectly simulated. This influence increased at 4 MeV (Fig. 11, which was difficult to evaluate. Therefore, the neutron efficiency at low energies was not displayed. Nevertheless, the experimental measurements clearly agree with the Geant4 simulation results, which demonstrates the reliability of the detection array.

Fig. 15Full-screen View

(Color online) The efficiency of the detection array with 48 scintillation detectors. The red data points with error bars are measured with ²⁵²Cf source and compared to the Geant4 simulation

Conclusions and outlook

An array composed of 48 liquid scintillation detectors and a PPAC was developed in CIAE to measure the PFNS of the actinide nuclei. Efficiency and energy calibrations were performed for all the liquid scintillators, and their efficiency consistency was found to be better than 5%. The time resolutions of the PPAC and liquid scintillator were measured to be 1.08 ns and 1.16 ns using ²⁵²Cf and ²⁰⁷Bi sources, respectively. The PSD of the liquid scintillator was utilized to identify neutron and γ signals on an event-by-event basis, and the FOM was deduced as 1.12 at 200 keVee threshold. The contribution from multiple scattered neutrons to the PFNS was evaluated using Geant4 simulations, and those originating from the environment were found to be comparable to the crosstalk between the detectors. The neutron efficiency of the entire detection array was calibrated by measuring the ²⁵²Cf spontaneous fission source and was demonstrated to be consistent with the Geant4 simulation results, which verified the reliability of the detection array.