Theory

In neutron radiography, incident neutrons react with ⁶LiF in the scintillation screen and emit ZnS fluorescence. Conventional imaging is typically achieved through exposure to scintillation screens, integrating the fluorescence distribution I(t, s) over time, as follows: $I(s)={\displaystyle \underset{\text{Exposure}-\text{time}}{\int }}I(t\mathrm{,}s)\text{d}t$ (1) where I(t) represents the light intensity distribution in the image; s is the spatial position; and t is exposure time.

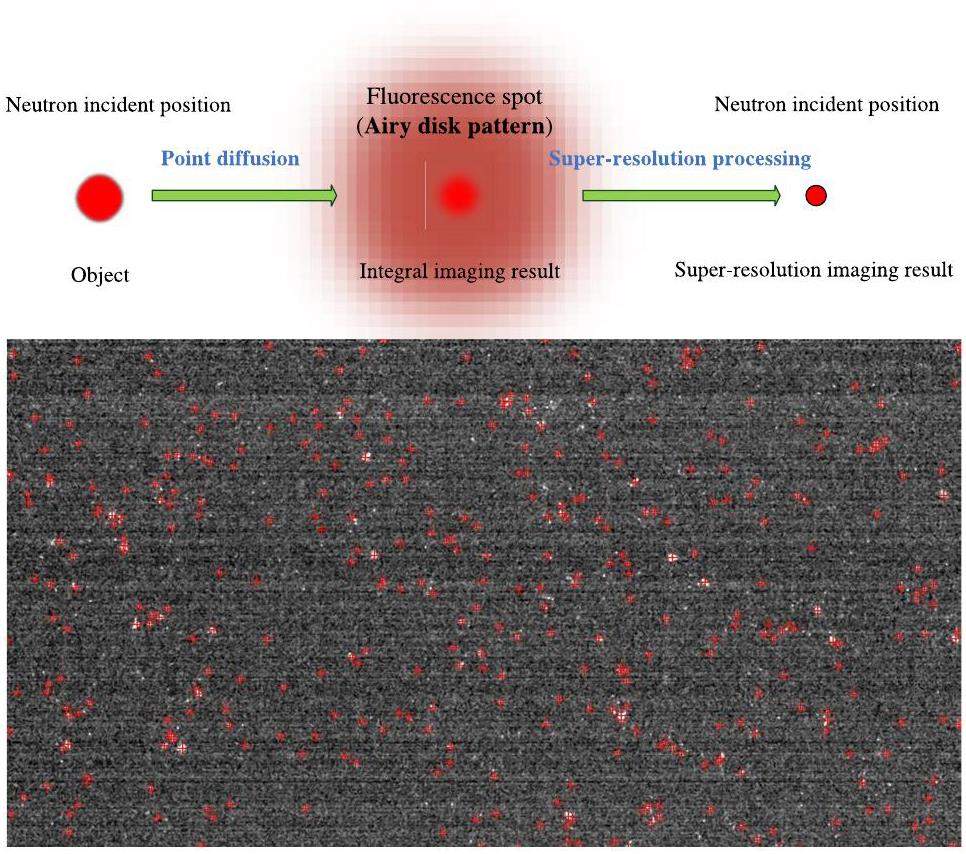
This work achieved single-neutron detection by detecting the fluorescence spots generated by neutron reactions individually, subsequently calculating the precise position of the incident neutron using a reconstruction algorithm. Using a dot with a precise location to replace the fluorescent Airy spot (light clusters), point diffusion and blurring during imaging can be reduced. Finally, a large number of light-dot distributions are added to form a higher-resolution neutron image.

Theoretically, single-neutron detection is equivalent to the time differential of the photon distribution I(t, s)dt. If the light-dot distributions are directly superimposed, the resulting image is equivalent to traditional imaging ${\displaystyle \int I(t\mathrm{,}s)}\text{d}t$. If they are superimposed after reconstructing P(I(t, s)dt), super-resolution imaging can be achieved. $I^{\text{HR}}\left(s\right)={\displaystyle \underset{\text{All}-\text{exposure}-\text{time}}{\int }}P[I(t\mathrm{,}s)]\text{d}t$ (2) where I^HR(s) represents the high-resolution image, and P(·) represents the reconstruction process.

Although this method can effectively achieve super-resolution imaging, it also places higher requirements on detection technology and the reconstruction algorithm. To detect a single event experimentally, the detection system must obtain a distinguishable weak light signal under intrinsic noise. During computations, each event in each frame is extracted and calculated. Considering the substantial computational resources and time required by the large number of neutron events, the efficiency of the algorithm should be improved. For weak light sources, the main problems are experimental detection and positioning calculations, making it critical to distinguish between noise and weak light signals. Thus, algorithms still need to improve noise discrimination.

Experiment

The most basic task accomplished in this experiment was to detect a single neutron event. Measuring each neutron radiation capture event under a continuous neutron beam, requires individual measurements of the fluorescence produced by the event and its spatial distribution. The spatial distribution of fluorescence is the basis of traditional and super-resolution imaging. The fluorescence distribution can be directly superimposed during data processing to obtain an image, equivalent to that of conventional integral imaging. Alternatively, the detection results for single neutrons can be processed to achieve super-resolution imaging.

The guiding principle of the experiment was single-neutron detection and reconstruction, as shown in Fig. 1. (I) In Fig. 1(a), traditional imaging detects all the neutrons during a single exposure, which is equivalent to time integration. Each Gaussian-like spot overlaps with the others, eventually forming an image with a blurred result. (II) In Fig. 1(b), single-neutron detection aims to detect neutrons individually, to obtain individual spot distributions. If reconstruction is not performed, all spots that directly overlap are equivalent to those in the traditional imaging method. (III) In Fig. 1(c), single-neutron super-resolution imaging aims to reconstruct the precise position of each neutron event, spot by spot. By superimposing the reconstructed points with small-scale distribution (pixel level), the spatial resolution of the imaging can be significantly improved.

Fig. 1Full-screen View

(Color online) Imaging method sketch: (a) Integral imaging (traditional imaging method); (b) Integral imaging based on single neutron detection; (c) Super-resolution imaging based on single neutron detection

The measurements were conducted at a Cold Neutron Radiography Facility (CNRF) located at the C1 beam tube of the China Mianyang Research Reactor (CMRR). The neutrons emitted from the C1 beam tube have a cold neutron spectrum with a characteristic wavelength of 0.26 nm (approximately 0.121 eV). The neutron flux can reach 3.41×10⁸ cm^-2s^-1, and the neutron flux at the sample position can reach 8×10⁶ cm^-2s^-1 [41]. Various collimation ratios (tube lengths and aperture sizes) were available, and the aperture size used in this study was ϕ 10 cm. The main components of the neutron imaging instrument include a ⁶LiF^-ZnS scintillator screen, mirror, optical lens group, image intensifier, and sCMOS camera. The CNRF facility and its imaging system are shown in Fig. 2 [42].

Fig. 2Full-screen View

(Color online) Experimental setup (a) Sketch of Cold Neutron Radiography Facility; (b) Sketch of imaging system at CNRF

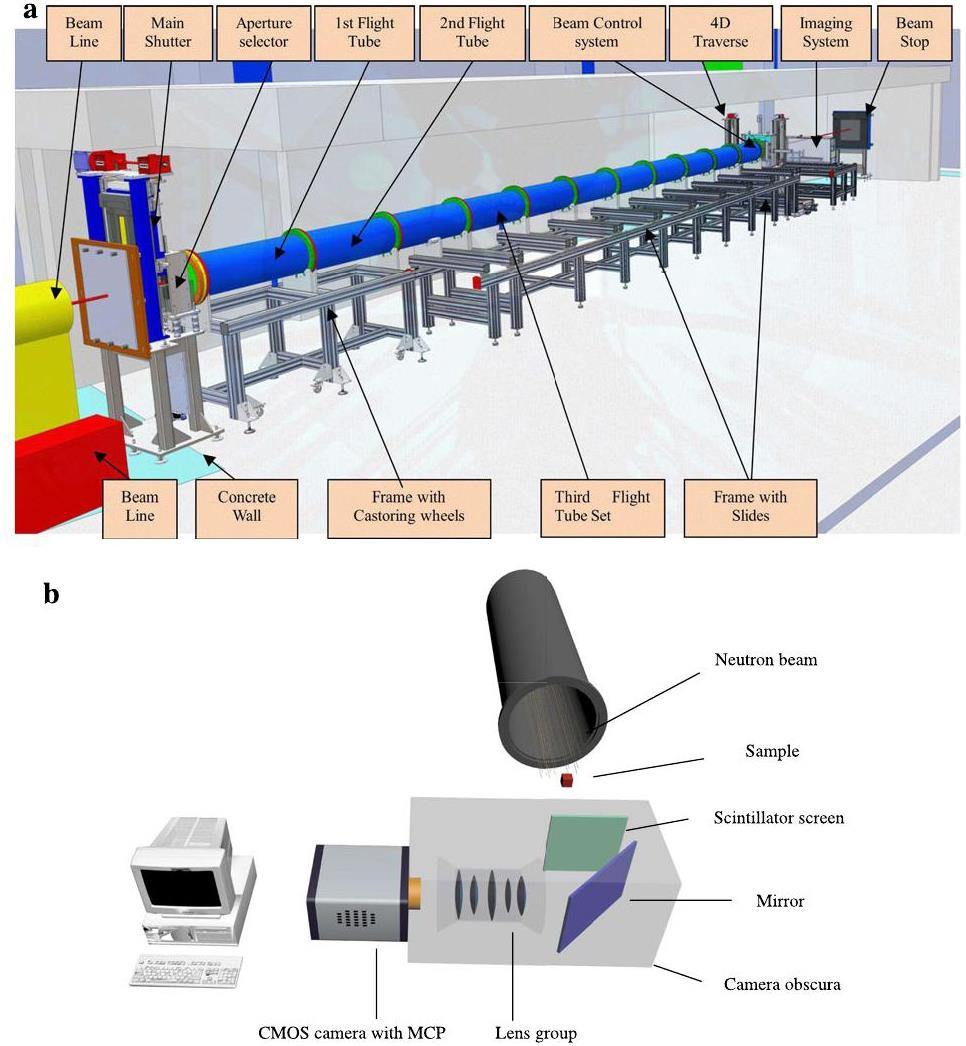
The ⁶LiF^-ZnS scintillation screen used in CNRF is also the most widely used and cost-effective neutron-scintillation screen. Aluminum with a small cross section was used as the base material of the scintillator screen, coated with a scintillator material thickness of 100 μm. The scintillator screen was composed of neutron converter material ⁶LiF, fluorescent material ZnS(Ag), and binder epoxy resin at a mass ratio of 1:2:1.29. The overall density was 2.845 g/cm³. The typical size of ⁶LiF and ZnS particles is approximately 1.5 μm-5 μm. The characteristic wavelength of the fluorescence spectrum was 450 nm, and fluorescence decay time was 200 ns.

The camera used was an ANDOR iStar-sCMOS, which provides high-resolution and high-frame-rate measurements. This camera can capture 12-bit or 16-bit images with an image array size of 2560×2560. The camera read images at a frame rate of 50 fps with full-frame resolution and 16 bit depth. An MCP was installed in the iStar-sCMOS camera as an image intensifier, which provided a maximum gain of 4096 times. This facilitates the detection of weak fluorescence. MCP has a peak quantum efficiency (QE) of up to 50% and spectral coverage of 120 to 1100 nm. MCP uses P46 phosphor with a light decay time of 200 ns (2 ms for P43), which is the main limitation to the optical interframe time (300 ns). The optical-resolution limit of the MCP (P46 phosphor) produced by Andor was 35 μm.

When collecting images, the field of view size was adjusted to 27 mm×27 mm to cover the entire sample. The sample used was a gadolinium resolution grating manufactured by the Paul Scherrer Institute. To minimize blurring caused by beam divergence, a resolution grating was placed close to the detector. The gain of MCP was set to 2000. The detector acquired images at a resolution of 2560×2560 pixels and read out a region of interest of 2560×1360 pixels at a higher detection frame rate. The acquisition was conducted in 12 bit low-noise mode. To detect the light spots generated by single neutrons and avoid the stacking of light spots as much as possible, the exposure time of the detector was set to 2 ms. After cooling the camera sensor to 0 ℃, 190 thousand images were collected. Once the test was completed, the beam aperture was closed and five thousand dark field images were acquired for noise removal.

Reconstruction method

Theoretically, each interaction on the scintillation screen material produces a star-shaped spot of light. In this experiment, the light spots produced by each capture reaction were recorded under a very short exposure time (millisecond). During reconstruction, the position of each light spot was calculated, and a value was assigned to the corresponding pixel. Reconstructing each nuclear event for each frame and eventually stacking all the frames enables high-resolution imaging. Each reconstruction calculation was performed for a single event, whereby the imaging technique transformed from a frame-based to an event-based system.

In single-neutron super-resolution imaging, the key steps of the reconstruction algorithm are as follows: (i) Processing image noise and extracting fluorescence signals. (ii) Calculating the location of neutron capture events and reducing the point-diffusion effect produced by the imaging device. Combining single-neutron detection with reconstruction enabled super-resolution imaging. A schematic representation of this principle is shown in Fig. 3.

Fig. 3Full-screen View

(Color online) Sketch of reconstruction principle

In this study, four advanced algorithms are proposed, and their reconstruction results are presented. The first is an improved centroid algorithm based on the existing algorithm, and the rest are the median filter centroid, median filter extremum, and Gaussian filter extremum algorithms. A schematic of the calculation process is presented in Fig. 4. Compared with the existing centroid algorithm (Fig. 4a), these algorithms offer additional advantages in terms of noise discrimination, and the calculated reconstructed images are more credible.

Fig. 4Full-screen View

(Color online) Sketch of the reconstruction algorithm

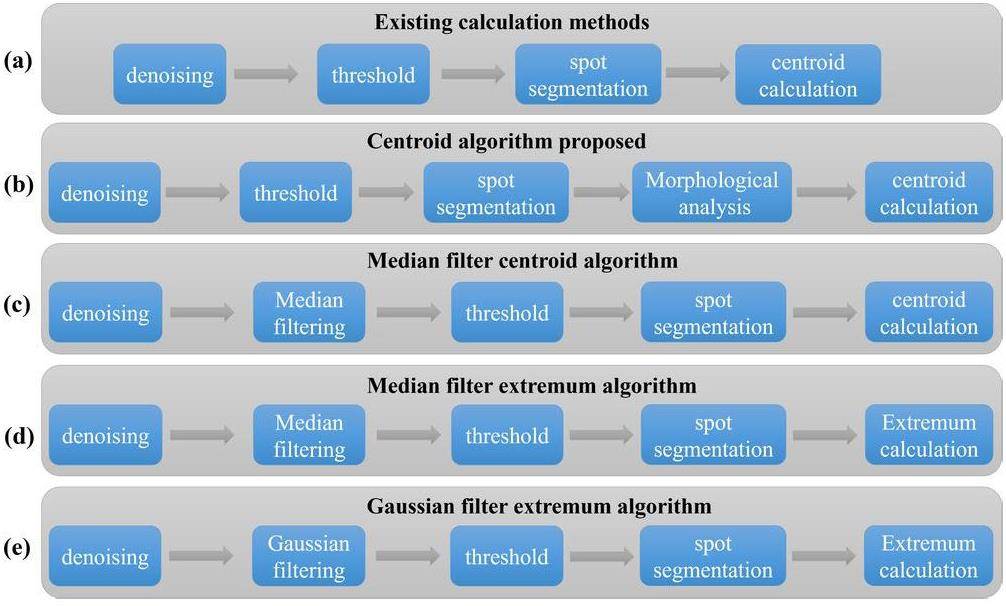
The calculation steps of the centroid algorithm (Fig. 4b) entail subtracting the background noise, spot segmentation, contour morphology analysis, and centroid calculation. In denoising, the image measured in the dark field can be removed as fixed noise, leaving only random noise. In spot segmentation, a threshold is set to eliminate random noise and low signal-to-noise ratio (SNR) light spot signals, and each spot area is segmented and processed. In contour analysis, the position, area, perimeter, and other morphological features of the contour are determined, and the relationship between the parent and child contours is established. In centroid calculation, the area and circumference of the contour can be considered as the condition for removing the low SNR signals. The centroid position of the light spot is then calculated to obtain a high-resolution image. Compared with the traditional method, which directly calculates the spot centroid, this method can remove noise more thoroughly and reconstruct a super-resolution image with higher credibility.

The median filter centroid algorithm is similar to the centroid algorithm (Fig. 4c). The difference is that a median filter is added after subtracting the background noise, and the filter kernel covers a radius of three pixels. The random noise in the image is close to the gray value signal and similar to the peak-shaped signal. However, the noise distribution range is smaller. Median filtering eliminates random noise that is similar to the signal. The advantage of median filtering is that it can remove noise with less signal loss. However, the disadvantages are that it changes the signal distribution and flattens the peak of the spot, which can change the centroid position.

The median filter extremum and Gaussian filter extremum algorithms are faster reconstruction methods (Figs. 4d and 4e). The calculation steps of these two algorithms include background subtraction, median/Gaussian filtering, spot segmentation, and local extreme value calculation. Compared with the centroid algorithm, the extremum algorithm has less computation, faster reconstruction speed, and a better noise reduction effect.

The addition of the median and Gaussian filtering operations can solve these two problems. First, for the amount of data (a large number of images x hundreds of light spots), the faster algorithm clearly has more potential for development. Direct filtering of the entire image is faster than analyzing the morphological characteristics of the light spots individually. In addition, in weak-light detection, such as neutron event imaging, noise elimination is an important task. Although weak noise with low gray values can be removed by thresholding, noise with large gray values in small areas (compared to gray signal areas) still remains in weak-light detection. Removing this signal-like noise using a centroid algorithm is difficult. However, the operation of filtering and threshold combination can eliminate the noise with large gray values in small areas, to better distinguish between noise and signal. Compared with median filtering, Gaussian filtering can reduce the gray value of noise to a greater extent and further enhance the signal-noise discrimination ability.

The addition of median and Gaussian filtering operations, can solve these two problems. First, for the amount of data (a large number of images × hundreds of light spots), the faster algorithm clearly has more potential for development. Directly filtering the entire image is faster than analyzing the morphological characteristics of the light spots individually. In addition, in weak-light detection, such as neutron event imaging, noise elimination is an important task. Although weak noise with low gray values can be removed by thresholding, noise with large gray values in small areas (compared to gray signal areas) remains in weak-light detection. Removing this signal-like noise using a centroid algorithm is difficult. However, the operation of filtering and threshold combination can eliminate the noise with large gray values in small areas and further enhance the signal-noise discrimination ability.

Experimental Results and Evaluation

For the reactor power near 10 MW, 1.9E5 images and 5E3 background images were collected at approximately 1.3 Tb. The original images are shown in Fig. 5. The raw data contained light spots produced by neutron capture events, as well as a large amount of noise. The image noise obtained by the CMOS sensor is mainly divided into random and fixed-pattern noise.

Fig. 5Full-screen View

Raw image data

The fixed pattern noise is primarily caused by the reset voltage deviation, which in turn is caused by factors such as the metal–oxide semiconductor field-effect transistor (MOS FET) threshold voltage deviation in the pixel, gain deviation of the source follower, and gain and bias of the column amplifier. This is a type of non-transient spatial noise. Therefore, it can be eliminated by using a multiframe averaging method. The average noise value of 5000 background images can be used to eliminate the fixed-pattern noise to a certain extent.

The numerous sources of random noise include power voltage fluctuations, substrate coupling between CMOS sensors and peripheral devices, and reset and readout processes of pixel transistors, which mainly comprise dark current, transfer, reset, flicker (1/f), and shot noise. The spatial distribution of random noise is not fixed; therefore, its direct removal is difficult. However, it can be distinguished based on the gray value and contour features during reconstruction. The morphological analysis link in the centroid algorithm (Fig. 4b) was used to analyze the area, perimeter, shape, and other characteristics of the light spot.

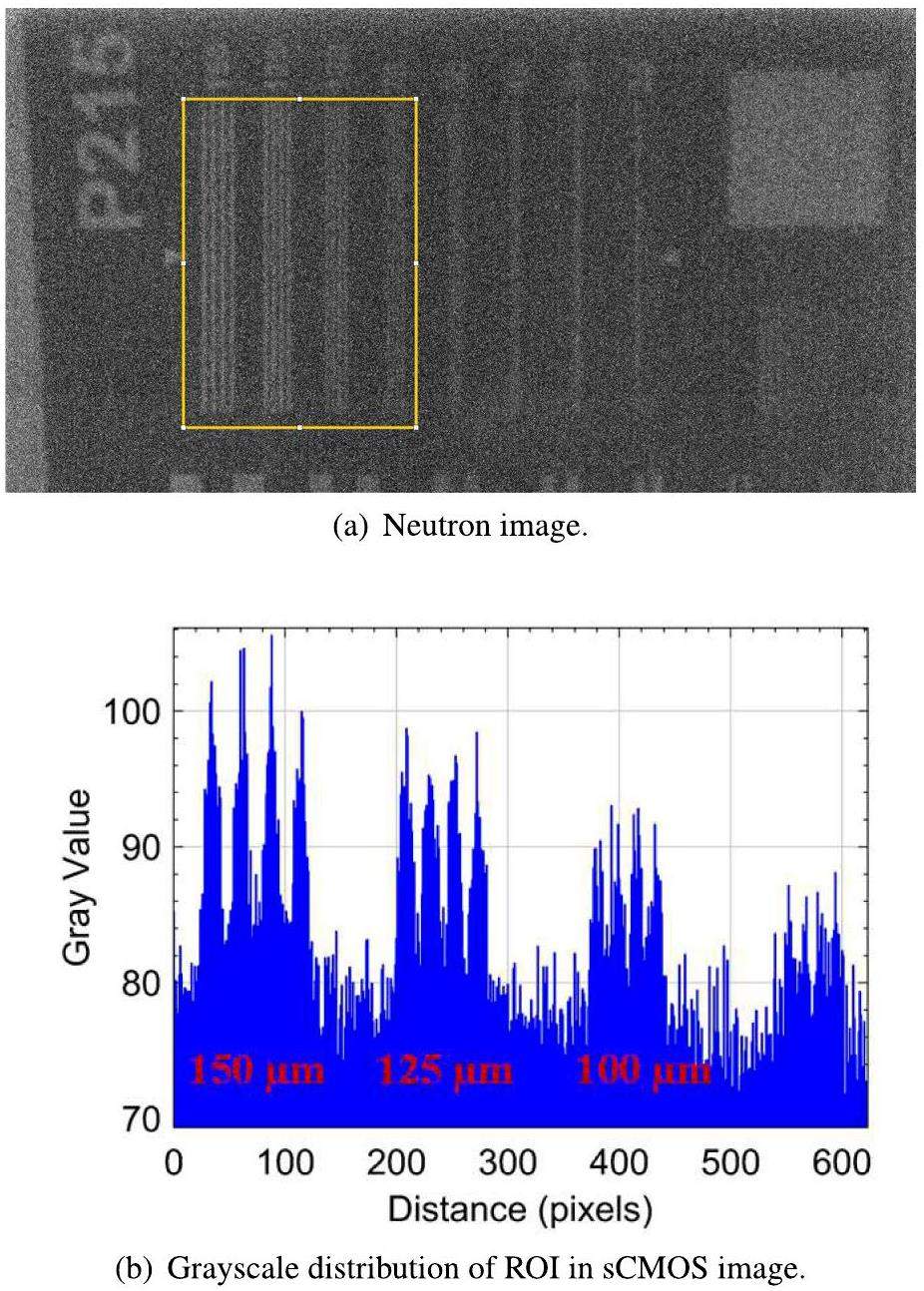
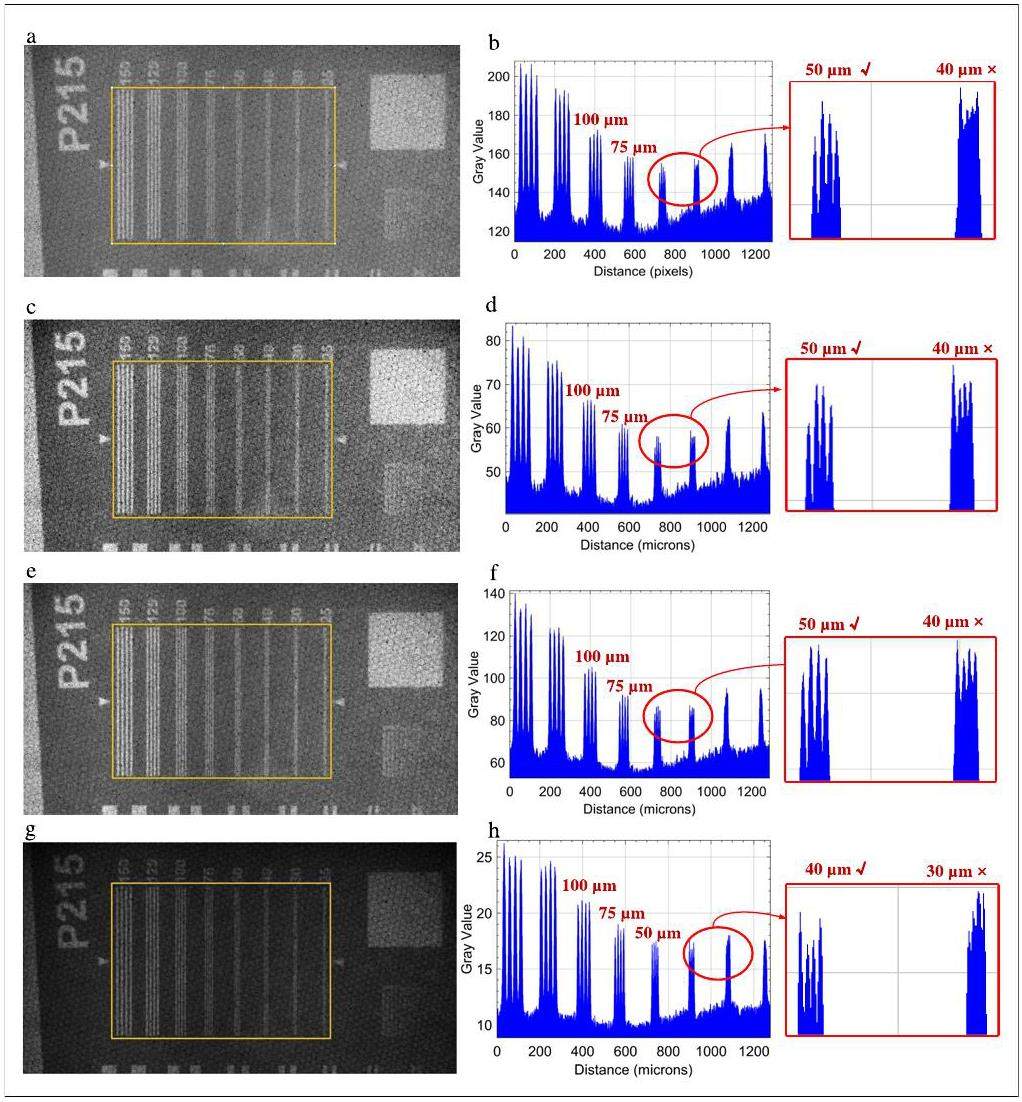
Comparing the effects of neutron event imaging requires the results of traditional integral imaging. By subtracting the multiframe background average from the original image data and then setting a threshold to remove the noise with low gray value, integral imaging was performed with 2 ms exposure. The traditional integral imaging results were obtained by superimposing 1.9E5 frames, as shown in Fig. 6, where the 125 μm stripes of the resolution grating are clearly visible at a field of view of 2.7 cm×2.7 cm. There are four easily distinguishable peaks in the grayscale distribution map. The 100 μm stripes are difficult for the human eye to distinguish. With four peaks, the gray distribution is not ideal. Therefore, the resolution of the conventional method is considered to be 125 μm and barely 100 μm.

Fig. 6Full-screen View

(Color online) Traditional integral imaging and its resolution level

In image reconstruction, the centroid, median filter centroid, median filter extremum, and Gaussian filter extremum algorithms were used to calculate the positions of neutron capture occurrence events in 1.9E5 images. High-resolution images were obtained. The results of the super-resolution experiments are shown in Fig. 7. After analyzing, the spatial resolution of the super-resolution image was significantly improved, and the results are shown in Table 1.

Fig. 7Full-screen View

(Color online) Super-resolution reconstruction results, and gray-scale distribution of resolution fringes. (a) Reconstruction results of the centroid algorithm; (b) Distribution of resolution fringes calculated by centroid algorithm; (c) Reconstruction results of median filter centroid algorithm; (d) Distribution of resolution fringes calculated by median filter centroid algorithm; (e) Reconstruction results of median filter extremum algorithm; (f) Distribution of resolution fringes calculated by median filter extremum algorithm; (g) Reconstruction results of Gaussian filter extremum algorithm; (h) Distribution of resolution fringes calculated by Gaussian filter extremum algorithm

To more accurately evaluate the super-resolution effect of single-neutron imaging, the image can be evaluated subjectively. From an objective aspect, line pair gray analysis and modulation transfer function were used to evaluate the resolution improvement effect.

The reconstruction results of the centroid algorithm shown in Fig. 7(a) and (b) can achieve a resolution of 50 μm. In the gray analysis, 50 μm stripes can be clearly distinguished, whereas 40 μm stripes cannot be distinguished.

The median filtering centroid algorithm in Figs. 7(c) and (d) and median filtering extremum algorithm in Fig. 7(e) and (f) have similar effects. Both algorithms can achieve resolutions between 50 μm and 40 μm. In grayscale analysis, the 50 μm stripes can be clearly distinguished, whereas the 40 μm stripes can barely be distinguished. This improvement in resolution indicates that median filtering can eliminate random noise. Because median filtering changes the signal distribution, it can further reduce the effect of noise on neutron event discrimination. In addition, the extremum algorithm has a faster reconstruction speed (in this experiment, five times that of the centroid algorithm).

According to the reconstruction results in Figs. 7(g) and (h), the Gaussian filter extremum algorithm can achieve a resolution of 40 μm. The Gaussian filter extremum algorithm obtained the best resolution and fastest reconstruction by virtue of its excellent random noise reduction and an ability to maintain constant peaks.

After comparing various algorithms, the results show that the Gaussian filter extreme-value algorithm has the best effect, as reflected by the optimal resolution level. The reconstructed image quality has higher clarity and better subjective visualization. In addition, it has the advantages of a small number of calculations and high speed.

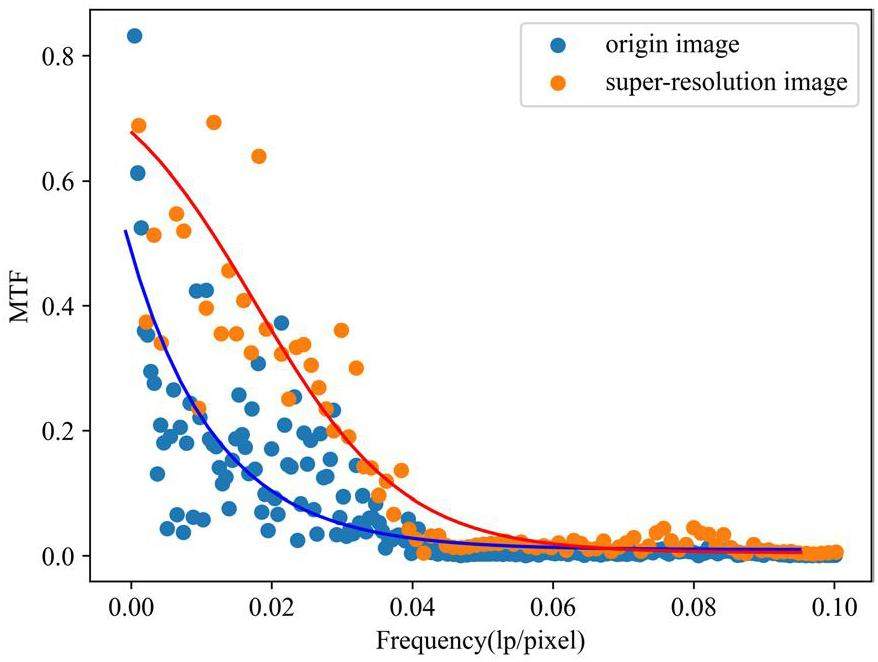
The modulation transfer function (MTF) is an important optical system evaluation indicator and can be used to calculate the resolution. Although the method of observing line pairs is the most direct and reliable, MTF can still be used as an additional method for verification.

An edge-to-edge method was selected for the calculation of the MTF curves. In terms of calculation objects, given the excellent performance of the Gaussian filter extremum algorithm, its reconstructed image was used as the representative of super-resolution. The MTF curves of the original and super-resolution images are compared in Fig. 8. The image resolutions calculated from the curves at 50% and 10% MTF are shown in Table 2.

Fig. 8Full-screen View

(Color online) MTF curves of the original and super-resolution images

At the same MTF, the super-resolution image had higher-frequency line pairs, such that the resolution level was also higher. The resolution obtained at 50% MTF, which corresponds to the most sensitive human eye, was 41.7 μm. The resolution obtained by directly observing the grayscale distribution of the line pairs with the human eye was 40 μm. Regardless of observing line pairs or analyzing MTF to assess resolution, the final results demonstrate that the experimental approach and reconstruction algorithm for single-neutron imaging are solutions that effectively improve imaging resolution.

Algorithm feature mining

To more concretely demonstrate the functions and characteristics of the algorithm, a small area with a high signal-to-noise ratio was intercepted from the original image for independent calculations, as shown in Fig. 9.

Fig. 9Full-screen View

(Color online) A small area of raw image data (86 × 80 pixels)

The specific calculation steps and processing effects of the centroid algorithm are illustrated in Fig. 10. (I) Most of the random noise in Fig. 10(a) can be removed by setting threshold segmentation spots. However, according to Fig. 10(b), noisy areas with high gray values remain, and the threshold cannot be further increased to remove noise to minimize the loss of the neutron signal. (II) Contour feature discrimination is a feasible method for further processing. The contour features are calculated using Suzuki85 boundary tracking algorithm, as shown in Fig. 10(c). (III) Neutron signals can be filtered out based on contour features to obtain the distribution of the pixel positions where the neutron signals are located, as shown in Fig. 10(d).

Fig. 10Full-screen View

(Color online) Centroid algorithm: (a) Grayscale distribution of original data; (b) Grayscale distribution after spot segmentation; (c) Contour line of light spot; (d) Grayscale distribution of reconstruction results

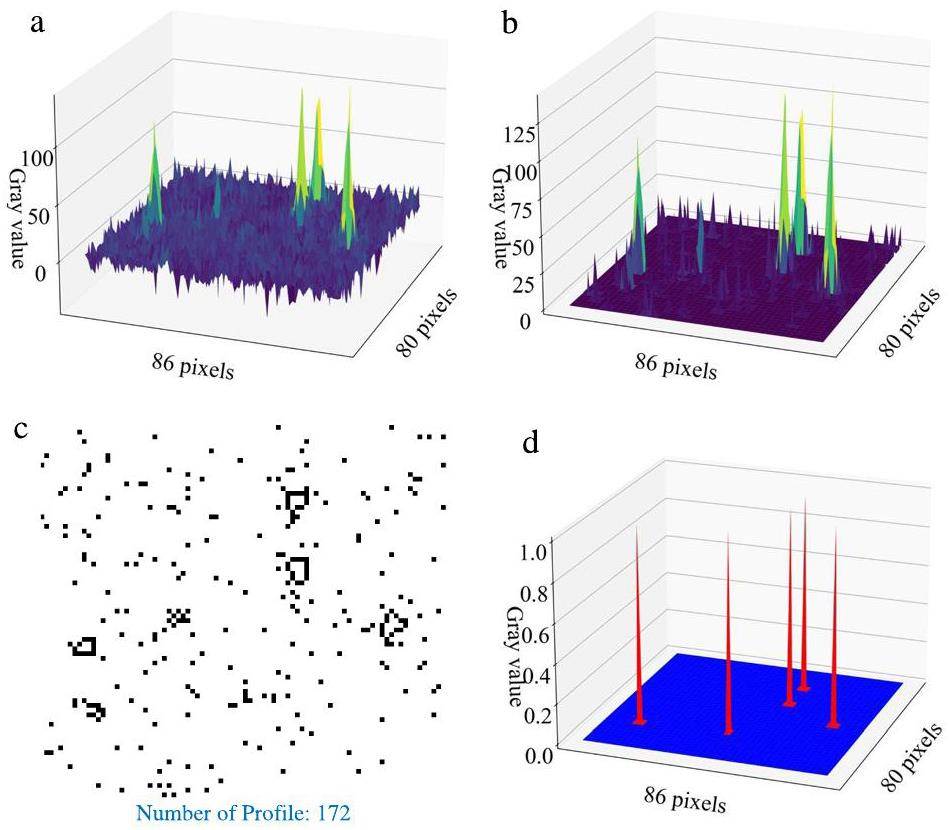
The centroid algorithm can analyze light spots individually and perform processing based on the shape, area, perimeter, and other image moment information. The centroid algorithm has many adjustable parameters, including the threshold and spot image moment parameters. However, the disadvantage is that the effect of noise elimination is poor, and the amount of calculation is large.

The Gaussian filter algorithm can improve the resolution from 125 μm to 40 μm. To more concretely demonstrate the functions and characteristics of the algorithm, the intermediate calculation results are shown in Fig. 11. Through Gaussian filtering, the random noise in Fig. 11(a) is reduced and smoothed, to obtain the result in Fig. 11(b). The distribution of light spots with low SNR and random noise is generally smaller. Gaussian filtering can significantly reduce the grayscale for a better filtering effect. Therefore, setting a lower threshold after Gaussian filtering can effectively segment the signal spots as shown in Fig. 11(c). Finally, the single-pixel distribution of the neutron signal was reconstructed, as shown in Fig. 11(d).

Fig. 11Full-screen View

(Color online) Gaussian filter algorithm: Grayscale distribution of (a) original data; (b) after filtering; (c) after spot segmentation; (d) reconstruction results

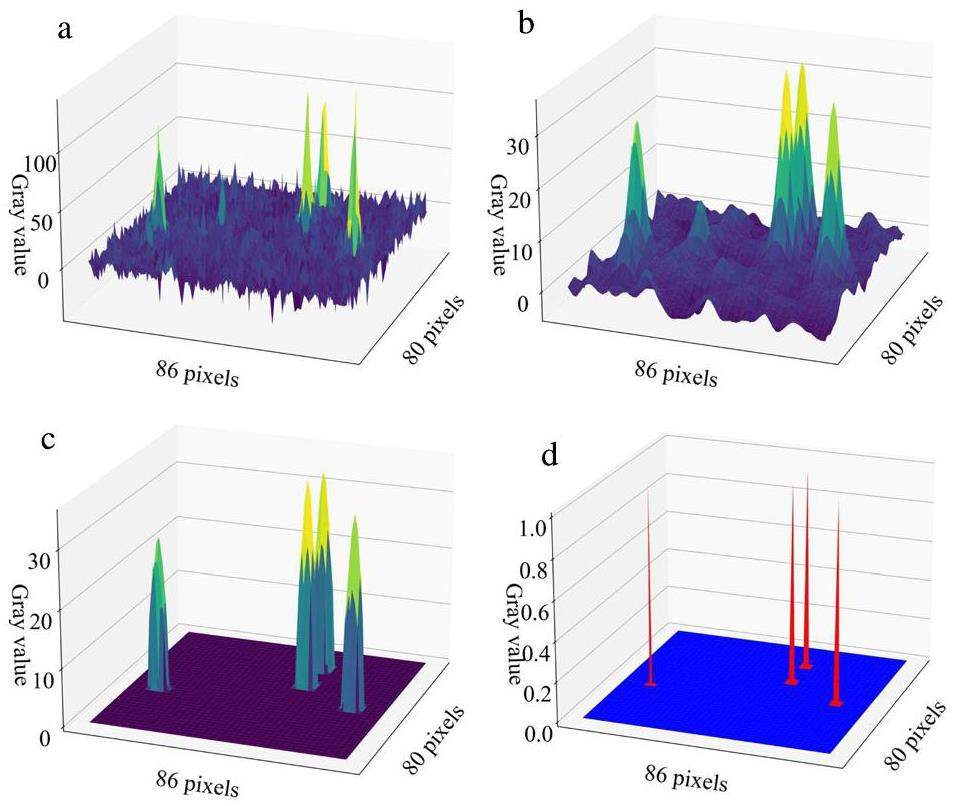
Gaussian filtering algorithms not only have a stronger signal-to-noise screening capability but also are faster. In addition, the algorithm can flexibly adjust the array size of the Gaussian filter kernel, sigma value, and spot segmentation threshold. These variable parameters enable the algorithm to remain well adapted under different experimental conditions, ensuring effective screening of neutron signals and noise.