Introduction
The neutron time-of-flight (ToF) measurement method is used to determine the neutron kinetic energy by measuring the velocity based on the relationship between the velocity and kinetic energy of a neutron when its flight path length is constant. This technique is widely used in neutron cross-sectional measurements [1-6] and large neutron spectrometers [7-13]. However, the accuracy of ToF measurements relies on the precision of the nuclear signal. Previously, the measurement of neutron flight times relied on large-scale analog circuits for signal amplification, timing conversion, and amplitude analyses. However, the transmission of analog signals often results in distortion and system instability. Hence, a waveform digitizer was introduced to convert continuous analog waveform signals into discrete digital forms. It provided time information and captured complete waveform information in digital form to overcome these issues, thereby exhibiting enhanced anti-interference capability and measurement accuracy [14, 15]. Additionally, digital signals can be transmitted using more stable digital methods, thereby minimizing the risk of signal distortion.
However, obtaining fast neutron ToF data at high frequencies can be challenging because it requires a narrow detector signal width. This requires the capability to be receive and process a higher signal frequency, while complying with the requirements of the Nyquist-Shannon sampling theorem. This method requires an analog-to-digital converter with a higher sampling frequency, which leads to challenges such as high-power consumption and increased costs. Moreover, the high sampling rates of the analog-to-digital converters result in large data volumes, placing significant burden on data transmission, storage, and processing. Therefore, there is an urgent need to develop an approach to alleviate the challenges associated with neutron ToF data transmission, storage, and energy consumption. Compressed sampling is a potential solution that allows simultaneous direct compression of signals during the sampling process, enabling signal recovery from a reduced number of measurements (below the Nyquist-Shannon sampling rate) [16, 17]. Thus, data can be effectively compressed with compressed sampling, thereby reducing the amount of data transmission and energy consumption in neutron ToF measurements.
Compressed sampling technology is widely applied to nuclear data processing and acquisition in nuclear physics and related fields. Wang et al. proposed a new compressed sampling framework integrating a discrete wavelet transform, Bernoulli measurement matrix, and sparsity adaptive matching pursuit for reconstructing neutron TOF signals [18]. Bin et al. used the compressed sampling framework of the SL0 algorithm to reconstruct the neutron spectrum expansion for Bonner sphere spectrometer measurements [19]. Additionally, Liu et al. proposed a compressed sensing-based coded-aperture method to optimize gamma-ray imaging technology and achieve higher imaging quality and faster imaging speed [20]. Jeong et al. employed a compressed sensing iterative algorithm with a coded-aperture mask to accurately reconstruct gamma camera images [21]. Kahuguna et al. investigated a compressed sensing-based method for flow mapping in nuclear reactors, which reduced the sampling volume and cost, while maintaining mapping accuracy [22]. Vargas et al. designed a neutron energy spectrum system based on compressed sensing measurements and revealed the energy characteristics of the neutron field using the theoretical framework of compressed sensing [23].
In our previous work [18], to address the limitation of applying conventional algorithms at low sampling rates for signal reconstruction, we have proposed a compressed sampling framework to sample neutron ToF signals per discrete wavelet transform (reverse biorthogonal 5.5, rbio5.5) + Bernoulli measurement matrix + sparsity adaptive matching pursuit (SAMP) reconstruction algorithm. Experiments were performed to verify the feasibility of the compressed sampling theory for neutron ToF signal acquisition. We also address the issues of massive data storage and processing when acquiring neutron ToF signals. Experimental results showed a percentage root-mean-square difference (PRD) of 6.7348%, correlation coefficient (CC) of 0.9977, and reconstruction time of 0.1108 s at a sampling rate of 20% of 2.5 Gs/s for neutron ToF signals generated from an electron-beam-driven photoneutron source.
These methods used the sparsity of nuclear data and employed compressed sampling for compression and reconstruction. However, traditional compressed sampling reconstruction methods encounter two main challenges. First, these methods failed to account for the specific characteristics and structure of the original signal in the universal random matrix, leading to suboptimal performance. Second, these methods requires multiple iterations to solve optimization problems owing to an increase in the dimensions of the solution space with an increase in the length of the signal frame, resulting in a longer reconstruction time. Therefore, traditional compressed sampling was introduced to significantly reduce data redundancy and energy costs. However, traditional compressed sampling still has some limitations in practical applications because traditional iterative algorithms are unsuitable for reconstructing numerous neutron ToF signals. Therefore, we introduced a deep-learning-based compressed sampling (DL-CS) algorithm to accurately recover the original signal at lower sampling frequencies, especially when dealing with a large number of neutron ToF signals.
The DL-CS algorithm does not rely on prior knowledge of the signal. Hence, it is robust. In other words, the original signal does not need to be inherently sparse or in the k-space. Instead, the algorithm designs a suitable deep neural network (DNN) based on signal characteristics and provides a network with substantial training data. This data-driven approach allows the network to learn hidden patterns in data, thereby enabling signal reconstruction. Furthermore, DL-CS can leverage the parallel computing power advantages of graphics processing unit (GPU) graphics cards for rapid signal reconstruction. Therefore, DL-CS has a better compression performance than traditional compressed sampling algorithms, as it effectively balances the trade-off between the compressed sampling reconstruction speed and quality.
When compressing neutron ToF signals, deep learning uses a combination of the sparse representation theory and DNN joint learning to obtain a signal-measurement matrix. The sparse representation theory holds that sparse signals can be recovered with fewer measurements. The deep neural network adjusts its weight parameters by training on a dataset to adapt to the signal characteristics and minimize reconstruction errors. An effective signal measurement matrix can be acquired for signal optimization and reconstruction. Regarding neutron ToF signal reconstruction, traditional iterative reconstruction algorithms perform better for sparse signals but are not as effective for non-strictly sparse signals. These algorithms also face challenges in achieving satisfactory reconstruction quality at high compression ratios and for small signal frame sizes. Furthermore, their performance deteriorates with low compression ratios and large signal frame sizes, where reconstruction time increases significantly as the number of tests grows. Therefore, the deep learning method exhibited better reconstruction results than the traditional approaches for reconstructing compressed physiological signals, particularly those with high-compression-ratio sampling.
We explored a data-driven deep learning method called the iterative shrinkage algorithm compressed sampling network (ISACSNet) to address these issues, compress the neutron ToF signal, and reconstruct the measurement values. This method directly models the mapping relationship between the dimensions of the rising measurements and original signals without considering prior information regarding the neutron ToF signal. Multiple convolution layers were employed to obtain the initial neutron ToF signal measurements. Moreover, a convolution layer increased the measurement dimensions, ensuring that the signal preserved its original shape. We also used multiscale convolutions to learn different signal features. Finally, a combination of long short-term memory (LSTM) and self-attention was used to improve the quality of the initial reconstruction signal and realize nonlinear reconstruction of the signal.
This study introduced a deep compressed sampling method for analyzing neutron ToF signals to address some of the constraints associated with traditional compressed sampling using ISACSNet, which combines inception blocks, LSTM, and self-attention. This deep compression sampling significantly improves the reconstruction accuracy and speed compared to traditional compression sampling. This study also proposes a measurement matrix based on the features of neutron ToF signals. This measurement matrix achieved a reconstruction accuracy superior to those of Bernoulli matrices at all sampling rates. Furthermore, this study evaluated the capability of deep compressed sampling in terms of the reconstruction accuracy and speed for neutron ToF signals using the PRD, correlation coefficient, and reconstruction time.
Materials and methods
Neutron ToF signals
This study focused on neutron ToF measurements using a photoneutron source powered by a 45-MeV electron beam pulsed at 8 ps. The ToF measurements were conducted over a distance of 5 m. In this experiment, an electron linear accelerator (e-LINAC), a target, and a neutron ToF detection system were used, as shown in Fig. 1 [24]. At the accelerator laboratory of Tsinghua University, an ultrashort pulsed electron linear accelerator was used to generate an electron beam pulse. The pulse was directed toward a Ta target located approximately 2 cm in front of the e-LINAC Ti window. The interaction between the electron beam and Ta-target resulted in the conversion of electrons to neutrons through the
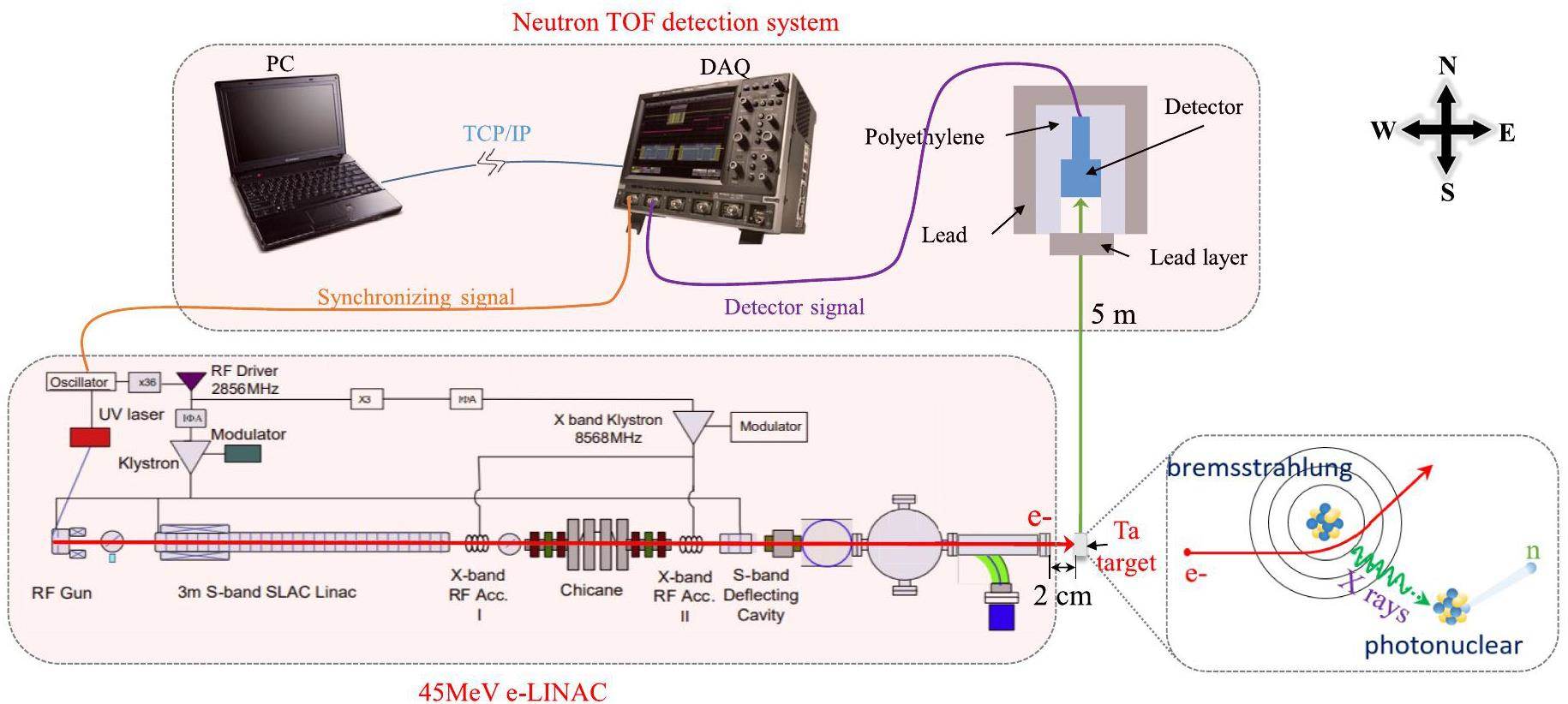
In the neutron ToF detection system, a φ 100 mm × 100 mm EJ299-33A plastic scintillator was coupled to a Hamamatsu R13089 photomultiplier tube to detect neutron signals. Neutron signal acquisition was performed using a LeCroy WaveRunner 64 Mix 600 MHz oscilloscope at a sampling rate of 2.5 Gs/s. Data acquisition was performed using a synchronization signal provided by the e-LINAC, and it was controlled by a computer connected via the transmission control protocol/internet protocol (TCP/IP) protocol. During offline processing, constant fraction timing was employed to accurately determine the arrival time of photons and neutrons.
The proposed approach was simulated using MATLAB R2021a and PyCharm on a Windows 10 operating system. The computer was equipped with an Intel Corei7-6500U CPU @ 2.50 GHz processor and 8 GB memory to process the neutron ToF signal from the EJ299 neutron 10k dataset. The dataset included the 104 neutron signals detected by the EJ299-33A plastic scintillator.
Compressed sampling
Compressed sampling is a novel signal-processing technique designed to efficiently compress signals. This technique allows sub-Nyquist rate sampling of analog signals and the reconstruction of singles with less sampled data. Compressed sampling relies on the sparsity and incoherence of a signal, indicating that the signal contains only a few nonzero elements in a specific transform domain. By applying a sparse transformation, signals can be sampled at rates significantly lower than the traditional sampling requirements. Then, a reconstruction algorithm can restore the original signal from the relatively fewer sampled data. A transform domain for the neutron ToF signal exists in the neutron pulse signals, and it randomly changes into a nonstationary signal with low-frequency components. Therefore, the neutron ToF signal exhibited sparsity, enabling compressed sampling for signal reconstruction. The compressed sampling framework was divided into three steps, as illustrated in Fig. 2. The first step involved sparsifying the signal, followed by designing a measurement matrix to sample the sparsified signal. Finally, the original signal is reconstructed using the sampled observations through a reconstruction algorithm.

Deep network for compressed sampling reconstruction
Traditional reconstruction algorithms can be tedious and time-consuming because of their iterative nature, which requires significant computational power. In contrast, deep-learning-compressed sampling uses neural networks to simplify the entire process by learning the mapping from the input to the output in an end-to-end manner. This technique reduces the need for manual parameter adjustments and streamlines the entire system. Additionally, unlike traditional compressed sampling, deep learning models automatically learn signal features through convolutional layers, eliminating the need for manually designing measurement matrices. However, deep-learning-compressed sampling requires more data for training, particularly in end-to-end learning, which can be advantageous in scenarios with abundant measurement data.
Figure 3 illustrates the ISACSNet workflow, where the original neutron ToF signal with a size of 1024 × 1 serves as the input, and a reconstructed signal of 1024 × 1 is generated as the output. ISACSNet comprises four key modules that are essential for its functionality.
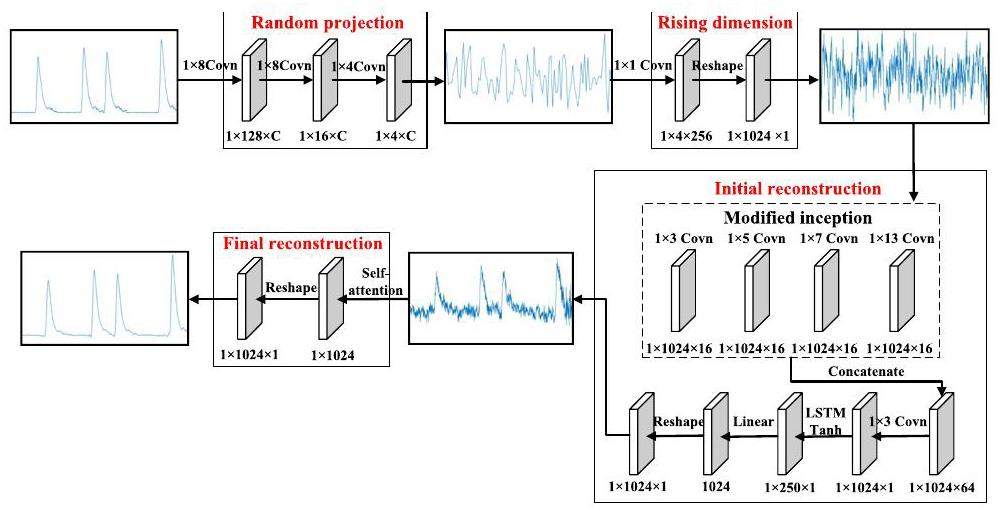
(1) Random projection module: The number of channels in the convolutional layers is adjusted to represent the various sampling rates in the training set. Moreover, the neutron ToF signals undergo simultaneous sampling and compression through multilayer convolution to yield measurements.
(2) Rising dimension module: The acquired measurements are processed through a convolutional layer to expand their dimensionality, while keeping the resulting signal consistent with the original neutron ToF signal.
(3) Initial reconstruction modules: By expanding the dimensions, we leverage the inception module to learn the features of the signals at different scales. The learned features are integrated, passed through a convolution layer, and ultimately processed using the LSTM module to achieve the initial reconstruction.
(4) Secondary reconstruction module: We employ self-attention to restore the initial reconstruction signal and enhance the signal quality.
Random projection
In the compression process of traditional compressed sampling, a fixed measurement matrix is replaced by three sequential convolution layers owing to the substantial storage requirements of the fixed measurement matrix and the necessity to satisfy the restricted isometry property principle [25]. The convolution operation is a critical factor because it can be represented as a matrix multiplication [26]. This process is described as follows.
The kernel size of the three convolution layers are 1 × 8, 1 × 8, and 1 × 4, with the strides of 8, 8, and 4, and the number of filters is denoted as C, where C=256 × Sampling rate, in which sampling rate is the ratio of the number of measurement sampling points to the original signal. Therefore, after the convolution operation, the length of the signal will be reduced to a quarter of its original length. Following all three consecutive convolutional layers, a measurement of size 1 × 4 × C is obtained.
Rising dimension
The measured dimensions were significantly smaller than those of the original signals. Therefore, the measurement dimensions must be increased to match the original signal before initiating the reconstruction of the initial measurement. The most effective way to achieve this is by employing a convolution layer with a kernel size of 1 × 1, stride of 1, and 256 filters, and then a leaky rectified linear unit (LeakyReLU) activation function. This nonlinearity ensures that the measurements match the initial dimensions. After the initial signal passed through the first convolution layer, the measurement dimensions were 1 × 4 × 256 pixels. Subsequently, a reshaping layer was applied to convert the signal from 1 × 4× 256 to 1 × 1024 × 1.
Initial reconstruction
The inception module is a powerful tool for learning signal features at multiple scales, making it an essential component of neutron ToF signal analyses. With a design concept that combines multiscale feature extraction, dimension reduction, and expansion, the neutron ToF signal is time-sequential, with different stages exhibiting multiscale characteristics. This technology can simultaneously capture features at different scales by using convolutional kernels of various sizes. This multiscale feature extraction enables the network to simultaneously focus on local and global information, thereby capturing signal characteristics.
Therefore, we highlighted the challenges in determining the optimal convolutions to achieve the best convolutional effect for the convolutional layers. It is vital to incorporate convolutional layers of various sizes into an inception module. The network learns features of different dimensions using convolution kernels of various sizes (1 × 3, 1 × 5, 1 × 7, and 1 × 13), thereby gathering information from distinct perceptual domains. This approach can significantly improve the network performance. Skip connections were used in convolution to prevent a decline in network performance and enhance the reconstruction accuracy. This powerful technique is illustrated in Fig. 4.

Moreover, the skip connections employed in signal processing do not increase the network parameters or computational complexity because they involve the addition of feature maps rather than multiplication. Therefore, skip connections are well suited for signal processing. The overall process is as follows:
When the inception module outputs four branches, feature maps are stacked together through a concatenation operation, and the integrated feature maps are mapped to be consistent with the original neutron ToF signal through a 1 × 1 convolution kernel. This process can be expressed as follows:
Recurrent neural network (RNN) is a deep neural network extensively employed for modeling time-series data. LSTM, a variant of the RNN, effectively addresses the gradient explosion or vanishing problems encountered in RNNs. To the best of the our knowledge, LSTM [27] has not yet been applied to the compression sampling of neutron ToF signals. In this regard, LSTM was used to extract local temporal features from the initial reconstruction signal output of the inception module, thereby improving the overall performance of signal reconstruction.
The LSTM unit comprised various components including a storage unit, an input gate, an output gate, and a forgetting gate. The activation and current-status updates for each gate were calculated as follows:
The LSTM network had a hidden layer of 250 cells, and the activation function was tan h, which is linear. The dense-layer output was 1024, and the final output dimensions were 1024 × 1. Finally, through the initial reconstruction module, the different captured features were integrated and mapped to keep the original neutron ToF signal dimensions consistent. This process can be expressed as follows:
Secondary reconstruction
Attention mechanisms have revolutionized computer vision, allowing targeted focus on critical regions of an image, while disregarding irrelevant parts. The application of attention mechanisms has led to significant progress in various aspects of computer vision, such as image classification, object detection, and semantic segmentation. The human brain has a similar cognitive process: quickly identifying crucial areas within complex visual scenes and processing them in greater detail. This cognitive process within the visual system is represented by the following equation:
Therefore, self-attention is a valuable tool for assisting models in understanding the connections between different positions within a sequence. It complements convolution by facilitating the modeling of long-range and multilevel dependencies among signal regions. The approach used by the model involves encoding each element of the sequence and analyzing the similarity between them to determine the most critical and contextually relevant elements.
Ultimately, the reconstruction network primarily comprises a self-attention module that plays a pivotal role in signal reconstruction by effectively capturing local temporal information and positional relationships. This technique enhances the quality of the reconstruction. This process is expressed as follows:
Performance metrics
The proposed ISACSNet was validated using a neutron ToF signal database. This database is divided into two parts: a training set that contains 15,000 signals with dimensions of 1024 and a testing set that comprises 100 signals with dimensions of 1024.
(1) The sampling ratio represents the degree of signal sampling during an experiment. The sampling ratio is defined as follows:
(2) The PRD is used to evaluate the quality of signal reconstruction, and it is defined as follows:
(3) The correlation coefficient reflects the degree between the original and reconstructed neutron ToF signals, similar to the variations per unit, and it is defined as follows:
Results and discussion
In this section, we evaluate the performance of the proposed ISACSNet for compressed sampling reconstruction. We also describe the datasets used for training and testing, along with some training details. A series of experiments were performed using the correlation coefficient, PRD, and reconstruction time as evaluating metrics for reconstructive performance. Subsequently, the reconstruction performance of ISACSNet was tested and compared with those of iterative hard thresholding (IHT) [29-31], basis pursuit (BP) [32-34], SAMP [35-38], temporal multiple measurement vector sparse bayesian learning (T-MSBL) [39-42], and focal underdetermined system solver (FOCUSS) [43-45] in different aspects. The above comparison algorithms involve iterative thresholding, convex optimization, greedy iteration, statistical class, and nonconvex optimization.
Dataset and training details
Our experiment used a neural network trained on 15,000 sets of neutron ToF signals, each with dimensions of 1024. Our final test signals consisted of 100 neutron ToF signals that were distinct from the training set but with the same signal dimensions.
The basic network parameters are described in Sect. 3. For other hyperparameters of Adam, we set the initial learning rate to 0.0005 and the first- and second-moment decay rates to 0.9 and 0.999, respectively. The epoch number of ISACSNet was set to 200, and the batch size was set to 16. We used the mean-squared loss as the loss function during training. Our proposed method was run on PyTorch 1.12.1 (a deep learning framework) on a Windows 10 64-bit operating system with an 8 GB RAM configuration. For other hyper-parameters of Adam, we set the exponential decay rates for the first- and second-moment estimates to 0.9 and 0.999, respectively. We trained our model for 100 epochs, and each epoch iterated 1400 times with a batch size of 64.
Comparison of different compression methods
This study used a different approach to compress signals by using sequential convolutional layers instead of a fixed random matrix. We validated the effectiveness of the compression module by comparing it with the Bernoulli random matrix, while keeping the rest of the model unchanged. Table 1 shows the performance of different compression methods using our compression method and the Bernoulli matrix for various traditional compressed-sampling reconstruction algorithms. We investigated five different sampling ratios from 1% to 50% using PRD as the assessment criteria to evaluate the performance of the compression methods. The results indicate that our compression method consistently outperformed the Bernoulli random matrix in different compressed sampling reconstruction algorithms, regardless of the sampling ratios. For instance, even with a low sampling ratio of 10% in the SAMP algorithm, the PRDs achieved using the Bernoulli random matrix and proposed compression method were 27.31% and 21.04%, respectively; the PRD of the proposed matrix is 6.27% lower than that of the Bernoulli random matrix for the SAMP algorithm.
| Algorithm | Sampling ratio (%) | ||||
|---|---|---|---|---|---|
| 1 | 5 | 10 | 25 | 50 | |
| IHT | 103.04/93.22 | 75.03/53.36 | 47.08/35.37 | 7.89/5.04 | 2.50/2.45 |
| BP | 106.11/93.54 | 66.79/36.99 | 31.64/15.30 | 4.68/4.24 | 2.06/2.05 |
| SAMP | 100/99.98 | 76.01/75.14 | 27.31/21.04 | 3.71/3.64 | 2.49/2.41 |
| T-MSBL | 99.14/99.13 | 91.25/90.01 | 28.93/26.17 | 3.84/3.19 | 2.60/1.99 |
| FOCUSS | 106.58/94.50 | 70.784/42.46 | 37.43/23.83 | 8.22/8.21 | 3.35/3.12 |
Figure 5 illustrates the PRD improvement rates of different algorithms at various sampling rates. The figure shows that the compression approach outperformed the Bernoulli matrix in terms of signal reconstruction accuracy at different sampling rates. This advantage is particularly evident at a relatively low sampling rate because our method is specifically tailored to the unique characteristics of neutron ToF signals, enabling it to capture the signal characteristics more effectively than the traditional universal measurement matrix.

Comparison with traditional CS methods
In this section, ISACSNet is compared with five traditional compressed sampling methods in terms of two aspects. The Bernoulli random matrix was selected as the measuring matrix for traditional compressed sampling methods. We used PRD and correlation coefficient to evaluate the errors between the different techniques and reconstructed neutron ToF signals. We also investigated the signal reconstruction times of different methods.
Evaluation of reconstruction performance
This section compares ISACSNet with different types of traditional reconstruction algorithms to determine the reconstruction accuracy. Using the Bernoulli random matrix as the measurement matrix, we employed PRD and correlation coefficient to assess the reconstruction error of the neutron ToF signal.
Figure 6 illustrates the average PRD of the neutron ToF signal test sets under different sampling rates for various methods. The x-axis represents the sampling rate, and the y-axis represents the average percentage of residuals. Our approach consistently achieved the lowest PRD values among the six methods, indicating that it consistently exhibited the lowest reconstruction errors and maintained a relative stability. Under the same sampling ratio conditions, the reconstruction performance of the proposed method surpassed that of the other methods. For instance, at a sampling ratio as low as 10%, our method outperformed (PRD value: 47.08%) other popular methods, such as IHT, BP, SAMP, T-MSBL, and FOCUSS, which exhibited PRD values of 31.64%, 27.31%, 28.93%, 37.43%, and 3.81%, respectively. As shown in Fig. 6, the performance of the DL-CS method is significantly better than those of the traditional compressed sampling methods at low sampling ratios. For example, at a sampling ratio of 1%, the PRD of the proposed method is only 9.17%.

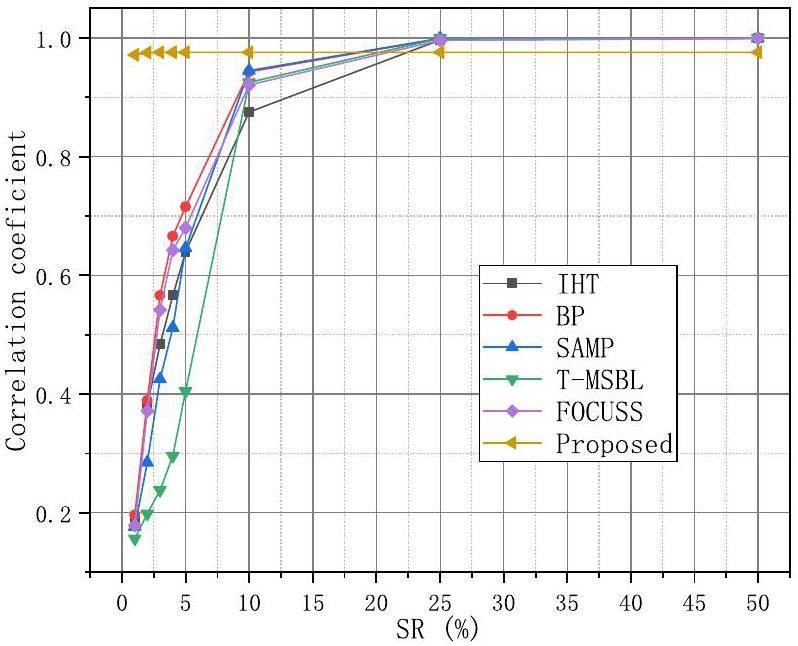
The correlation coefficients for various reconstruction algorithms when reconstructing a test signal of size 1024 with different sampling ratios are provided in Fig. 7 and Table 2. The proposed method achieved a correlation coefficient of 0.9715 at a sampling ratio of 1%, whereas the correlation coefficients for the other methods were all below 0.2. Additionally, as the sampling ratio increased, our approach tended to stabilize, maintaining correlation coefficient values above 0.9715, outperforming the other methods. This approach highlights its advantages at low sampling ratios, demonstrating its effectiveness in achieving good reconstruction results.
| Algorithm | Sampling ratio (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 10 | 25 | 50 | |
| IHT | 0.18654 | 0.38093 | 0.48366 | 0.56611 | 0.63952 | 0.87511 | 0.99654 | 0.99969 |
| BP | 0.19645 | 0.38931 | 0.56623 | 0.66587 | 0.71543 | 0.94302 | 0.99891 | 0.99979 |
| SAMP | 0.1764 | 0.28497 | 0.42514 | 0.51171 | 0.64611 | 0.94507 | 0.99928 | 0.99968 |
| T-MSBL | 0.1564 | 0.19842 | 0.23829 | 0.29563 | 0.4049 | 0.92543 | 0.99926 | 0.99966 |
| FOCUSS | 0.17838 | 0.37162 | 0.54205 | 0.64221 | 0.6799 | 0.92114 | 0.99646 | 0.99942 |
| Proposed | 0.9715 | 0.9753 | 0.9756 | 0.9757 | 0.9758 | 0.9759 | 0.976 | 0.976 |
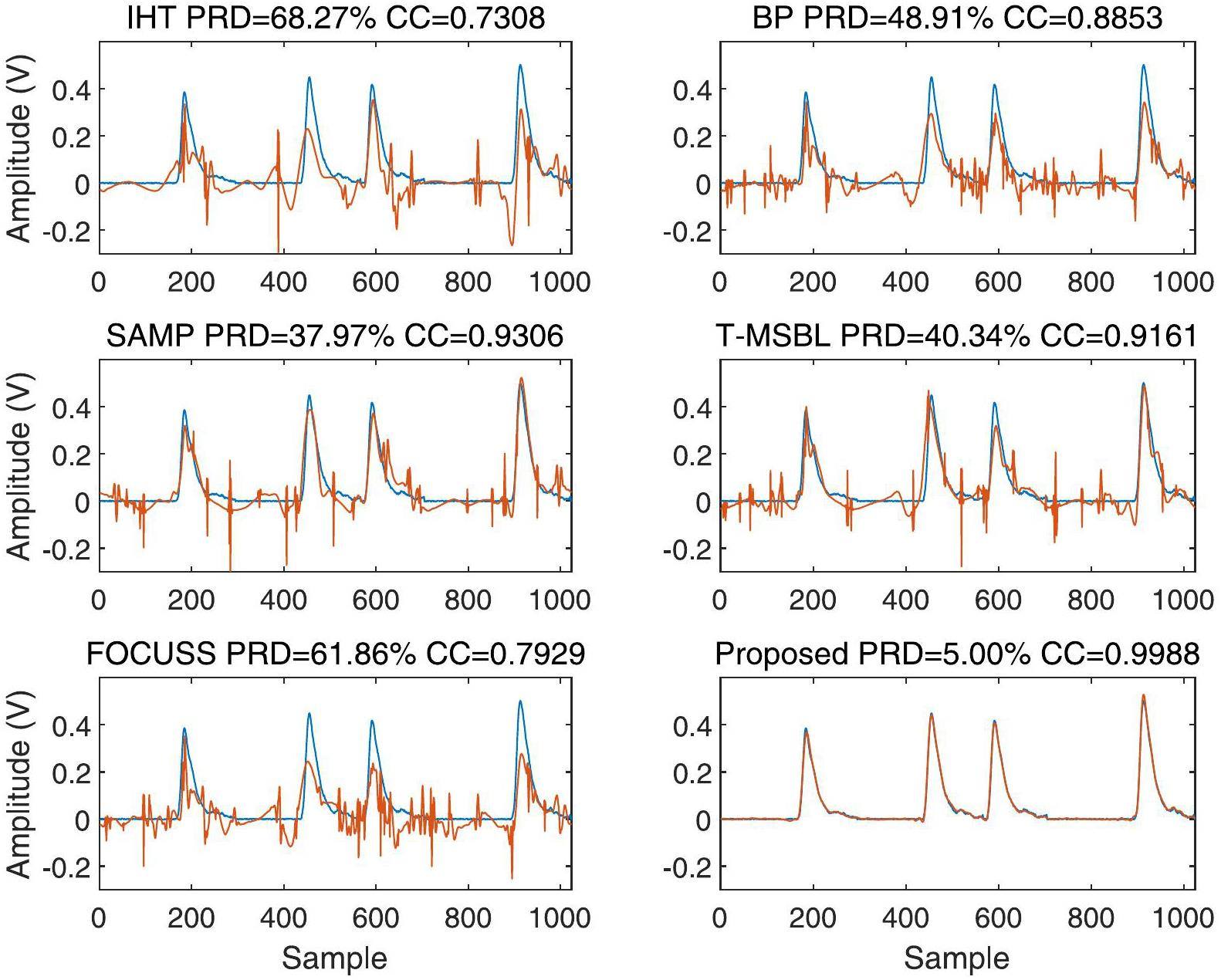
Figure 8 illustrates the original and reconstructed signals obtained using the different reconstruction methods at a sampling ratio of 10%. Our proposed reconstruction method outperformed traditional compressed sensing methods at a sampling rate of 10%, with a PRD of 5% and correlation coefficient of 0.998 (Fig. 8) and showing a better reconstruction performance with the reconstructed signal peaks closer to the original signal.
Investigation of reconstruction time
The reconstruction time of a signal plays a critical role in neutron ToF compressed sampling. We reconstructed 100 signals from the test set by using different algorithms at various sampling rates. We also evaluated the reconstruction performances of the different algorithms by comparing their average reconstruction times.
Table 3 and Fig. 9 show the reconstruction times of the different test algorithms at different sampling rates. As shown in Fig. 9, the proposed ISACSNet method had the shortest and most stable reconstruction times. As shown in Table 3, for sampling ratios in the range of 1–50%, the proposed method required a reconstruction time of 0.0108–0.0136 s.
| Algorithm | Sampling ratio (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 10 | 25 | 50 | |
| IHT | 0.00459 | 0.00534 | 0.00753 | 0.00878 | 0.01455 | 0.01845 | 0.12051 | 0.55543 |
| BP | 0.08245 | 0.09047 | 0.10416 | 0.12012 | 0.17071 | 0.38656 | 2.74138 | 22.87237 |
| SAMP | 0.0012 | 0.00258 | 0.009 | 0.0114 | 0.02011 | 0.0351 | 0.09959 | 0.17924 |
| T-MSBL | 0.06378 | 0.11472 | 1.05917 | 2.45918 | 5.33227 | 8.44691 | 7.56503 | 9.26934 |
| FOCUSS | 0.02076 | 0.02905 | 0.05986 | 0.10479 | 0.13794 | 0.52653 | 1.66972 | 2.06762 |
| Proposed | 0.0126 | 0.011 | 0.0108 | 0.0116 | 0.0136 | 0.0108 | 0.0111 | 0.0113 |

At the same sampling rate, our proposed algorithm could reconstruct 1024 signals, which is one to four orders of magnitude faster than the other methods. Our proposed method fully exploits the computational power of the graphics card, resulting in shorter processing times compared to traditional methods that rely solely on CPU computation. This advantage is evident because traditional iterative methods struggle with parallel transformation when solving optimization problems. Each layer of deep learning is designed for parallel computation. By leveraging the parallel computing power of the GPU, our method enables high-speed inference. Even if traditional generation selection methods can be parallelly modified and executed on a GPU, they cannot match the efficiency of deep learning owing to the numerous assumptions and limitations in their theoretical design. Therefore, the deep learning reconstruction network proposed in this study capitalizes on hardware parallelization, resulting in significantly shorter reconstruction times compared to traditional compressed sampling methods.
Conclusion
This study proposes a new approach for tackling two critical compressed sampling theory issues by incorporating deep learning techniques. This paper presents a sampling operator tailored for neutron ToF signals and a non-iterative fast reconstruction algorithm called ISACSNet. The proposed DNN model comprises four main modules: random projection, dimensional expansion, initial reconstruction, and secondary reconstruction. Unlike the traditional compressed sampling theory, which uses fixed random matrices, this model employs sequential convolutional layers to compress the neutron ToF signals. In addition, the model uses a modified inception block, LSTM, and self-attention to learn the mapping relationship between the measurements and original signal directly without requiring prior knowledge.
We performed extensive experiments on the neutron ToF signal database and demonstrated that our compression approach outperformed Bernoulli's in terms of PRD. Specifically, when the sampling ratio was below 10%, the PRD was 5%, and the correlation coefficient was 0.9988; furthermore, the reconstruction time was 0.0108 s. The PRD and correlation coefficient significantly exceeded those of the other methods. As the sampling ratio increased, the reconstruction time did not increase substantially with the signal length, thereby effectively improving the reconstruction efficiency of longer signals.
Our proposed deep-learning compression method outperformed traditional compressed sampling approaches, enabling accurate and fast reconstruction of the original signals at lower sampling frequencies when dealing with a large number of neutron ToF signals. Future studies will explore hardware structures suitable for neutron ToF signals and deploy them in ToF systems.
Measurement of the 235U(n,f) cross section relative to the 6Li(n,t) and 10B(n,a) standards from thermal to 170 keV neutron energy range at n_TOF
. Eur. Phys. J. A 55, 120 (2019). https://doi.org/10.1140/epja/i2019-12802-7Measurements of differential and angle-integrated cross sections for the 10B(n, α)7Li reaction in the neutron energy range from 1.0 eV to 2.5 MeV
. Chinese Physics C 43, 51-78 (2019). https://doi.org/10.48550/arXiv.1910.03373Neutron capture cross section of 232Th measured at the n_TOF facility at CERN in the unresolved resonance region up to 1 MeV
. Phys. Rev. C 73,Neutron capture measurement at the n TOF facility of the 204Tl and 205Tl s-process branching points
. J. Phys. Conf. Ser. 1668,Measurement of the neutron-induced total cross-sections of natPb from 0.3 eV to 20 MeV on the Back-n at CSNS
. Nucl. Sci. Tech. 35, 18 (2024). https://doi.org/10.1007/s41365-024-01370-zDetermination of the 232Th (n,γ) cross section from 10 to 200 keV at the Back-n facility at CSNS
. Eur. Phys. J. A 59, 224 (2023). https://doi.org/10.1140/epja/s10050-023-01126-0Developing time of flight polarized neutron capability at the China Spallation Neutron Source
. Nucl. Sci. Tech. 34, 146 (2023). https://doi.org/10.1007/s41365-023-01286-0On a Two-Mode Time-of-Flight Neutron Reflectometer for the DARIA Compact Neutron Source
. Nucl. Sci. Tech. 17, 818-825 (2023). https://doi.org/10.1134/S1027451023040171Miniaturized time-of-flight neutron spin flipper using a high-superconductor
. Nucl. Sci. Tech. 34, 145 (2022). https://doi.org/10.1007/s41365-022-01134-7Back-n white neutron facility for nuclear data measurements at CSNS
. J. Instrum. 12,Progress on The Time-of-Flight Ultra Small Angle Neutron Scattering Instrument at SNS
. J. Phys. Conf. Ser. 1021,Developing time-of-flight polarized neutron capability at the China Spallation Neutron Source
. Nucl. Sci. Tech. 34, 146 (2023). https://doi.org/10.1007/s41365-023-01286-0Highly efficient GEM-based neutron detector for China Spallation Neutron Source
. Nucl. Instrum. Meth. 953,Real-time digital trigger system for GTAF-II at CSNS Back-n white neutron source
. J. Instrum. 16, 10029 (2021). https://doi.org/10.1088/1748-0221/16/10/P10029neutron ToF spectroscopy measurement using a waveform digitizer
. Chinese Phys. C 40,Compressed sensing
. IEEE T. Inform. Theory 52, 1289-1306 (2006). https://doi.org/10.1109/TIT.2006.871582Compressive sampling
. Proc. Int. Cong. Math. 3, 1433-1452 (2006). https://doi.org/10.4171/022-3/69Compressed sampling for neutron ToF signals based on SAMP algorithm
. IEEE Sens. J. 24, 8517–8525 (2024). https://doi.org/10.1109/JSEN.2024.3360332Study on unfolding method of neutron spectrum of BSS (Bonner Sphere Spectrometer) based on compressed sensing
. Nucl. Instrum. Meth. A 925, 217-222 (2019). https://doi.org/10.1016/j.nima.2019.02.026A novel coded aperture for γ-ray imaging based on compressed sensing
. Nucl. Instrum. Meth. A 1021,MCNP-polimi simulation for the compressed-sensing based reconstruction in a coded-aperture imaging CAI extended to partially-coded field-of-view
. Nucl. Eng. Technol. 53, 199-207 (2021). https://doi.org/10.1016/j.net.2020.02.011Sensor position optimization for flux mapping in a nuclear reactor using compressed sensing
. Ann. Nucl. Energy 159,Development of a neutron spectroscopic system utilizing compressed sensing measurements
. EDP Sciences 106, 07002 (2016). https://doi.org/10.1051/epjconf/201610607002Investigation of fast neutron resonance transmission analysis based on the ultrashort pulsed electron beam-driven photoneutron source
. Nucl. Instrum. Meth. 14, P05004-p05004 (2019). https://doi.org/10.1088/1748-0221/14/05/P05004The restricted isometry property and its implications for compressed sensing
. C. R. Math. 346, 589-592 (2008). https://doi.org/10.1016/j.crma.2008.03.014Sequential convolution and runge-kutta residual architecture for image compressed sensing
. Compres. Sens. 12354, 232-248 (2020). https://doi.org/10.1007/978-3-030-58545-7_14Long short-term memory
. Neural Comput. 9, 1735-1780 (1997). https://doi.org/10.1162/neco.1997.9.8.1735Attentional control and the self: The self-attention network (SAN)
. Cogn. Neurosci. 7, 5-17 (2016). https://doi.org/10.1080/17588928.2015.1044427A new and improved quantitative recovery analysis for iterative hard thresholding algorithms in compressed sensing
. IEEE T. Inform. Theory 61, 2019-2042 (2014). https://doi.org/10.1109/TIT.2015.2399919Iterative hard thresholding for compressed sensing with partially known support
. INT Conf. Acoust Spee. 27, 4028-4031 (2011). https://doi.org/10.1109/ICASSP.2011.5947236An Iterative Hard Thresholding Algorithm based on Sparse Randomized Kaczmarz Method for Compressed Sensing
. Int. J. Comput. Intell. 17, 1850015.1-1850015.8 (2018). https://doi.org/10.1142/S1469026818500153Consistent Basis Pursuit for Signal and Matrix Estimates in Quantized Compressed Sensing
. IEEE Signal Proc. Let. 23, 25-29 (2015). https://doi.org/10.1109/LSP.2015.2497543Atomic decomposition by basis pursuit
. SIAM Rev. 43, 129-159 (2001). https://doi.org/10.1137/S1064827596304010ECG Signal Denoising and Reconstruction Based on Basis Pursuit
. Appl. Sci. 11, 1591 (2021). https://doi.org/10.3390/app11041591Fast sparsity adaptive multipath matching pursuit for compressed sensing problems
. J. Electron Imaging 26, 033007.1-033007.9 (2017). https://doi.org/10.1117/1.JEI.26.3.033007Compressive sensing of block-sparse signals recovery based on sparsity adaptive regularized orthogonal matching pursuit algorithm
. (2012). https://doi.org/10.1109/ICACI.2012.6463352Sparsity Adaptive Matching Pursuit Detection Algorithm Based on Compressed Sensing for Radar Signals
. Sensors 17, 1120.1-1120.14 (2017). https://doi.org/10.3390/s17051120Sparse Signal Recovery With Temporally Correlated Source Vectors Using Sparse Bayesian Learning
. IEEE J. Sel. Top. Signal 5, 912-926 (2011). https://doi.org/10.1109/JSTSP.2011.2159773Distributed Compressive Sensing via LSTM-Aided Sparse Bayesian Learning
. Signal Process. 176, 107656.1-107656.33 (2020). https://doi.org/10.1016/j.sigpro.2020.107656A compressed sensing image reconstruction algorithm based on block sparse bayesian learning and multiple measurement vector
. ICIC Express Letters 9, 2009-2014 (2015).k-t FOCUSS: a general compressed sensing framework for high resolution dynamic MRI
. Magn. Reson. Med. 61, 103-116 (2009). https://doi.org/10.1002/mrm.21757Improved FOCUSS method for reconstruction of cluster structured sparse signals in radar imaging
. Science China (Information Sciences) 55, 1776-1788 (2012). https://doi.org/10.1007/s11432-012-4628-1Fully cooperative and distributed focal underdetermined system solver compressive sensing recovery algorithm for wireless sensor networks
. Int. J. Commun. Syst. 35,The authors declare that they have no competing interests.

