Calculation process

For infinite bunches, the space charge forces on each bunch can be calculated based on the reference bunch. Owing to the space symmetry, the forces on other bunches are identical to those on the reference bunch. In the axial direction, the space charge forces cancel each other. However, in the radial direction, the forces superimpose, leading to faster bunch radius growth compared with a single-bunch.

First, an analytical expression was determined for the single-bunch space charge forces which was then solved for infinite bunches. Furthermore, when the bunch train expanded so that adjacent bunches overlapped, a mirror folding method was employed to confine it to the original spacing. To improve the computing performance, the macroparticle and PIC methods were used. Additionally, the six-dimensional phase space was simplified into a four-dimensional phase space, according to the axial symmetry of the bunches. The calculation process of the algorithm is shown in Fig. 1.

Fig. 1Full-screen View

Calculation process

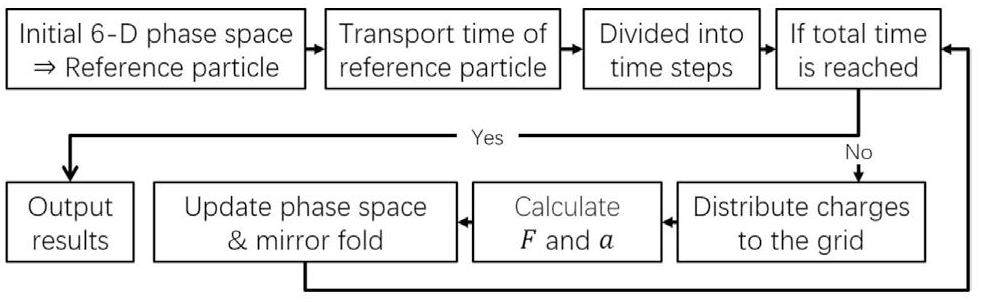
A brief description of the calculation process is as follows:

(1) Input file and reference particle Using the input initial six-dimensional phase space of N macroparticles, convert the x, y, z coordinates to r,z coordinates in the polar coordinate system, ignoring the position and velocity in the ϕ direction. Define a reference particle at the average position of the bunch.

(2) Transport time and iteration steps As the reference particle is in the center of the bunch, it is not affected by space charge forces. Considering its initial speed and the external electromagnetic fields, solve its total transport time and then divide it into iteration time steps. For the calculation of the entire bunch, the computing ends only if the total transport time is reached.

(3) First system conversion Before each iteration, convert the laboratory system into the bunch system, as the calculation of space charge forces is easier.

(4) Grid division According to the position distribution of particles, determine the upper and lower bounds of the uniform grid by considering their maximum value, average value, and standard deviation. Distribute macro-particle charges to each lattice point of the grid by linear interpolation. Extreme macro-particles with positions exceeding the grid range are assigned to the nearest grid boundary point.

(5) Space charge forces calculation Calculate the total space charge forces on (Nr+1)× (Nz+1) grid points based on the ring-charge model. Each macroparticle uses the value of the closest grid point.

(6) Second system conversion Convert the space charge forces in the bunch system back into the laboratory system.

(7) Iteration update Considering both the space charge forces and external electromagnetic fields, for each macroparticle, solve their acceleration and update their positions and velocities to obtain their new phase space in the laboratory system.

(8) Repeat steps (3) to (7) iteratively until the results are obtained.

The algorithm uses the Euler method for iterations because the relationship between the accelerations and positions is sufficiently complex that the commonly used fourth-order Runge-Kutta method [34, 35] is unsuitable. Although the Euler method is known to have relatively large errors [36], the overall error of the PIC algorithm was found to be acceptable, as shown in the results and discussion sections.

PIC method and grid division

To simplify the computational process, a macroparticle approach was employed in which a certain number of electrons were treated as a single entity.

Owing to the interdependence between the positions and the resulting space charge forces, ordinary differential equations (ODEs) could not be used directly. Numerical calculations and time-based iterations are typically used to address this issue. Within each iteration, a single macroparticle receives space charge forces from the other (N-1) macroparticles. Consequently, the complexity of the algorithm for each iteration is approximately N².

The PIC method was utilized to effectively reduce algorithm complexity [37, 38]. It divides the spatial region into a grid and allocates the quantities of particles, such as the charge and force, to the grid points for calculation. This reduces the computational complexity of each iteration from N² to $N_1^2{N}_2^2$, where N₁ and N₂ represent the number of grids in both directions.

In the multi-bunch model, a key assumption is that the bunch exhibits angular symmetry, allowing the velocity of the bunch in the azimuthal direction (ϕ) to be neglected. This simplification enables the establishment of an r-z grid in a cylindrical coordinate system. The radial direction (r) represents the transverse dimensions of the bunch, and the vertical axis (z) represents the longitudinal dimensions. The radial grid starts at r=0 and does not include negative parts.

In this study, uniform grid division was employed. When a macroparticle charged q fell within the grid region, its charge was linearly distributed to four nearby lattice points, and the space charge forces were calculated using only the parameters on the grid. Note that as the bunches expanded over time, it was necessary to update the grid.

Analytical calculation of a single-bunch

In this section, analytical expressions are obtained for the space charge forces of a single-bunch. Each point in the r-z grid represents a ring charge (except r=0, which is a point charge). In this model, the Coulomb repulsion of the ring charge q₂ toward the point particle q₁ is solved, as shown in Fig. 2. The left side shows the projection on the plane z=0, and the right side shows the relationship in space.

Fig. 2Full-screen View

(Color online) Repulsion between the microelement dq₂ and particle q₁

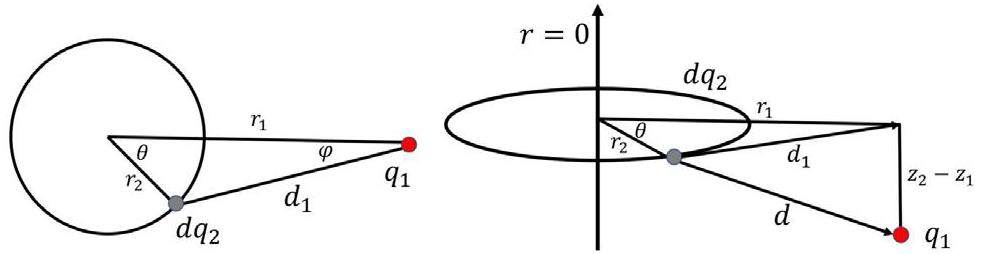
Taking r₁ as the positive direction of the axis x, the cylindrical coordinate system can be transformed into a spatial rectangular coordinate system. In Fig. 2, the microelement $d{q}_2=q_{2}dl/2\pi r_2=q_{2}d\theta /2\pi$, where dl is the length of the microelement. The coordinate of the microelement is (r₂, r₂, z₂), whereas the coordinate of the point particle is (r₁, 0, z₁). The distance between them is: $d=\sqrt{{\left(r_1-r_2\cos \theta \right)}^2+{\left(r_2\sin \theta \right)}^2+{\left(z_1-z_2\right)}^2}$ (1) The Coulomb repulsions in the r and z directions, respectively, are as follows: $d{F}_r=\frac{q_{1}d{q}_2}{4\pi {\epsilon }_0}\frac{1}{d^2}\frac{\left(r_1-r_2\cos \theta \right)}{d}$ (2a) $d{F}_z=\frac{q_{1}d{q}_2}{4\pi {\epsilon }_0}\frac{1}{d^2}\frac{\left(z_1-z_2\right)}{d}$ (2b) By integrating along the ring, the forces in both directions are obtained as follows: ${F^{\prime }}_r=\frac{q_1{q}_2}{4\pi {\epsilon }_0}{I}_1$ (3a) ${F^{\prime }}_z=\frac{q_1{q}_2}{4\pi {\epsilon }_0}{I}_2$ (3b) where $I_1={\displaystyle {\int }_0^{\pi }}\frac{\left(r_1-r_2\cos \theta \right)}{\pi {\left[A_r+{\left(z_1-z_2\right)}^2\right]}^{\frac{3}{2}}}\text{d}\theta$ (3c) $I_2={\displaystyle {\int }_0^{\pi }}\frac{\left(z_1-z_2\right)}{\pi {\left[A_r+{\left(z_1-z_2\right)}^2\right]}^{\frac{3}{2}}}\text{d}\theta$ (3d) $A_r={\left(r_1-r_2\cos \theta \right)}^2+{\left(r_2\sin \theta \right)}^2$ The integrations are used in the subsequent calculation of infinite bunches. The results are as follows: $I_1=\frac{A_{2}ellipticE\left(A_1\right)+A_{3}ellipticK\left(A_1\right)}{\pi A_4}$ (4) $I_2=\frac{2\left(z_1-z_2\right)ellipticE\left(A_1\right)}{\pi A_4}$ (5) where $\begin{array}{ll}{A}_1\hfill & =\frac{4r_1{r}_2}{{\left(r_1+r_2\right)}^2+{\left(z_1-z_2\right)}^2}\hfill \\ A_2\hfill & =r_1{}^2-r_2{}^2-{\left(z_1-z_2\right)}^2\hfill \\ A_3\hfill & ={\left(r_1-r_2\right)}^2+{\left(z_1-z_2\right)}^2\hfill \\ A_4\hfill & =r_1{A}_3\sqrt{{\left(r_1+r_2\right)}^2+{\left(z_1-z_2\right)}^2}\hfill \end{array}$ ellipticE and ellipticK are elliptic integral functions which are time-consuming to calculate. The approximation methods are discussed subsequently in this paper.

Analytical calculation of infinite bunches

To calculate the space charge forces in the radial direction for infinite bunches, the ring charges are divided into groups. In each group, the r coordinates of the ring charges are the same, whereas their z coordinates differ by distance D, which is equal to the spacing between adjacent bunches.

By replacing $\text{Δ}z=z_1-z_2$ in equations 3(c) and (d) with $\text{Δ}z=z_1-z_2+kD(k=\mathrm{0,}\mathrm{1,}\mathrm{2,}\dots )$, the space charge force of any ring charge group towards the point charge in the reference bunch can be obtained. By adding the forces of each group, the following expression for the radical force is obtained: $E_{r\mathrm{,}k}={\displaystyle \sum _{k=-\infty }^{+\infty }}\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{2}{2\pi }{\displaystyle {\int }_0^{\pi }}\frac{\left(r_1-r_2\cos \theta \right)}{{\left[A_r+\text{Δ}{z}_k{}^2\right]}^{3/2}}\text{d}\theta$ (6) This expression can be simplified as follows: $E_{r\mathrm{,}k}=\frac{q_1{q}_2}{4{\pi }^2{\epsilon }_0}{\displaystyle {\int }_0^{\pi }}{\displaystyle \sum _{k=-\infty }^{+\infty }}\frac{c}{{\left[a+{\left(k-b\right)}^2\right]}^{\frac{3}{2}}}\text{d}\theta$ (7) where $\begin{array}{l}a=A_r/D^2\ge 0\\ b=\left(z_2-z_1\right)/D\in \left[-\mathrm{1,1}\right]\\ c=\left(r_1-r_2\cos \theta \right)/D^3\\ z_1\mathrm{,}{z}_2\in \left[-D/\mathrm{2,}D/2\right]\end{array}$ The sum of the infinite series is calculated as follows: $S_{\text{total}}={\displaystyle \sum _{k=-\infty }^{+\infty }}\frac{c}{{\left[a+{\left(k-b\right)}^2\right]}^{\frac{3}{2}}}$ (8) where a >0, b∈[-1,1]. This summation can be proven to converge using the following method: $\begin{array}{ll}\left|\frac{S_{\text{total}}}{c}\right|=\hfill & {\displaystyle \sum _{k=-\infty }^{+\infty }}\frac{1}{{\left[a+{\left(k-b\right)}^2\right]}^{\frac{3}{2}}}\le {\displaystyle \sum _{k=-\infty }^{+\infty }}\frac{1}{{\left(k-b\right)}^3}\hfill \\ \hfill & \le \frac{1}{{\left\{b\right\}}^3}+{\displaystyle \sum _{k=1}^{+\infty }}\frac{2}{k^3}<\frac{1}{{\left\{b\right\}}^3}+\frac{5}{2}\hfill \end{array}$ where {b} denotes the fractional proportion of b.

Equation (8) does not have an analytical solution. However, if this summation is approximated as its corresponding integral, the following simple solution can be obtained: $\begin{array}{ll}{S}_{\text{int}}=\hfill & {\displaystyle {\int }_{-\infty }^{+\infty }}\frac{c}{{\left[a+{\left(k-b\right)}^2\right]}^{\frac{3}{2}}}\text{d}k\hfill \\ \hfill & =\frac{2c}{a}\hfill \end{array}$ (9) When $\left|k\right|$ is small, the relative error between the series and integral is large. Therefore, rather than directly using the entire integral for the approximation, it is only used when $\left|k\right|$ is large. For $\left|k\right|\le k_0$, the original series is used. The final expression of the approximation is: $\begin{array}{ll}{S}_{\text{ap}}=\hfill & {\displaystyle \sum _{k=-k_0+0.5}^{k_0-0.5}}\frac{c}{{\left[a+{\left(k-b\right)}^2\right]}^{\frac{3}{2}}}\hfill \\ \hfill & +S_{\text{int}}-{\displaystyle {\int }_{-k_0}^{+k_0}}\frac{c}{{\left[a+{\left(k-b\right)}^2\right]}^{\frac{3}{2}}}\text{d}k\hfill \end{array}$ (10) where k₀ is a half integer. For example, when k₀=2.5, the interval to be eliminated by the integral approximation is [-2.5, 2.5], which is replaced by the original series of the region $k\in \left[-\mathrm{2,}2\right]$.

The approximation error is determined using the following method. In the bunch system, the bunch shape factor $A=R/\gamma L_{\text{lab}}$. Suppose that the radius and length of a single-bunch are comparable; A is close to 1 thus, in equation (11), $a\in \left[\mathrm{0,}1\right]$ and $b\in \left[-\mathrm{1,}1\right]$. Under such circumstances, when k₀=1.5, the maximum relative error between S_ap and S_total is 3%; when k₀=2.5, it is reduced to 0.5%. It is important to note that when θ varies from 0 to π, a and b change within their respective ranges and the average relative error is significantly smaller than the maximum error. Therefore, after integrating θ into $\left[\mathrm{0,}\pi \right]$, the relative error in the integral approximation is small. As k₀ increases, the relative error of the algorithm decreases significantly. However, the computational workload for series summation increases. For example, when k₀=2.5, the computational workload of the multi-bunch PIC algorithm is approximately $2k_0+2=7$ times that of the single-bunch algorithm.

In equation (10), S_int is a simple expression derived from equation (9), and the series part of $\left[-k_0+\mathrm{0.5,}{k}_0-0.5\right]$ can be obtained by applying the single-bunch algorithm 2k₀ times. Thus, the focus of the calculation is the integration of the last term. Integrating θ yields: $\begin{array}{ll}{I}_k\hfill & ={\displaystyle {\int }_0^{\pi }}{\displaystyle {\int }_{-k_0}^{+k_0}}\frac{c}{a+{\left(k-b\right)}^2{}^{\frac{3}{2}}}\text{d}k\text{d}\theta \hfill \\ \hfill & ={\displaystyle {\int }_0^{\pi }}\frac{c}{a}\frac{k_0-b}{\sqrt{a+{\left(k_0-b\right)}^2}}+\frac{k_0+b}{\sqrt{a+{\left(k_0+b\right)}^2}}\text{d}\theta \hfill \end{array}$ Substituting a, b, c yields: $\begin{array}{ll}{I}_k\hfill & ={\displaystyle \sum _{i=1}^2}{\displaystyle {\int }_0^{\pi }}\frac{\left(r_1-r_2\cos \theta \right)\text{Δ}{z}_i}{A_{r}D{\left[A_r+\text{Δ}{z}_i{}^2\right]}^{1/2}}\text{d}\theta \hfill \\ \hfill & =I_{k1}+I_{k2}\hfill \end{array}$ The calculation result of the integral is: $I_k=\{\begin{array}{c}\frac{1}{D}{\displaystyle \sum _{i=1}^2}\frac{\text{Δ}{z}_i}{\sqrt{4r^2+\text{Δ}{z}_i^2}}\frac{ellipticK\left(\frac{4r^2}{4r^2+\text{Δ}{z}_i^2}\right)}{r}\mathrm{,}{r}_1=r_2=r;\\ \frac{1}{D}{\displaystyle \sum _{i=1}^2}\text{Δ}{z}_i\frac{\left(r_1+r_2\right)ellipicK\frac{4r_1{r}_2}{{\left(r_1+r_2\right)}^2+\text{Δ}{z}_i^2}+\left(r_1-r_2\right)ellipicPi\left[\frac{4r_1{r}_2}{{\left(r_1+r_2\right)}^2}\mathrm{,}\frac{4r_1{r}_2}{{\left(r_1+r_2\right)}^2+\text{Δ}{z}_i^2}\right]}{r_1\left(r_1+r_2\right)\sqrt{{\left(r_1+r_2\right)}^2+\text{Δ}{z}_i^2}}\mathrm{,}\\ r_1\ne r_2\end{array}$ (11) where $\text{Δ}{z}_1=z_1-z_2+k_{0}D\mathrm{,}\text{Δ}{z}_2=z_1-z_2-k_{0}D$.

Utilizing equations (7)-(11), the radial analytical expressions of the space charge forces are obtained for infinite bunches in the bunch system.

In the radial direction, the space charge forces from different bunches are in the same orientation, so each term in the sum of the series is positive, which would be suitable for approximation by integration. However, in the longitudinal direction, these forces cancel. Consequently, this integration is zero, which may lead to unacceptable errors. Therefore, an alternative method was used to approximate the summation. In the longitudinal direction, equation (8) becomes: $S_{\text{total}-\text{z}}={\displaystyle \sum _{k=-\infty }^{+\infty }}\frac{k-b}{{\left[a+{\left(k-b\right)}^2\right]}^{\frac{3}{2}}}$ (12) where $a>\mathrm{0,}b\in -\mathrm{1,1}$. When k≥2, equation (12) is expanded based on 1/k as follows: $S_k=\frac{1}{k^2}\frac{\left(1-\frac{b}{k}\right)}{{\left[{\left(1-\frac{b}{k}\right)}^2+\frac{a}{k^2}\right]}^{\frac{3}{2}}}$ $S_{-k}=-\frac{1}{k^2}\frac{\left(1+\frac{b}{k}\right)}{{\left[{\left(1+\frac{b}{k}\right)}^2+\frac{a}{k^2}\right]}^{\frac{3}{2}}}$ $\begin{array}{c}{S}_{\pm k}=S_k+S_{-k}=\frac{4b}{k^3}+\frac{4\left(-3ab+3b^3\right)}{k^5}\\ +\frac{3}{2}\frac{\left(15a^{2}b-4a{b}^3+8b^5\right)}{k^7}+O\left(\frac{1}{k^9}\right)\end{array}$ (13) where $a=\left(r_1^2+r_2^2-2r_1{r}_2\right)/D^2\ge 0$. As a only appears in the numerators, after substituting a and b, equation (13) can be simply integrated with θ on 0, π. Similar to the previous section, the original series is used when |k| <k₀ and its Taylor expansions are used for the remaining part. Considering that ${\displaystyle {\sum }_{k=1}^{+\infty }\frac{1}{k^i}}$, i=3, 5, 7 are mathematically known constants, after summing k on $\left[k_0\mathrm{,}+\infty \right)$ for equation (13), the approximate expression of equation (12) is obtained.

Calculations are conducted in the bunch system, where $D_{\text{bunch}}=\gamma D_{\text{lab}}$, such that $a_{\text{max}}={\left(\frac{R}{\gamma D_{\text{lab}}}\right)}^2=A_D^2$. When $a\in \mathrm{0,}\mathrm{1,}b\in \left[-\mathrm{1,}1\right]$, a uniform sample is taken to evaluate the approximation effect, and the results validate the approximation method. When k₀=2.5, $rms\left(I_{kz}\right)=35.72$ whereas $rms\left(\text{Δ}{I}_{kz}\right)=0.0035$, where Ikz is the value after integrating equation (12) with θ, summed by k cutting at |k|=100. $\text{Δ}{I}_{kz}$ is the error between Ikz and its approximation. When k₀ becomes 3.5, $rms\left(\text{Δ}{I}_{kz}\right)$ decreases to 0.00048. However, by analyzing quation (13), such an approximation is sensitive to a and k₀. A large a may significantly reduce the accuracy. Consequently, $k_0\ge \sqrt{2}{A}_D$ to maintain the approximation effect.

When calculating the space charge forces, k₀ is taken as $k_{0x}$ and $k_{0z}$, respectively, in different directions to balance the accuracy and efficiency of the algorithm.

Acceleration in a laboratory system with space charge forces and external fields

Thus far, the radial and longitudinal space charge forces have been determined in the bunch system. Before converting from a bunch to a laboratory system, the infinite-bunch model is considered, in which the Lorentz force in the radial direction is opposite to the Coulomb repulsion and differs in size by a factor β². Therefore, the total radial force in the laboratory system is $1/{\gamma }^2$ times the Coulomb repulsion in the bunch system [39]. The expression for the radial force is: $\begin{array}{ll}{F}_r\hfill & =\frac{qIr}{2\pi {\epsilon }_0\beta c{a}^2}\left(1-{\beta }^2\right)\hfill \\ \hfill & =\frac{qIr}{2\pi {\epsilon }_0\beta c{a}^2}\frac{1}{{\gamma }^2}\hfill \end{array}$ (14) This result is used in the subsequent Results and Discussion sections. It is assumed that the laboratory system is a S system, whereas the bunch system is a S' system, which moves at a speed $u=\beta c$ in direction z. According to the relativistic transformation, the forces in the laboratory system are as follows: $\{\begin{array}{c}{F}_r=\frac{{F^{\prime }}_r}{\gamma }+F_{r\mathrm{,}\text{ex}}\\ F_z={F^{\prime }}_z+F_{z\mathrm{,}\text{ex}}\end{array}$ (15) where $F_{r\mathrm{,}\text{ex}}\mathrm{,}{F}_{z\mathrm{,}\text{ex}}$ are the external electromagnetic field forces; ${F^{\prime }}_r\mathrm{,}{F^{\prime }}_z$ are the space charge forces in the bunch system; and $F_r\mathrm{,}{F}_z$ are the total forces in the laboratory system.

The expression for the acceleration in the case of relativity is: $\overrightarrow{a}=\frac{\overrightarrow{F}}{\gamma m_0}-\frac{\overrightarrow{v}\left(\overrightarrow{v}\cdot \overrightarrow{F}\right)}{\gamma m_0{c}^2}$ (16) Using the acceleration in equation (16), the particle phase space is updated after each iteration.

Mirror method for overlapping bunches

As the bunches expand such that adjacent bunches overlap, a mirroring technique is used, as shown in Fig. 3. The overflowing part outside the bunch interval is folded back into the original bunch range using mirror symmetry. This ensures consistency in the grid and the algorithm used in the previous sections. The mirroring process involves reflecting macroparticle positions longitudinally and reversing their longitudinal velocities, while keeping their transverse positions and velocities constant. After updating the phase spaces of macroparticles in each iteration, a mirror operation is performed.

Fig. 3Full-screen View

(Color online) Mirror Method

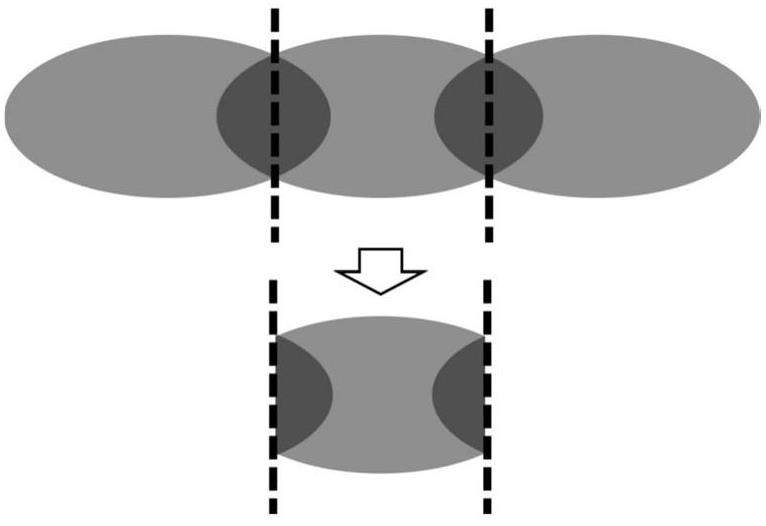
This operation serves two purposes. First, it restricts the longitudinal length of the bunches to the bunch interval D, simplifying the longitudinal grid update. Second, it focuses on the calculation of a single reference bunch rather than computing the complex effects of overlapping bunches.

Approximation of elliptic integral functions

The analytical expressions for the space charge forces involve three elliptic integral functions: $ellipticE\left(x\right)\mathrm{,}ellipticK\left(x\right)$, and $ellipticPi\left(x\mathrm{,}y\right)$. However, their computational complexity is high, and existing approximations often rely on iterative methods, resulting in a significant computation time [40, 41]. This section introduces simple and fast approximation methods for elliptical integrals with improved accuracy.

For convenience: $x=\frac{4r_1{r}_2}{{\left(r_1+r_2\right)}^2+{\left(z_1-z_2+kD\right)}^2}$ (17) where x is the argument of the functions ellipticE and ellipticK. Note that when calculating the space charge forces on the grid points, the macroparticle under the forces is treated as a point charge. Therefore, the self-force of one grid point is neglected, which means that in equation (17), ${\left(r_1-r_2\right)}^2+{\left(z_1-z_2\right)}^2\ne 0$.

The function ellipticE is a complete elliptic integral of the second type, which is smooth when $x\in \left[\mathrm{0,}1\right]$. Consequently, a fourth-order polynomial can be used to approximate the function. As shown in Fig. 4(a), the blue line depicts the function ellipticE in its defined domain. The orange line describes the relative error of the polynomial approximation and original function, which mainly ranges from 0.2%. Only when x is close to 1, the relative error increases to 1%. The approximation has a root mean square error (RMSE) of 0.0012.

Fig. 4Full-screen View

(Color online) Fit of elliptic integrals

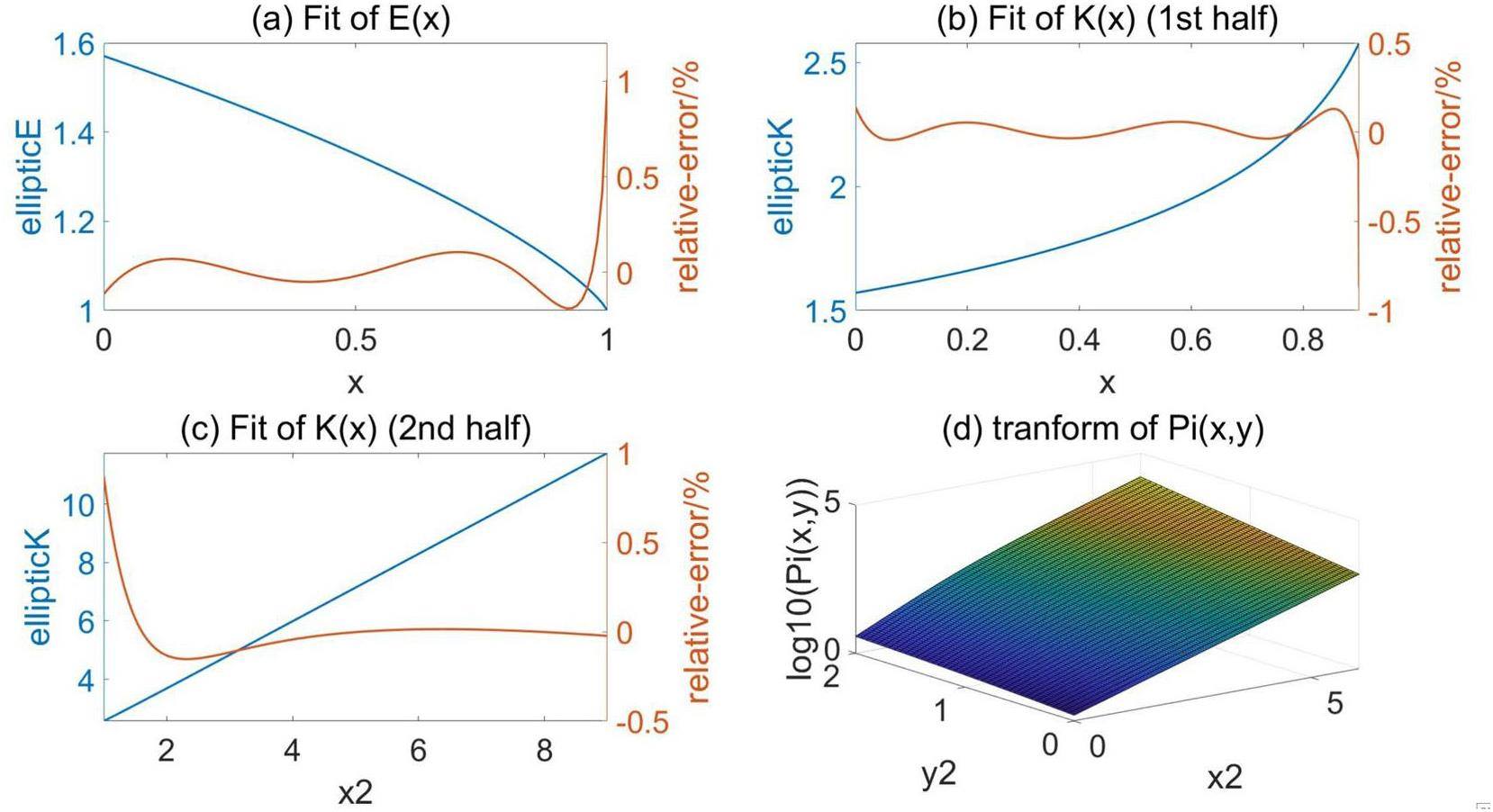
The function ellipticK cannot be directly approximated by polynomials, because when $x\to \mathrm{1,}ellipticK\left(x\right)\to +\infty$. Thus, a sixth-order polynomial is used to fit it when $x\in \left[\mathrm{0,}0.9\right]$, which has a RMSE of 0.00089. As shown in Fig. 4(b), the blue line represents the value of the function on $\left[\mathrm{0,}0.9\right]$, whereas the orange line represents the relative error of the approximation, which varies within 0.2%. Subsequently, a separate method is used for the function ellipticK when $x\in \left[\mathrm{0.9,}1\right]$.

In equation (17), x cannot reach the upper limit 1. Deriving the maximum value of x is conducive to constructing an approximation. When calculating the space charge forces on uniform grid points: $\begin{array}{l}{r}_1=N_1\text{Δ}r\mathrm{,}{r}_2=N_2\text{Δ}r\mathrm{,}{N}_1\mathrm{,}{N}_2=\mathrm{0,}\mathrm{1,}\mathrm{2,}\dots \mathrm{,}{N}_r\\ z_1=N_3\text{Δ}z\mathrm{,}{z}_2=N_4\text{Δ}z\mathrm{,}{N}_3\mathrm{,}{N}_4=\mathrm{0,}\mathrm{1,}\mathrm{2,}\dots \mathrm{,}{N}_z\end{array}$ where $N_r\mathrm{,}{N}_z$ are the number of grids in both directions, $\text{Δ}r$ and $\text{Δ}z$ are their unit lengths, $m=\text{Δ}r/\text{Δ}z$. To estimate the maximum value of x, k=0 is included in equation (17): $x=\frac{4N_1{N}_2}{{\left(N1+N_2\right)}^2+\frac{{\left(N_3-N_4\right)}^2}{m^2}}$ (18) Variable substitution is then performed as follows: $\begin{array}{ll}{x}_1\hfill & =\frac{1}{1-x}\hfill \\ \hfill & =\frac{{\left(N_1+N_2\right)}^2+\frac{{\left(N_3-N_4\right)}^2}{m^2}}{{\left(N_1-N_2\right)}^2+\frac{{\left(N_3-N_4\right)}^2}{m^2}}\hfill \end{array}$ (19) When $x\to \mathrm{1,}{x}_1\to \infty \mathrm{,}ellipticK\left(x\right)\to \infty$, the variable can be changed from x to x₁ and the function $K\left(x\right)$ can be constructed for approximation. Note that ${\left(N_1-N_2\right)}^2+{\left(N_3-N_4\right)}^2\ne 0$. To let x₁ reach its maximum value, there are only two possible situations:

(a) $N_1=N_2=N_r\mathrm{,}\left|N_3-N_4\right|=1\Rightarrow x_1=\frac{1}{1-x}={\left(2N_{r}m\right)}^2+1$

(b) $N_3=N_4\mathrm{,}\left|N_1-N_2\right|=\mathrm{1,}\min \left(N_1\mathrm{,}{N}_2\right)=N_r\Rightarrow x_1=\frac{1}{1-x}={\left(2N_r-1\right)}^2+1$

For simplicity, m=1 is considered when: $\text{max}\left(x_1\right)={\left(2N_r\right)}^2+1\approx 4N_r^2$ (20) Taking Nr=30, $\text{max}\left(x_1\right)\approx 3600$. If $\text{max}\left(x_1\right)\approx {10}^6$, then Nr can be set to 500, which is sufficient for most PIC algorithms.

After converting the variable from x to x₁, the function $ellipticK\left(x\right)-x_1$ is fitted well with the power function. It follows that: $x_2=lg\left(x_1\right)=\text{lg}\left[1/\left(1-x\right)\right]$ (21) Consequently, $x\in \left[1-{10}^a\mathrm{,1}-{10}^b\right]\Rightarrow x_2\in \left[a\mathrm{,}b\right]$. $x_2\in \left[\mathrm{1,}9\right]$ is used with evenly spaced x₂ sequences as independent variables. Although the function $ellipticK\left(x\right)-x$ is difficult to approximate directly, the function $ellipticK\left(x\right)-x_2$ is close to a straight line, as shown by the blue line in Fig. 4(c). Therefore, a second-order polynomial is used for the approximation, which has a RMSE of 0.0041. The orange line indicates the relative error.

The total expression of this approximation is: $K(x)={\displaystyle \sum _{i=1}^3}{p}_i*\text{lg}{\left[1/\left(1-x\right)\right]}^{3-i}$ If a finer grid is required, a further approximation can be achieved by involving a larger x₂ using the same method.

The third function ellipticPi is approximated in a manner similar to that for ellipticK. ellipticPi is the complete elliptic integral of the third type, which is expressed as: $\begin{array}{ll}ellipticPi\left(x\mathrm{,}y\right)\hfill & =Pi\left(x\mathrm{,}y\right)=Pi\left(x\mathrm{,}\frac{\pi }{2}|y\right)\hfill \\ \hfill & ={\displaystyle {\int }_0^{\pi /2}}\frac{1}{\left(1-x{{\displaystyle \sin }}^2\theta \right)\sqrt{1-y{{\displaystyle \sin }}^2\theta }}\text{d}\theta \hfill \end{array}$ The function $Pi\left(x\mathrm{,}y\right)$ is constructed to approximate $ellipticPi\left(x\mathrm{,}y\right)$. After converting the parameters from x, y, $Pi\left(x\mathrm{,}y\right)$ to x₂, y₂, Z, the function $Z\left(x\mathrm{,}y\right)-x_2\mathrm{,}{y}_2$ can be fitted well with the following polynomials: $\begin{array}{c}{x}_2=\lg \left(x_1\right)=\text{lg}\left[1/\left(1-x\right)\right]\\ y_2=\lg \left(y_1\right)=\text{lg}\left[1/\left(1-y\right)\right]\\ Z=\lg \left[Pi\left(x\mathrm{,}y\right)\right]\\ x=\frac{4r_1{r}_2}{{\left(r_1+r_2\right)}^2}\mathrm{,}{r}_1\ne r_2\\ y=\frac{4r_1{r}_2}{{\left(r_1+r_2\right)}^2+{\left(z_1-z_2+k_{0}D\right)}^2}<x<1\end{array}$ (22) Considering that $k_{0}D$ in the denominator restricts the maximum value of y, $\max \left(x_2\right)=6$ and $\max \left(y_2\right)=2$ are used, when the function $Z\left(x\mathrm{,}y\right)-x_2\mathrm{,}{y}_2$ is close to a flat surface, as shown in Fig. 4(d). This can be fitted well by a third-order polynomial with a RMSE of 0.0021.

By replacing the time-consuming calculations of the three elliptic integrals with simpler and faster approximation computations, the algorithm significantly improves the computational efficiency while providing reasonably accurate results. Before the approximation, the algorithm has an excessive computational time, which is significantly shortened by the approximation, although it remains slower than that of ASTRA. The accuracy and calculation time of the algorithm are presented in the Results section.

Comparison with infinite-bunch model results

The proposed algorithm is designed to calculate the space charge forces exerted by infinite bunches with uniform spacing. First, a special situation is considered. When the bunches are simplified uniform cylinders, and the distance between them is equal to their length, the adjacent bunches are connected end-to-end, forming a uniform, infinite-bunch, as shown in Fig. 5(a). In this section, the bunch spacing D of the proposed algorithm is equal to the bunch length L₀ and its results are compared with the infinite uniform bunch model.

Fig. 5Full-screen View

(Color online) Comparison between multi-bunch and single-bunch algorithms

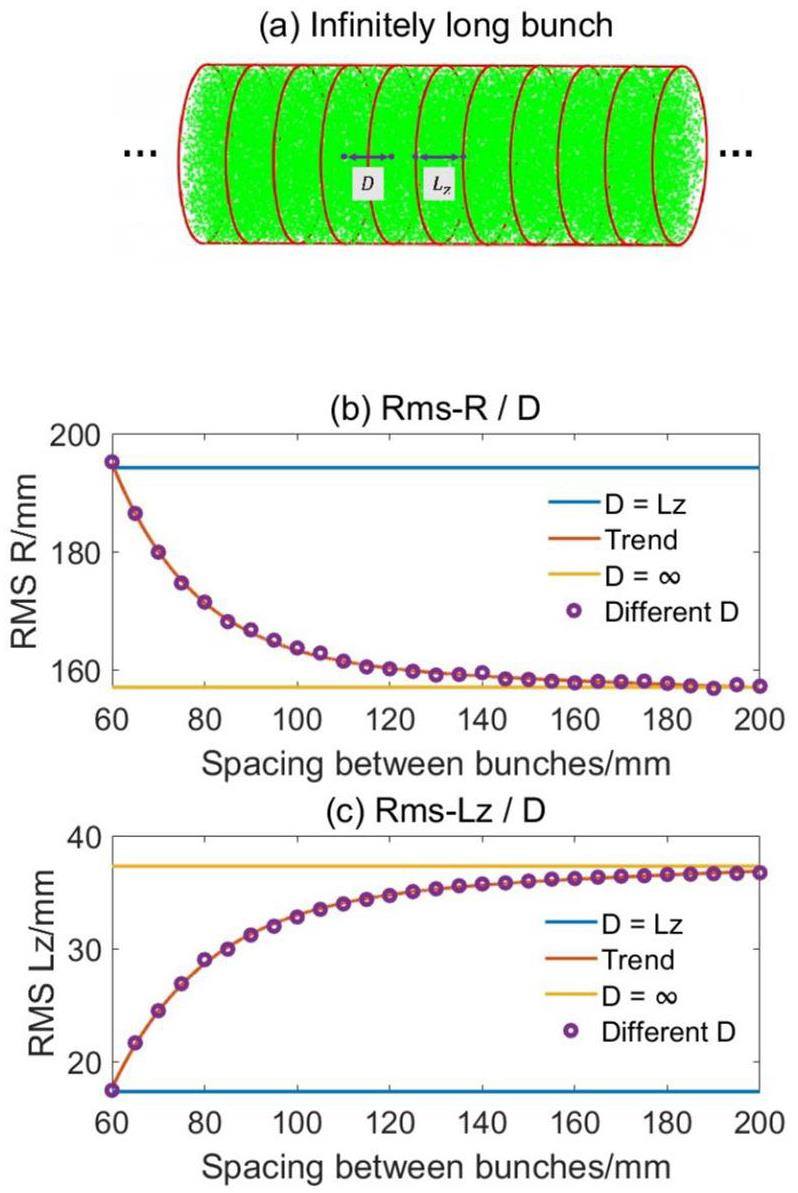
The analytical expression of the space charge forces for this model is shown in Eq. (14). As the bunch length of this model is infinite, the bunch does not expand longitudinally because of the symmetry. Thus, its equivalent current can be used as a constant parameter to describe the space charge forces. During the transverse expansion, the particle accelerations are proportional to their radii. If the particles in the bunch have no initial transverse velocities, the ratio of radii among the particles remains constant and the bunch remains uniform after the action of space charge forces. Therefore, the calculation results of this model can be simply verified.

The results for an infinite uniform bunch can also be obtained by utilizing the ASTRA single-bunch algorithm. In the proposed algorithm, a case in which infinite bunches are concatenated is calculated. In ASTRA, the number of bunches can be reduced from infinity to 100 and spliced into a long bunch. When the length of the entire bunch is such that its longitudinal expansion under space charge forces can be neglected, the equivalent current remains constant during transport. Under these circumstances, the transverse expansion is approximately equal to that of an infinite uniform bunch model.

The proposed algorithm took 380 s to calculate 6000 macroparticles, with iteration steps of 4000 and $k_{0r}=\mathrm{2.5,}{k}_{0z}=\mathrm{3.5,}{N}_r=\mathrm{25,}{N}_z=30$. When the same parameters were used, including macroparticle numbers for each single bunch, iteration steps, and mesh density, the calculation of a long bunch containing 100 single bunches using ASTRA would take 2460 s. However, such a long uniform bunch would have limited longitudinal expansion, making longitudinal calculations unimportant. Finally, 6000 macroparticles and 30 longitudinal meshes were used for the entire long bunch in ASTRA, which shortened the calculation time to 17 s.

The comparison results are summarized in Table 1, where R₀ and L₀ are the initial radius and length of a single bunch, respectively, and γ is the Lorentz factor. The charge within the length L₀ is q₀ = -5 nC. The distance D between different bunches is equal to L₀, such that $A_D=R_0/\left(\gamma D\right)=A$. Nr and Nz are the numbers of grids and A is the shape factor of the bunch in the bunch system. For convenience of comparison, the algorithm takes $k_{0z}=3.5$ in all calculations. If A is larger, then $k_{0z}$ must be increased to satisfy $k_{0z}>\sqrt{2}{A}_D=\sqrt{2}A$.

A is related to the grid division. For example, a large A indicates that the transverse length of the bunch is greater than its longitudinal length. Therefore, the grid in the r direction should be divided finer than that in the z direction to increase the accuracy of the PIC algorithm. Considering that the space charge forces were calculated in the bunch system, γ is also included in the expression for A. L is the transport distance of the bunch. R₀ is the root mean square (RMS) radius of the final bunch, which is calculated using the ASTRA long bunch. RE(R₁) and RE(R₂) are the relative errors with R₀ from the multi-bunch PIC algorithm and infinite uniform bunch model, respectively. L₀ is the ASTRA RMS length result and RE(L₁) is the multi-bunch PIC algorithm relative error. The analytical model only calculates transversely; therefore, there is no length result. As shown in Table 1, although the PIC algorithm adopts a rough mesh division because Nr and Nz are small, most relative errors with an infinite uniform bunch model are approximately 1%, validating the PIC algorithm.

Comparison with ASTRA single-bunch model results

The PIC algorithm was further validated by varying the spacing of the bunches while maintaining the constant parameters of a single-bunch. By gradually expanding the spacing of the bunches, the behavior of the multi-bunch algorithm is compared with the results obtained from ASTRA's single-bunch method. As the spacing of the bunches increases, the infinite-bunch model gradually degenerates into a single-bunch model. Hence, if the PIC algorithm results ultimately converge with those of ASTRA, this provides further evidence for the validity and rationality of the PIC algorithm.

Using the same parameters as in Section A, the multi-bunch calculation time of the proposed algorithm is 380 s, whereas that of the ASTRA single-bunch model is 20 s.

The comparison results between ASTRA and the multi-bunch algorithm with different bunch spacings are presented and discussed in Fig. 5.

The initial parameters of the single-bunch algorithm are q₀ = -5 nC,R₀ = 50 mm,L₀ = 60 mm, and γ = 5, L = 50 m. D represents the spacing between bunches used in the multi-bunch algorithm, and R represents the RMS value of the radius of the bunches. As shown in Fig. 5(a), when the spacing between the bunches is equal to the length of the bunches, the multi-bunch algorithm result is equal to that of the infinite-bunch model, as shown by the blue line in Fig. 5(b)(c). The results of different D values from the multi-bunch algorithm are shown as purple points, where R decreases as D increases, whereas Lz increases. When D reaches double that of L₀, the transverse expansion of the bunches due to space charge forces is reduced by approximately 20% compared to the infinite-bunch model. When D reaches triple that of L₀, the result of the multi-bunch algorithm is sufficiently close to that of the ASTRA single-bunch algorithm, as shown by the yellow line. The orange line shows the fitted trend as D increases. The position relationship of the three lines indicates that the multi-bunch algorithm and ASTRA single-bunch algorithm agree well. Moreover, it should be noted that if another set of parameters is used, when the results of the multi-bunch algorithm are close to those of the single-bunch algorithm, the requirement for $D/L_0$ may be different. One purpose of the PIC algorithm is to estimate such differences.

Comparison with PARMELA and ASTRA several-bunch results

PARMELA can calculate the space charge forces for several bunches, whereas ASTRA can only handle a single-bunch. However, if a file is input with an initial phase space of several bunches, ASTRA can also calculate their space charge forces, even though they are treated as a long bunch. Consequently, the mesh division of ASTRA is relatively approximate, which may result in slightly larger errors.

By utilizing ASTRA and PARMELA, the space charge forces of several bunches can be calculated. As the number of bunches gradually increases, their results gradually approach those of infinite bunches. This confirms the reliability of the PIC algorithm.

Using the same parameters as in Section A, the multi-bunch calculation time of the proposed algorithm is 380 s. When keeping the macroparticle numbers for each bunch and the mesh density constant, as the number of bunches increases from 1 to 19, the calculation times of ASTRA are 14, 36, 57, 79, 102, 125, 149, 173, 213, 241 s.

The results obtained using the three algorithms are shown in Fig. 6. The initial parameters of a single-bunch were q₀ = -2 nC,R₀ = 50 mm,L₀ = 10 mm, γ = 8, L = 50 m, and D=15 mm. R represents the final RMS value of the radius of the bunches, and N represents the number of bunches used in the PARMELA and ASTRA simulations. For example, N=5 indicates the existence 2 bunches on each side of the reference bunch. To ensure symmetry, N=1, 3, 5, … Fig. 6(a) shows the ASTRA results for N=5. As indicated by the green points, the longitudinal expansion of the central bunch is suppressed compared to that of the bunches at the edge. Therefore, to unify the standards, the ASTRA RMS results used subsequently were all obtained from the central bunch, rather than the entire bunch train.

Fig. 6Full-screen View

(Color online) Comparison between infinite-bunch and finite-bunch models

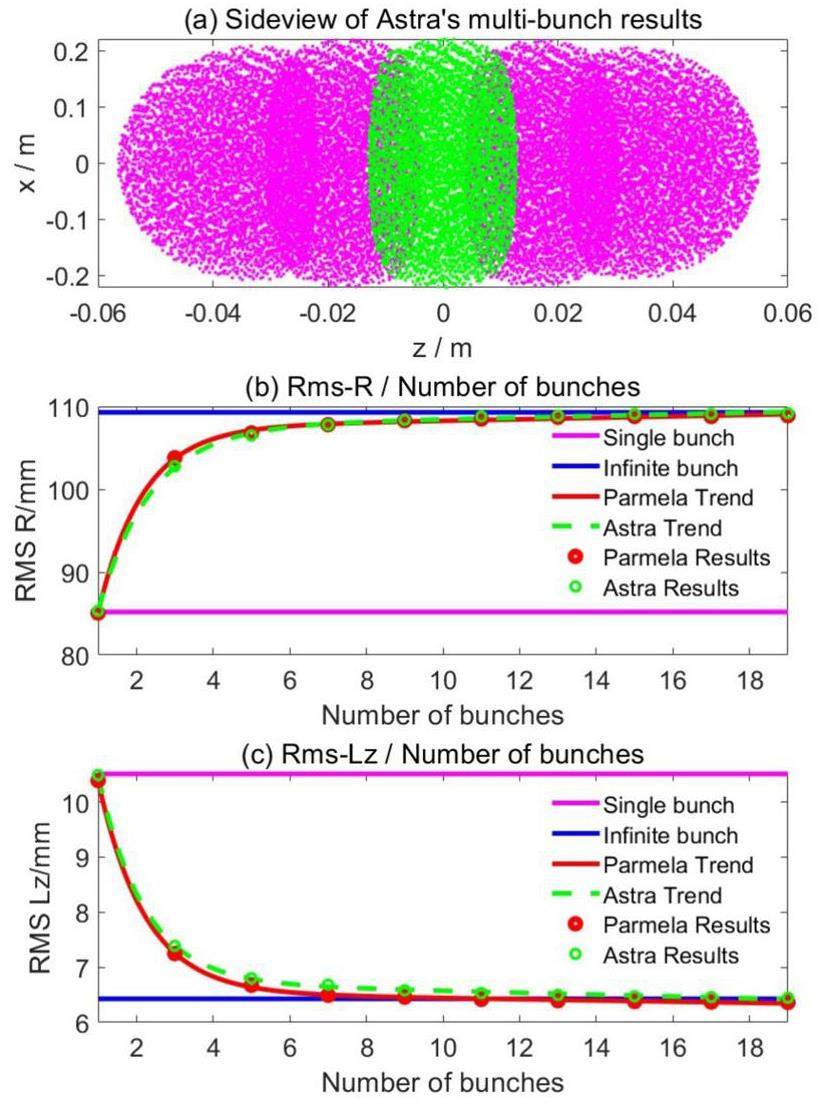
As the number of bunches (N) increases, the results of ASTRA and PARMELA are indicated by green and red points, respectively, as shown in Fig. 6(b)(c). The trends are represented by the curves of the corresponding colors. When N=1, both results fit well with the single-bunch results of the proposed algorithm by setting D to be sufficiently large, as indicated by the pink line. When the number of bunches $N\ge 9$, both results approach those obtained from the PIC algorithm, which sets the number of bunches to infinity (∞), as shown by the blue line.

The overall convergence between the finite- and infinite-bunch models validates the capability of the latter algorithm to predict space charge forces for industrial accelerator systems.

Comparison with ASTRA external field results

In this section, by setting D to be sufficiently large, the PIC multi-bunch algorithm is degraded to a single-bunch algorithm. Subsequently, the single- and multi-bunch results of the PIC algorithm are compared with those of ASTRA in the field of an S-band standing wave accelerator, with an axial electric field as shown in Fig. 7(a). The field has a frequency of 2856 MHz and its maximum electric field strength is 18.087 MV/m.

Fig. 7Full-screen View

(Color online) Comparison with ASTRA in an external field. (a): External electric field along the z axis; (b)-(f): rms-x, rms-divergence, average kinetic energy, rms-length and capture rate, and the energy spread of the beam during transport, respectively

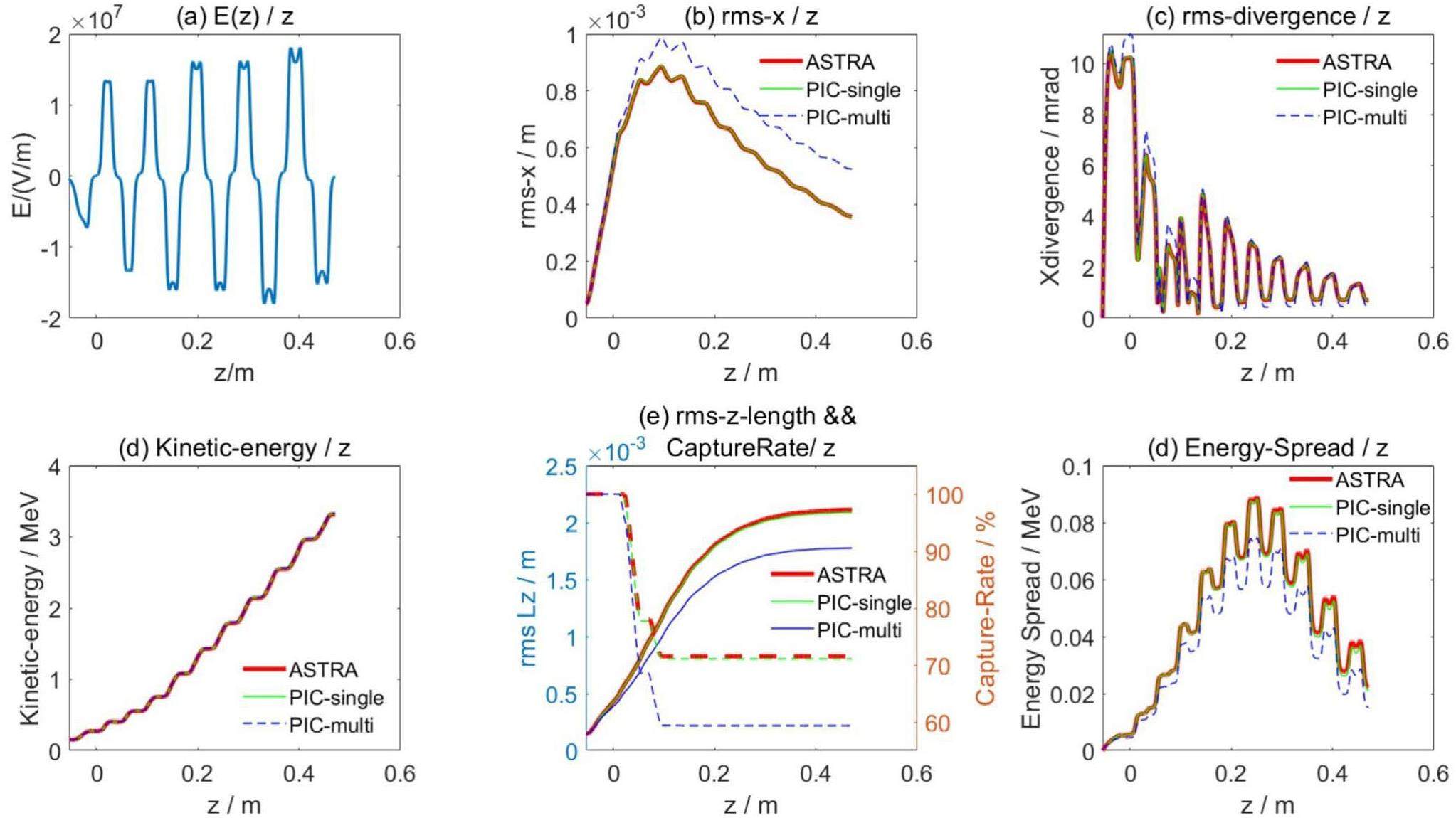
A uniform bunch was used to calculate the transport process. When a low energy bunch was used in the S-band field, its length increased so much that it exceeded the range of the accelerating tube, which caused significant problems in the longitudinal calculation. Hence, a higher energy bunch was used to validate the calculation capabilities of the proposed algorithm in an external field. The initial parameters of the single-bunch were q₀=-4 pC,R₀=0.1 mm,L₀=0.5 mm, and γ=1.3, L=L_cell=0.5255 m. D=1×10³ m was used to degrade the bunch train with infinite bunches into a single-bunch. In this section, the number of iteration steps was 4000, the number of macroparticles was 10000, and k_0r=2.5, k_0z=5.5, N_r=30, N_z=40. It took the proposed algorithm 780 s and ASTRA 42 s to complete the single-bunch calculations.

For the multi-bunch calculations of the standing-wave accelerating field, a bunch train with a spacing equal to its RF period should be used, which is 67.1 mm for 2856 MHz and $\gamma =1.3$. However, such a bunch train is not suitable for validation because the RF period is too long compared with the bunch length. Considering the same mesh density as a single-bunch, calculating 11 bunches in ASTRA would require more than 50000 meshes longitudinally, which is unrealistic. Experimentally, ASTRA was used to calculate 11 bunches with 5000 longitudinal meshes, which required more than 14 h. The results showed that the bunch train expands to over 1000 mm longitudinally, which is almost double the accelerating field length. Finally, a small D as 2 times L₀ was used, which indicated that the bunch spacing was equal to the bunch initial length. Such a parameter would be convenient for validating the ability of the proposed algorithm to calculate in an external field, as fewer longitudinal meshes are needed. For high-frequency accelerators, it is more practical to adopt D as the RF period.

Furthermore, the π-mode S-band field contains only 11 cells, which is fewer than six RF periods. Consequently, when the number of bunches exceeds seven, some bunches would exit the field before others have entered. When the bunch train has only a few bunches, such as five bunches, the proposed algorithm can help provide the upper limit of the space charge force. When the field has an adequate number of cavities, such as 30, the proposed algorithm has additional computational advantages.

A comparison of the results of the three algorithms is presented in Fig. 7(b)-(f).

Figure 7(b) shows the RMS values of the bunches in the x direction. The PIC single-bunch results agreed well with those of ASTRA, with a relative error of less than 0.5%. The blue dashed line shows the results of the multi-bunch algorithm, under which circumstances the expansion of the bunches is more obvious because of the increased space charge forces.

Figure 7(c) shows the beam divergences of the three algorithms. The two single-bunch results fit well. The multi-bunch divergence is larger when the radius is small. When the multi-bunch radius is much larger than that of the single-bunch, its divergence decreases.

Figure 7(d) compares the beam energies of the three algorithms, all of which were accelerated from 153 keV to approximately 3.33 MeV. The relative error between the two single-bunch algorithms is less than 0.6%.

Figure 7(e)(f) depicts the RMS length and capture rate when a simple circular aperture with a radius of 1.5 mm was added and the energy divergence of the three algorithms. The two single-bunch results fit well. As indicated by the solid lines in Fig. 7(e), the bunch length exhibits a maximum relative error of 1%, whereas in Fig. 7(f), the energy spread is 5% at certain points. As indicated by the dashed lines in Fig. 7(e), the final capture rates of ASTRA and the single-bunch of the proposed algorithm were 71.5% and 71.7%, respectively, whereas the multi-bunch capture rate was 59.9%. The blue line shows the results of the multi-bunch, where the longitudinal expansion of the bunches is suppressed.

In this case, the multi-bunch space charge forces have a significant impact on the transverse and longitudinal evolutions of the bunches. The transverse expansion was intensified, whereas the longitudinal expansion was suppressed. Both effects interfere with the capture rate, which is reduced by approximately 10%. After this comparison with ASTRA, the ability of the proposed algorithm to calculate multi-bunch space charge forces in accelerating fields was demonstrated.

However, it should also be noted that in this example, to reduce the burden of the longitudinal calculation, D was not considered as the S-band RF period because it was too long. As a result, the accelerating phase of each bunch is different, which is not considered in the proposed algorithm; hence, the capture ratio in Fig. 7(e) includes only the loss on the aperture owing to the large beam radius. If the external field has higher frequency or adequate cavities, the proposed algorithm would be able to take D as the RF period and provide more valuable results. In future studies, work should focus on optimizing the longitudinal calculation capabilities of the algorithm until it can calculate the bunching process of low energy beams more accurately.