Introduction
Radiation-shielding designs for reactors aim to minimize the external radiation dose (ALARA) by selecting appropriate shielding materials and structures to meet the radiation-safety requirements of the personnel [1, 2]. Additionally, with the development of new types of nuclear reactors in various fields, the shielding design needs to balance safety standards with the consideration of miniaturization and lightweight design, such as for marine, transportable, and space reactors [2-5]. Consequently, the radiation-shielding design for newly developed reactors presents a typical multi-objective optimization problem, as it involves multiple design objectives and parameters, including the radiation dose, volume, and weight (Fig. 1.
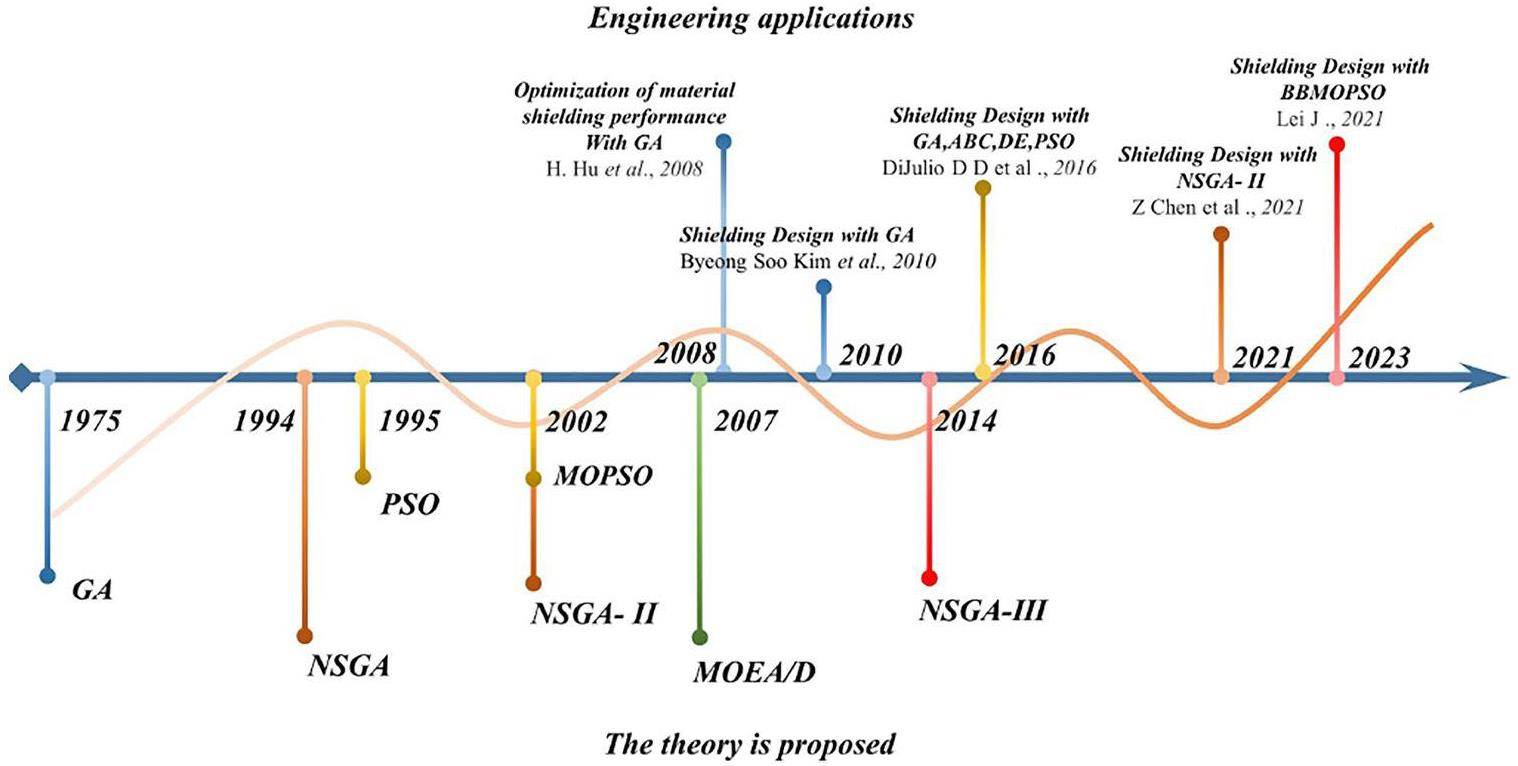
Conventional shielding-design methods rely heavily on expert knowledge, and require manual iterations to achieve acceptable results. With the development of evolutionary optimization algorithms, some researchers have begun to employ single-objective optimization algorithms, such as the genetic algorithm (GA), particle swarm optimization, and differential evolution, to optimize the radiation dose as a single objective [5-7]. In recent years, studies have also utilized multi-objective (two or three objectives) optimization algorithms, such as the non-dominated sorting genetic algorithm II (NSGA-II) and multi-objective particle swarm optimization, to optimize the volume-dose trade-off as multiple objectives [8-12]. This means that evolutionary algorithms have received considerable attention and can provide new opportunities for complex shielding-optimization problems.
However, in practical shielding-optimization designs, the number of objectives to be optimized often exceeds four, resulting in a typical many-objective problem (four or more objectives to be optimized) [13, 14]. Conventional multi-objective optimization algorithms exhibit suboptimal performance when dealing with many-objective optimization problems [15, 16], failing to meet the requirements of achieving a global optimal solution in the shielding design. Therefore, in this study, we propose a reference point-based many-objective artificial bee-colony algorithm (RP-MOABC) and reference point-based non-dominated sorting algorithm (RP-NSGA) to solve many-objective shielding-optimization problems.
The remainder of this paper is organized as follows. Section 2 presents the mathematical model of the many-objective optimization problem in reactor radiation shielding and discusses the encoding methods for shielding design. In Sect. 3, we provide an overview of the fundamental principles of the proposed genetic-and bee-colony-based optimization algorithms. We also outline a detailed framework for their application in radiation-shielding designs. Section 4 presents the numerical models of reactor-shielding design applications, along with the corresponding numerical results. Finally, the concluding section summarizes the key findings and conclusions of this study.
Many-objective optimization problem in reactor radiation-shielding design
This section provides a concise overview of reactor radiation-shielding design and the associated mathematical model for the many-objective shielding-optimization problem. It begins with a brief explanation of the principles underlying the shielding design for neutrons and gamma rays in reactors. Next, a mathematical model is proposed to address the many-parameter, -objective, and -constraint reactor-shielding design. Finally, a special encoding method is proposed to represent the shielding parameters (such as the number of shielding layers, types of shielding materials, and their compositions), facilitating the optimization process.
Principles of radiation-shielding design
The primary objective of reactor radiation shielding is to design a shielding system composed of multi-layer and multi-material structures that surround the core facilities within the reactor, ensuring that the personnel are in an environment where the radiation dose meets the specified limits. This is achieved by utilizing suitable shielding materials and geometric configurations combined with multi-layered and multi-component structures to shield the radiation sources. The selection and arrangement of materials in each layer are based on their specific shielding capabilities and nuclear interactions with radiation particles, with the aim of minimizing radiation levels to the maximum possible extent.
The principles governing the design of radiation shielding are based on the interactions between the radiation particles and materials. Radiation predominantly comprises neutrons and gamma rays. Neutron interactions include absorption and scattering, which is further categorized into elastic and inelastic scattering. For neutron shielding, the secondary gamma rays generated during inelastic scattering reactions must be considered. The interactions of gamma rays include Compton scattering, photoelectric absorption, and pair production. Typically, neutron shielding requires materials containing heavy and light isotopes, such as light water, boron carbide, and polyethylene [17, 18]. Conversely, gamma-ray shielding requires materials with high-Z isotopes, including lead, concrete, and steel [19].
Many-objective mathematical model for radiation-shielding design
Many-objective optimization in practical applications aims to achieve multiple optimized objectives within specific constraints. However, owing to the inherent conflicts between these objectives, optimizing one objective is typically achieved at the expense of deteriorating the others. As a result, a unique optimal solution is elusive; instead, a set of Pareto-front solutions consisting of non-dominated individuals is obtained [20]. Radiation-shielding design presents a typical many-objective optimization problem in nuclear engineering. The goal is to minimize the mass and volume of the total shielding system while ensuring that the external-radiation dose satisfies the ALARA principle. However, weight, volume, and radiation dose are conflicting objectives that cannot be optimized simultaneously. In this study, we focus on minimizing the total weight, total volume, and axial and radial radiation doses outside the shielding layers. These objectives are influenced by various parameters, including the thickness of the shielding layer, materials used, and the composition of the materials used. Additionally, constraints are imposed on the fast-neutron, thermal-neutron, and gamma-ray flux rates outside the shielding layers during the optimization process. Reactor radiation-shielding design involves many objectives, parameters, and constraints. To address these challenges, the mathematical model in Eq. (1) is proposed:
Encoding methods of radiation-shielding model
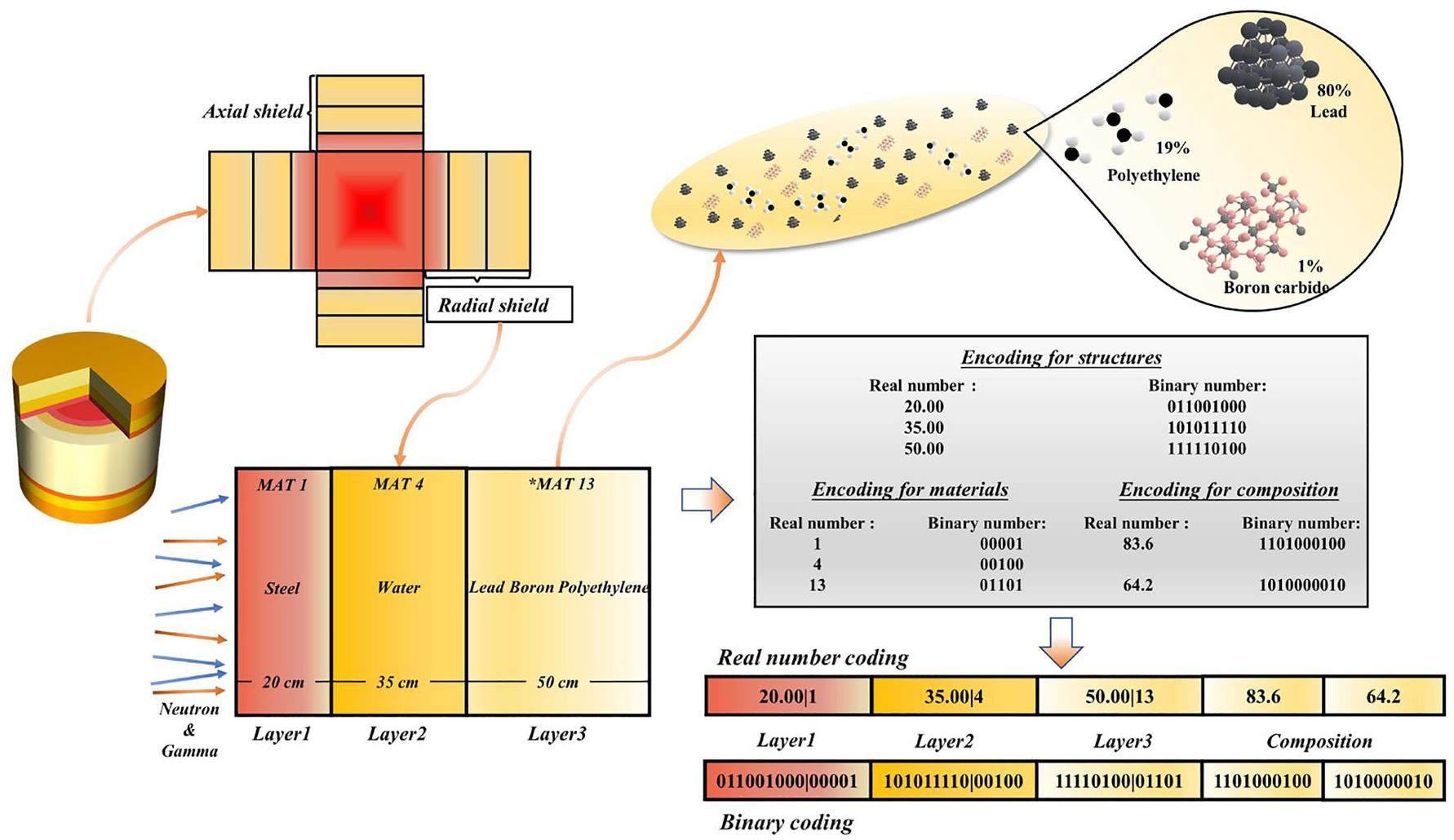
In recent years, the development of radiation-shielding designs has progressed significantly, and a series of studies combining evolutionary algorithms with various types of shielding designs have emerged. However, the decision vector in this type of research only covers the shielding structure and shielding-material-type changes, and no material-composition-optimization research has been previously carried out. In this study, the reactor-shielding model is simulated for the many-parameter problem in shielding optimization using both binary encoding and real-number encoding, which can be encoded to characterize the shielding-model geometry, material type and material composition, and coupled with a variety of evolutionary algorithms for calculation.
Fig. 2 illustrates the encoding process for the simple shielding scheme. First, the thicknesses of the shielding layers and the corresponding index numbers for the shielding materials are obtained. The composition is determined for materials with variable compositions, such as borated and lead-borated polyethylene. Second, the above parameters are encoded in real or binary numbers. The composition content, which is subject to fixed-sum constraints, is transformed using spherical-coordinate conversion [21], as in Eq. (2) prior to encoding. Finally, the encoding design is completed for all shielding layers. The purpose of encoding is to combine the shielding model with the evolutionary algorithm such that the model parameters can be optimized by the algorithm, and the final shielding scheme can be obtained for the reference of the designer.
Many-objective evolutionary algorithms for radiation-shielding design
Scheme of radiation-shielding optimization with many-objective evolutionary algorithm
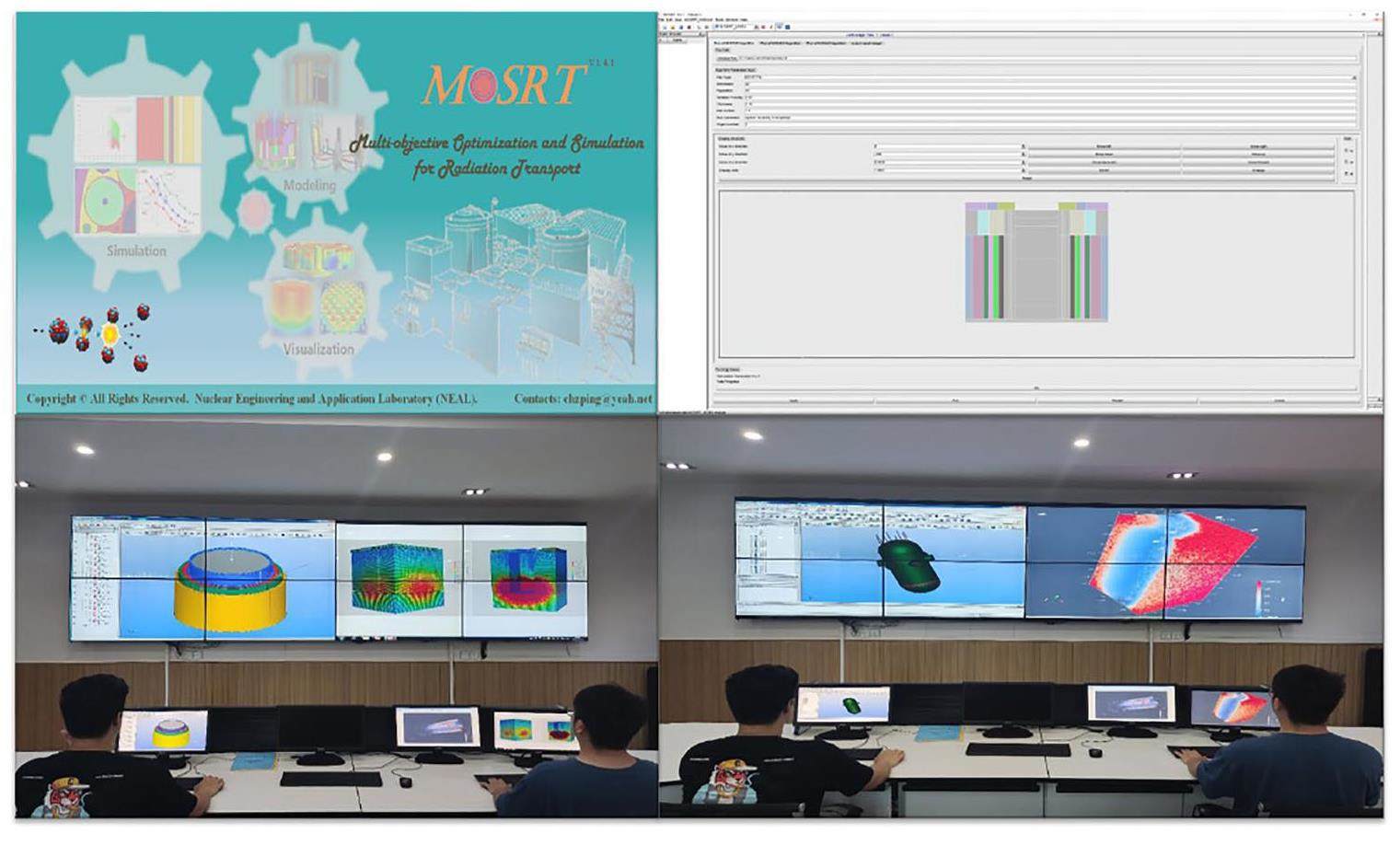
In this study, shielding-optimization methods are proposed by combining many-objective evolutionary algorithms with particle-transport calculation software that can optimize the reactor primary-shielding structures, material types, and material compositions to obtain optimal shielding-design schemes through an automated process. These methods are embedded into the multi-functional radiation-transport simulation platform (MOSRT) developed by the NEAL team [22, 23].
A schematic of the many-objective optimization of the radiation-shielding design is shown in Fig. 3, and the steps are described as follows.
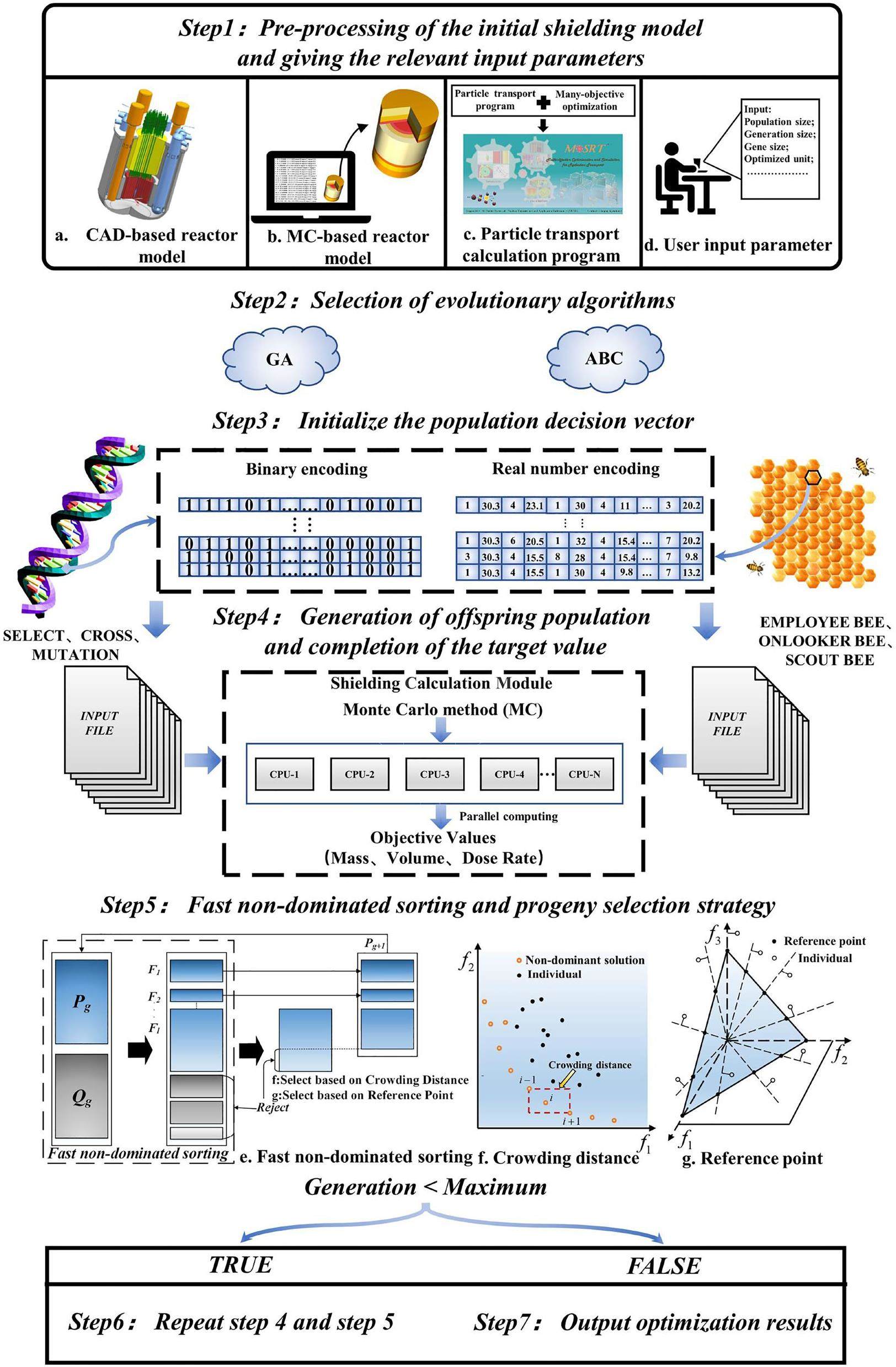
(1) Preprocessing of the initial shielding model is performed using the MOSRT software. First, the CAD model of the reactor geometry is modeled with MOSRT, and the model is automatically converted into a particle-transport calculation model. The shielding regions to be optimized are labeled. Finally, the initial running parameters are set, including the maximum number of iterations g, population size N, and optimization-objective number M.
(2) The evolutionary algorithm is selected. In this study, the genetic and ABC algorithms are invoked as evolutionary algorithms to optimize the weight, volume, and region-specific radiation-dose rate of the reactor radiation-shielding model.
(3) The decision-vector encoding method (real-number encoding or binary encoding) is chosen based on the requirements, and the initial parent population
(4) The initial offspring population
(5) A fast non-dominated sorting strategy is applied to the merged population, and each algorithm uses the reference-point selection strategy [25] to generate the new parent population
(6) Steps (4) and (5) are repeated if the maximum number of iterations is not reached, and the parent population
(7) The optimization process is completed, and the optimization results of each algorithm are thoroughly compared and analyzed.
Evolutionary strategy based on genetic algorithm
The GA [27] is a classical evolutionary strategy for simulating inheritance and evolution in nature. It searches for the solution space of optimization problems through operations such as selection, crossover, and mutation. GAs based on different evaluation strategies exhibit significant differences in performance when solving various problems [28]. The following section explains the basic operations of GAs.
Selection: In this study, a binary tournament-selection operation is used, where two individuals (the individual in the paper means a specific shielding scheme) are taken from the current population at a time, the dominance relationship between the two individuals is judged, and the individual in the dominant position is selected for subsequent crossover and mutation. If two individuals do not dominate each other, one individual is randomly selected for the subsequent genetic steps. The determination of the dominance relationship will be explained in Sect. 3.4.1.
Crossover: The crossover operation mimics the process of hybridization in biological evolution. It selects the chromosomal segments (genes) of two or more parent individuals for exchange to generate new offspring. In this study, we use a single-point crossover operation for GAs with binary encoding and a simulated binary crossover operation for GAs with real-number encoding.
Mutation: The mutation operation introduces a degree of randomness to the algorithm by changing some gene values on individual chromosomes to generate new individuals. The mutation operation can increase the diversity of the population and prevent it from falling into a locally optimum solution. The mutation operation can randomly select some genes of an individual to be changed, or mutate each gene on the chromosome with a particular probability. In this study, we use the bit-flip mutation operation for GAs with binary encoding and polynomial mutation operations for GAs with real number encoding.
Evolutionary strategy based on artificial bee-colony algorithm
The ABC [29, 30] algorithm is a global optimization technique based on swarm intelligence. It draws inspiration from the foraging behavior of bee colonies, where individual bees perform specific tasks and share information to collectively find the optimal solution to a problem. This study builds on the fundamental ABC algorithm and introduces improvements by employing two methods: a differential evolution search [31] and golden sine search [32]. The following sections explain the search strategies of the algorithm.
Employed bee search: In this phase, a number of hired bees consistent with the population size will be dispatched to search for historical food sources (solution space). In this study, the bee population searches using a differential-search method based on an elite strategy. Individuals in the Pareto optimal set (the Pareto optimal set will be explained in Sect. 3.4.2.) are randomly used as bootstrap terms, and the differential evolution operator is used to generate new solutions, as shown in Eq. (3):
The elite-guided search mechanism is an exploitation operation that unavoidably reduces the diversity of the population, and may cause the algorithm to converge locally. To better balance the global-search and local-exploitation capabilities, this study proposes a solution-space search method based on the golden sine function:
The employed bees use Eq. (3) and Eq. (4) for searching with equal probabilities to balance the diversity and local-search capability of the population.
Onlooker bee search: The onlooker bees perform repeated optimization on the excellent food sources based on the roulette-wheel selection. The specific optimization operations are the same as those of the employed bees, and the onlooker-bee evaluation function is as follows:
The roulette-wheel selection probability is defined as
Scout bee search: A food source is randomly selected from the last Pareto layer, its decision vector is randomized, and its corresponding objective values are reset.
Evaluation method of shielding scheme based on Pareto domination
Pareto domination of the shielding schemes
When evaluating the performance of different shielding-design schemes, in the case of a single objective (such as shield weight), a smaller shield weight indicates better performance of the design scheme. However, for multiple objectives, each shielding-design scheme has multidimensional attributes (such as shield weight, volume, and dose rate). The performance of shielding schemes cannot be evaluated simply based on numerical magnitudes.
First, the decision vectors must be decoded and converted into particle-transport program-input files, and the population objective values are calculated using the particle-transport program, as shown in Eq. (7):
Fast non-dominated sorting strategy
Based on the Pareto-domination judgment method, fast non-dominated sorting (Fig. 3(e)) of the populations can be performed to divide the different levels of the non-dominated layers. First, all schemes in the population are judged for domination, and all schemes that are not dominated by others are removed from the population and constitute the non-dominated layer
The schemes at each level of the non-dominated layer are not dominated by each other, and the smaller the level of the non-dominated layer, the better the integrated performance of the schemes in the layer. The
Pareto-set-selection strategy
When offspring are generated, the parent set
Selection strategy based on crowding distance
Conventional multi-objective optimization algorithms use the crowding distance to compare schemes in non-dominated layers. Further judgment is made by calculating the CD value for each scheme. The calculation method is given in Eq. (11) and Fig. 3(f):
Selection strategy based on reference point
In the reference-point selection strategy [34, 35], the reference points are first predefined in the normalized hyperplane and the number of reference points should be close to the population size, which is defined by Eq. (12):

We define
After associating the reference points with the scheme in
If the selected
If
Numerical evaluation for radiation-shielding optimization problems
Two sets of numerical simulations are conducted, as follows:
(1) The GA and ABC algorithms are combined with Pareto-frontier-selection strategies based on the reference-point strategy or crowding-distance strategy, respectively, to test the optimization of a simple three-dimensional (3D) shielding problem, and the optimization performance of each strategy is compared.
(2) Constrained many-objective optimization of a complex shielding problem is conducted using the proposed optimization method and is compared with the initial shielding scheme.
In the following sections, we refer to the algorithms based on the reference-point-selection strategy as RP-NSGA and RP-MOABC, and those based on the crowding-distance strategy as CD-NSGA and CD-MOABC. The neutron database used in the simulation is ENDF/B-VIII.0 [36], and the photon database is MCPLIB84. The neutron flux-dose rate and photon flux-dose rate conversion factors used are NCRP-38 and ANSI/ANS 1977 [37], respectively. Particle-transport simulations are conducted using the Monte Carlo code MagicMC [38], and the overall optimization process, including evolutionary algorithms and the Monte Carlo code, are integrated into the self-developed software MOSRT (Fig. 5.
Many-objective optimization for a simple 3D shielding problem
The first problem focuses on the multiple objectives of a simple 3D shielding structure, as shown in Fig. 6(a). The optimization objectives are to determine the total volume and weight of the R1-R10, U1-U5, and L1-L5 shielding layers as well as the radial lateral, axial upward, and axial downward dose rates of the shielding layers. The thickness of each shielding layer in the optimized model ranges from 0.3 cm to 13 cm. The reactor consists of a homogenized core with a height of 167.6 cm and radius of 78.8 cm. The source term is set as a fixed source with a probability distribution based on the Watt-fission spectrum. A comparative analysis of the optimization performance of each algorithm is performed using the average objective value and hypervolume [39] value.
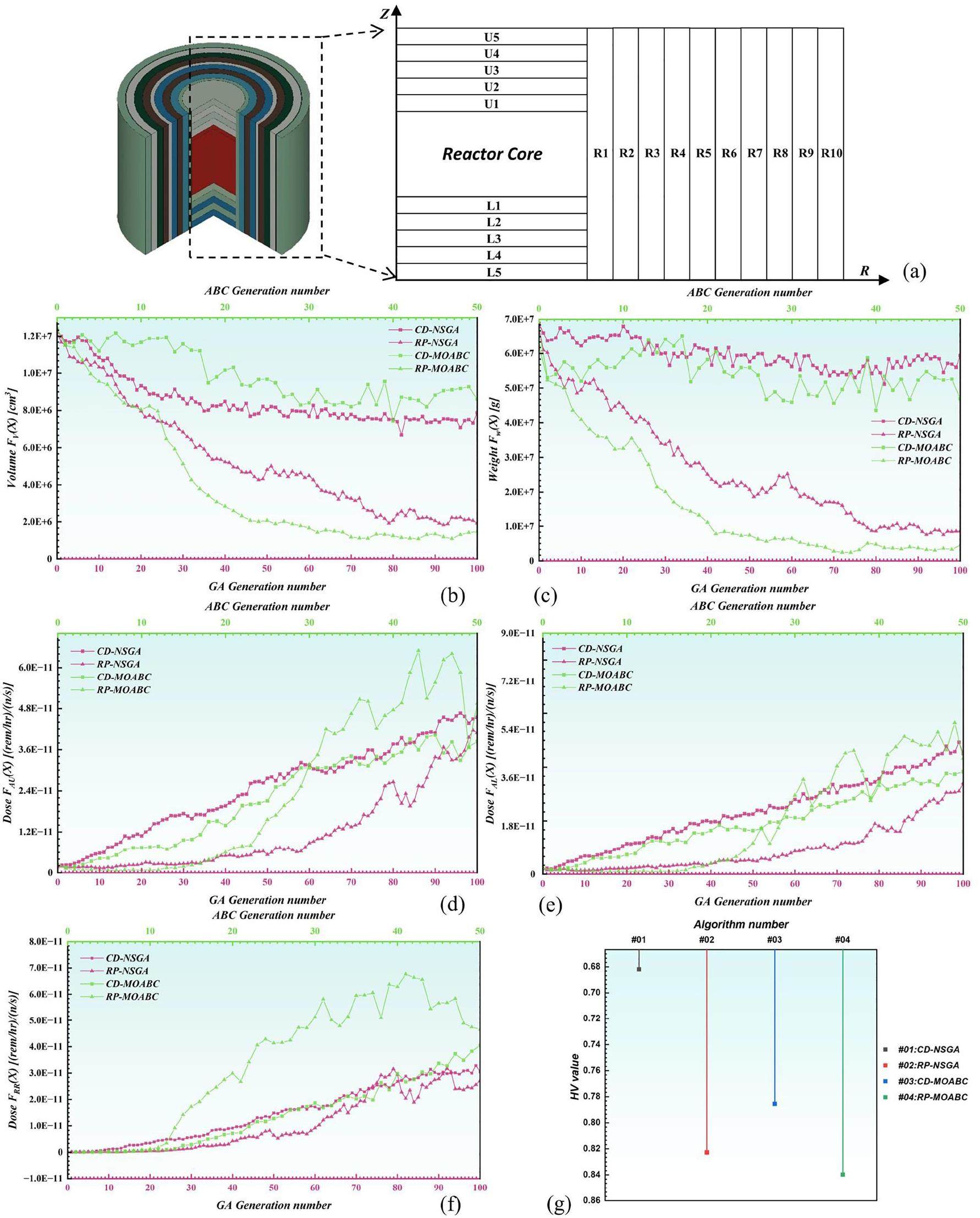
In this problem, GA-based algorithms use binary encoding and ABC-based algorithms use real number encoding. The population size of all algorithms is set to 210, and the number of reference points of the algorithms using the RP strategy is 210 (the number of divisions H=6). The number of MC transported particles is 1.0×107.
For the shielding-optimization process, the time complexity is mainly related to the number of evolutionary generations g and the population size N, where the total time complexity of the GA is
As observed in the average objective values shown in Fig. 6(b-f), the algorithms based on the reference-point strategy show excellent optimization results in terms of the weight and volume objectives. Compared with the conventional crowding-distance strategy, the average volume and weight values for the shielding schemes in the final generation of RP-NSGA are only 24.5% and 14.5% of those of CD-NSGA, and the average volume and weight values of RP-MOABC are only 17.3% and 9.77% of those of CD-MOABC. Regarding the dose rates in each region, the results in the final generation of each strategy are not significantly better or worse; the distribution of the results is relatively close, and the algorithm with relatively better performance is RP-NSGA. Overall, based on the average objective values, the algorithms using the reference-point strategy exhibit better convergence results.
To further evaluate the comprehensive performance of each algorithm scientifically, the hypervolume (HV) is chosen as the quantified factor to measure the convergence and distribution of the shielding schemes. The HV metric is a widely used performance evaluation method for engineering optimization problems, and does not require a real Pareto front to judge the strengths and weaknesses of a set of population schemes. The HV metric is calculated as shown in Eq. (14):
Constrained many-objective optimization for a complex 3D shielding problem
The second problem focuses on conducting a constrained many-objective optimization for the complex shielding structures shown in Fig. 7(a). For the constraint objectives, the thermal neutron-flux rate on the outermost shielding layer of the primary shielding system must be less than 1.0×105 n/(cm2·s), the fast neutron-flux rate must be less than 1.0×103 n/(cm2·s), and the gamma-ray energy-flux rate must be less than 6.0×106 MeV/(cm2·s). The optimization objectives include the total volume and weight of shielding layers R1–R8 and U1–U3, as well as the dose rates in the radial and axial upward directions of the shielding layers. The variable parameters are the shielding-layer thickness, shielding-layer materials, and partial material compositions (boron polyethylene, lead boron polyethylene, tungsten alloy). The thickness of each shielding layer in the optimized model ranges from 15 cm to 80 cm. The reactor consists of a homogenized core with a height of 167.6 cm and radius of 78.8 cm. The source term is set as a fixed source with a probability distribution based on the Watt-fission spectrum.
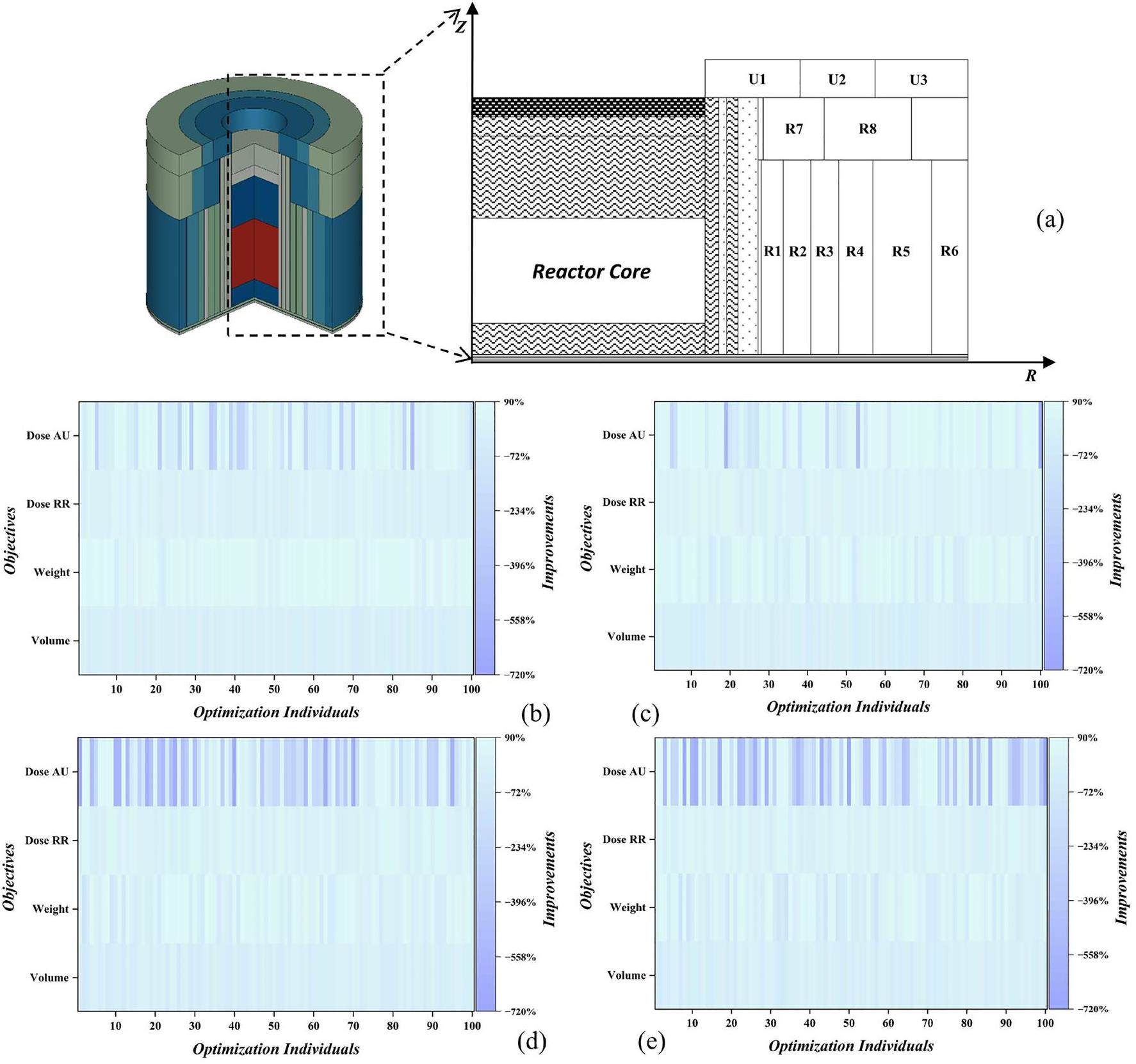
In this problem, GA- and ABC-based algorithms use real-number encoding. The population size of all the algorithms is set to 100, and the number of reference points of the algorithms using the RP strategy is 84 (the number of divisions H=6). The number of MC transported particles is 2.0×108. For computational efficiency, eight AMD EPYC 7H12 CPUs (Dual 128 core, 2.6 GHz) are used for massive parallel computation.
A heat map of the optimization ratio is plotted for the last generation of optimized shielding schemes compared to the initial shielding scheme, where the optimization ratio is defined in Eq. (15):
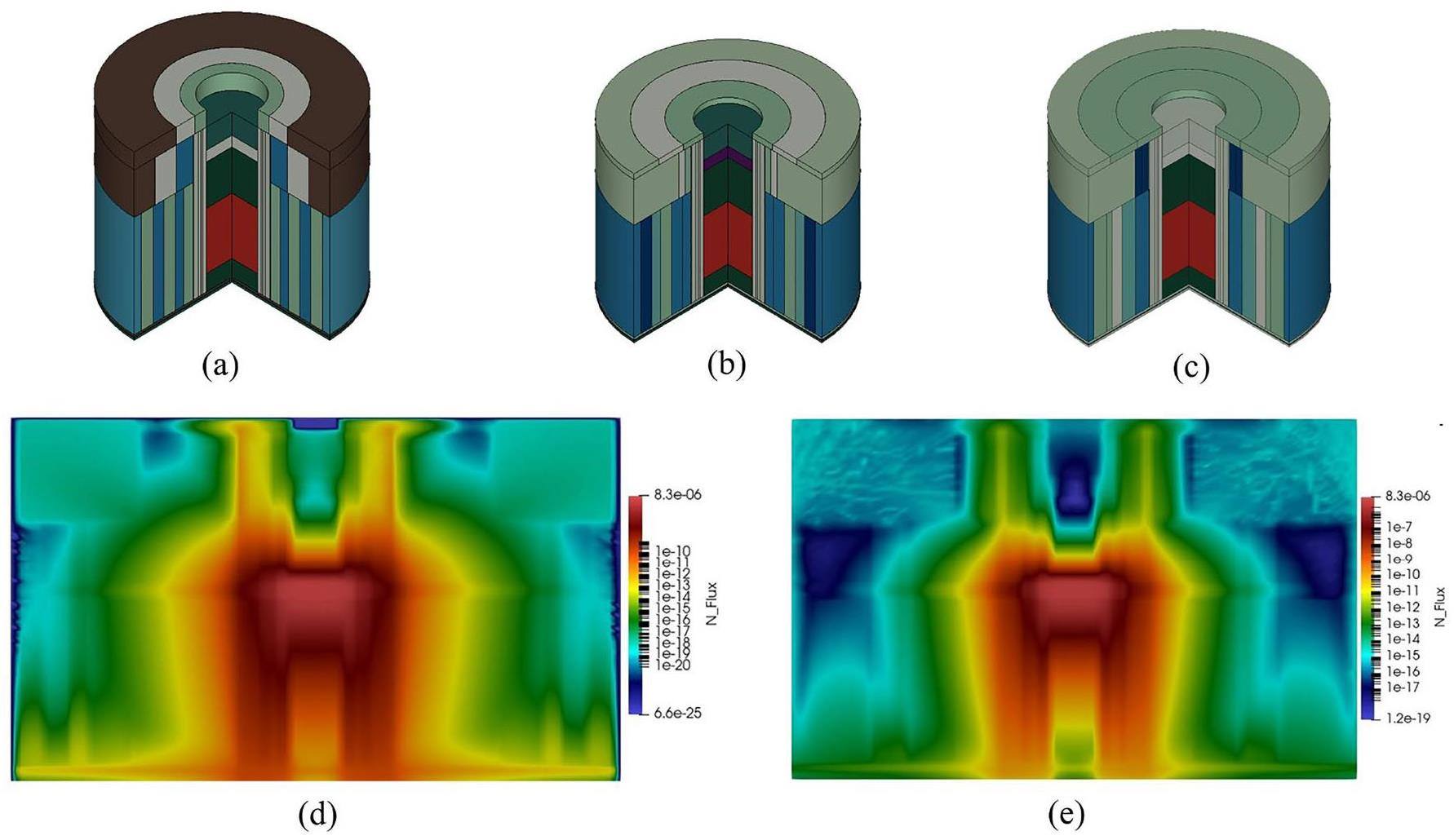
In practical engineering shielding-design problems, the final design scheme can be selected from a Pareto set of optimization schemes based on specific requirements. In this study, the miniaturization schemes obtained by the RP-NSGA algorithm (Shield #1) and RP-MOABC algorithm (Shield #2) are selected for demonstration. The shielding structure is shown in Fig. 8(b-c), the dose field distribution is shown in Fig. 8(d-e), and the specific parameters and optimization effects are listed in Tables 1, 2, 3 and 4. The dose rates are computed with the MagicMC Monte Carlo code using the global variance-reduction method [40-43] with a statistical error of less than 5%.
| Shielding Scheme No. | Borated Polyethylene | Lead-Borated Polyethylene | Tungsten Alloy | |||||
|---|---|---|---|---|---|---|---|---|
| B4C (%) | PE (%) | Pb (%) | B4C (%) | PE (%) | W (%) | Ni (%) | Fe (%) | |
| Initial shield | 80.30 | 19.70 | 53.17 | 2.34 | 44.49 | 98.66 | 0.94 | 0.40 |
| Shield #1 | 76.85 | 23.15 | 80.17 | 0.99 | 18.83 | 90.53 | 6.63 | 2.84 |
| Shield #2 | 30.34 | 69.66 | 90.00 | 0.50 | 9.50 | 90.62 | 6.57 | 2.81 |
| Shielding Scheme No. | Volume | Weight | Radial dose rate | Axial upper dose rate | ||||
|---|---|---|---|---|---|---|---|---|
| Numeric (cm3) | OR (%) | Numeric (g) | OR (%) | Numeric (rem/hr) | OR (%) | Numeric (rem/hr) | OR (%) | |
| Initial shield | 1.01×108 | - | 9.11×108 | - | 9.90×100 | - | 9.95E-1 | - |
| Shield #1 | 8.17×107 | 18.95 | 4.44×108 | 51.19 | 9.36×100 | 5.44 | 7.75E-1 | 22.09 |
| Shield #2 | 8.15×107 | 19.12 | 6.88×108 | 24.50 | 9.77×100 | 1.32 | 5.31E-1 | 46.62 |
| Shielding Scheme No. | Radial outermost shield | Axial topmost shield | ||||
|---|---|---|---|---|---|---|
| Thermal neutron (n/(cm2·s)) | Fast neutron (n/(cm2·s)) | Photon (MeV/(cm2·s)) | Thermal neutron (n/(cm2·s)) | Fast neutron (n/(cm2·s)) | Photon (MeV/(cm2·s)) | |
| Initial shield | 1.06×102 | 6.15×102 | 3.56×105 | 1.94×102 | 7.39×101 | 5.35×105 |
| Shield #1 | 6.01E-2 | 3.57×100 | 5.28×105 | 2.53×100 | 2.53×100 | 2.88×105 |
| Shield #2 | 2.34×101 | 3.02×102 | 3.95×105 | 5.96×100 | 1.81×102 | 1.01×105 |
| Shielding layer No. | Initial shield | Shield #1 | Shield #2 | |||
|---|---|---|---|---|---|---|
| Thickness (cm) | Material type | Thickness (cm) | Material type | Thickness (cm) | Material type | |
| R1 | 28.7 | B-Steel | 28.2 | Pb-B-PE | 40.0 | Pb-B-PE |
| R2 | 25.8 | Pb-B-PE | 33.3 | Pb-B-PE | 40.0 | B4C |
| R3 | 35.4 | W-Ni-Fe | 34.7 | W-Ni-Fe | 29.8 | H2O |
| R4 | 32.2 | Pb-B-PE | 31.0 | B4C | 15.0 | W-Ni-Fe |
| R5 | 36.9 | W-Ni-Fe | 33.2 | B-PE | 40.0 | W-Ni-Fe |
| R6 | 21.8 | W-Ni-Fe | 22.0 | Pb-B-PE | 15.0 | Pb-B-PE |
| R7 | 50.0 | Pb-B-PE | 20.0 | W-Ni-Fe | 20.0 | B-Steel |
| R8 | 66.8 | H2O | 20.3 | H2O | 20.0 | B-PE |
| U1 | 34.1 | W-Ni-Fe | 64.3 | W-Ni-Fe | 74.4 | W-Ni-Fe |
| U2 | 58.0 | H2O | 78.5 | H2O | 80.0 | W-Ni-Fe |
| U3 | 46.4 | Air | 20.0 | Air | 20.0 | Air |
Conclusion
With the development of new nuclear-reactor types, this study introduces two many-objective evolutionary algorithms based on a reference-point-selection strategy, and applies them to many-objective radiation-shielding optimization problems. The basic principles of the proposed evolutionary algorithms for shielding optimization are described in detail. The algorithms efficiently and accurately deliver an optimal set of shielding schemes that are more compact and lightweight and have lower dose rates. This study conducts a performance assessment based on a simple 3D shielding problem, with the results indicating superiority over evolutionary algorithms that rely on crowding-distance strategies. However, for the optimization of a complex shielding problem with multiple constraints for practical applications, the algorithms proposed in this study are able to obtain optimized design schemes with superior objective values compared to the initial scheme. Furthermore, by incorporating the composition of the shielding materials into the optimization process, the algorithms enhance the diversity and creativity of the shielding design. In summary, optimization algorithms can effectively identify excellent shielding schemes in the early stages of radiation-shielding design for nuclear reactors. This study provides significant guidance for radiation-shielding design and provides supplementary data during the conceptual design phase of novel nuclear facilities with limited engineering experience.
The technology of shielding design for nuclear reactor: a review
. Prog. Nucl. Energ. 161,SP100 space reactor design
. Prog. Nucl. Energ. 42(3), 323-59 (2003). https://doi.org/10.1016/S0149-1970(03)90003-5Shielding design of a megawatt-scale heat pipe reactor core
. Nucl. Tech. 46(02),A preliminary study to metaheuristic approach in multilayer radiation shielding optimization
. Mater. Sci. Eng. 298(1),Use of a genetic algorithm in the search for a near-optimal shielding design
. Ann. Nucl. Energy. 37(2), 120-129 (2010). https://doi.org/10.1016/j.anucene.2009.11.014Semi-empirical and semi-quantitative lightweight shielding design method
. Nucl. Sci. Tech.34(3), 43 (2023). https://doi.org/10.1007/s41365-023-01187-2Metaheuristic optimization method for compact reactor radiation shielding design based on genetic algorithm
. Ann. Nucl. Energy. 134, 318-329 (2019). https://doi.org/10.1016/j.anucene.2019.06.031Radiation shielding optimization design research based on bare-bones particle swarm optimization algorithm
. Nucl. Eng. Technol. 55(6), 2215-2221 (2023). https://doi.org/10.1016/j.net.2023.02.018A novel multi-objective shielding optimization method: DNN-PCA-NSGA-II
. Ann. Nucl. Energy. 161,Multi-objective optimization strategies for radiation shielding design with genetic algorithm
. Comput. Phys. Commun. 260,Radiation shielding optimization of space reactor based on intelligent decision support system
. Nucl. Tech. 45(05), 65-75 (2022). https://doi.org/10.11889/j.0253-3219.2022.hjs.45.050601 (in Chinese)Evolutionary many-objective optimization: A comparative study of the state-of-the-art
. Ieee Access, 6, 26194-26214 (2018). https://doi.org/10.1109/ACCESS.2018.2832181Hyperplane Assisted Evolutionary Algorithm for Many-Objective Optimization Problems
. Ieee. T. Cybernetics. 50(7), 3367-3380 (2020). https://doi.org/10.1109/TCYB.2019.2899225An evolutionary many-objective optimization algorithm based on dominance and decomposition
. Ieee. T. Evolut. Comput. 19(5), 694-716 (2014). https://doi.org/10.1109/TEVC.2014.2373386Evolutionary many-objective optimization: A short review
. Ieee C Evol Computat. 2419-2426 (2008). https://doi.org/10.1109/CEC.2008.4631121Study on the design and experimental verification of multilayer radiation shield against mixed neutrons and γ-rays
. Nucl. Eng. Technol. 52(1), 178-184 (2020). https://doi.org/10.1016/j.net.2019.07.016Simulations of mass attenuation coefficients for shielding materials using the MCNP-X code
. Nucl. Sci. Tech. 28, 95 (2017). https://doi.org/10.1007/s41365-017-0253-4Research on the shielding performance and optimization of new type foam metal matrix composite shielding materials
. Nucl. Instrum. Meth. B. 516, 31-37 (2022). https://doi.org/10.1016/j.nimb.2022.02.005Guiding Evolutionary Multiobjective Optimization With Generic Front Modeling, Ieee
. T. Cybernetics. 50, 1106-1119 (2020). https://doi.org/10.1109/TCYB.2018.2883914Optimization research on neutron shielding material component based on genetic algorithm
. Radiat. Prot. 40(01) 38-44 (2020). (in Chinese)Development and verification of radiation shielding optimization design platform for marine reactor
. Nuclear Power Engineering. 43(1), 221-228 (2022). https://doi.org/10.13832/j.jnpe.2022.01.0208 (in Chinese)CAD-based inversion visualization of monte Carlo Computational model based on SALOME
. High Power Laser And Particle Beams. 35(03), 168-174 (2023). https://doi.org/10.11884/HPLPB202335.220276 (in Chinese)Development and benchmarking of the Weight Window Mesh function for OpenMC
. Fusion. Eng. Des. 170,Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems
. Siam. J. Optimiz. 134, 631-657 (1998). https://doi.org/10.1137/S1052623496307510A fast and elitist multi objective genetic algorithm: NSGA-II
. Ieee. T. Evolue. Comput. 6(2), 182-197 (2002). https://doi.org/10.1109/4235.996017Genetic algorithms and their applications
. Ieee. Signal. Proc. Mag. 13(6), 22-37 (1996). https://doi.org/10.1109/79.543973Study on many-objective optimization method for reactor 3D shielding structure based on Genetic Algorithm
. Nucl. Tech. 45(11), 101-111 (2022). https://doi.org/10.11889/j.0253-3219.2022.hjs.45.110603 (in Chinese)An elitism based multi-objective artificial bee colony algorithm
. Eur. J. Oper. Re. 245(1), 168-193 (2015). https://doi.org/10.1016/j.ejor.2015.03.005A multi-objective artificial bee colony algorithm
. Swarm. Evol. Comput. 2, 39-52 (2012). https://doi.org/10.1016/j.swevo.2011.08.001Recent advances in differential evolution: a survey and experimental analysis
. Artif. Intell. Rev. 33, 61-106 (2010). https://doi.org/10.1007/s10462-009-9137-2Golden Sine Algorithm: A Novel Math-Inspired Algorithm
. Adv. Electr. Comput. En. 17, 71-78 (2017). https://doi.org/10.4316/AECE.2017.02010A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization
. Appl. Math. Comput. 186(2), 1407-1422 (2007). https://doi.org/10.1016/j.amc.2006.07.134An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach
. Ieee. T. Evolue. Comput. 18(4), 602-622 (2013). https://doi.org/10.1109/TEVC.2013.2281534An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints
. Ieee. T. Evolue. Comput. 18(4), 577-601 (2013). https://doi.org/10.1109/TEVC.2013.2281535ENDF/B-VIII. 0: the 8th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data
. Nucl. Data. Sheets. 148, 1-142 (2018). https://doi.org/10.1016/j.nds.2018.02.001An historical review and current status of buildup factor calculations and applications
. Radiat. Phys. Chem. 41, 631-672 (1993). https://doi.org/10.1016/0969-806X(93)90317-NDevelopment and Verification of a Monte Carlo Calculation Program Magic for Dose of Boron Neutron Capture Therapy
. Modern Applied Physics 14(04), 41-48 (2023). https://doi.org/10.12061/j.issn.2095-6223.2023.040202 (in Chinese)SMS-EMOA: Multiobjective selection based on dominated hypervolume
. Ieee World Congress On Computational Intelligence. 282–288, (2016). https://doi.org/10.1109/FSKD.2016.7603187Single-step Monte Carlo criticality algorithm
. Comput. Phys. Commun. 279,Pointing probability driven semi-analytic Monte Carlo method (PDMC)–Part I: global variance reduction for large-scale radiation transport analysis
. Comput. Phys. Commun. 291,SP3-coupled global variance reduction method based on RMC code
. Nucl. Sci. Tech. 32, 122 (2021).https://doi.org/10.1007/s41365-021-00973-0Mesh-based activation analysis for structural materials in nuclear reactor
. Nucl. Tech. 45(08), 080601-080601 (2022). https://doi.org/10.11889/j.0253-3219.2022.hjs.45.080601 (in Chinese)The authors declare that they have no competing interests.


