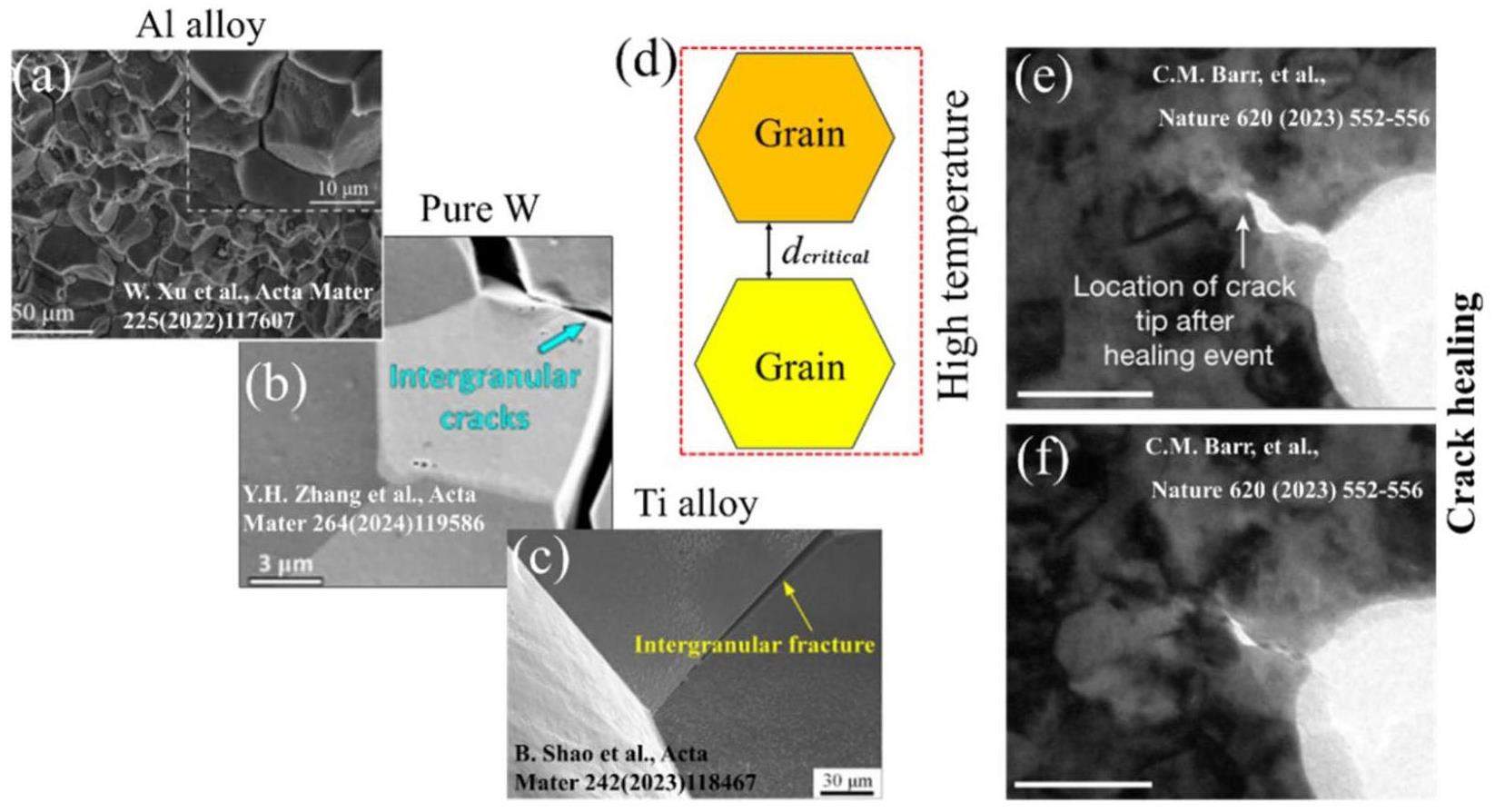
Introduction

Growing demand for clean energy has accelerated the development of the nuclear energy industry. Nuclear reactor components must operate in environments with high temperatures, stresses, irradiation, and hydrogen concentrations [1-6] and may develop nanocracks. Therefore, their safe operation requires an understanding of the stabilization behavior of these nanocracks at high temperatures. Al alloys have a small thermal neutron absorption cross-section, excellent plasticity, favorable thermal conductivity, and machinability, and are widely applied in nuclear reactor cladding shells and pressure vessels [1, 2]. The best candidate metal for the first wall is W owing to its high melting point, high-temperature strength, high thermal conductivity, and resistance to irradiation damage [3, 4]. However, the harsh, high-temperature, high-stress, and highly corrosive environment inside reactors requires Al and W alloys with exceptional stability and strength. Although Ti is commonly used to store nuclear waste, it is susceptible to grain boundary (GB) embrittlement [5]. In this study, Al, W, and Ti alloys were investigated to understand the high-temperature stability of GB cracks.

Over the past few decades, alloys containing Al, W, and Ti with microstructures that resist deformation, cracking, and failure (e.g., crack initiation, propagation, and extension) have been successfully developed [1-5]. However, few studies have investigated alloy failure prevention or remediation. For metals, most self-healing methods rely on temperature and stress, which activate atomic diffusion for crack healing. For example, stress-driven GB migration, which may originate from inhomogeneous stresses, is widely observed in nanocrystalline metals; this GB migration can promote crack healing [6]. If localized compressive stresses drive crack healing at the GBs, then concentrated tensile stresses near the GBs may damage the structure in this vicinity; that is, crack healing requires a stable structure that can store additional energy [4, 5]. The GB crack healing is closely related to GB migration; therefore, the stability and characteristics of this migration should be investigated. The complementary process of high-temperature-driven microstructural evolution can also promote GB crack healing; the disappearance of GB microcracks is driven by atomic diffusion after atoms break GB crack bonds at high temperatures [6-9]. However, an accurate mechanical model of alloy crack migration at high temperatures has not yet been developed. To date, design strategies for self-healing materials have only been proposed for polymers and composites [10].

Temperature affects both GB nanocrack sprouting and healing. This can promote crack healing by activating the structures within the grains. At low temperatures (e.g., 0, 293, or 373 K), GB nanocracks heal through mechanical or chemical mechanisms, and the GB crack stability is dependent on the GB characteristics and crack surfaces. At high temperatures, binding at the crack surface may enhance GB crack stability, and random atom diffusion on the crack surface may contribute to healing [6]. Furthermore, low temperatures inhibit the formation of amorphous nano-cracked structures. Few crack formation and extension theories explain crack stability and healing, and research on the stabilization behavior of nanocrack surfaces (e.g., diffusion, clustering, and atom disordering) at high temperatures are rare [7, 8]. Nanocrack sprouting is a representative GB structure behavior that relies solely on the localized energy or diffusion of individual atoms to confirm that the stability of a nano-cracked surface is inappropriate [8]. GB self-healing is closely related to the cracking state.

To investigate the adsorption behavior of crack surfaces and the healing behavior after complete GB fracture, we selected face-centered cubic (FCC) Al, body-centered cubic (BCC) W, and hexagonal close-packed (HCP) Ti alloy GBs and separated them into crack surfaces. The structure of the nanocracks, as they evolved from sprouting to expansion to fracture, was established within the coherent lattices for ∑3 and ∑5 GBs. Finally, nanocrack structural stabilization and healing were simulated at 0, 293, and 373 K.

Calculation details

Weld, creep, and stress concentrations accelerate the sprouting of GB cracks, which significantly compromises the safe operation of nuclear reactors [7, 8]. Table 1 and Fig. 1 present the GB fracture modes of Al, pure and alloyed W, and Ti alloys at room and high temperatures. W failure is accelerated by intergranular fractures at low temperatures. Barr et al. [6] reported the self-healing of fatigue cracks in pure metals. Qiu et al. [9] quantitatively evaluated the room-temperature self-healing behavior of nanodiamond composites. Understanding the self-healing mechanisms of cracks in high-temperature and -stress environments can extend the service life of nuclear metals. However, experimentally investigating the crack-healing process is difficult [6, 7]; therefore, the present study combined simulations and thermodynamics to quantify the synergistic effects of temperature, stress, and GBs on crack healing. The GB crack structure of the metal is listed in Table 1. The fracture modes of Ti alloys at 298, 1023, and 1203 K are intergranular, proving that Ti GB cracks are not healed (Table 1). Meanwhile, crack healing in W was demonstrated in [3].

Fig. 1Full-screen View

(Color online) GB cracking of metals at high temperature: (a) Al alloy [1], (b) pure W [3], and (c) Ti alloy [5]. (d) GB separation at high temperature. (e, f) Crack healing [6]

Figure 2 shows the GBs of the lattices investigated in this study. The red dashed line represents the GB plane. The HCP Ti twins, namely, (10-11) and (10-12), are defined as compression and tensile twins, respectively. Figure 2(g) shows the separation of a GB into two nano-cracked surfaces; the yellow area represents the GB nanocrack and d represents the crack width. Details regarding the calculation of d are given in [10].

Fig. 2Full-screen View

(Color online) Lattice GBs: (a) ∑3(111) and (b) ∑5(210) GBs of FCC (Al), (c) ∑3(111) and (d) ∑5(210) GBs of BCC (W), and (e) ∑3(10-11) and (f) ∑3(10-12) GBs of HCP (Ti). (g) GB nanocrack formation after GB separation

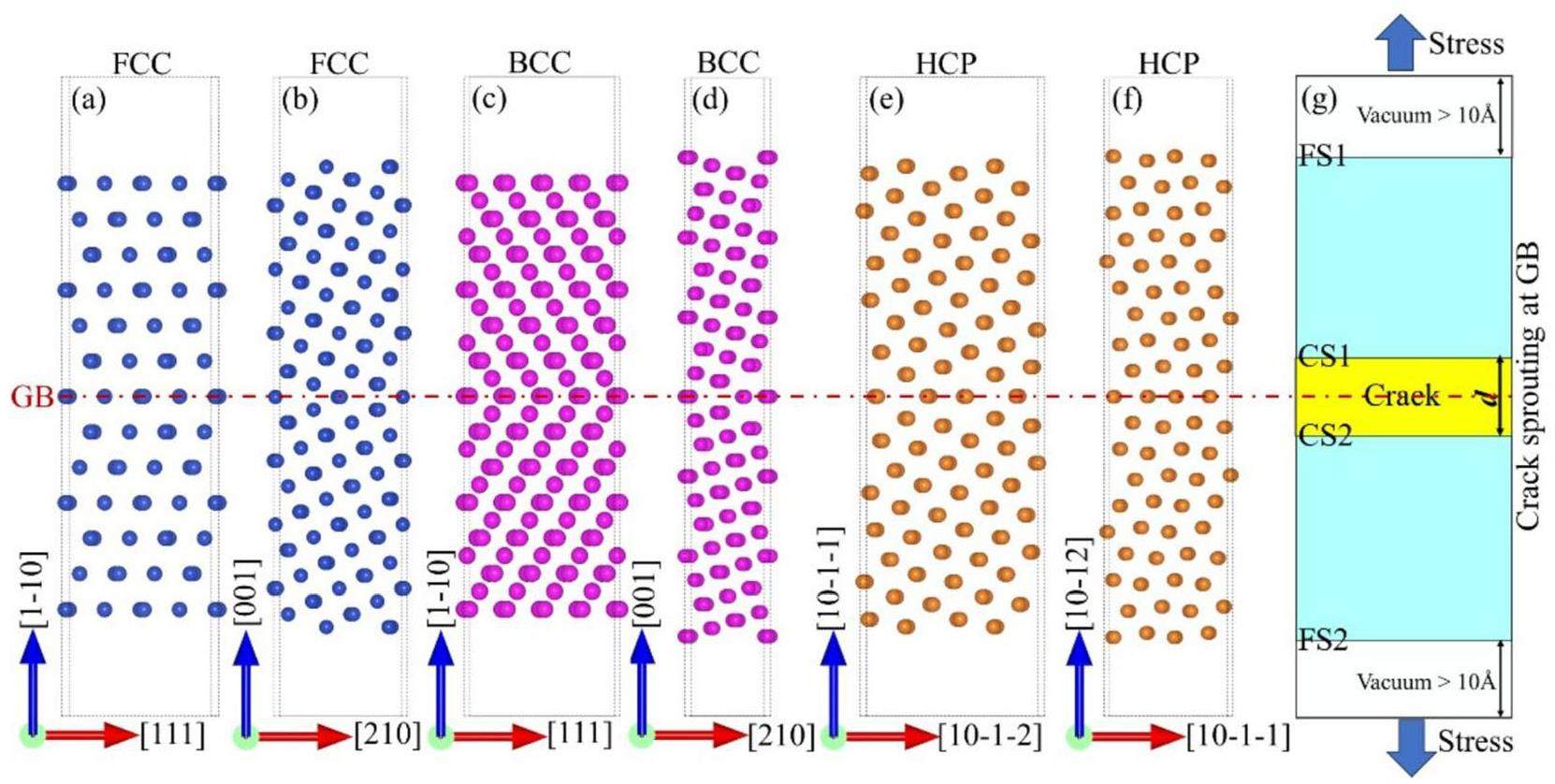
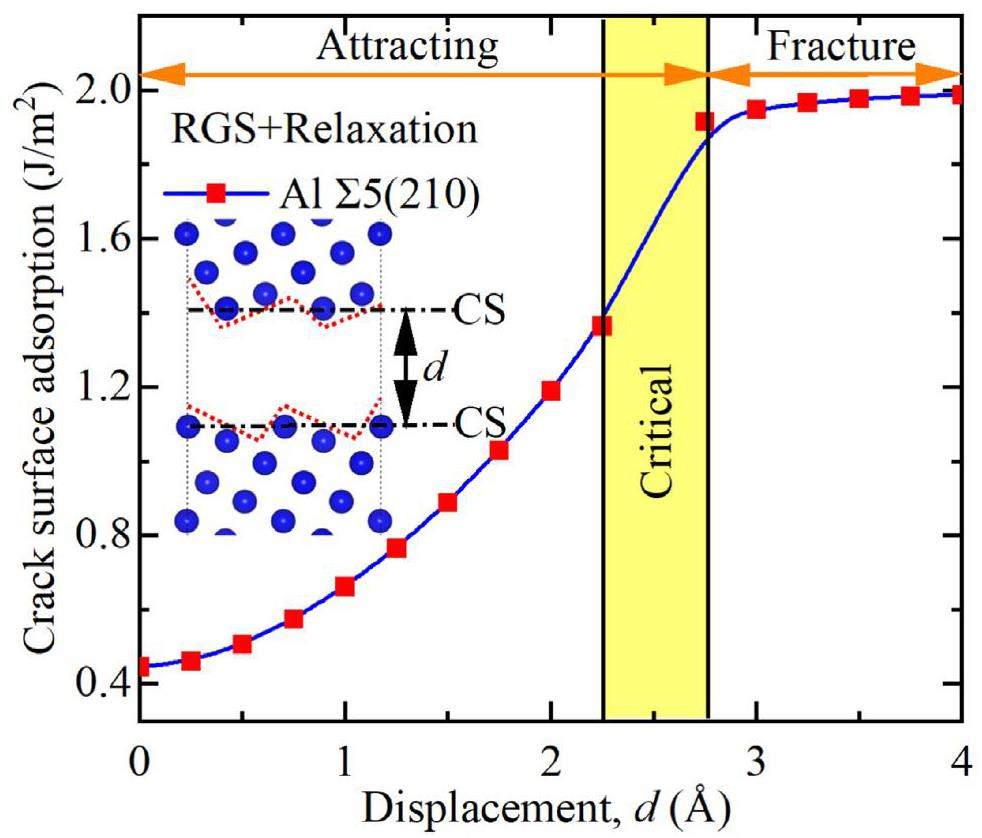
Figure 3 shows the rigid grain shift (RGS) [10]. In this model, the GB is subjected to tensile stress during relaxation between 0 and 373 K. First, a small displacement increment d is added in the direction perpendicular to the GB plane, achieving complete separation and forming two crack surfaces (CS in the figure). For each d, two calculations were performed with a fixed supercell length to obtain the RGS and relaxation at 423 K and the desired temperature. The relaxed cracks have an attraction energy E_attract (Eq. (1)), which is plotted against the displacement of the selected ∑5 (210) GB in Fig. 3. GB separation resulted in the formation of two zigzag crack surfaces (dashed red lines). However, this GB separation may be accompanied by GB self-healing; a strong attraction at the crack surface drives crack healing if E_attract < 0, however, complete GB separation occurs if E_attract = 0.

Fig. 3Full-screen View

(Color online) Crack attraction energy versus displacement of selected Al ∑5 (210) evaluated via the RGS+relaxation methodology

The interaction at the cracked surface for a GB separation distance of d can be characterized as $\text{Δ}{\gamma }_{\text{n}}^{\text{CS}}={\gamma }_{\text{d}}^{\text{CS}}-n{\gamma }_{\text{FS}},$ (1) where ${\gamma }_{\text{d}}^{\text{CS}}$ is the total energy corresponding to the formation of a cracked surface after GB separation and γ_FS is the total energy of the free surface (Fig. 2(g)) [10-12]. After GB separation, the structure underwent cracking, resulting in two cracked surfaces and two fracture surfaces (FSs). Therefore, when n = 4, negative $\text{Δ}{\gamma }_{\text{n=4}}^{\text{CS}}$ indicates the mutual attraction of cracked surfaces (E_attract). Given that the attraction of cracked surfaces is positively correlated with the GB strength, $\text{Δ}{\gamma }_{\text{n=4}}^{\text{CS}}$ = 0 when the GB is broken and no attraction is observed on the cracked surfaces. ${\gamma }_{\text{d}}^{\text{CS}}$ is calculated as follows: ${\gamma }_{\text{d}}^{\text{CS}}=\frac{\left(E_{\text{d}}^{\text{CS}}-\alpha {\mu }_X\right)}{A}\mathrm{,}$ (2) where $E_{\text{d}}^{\text{CS}}$ is the total energy after GB separation, ${\mu }_{X\text{=Al,W,Ti}}$ is the atomic chemical potential [13], α is the atomic number, and A is the GB area. At high temperatures, the GB cracked structure may be disordered and amorphous in the cracked region. The GB energy per unit volume can be expressed by the energy density as follows: ${\rho }_{\text{E}}=C\times \frac{E_{\text{d}}^{\text{CS}}-E_{\text{GB}}}{V_{\text{d}}-V_0}\mathrm{,}$ (3) where the energy density (i.e., stress) is measured in Pa, E_GB is the total GB energy, and C = 1.6 × 10¹¹.

First-principles calculations were performed using the density functional theory in the Vienna Ab initio Simulation Package software [14]. Electron-ion interactions were modeled using the projector-augmented wave method [15]. The generalized gradient approximation [16] of the exchange-correlation energy was used in this study. The total energy was converged to within 10^-5 eV, whereas the atomic forces were converged to within 0.02 eV/A°. The cutoff energy in the calculation was 400 eV. Ab initio molecular dynamics [13] simulations were performed to analyze the dynamic properties of the supported cracks. The calculations were performed with optimized configurations and fixed lattice parameters for durations of at least 5 ps to more than 20 ps with a 1-fs time step. A canonical ensemble (NVT) and a Nosé–Hoover thermostat were used. The temperature was set to 293 or 373 K. Table 2 lists the lattice parameters, atomic counts, sizes, K-points, GB energies, and surface energies of the assessed GB structures. The GB and surface energies are consistent with the results reported in the literature [11, 17, 18], confirming the precision of our calculations.

Results

Based on the simulation results, the following conclusions could be drawn:

1) The energy density is derived from the crack surface energy; low-energy crack surfaces have high stability, and GBs are highly resistant to nanocrack healing.

2) At high energies, crack surfaces have low stability; however, atoms on crack surfaces have a high diffusion drive, and their diffusion is accelerated by high temperatures.

3) Crack surface stability is influenced by the energy and strength of the bonds between the atoms on the crack surface. For example, low-energy and strongly bonded GB cracks are stable but are unlikely to heal.

4) The developed model for high-temperature GB migration is accurate and well-suited for describing the target service environment.

3.1

Relationship between crack width and energy

Crack healing, modulated by localized stress and GB migration, challenges the fundamental theory for structural material lifetime evaluation. A nanocrack structural evolution simulation from sprouting to expansion to fracture was established within coherent lattices with ∑3 and ∑5 GBs, and the stabilization and healing of nanocrack structures were simulated at 0, 293, and 373 K. Figure 4 shows the results for 0 K. We applied tensile stress in the z-direction (i.e., at the vertical GB) to induce GB separation and calculated the effect of the GB crack width d on the energy density and crack surface adsorption using Eqs. (1) and (3) (Figs. 4(a) and (b)).

Fig. 4Full-screen View

(Color online) Simulation results for 0 K: (a) energy density, (b) crack surface adsorption, (c) critical crack surface adsorption, (d) atomic deformation volume of atoms after nanocrack healing, (e) atomic deformation volume after complete GB fracturing, (f) ∑3(111) charge density (e/Bohr³) of Al at 0 and 2.25, and (g) ∑5(210) charge density of Al at 0 and 2.25

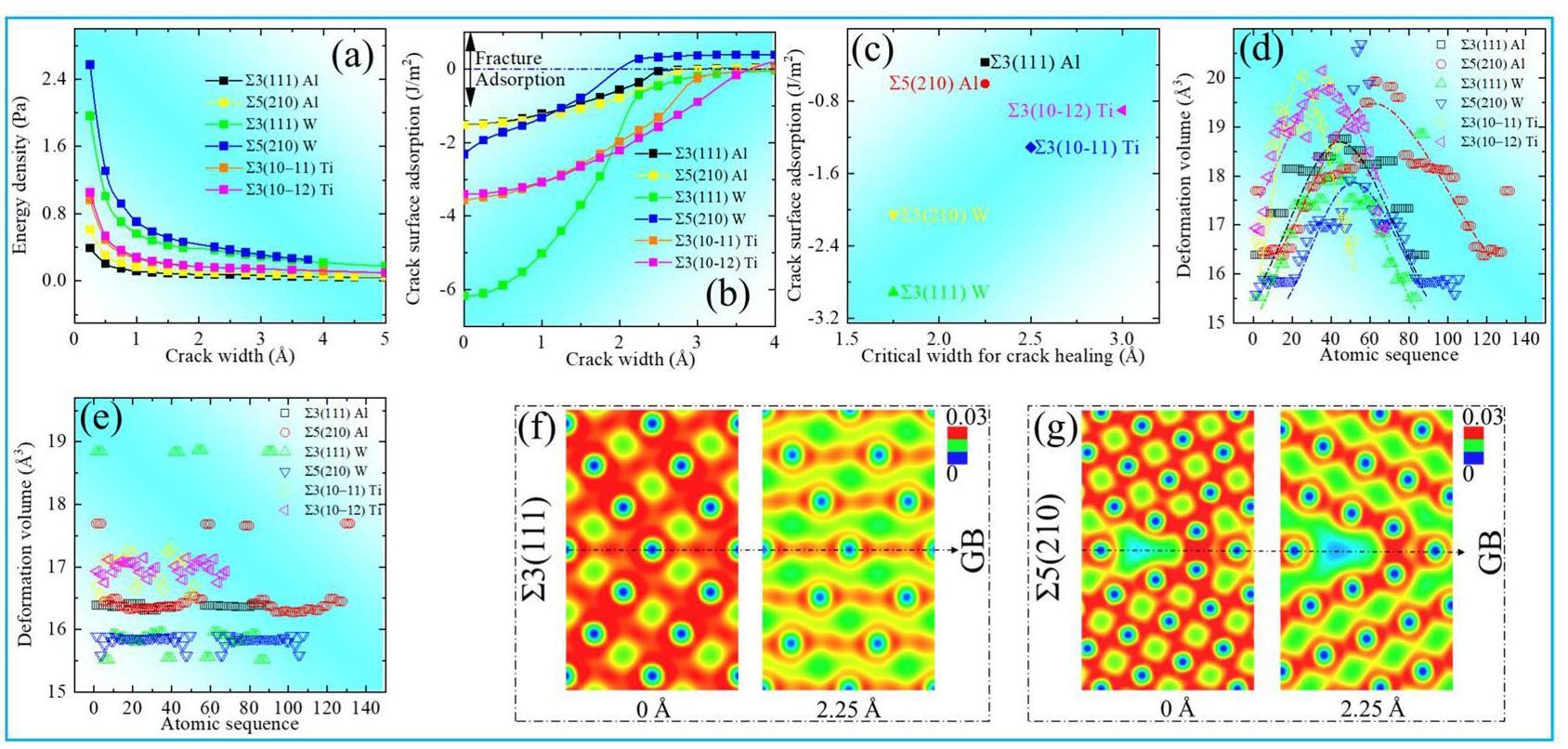
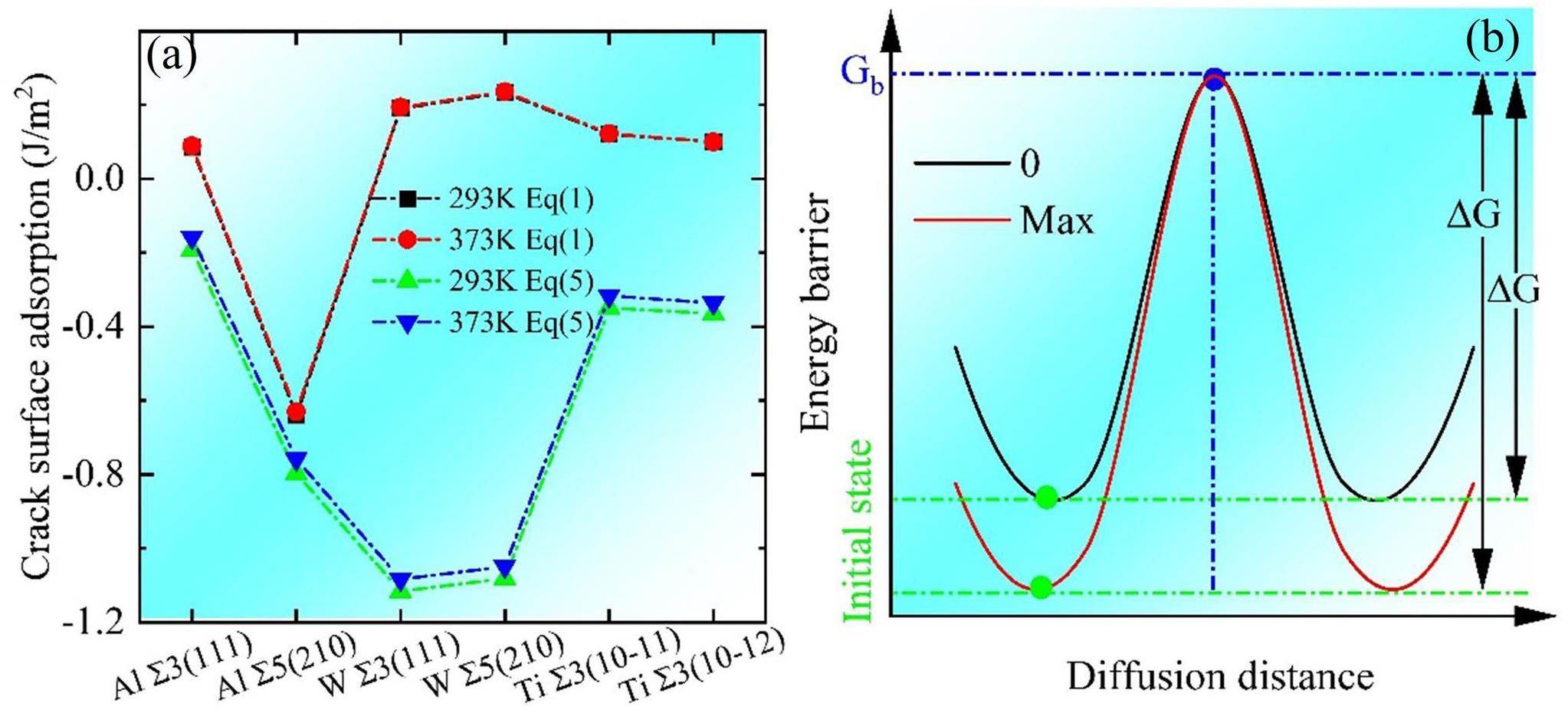
As shown in Fig. 4(a), low energy density is associated with high stability in the GB cracking system. The energy density was derived from the crack surface energy using Eq. (3) and is directly proportional to 1/d. The energy density order at 0 K is as follows: ∑5(210) W (highest energy, lowest stability) > ∑3(111) W > ∑3(10-12) Ti ≈ ∑3(10-11) Ti > ∑5(210) Al > ∑3(111) Al (lowest energy, highest stability). For d < 1 Å, the GB energy density is high; however, when it is between 4 and 5 Å, the energy density approaches 0 Pa, indicating that the GB has completely fractured and separated into two free cracked surfaces. In Fig. 4(b), the negative and positive crack surface adsorption indicates mutual attraction and no attraction, respectively, between GB cracks. The surface adsorption of ∑3(111) W is maximized at d < 2 Å. The adsorption energies of the Ti (10-11) and (10-12) GBs are similar, and that of Al ∑5(210) is slightly higher than that of Al ∑3(111), indicating that W ∑3(111) exhibits the highest resistance to GB crack widening. Figures 4(a) and 4(b) reveal that crack sprouting is inhibited at GBs with high energy densities, and that GB fracturing is accelerated at GBs with low energy densities. The presence of a GB crack with width d < d_Critical indicates GB healing. Figure 4(c) shows the relationship between d_Critical and crack surface adsorption. When d > d_Critical, the interaction between GB cracks vanishes and the GB fractures. Crack extension originates from the accumulation of minor interatomic strains. We quantified these strains in terms of the atomic deformation volume, also known as the Voronoi volume [11].

Figure 4(d) shows the atomic deformation volume on a GB at d = d_Critical, revealing a parabolic feature with increasing atomic order. After crack healing, the atomic deformation volume at the GB approached the vertex of the parabola. Figure 4(e) shows the atomic deformation volume after complete cracking, revealing that the deformation volume is stable. Figures 4(f) and 4(g) show the Al charge densities at d =0 Å and d_Critical = 2.25 Å. After crack healing, the charge density of ∑3(111) Al is lower than that of ∑5(210) Al, indicating an increase in the interatomic bonding of ∑5(210) Al after healing.

At 0K, microcrack healing does not occur after GB fracturing [6]. Therefore, we performed simulations at room temperature (293 K) and the destressed annealing temperature (373 K) to evaluate the non-mechanical healing of nanocracks and microcracks after complete GB fracturing (Figs. 5(a) and (b)). Figures 5(c) and (d) reveal the stability of the GB structure and crack surface energy, as calculated using Eq. (1) for 293 and 373 K. As shown in Fig. 5(c), ∑5(210) Al has the lowest crack surface attraction at both temperatures, suggesting that ∑5(210) Al cracks are stable and cannot be healed. However, the positive crack surface adsorption of W, Ti, and ∑3(111) Al reveals that the temperature presumably results in atomic diffusion at the crack surface, promoting crack healing.

Fig. 5Full-screen View

(Color online) Simulation results for room and annealing temperatures. GB energy fluctuations at (a) 293 and (b) 373 K. (c) Average energy density at both temperatures. Atomic volume density at (d) 293 and (e) 373 K. Charge density of (f) ∑3(111) Al and (g) ∑5(210) Al at 0, 293, and 373 K

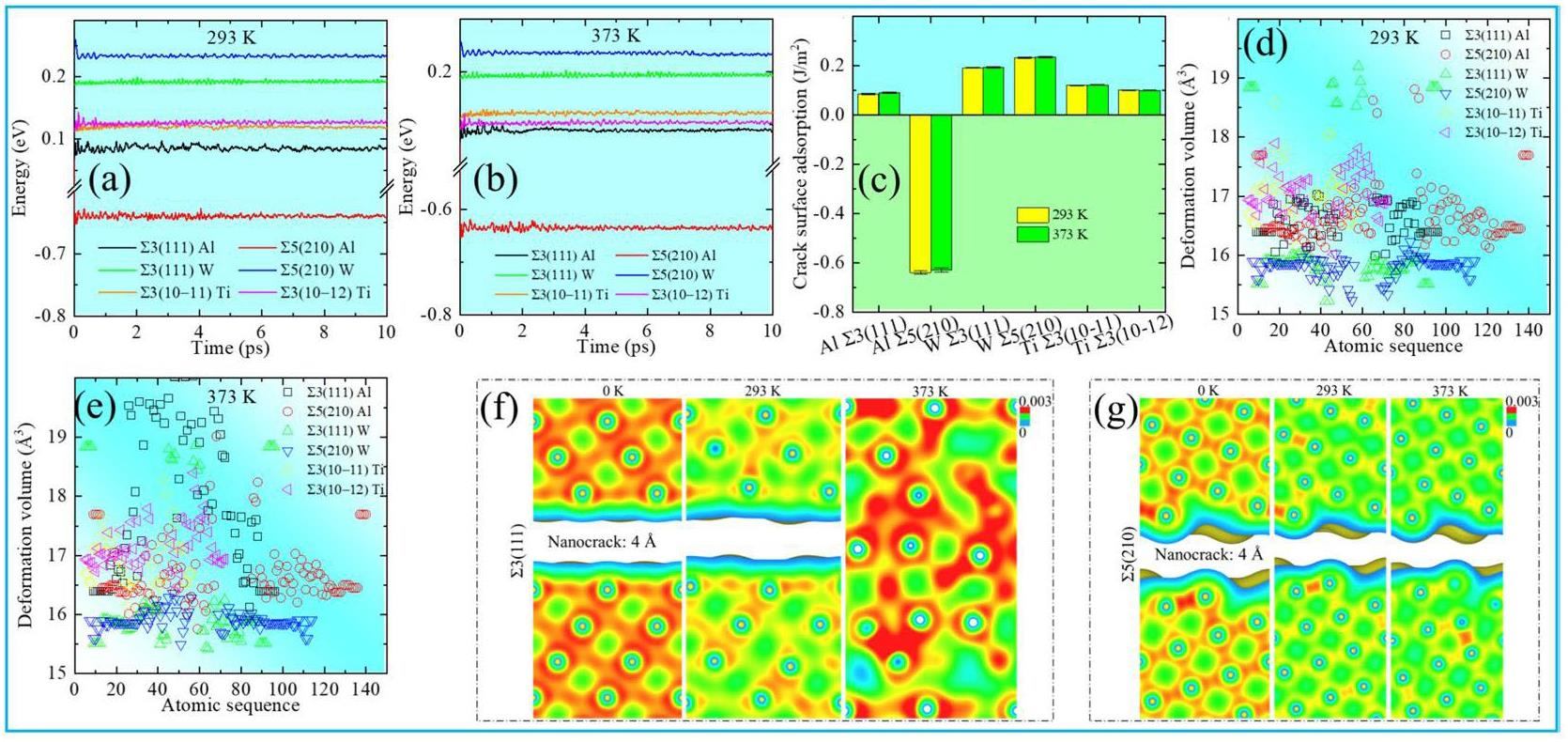
Figures 5(d) and (e) show the atomic deformation volumes at 293 and 373 K, respectively; the temperature and atomic volume density are positively correlated. Figures 5(f) and (g) present the charge densities of Al at 0, 293, and 373 K at d_Critical. As shown in Fig. 5(f), although crack healing is not promoted at 0 or 293 K, GB cracks disappear at 373 K; this crack healing is attributed to atomic diffusion. The high temperature (373 K) prevented the formation of an amorphous crack structure. At 0, 293, and 373 K, the cracks in W and Ti did not heal.

We calculated the energy fluctuations and charge density differences between W and Ti at 573 and 1203 K (Fig. 6) according to the experimental results presented in Table 2. The charge-transfer behavior of Al at 293 and 373 K is also shown in Fig. 6. The charge density difference (Δρ) is calculated as follows: $\text{Δ}\rho ={\rho }_{\text{T}}-{\rho }_0$ (4) where ρ_T and ρ₀ are the crack charge densities at high temperatures and at 0 K, respectively. The isosurface value of the charge density was set as 0.03 e/Bohr³. First, Figs. 6(a) and (b) show the Δρ of Al at 293 and 373 K, respectively, where the charge accumulates on the cracked surface and cracked region of ∑3(111) Al, and the Δρ of ∑5(210) Al is lower, implying a weaker charge transfer tendency at high temperatures (293 and 373 K) for ∑5(210). Next, Figs. 7(a) and (d) show the energies of W and Ti, respectively, at high temperatures (573 and 1203 K). Figures 7(b) and (c) show the Δρ and atomic structure of ∑3(111) W and ∑5(210) W at high temperatures, respectively, where the crack structure of ∑5(210) W is ordered to heal at 573 and 1203 K, while the Δρ of the healed region is the highest at this temperature. Figures 7(e) and (f) shows the Δρ of ∑3(10-11) Ti and ∑3(10-12) Ti at high temperatures, respectively, where the crack structure of Ti remains stable and the charge density near the crack surface is higher.

Fig. 6Full-screen View

(Color online) Charge density difference in Al at high temperatures: (a) ∑3(111) and (b) ∑5(210)

Fig. 7Full-screen View

(Color online) (a) Energy fluctuations of W at 573 and 1203 K. High-temperature charge difference densities for (b) ∑3(111) and (c) ∑5(210). (d) Energy fluctuations of Ti at 573 and 1203 K. High-temperature charge difference densities for (e) ∑3(10-11) and (f) ∑3(10-12)

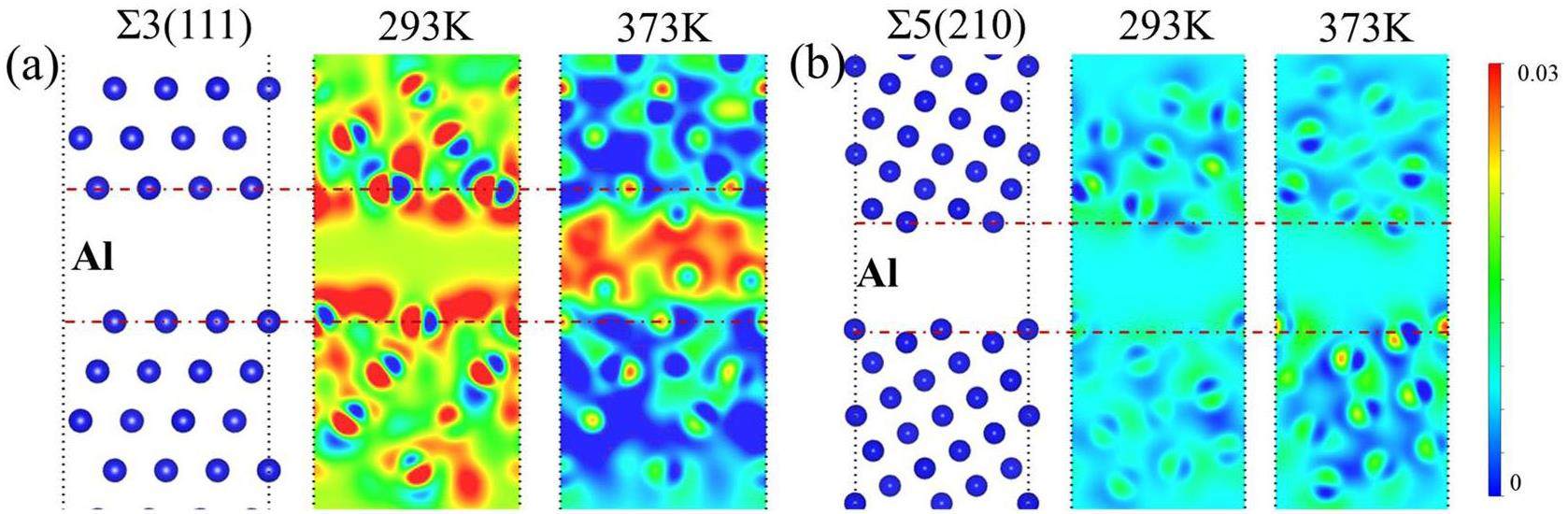
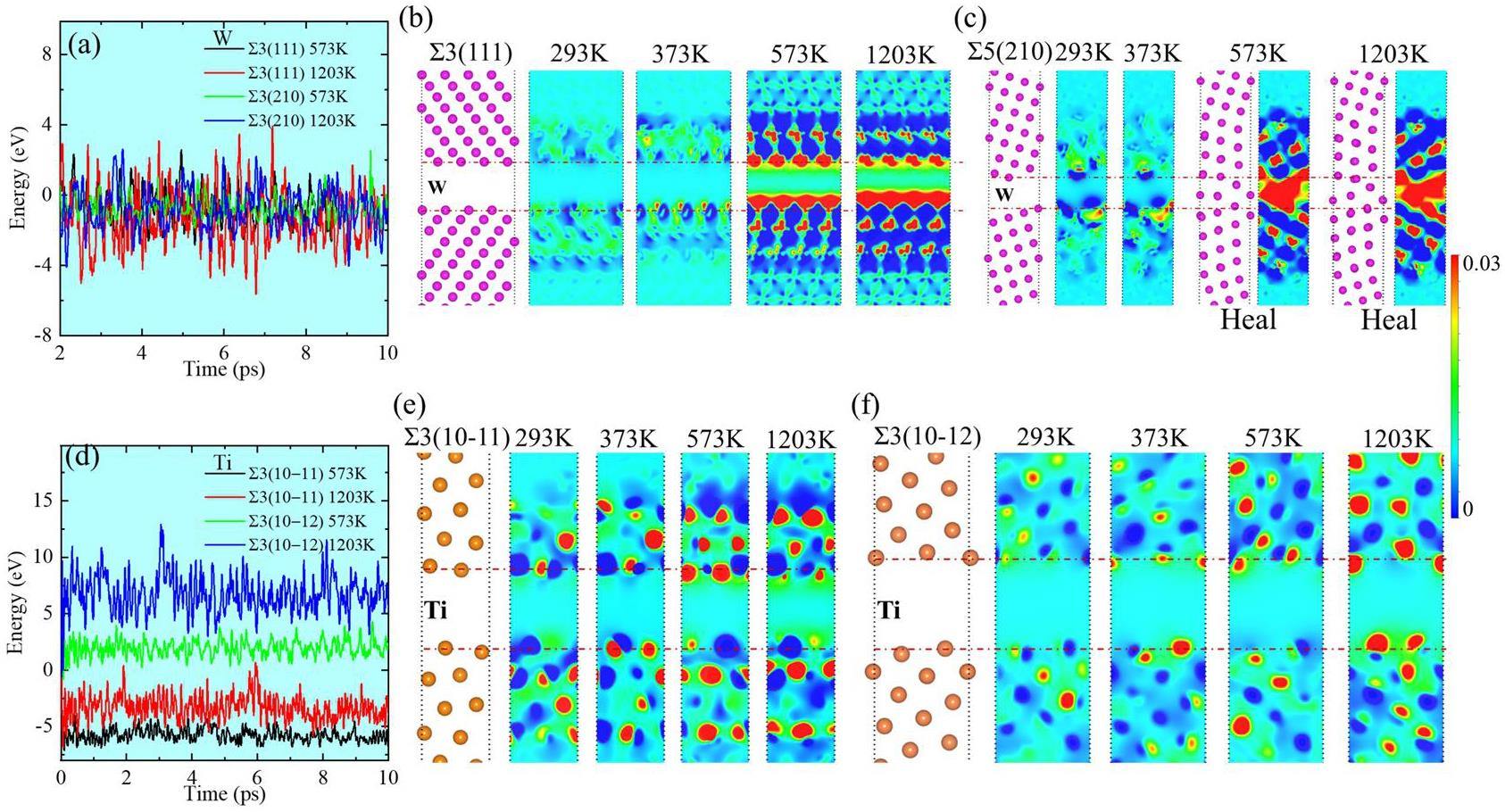
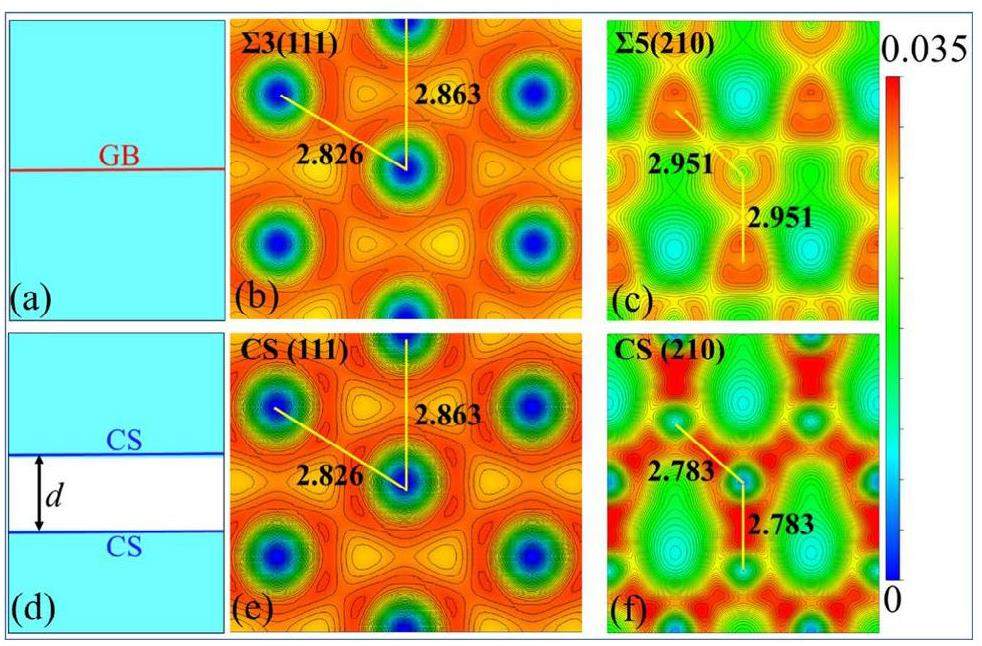
Figure 8 shows the charge densities of Al alloys with intact GBs (top) and crack structures (bottom), which are depicted in Figs. 8(a) and 8(d), respectively. For the non-cracked alloys, the charge density of ∑3(111) Al (Fig. 8(b)) was higher than that of ∑5(210) Al (Fig. 8(e)); their interatomic bond lengths are 2.826 and 2.863, respectively. However, for cracked structures, the charge density of CS (210) Al (Fig. 8(c)) was lower than that of CS (111) Al (Fig. 8(f)); after cracking; the bond length of (111) Al is unchanged, whereas that of (210) Al has contracted to 2.951 Å. This implies that CS (210) Al has a greater bond strength than CS (111) Al. Therefore, crack healing is determined by both the crack adsorption energy and bonding, and crack surfaces with low energy and weak bonding exhibit superior crack healing.

Fig. 8Full-screen View

(Color online) (a) GB and (b) cracked surfaces (CSs). Charge density (e/Bohr³) on the GB for (c) ∑3(111) Al and (d) ∑5(210) Al. Charge density on the CS for (e) ∑3(111) Al and (f) ∑5(210) Al

The bonding or antibonding state of the crack structure as a whole can be considered in terms of the normalized localized density of states (LDOS), which is calculated as follows: $\text{Δ}\text{LDOS}={\text{LDOS}}_{\alpha }-{\text{LDOS}}_{\beta }\mathrm{,}$ (5) where ${\text{LDOS}}_{\alpha }$ and ${\text{LDOS}}_{\beta }$ are the densities of states of α and β, respectively; ΔLDOS ≈ 0 implies interatomic bonding. α is the structure containing cracks and β is the Al GB. Figure 9 shows ΔLDOS after the complete splitting of the Al GB. When E₀ < 0, ΔLDOS ≈ 0 implies the bonding state. When E₀ > 0, ΔLDOS exhibits a large fluctuation range, while the strongest antibonding state occurs on ∑3(111). As can be seen, ∑3(111) Al has no significant bonding tendency when the GBs are fully separated.

Fig. 9Full-screen View

(Color online) LDOS for ∑3(111) and ∑5(210) Al

3.2

Qualitative analysis of high-temperature cracked surfaces

At high temperatures, any surface disorder can be assumed to occur at the beginning of surface melting [19-21]. The healing behavior of GB nanocracks is closely linked to $\text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}$. The relationship between entropy S and the crack surface interaction energy $\text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}$ for complete GB fracturing at temperature T [21] is as follows: $S=-\frac{\partial \text{Δ}{\gamma }_{\text{T}\mathrm{,}\text{n=4}}^{\text{C}S}}{\partial T}.$ (6) For high-temperature melting [21], ${\gamma }_{\text{melting}}^{\text{CS}}=\frac{\text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}+\frac{\partial \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}}{\partial T}\left(T_{\text{m}}-T\right)}{1.2}$ (7) with T = 0, 293, or 373 K. The melting points (T_m) of Al, W, and Ti are 993, 3693, and 1490 K, respectively. Figure 10(a) shows the $\text{Δ}{\gamma }_{T\mathrm{,}n=4}^{\text{CS}}$ values of the GBs that exhibit similar trends at 373 and 293 K [21]. However, if the cracked surface begins to melt or the atoms escape surface confinement, the data shown in Fig. 10(a) and Eq. (1) are not valid. Therefore, ${\gamma }_{\text{Critical}}^{\text{CS}}$ at high temperatures can be obtained using Eq. (7). Figure 10(a) shows ${\gamma }_{\text{Critical}}^{\text{CS}}$ for the GBs; the trends are similar at 293 and 373 K, and the corresponding values for Al ∑3(111) are 0.37 and 0.40 J/m², respectively. Furthermore, ${\gamma }_{\text{Critical}}^{\text{CS}}$ for Al ∑3(111) was the lowest at 373 K. It is worth noting that, as mentioned before, cracked surfaces heal only for Al ∑3(111) (Fig. 10(f)), which implies that the healing behavior of Al ∑3(111) may be related to ${\gamma }_{\text{Critical}}^{\text{CS}}$. This phenomenon can be explained by diffusion energy barriers [22]: $P_{\text{T}}=\exp \left(-\frac{G_{\text{b}}-A\times {\gamma }_{\text{Critical}}^{\text{CS}}}{KT}\right),$ (8) where $G_{\text{b}}$ and K are the diffusion energy barrier and the Boltzmann constant, respectively, and $\text{Δ}G=G_{\text{b}}-A\times {\gamma }_{\text{Critical}}^{\text{CS}}$. This equation was used to determine the diffusion resistance of healing surface atoms. In Fig. 10(b), the green and blue points represent the initial atomic states and energy barrier sites, respectively. The results shown in Fig. 10(b) imply that $\text{Δ}G$ is the largest for Al ∑3(111), the coordination number of atoms on the crack surface of Al ∑3(111) is higher than that of Al ∑5(210), and the crack-healing behavior of Al ∑3(111) may be attributed to its low crack surface energy [23].

Fig. 10Full-screen View

(Color online) (a) Interaction energies of cracked surfaces, as obtained using Eqs. (1) and (5). (b) Schematic of a diffusion energy barrier

3.3

High-temperature crack extension modeling

Crack healing is closely associated with GB migration. Under tensile loading, the spacing between crack surfaces increases, resulting in nanocrack growth. According to thermodynamic strength theory [24-28], a nanocrack separates into two free surfaces when the external work done by the loading surpasses the interaction energy between the nanocrack surfaces: $\sigma \left(d_{\text{Critical}}-d\right)\ge \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}$ (9) where d_Critical-d is the working distance. This process is equivalent to externally driving a nanocrack to overcome an energy barrier with height $A\times \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}$. Eq. (9) is equivalent to the energy release rate criterion in fracture mechanics. Therefore, the critical stress for nanocrack separation can be derived as follows: ${\sigma }_{\text{cr}}\left(T\mathrm{,}d\right)=\text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}/\left(d_{\text{Critical}}-d\right)\mathrm{.}$ (10) The critical stress ${\sigma }_{\text{cr}}$ is not the minimum stress required for nanocrack separation; Eq. (10) does not account for the contribution of thermal-activation effects. Overcoming the thermally activated barrier is certainly involved in determining this rate. That is, the separation stress of a nanocrack (denoted σ_s) is influenced by the separation rate. This separation rate can be considered as the rate of a thermally activated process, which can be quantified using the Arrhenius equation, as follows: $v=v_0\text{exp}\left(-A\frac{\text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}-{\sigma }_{\text{s}}{d}_{\text{Critical}}}{\kappa T}\right),$ (11) where v₀ denotes the separation rate under stress σ_cr and is called the characteristic separation rate. Eq. (11) can be rewritten as ${\sigma }_{\text{s}}\left(T\mathrm{,}d\mathrm{,}v\right)={\sigma }_{\text{cr}}\left(T\mathrm{,}d\right)+\frac{KT}{A\left(d_{\text{Critical}}-d\right)}\ln \frac{v}{v_0}\mathrm{.}$ (12) When considering thermal activation effects, an additional term $\frac{KT}{A\left(d_{\text{Critical}}-d\right)}\ln \frac{v}{v_0}$ is introduced into the separation stress expression. This term indicates that when the actual separation rate of nanocrack v is lower than v₀ for a given T and d, ${\sigma }_{\text{s}}\left(T\mathrm{,}d\mathrm{,}v\right)<{\sigma }_{\text{cr}}\left(T\mathrm{,}d\right)$. Because $KT\ll A\times \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}$, the thermally activated term is negligible at low temperatures. As mentioned, $\text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}\approx 1.2{\gamma }_{\text{melting}}^{\text{CS}}-\frac{\partial \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}}{\partial T}\left(T_{\text{m}}-T\right)$ at high temperatures; therefore, we have $\begin{array}{c}{\sigma }_{\text{s}}\left(T\mathrm{,}d\mathrm{,}v\right)=\frac{1}{d_{\text{Critical}}-d}[1.2{\gamma }_{\text{melting}}^{\text{CS}}-T_{\text{m}}\frac{\partial \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}}{\partial T}\\ +T\left(\frac{\partial \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}}{\partial T}+\frac{K}{A}\ln \frac{v}{v_0}\right)].\end{array}$ (13) Equation (13) reveals that the high-temperature separating stress is directly proportional to the temperature, with a slope of $\frac{1}{d_{\text{Critical}}-d}\left(\frac{\partial \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}}{\partial T}+\frac{K}{A}\ln \frac{v}{v_0}\right)$. As $\frac{\partial \text{Δ}{\gamma }_{\text{T}\mathrm{,}n=4}^{\text{CS}}}{\partial T}=-S<0$ and v<v₀, the slope is negative. Figure 11 shows the trend of the stress (energy density) with temperature for ∑3(111) Al healing (Fig. 11(f)), which is accurately represented by Eq. (13). Therefore, the crack separation model described in this section is applicable for separation stress assessment at high temperatures. Notably, this model suggests a correlation between the separation stress and rate; therefore, different rates result in different separation stress sensitivities to temperature. A more comprehensive investigation of this phenomenon will be conducted in future work.

Fig. 11Full-screen View

(Color online) Linear relationship between stress and temperature

Discussion

Al (FCC), W (BCC), and Ti (HCP), among other metals, are subjected to high temperatures and stresses in nuclear reactors, and GB cracking is a common failure mode [29-34]. After GB separation, the GB cracking energy determines the stability and healing ability of the cracks [10]. In their latest research, Barr et al. [6] observed weak-fatigue crack initiation and extension in a 40-nm Pt foil; crack healing occurred at approximately 664,000 cycles, and substantial microstructural evolution accompanied crack healing, including the migration of twin GBs. Additionally, GB migration and crack healing occurred near room temperature, and fatigue cracks in pure metals self-healed at room temperature. They reported that the attraction between the two cracked surfaces was related to the self-healing of the cracks, which is consistent with our results. According to a report by Belytschko et al. [35], the non-linear strain that occurs in the yield and maximum-strength regions owing to bond breakage leads to stress reduction, whereas the formation of new bonds as the deformation process progresses leads to an increase in stress.

Currently, macroscopic mechanical models focus on the failure behavior of grains and GBs at room temperature. A quantitative relationship among the yield strength, modulus of elasticity, Poisson's ratio, and temperature was previously established to predict the yield strength at different temperatures and strain rates [36]. Li et al. developed a temperature-dependent yield strength model for metallic materials based on the equivalence between thermal energy and distortion strain energy [37]. The advantages of their model were its generality and ability to easily predict the temperature-dependent yield strength at arbitrary temperatures. However, the model uses macroscopic quantities to simulate the quantitative relationship between yield strength and temperature for certain metallic materials; it does not consider microscopic quantities.

In mechanical modeling, nanocracks are commonly considered as structural damage, and the effective properties of a material are determined via the damage mechanics approach [38]. The incorporation of temperature into the damage model is essential for evaluating its influence on the mechanical properties of materials, thereby establishing a thermomechanical damage constitutive model [39-46]. However, the damage mechanics approach requires the introduction of many fitting parameters, the physical meaning of which remains unclear. Determining the physical meaning of these parameters is a worthy research endeavor. In Section C, we outline a thermodynamic method for calculating the separation stress of nanocracks. The present density functional theory results confirm the effectiveness of this method. According to Eq. (11), the temperature dependence of the strength of materials containing crack damage is determined by the interaction energy between the cracks and the tensile rate. Accordingly, the results of this study provide atomic-scale support for the development of a rate-dependent thermomechanical model for nuclear reactor materials.

Conclusion

The healing behavior of nanocracks was demonstrated in a previous study. However, nanocrack recovery and healing on an atomic or electronic scale, and the energies affecting this healing behavior have not been described. Therefore, we selected GBs in alloys with FCC, BCC, and HCP structures and simulated the separation of the GBs into crack surfaces to investigate the adsorption behavior of the crack surfaces and the healing behavior after complete GB fracture. Based on the results, the main conclusions of this study can be summarized as follows:

(1) Microcrack healing is closely related to the crack surface energy. Ordered and disordered atom arrangements on the surface result in stable and unstable crack surfaces, respectively. Adsorption on a nanocrack surface determines the critical width of nanocracks.

(2) The adsorption force on a cracked surface is positively correlated with the GB strength (stress), and the adsorption force on the cracked surface is zero at 0 K once the GB has separated (i.e., complete fracture); that is, no interaction remains between the crack surfaces. However, high temperature drives atomic diffusion on the crack surface, and the GB cracks begin to heal. Al ∑3(111) nanocracks heal at high temperatures, and their healing behavior is closely related to the surface energy.

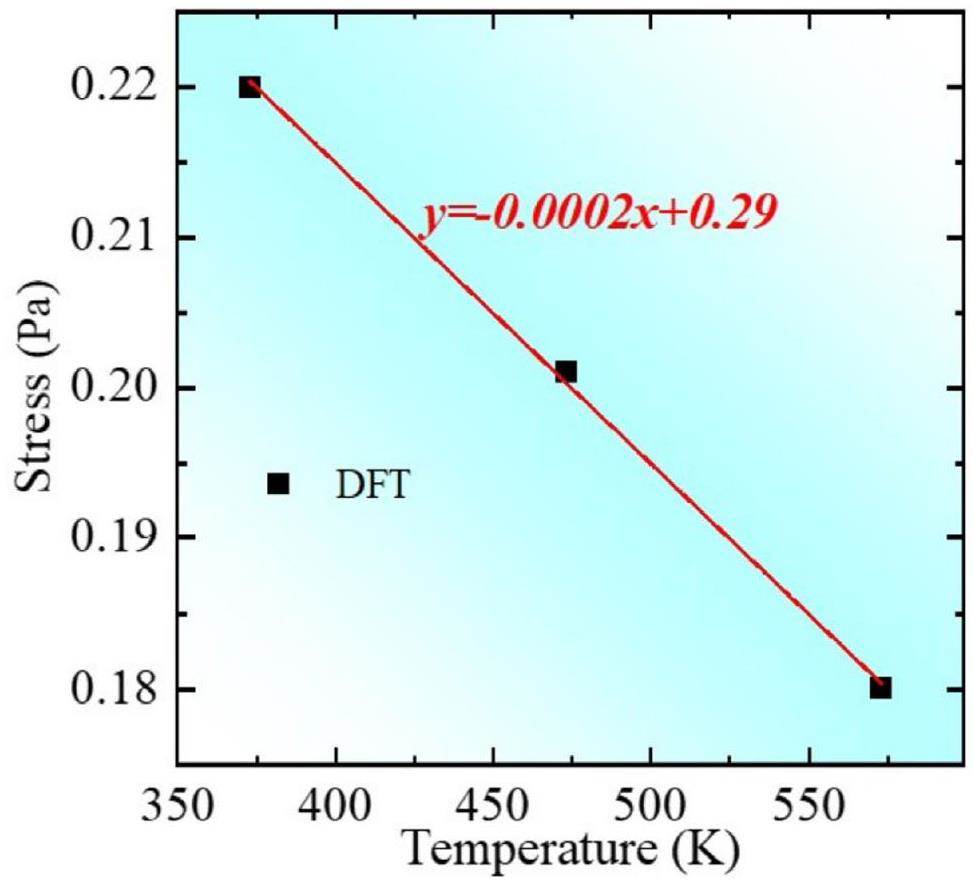
(3) Relying on the global non-equilibrium energy criterion, a high-temperature model for GB migration was developed in this study, namely, σ_s(T, d, v). Introducing temperature improves the model for metals in nuclear reactors. It was found that temperature is negatively correlated with stress, and the slopes of the temperature–stress relationship curves were consistent with the predicted values.