Theory of PFNUL

Figure 1 illustrates the principles of the PFNUL technique. The D-T neutron generator emits fast neutrons (called source neutrons) in a pulsed manner into the downhole formation, and these fast neutrons are slowed by elastic scattering, inelastic scattering, and other nuclear interactions with the formation rock. Fast neutrons are rapidly slowed down to epithermal neutrons (E) (epithermal neutron lifetime ≤t₁) and thermal neutrons (T), which stay in the stratum for a long time (≤ 5000 μs) in the form of “thermal motion”, during which they undergo radiative capture, fission, and other nuclear interactions with the nuclei of the material atoms, and are ultimately absorbed by the material (neutron fading). During a single pulsed neutron measurement cycle, the epithermal and thermal neutron time spectra in the formation are collected by an epithermal neutron detector and a thermal neutron detector, respectively, in which the slowed-down thermal neutrons are prone to undergo fission reactions with 235U in the formation and thereby produce 2-3 uranium fission-transient neutrons that prolong the epithermal neutron fading time ($\ge t_{\text{1}}$), as shown in Fig. 1(b). This prolonged Δt portion of the epithermal neutrons is positively correlated with the uranium content.

Fig. 1Full-screen View

(Color online) (a)Principle of PFNUL. (b)Epithermal and thermal neutron time spectrum for no-uranium and uranium cases

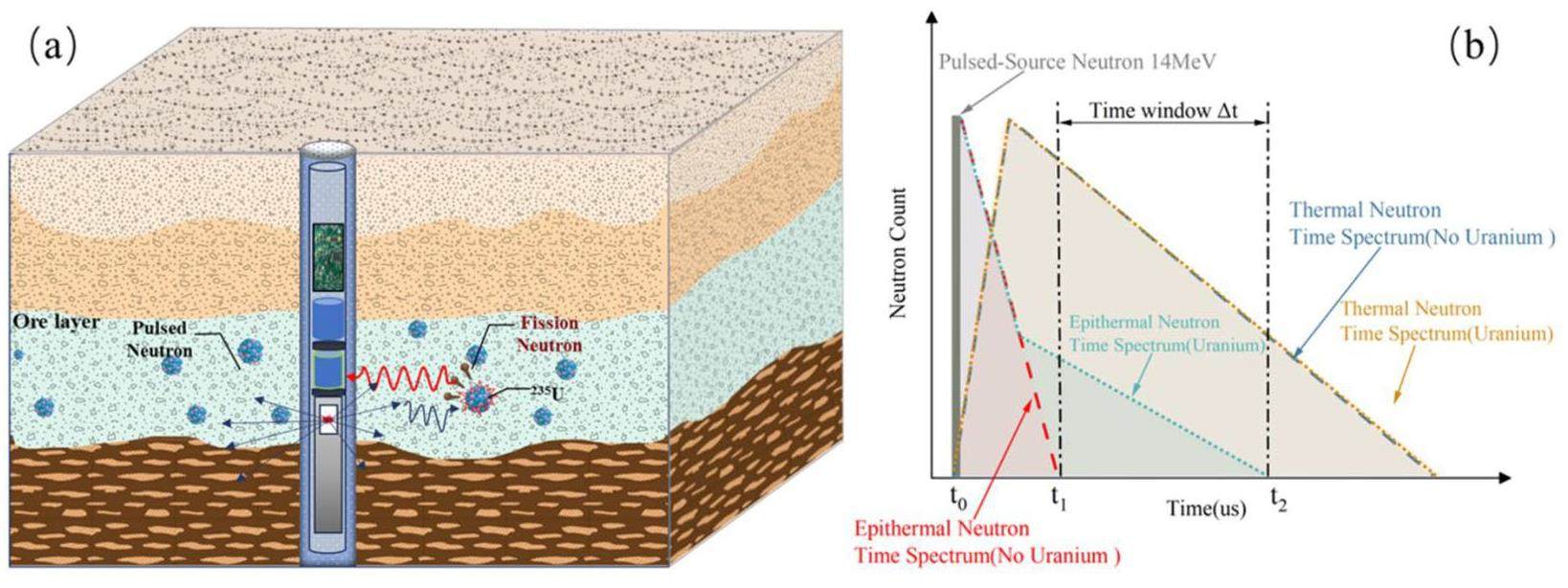
Uranium quantification by epithermal neutrons

In 1972, Czubek proposed a novel direct uranium logging method that utilized a 14 MeV pulsed neutron source to continuously irradiate a uranium-bearing formation and measure the formation fission neutron time distribution at the end of the source neutron pulse [17]. Czubek theoretically demonstrated the feasibility of determining the uranium content by measuring the prompt fission epithermal neutron time spectrum resulting from the fission of the formation 235U thermal neutron nucleus. Based on the energy, time, and space distributions of neutrons in the medium under isotropic pulsed neutron point source conditions, Czubek obtained the formula for the count rate of epithermal fission neutrons within the measurement time window by using an epithermal neutron detector record and derived that for an epithermal neutron detector with a determined performance, the epithermal neutron counts of the detector are only related to the source neutron yield Q when the parameters such as the measurement timing of the logging system, formation uranium content q_u, formation density ρ, and formation neutron characteristic function $f\left(t_{\text{s}}\mathrm{,}{\displaystyle \sum {}_{\text{a}}}\right)$ are fixed: $\text{Epi}\text{.Count}=K_{\text{E}}\cdot Q\rho q_{\text{u}}\cdot f\left(t_{\text{s}}\mathrm{,}{\displaystyle \sum {}_{\text{a}}}\right)$ (1) where Epi.Count is the count of epithermal neutrons in the measurement time window, K_E is the scale factor for the system and denotes the coefficient of proportionality between the epithermal neutron counts and uranium content q_u, ∑_a is the macroscopic thermal neutron absorption cross-section of the formation, and t_s is the average slowing time of the fast neutrons. However, a single epithermal neutron time spectrum is susceptible to fluctuations in the neutron source yield.

Uranium quantification of the epithermal neutron–thermal neutron ratio (E/T)

The epithermal fission neutron counting model proposed by Czubek in 1972 is an absolute method of uranium content quantification that requires compensatory measurements of parameters, including the source neutron yield (Q), formation density (ρ), and macroscopic thermal neutron absorption cross-section (∑_a). In 1978, Givens et al. proposed a relative uranium content measurement method in which a thermal neutron detector was added to the logging equipment to measure the formation thermal neutron time spectrum. The uranium content was quantified by measuring the ratio of the uranium fission neutron counts to the thermal neutron counts of the formation [34]. The epithermal fission neutron counts versus thermal neutron counts (Ther.Count) contributed by the ²³⁵U thermal neutron nuclear fission reaction within the detector measurement timeframe are given by Eq. (2): $\{\begin{array}{l}\text{Epi}\text{.Count}={\epsilon }_{\text{epi}}{N}_{\text{u}}{\sigma }_{fU}g\left(S\mathrm{,}{\sum }_{\text{a}}\mathrm{,}{t}_{\text{b}}\mathrm{,}{t}_{\text{c}}\right)f\left({\sum }_{\text{a}}\mathrm{,}{t}_{\text{c}}\right)\hfill \\ \text{Ther}\text{.Count}={\epsilon }_{\text{ther}}g\left(S\mathrm{,}{\sum }_{\text{a}}\mathrm{,}{t}_{\text{b}}\mathrm{,}{t}_{\text{c}}\right)f\left({\sum }_{\text{a}}\mathrm{,}{t}_{\text{c}}\right)\hfill \end{array}$ (2) where ${\epsilon }_{\text{epi}}$ is the detection efficiency of the epithermal neutron detector, N_u is the ²³⁵U atomic number density of the formation, ${\sigma }_{\text{fU}}$ is the ²³⁵U nuclear fission reaction cross-section, $g\left(S\mathrm{,}{\sum }_{\text{a}}\mathrm{,}{t}_{\text{b}}\mathrm{,}{t}_{\text{c}}\right)$ is the thermal neutron flux density of the formation at the end of the waiting time t_b, S is the source neutron yield, ∑_a is the macroscopic thermal neutron absorption cross-section of the formation, $f\left({\sum }_{\text{a}}\mathrm{,}{t}_{\text{c}}\right)$ is the thermal neutron flux at measurement time t_c, and ${\epsilon }_{\text{ther}}$ denotes the detection efficiency of the thermal neutron detector.

The $g\left(S\mathrm{,}{\sum }_{\text{a}}\mathrm{,}{t}_{\text{b}}\mathrm{,}{t}_{\text{c}}\right)$ term represents the thermal neutron source that causes the ²³⁵U thermal neutron nuclear fission reaction, and any factor affecting the thermal neutron flux of the formation affects the epithermal fission neutron flux. The macroscopic thermal neutron absorption cross-section of the formation can affect its thermal neutron flux. To correct the influence of the formation parameters and other factors on the thermal neutron flux of the formation, Givens et al. proposed an epithermal neutron–thermal neutron counting model. The model equations contain the same thermal neutron correlation terms. Hence, the influencing factor correlation terms of the formation can be eliminated by the ratio method $g\left(S\mathrm{,}{\sum }_{\text{a}}\mathrm{,}{t}_{\text{b}}\mathrm{,}{t}_{\text{c}}\right)$ and $f\left({\sum }_{\text{a}}\mathrm{,}{t}_{\text{c}}\right)$ on the epithermal neutron flux counting. Moreover, the relationship between the epithermal fission neutron-thermal neutron counting ratio and ²³⁵U atomic number density of the stratum is obtained via the ratio method, as shown in Eq. (3): $\frac{\text{Epi}\text{.Count}}{\text{Ther}\text{.Count}}=\frac{{\epsilon }_{epi}{N}_{\text{u}}{\sigma }_{fU}}{{\epsilon }_{\text{ther}}}$ (3) In logging equipment, Givens et al. arranged thermal neutron and epithermal fission neutron detectors with equal source spacing to ensure that the thermal neutron correlation terms $g\left(S\mathrm{,}{\sum }_{\text{a}}\mathrm{,}{t}_{\text{b}}\mathrm{,}{t}_{\text{c}}\right)$ and $f\left({\sum }_{\text{a}}\mathrm{,}{t}_{\text{c}}\right)$ at the positions of the thermal neutron and epithermal neutron detectors in Eq. (2) were equal. However, in practical engineering applications, an equal source-spacing thermal neutron and epithermal fission neutron detector arrangement is not achievable, owing to the limitation of the spatial location. Therefore, the authors proposed the use of a double neutron detector with upper and lower structures for the acquisition of the time spectra of epithermal neutrons (E) and thermal neutrons (T), respectively, as shown in Fig. 1(a), and constructed the E/T values to eliminate the fluctuating effects of the neutron source yields. During the life cycle of a neutron, thermal neutrons are prone to fission with ²³⁵U within the medium and produce uranium fission transient neutrons, thereby prolonging the epithermal neutron fading time, as shown in Fig. 1(b), which is the theoretical basis for detecting the occurrence of uranium fission, as well as for uranium ore quantification using pulsed neutron logging. According to the theory of uranium fission, in a homogeneous medium (saturated ore layer), at any time t after all the primary pulsed neutrons have been slowed down to thermal neutrons (denoted as the t₁ moment), the total number of existing epithermal neutrons in the medium n_E(t) is proportional to the total number of existing thermal neutrons n_T(t) versus the uranium content (or ²³⁵U content): $\frac{n_{\text{E}}\left(t\right)}{n_{\text{T}}\left(t\right)}=\frac{n_{\text{E}}\left(t_{\text{1}}\right)\cdot e^{-\left(t-t_{\text{1}}\right)/{\tau }_{\text{E}}}}{n_{\text{T}}\left(t_{\text{1}}\right)\cdot e^{-\left(t-t_{\text{1}}\right)/{\tau }_{\text{T}}}}=K_{\text{U}}\cdot q_{\text{u}}$ (4) Equation (4) shows that after the slowing down of primary neutrons to thermal neutrons, the total amount of existing epithermal neutrons n_E(t) and thermal neutrons n_T(t) in the homogeneous medium decay according to the negative exponential law, i.e., the time spectrum of epithermal neutrons and thermal neutrons at this time period, is the decay time spectrum [35]. The decay rates are described by $1/{\tau }_{\text{E}}$ and $1/{\tau }_{\text{T}}$ (τ_E and τ_T are the time constants for the fading times of epithermal and thermal neutrons, and their values are closely related to the stratum rock, drilling medium, and neutron nuclear interaction ability). Moreover, K_U denotes the positive coefficient of the ratio of the total amounts of existing epithermal and thermal neutrons in the formation rock to the uranium content q_u after the moment of t₁. Thus, determining the time window parameters t₁ and t₂ shown in Fig. 1(b) is critical; otherwise, the epithermal neutrons produced by the neutron source affect the accuracy of uranium quantification, as discussed below.

If a logging probe measures the double neutron time spectra of n_E(t) and n_T(t) at a certain measurement point along the well axis, then the epithermal neutron attenuation at Δt is N_E(Δt), the thermal neutron attenuation is N_T(Δt), and the ratio of the two attenuations is called the "Epithermal/Thermal" (E/T) ratio value. The detected epithermal neutron attenuation N_E(Δt) and thermal neutron attenuation N_T(Δt) come from the upper and lower structural distributions of ³He orthotropic technology tubes, respectively. $\{\begin{array}{l}{N}_{\text{E}}\left(\text{Δ}t\right)={\eta }_{\text{E}}{\displaystyle {\int }_{t_{\text{1}}}^{t_{\text{2}}}}{n}_{\text{E}}\left(t\right)dt={\eta }_{\text{E}}\cdot n_{\text{E}}\left(t_{\text{1}}\right){\tau }_{\text{E}}\left(1-e^{-\text{Δ}t/{\tau }_{\text{E}}}\right)\hfill \\ N_{\text{T}}\left(\text{Δ}t\right)={\eta }_{\text{T}}{\displaystyle {\int }_{t_{\text{1}}}^{t_{\text{2}}}}{n}_{\text{T}}\left(t\right)dt={\eta }_{\text{T}}\cdot n_{\text{T}}\left(t_{\text{1}}\right){\tau }_{\text{T}}\left(1-e^{-\text{Δ}t/{\tau }_{\text{T}}}\right)\hfill \end{array}$ (5) Hence, the E/T ratio is proportional to the formation rock formation. $\text{E/T}(\text{Δ}t)=\frac{N_{\text{E}}\left(\text{Δ}t\right)}{N_{\text{T}}\left(\text{Δ}t\right)}=K_{\text{E/T}}\cdot q_{\text{u}}$ (6) In Eqs. (5) and (6), ${\eta }_{\text{E}}$ is the effective detection efficiency of epithermal neutron attenuation, which indicates the ratio of detected epithermal neutron attenuation to the actual epithermal neutron attenuation; similarly, ${\eta }_{\text{T}}$ is the effective detection efficiency of thermal neutrons, and K_E/T is the conversion factor that indicates the positive coefficient of the E/T to the uranium content q_u. Moreover, this conversion factor is the covariate determined by the factors of logging instrument, stratum rock, drilling medium, etc. Once the logging instrument, formation rock, and drilling medium are fixed (particularly the logging instrument), K_E/T remains constant.

In the above equation, K_E/T is considered the known variable, E/T(Δt) is the measured variable, and q_u is the variable to be solved. For this reason, it is necessary to construct accurate uranium model wells that are similar to field wells in terms of lithological structure, material composition, and medium in the wells and then use the PFNUL instrument to scale the model wells with known uranium contents to determine the derived K_E/T, carry out actual field logging, and then substitute it into Eq. (6) to determine the uranium content of the field wells q_u. Therefore, determining the dimensional parameters of the uranium model wells is also important in this study.

In Eqs. (6), E/T(Δt) is added to the epithermal neutrons, thermal neutrons, and fading time correction, which are attributable to the negative exponential decay law of epithermal neutrons and thermal neutrons, respectively, as well as the decay time spectrum of negative exponential fitting in finding the value of τ_E,τ_T. Because the values of τ_E and τ_T in a homogeneous medium are relatively stable, the fading time correction coefficient can also be set to the value of K_E/T. Moreover, when the t₂ value is large, the count rate of the tail of the epithermal neutron time spectrum has a large statistical rise and fall (which may also include the uranium fission delayed neutrons), when the frequency of the pulsed neutron emission reaches or exceeds 1000 Hz, then it must be ≤ 1000 μs. Therefore, it is recommended that the value of Δt be set between 600 and 1000 μs.

The advantages of this method lie in the following: extracting the secondary neutron extinction law from the epithermal neutron time spectrum and the primary neutron slowing law from the thermal neutron time spectrum to select the appropriate time window parameters, define the "Epithermal/Thermal" ratio based on the two-neutron time spectrum, and construct a real-time algorithm for uranium ore quantification. Thus, the "direct uranium measurement" and quantification via the prompt neutron logging of uranium fission was realized.

Time windows (Δt)

In this study, the Monte Carlo method was used to establish a model of a PFNUL instrument with a ratio of epithermal neutrons to thermal neutrons and a model of cylindrical saturated uranium ore with reference to the actual model [36-38], as shown in Fig. 2(a). Among them, the outer diameter of the probe tube was 5.5 cm, and the length of the probe tube was 284 cm. The pulsed neutron source was a 14 MeV D-T pulsed neutron source with a pulse width of 10 μs, and the two ³He detectors were distributed in an upper and lower structure, with the upper ³He detector wrapped with 1 mm cadmium and 4 mm polyethylene for epithermal neutron (energy range of 0.7-1000 eV) time-spectrum acquisition and the lower ³He detector. The neutron source and center of the epithermal neutron detector had a source distance of 15.15 cm, and the neutron source and center of the thermal neutron detector had a source distance of 43.7 cm. The uranium content of the stratum was set to be 0%, 0.0280%, 0.0684%, and 0.0982%, respectively, and the results of the simulated time spectrum are shown in Fig. 2(b).

Fig. 2Full-screen View

(Color online) (a) Uranium logging model. (b) Time spectrum of epithermal and thermal neutrons and Δt for the uranium signature information acquisition, where E_n denotes the normalized counts of the epithermal neutron time spectrum and T_n denotes the normalized counts of the thermal neutron time spectrum

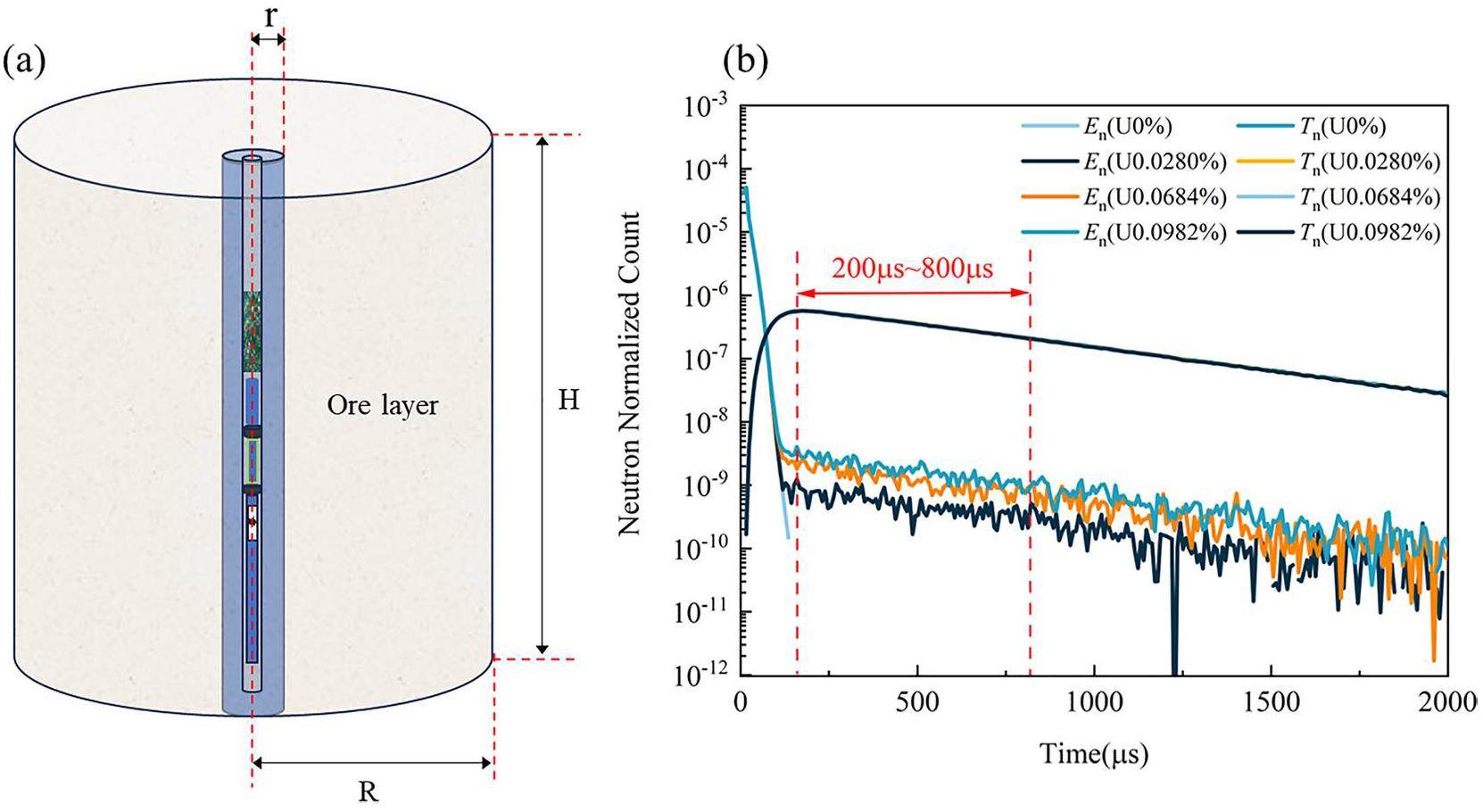
Figure 2(b) shows that the thermal neutron time spectra are the same in both the uranium-bearing and non-uranium-bearing layers. This means that regardless of whether the ore layer contains uranium, as long as the formation rocks, drilling conditions, and other factors remain unchanged, the difference in the macroscopic absorption cross-section of the thermal neutrons is small (almost the same). At any time ($t\ge t_{\text{1}}$), the number of existing thermal and epithermal neutrons in the formation rocks with a law of change over time is a negative exponential decay function. In the epithermal neutron time spectrum of the pure sandstone model (0% uranium content), there are no counts after 200 μs, and all neutrons produced by the neutron source are converted to thermal neutrons after 200 μs, which is the value of t₁ in Eqs. (5). Then, in the epithermal neutron time spectrum with uranium contents of 0.0280%, 0.0684%, and 0.0982%, respectively, the epithermal neutron counts after 200 μs are all produced by the decelerated production of fast neutrons from the uranium fission reaction, and the number is related to the uranium content. When the time is after 800 μs, the epithermal neutron counts in the model of uranium-containing layers are less distinguishable, and the statistical rise and fall of the epithermal neutrons after this moment are larger and may also be credited to the uranium fission slow-generating neutrons. Hence, the t₁ and t₂ of the uranium characterization information acquisition for the E/T counts are taken to be 200 and 800 μs respectively.

Standard model wells

The ideal standard model well size should be as large as possible, beyond the effective detection range. Therefore, the determination of the appropriate height (H in Fig. 2(a)) and radius (R in Fig. 2(a)) of the standard model is important. Using the Monte Carlo method, based on the aforementioned neutron logger model, the size of the mineral layer model gradually increases with the detector performance, source term, and formation medium unchanged. Moreover, the appropriate height and diameter of the standard model well are determined according to the variation of the E/T ratio. Figure 2(a) shows the model. Considering that the neutron counts measured by the uranium fission neutron logger are affected by the uranium content of the formation and the size of the borehole radius r, we set the uranium content of the formation to be 0.0280%, 0.0684%, and 0.0982% and the radius of the borehole to be 3, 7, 11, and 16.5 cm, respectively. Then, we change the model height and simulate the uranium fission neutron logging E/T ratio counts using the Monte Carlo software. The height of the saturated uranium model is determined based on the stability of the E/T ratio. Under the same conditions, the radius of the model was changed, and Monte Carlo software was used to simulate the E/T ratio counts. The radius of the saturated uranium logging model was determined according to the stability of the E/T ratio. Figure 3 shows the simulation results.

Fig. 3Full-screen View

(Color online) (a–c) Simulation results of the saturated uranium model radius R. (d–f) Simulation results of the saturated uranium model height H

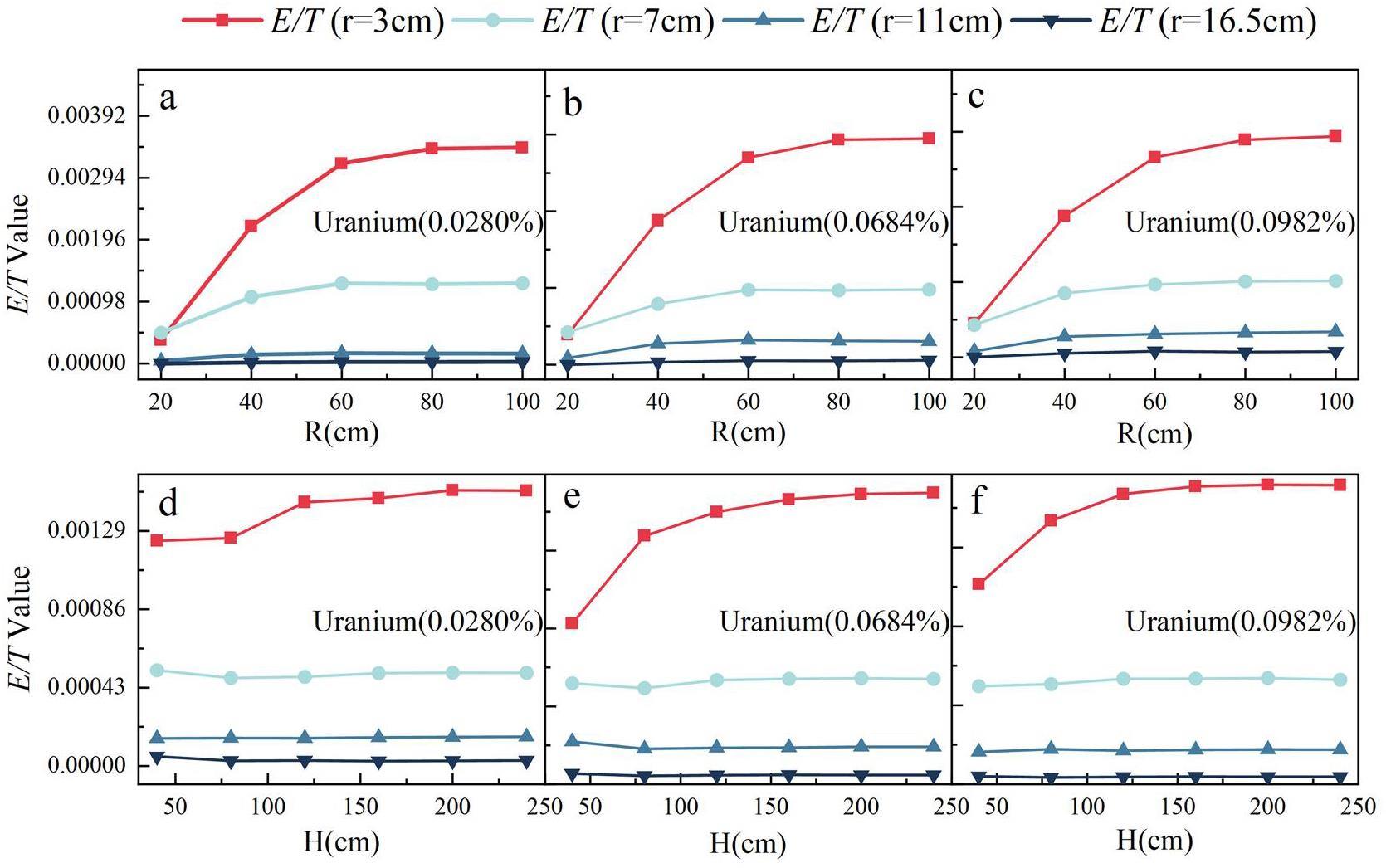
Figures 3(a–c) show the changes in the E/T value with the model height. The results show that the E/T ratio detected by the uranium fission transient neutron logger increases with an increase in the logging model radius R. However, after the model radius reaches a certain value, the E/T ratio does not change significantly with a further increase in the model height. In addition, with a smaller the borehole radius r, changes of the model radius R will lead to more drastic changes of the E/T ratio. The changes in the E/T value are relatively insignificant with changes in the model height when the borehole radius exceeds 7 cm. Thus, the simulation results show that for the radius R of the saturated ore layer, R ≥ 60 cm.

The changes in the E/T value with respect to the model radius are shown in Fig. 3(d–f). The results show that with an increase in the logging model height H, the E/T value detected by the PFNUL instrument is more significantly increased when the borehole radius is 3 cm. In contrast, the changes in the E/T value with changes in the model height are relatively insignificant when the borehole radius exceeds 3 cm. The number of E/T values does not change significantly with an increase in the model height and is less affected by the borehole radius r. After the model reached a certain height, the number of E/T values did not change significantly with an increase in the model height and was less affected by the borehole radius r. Therefore, the simulation results show that H ≥ 120 cm for the height of the saturated layer.

After the simulation, it was determined that the height of the saturated uranium ore model H ≥ 120 cm, radius R ≥ 60 cm, and measurement results of the neutron detector under the model of the ore layer of this size were the same as those of the infinite ore layer.

The experimental model used in this experiment was the Nu series of the sandstone-type uranium ore standard model wells constructed by the Airborne Survey and Remote Sensing Center of Nuclear Industry (ASRSCNI), as shown in Fig. 4(a). Models Nu-1, Nu-2, and Nu-3 are uranium-bearing models (red) with uranium contents of 0.0281%, 0.0685%, and 0.0983%, respectively. The Nb-4 model, in which the uranium taste is much lower than the boundary taste, is defined as a pure sandstone model without uranium and is a background count test model (green). The borehole radius r of each uranium cylinder model drill hole is 9 cm, the model radius R is 70 cm, and the height is 180 cm. Moreover, a 90 cm thick concrete roof is set on the model, a 30 cm thick concrete base is set under the model, and extension holes are set below the base at a depth of 260 cm. The size of the model meets the requirements of the saturation model. Figure 4(b) shows the PFNUL instrument, which contains two sets of ³He tubes in the well-logging instrument, a polyethylene neutron moderating material wrapped around the epithermal neutron detector, a cadmium metal skin wrapped around the moderating material, a high-voltage power supply for the detector, a preamplifier, shaping and screening circuitry, a pulse counter to record the output signals from the dual neutron detector, a time spectrum analysis, and cache circuits to record the output signals of the dual neutron detectors.

Fig. 4Full-screen View

(Color online) (a) Standard model wells for Nu-series sandstone-type uranium mines. (b) PFNUL instrument

Simulated scale factor

According to the simulation results, to find the conversion relationship between the E/T ratio and uranium content, considering the reduction of the influence of the statistical rise and fall on the counting results, the simulated time spectra with different uranium contents (pure sandstone, 0.0280%, 0.0684%, and 0.0982%) are taken as the starting and ending times of 200–800 μs, and the total counts of epithermal and thermal neutrons and neutrons are calculated. The scale curve of the uranium fission prompt neutron instrument for this study was compared with the E/T value curve calculated from the experimental raw data, as shown in Fig. 5.

Fig. 5Full-screen View

(Color online) PFNUL simulation scale curve

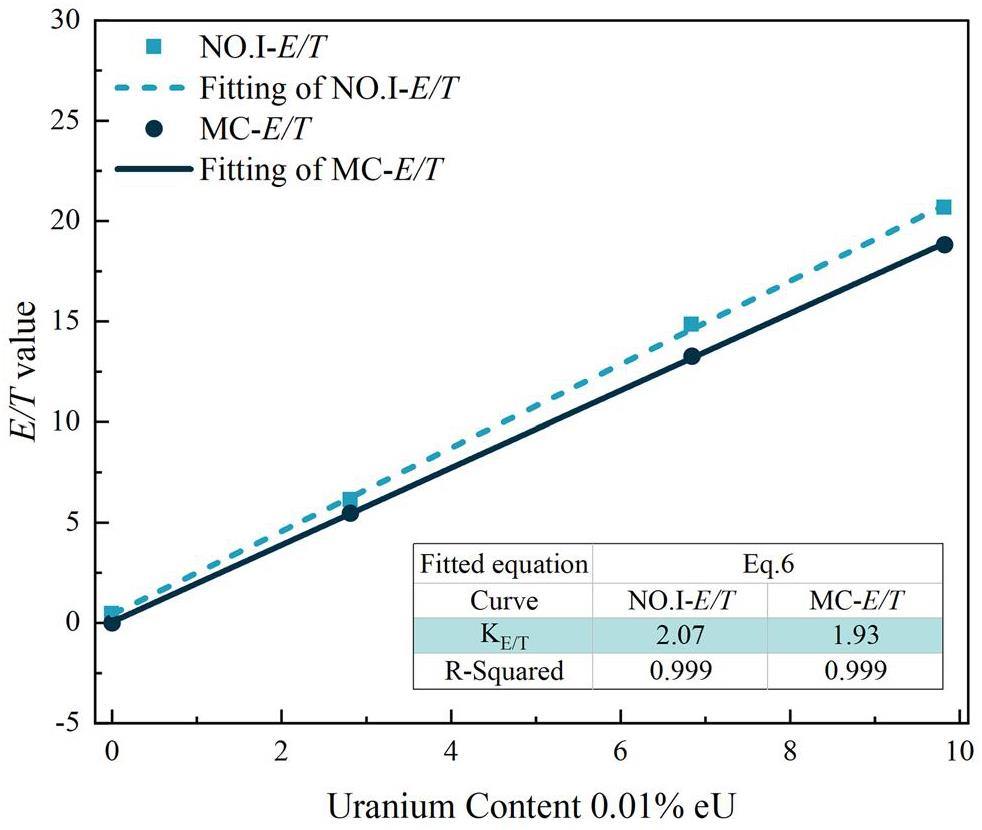
Figure 5 shows a comparison of the simulated correspondence between the uranium content and E/T ratio and the experimental results, which can be fitted using Eqs. (6). The conversion coefficient of the simulated results of the uranium content and E/T value K_E/Tmc=1.93(0.01%eU/cps) exhibit a fit of R²=0.999, and the same can be obtained from the experimental data with a conversion coefficient of K_E/T=2.07(0.01%eU/cps). The deviation of simulation and experiment comparison is 7.25%. The simulation results are in line with the principle of PFNUL, based on the ratio of epithermal to thermal neutrons.

Time spectra of different neutron yields

Owing to the consumption of the experiments and tritium, the neutron yield of the D-T neutron tube changed with use. To investigate the effect of the neutron yield on the accuracy of uranium quantification, four sets of experiments were conducted, in which the neutron intensity of the D-T neutron source was varied slightly. The neutron source intensity was based on Experiment No. 1, and the relative intensities of the neutron sources of the remaining experiments were calculated, as shown in Table 1.

As shown in Fig. 6, four sets of neutron time spectra and epithermal neutron time spectra were measured using a logging instrument at different neutron source intensities in the Nu series sandstone uranium logging model (Fig. 4(a)) from the ASRSCNI.

Fig. 6Full-screen View

(Color online) (1)Neutron time spectrum test results of Experiment 1 (2)Neutron time spectrum test results of Experiment 2 (3)Neutron time spectrum test results of Experiment 3 (4)Neutron time spectrum test results of Experiment 4

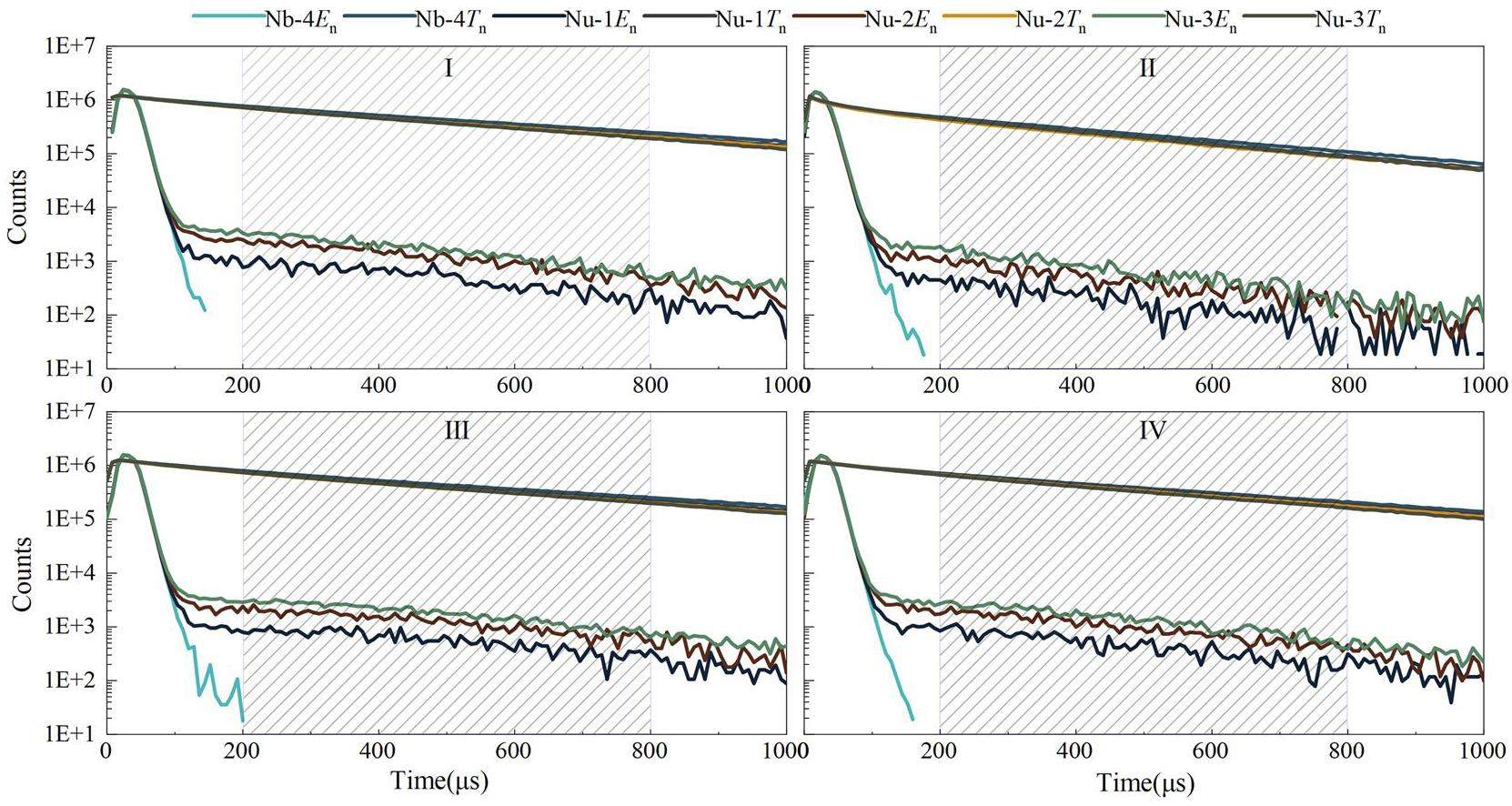
Effect of the neutron source strength on the epithermal neutron counts and E/T values

As listed in Table 1, the relative intensities of the neutron sources in the four experiments were not equal. Figure 7 shows the changes in the E/T values and epithermal neutron counts measured in the standard uranium mine model with the changes in the intensity of the neutron sources in the four experiments.

Fig. 7Full-screen View

(Color online) Variation of E/T values and epithermal neutron counts

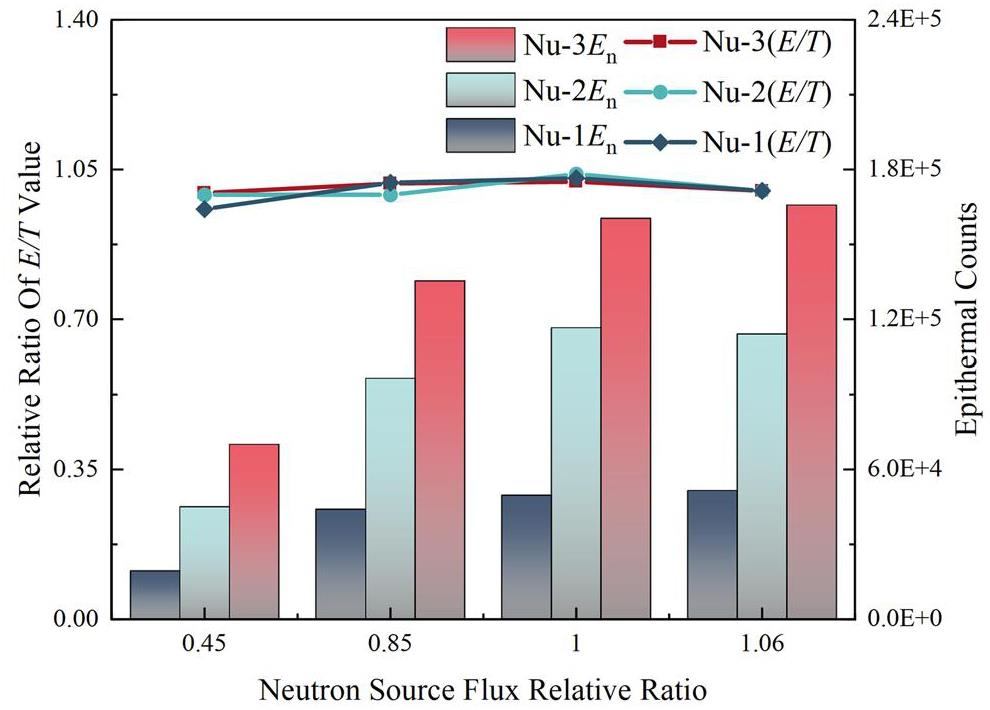
Figure 7 shows that different neutron source intensities have a significant influence on the counts of epithermal neutrons, which results in significant changes in the epithermal neutron counts; however, there is no significant change in the E/T values under different neutron source intensities. The relative standard deviation (RSD) was used to measure the stability of the E/T value and epithermal neutron counts under different neutron source intensities [39, 40]. The calculation formula is as follows: $\text{RSD}=\frac{\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2}}{n-1}}}{\overline{x}}\times 100\%$ (7) where x is the epithermal neutron count or the E/T value for the same uranium model, i denotes the corresponding experimental group, and $\overline{x}$ is the mean value.

The RSD values of the epithermal neutron counts and E/T values for different uranium contents in each group of experiments were calculated, as shown in Table 2. The maximum value of the standard deviation of the counts of epithermal neutrons reaches 36.32%, whereas the relative standard deviation of the E/T values is relatively stable, with a maximum value of only 3.2%, proving that the fluctuation of the neutron yield has a large impact on the counts of epithermal neutrons, whereas its impact on the E/T values is small.

Variation of the scale factor for different neutron source intensities

Based on the experimental data, we calculated the epithermal neutron counts for different neutron source intensity test data with different uranium contents within a time of 200–800 μs, and we linearly fitted the relationship between the epithermal neutron counts and uranium content, as shown in Fig. 8(a). The figure clearly shows that the epithermal neutron counts and uranium content have a good linear relationship; however, the epithermal neutrons of the same uranium content change with the relative intensity change of the neutron source. The fluctuation of neutron tube production in the process of uranium measurement has a greater impact on the results of the counting of epithermal neutrons, which directly affects the uranium measurement accuracy. After the time normalization of the experimental time spectrum, the counts of epithermal and thermal neutrons from 200–800 μs for different uranium contents in the four sets of experimental data were calculated. Additionally, the corresponding E/T values were calculated. Finally, the corresponding relationship curves were obtained based on the linear fitting of the E/T values to the uranium content, as shown in Fig. 8(b).

Fig. 8Full-screen View

(Color online) (a) Fitted curves of the epithermal neutron counts versus the uranium content. (b) Fitted curves of the E/T values versus the uranium content for four groups of experiments

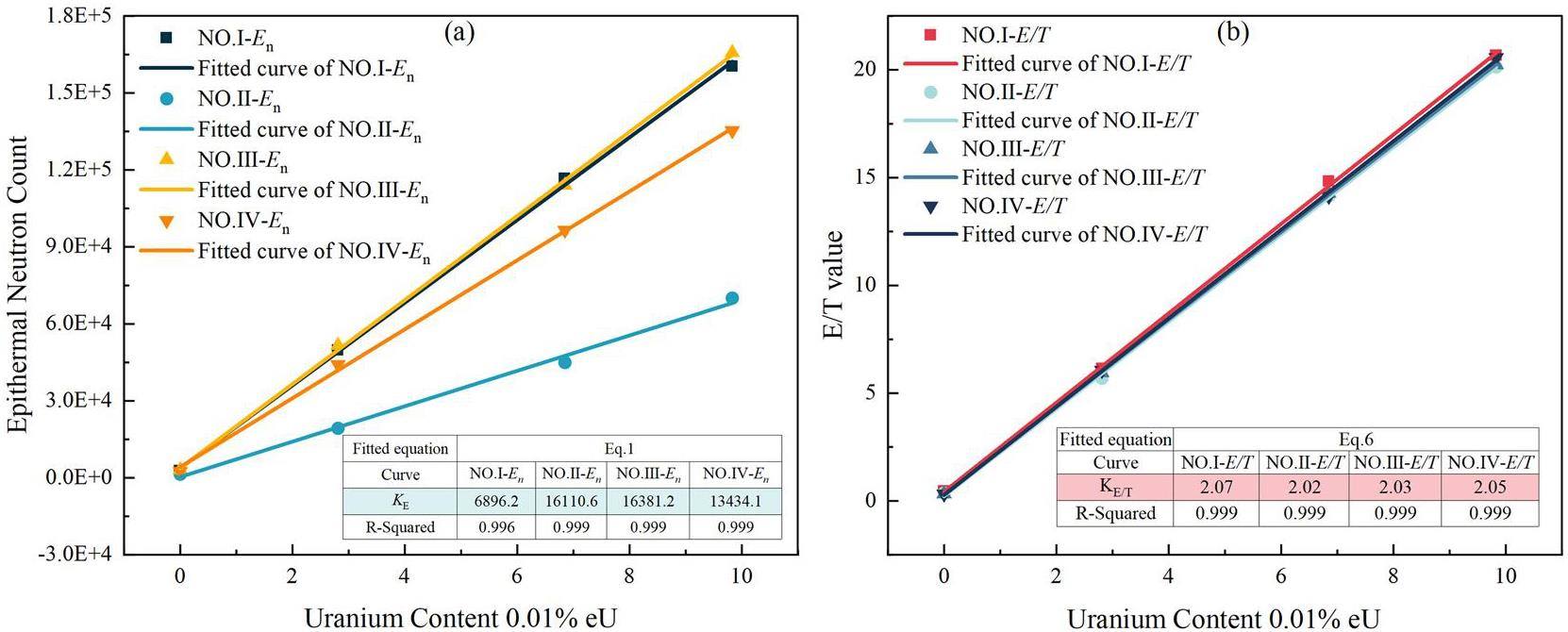
The linear fitting results showed that the uranium quantitative scale factors K_E based on epithermal neutron counting without relevant correction factors in the four sets of experiments conducted were 6896.2, 16110.6, 16381.2, and 13434.1. The RSD value was 33.41%, and the uranium quantitative scale factors K_E/T based on the E/T value were 2.07, 2.02, 2.03, and 2.05, respectively. The RSD value was 1.09%. It has been proven that the E/T-based uranium quantification method based on the double neutron time spectrum can effectively and accurately analyze uranium quantification and that the scale factor is not affected by the neutron tube yield, which can effectively improve the service life of the neutron logging instrument.