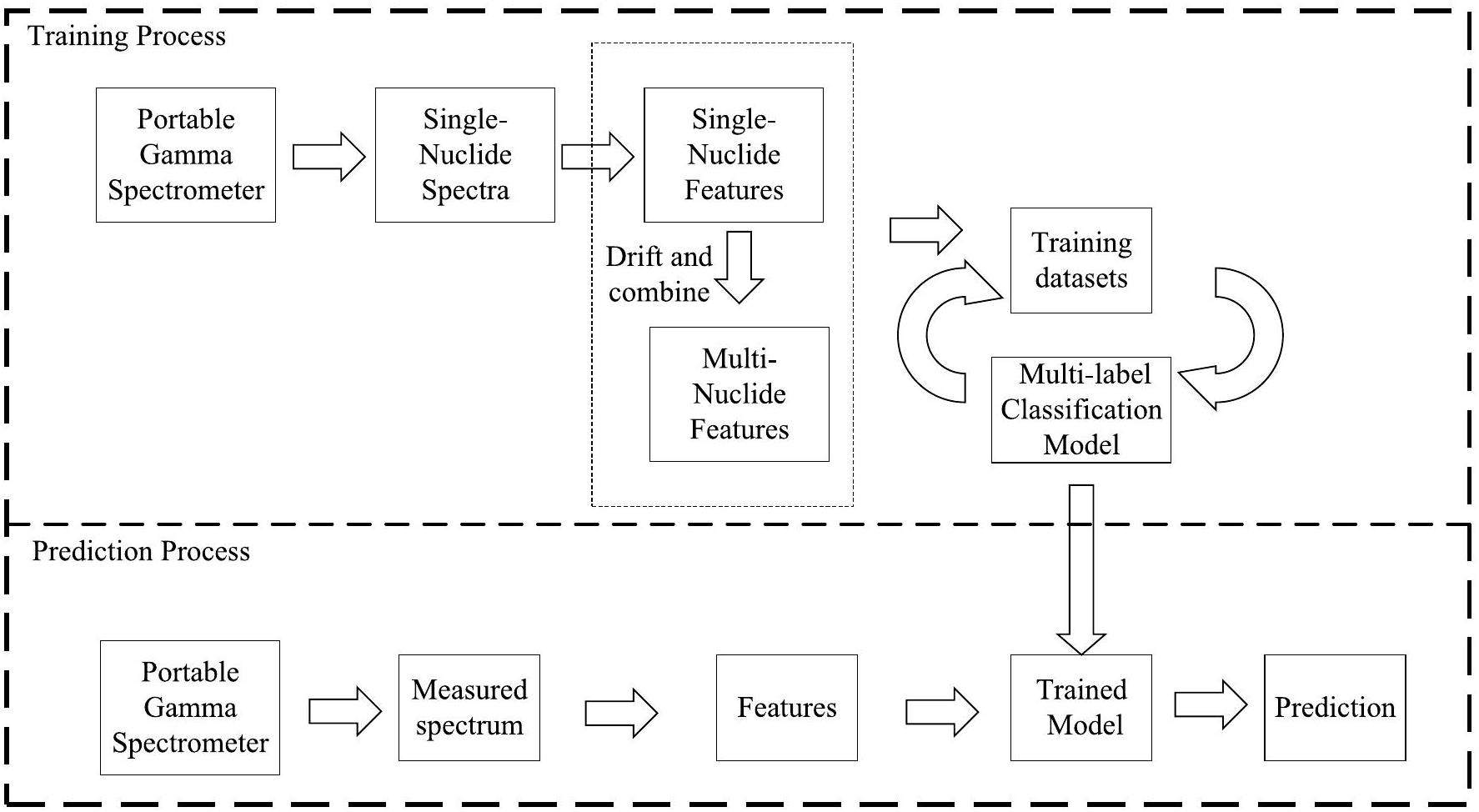
Multi-label classification

As shown in Fig. 2, the classification neural network for single-label and multi-label can have the same network topology construction. o={o₁, o₂ …, o₅} is the output vector of the classification neural network. In single-label classification, the output vector satisfies ∑o=1, assuming o₃ is the maximum value, its prediction vector y={y₁,y₂…,y₅} yields {0, 0, 1,, 0, 0}, which indicates that the input feature vector only belongs to the 3-rd label. In the multi-label classification case, its output vector satisfies ${\displaystyle \sum }o\ne 1$, assuming that all of the ${\tilde{o}}_1\mathrm{,}{\tilde{o}}_3\mathrm{,}{\tilde{o}}_5$ are higher than a given threshold, the prediction vector y={y₁,y₂…,y₅} yields {1, 0, 1, 0, 1}, indicating that the input feature vector belongs to the 1-st, the 3-rd, and the 5-th labels at the same time, which meets the requirement of multiple nuclides identification.

Fig. 2Full-screen View

Classification neural network

Although single-label and multi-label classification neural networks can have the same network topology, there are differences in the activation and loss functions. To avoid the logical redundancy of the traditional nuclide matching method and the high resource consumption of existing neural network algorithms, a loss function optimization method was designed to handle the multi-label output and optimize the loss function.

The designed neural network had an input layer, two hidden layers, and an output layer. All the layers were fully connected. The computational formula between two layers can be defined as $\text{o}=f(\text{l}\text{W}+\text{b})$ (1) where o, l, W, b denote the data vector of the current layer, data vector of the previous layer, weight matrix, and bias vector, respectively. When the network is trained to converge, the weight matrix of each layer will be fixed. f(·) is the activation function, which introduces nonlinear factors so that the network can learn and represent complex nonlinear relationships. The data in the input layer are a feature vector consisting of the characteristic energies of the measured spectrum, and its dimension is discussed in the following subsection. For the output layer, the output data are a 12-dimensional prediction vector indicating the existence probability of the 12 types of target nuclides (the background spectra are also regarded as nuclide spectra). The sigmoid activation function was selected as the activation function for the output layer, differing from the softmax function in single-label classification. It can be defined as, $\sigma (x)=\frac{e^x}{1+e^x}\mathrm{,}$ (2) and its derivative ${\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$. The sigmoid function effectively maps the network output data to a range between 0 and 1 and is particularly suitable for models where the output needs to be interpreted as a probability.

The loss function in the neural network quantifies the difference between the predicted and true values, which is considered as the difference between the real probability distribution and the predicted probability distribution for this network design. The output of the k-th node Ok can be regarded as the predicted presence probability of the k-th target nuclide and obeys the Bernoulli distribution. The probability density function can then be defined as $P\left(Y_k\right)=O_k{}^{Y_k}{\left(1-O_k\right)}^{1-Y_k}\mathrm{.}$ (3) In a sample set Y containing N samples, the occurrence frequency of an event Yk can be determined; however, its true probability ${\tilde{O}}_k$ remains unknown. To estimate ${\tilde{O}}_k$, the maximum likelihood estimation method is applied. The likelihood function is $\begin{array}{ll}\log P(Y)\hfill & =\log {\displaystyle \prod _{i=1}^N}P\left(Y_k^i\right)={\displaystyle \sum _{i=1}^N}\log P\left(Y_k^i\right)\hfill \\ \hfill & ={\displaystyle \sum _{i=1}^N}\left(Y_k^i\log O_k+\left(1-Y_k^i\right)\log \left(1-O_k\right)\right).\hfill \end{array}$ (4) By taking the derivative of (4), and setting it equal to zero, the estimated ${\overline{O}}_k$, representing the maximum point of (4), can be calculated. During one training epoch of the neural network, all N samples are utilized; thus, the loss function for the k-th node can be defined as ${\text{Loss}}_k=-{\displaystyle \sum _{i=1}^N}\left(Y_k^i\log O_k+\left(1-Y_k^i\right)\log \left(1-O_k\right)\right)\mathrm{,}$ (5) where Yk represents the true k-th label of the input sample. By continuously minimizing the optimized loss function, the predicted existence probability and the true existence probability are realized.

For the undefined network hyperparameters, a hyperparameter optimization process was implemented. In this process, random search is commonly employed to select hyperparameters and evaluate model performance. This approach identifies optimal hyperparameters over a wide range and provides an initial training set. By analyzing training results, the hyperparameter region converges more easily. The Keras-Tuner toolkit was utilized for hyperparameter searching, with the node numbers of the first and second hidden layers set to 30 and 26, respectively. The dropout rate for hidden layer neurons was 0.5, and the learning rate was set to 0.001.

The designed multilabel classification neural network was built, trained, and tested using the Keras library in Python 3.9. The backpropagation algorithm employed the Adam optimizer to adjust network parameters and minimize the loss function [33]. The number of training epochs was set to 20,000.

Features extraction

In this section, a portable gamma spectrometer was used to measure the spectra of 12 target nuclides (including the background case) with a dose rate of d≈0.5 μSv/h and a measurement time of t_m=60 s. The self-developed portable gamma spectrometer is shown in Fig. 3. It comprises a 0.5 × 1 × 2-inch CsI scintillator detector and a signal processing circuit. Signals from the scintillator detector were amplified, shaped, counted, and analyzed using a signal processing circuit equipped with a low-power ARM chip operating at 200 MHz. Unlike existing portable gamma spectrometers [34], energy calibration was performed using LuO powder surrounding the scintillator crystal. By analyzing fluctuations in the decay characteristic energies of ¹⁷⁶Lu in LuO, energy-scale coefficients were adjusted to achieve energy calibration. The measured nuclides included the industrial nuclides (²⁴¹Am, ¹³³Ba, ⁶⁰Co, ¹³⁷Cs, ¹⁵²Eu, ²²Na, ⁵⁴Mn), the natural nuclides (⁴⁰K) and the medical nuclides (¹³¹I, ¹⁷⁷Lu, ^99mTc). The measured gamma spectra were used as original samples, and features were extracted to construct the training datasets.

Fig. 3Full-screen View

(Color online) Portable gamma spectrometer for spectra measurements

The characteristic energies of the spectra were used as elements in the feature vectors, enhancing the robustness of the algorithm, generalizability, and interpretability under higher dose rates or longer measurement times. Portable gamma spectrometers with scintillator detectors typically exhibit low energy resolution and can identify only a limited number of nuclides. To achieve multiple nuclide identification within three types of nuclides, the feature vector size was set to eight elements (empty elements were filled with zeros). This significantly reduced the number of input nodes and the computational burden of the neural network [22]. The following peak-searching algorithm was designed for feature extraction.

Considering the computing power of the gamma spectrometer and the reliability of the spectral data after smoothing, the smoothing algorithm employs the 7-point barycenter method, which is expressed as $\begin{array}{c}{s}_i=\frac{1}{64}(20s_i+15s_{i-1}+15s_{i+1}\\ +6s_{i-2}+6s_{i+2}+s_{i-3}+s_{i+3}),\end{array}$ (6) where si represents the number of the i-th channel in the spectrum. The symmetry method was used to handle the boundaries of the spectra. The smoothing weight factors are positive, and the smoothed spectrum data exhibit good performance, particularly for spectra with a high background count.

In the spectra measured by the spectrometer, the background primarily originates from uranium, thorium, potassium, and their decay offspring in the environment. In addition, the shielding of materials can further complicate the spectra owing to significant scattering in the spectra. This places higher demands on the spectral feature extraction method. A symmetric zero area peak-searching algorithm was implemented to suppress high background levels and resolve overlapping peaks. The symmetric zero area method uses a symmetric window function with zero area to convolve with the obtained spectra and applies specific criteria to filter valid peaks in the transformed spectra. Its expression is defined as ${\tilde{s}}_i={\displaystyle \sum _{j=-t}^t}{G}_j{s}_{i+j}\mathrm{,}$ (7) where ${\displaystyle \sum _{j=-t}^t}{G}_j=0$. The first derivative of the Gaussian function was utilized as the window function: $G_j=\frac{j}{{\sigma }^2}{e}^{-j^2/2{\sigma }^2}\mathrm{,}$ (8) where $j\in \{-t\mathrm{,}-t+1\cdots \mathrm{,}0\cdots t-\mathrm{1,}t\}$ and σ is the variance of the Gaussian function. In the transformed spectrum, the zero point is an alternative point to the peak position. To minimize the influence of miscellaneous peaks and boundary noise during peak searching, two criteria are applied: the area ratio between two adjacent zero points f₁ and the distance between two adjacent zero points f₂ are taken as the discrimination standard. Hence, $\frac{\min \left\{\left|{\displaystyle {\sum }_{j=z_{i-1}}^{z_i}{\tilde{s}}_j}\right|\mathrm{,}\left|{\displaystyle {\sum }_{j=z_i}^{z_{i+1}}{\tilde{s}}_j}\right|\right\}}{\max \left\{\left|{\displaystyle {\sum }_{j=z_{i-1}}^{z_i}{\tilde{s}}_j}\right|\mathrm{,}\left|{\displaystyle {\sum }_{j=z_i}^{z_{i+1}}{\tilde{s}}_j}\right|\right\}}<f_1,$ (9) ${\tilde{s}}_j-{\tilde{s}}_{j-1}>f_2\mathrm{,}{\tilde{s}}_{j+1}-{\tilde{s}}_j>f_2,$ (10) where z_i denotes the i-th zero point of the transformed spectrum. To ensure that the sensitivity of peak searching remains unaffected by statistical fluctuations in the spectrum, the standard deviation of the transformed spectrum is used. Specifically, when the positive extreme value of the transformed spectra divided by the standard deviation exceeds the set threshold f, the point is identified as the peak position. $\frac{{\tilde{s}}_i}{\text{Δ}{\tilde{s}}_i}=\frac{{\displaystyle {\sum }_{j=-t}^t{G}_j{s}_{i+j}}}{\sqrt{{\displaystyle {\sum }_{j=-t}^t{G}_j^2{s}_{i+j}}}}>f\mathrm{.}$ (11) Figure 4 illustrates the peak-searching process for the background, single, and multiple nuclide spectra. The characteristic decay energies of ¹⁷⁶Lu (201.8 keV and 306.8 keV) were used for energy calibration, as shown in Fig. 4c. The two full-energy peaks, marked by blue circles, are derived from the characteristic gamma photons emitted by ¹⁷⁶Lu. For the portable gamma spectrometer, energy calibration was performed periodically during the background measurement but not during the identification process. To ensure the stability of energy calibration and minimize interference from ¹⁷⁶Lu in nuclide identification, different values for f₁,f₂, and f were selected, as shown in Fig. 4c and i.

Fig. 4Full-screen View

(Color online)Peak-searching processes for the background, single nuclide (¹³⁷Cs), and multiple nuclides (²⁴¹Am-⁶⁰Co-¹³⁷Cs). (a), (d), and (g) are the smoothing processes for background, single nuclide, and multiple nuclides cases, respectively. (b), (e), and (h) are the convolution processes. (c), (f), and (i) show the peak-search results

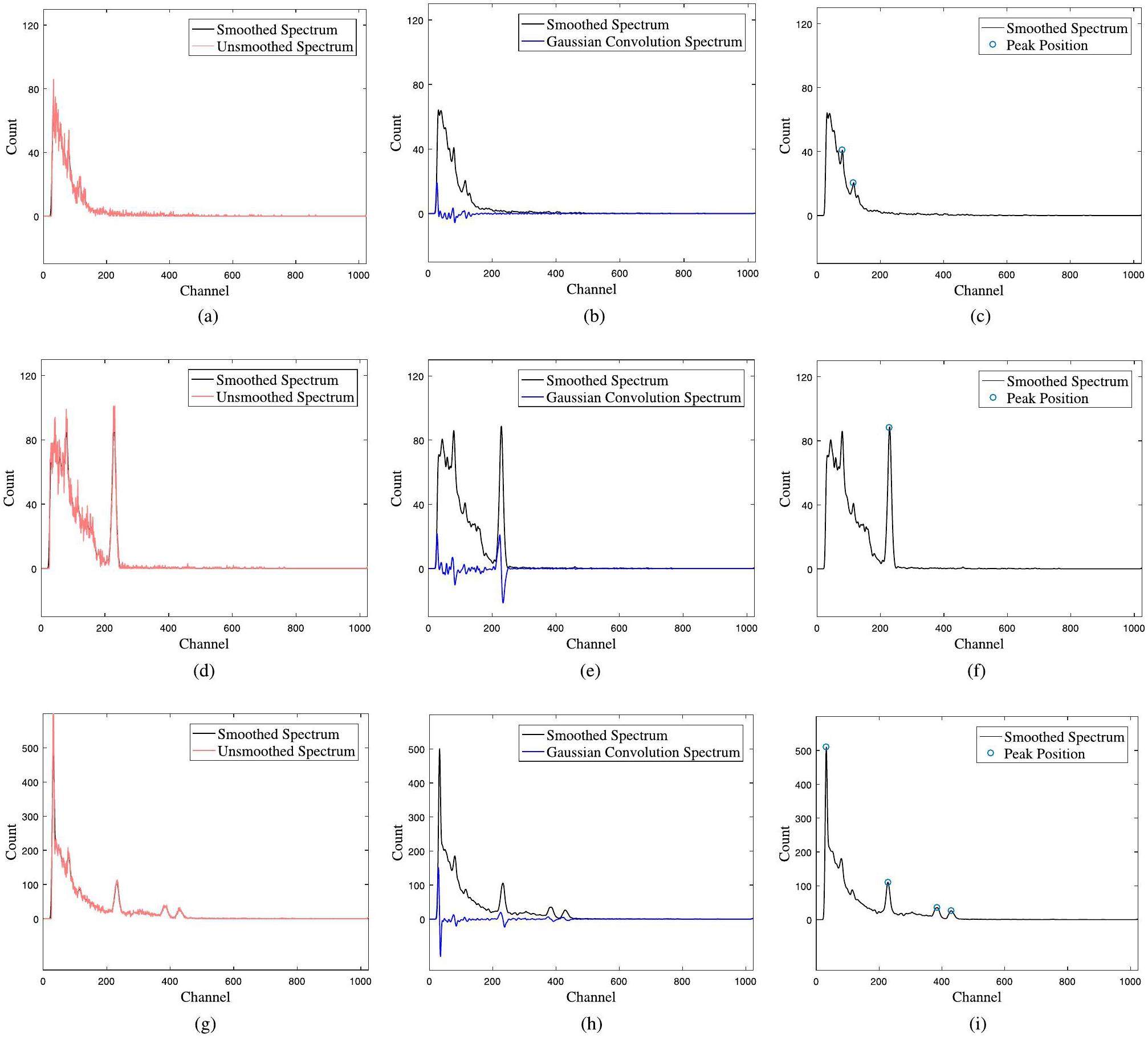
In Figs. 4a, d, and g, the smoothing algorithm demonstrates good performance, ensuring the non-negativity of the spectra around peak regions. The transformation process also effectively removes the background, as shown in Figs. 4b, e, and h. The peaks marked with blue circles in Figs. 4f and i represent the full-energy peaks of the single (¹³⁷Cs) and multiple nuclides (²⁴¹Am-¹³⁷Cs-⁶⁰Co) cases, respectively, indicating the effectiveness of the designed peak-searching algorithm.

Datasets construction

Using the designed feature extraction algorithm, the full-energy peaks of 12 nuclides were obtained from 1200 measured spectra (100 spectra for each nuclide). The characteristic energies were calculated based on the energy-scale coefficients of the spectrometer. Table 1 lists the characteristic energies of the measured nuclides obtained using the peak-searching algorithm and energy calibration. The designed peak-searching algorithm proves effective for gamma rays with high branching ratios emitted by the nuclides.

The data listed in Table 1 demonstrates a noticeable error between the obtained energies and the standard characteristic energy. Simultaneously, considering the drift problem of the detector under varying working environment temperatures, the extracted datasets for a single nuclide were expanded within a range of ±2%. Consequently, the training dataset size for a single nuclide increased from 100 to 500. Then, the different expanded single-nuclide characteristic energies were combined to create multiple-nuclide characteristic energy vectors, with the number of nonzero elements kept at eight or fewer. The multiple-nuclide labels were formed by linearly superposing single-nuclide labels. This process generated datasets containing 18,500 input feature vectors. All input feature vectors were normalized and randomized to reduce positional sensitivity and enhance the generalizability of the model.

Identification accuracy indicators

Hamming Loss is a common evaluation metric in machine learning and classification problems, particularly for multilabel classification tasks where each sample can have multiple labels. It measures the dissimilarity between predicted and actual labels using the Hamming distance, which quantifies the number of differing bits between two binary strings. Specifically, Hamming Loss is calculated as the average number of misclassified labels across an entire test dataset. Hamming Loss evaluates not only individual label predictions but also overall sample predictions. In addition, it is easy to understand and calculate, providing an intuitive measure of classifier performance on test datasets. A lower Hamming Loss indicates higher model accuracy. The calculation formula is as follows: $\text{HL}=\frac{1}{mq}{\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^q}I\left(y_j^i\ne {\tilde{y}}_j^i\right)\mathrm{,}$ (12) where m is the number of tested samples, q is the label dimension, $y_j^i$ is the j-th element of the real label for the i-th sample, and ${\tilde{y}}_j^i$ is the j-th element of the prediction for the i-th sample.

However, Hamming Loss has certain limitations. It primarily focuses on overall similarity and can fail to capture local characteristics. To address this issue, this study introduces a stricter evaluation method called the exact match ratio (EMR). This method considers only cases where the prediction matches the true label exactly as effective results. EMR is defined as $\text{EMR}=\frac{1}{m}{\displaystyle \sum _{i=1}^m}I\left(y^i={\tilde{y}}^i\right)\mathrm{,}$ (13) where m is the number of tested samples, yi is the real label for the i-th sample, ${\tilde{y}}^i$ is the prediction for the i-th sample, and I(·) is the indicator function.

The EMR method is stricter than Hamming Loss because partially correct predictions are not considered effective. Nonetheless, for both metrics, a smaller value always indicates better network model performance.

Identification Test

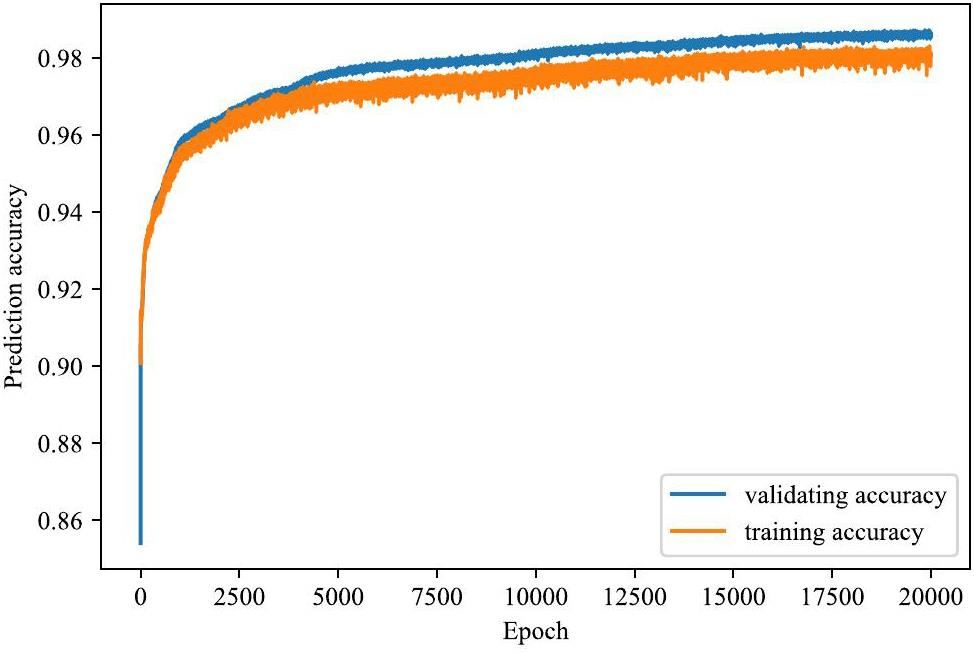
In this study, 14800 gamma spectra were used as training and validation datasets, while 3700 gamma spectra were used as test datasets. The training accuracy iteration processes for both the training and validation datasets were recorded over 20000 epochs, as shown in Fig. 5. The validation accuracy converged to 0.967. Two types of identification tests were performed: a validation test using 3700 validation spectra and an actual test using 900 spectra measured under both unshielded and shielded conditions.

Fig. 5Full-screen View

(Color online) Iteration processes of the training and validation datasets

Using the trained network, validation datasets including single, double, and triple nuclides were tested. Table 2 lists the average neural network output for each node under a single-nuclide case, where the background case is also considered as a type of single-nuclide case. The 12 values in each row of Table 2 represent the average output of the 12 network output nodes for a specific nuclide case. Figure 6 illustrates the distribution of the network output for the corresponding nodes under a single-nuclide case. The bold numbers in Table 2 and the red lines in Fig. 6 indicate the average output of the corresponding nodes.

Fig. 6Full-screen View

Network output of the corresponding nodes under the single nuclide case

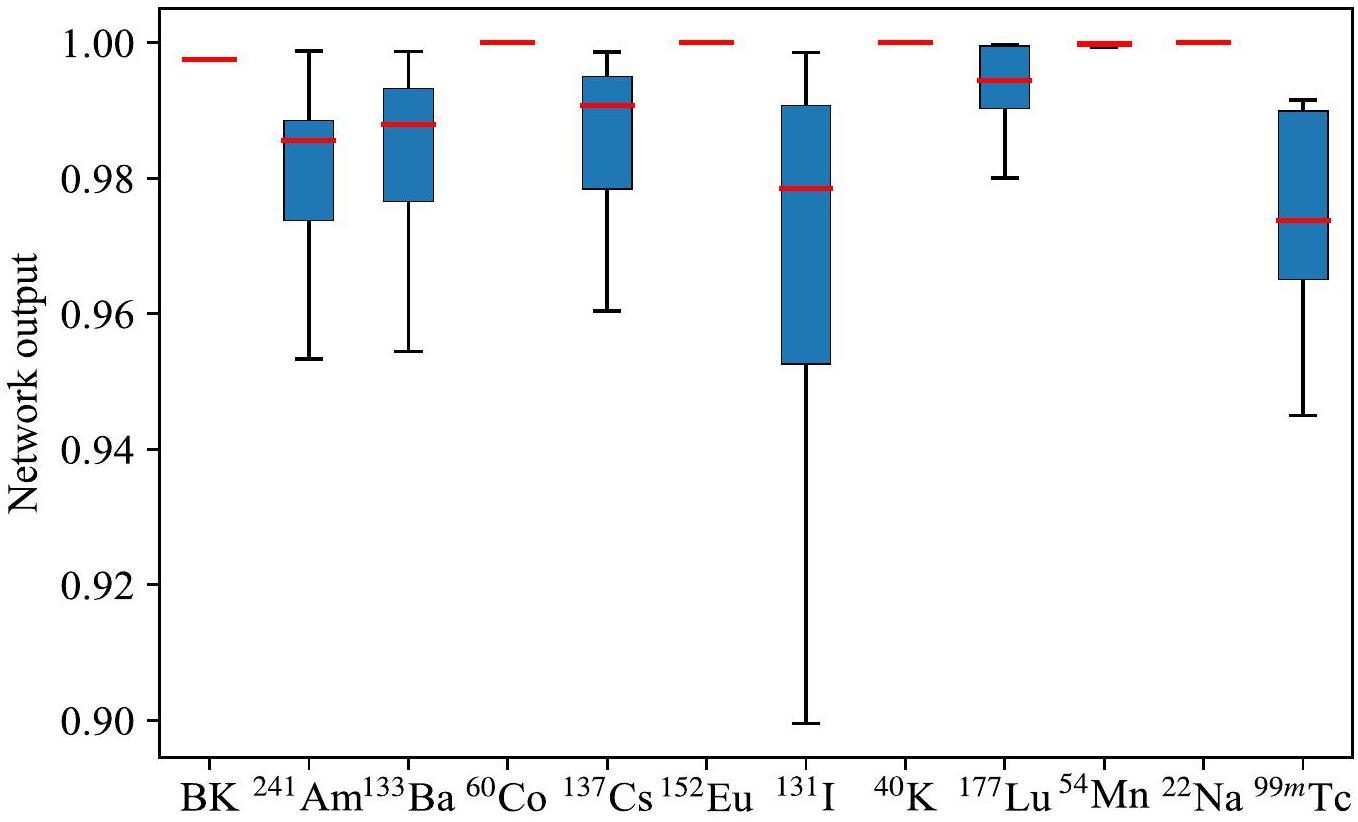
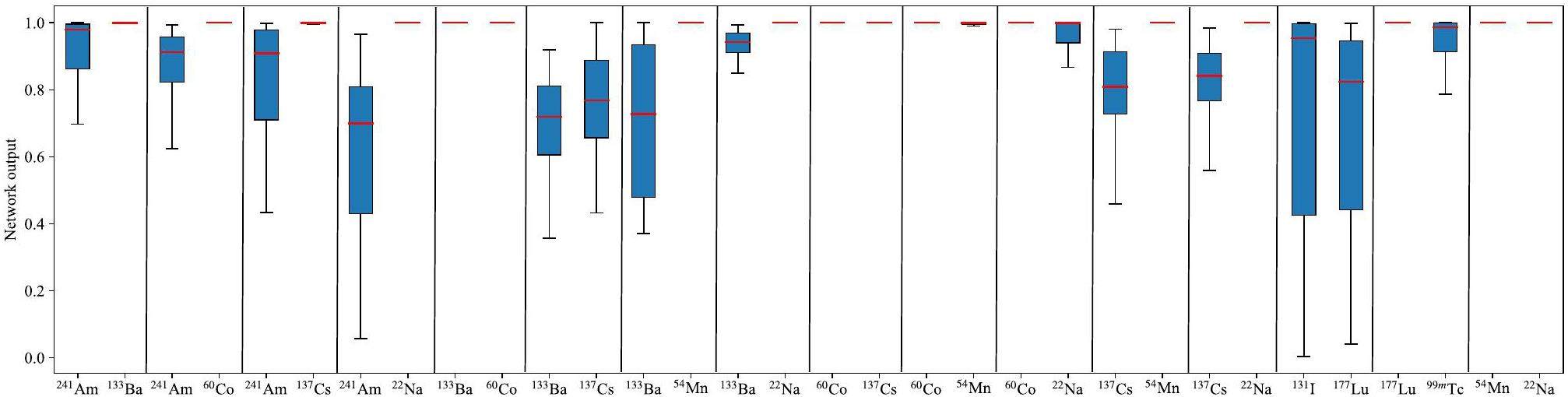
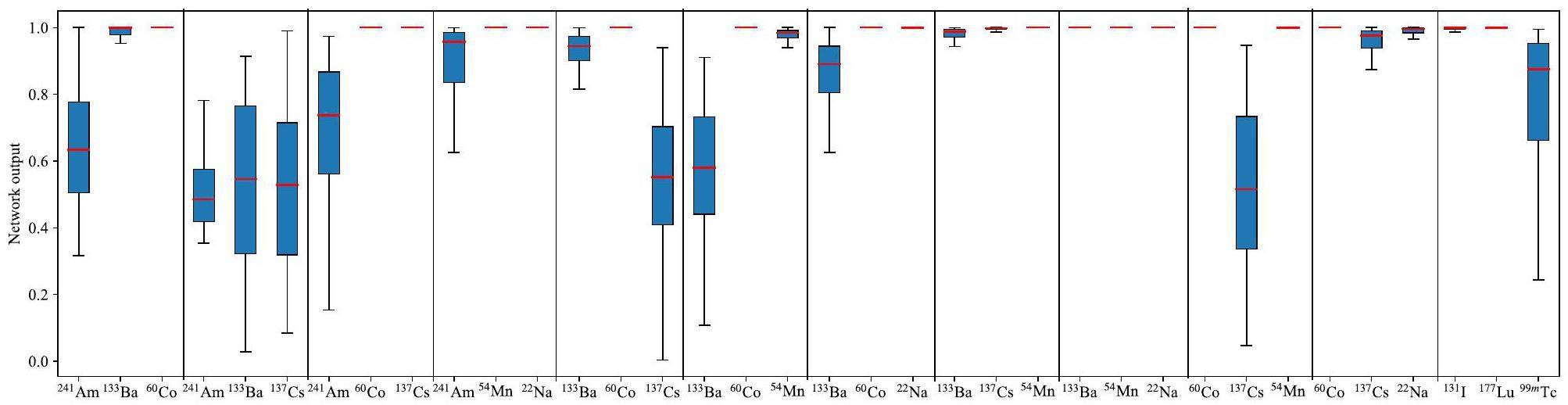
Tables 3 and 4 list the average neural network output for each node under dual- and triple-nuclide cases, where the background case is not considered. This is because the dual- and triple-nuclide cases with the background included can be reduced to single- and dual-nuclide cases, respectively. The 12 values in each row of Tables 3 and 4 represent the average output of the 12 network output nodes for a specific multiple-nuclide case. Based on possible combinations of target nuclides in industrial and medical processes, 16 dual-nuclide cases and 12 triple-nuclide cases were tested. Figure 7 and Fig. 8 illustrate the distribution of the network output for the corresponding nodes under dual- and triple-nuclide cases. The bold numbers in Tables 3 and 4 and the red lines in Fig. 7 and Fig. 8 demonstrate the observations listed in Table 2 and shown in Fig. 6.

Fig. 7Full-screen View

Network output of the corresponding nodes under dual nuclides case

Fig. 8Full-screen View

Network output of the corresponding nodes under the triple nuclide case

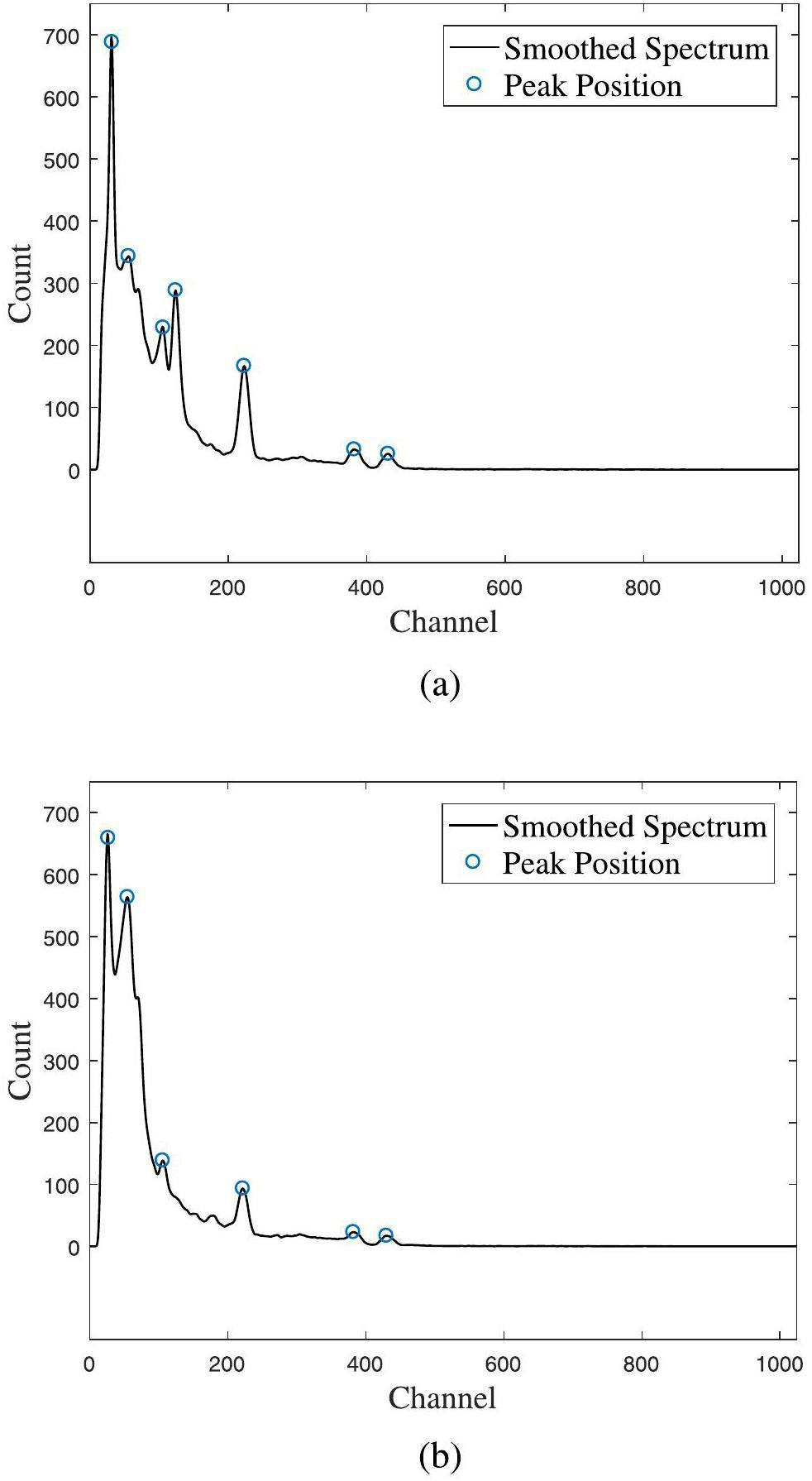
After the identification test using validation datasets, an actual test of the identification method was conducted under unshielded and shielded conditions (using a 10 mm lead brick). To verify the validity and feasibility of the algorithm in scenarios with energy resolution challenges and complex background interference, several types of single, double, and triple nuclides were randomly selected for 100 repeated identification tests under both conditions. All the shielded spectra were excluded from the training datasets, but the nuclides were included in the output layer. Figure 9 illustrates the peak-searching results for unshielded and shielded multiple-nuclide cases. Figure 9a shows peak-searching results for the unshielded ¹³³Ba-⁶⁰Co-¹³⁷Cs case, and Fig. 9b shows the results for the shielded case.

Fig. 9Full-screen View

Peak-searching results of the unshielded and shielded triple nuclides (¹³³Ba-⁶⁰Co-¹³⁷Cs) case. (a) Unshielded triple nuclides case; (b) Shielded triple nuclides case

Identification accuracy

As shown in Fig. 6, for single nuclides with similar decay energies, the average output of the corresponding nodes is relatively lower than that for other nuclides. For example, the decay characteristic energies of 364.5 keV and 637.0 keV for ¹³¹I are close to the 356.0 keV of ¹³³Ba and the 661.7 keV of ¹³⁷Cs, indicating that there are small differences between their input vectors after normalization. A similar situation occurs between ²⁴¹Am, ¹⁷⁷Lu, and ^99mTc. These small differences are likely to be treated as noise signals, causing a drop in the output of the corresponding nodes. The results in Table 3 show that the outputs of the corresponding nodes are significantly different from those of other nodes.

For the dual-nuclide case results in Fig. 7 and Table 4, and the triple-nuclide case results in Fig. 8 and Table 4, the decline in the output of the corresponding nodes is caused not only by similar decay characteristic energies but also by mutual interference within the dual- and triple-nuclide training datasets. For example, in the ²⁴¹Am-¹³³Ba-⁶⁰Co case, the weight of ²⁴¹Am (normalized characteristic energy value of ²⁴¹Am) in its input vector is close to zero after normalization because since the normalization process is performed by dividing all the feature input vectors by the largest characteristic energy value in the datasets. The characteristic energy of ²⁴¹Am and the largest characteristic energy were 63.2 and 1452.1 keV, respectively. This causes a decline and an increase in the ²⁴¹Am node in the ²⁴¹Am-¹³³Ba-⁶⁰Co and ¹³³Ba-⁶⁰Co cases. Nevertheless, the 12 values of each row in Tables 3 and 4 also show a relatively significant difference between the correct and other nodes, and by choosing an appropriate threshold, a high identification accuracy can be obtained.

Based on the analysis in the table above, the threshold for determining the presence or absence of nuclides was set at 0.4. If the output of a node exceeds 0.4, then it is considered to indicate the presence of the corresponding nuclide, and vice versa. Using this threshold, the Hamming Loss and EMR were calculated as 0.013 and 0.052, respectively. The accuracy of complete identification was 1-EMR=94.8%. Compared to the full-spectrum identification method with an accuracy of 90.0% (considering only six kinds of nuclides) [22], the proposed algorithm demonstrates higher accuracy and a superior ability to identify multiple nuclides. Moreover, as shown in Fig. 9, the full-energy peak positions can be accurately determined in both unshielded and shielded multiple-nuclide cases (¹³³Ba-⁶⁰Co-¹³⁷Cs), highlighting the effectiveness of the peak-searching method. After 100 repetitions for each case, the Hamming Loss, EMR, and the accuracy of complete identification for each case with the chosen threshold are listed in Table 5. The total Hamming Loss and EMR were 0.007 and 0.016, respectively, with an overall accuracy of 1 - EMR = 98.4% for the actual test. As shown in Fig. 9b, the energy resolution and complex background interference caused by the shielding can change the shape and characteristics of the peaks, which leads to biased network input. Nevertheless, good identification results were achieved for both unshielded and shielded cases, demonstrating the effectiveness and robustness of the algorithm.

This algorithm could be further developed to include additional standard nuclides. Incorporating new standard nuclides typically reduces identification accuracy. This study considered eleven common nuclides and their combinations. To include new sources, their gamma spectra must be measured, or their full-energy peak data directly. These characteristic energies can then be combined with those of existing nuclides to update the training datasets. The directly used full-energy peak data should account for uncertainties based on detector performance (e.g., peak drifting or resolution changes). The output layer should also be expanded to include all considered nuclides. Expanding the number of output nodes slightly increases resource consumption and reduces the identification accuracy of the chip. However, previous neural network identification methods require expanding the output layer to include not only the considered nuclides but also their combinations, leading to significant chip resource consumption. The decrease in identification accuracy primarily depends on the proximity of characteristic energies of the new nuclides to those of existing nuclides; greater differences result in smaller effects.

Complexity analysis

Time and space complexities are fundamental concepts in algorithm analysis and are used to describe the time and space resources required by an algorithm during execution.

Time complexity refers to the computational work needed to execute an algorithm and reflects the growth in execution time as input size increases. Specifically, the time complexity is expressed as a function that relates the number of basic operations (e.g., addition, comparison, and assignment) performed by an algorithm to the input size, typically described using the notation O(·). Space complexity refers to the amount of memory required to execute an algorithm and reflects the growth in required storage space as the input size increases. Similar to time complexity, space complexity is described using O(·).

In this study and other related studies, the time and space complexities of algorithms primarily stem from the forward computation of neural networks and convolutional computations. Since neural network training is typically performed on high-performance computers, only the time and space complexities during the prediction process were considered. The time and space complexities of the designed algorithm are given by $\text{Time}\sim O\left(mk+{\displaystyle \sum _{l=1}^D}{C}_{l-1}{C}_l\right)\mathrm{,}$ (14) $\text{Space}\sim O\left(k+{\displaystyle \sum _{l=1}^D}{C}_{l-1}{C}_l\right)\mathrm{,}$ (15) where m is the size of the data, k is the length of the convolution kernel, D is the network depth, and C_l-1 and Cl represent the numbers of input and output nodes, respectively, in the l-th layer. The network depth D is typically set to three or four. In this study, a low-consumption design was implemented with parameters set as C₀ = 8 and CD = 12, corresponding to the number of target nuclides. The time and space complexities of traditional artificial neural network (ANN) algorithms [22, 35] are given by $\text{Time}\sim O\left({\displaystyle \sum _{l=1}^{\overline{D}}}{\overline{C}}_{l-1}{\overline{C}}_l\right)\mathrm{,}$ (16) $\text{Space}\sim O\left({\displaystyle \sum _{l=1}^{\overline{D}}}{\overline{C}}_{l-1}{\overline{C}}_l\right)\mathrm{.}$ (17) Equations (16) and (17) are structurally similar to Equations (14) and (15). However, the input dimension ${\overline{C}}_0$ and the output dimension ${\overline{C}}_{\overline{D}}$ are usually taken as the dimension of the spectra and the combination of the target nuclides, which yields ${\overline{C}}_0\ge 1024$ and ${\overline{C}}_{\overline{D}}={\displaystyle {\sum }_{l=1}^S{C}_o^l}$, where $C_o^l=o!/(l)!(o-l)!$ and S are the number of identifiable nuclides under the multiple nuclides case. The time and space complexities of the CNN are given by $\text{Time}\sim O\left({\displaystyle \sum _{l=1}^{\tilde{D}}}{M}_l^2{K}_l^2{\tilde{C}}_{l-1}{\tilde{C}}_l\right)\mathrm{,}$ (18) $\text{Space}\sim O\left({\displaystyle \sum _{l=1}^{\tilde{D}}}{K}_l^2{\tilde{C}}_{l-1}{\tilde{C}}_l\right)\mathrm{,}$ (19) where Ml and Kl denote the side lengths of the feature map and kernel, respectively. CNNs usually consist of multiple convolutional, pooling, and fully connected layers with high dimensions, which significantly increase their time and space complexities [36, 37]. Comparing the above formulas reveals that the algorithm designed in this study achieves shorter running times and lower resource consumption. Practical testing shows that it can be executed within 2 s on an ARM chip.