Introduction

Terahertz (THz) radiation has been utilized in numerous applications over the past few decades owing to its unique properties. Terahertz radiation has diverse applications, particularly in the fields of biology, medicine, and magnetic and quantum materials. It is particularly useful in THz imaging for nondestructive material analysis because of its ability to penetrate materials of various densities. Its high absorption by water makes it invaluable for probing diseased tissues [1, 2] and monitoring skin and tissue hydration levels [3]. Moreover, the alignment of the THz frequency band with the rotational and vibrational modes of numerous molecules allows the intermolecular bonds and ultrafast dynamic processes to be studied using THz spectroscopy [4] and pump-probe experiments [5]. These advanced techniques have applications in molecular modeling, DNA identification, and crystal polymorphism analysis [6-8]. Beyond its applications in biology, THz radiation is also well suited for applications in materials science such as investigating magnetoconductivity in two-dimensional quantum systems and quasi-particle excitations in solids and magnetic systems, manipulating the dynamic states of matter, and characterizing polymers, liquid crystals, and metamaterials [9-11].

The advantages of THz radiation in various applications have led to numerous studies on the development of THz light sources, detectors, and experimental techniques. The quality of the radiation source is a crucial consideration in applications requiring high-brightness THz radiation. Accelerator-based light sources are among the most powerful sources of THz radiation. THz light sources have been developed by several accelerator centers and laboratories based on various techniques. In particular, free electron lasers (FELs) provide intense, coherent, and ultrafast radiation pulses with possible wavelength tunability. Wavelength tunability is typically not available in conventional lasers, in which the electrons are bound to atoms or molecules [12].

Accelerator-based FELs can be realized using various approaches depending on the desired radiation wavelength and intended applications. A popular approach is stimulated emission radiation, which is commonly used to realize FELs with wavelengths ranging from the mid-infrared to X-ray region. In this process, electron bunches emit radiation while traveling through a sinusoidal magnetic field structure, such as that in an undulator magnetic field, and interact with radiation either from the electron bunches themselves or from an external light source. The co-propagating radiation modulates the longitudinal velocity of the electrons in the bunch, causing them to bunch into small groups via the so-called microbunching process [13]. Because the bunch length of the microbunch is shorter than the wavelength, the electrons in the microbunch radiate coherently to produce high-intensity radiation with a narrow spectral width. The radiation wavelength can be adjusted by tuning the electron beam energy or undulator magnetic field. Well-known examples of FELs based on the stimulated emission radiation process include self-amplified spontaneous emission FELs [14, 15], seeded FELs [16], and oscillator FELs [17].

At long wavelengths, such as those in THz radiation, electron beams with high currents are required to provide sufficient gain within a practical interaction length during the microbunching process. Therefore, stimulated emission radiation may not be practical under certain accelerator conditions. Another efficient technique for realizing a FEL in this wavelength range is the super-radiant or prebunched FEL technique [18]. In this technique, femtosecond to sub-picosecond electron bunches with relatively high charges are produced and injected into an undulator magnetic field. In contrast to stimulated emission, microbunching does not occur because the lengths of the electron bunches are already equal to or shorter than the radiation wavelength. Consequently, coherent radiation is spontaneously emitted from an ultrashort pre-bunched electron beam as it travels through the undulator poles along the beam trajectory. The constructive interference between overlapping emitted radiation leads to the proper addition of radiation along the forward direction, resulting in an enhanced radiation intensity proportional to the square of the electron number ($I\propto N^2$). In this case, the intensity of the FEL pulse is very high because the radiation is coherently emitted from the entire electron bunch rather than from microbunches.

Super-radiant THz FEL sources have been established and developed in several research facilities worldwide such as the TELBE facility at ELBE (Helmholtz-Zentrum Dresden-Rossendorf, Germany) [19], the compact THz coherent undulator radiation source at KU FEL (Kyoto University, Japan) [20], the THz FEL facility at NSRRC (National Synchrotron Radiation Research Center, Taiwan) [21], and the super-radiant THz undulator source at EU-XFEL (European X-Ray Free-Electron Laser Facility, Germany) [22]. At ELBE, Kyoto University, and NSRRC, electron bunches with energies of less than 40 MeV are compressed to femtosecond-scale lengths, whereas at EU-XFEL, the bunch length of the GeV electron beam is on the order of sub-femtoseconds. These facilities have achieved intense and narrow-bandwidth THz radiation with pulse energies on the order of microjoules. The super-radiant THz undulator source at EU-XFEL has the potential to produce high radiation pulse energies on the order of millijoules by utilizing a photocathode radio-frequency (RF) gun, a superconducting L-band radio-frequency (RF) linear accelerator (linac), and a superconducting undulator magnet. However, the establishment of such large facilities requires advanced technology and expensive components. More compact super-radiant THz FEL sources utilizing electron beams with energies in the tens of MeV range have been built at smaller facilities and universities.

An accelerator-based coherent THz-FEL source is being established at the PBP-CMU Electron Linac Laboratory (PCELL) with the aim of providing an experimental station for utilizing the unique capabilities of THz-FEL. This paper reports on and discusses the design and beam dynamics simulation of the super-radiant THz-FEL beamline. The methodology for producing short electron bunches with the proper charge and peak current for the prebunched FEL is described in Sect. 2. Start-to-end beam dynamics simulations for the expected performance of the accelerator and magnetic bunch compressor systems are presented in Sect. 3. Finally, the properties of the expected THz FEL calculated based on the simulated beam parameters are presented in Sect. 4.

Facility overview

An accelerator-based coherent infrared light source with three radiation stations and beamlines utilizing different techniques comprising coherent THz transition radiation (THz-TR), super-radiant THz-FEL, and oscillator mid-infrared FEL (MIR-FEL) is currently under construction at PCELL. A schematic of the accelerator system with all three stations and beamlines is shown in Fig. 1. With these three radiation sources, our facility will become the first light source of its kind in Thailand and Southeast Asia with the aim of providing experimental stations utilizing MIR and THz radiation generated using the aforementioned techniques. In this study, we focus on the development of the super-radiant THz-FEL source. The accelerator system consists of an S-band thermionic cathode RF electron gun [23], an alpha magnet serving as a pre-bunch compressor and energy filter [24], an S-band travelling-wave RF linac, and beam focusing / steering elements in the form of quadrupole magnets and square-frame dipole coils [25]. A 180° magnetic bunch compressor and a beamline for generating THz-FEL radiation are located downstream of the linac.

Fig. 1Full-screen View

(Color online) Schematic layout of accelerator-based coherent infrared light source at Chiang Mai University. The super-radiant THz-FEL beamline is shown in the middle branch of the system

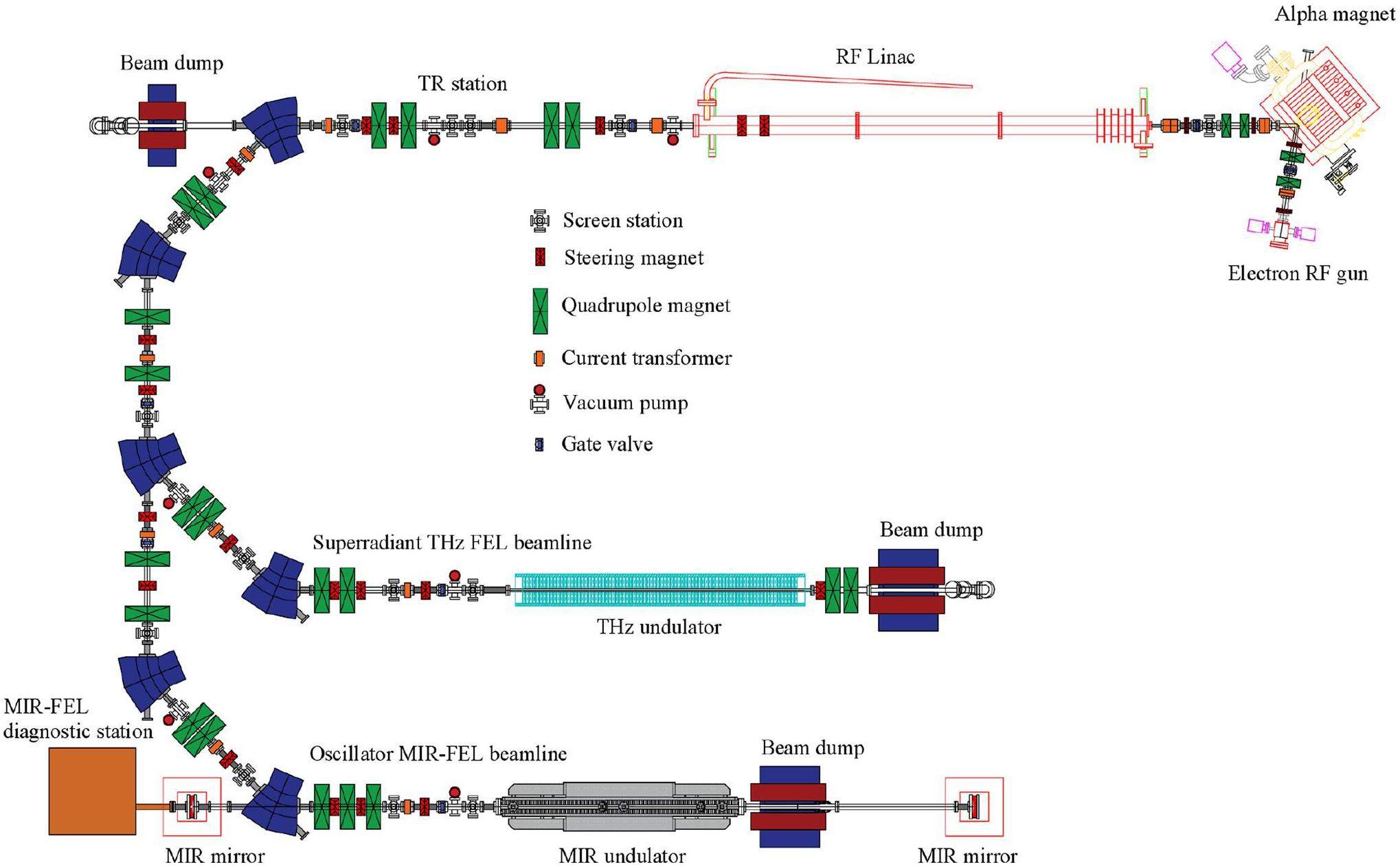
The super-radiant THz-FEL requires a high-brightness electron beam with a bunch length equal to or shorter than the radiation wavelength. At PCELL, our goal is to produce THz-FEL radiation with a frequency of up to 3 THz corresponding to a wavelength of 100 μm. Therefore, the electron bunch length should be at least 100 μm or 300 fs. Such ultrashort bunches are achieved through three bunch compression processes for optimizing the electron beam at our facility. In addition, achieving a super-radiant THz FEL with the desired properties requires an undulator magnet with suitable characteristics. These issues are briefly described and discussed in this section.

Start-to-end beam dynamics simulations

The electron beam properties must be numerically optimized prior to installing the accelerator components. Start-to-end simulations of the beam dynamics throughout the accelerator system were performed using the ASTRA code [30] to determine the appropriate operational parameters for the super-radiant THz-FEL beamline. The optimization process is divided into two parts, one from the RF gun to the alpha magnet and the other from the alpha magnet to the entrance of the undulator magnet. The parameters considered in the simulation comprise the alpha magnet gradient, linac RF phase, and field strengths of all the magnets in the magnetic bunch compressor. The quadrupole and steerer magnetic fields along the beamline were adjusted to achieve low emittance and low energy spread. The 3D electromagnetic field inside the RF gun for the optimization process was obtained using CST Microwave Studio 2012 simulations [31]. The magnetic field distributions for all the magnets were obtained using CST EM Studio 2018 simulations [32]. An optimized electron beam characterized by a short bunch length, high bunch charge, small emittance, and low energy spread is expected to be obtained at the undulator entrance.

In the ASTRA simulation, the space charge effects were accurately modeled using cylindrical and 3D mesh cells. For the RF gun simulation, we used cylindrical meshes with 50 radial and 200 longitudinal mesh cells, as presented in [33]. This choice was made because electrons are uniformly emitted from the cathode and the electric field is predominantly aligned along the gun cavities, resulting in a considerably round transverse beam shape at the gun exit. However, 3D mesh cells were employed for other components such as the alpha magnet field, especially when asymmetric electron beam distributions are present. The mesh cell quantity has a significant influence on the simulation accuracy, impacting both the transverse and longitudinal beam distributions at specific locations during transportation. Determining the appropriate number of mesh cells involves achieving a balance between the number of macro-particles per cell and the smoothness of the space charge fields. The appropriate 3D mesh cell numbers for the alpha-to-undulator section along the x, y, and z axes were determined to be 32, 32, and 4, respectively [34].

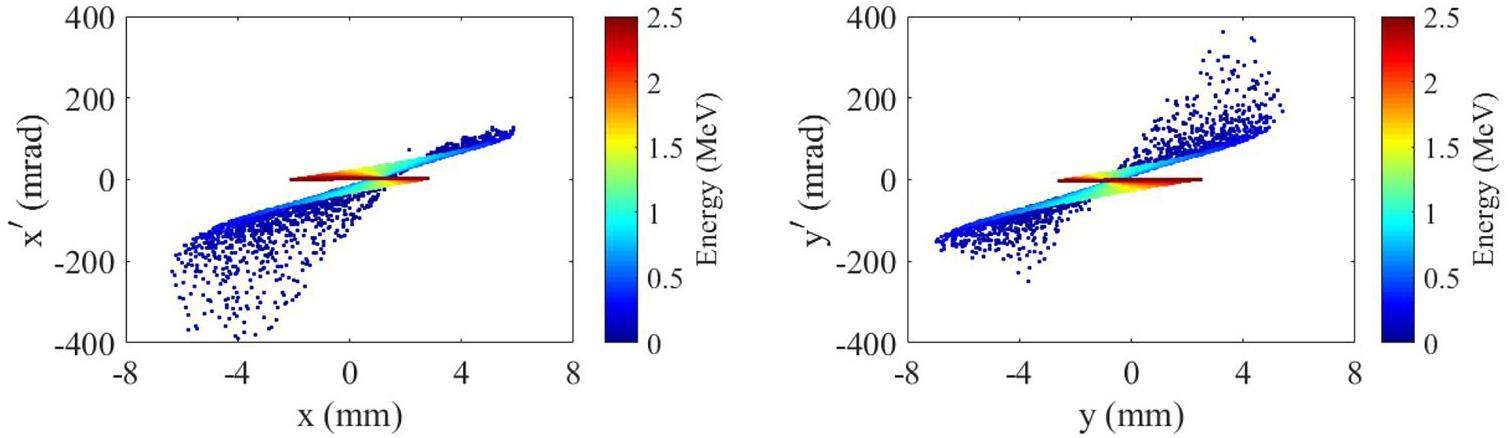
Electron beam optimization was performed from the RF gun to the undulator entrance for various operational parameters. The optimization process comprises the three primary steps of alpha magnet gradient optimization, linac phase optimization, and two-parameter investigation. A dynamic simulation of a single-bunch electron beam in the RF gun was first conducted. In the simulation, two million macroparticles with a diameter of 6 mm are uniformly emitted from the cathode surface. Each macroparticle carries a charge of 0.45 fC, as determined from the average current of 2.6 A measured at the gun over a RF period. A kinetic energy of 0.165 eV corresponding to a cathode temperature of 1000 degree Celsius was assumed. The average electric fields in the RF gun cavities were adjusted to achieve a maximum electron beam kinetic energy of 2.5 MeV in accordance to the specifications provided in [31]. The electron bunch exiting the RF gun has a charge of 224 pC, average energy of 2 MeV, maximum energy of 2.5 MeV, and energy spread of 0.62 MeV. The transverse phase spaces of the electron beam at the gun exit are presented in Fig. 2. The simulation results show that the electron beam produced by the gun exhibits an asymmetric transverse distribution, as shown in Fig. 3 (a). This asymmetry arises from the influence of the dipole field introduced by the open holes of the side-coupling cavity and the RF waveguide input port of the RF gun [31]. At the gun exit, high-energy electrons are concentrated at the head of the bunch with a well-correlated relationship between energy and time (see Fig. 3 (row 1)). These electrons are subsequently compressed by the alpha magnet downstream of the RF gun, as shown in Fig. 3 (b). Two million macroparticles are emitted from the cathode. Approximately 25% of these particles are then accelerated through the RF gun. Consequently, the electron bunch exiting the RF gun contains approximately five hundred thousand macroparticles, which then proceed to the alpha magnet. The number of macroparticles at the exit of the alpha magnet varies depending on the desired bunch charge. For instance, a 50 pC electron bunch consists of approximately one hundred thousand macroparticles.

Fig. 2Full-screen View

(Color online) Horizontal (x, x') and vertical (y, y') phase spaces of electron bunch at RF gun exit

Fig. 3Full-screen View

(Color online) Transverse and longitudinal distributions of electron beam at (a) RF gun exit, (b) alpha exit, (c) linac exit, and (d) undulator entrance

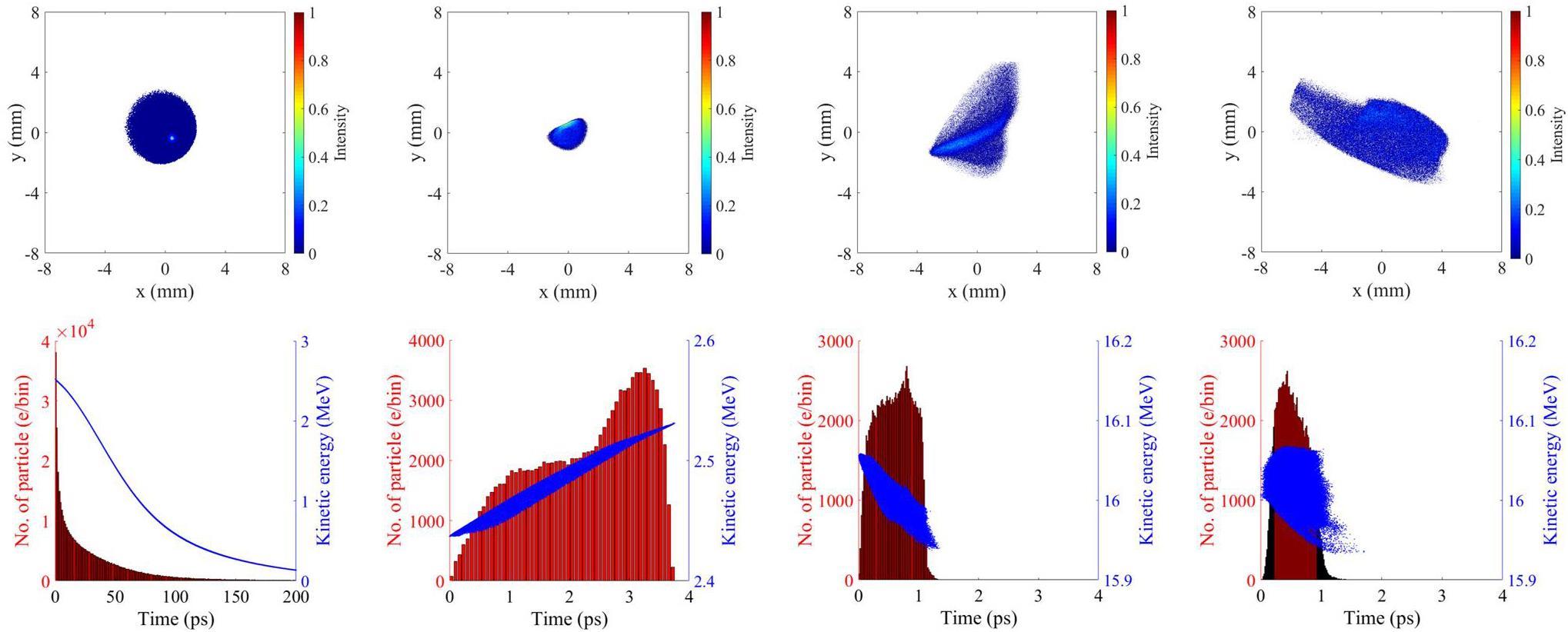
The electron bunch is then further accelerated through the linac structure. The PCELL accelerator system utilizes a SLAC-type S-band traveling wave RF linac operating in the 2π/3 mode. This linac structure, which is known as a disk-loaded cylindrical waveguide, consists of a series of conducting disks with a central hole. The traveling wave fields of a SLAC-type linac obtained from the SSRL SLAC website [35] were incorporated into the ASTRA simulation. The RF phase of the linac was determined relative to a cosine wave. The structure of the disk-loaded cylindrical waveguide was modeled as a linac aperture. Furthermore, beam loading effects were considered in the simulation although the RF pulse width and power dissipation in the linac wall were not included. The beam dynamics optimization initially focused on an electron beam with an average energy of 16 MeV. The linac gradient was therefore adjusted to obtain this energy value. The combination of the bunch compression processes in the alpha magnet and velocity bunching in the linac results in an electron bunch with a sub-picosecond length, as shown in Fig. 3(c).

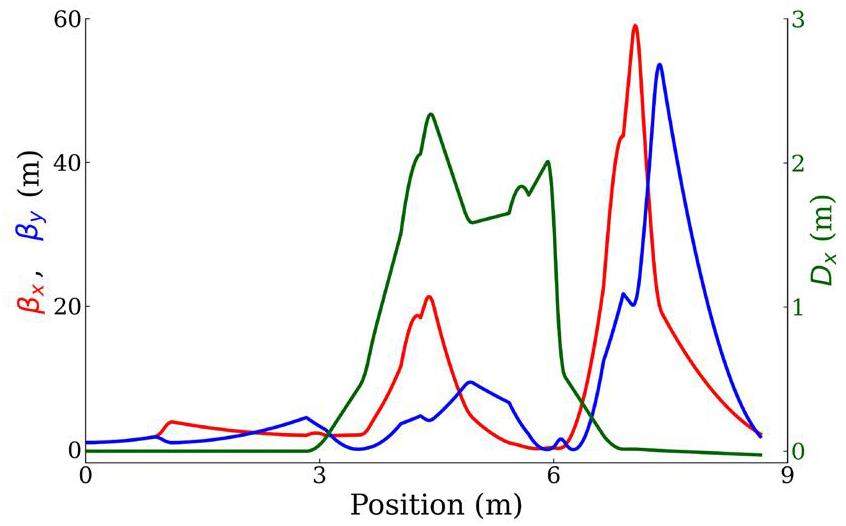
Within the 180°-bunch compressor system, the strengths of the four dipole magnets were adjusted to achieve a bending angle of 45°. The R56 value of 1.04 m for the bunch compressor indicates the transformation of the longitudinal positions relative to the momentum deviations of the electrons within a bunch. Full compression can only be achieved when the calculated R56 is properly matched with the optimized longitudinal phase space of the electron beam at the entrance of the bunch compressor. Quadrupole doublets and a steering magnet were then strategically positioned between the dipole magnets. To accommodate different alpha magnet gradients and linac phases, the strengths of the quadrupole fields in the bunch compressor were uniquely tailored to manipulate the electron distributions within the bunch while the steering magnets were simultaneously tuned to control the electron beam trajectory. An appropriate distribution of high- and low-energy electrons on the x-z plane facilitates the smooth rotation of the longitudinal phase space of the electron bunch along the 180° bunch compressor. Consequently, the electron bunch undergoes significant shortening downstream of the compressor system, as illustrated in Fig. 3 (d). The beta functions and horizontal dispersion along the beam transport line of the magnetic bunch compressor in Fig. 4 show that the electron beam travels along a dispersive trajectory with a momentum deviation under appropriate strengths of the quadrupole magnets within the bunch compressor.

Fig. 4Full-screen View

(Color online) Transverse beta functions (βx, βy) and horizontal dispersion (Dx) along transport line from linac exit to undulator entrance of 16 MeV electron beam

3.1

Alpha magnet gradient optimization

The alpha magnet located downstream of the RF gun is used to rotate the longitudinal phase space distribution of the electron beam. This is essential for proper compression during velocity bunching by the linac and within the magnetic compressor system. Furthermore, energy slits inside the alpha magnet vacuum chamber are utilized as energy filters to remove low-energy electrons from the tail of the bunch. A useful fraction of the electron beam with low energy spread and a specific bunch charge departs from the alpha magnet. A bunch charge of 50 pC was set for this optimization. The RF phase of the linac was set to 0° corresponding to the maximum acceleration condition (on-crest acceleration).

The electron bunch is vertically focused and rotated clockwise in longitudinal phase space as it moves through the alpha magnet, resulting in the transverse and longitudinal distributions shown in Fig. 3(b). The electron trajectory in the alpha magnet at a high alpha magnet gradient is longer than that at a low gradient. Consequently, the electron bunch length shortens and the positive energy chirp of the beam increases as the gradient of the alpha magnet increases. Furthermore, the transverse phase space distribution exhibits a larger divergence and emittance in the vertical direction when a higher alpha magnet gradient is applied. The gradient of the alpha magnet in the PCELL laboratory can be varied up to 460 G/cm owing to limits due to the heating of the coils of the alpha magnet and its water cooling system.

The alpha magnet gradient optimization results are shown in Fig. 5(a). After passing through the two compression processes of alpha magnet compression and linac velocity bunching, the electron bunch has a minimum RMS bunch length of approximately 315 fs for alpha magnet gradients in the range of 405 - 450 G/cm. When the electron bunch moves through the 180°-bunch compressor, the bunch length decreases for all values of the alpha magnet gradient and reaches the smallest value of 206 fs at an alpha gradient of 410 G/cm. Theoretically, the major factors affecting compression in the magnetic bunch compressor are the transverse distribution, energy spread, bunch length, and energy chirp of the electron bunch at the compressor entrance [28]. The transverse beam size and divergence at each alpha magnet gradient are appropriately controlled by the quadrupole magnets in the bunch compressor, whereas the energy spread at all alpha magnet gradients is less than 0.2% owing to energy filtering in the alpha magnet and on-crest acceleration in the linac. The electron bunch length and energy chirp at the 180° bunch compressor entrance therefore significantly influence the attainment of the shortest electron bunch length at the bunch compressor exit during alpha magnet gradient optimization.

Fig. 5Full-screen View

(Color online) (a) RMS bunch length at bunch compressor entrance compared to that at bunch compressor exit for different alpha magnet gradients. (b) Longitudinal phase spaces of electron bunch at bunch compressor entrance (left) and bunch compressor exit (right) for alpha magnet gradients of 360 G/cm (top row), 410 G/cm (middle row), and 460 G/cm (bottom row)

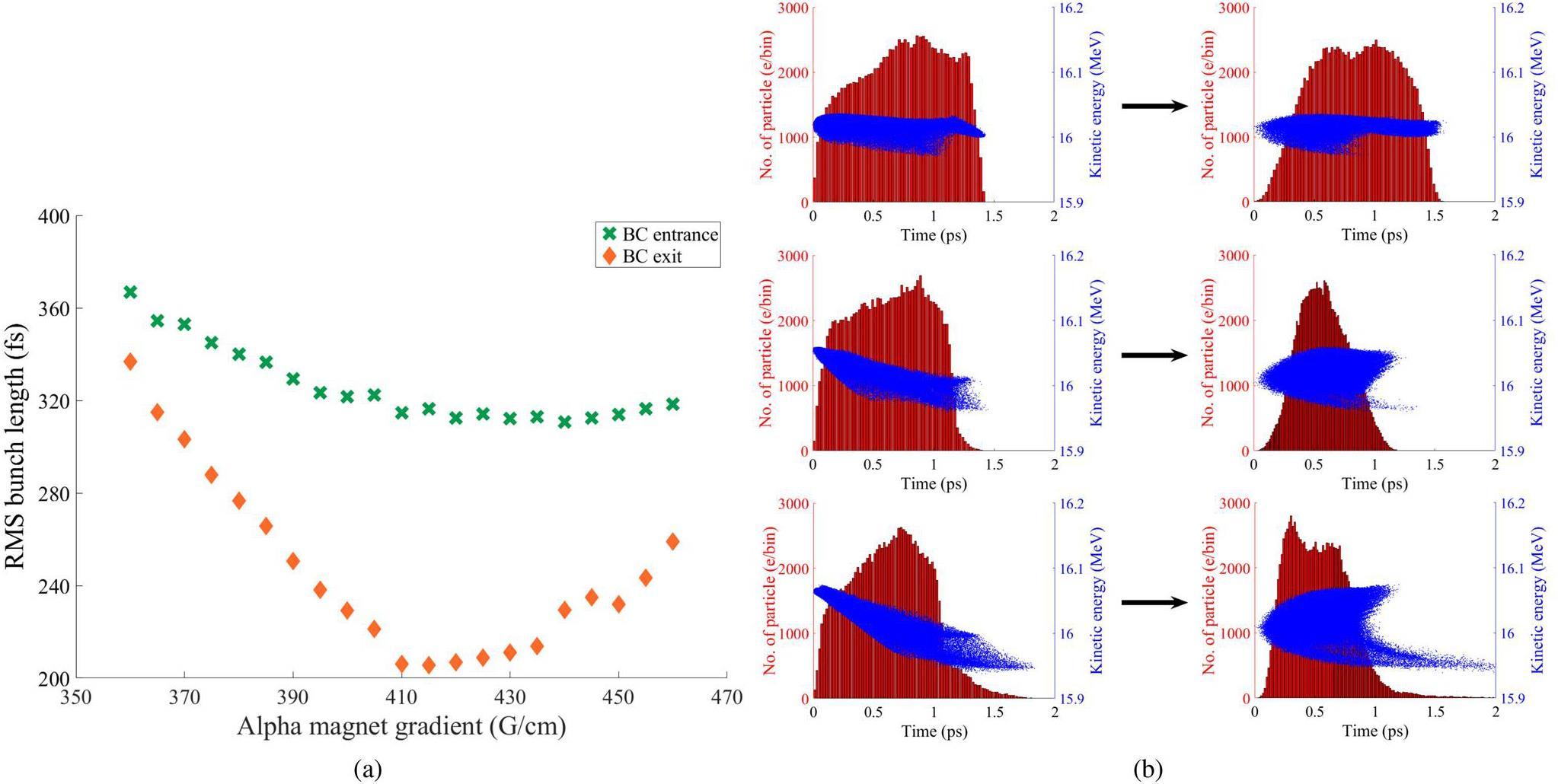
The electron bunches at the bunch compressor entrance exhibit various longitudinal characteristics at different alpha magnet gradients. At a gradient of 360 G/cm, the energy-time phase space has a nearly linear relationship and is uncompressed as the electron bunch moves through the magnetic bunch compressor system because of its dispersion condition, as shown in Fig. 5(b) (top row). In contrast, the electron bunch with a high-energy chirp at the entrance is overcompressed, as shown in Fig. 5(b) for the alpha gradient of 460 G/cm (bottom row). Therefore, optimum compression of the longitudinal beam phase space can be achieved in the magnetic compressor system for an initial electron beam with a short bunch length and a suitable energy chirp at the bunch compressor entrance.

3.2

Linac phase optimization

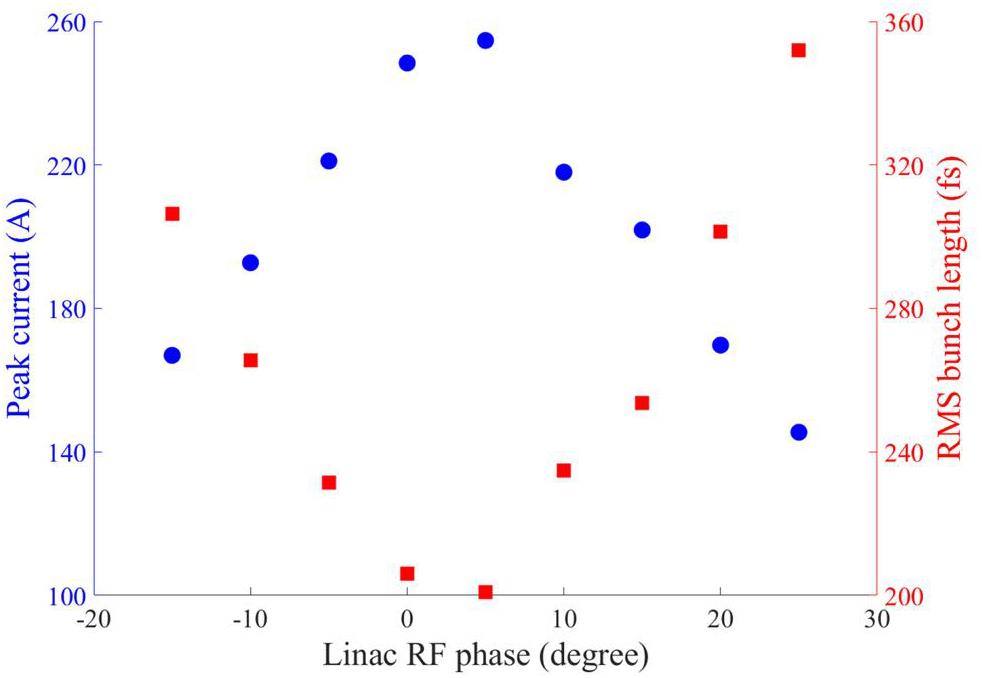
The linac RF phase is crucial for the velocity bunching process and electron beam characteristics at the 180° bunch compressor entrance. When an electron bunch is accelerated through the linac, the beam energy increases and the transverse momentum decreases, resulting in a reduction in the divergence angle and transverse emittance along the linac. Moreover, the longitudinal phase space at the linac exit is compressed by the velocity bunching process, as shown in Fig. 3(c). In this section, we present the optimization of the linac RF phase around the on-crest phase to obtain the minimum bunch length at the undulator entrance for the case of a 410 G/cm alpha magnet gradient. This gradient approximately corresponds to the minimum bunch length condition, as shown in Fig. 5(a). The accelerating electric field of the linac was adjusted simultaneously to obtain an average beam energy of 16 MeV for each linac phase.

The optimization results for the linac phase are shown in Fig. 6. At the undulator entrance, the shortest RMS bunch length and highest peak current can be achieved at the linac phase of 5°. The energy spread of the electron beam upstream of the bunch compressor increases from 0.07% to 0.31% as the accelerating phase of the linac varies from -15° to 25°. However, the energy spread remains unchanged after passing through the bunch compressor [34]. When the electron bunch encounters an off-crest linac RF phase, its energy spread, bunch length, and energy chirp at the 180° bunch compressor entrance change significantly, contributing to different longitudinal phase space rotations in the bunch compressor. Thus, the linac RF phase must be optimized for each alpha magnet gradient.

Fig. 6Full-screen View

(Color online) Peak current (blue circles) and RMS bunch length (red rectangles) of electron beam at undulator entrance for linac phase optimization

3.3

Two-parameter investigation

Different longitudinal electron beam distributions can be accelerated differently in the linac, resulting in different electron beam properties at the entrance of the 180° magnetic bunch compressor. Therefore, two-parameter optimization of the alpha magnet gradient and linac RF phase was performed to obtain the shortest electron bunch with the highest peak current at the undulator entrance. The linac RF phase was varied from -15° to 25° for alpha magnet gradients from 360 G/cm to 460 G/cm. The electron beam leaving the 180° bunch compressor system is transported and focused at the center of the undulator magnet. The RMS bunch length of the electron beam at the undulator entrance in the two-parameter investigation is shown in Fig. 7(a). Consequently, the minimum value of the RMS bunch length for each alpha magnet gradient can be obtained at the optimal linac RF phase. A lower alpha magnet gradient requires a larger off-crest linac phase to adjust the linear longitudinal phase space of the electron beam. In contrast, at high alpha magnet gradients, the energy-time phase space has optimal chirp for bunch compression and an almost on-crest linac phase is therefore suitable. RMS bunch lengths of 200 fs to 340 fs, corresponding to peak currents of 160 A to 250 A, can be achieved for alpha magnet gradients ranging from 360 G/cm to 460 G/cm. The optimal alpha magnet gradient for providing a 16 MeV electron beam with the shortest bunch length and highest peak current at the undulator entrance is 430 G/cm, as shown in Fig. 7(b).

Fig. 7Full-screen View

(Color online) (a) RMS bunch length at undulator entrance for optimization of alpha magnet gradient and linac RF phase. (b) Optimal peak current (blue circles) and RMS bunch length (red rectangles) for two-parameter optimization. (c) Contour plots of RMS bunch length and (d) peak current of electron beam at undulator entrance for different alpha magnet gradients and linac RF phases

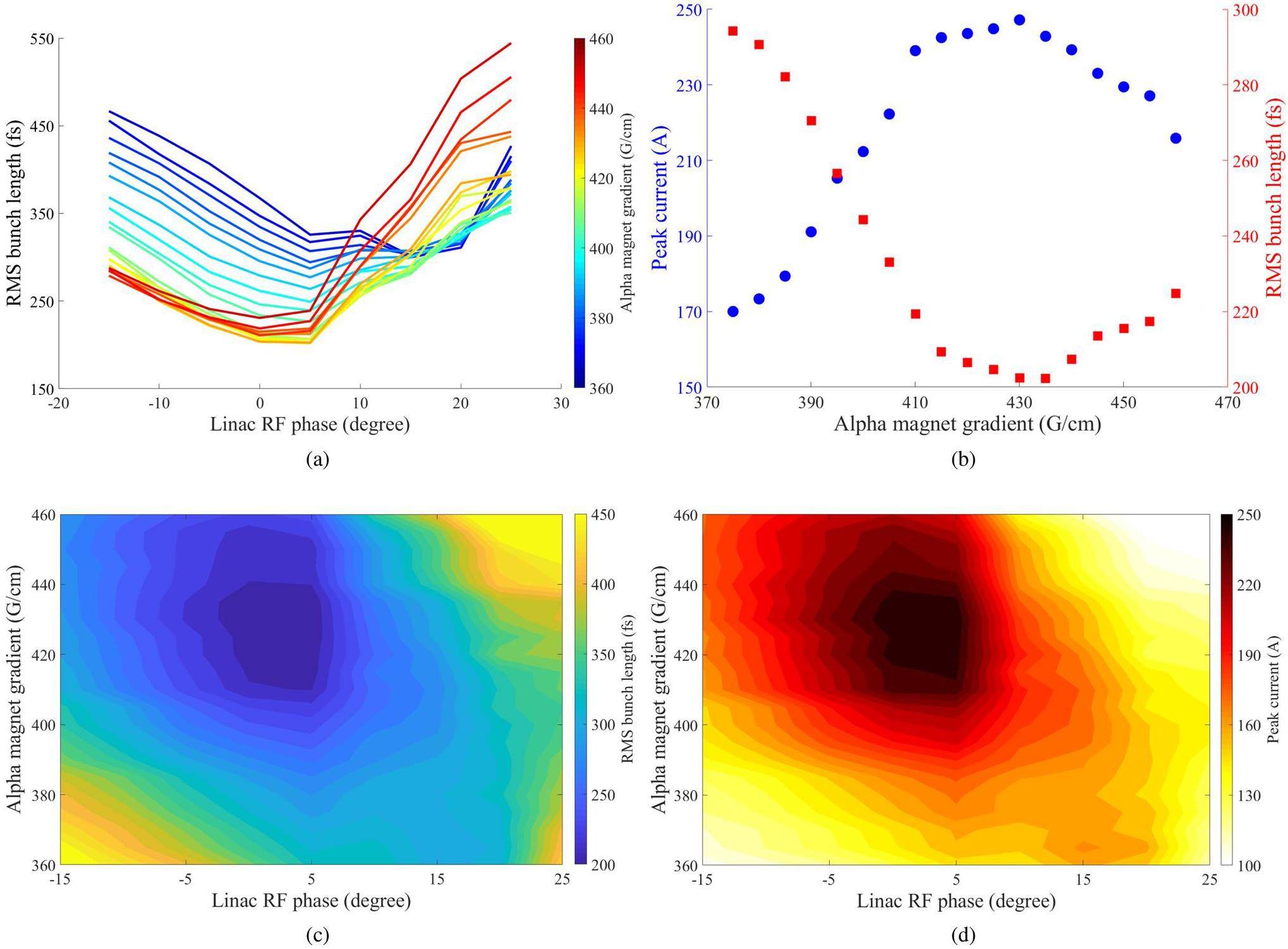
The variations of the electron bunch length and peak current at the undulator entrance with the alpha magnet gradient and linac RF phase are displayed in Fig. 7(c) and (d). The two-parameter optimization contour plots show that a short electron bunch length and high peak current can be obtained over the alpha gradient range of 410 G/cm to 440 G/cm and linac phase range of 0° to 5°. The minimum RMS bunch length is 202 fs and the highest peak current is 247 A. The energy spread is less than 0.2% and the normalized transverse emittance is approximately 15.05 πmm·mrad. The evolution of the electron bunch length along the PCELL accelerator system shown in Fig. 8(a) reveals that the three bunch compressor processes can efficiently shorten the electron bunch length along the beamline.

Fig. 8Full-screen View

(Color online) (a) Evolution of RMS bunch length (magenta solid line) and normalized transverse emittance (${ϵ}_{xy\mathrm{,}\text{norm}}$) (green dots) of 16 MeV electron beam with optimum compression condition. (b) Minimum RMS bunch length and corresponding energy spread of 16 MeV electron beam at undulator entrance for different bunch charges. (c) Electron current profiles of 10 MeV and 16 MeV electron bunches at undulator entrance. (d) Total pulse energy of super-radiant THz FEL and square modulus of form factor for 10 MeV and 16 MeV electron beams

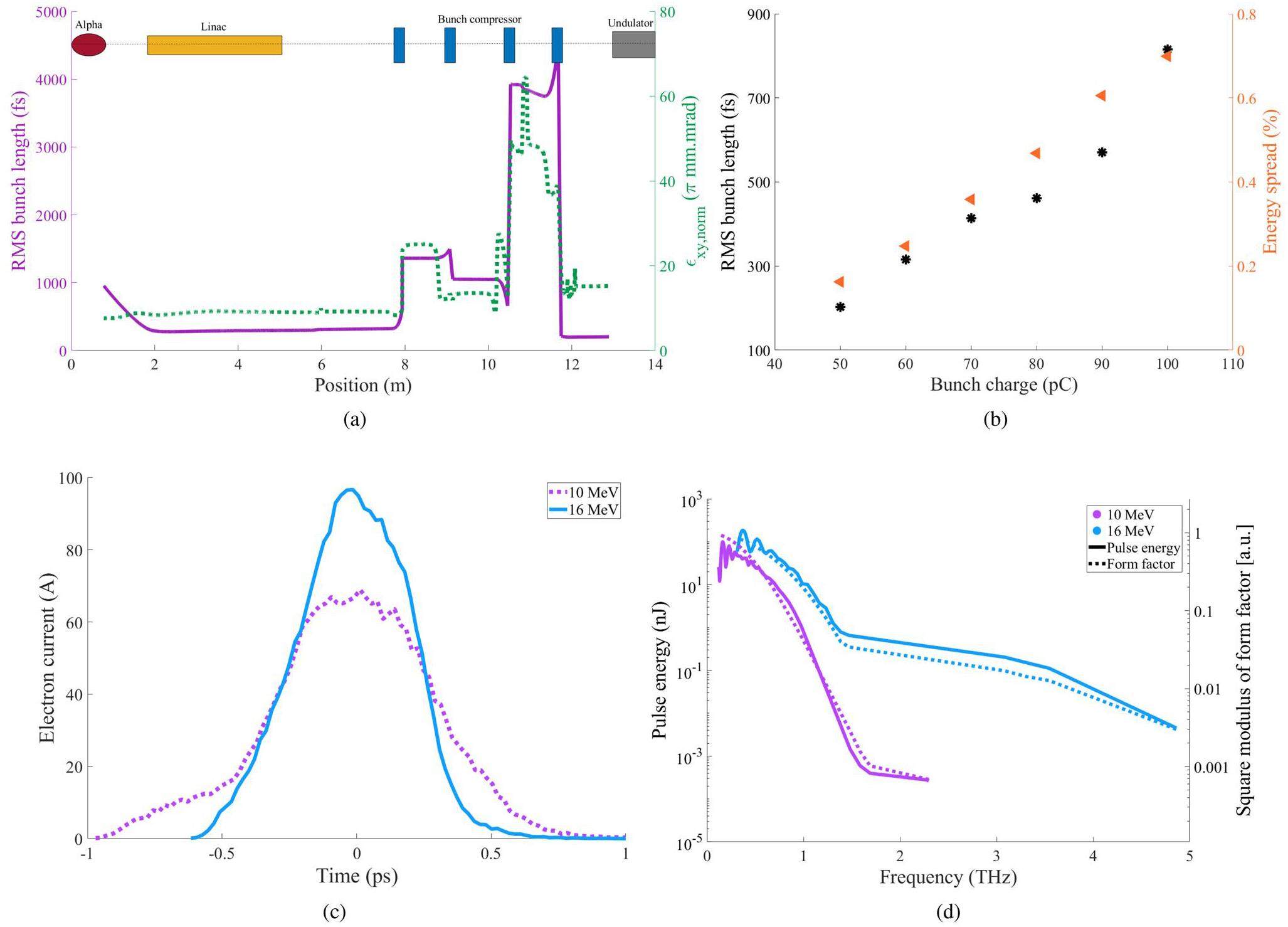
Furthermore, beam dynamic simulations were performed for a 10 MeV electron beam with a bunch charge of 50 pC using the same optimization processes as those for the 16 MeV beam. The linac gradient was adjusted to achieve an electron beam energy of 10 MeV at the linac exit and the dipole field strengths in the bunch compressor tuned to bend the 10 MeV beam at an angle of 45°. The optimized properties of both the 10 MeV and 16 MeV electron beams at the undulator entrance are summarized in Table 2.

Table 2Full-screen View

(Color online) Optimized properties of 10 MeV and 16 MeV electron beams with bunch charge of 50 pC at undulator entrance

Properties	10 MeV	16 MeV
RMS bunch length (fs)	303.4	202.3
Peak current (A)	165.7	247.0
Energy spread (%)	0.23	0.16
Norm. horizontal emittance (πmm·mrad)	8.21	10.64
Norm. vertical emittance (πmm·mrad)	5.67	10.64
Norm. transverse emittance (πmm·mrad)	9.97	15.05

Show more

For the 10 MeV electron beam, the shortest bunch length achieved is 303 fs at an alpha magnet gradient of 360 G/cm and linac RF phase of 10°. The peak current of the 16 MeV electron beam is approximately 1.5 times higher than that of the 10 MeV electron beam. These results suggest that a higher-energy electron beam can be compressed to a shorter bunch length and higher peak current than a lower-energy electron beam because of space charge effects, which have a greater impact on the latter. The two optimized electron beams are used to calculate the super-radiant THz radiation in Sect. 4.

Expected super-radiant THz-FEL properties

The coherence or super-radiant property of any radiation depends significantly on its source. Generally, radiation emitted by relativistic electrons is coherent when the electron bunch length is equal to or shorter than the radiation wavelength. The total radiated energy (W_tot), which is dependent on the radiation energy of a single electron ($W_{\text{1e}}$), number of electrons per bunch (N_e), and bunch form factor f(w), is given by [39] $W_{\text{tot}}=W_{\text{1e}}{N}_{\text{e}}\left[1+\left(N_{\text{e}}-1\right)|f\left(w\right){|}^2\right]\mathrm{.}$ (2) The first term in the brackets of Eq. (2) describes incoherent radiation. The second term corresponds to coherent radiation, for which the radiated power is proportional to the square of the electron number. The form factor can be derived from the Fourier transform of the longitudinal distribution of the electron bunch (F(t)). The influence of the transverse beam distribution can be excluded from the bunch form factor when the emitted radiation is observed in the forward direction or when the transverse beam size at the undulator entrance is small [40]. The longitudinal form factor of the electron beam is thus defined as [41] $f(w)={\displaystyle {\int }_{-\infty }^{\infty }}F(t)\text{exp}(2\pi iwt)\text{d}t\mathrm{.}$ (3) The longitudinal profile of the optimized electron beam along the PCELL beamline with all three compression conditions was used to obtain the form factor. Figure 8(c) shows the current profiles of 10 MeV and 16 MeV electron bunches at the undulator entrance.

The optimized properties of the compressed electron beams at the undulator entrance (Table 2) and the specifications of the undulator magnet in Table 1 were used in the SPECTRA code to calculate the total pulse energy of the super-radiant THz-FEL [42]. The angular flux density, which represents the number of photons emitted per second per solid angle within a relative photon energy bandwidth of 0.1%, was provided by SPECTRA. Figure 9 shows the angular flux density as a function of the radiation frequency for the first three harmonics and the fundamental harmonic at a frequency of 2.9 THz. To establish a common basis for quantifying the optical properties, the angular flux density was simplified to the spectral energy of a single electron. The on-axis radiation energy of a single electron at a specific central frequency can be obtained subsequently by integrating over all the frequencies of the fundamental harmonic peak following [22], as shown in Fig. 9. Thus, the total pulse energy of an electron bunch at a specific central frequency can be derived using Eq. (2). The specific central frequency of the fundamental harmonic for the PCELL accelerator was varied by adjusting the undulator parameter. The resultant total pulse energies of the super-radiant THz-FEL at the fundamental harmonic for different central frequencies, the corresponding undulator parameters, and the square moduli of the form factors for 10 and 16 MeV electron beams are shown in Fig. 8(d).

Fig. 9Full-screen View

(Color online) Angular flux density of undulator radiation for first three harmonics (top) and fundamental harmonic at frequency of 2.9 THz (bottom)

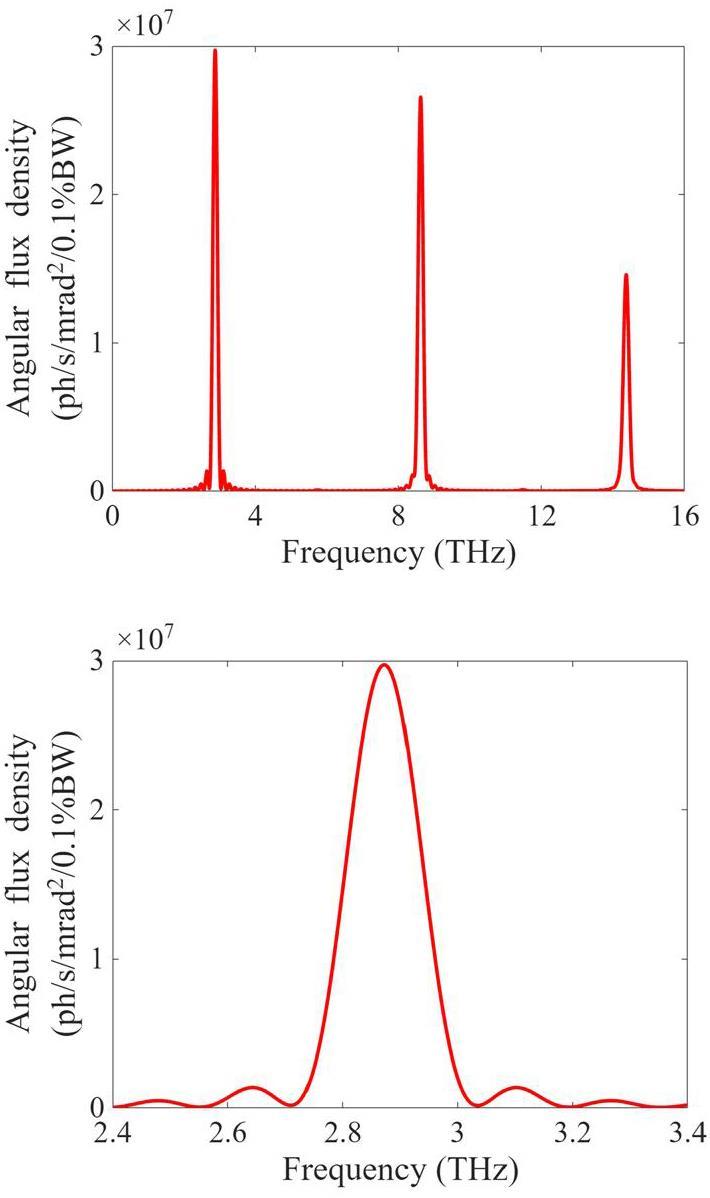
The total pulse energy as a function of the radiated frequency shows that the super-radiant THz spectrum consists of both coherent and incoherent emissions. The coherent emission is constrained by the form factor, which depends on the electron bunch length and radiation wavelength. The coherent radiation is approximately 10⁵ times (Ne times) higher than incoherent emission. This agrees well with the theoretical prediction that coherent radiation scales as the square of the number of electrons whereas incoherent radiation is proportional to the number of electrons. The 16 MeV electron beam, which has a shorter bunch length, generates super-radiant THz-FEL radiation with a broader spectrum and higher pulse energy than those of the 10 MeV electron beam. Total pulse energies in the range of 0.1 nJ to 100 nJ can be obtained at frequencies below 1 THz and 3.5 THz for 10 MeV and 16 MeV electron beams, respectively.

Conclusion

A super-radiant THz-FEL source was designed for the PCELL facility and start-to-end beam dynamics simulations completed. It was confirmed that the PCELL accelerator system can produce femtosecond electron bunches at the entrance of the undulator magnet by employing the three bunch compression processes. The combination of bunch compression in the alpha magnet and velocity bunching in the linac can provide an optimized electron beam with a bunch length as short as 365 fs. The alpha magnet gradient and linac RF phase were optimized to achieve an electron beam with an appropriate longitudinal beam phase space for the final compression process in the 180° bunch compressor. Under the optimal alpha magnet gradient, linac RF phase, and quadrupole field strengths in the 180-degree bunch compressor, the electron beam can turn 180 degrees and be simultaneously compressed to a bunch length of approximately 200 fs after leaving the compressor system. Electron beams with two energies (10 MeV and 16 MeV) were considered. The most promising optimization result suggests that a 16 MeV electron beam with a peak current of 247 A can be achieved at the undulator entrance. The electron beam can be used to generate super-radiant THz-FEL radiation with sub-microjoule pulse energies.

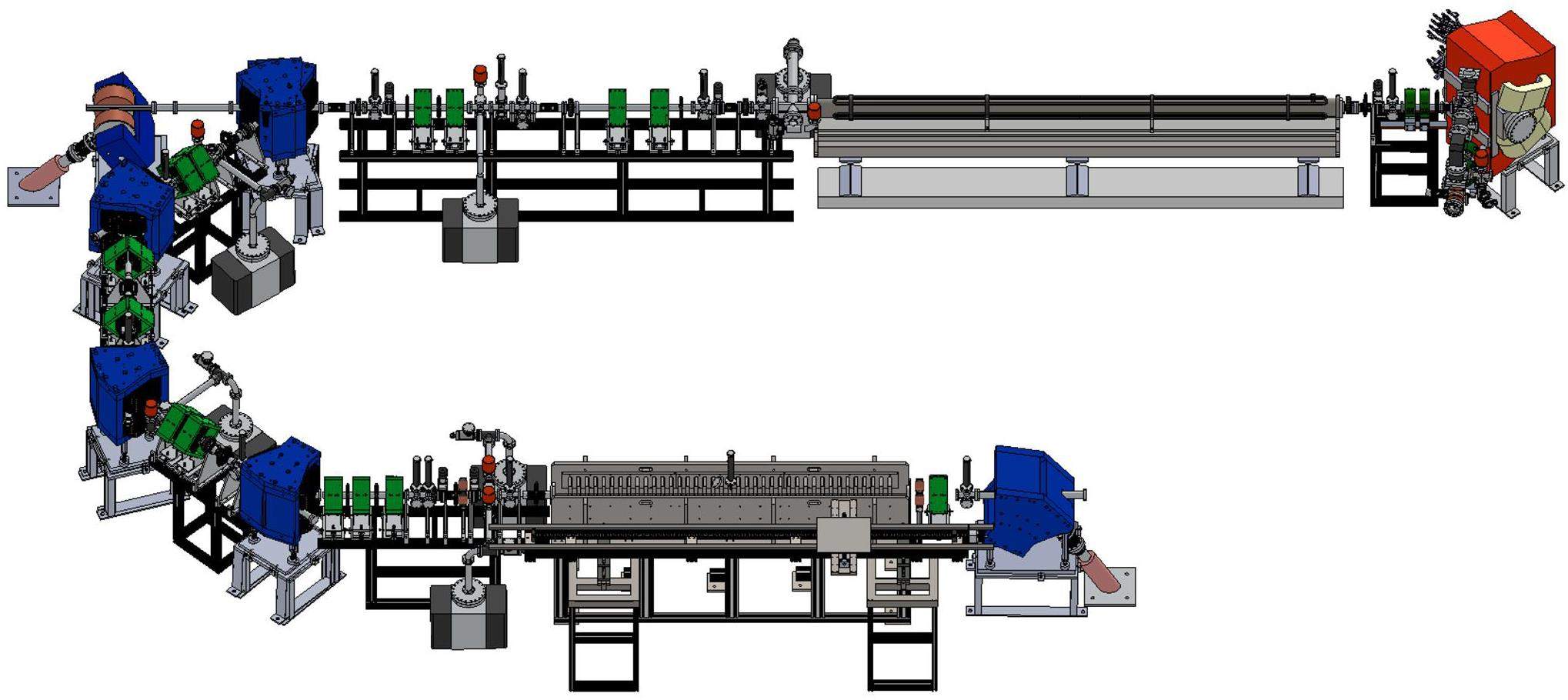
Based on the results of the beam dynamics simulations in this study, a three-dimensional engineering drawing for all the components of the accelerator system and the super-radiant THz-FEL beamline at PCELL was produced and presented in Fig. 10. In addition, an additional quadrupole magnet was incorporated before the undulator entrance to facilitate convenient adjustments to the transverse size of the electron beam during practical beam operation. The construction and installation of the components in this beamline following the engineering drawing are underway with installation and commissioning expected to be completed by mid-2024.

Fig. 10Full-screen View

Three-dimensional drawing of accelerator system and super-radiant THz-FEL beamline at Chiang Mai University