Introduction

Nuclear binding energies are important ground state properties that provide valuable information for probing nuclear structures [1-4] and serve as crucial inputs for some nuclear physics problems [5, 6]. For instance, binding energies play a key role in calculating the product cross sections for unknown nuclei using nuclear reaction models before synthesizing superheavy nuclei [7, 8]. They are also instrumental in identifying new nuclides in synthesis experiments of heavy and superheavy nuclei [9, 10] because α decay is one of the fundamental decay modes for most heavy and superheavy nuclei [11-13]. For α-emitters, there are two main α-decay observable properties, which are respectively α-decay energies and half-lives [14-18]. Thereinto, α-decay half-lives are strongly influenced by the α-decay energies, which can be calculated using the binding energies. Meanwhile, binding energies are also vital for calculating the properties of other radioactive decay modes, such as two-proton radioactivity [19] and heavy-cluster radioactivity [20]. Furthermore, the accuracy of binding energies has a significant impact on nuclear astrophysics studies, including r-process [21, 22], rp-process [23, 24], and the properties of neutron stars [25, 26]. Therefore, it is necessary to explore reliable theoretical models to calculate and predict the binding energies more accurately.

With the advancements in experimental nuclear physics facilities, binding energies of more than two thousand nuclei have been measured to date [27]. The accumulated experimental data provide a foundation for the development of theoretical models. In the past few years, numerous theoretical models and formulas have been proposed to calculate binding energies, including the Bethe-Weizsäcker formula [28, 29], the Thomas-Fermi (TF) model [30], the Hartree-Fock-Bogoliubov mean field model [31], and the finite-range drop model (FRDM) [32]. The theoretical binding energies calculated using these models and formulas are in good agreement with the experimental data. In Ref. [8], an improved binding-energy formula was proposed by incorporating additional physical terms into the standard Bethe-Weizsäcker formula, which consists of the shell effect and the neutron-proton correlations. The binding energies and α-decay energies can be well reproduced using this improved formula for heavy and superheavy nuclei with $Z\ge 90$ and $N\ge 140$. Although these current traditional models can provide theoretical guidance for studying binding energies, it is still worth exploring other models to provide more accurate calculations and predictions for future investigations of binding energies.

Machine learning has been widely used across many fields [33-38], as it can learn useful information from known systems and predict unknown properties within the same system using the obtained information. In the last decade, nuclear properties have been studied using various machine-learning methods based on available physical knowledge, including nuclear masses [39-41], nuclear charge radii [42], α-decay properties [43], and β -decay properties [44]. These nuclear properties can be well reproduced using machine learning. Recently, a new Bayesian machine learning mass model has been proposed [45], which can reproduce nuclear masses with the high accuracy required for the studies of r -process. As one of the popular machine-learning methods, the Gaussian process is a powerful nonparametric model, which is expected to model any distribution of the objectives [46]. Owing to its excellent flexibility in data modeling, the Gaussian process has been frequently applied in various studies [48, 47]. Notably, the Gaussian process can provide not only the theoretical values of the objectives but also the distribution of the calculated results, contributing to the visualization of the theoretical uncertainties [49]. Recently, the Gaussian process has been successfully exploited to predict the α-decay energies and half-lives of actinide nuclei [50]. Inspired by these previous works, it is of great interest to explore the reliability of the Gaussian process in the calculations of binding energies.

In this work, the Gaussian process has been extended to study the binding energies by directly modeling the experimental binding energies. The remainder of this paper is given as follows. In Sect. 2, the theoretical framework, consisting of the Gaussian process with the modified kernel function and the physically motivated feature space, is provided. In Sect. 3, the theoretical binding energies calculated using the Gaussian process are shown and discussed. Furthermore, the α-decay properties are reproduced and predicted based on the calculated binding energies. Finally, a comprehensive summary is presented in Sect. 4.

Theoretical Framework

In the present work, the binding energy for a nucleus is considered as a realistic observation $B_p=b_p+ð$ with noise $ð\sim \mathcal{N}\left(\mathrm{0,}{\sigma }_b^2\right)$. Here, $b_p=b\left(x_p\right)$ is a latent function that denotes the noise-free binding energy for the p th nucleus $x_p$ [51]. B_p denotes the realistic binding energy, and $ð$ is an independently identically distributed Gaussian noise. Given a set of n nuclei with known binding energies into a training set ${\left(x_p\mathrm{,}{B}_p\right)}_{p=1}^n$, we aim to model the underlying physical relationship between each nucleus and its binding energy using the Gaussian process. Within the framework of the Gaussian process, the values of latent function $b={\left(b_1\mathrm{,}{b}_2\mathrm{,}\cdots \mathrm{,}{b}_n\right)}^{\text{T}}={\left(b\left(x_1\right)\mathrm{,}b\left(x_2\right)\mathrm{,}\cdots \mathrm{,}b\left(x_n\right)\right)}^{\text{T}}$ are modeled by a joint Gaussian distribution, characterized by the values of a mean function ${\left(m\left(x_1\right)\mathrm{,}m\left(x_2\right)\mathrm{,}\cdots \mathrm{,}m\left(x_n\right)\right)}^{\text{T}}$ and the matrix of a covariance function ${\left[k\left(x_p\mathrm{,}{x}_q\right)\right]}_{n\times n}$ [46]. Therefore, the Gaussian process can be generally denoted as $b\left(x_p\right)\sim \mathcal{G}\mathcal{P}\left(m\left(x_p\right)\mathrm{,}k\left(x_p\mathrm{,}{x}_q\right)\right)$. The mean function $m\left(x_p\right)$ is often set as zero because of the lack of prior knowledge. The so-called kernel function $k\left(x_p\mathrm{,}{x}_q\right)$ can be written as a function of $|x_p-x_q|$, which is crucial for describing the similarities between pairs of nuclei. For the studies of binding energies, we choose a composite kernel function written as $k\left(x_p\mathrm{,}{x}_q\right)={\eta }_b^2\left[\left(1+\frac{\sqrt{3}{r}_b}{l_b}\right)\text{exp}\left(-\frac{\sqrt{3}{r}_b}{l_b}\right)+{\left(1+\frac{r_b^2}{2{\alpha }_b{d}_b^2}\right)}^{\text{}-{\alpha }_b}\right]$ (1) with $r_b=|x_p-x_q|$. The modified kernel function is a linear combination of two widely used kernel functions, which are the Matérn kernel function and the Rational Quadratic kernel function, respectively. Here, ηb, $l_b$, αb, and db are four hyperparameters of the Gaussian process. $l_b$, αb, and db can capture the relevant range of the binding energies for pairs of nuclei, and ηb is able to describe the correlation intensity between them. For the realistic binding energy B_p, the covariance function becomes $k\left(x_p\mathrm{,}{x}_q\right)\to k\left(x_p\mathrm{,}{x}_q\right)+{\sigma }_b^2{\delta }_{pq}$. δpq is a Kronecker delta where δpq = 1 for p = q and δpq = 0 for $p\ne q$. When describing a number of nuclei $X={\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)}^{\text{T}}$, the binding energies $B={\left(B_1\mathrm{,}{B}_2\mathrm{,}\cdots \mathrm{,}{B}_n\right)}^{\text{T}}$ are expressed as $B\sim \mathcal{G}\mathcal{P}\left(0\mathrm{,}K\left(X\mathrm{,}X\right)+{\sigma }_b^{2}I\right)$, where I is a diagonal matrix.

The central interest of this work is to predict unknown binding energies based on the knowledge learned from the training set using the Gaussian process. When predicting unknown binding energies for nuclei X_* with the training set $\mathcal{D}={\left(x_p\mathrm{,}{B}_p\right)}_{p=1}^n$, the joint Gaussian distribution of the training outputs B and the predicted outputs b_* can be written as [46] $\left[\begin{array}{c}B\\ b_{*}\end{array}\right]\sim \mathcal{N}\left(0\mathrm{,}\left[\begin{array}{cc}K\left(X\mathrm{,}X\right)+{\sigma }_b^{2}I& K\left(X\mathrm{,}{X}_{*}\right)\\ K\left(X_{*}\mathrm{,}X\right)& K\left(X_{*}\mathrm{,}{X}_{*}\right)\end{array}\right]\right).$ (2) For $n_{*}$ predicted nuclei, K(X, X), K(X, X_*), K(X_*, X), and K(X_*, X_*), respectively, denote $n\times n$, $n\times n_{*}$, $n_{*}\times n$, and $n_{*}\times n_{*}$ matrix evaluated at all pairs of training and predicted points. By conditioning the joint Gaussian distribution, the crucial predicted expressions for the Gaussian process are $b_{*}|\mathcal{D}\mathrm{,}{X}_{*}\sim \mathcal{N}\left(b_{*}\mathrm{,}\text{cov}\left(b_{*}\right)\right)$, where $\begin{array}{c}{b}_{*}=K\left(X_{*}\mathrm{,}X\right){\left[K\left(X\mathrm{,}X\right)+{\sigma }_b^{2}I\right]}^{-1}B\mathrm{,}\\ \text{cov}\left(b_{*}\right)=K\left(X_{*}\mathrm{,}{X}_{*}\right)-K\left(X_{*}\mathrm{,}X\right){\left[K\left(X\mathrm{,}X\right)+{\sigma }_b^{2}I\right]}^{-1}K\left(X\mathrm{,}{X}_{*}\right).\end{array}$ (3) Here, the values of b_* give the predicted binding energies for unknown nuclei. The variances of the predicted binding energies can be calculated by adding the noise variance ${\sigma }_b^2$ to the predictive variance given by cov(b_*).

As mentioned above, each nucleus is described by x_p, which is a vector of physical features determining the description of the corresponding binding energy. In the present work, our goal is to obtain good descriptions of the binding energies using the Gaussian process with as simple physical information as possible. Hence, we construct a physical feature space with nine features, where $x_p=\left(A_p\mathrm{,}{A}_p^{2/3}\mathrm{,}{Z}_p^2{A}_p^{-1/3}\mathrm{,}{\left(A_p/2-Z_p\right)}^2/A_p\mathrm{,}{A}_p^{-1/2}\mathrm{,}{\delta }_p\mathrm{,}|N_p-Z_p|/A_p\mathrm{,}{\pi }_p\mathrm{,}{v}_p\right)$. Here, A, Z, and N denote the mass, proton, and neutron numbers, respectively. The first six features are based on the Bethe-Weizsäcker formula [7, 28, 29, 52, 53]. A is introduced to model the proportional relationship between the binding energies and the nuclear volume, reflecting the saturation of nuclear force. A^2/3 is provided since the binding energies are expected to decrease on the nuclear surface. $Z^2{A}^{-1/3}$ is used to describe the influence of the Coulomb interaction between protons. ${\left(A/2-Z\right)}^2/A$ is the symmetry term that approximately estimates the balance between N and Z. $A^{-1/2}$ and $\delta =\left[{\left(-1\right)}^N+{\left(-1\right)}^Z\right]/2$ are used to describe the pairing energies with δ = 1, 0, -1 for the even-even, odd- A, and odd-odd nuclei. $|N-Z|/A$ is from the Wigner term, which originates from the neutron-proton correlations [1, 8]. Additionally, π and v include the shell information, where π (v) is calculated using the numbers of protons (neutrons) away from the nearest proton (neutron) magic numbers [54].

The aforementioned theoretical framework implies that five hyperparameters need to be determined, which are ηb, l_b, αb, db, and ${\sigma }_b$, respectively. These can be determined by optimizing the marginal likelihood using the training data [46].

Numerical results and discussions

In this section, we present and discuss the theoretical results of the nuclear binding energies calculated using the Gaussian process. First, we calculate the binding energies for nuclei with Z > 20 and N > 20 to evaluate the learning ability of the Gaussian process. The training set chosen in this work contains 2238 nuclei with known binding energies taken from AME2020 [55]. Each nucleus in the training set is presented as (x_p, B_p), where $x_p=\left(A_p\mathrm{,}{A}_p^{2/3}\mathrm{,}{Z}_p^2{A}_p^{-1/3}\mathrm{,}{\left(A_p/2-Z_p\right)}^2/A_p\mathrm{,}{A}_p^{-1/2}\mathrm{,}{\delta }_p\mathrm{,}|N_p-Z_p|/A_p\mathrm{,}{\pi }_p\mathrm{,}{v}_p\right)$ and $B_p=B_p^{\text{Expt}\text{.}}$. After the training process, the hyperparameters are determined as ${\eta }_b=1.814\times {10}^4{\text{MeV}}^{1/2}$, $l_b=1.821\times {10}^4$, αb = 1937.218, db = 414.771, and ${\sigma }_b=0.093{\text{MeV}}^{1/2}$. The larger value of ηb indicates a stronger dependence between pairs of nuclei. Meanwhile, the larger values of l_b, αb, and db result in a relatively larger correlation range, which means that the change of binding energies is comparatively smoother. Moreover, they also assist in avoiding the rapid growth of the error bars of the binding energies for nuclei away from the training data [46].

After the hyperparameters have been determined, the binding energies can be calculated using the Gaussian process. To test the accuracy of the calculated results, we calculate the absolute value of the deviation between the experimental result and the theoretical one for each nucleus, defined by $\left|{\text{Δ}}_B\right|=\left|B_p^{\text{Expt}\text{.}}-B_p^{\text{Theo}\text{.}}\right|\mathrm{.}$ (4) Here, $B_p^{\text{Expt}\text{.}}$ and $B_p^{\text{Theo}\text{.}}$ denote the experimental binding energy and theoretical result calculated using the Gaussian process for the p th nucleus, respectively. The numerical results show that all absolute values of the deviations are smaller than 0.423 MeV, indicating a small global deviation. We show the corresponding results in Fig. 1, in which the x- and y-axis indicate the neutron and proton numbers, respectively. The red squares depict the absolute values of the deviations, where darker colors are associated with larger deviations. The transverse and vertical dotted lines present N = 28, 50, 82, 126 and Z = 28, 50, 82, respectively. It can be seen clearly from Fig. 1 that the colors of most squares are lighter, reflecting that the deviations for most nuclei are below 0.1 MeV. Additionally, the binding energies for nuclei near the shell closure are also well reproduced using the Gaussian process. Next, we calculate the average deviation $\langle {\sigma }_B\rangle =\frac{1}{{\tilde{n}}_B}{\displaystyle \sum _{p=1}^{{\tilde{n}}_B}\left|B_p^{\text{Expt}\text{.}}-B_p^{\text{Theo}\text{.}}\right|}$ (5) and the standard deviation $\sqrt{{\sigma }_B^2}=\sqrt{\frac{1}{{\tilde{n}}_B}{\displaystyle \sum _{p=1}^{{\tilde{n}}_B}{\left(B_p^{\text{Expt}\text{.}}-B_p^{\text{Theo}\text{.}}\right)}^2}}$ (6) of the theoretical binding energies calculated using the Gaussian process for nuclei with Z > 20 and N > 20. Here, ${\tilde{n}}_B$ denotes the number of nuclei included in the calculations. The numerical values are $\langle {\sigma }_B\rangle =0.046\text{MeV}$ and $\sqrt{{\sigma }_B^2}=0.066\text{MeV}$, respectively. The small deviations show that the theoretical binding energies calculated using the Gaussian process with the modified kernel function in the physically motivated feature space are in good agreement with the experimental data. These results demonstrate the good learning ability of the Gaussian process in the studies of binding energies.

Fig. 1Full-screen View

(Color online) The absolute values of deviations between experimental binding energies and the theoretical results calculated using the Gaussian process across the nuclear chart. The darker colors indicate larger deviations of binding energies. Numerically, the largest absolute value of the deviations is $\left|{\text{Δ}}_B\right|=0.423$ MeV

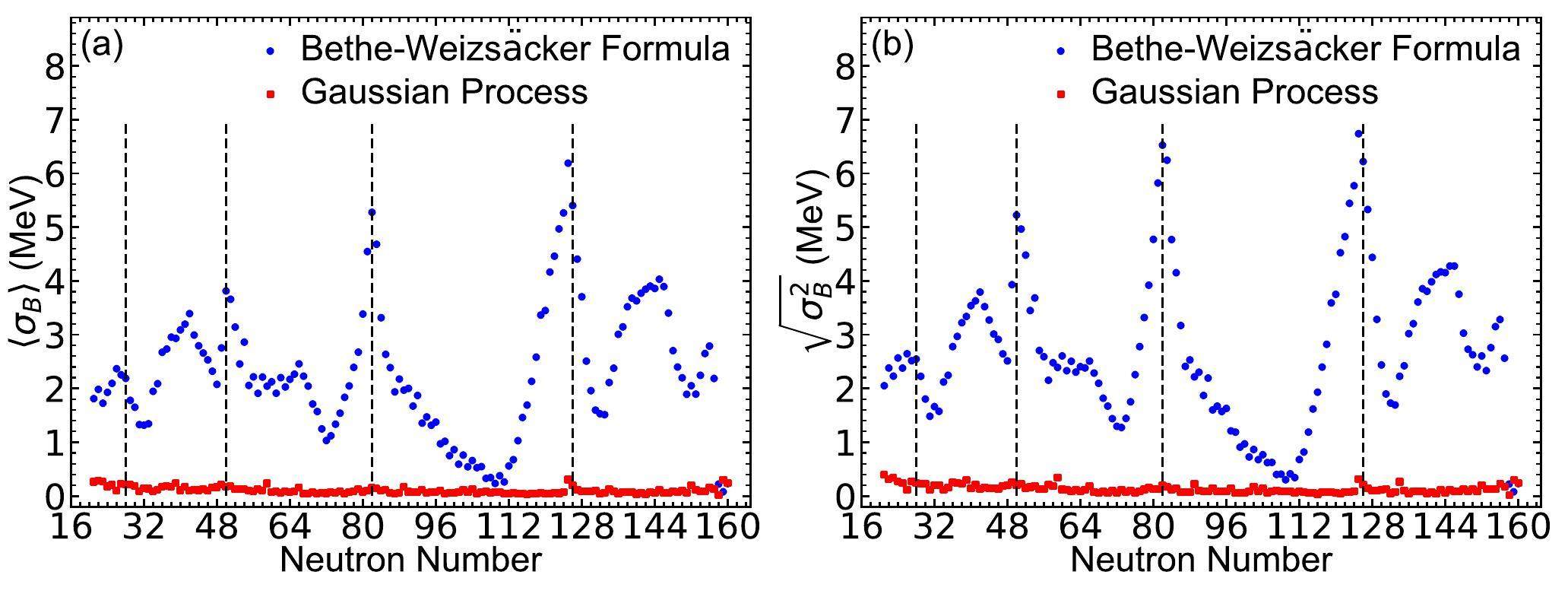
To further evaluate the learning ability and predictive power of the Gaussian process in the studies of binding energies, we perform cross validation for the Gaussian process. In this work, we introduce the isotone-fold cross-validation that nuclei in each isotonic chain will be predicted using the Gaussian process based on the information provided by the remaining isotonic chains in the training set. The average deviations and the standard deviations of the theoretical binding energies for nuclei in each isotonic chain are calculated, with results depicted in Fig. 2. For comparison, the average deviations and the standard deviations of the binding energies calculated using the Bethe-Weizsäcker formula for each isotonic chain are also provided in Fig. 2. In Fig. 2(a) and Fig. 2(b), the red squares denote the average deviations and the standard deviations calculated using the Gaussian process for each isotonic chain, respectively. The blue circles present the average deviations and the standard deviations calculated using the Bethe-Weizsäcker formula for each isotonic chain separately. It is straightforward to see that the deviations given by the Gaussian process are quite small, which means that the cross-validation result is pretty good. In addition, we can find that the deviations are significantly reduced compared with those given by the Bethe-Weizsäcker formula. These results reflect the good learning ability and predictive power of the Gaussian process. Numerically, the total average deviation and standard deviation of the cross-validation for nuclei in the training set are $\langle {\sigma }_B\rangle =0.100\text{MeV}$ and $\sqrt{{\sigma }_B^2}=0.144\text{MeV}$, respectively. The small deviations show that the predicted binding energies agree well with the experimental data, indicating that the binding energies can be well learned using the Gaussian process. Thus, we can conclude that the learning ability and predictive power of the Gaussian process are reliable for studying the binding energies.

Fig. 2Full-screen View

(Color online) The cross-validation results for nuclei in each isotopic chain calculated using the Gaussian process. In Fig. 2(a), the red squares and the blue circles depict the average deviations calculated using the Gaussian process and the Bethe-Weizsäcker formula, respectively. In Fig. 2(b), the red squares and the blue circles show the standard deviations calculated using the Gaussian process and the Bethe-Weizsäcker formula separately

Then, we further test the predictive power of the Gaussian process by calculating the binding energies for nuclei that are present in AME2020 but not in AME2012 using the Gaussian process. To perform this calculation, the training set is chosen to include nuclei that are provided in both AME2012 and AME2020. Based on the training set, we predict the binding energies for 108 nuclei that are provided in AME2020 but not in AME2012 using the Gaussian process. The theoretical average deviation and standard deviation for these nuclei are $\langle {\sigma }_B\rangle =0.216\text{MeV}$ and $\sqrt{{\sigma }_B^2}=0.304\text{MeV}$, respectively. These deviations are acceptable results in the calculations of binding energies, verifying that the predicted power of the Gaussian process is commendable. Therefore, based on these theoretical results, it can be concluded that the Gaussian process is a reliable model for the studies of nuclear binding energies.

Next, we would like to calculate and discuss the theoretical results calculated using the Gaussian process with different kernel functions and physical feature spaces. First, we calculate the binding energies using the Gaussian process with the Matérn kernel function and the Rational Quadratic kernel function, respectively. The corresponding deviations of the binding energies for 2238 nuclei are $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=\left(\mathrm{0.059,0.076}\right)$ MeV for the Matérn kernel function and $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=(\mathrm{0.121,0.166})$ MeV for the Rational Quadratic kernel function, respectively. The deviations for 108 new nuclei are $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=\left(\mathrm{0.278,0.415}\right)$ MeV for the Matérn kernel function and $(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2})=(\mathrm{0.193,0.249})$ MeV for the Rational Quadratic kernel function separately. Comparing with the deviations $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=(\mathrm{0.046,0.066})$ MeV for 2238 nuclei and $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=(\mathrm{0.216,0.304})$ MeV for 108 new nuclei calculated using the composite kernel function, it can be found that the deviations calculated with the composite kernel function are as small as those calculated using the Matérn kernel function for 2238 nuclei and show better results than those calculated using the Matérn kernel function for 108 new nuclei. The deviations calculated using the composite kernel function show results as good as those calculated using the Rational Quadratic kernel function for 108 new nuclei and are smaller than those calculated using the Rational Quadratic kernel function for 2238 nuclei. Therefore, the good interpolation power of the Gaussian process with the Matérn kernel function and extrapolation ability of the Gaussian process with the Rational Quadratic kernel function are inherited by the composite kernel function in the calculations of binding energies, which demonstrates that the modified kernel function is a good choice for the present work. Furthermore, we hope that the choice of the composite kernel function can provide a new idea for modeling other physical problems using the Gaussian process.

We continue to compare the average deviations and standard deviations for 108 new nuclei using the Gaussian process in different physical feature spaces. We first calculate the deviations for nuclei using the Gaussian process in the feature space consisting of six features taken from the Bethe-Weizsäcker formula, where the p th nucleus is described by $x_p=\left(A_p\mathrm{,}{A}_p^{2/3}\mathrm{,}{Z}_p^2{A}_p^{-1/3}\mathrm{,}{\left(A_p/2-Z_p\right)}^2/A_p\mathrm{,}{A}_p^{-1/2}\mathrm{,}{\delta }_p\right)$. The theoretical deviations are $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=(\mathrm{0.437,0.775})$ MeV. Then, we add the neutron-proton correlation and the shell information in the above feature space and compare the corresponding deviations. When the neutron-proton correlation is added in the feature space where $x_p=\left(A_p\mathrm{,}{A}_p^{2/3}\mathrm{,}{Z}_p^2{A}_p^{-1/3}\mathrm{,}{\left(A_p/2-Z_p\right)}^2/A_p\mathrm{,}{A}_p^{-1/2}\mathrm{,}{\delta }_p\mathrm{,}|N_p-Z_p|/A_p\right)$, the deviations become $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=(\mathrm{0.398,0.712})$ MeV. The reduction in the deviations shows that the neutron-proton correlation is necessary for calculating the binding energies. When the shell information is included in the feature space, where $x_p=\left(A_p\mathrm{,}{A}_p^{2/3}\mathrm{,}{Z}_p^2{A}_p^{-1/3}\mathrm{,}{\left(A_p/2-Z_p\right)}^2/A_p\mathrm{,}{A}_p^{-1/2}\mathrm{,}{\delta }_p\mathrm{,}{\pi }_p\mathrm{,}{v}_p\right)$, the deviations are $\left(\langle {\sigma }_B\rangle \mathrm{,}\sqrt{{\sigma }_B^2}\right)=(\mathrm{0.236,0.365})$ MeV. The results reflect that the introduced features π and v provide useful shell information for nuclei in the calculations of binding energies. Furthermore, it can be observed that the above deviations are larger than those calculated in the feature space with nine features established in the present work, indicating that our choice of feature space is reasonable. Notably, the importance of the physically motivated feature space has also been studied in the Bayesian neural network and the probabilistic Mixture Density Network [41, 39]. The physical feature space established in the present work is first studied in the Gaussian process on the research of binding energies.

It has been mentioned that the distribution of theoretical results can be provided by the Gaussian process. Here, we present the intervals of error bars for the theoretical results calculated in this work. The lengths of error bars at 95% confidence interval range from 0.213 MeV to 0.258 MeV in the studies of 2238 nuclei, while they range from 0.234 MeV to 4.022 MeV in the calculations of 108 new nuclei. These results show that the hyperparameters determined by the marginal likelihood are reasonable and that the theoretical binding energies calculated using the Gaussian process are reliable. Thus, we conclude that the Gaussian process with a modified kernel function and the physically motivated feature space is a reliable model for calculating binding energies.

Due to the successful calculations of the binding energies, it is expected that the α-decay energies, which are the differences among the binding energies of the parent nuclei, the daughter nuclei, and the α-particles, can be reproduced with good accuracy. Thus, we calculate the α-decay energies for 1169 nuclei with $50\le Z\le 110$ and compare the calculated results with the experimental data taken from AME2020 [27]. The deviations between the experimental α-decay energies and the theoretical results for these nuclei are depicted in Fig. 3. In Fig. 3, the blue circles denote the deviations and the red shadow shows the deviations $\left|Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}\right|\le 0.3$ MeV. The dashed line represents $\left|Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}\right|=0$ MeV and the two dash dotted lines present $\left|Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}\right|=0.5$ MeV, respectively. The deviations for the α-decay energies of the 1169 nuclei are all clearly below 0.5 MeV and the deviations for most of these nuclei are less than 0.3 MeV. These results show good agreement between the theoretical α-decay energies derived from the binding energies which are calculated using the Gaussian process and the experimental data. Furthermore, it has been found in previous studies that α-decay energies are strongly affected by the shell effect, which leads to larger deviations for nuclei near the closed shell [56]. In Fig. 3, the deviations for nuclei near the shell closure are also less than 0.3 MeV. It can reflect that π and v features can successfully model the shell effect with the Gaussian process. We also calculate the average deviation and standard deviation for these nuclei, given by $\langle {\sigma }_{\alpha }\rangle =\frac{1}{{\tilde{n}}_{\alpha }}{\displaystyle \sum _{p=1}^{{\tilde{n}}_{\alpha }}\left|Q_{\alpha }^{\text{Expt}\text{.,p}}-Q_{\alpha }^{\text{Theo}\text{.,p}}\right|}=0.047\text{MeV}$ (7) and $\sqrt{{\sigma }_{\alpha }^2}=\sqrt{\frac{1}{{\tilde{n}}_{\alpha }}{\displaystyle \sum _{p=1}^{{\tilde{n}}_{\alpha }}{\left(Q_{\alpha }^{\text{Expt}\text{.,p}}-Q_{\alpha }^{\text{Theo}\text{.,p}}\right)}^2}}=0.070\text{MeV}\mathrm{.}$ (8) Owing to the complexity of the quantum many-body theory, it is difficult to calculate the α-decay energies with deviations less than 0.1 MeV. These small deviations show that the α-decay energies agree well with the experimental results.

Fig. 3Full-screen View

The deviations between the experimental α-decay energies and the theoretical results for 1169 nuclei with $50\le Z\le 110$. The blue circles depict the deviations for these nuclei. The dashed line denotes $\left|Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}\right|=0$ MeV. The red shadow and the dash dotted lines present $\left|Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}\right|\le 0.3$ MeV and $\left|Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}\right|=0.5$ MeV, respectively

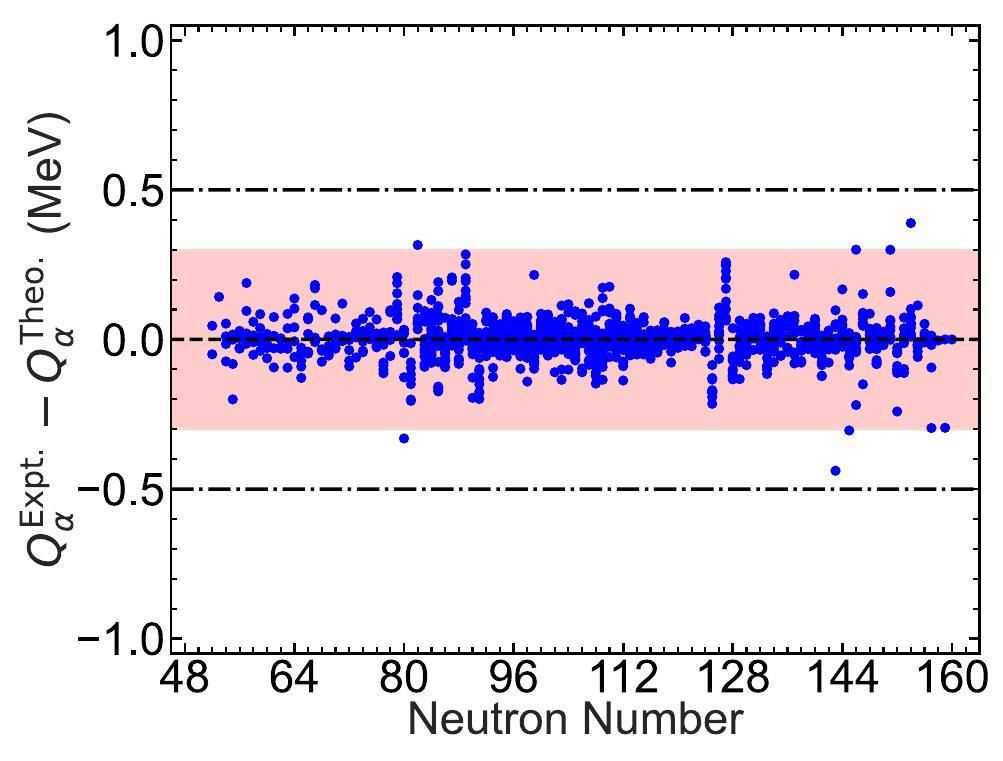
Recently, some actinide nuclei, including ²⁰⁴Ac [57] and ²⁰⁷Th [10], were synthesized experimentally. Theoretical α-decay properties provide useful references for these experiments. Here, we present the theoretical α-decay energies calculated using the Gaussian process for the actinide nuclei in Table 1. In Table 1, the first column lists the actinide nuclei. The second column denotes the experimental data and the third column presents the theoretical results. The fourth column gives the deviations $\text{Δ}{Q}_{\alpha }=Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}$ between the experimental results and the theoretical ones. The experimental α-decay energies for two new nuclides ²⁰⁴Ac and ²⁰⁷Th are taken from Ref. [57] and Ref. [10] separately. It can be clearly seen that the theoretical results obtained using the Gaussian process are in good agreement with the experimental data for the actinide nuclei. For the new nuclide ²⁰⁴Ac, the theoretical α-decay energy calculated using the Gaussian process is nearly equivalent to the experimental result, with a small deviation of $\text{Δ}{Q}_{\alpha }=Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}=0.0004$ MeV. For another new nuclide, ²⁰⁷Th, the deviation is $\text{Δ}{Q}_{\alpha }=Q_{\alpha }^{\text{Expt}\text{.}}-Q_{\alpha }^{\text{Theo}\text{.}}=0.051$ MeV, indicating that the calculated result is in good agreement with the experimental one. These results demonstrate that the α-decay energies for the actinide nuclei can be well reproduced by deriving from the theoretical binding energies calculated using the Gaussian process. Overall, the above results show the reliability of the Gaussian process in the calculations of nuclear binding energies and α-decay properties.

Finally, we predict the α-decay energies for some unknown actinide nuclei using the Gaussian process. With the predicted α-decay energies, we also calculate the α-decay half-lives using the new Geiger-Nuttall law (NGNL) [58]. The corresponding results are given in Table 2. In Table 2, the first column lists the α-emitters. The second and third columns present the α-decay energies calculated using the Gaussian process and the FRDM, respectively. The fourth and fifth columns give the predictive α-decay half-lives calculated using the NGNL with the α-decay energies predicted by the Gaussian process and the FRDM, respectively. It can be found that most predicted α-decay energies agree well with those calculated using the FRDM. Nevertheless, the predicted α-decay energies for Einsteinium, Fermium, Mendelevium, and Nobelium are relatively larger than those given by the FRDM, which results in different α-decay half-lives. We hope that future experimental α-decay properties for Einsteinium, Fermium, Mendelevium, and Nobelium can provide useful information for improving the Gaussian process. The α-decay properties predicted by the Gaussian process can complement existing theoretical models and provide valuable guidance for future studies of α decay. In addition, some actinide isotopes are being synthesized at the Heavy Ion Research Facility in Lanzhou (HIRFL), China. Therefore, it is expected that the predicted α-decay properties can be used as theoretical references for identifying new nuclides in the future.

Summary

In this work, the Gaussian process with a composite kernel function is applied to study the binding energies. First, we calculate the binding energies for 2238 nuclei with Z > 20 and N > 20 within the framework of the Gaussian process using a physically motivated feature space. The calculated average deviation and standard deviation are 0.046 MeV and 0.066 MeV, respectively. The results demonstrate that the binding energies are successfully modeled by the Gaussian process, reflecting the good learning ability of the Gaussian process in the calculations of binding energies. Then, we calculate the binding energies for 108 nuclei, which are newly included in AME2020. The calculated results are in good agreement with the experimental data, which indicates the good predictive power of the Gaussian process in the studies of binding energies. Moreover, the application of the composite kernel function provides a novel perspective in studying other physical problems using the Gaussian process. Next, we calculate the α-decay energies due to the successful calculations of the binding energies using the Gaussian process. The average deviation and the standard deviation for 1169 nuclei with $50\le Z\le 110$ are 0.047 MeV and 0.070 MeV, respectively. Notably, the theoretical α-decay energies for the new nuclides ²⁰⁴Ac and ²⁰⁷Th are well reproduced with Δ Qα = 0.0004 MeV for ²⁰⁴Ac and Δ Qα = 0.051 MeV for ²⁰⁷Th. The good results also show that the Gaussian process is reliable for the studies of binding energies. Finally, the α-decay properties for the actinide nuclei are predicted using the Gaussian process. We expect the predicted results will be useful for future studies of the binding energies and the α-decay properties.