Gamow coupled-channel approach(GCC)

In this study, we used a GCC approach [50, 51], which is a three-body model describing ¹⁸Mg in terms of two valence protons and a core (¹⁶Ne). To describe the three-body asymptotic behavior, the coordinates of ¹⁸Mg can be expressed in Jacobi (relative) coordinates: $\begin{array}{l}x=\sqrt{{\mu }_x}\left(r_{i_1}-r_{i_2}\right)\mathrm{,}\\ y=\sqrt{{\mu }_y}\left(\frac{A_{i_1}{r}_{i_1}+A_{i_2}{r}_{i_2}}{A_{i_1}+A_{i_2}}-r_{i_3}\right)\mathrm{,}\end{array}$ (1) where r_i denotes the position vector of the ith cluster; $i_1=p_1$, $i_2=p_2$, and i₃=¹⁶Ne for the T-coordinate and i₁=¹⁶Ne, $i_2=p_1$, and $i_3=p_2$ for the Y-coordinate, as shown in Fig. 1(a,b). Ai is the mass number of the ith cluster. ${\mu }_x=\frac{A_{i_1}{A}_{i_2}}{A_{i_1}+A_{i_2}}$ and ${\mu }_y=\frac{\left(A_{i_1}+A_{i_2}\right)A_{i_3}}{A_{i_1}+A_{i_2}+A_{i_3}}$ are the reduced masses associated with $x$ and $y$, respectively. These parameters can be used to describe the hyperradius $\rho =\sqrt{x^2+y^2}$, which is transformation-invariant among different sets of Jacobi coordinates.

Fig. 1Full-screen View

(Color online) Schematic of three-body ¹⁶Ne + p + p system in Jacobi-T (a) and Jacobi-Y (b) coordinates. Momentum scheme (c) of three-body system

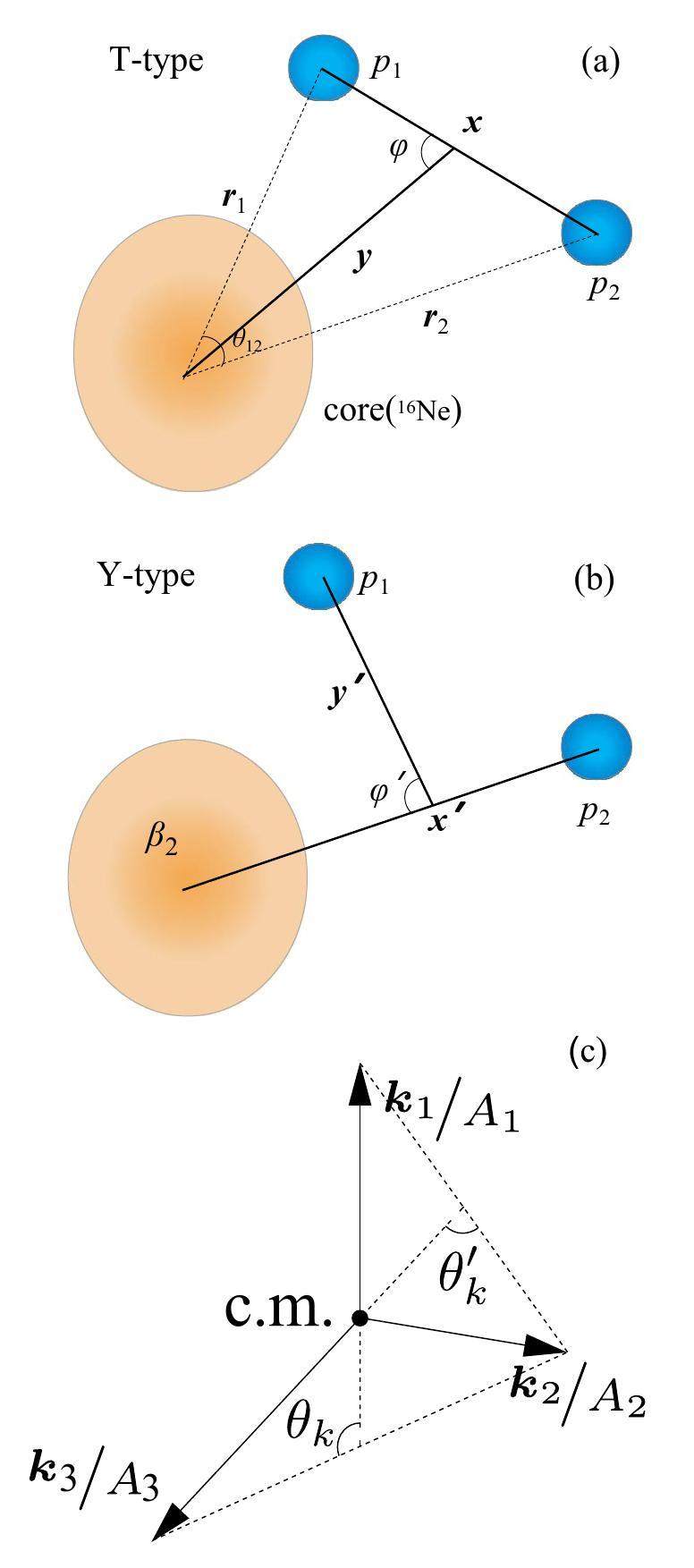
As the experimental measurements are performed in the momentum space, the relative momentum is defined as follows: $\begin{array}{l}{k}_x={\mu }_x\left(\frac{k_{i_1}}{A_{i_1}}-\frac{k_{i_2}}{A_{i_2}}\right)\mathrm{,}\\ k_y={\mu }_y\left(\frac{k_{i_1}+k_{i_2}}{A_{i_1}+A_{i_2}}-\frac{k_{i_3}}{A_{i_3}}\right)\mathrm{,}\end{array}$ (2) where k_i denotes the linear momentum of the ith cluster; θk and ${{\theta }^{\prime }}_k$ are the opening angles of (k_x, k_y) in the Jacobi-T and Jacobi-Y coordinates, respectively, as shown in Fig. 1(c), respectively. $E_{\text{pp}}=\frac{{\hslash }^2{k}_x^2}{2{\mu }_x}$ represents the kinetic energy of the relative motion of the two emitted protons, and $E_{\text{core}-\text{p}}$ signifies that of the ¹⁶Ne–p pair.

The total wave function in the Jacobi coordinates of the mother nucleus, which couples with the p–p pair and ¹⁶Ne, can be expressed as ${\Psi }^{J\pi }={\displaystyle \sum }{\left[{\text{Φ}}^{J_{\text{p}}{\pi }_{\text{p}}}\otimes {\varphi }^{J_{\text{c}}{\pi }_{\text{c}}}\right]}^{J\pi }\mathrm{,}$ (3) where ${\varphi }^{J_{\text{c}}{\pi }_{\text{c}}}$ denotes the wave function of the core ¹⁶Ne, and ${\text{Φ}}^{J_{\text{p}}{\pi }_{\text{p}}}$ represents the wave function of the valence nucleons, which can be expressed as ${\text{Φ}}^{J_{\text{p}}{\pi }_{\text{p}}}={\rho }^{-5/2}{\displaystyle \sum _{\gamma \text{n}K}{C}_{\gamma \text{n}K}^{J_{\text{p}}\pi M}}{\text{B}}_{\gamma \text{n}}^{J_{\text{p}}\pi }\left(\rho \right){\mathcal{Y}}_{\gamma K}^{J_{p}M}\left(\Omega \right)\mathrm{,}$ (4) where ${\text{Y}}_{\gamma K}^{J_{\text{p}}M}\left(\Omega \right)$ reprsents the hyperspherical harmonic of the hyper-angle. The hyperradial part is expanded in the Berggren ensemble, a complete basis in the complex-momentum plane including bound, decaying, and scattering states [50, 52, 53]. K is the hyperspherical quantum number, and $\gamma =\left\{s_1\mathrm{,}{s}_2\mathrm{,}{S}_{12}\mathrm{,}S\mathrm{,}{\mathcal{l}}_x\mathrm{,}{\mathcal{l}}_y\mathrm{,}L\mathrm{,}{J}_{\text{p}}\mathrm{,}{J}_{\text{c}}\right\}$ contains the other numbers. Using the Berggren basis, the inner and asymptotic regions of the Schrödinger equation can be addressed on the same footing, providing a natural connection between the nuclear structure and decay aspects of the problem.

The ¹⁶Ne + p + p Hamiltonian of GCC can be expressed as $\widehat{H}={\displaystyle \sum _{i=\text{c}\mathrm{,}{p}_1\mathrm{,}{p}_2}\frac{{\widehat{p}}_i^2}{2m_i}}+{\displaystyle \sum _{i>j=1}^3{V}_{ij}}\left(r_{ij}\right)+{\widehat{H}}_{\text{c}}-{\widehat{T}}_{\text{c}\mathrm{.}\text{m}\mathrm{,}}$ (5) where ${\widehat{p}}_i^2/\left(2m_i\right)$ represents the kinetic operators of each particle, $V_{ij}\left(r_{ij}\right)$ denotes the interaction between clusters i and j, ${\widehat{H}}_{\text{c}}$ is the core Hamiltonian given by the excitation energies of the core, and ${\widehat{T}}_{\text{c}\mathrm{.}\text{m}\mathrm{.}}$ denotes the center-of-mass term. In Jacobi coordinates, the center of mass is automatically eliminated. In this study, the proton-core interaction V_pc, including the central, spin–orbit, and Coulomb terms, is approximated by a Woods–Saxon (WS) average potential [54-57].

To address the antisymmetrization between core and valence protons, a supersymmetric transformation method [58-60] was employed. This method introduces an auxiliary repulsive “Pauli core” in the original core-p interaction to eliminate Pauli-forbidden states.

Consequently, the acquired eigenstate possesses a complex energy denoted by $\tilde{E}=E-i\text{Γ}/2$, where Γ represents the decay width. To elucidate the dynamics and asymptotic correlations inherent in the 2p decay, the wave function ${\Psi }_{\text{GCC}}^{J\pi }$, derived within the complex framework, should be decomposed into real-momentum scattering states by applying the Fourier–Bessel series expansion. This approach is instrumental in reinstating the Hermitian characteristics of the Hamiltonian matrix and ensuring the conservation of total density. The initial wave packet, ${\Psi }_{\text{TD}}^{J\pi }\left(t=0\right)$, thus generated, can evolve over extended durations and distances within a time-dependent (TD) framework, as shown in Refs. [61, 62].

Hamiltonian and parameters

Magnesium isotopes often exhibit significant deformation. However, due to the lack of definitive experimental data on their deformation, the deformation factor is adopted from their mirror nucleus, ¹⁸C, which exhibits a quadrupole deformation, β₂, of approximately 0.3, as reported in [63]. The ground and 2⁺ states of the deformed core were considered through non-adiabatic coupling with the valence nucleons, and the corresponding energies were obtained from experimental data [63]. A previous study [38] reported significant mirror symmetry breaking in the ¹⁶Ne-¹⁶C mirror pair due to different configurations [64, 65]. However, the excitation energies of their first 2⁺ states are remarkably similar, with ¹⁶Ne at 1.77(0) MeV and ¹⁶C at 1.76(6) MeV. Consequently, the breaking of mirror symmetry within the current framework cannot easily be described.

In a three-body system (¹⁶Ne + p + p), the interaction between the two protons is described by the finite-range Minnesota force, adhering to the original parameters specified in Ref. [66]. This interaction is further supplemented by a two-body Coulomb force applied to protons. The core-proton (core-p) effective interaction was modeled using a WS potential (with a spin–orbit term) and one-body Coulomb interaction. The parameters of the WS potential, except for the potential depth V₀ and– the spin–orbit strength V_s.o., were retained as default values, as detailed in Ref. [67]. The spin–orbit strength was set to 24 MeV. Additionally, the depth V₀ was finely adjusted to accurately replicate the experimental ground state decay energy, $Q_{\text{2p}}\left(0_{\text{g}\text{.s}\text{.}}^{+}\right)$ = 3.44 MeV, and the energy of the first 2⁺ state, $E_x\left(2_1^{+}\right)$ = 1.84 MeV, of ¹⁸Mg, as discussed in Ref. [29].

The three-body configurations in Jacobi coordinates are labeled by quantum numbers $\left(K\mathrm{,}{\mathcal{l}}_x\mathrm{,}{\mathcal{l}}_y\mathrm{,}S\right)$, where ${\mathcal{l}}_x$ represents the orbital angular momentum of the proton (neutron) pair with respect to their center of mass, ${\mathcal{l}}_y$ is the orbital angular momentum of the pair with respect to the core, and S denotes the total intrinsic spin of the emitted nucleons. Three-body calculations were performed in the model space defined by $\max \left({\mathcal{l}}_x\mathrm{,}{\mathcal{l}}_y\right)⩽8$ with a maximal hyperspherical quantum number $K_{\text{max}}=20$. For the hyperradial part, we used the Berggren basis for the $K⩽3$ channels and the harmonic oscillator basis with an oscillator length of 1.75 fm and N_max = 20 for the remaining channels. For the GCC calculation of the initial state, the complex momentum contour defining the Berggren basis is given by the path $k=0\to 0.3-0.1i\to 0.4-0.05i\to 0.5-0.03i\to 0.8\to 1.2\to 2\to 4\to 6$ (all in fm^-1). For time-dependent evolution, the inner part (< 15 fm) of the initial state was expanded and propagated with a real-momentum contour, which followed $k=0\to 0.1\to 0.13\to 0.15\to 0.16\to 0.17\to 0.185\to 0.2\to 0.225\to 0.24\to 0.25\to 0.65\to 0.8\to 1.2\to 2\to 4\to 6\to 8$ (all in fm^-1). Each segment was discretized into 30 scattering states. In practice, interactions within a sphere of radius 250 fm were considered. However, because the wave function is defined in the momentum space and evolves from a highly localized initial wave packet, this cutoff has no practical effect on the investigated physical observables.

Structure information of ¹⁸Mg and ¹⁸C

A highly proton-rich nucleus, ¹⁸Mg, located far from the β-stability line, has been recently identified as a 4p emitter [29]. The 4p decay proceeds through a two-step 2p decay via the intermediate ground state of ¹⁶Ne. To elucidate the internal structure of ¹⁸Mg and its influence on decay properties, we begin by examining the spectrum and valence-proton configurations of ¹⁸Mg and comparing them with its mirror partner, ¹⁸C. The mirror pair, due to isospin symmetry, typically exhibits similar properties across many aspects. However, Coulomb interactions introduce discrepancies in their thresholds. Consequently, ¹⁸Mg is particle-unbound, with a 2p separation energy of S_2p(¹⁸Mg) = -3.44 MeV, whereas ¹⁸C is bound to a 2n separation energy of S_2n(¹⁸C) = 4.92 MeV, as determined experimentally.

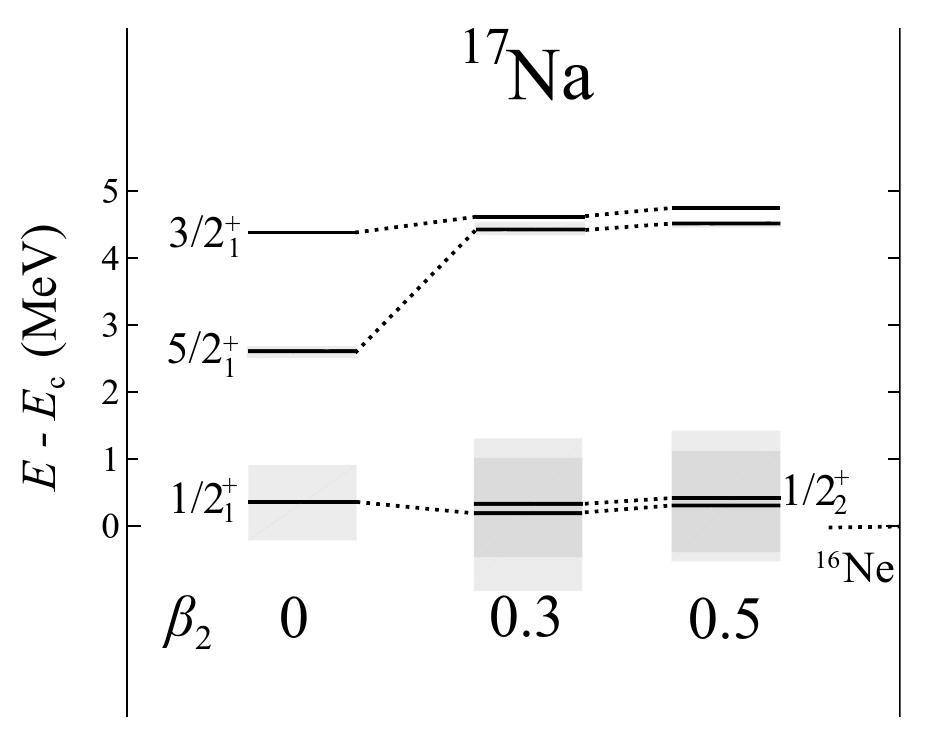
The calculated spectra of ¹⁸Mg and ¹⁸C align qualitatively, if not quantitatively, with the experimental data (Fig. 2). Specifically, the excitation energy of the first 2⁺ state is slightly underestimated for ¹⁸Mg. Meanwhile, although only one 2⁺ state is observed experimentally, our calculation predicts two low-lying 2⁺ states, similar to the situation in its mirror system ¹⁸C. The ground state of ¹⁸Mg is less unbound than those of ¹⁷Na and ¹⁶Ne. Considering the large decay width of ¹⁷Na, the ground state of ¹⁸Mg might have a “democratic” decay mode, which exhibits open 1p and 2p decay channels. This suggests potential competition between 1p and 2p decay modes during the decay process of ¹⁸Mg. To determine the primary decay mechanism, we used a time-dependent approach to analyze the corresponding decay dynamics (see the discussion below).

Fig. 2Full-screen View

The calculated spectra and decay widths (shaded areas) of ¹⁸Mg-¹⁸C pair and related neighboring nuclei ¹⁷Na and ¹⁷C. Experimental data were obtained from Refs. [29, 63]

However, due to the Coulomb interaction, ¹⁸Mg is less bound than its mirror partner, indicating a greater continuum effect. As presented in Table 1, the sd-shell effect significantly influences the ground-state configuration of valence neutrons in ¹⁸C, favoring the configurations (K, ${\mathcal{l}}_x\mathrm{,}{\mathcal{l}}_y\mathrm{,}S$) = (4,0,0,0) and (4,1,1,1), which primarily correspond to the d orbital. However, for ¹⁸Mg in its ground state, the (0,0,0,0) configuration (s orbital) is essential. This is because ¹⁸Mg better interacts with the continuum than ¹⁸C, rendering the s-wave component favorable owing to its reduced centrifugal barrier. This effect is also observed in the spectral analysis of the odd-A neighboring nuclei ¹⁷Na and ¹⁷C, where the 1/2⁺ state in ¹⁷Na, despite being unbound, benefits from additional binding from the continuum, establishing it as the ground state. Conversely, the state sequence in the mirror nucleus ¹⁷C exhibits a different arrangement. This discrepancy in the energy levels between particle-bound and unbound mirror systems is a characteristic of the Thomas–Ehrman shift [68-70].

Regarding the 2⁺ states, although the pure s-wave component is forbidden by the angular momentum selection rule, the influence of the continuum is still noticeable, causing the configuration (K, ${\mathcal{l}}_x\mathrm{,}{\mathcal{l}}_y\mathrm{,}S$) = (2,0,2,0) to be pronounced in ¹⁸Mg, where the K quantum number represents the three-body centrifugal barrier. This leads to similar excitation energies for the 2⁺ states of ¹⁸C and ¹⁸Mg, although different continuum effects are involved in these systems.

The internal structures of ¹⁸C and ¹⁸Mg also exhibit moderate mirror symmetry breaking, which is similar to that of the ¹⁶C-¹⁶Ne mirror pair. As illustrated by the density distributions of the valence nucleons shown in Fig. 3, the ground state of ¹⁸Mg exhibits a more expansive distribution than that of ¹⁸C, although both nuclei possess di-nucleon, cigar-like structures, and a small triangular component internally. This discrepancy is due to the significant s-wave component and unbound nature of ¹⁸Mg. Meanwhile, the internal structures of the $2_1^{+}$ states appear analogous to the ground for both ¹⁸Mg and ¹⁸C because most components are built upon the excited state of the daughter nuclei.

Fig. 3Full-screen View

(Color online) 2p (left) and 2n (right) density distributions in Jacobi-T coordinate predicted for the ground and first excited states of ¹⁸Mg (left) and ¹⁸C (right), respectively

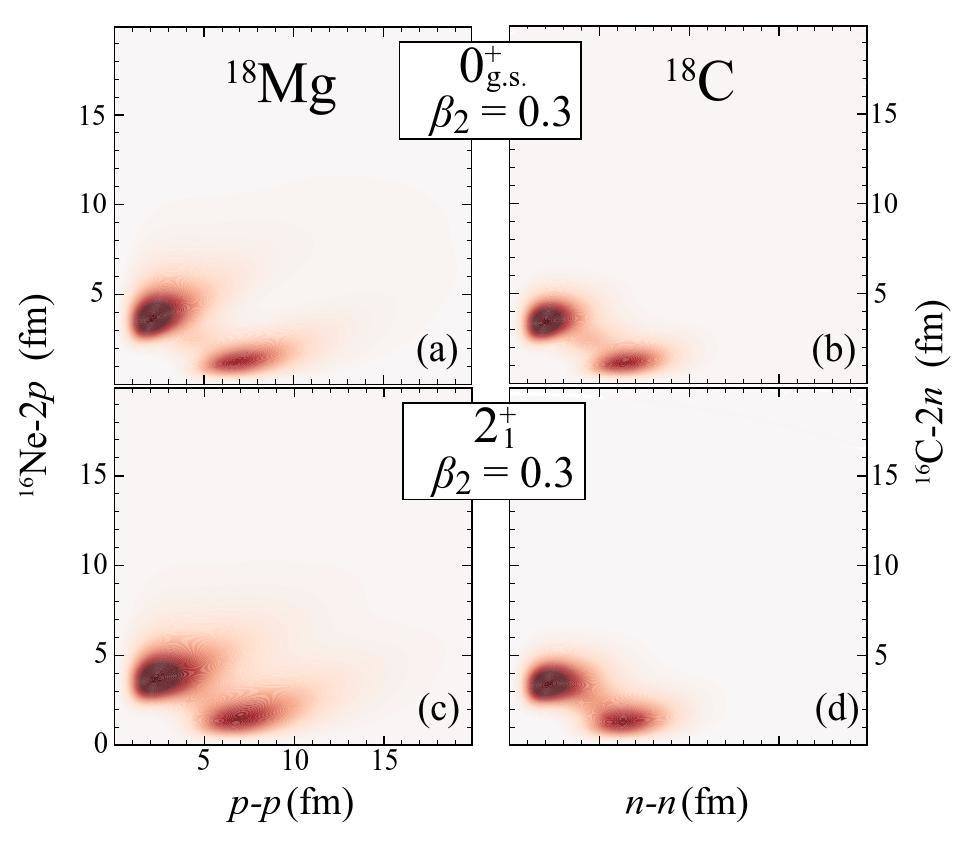
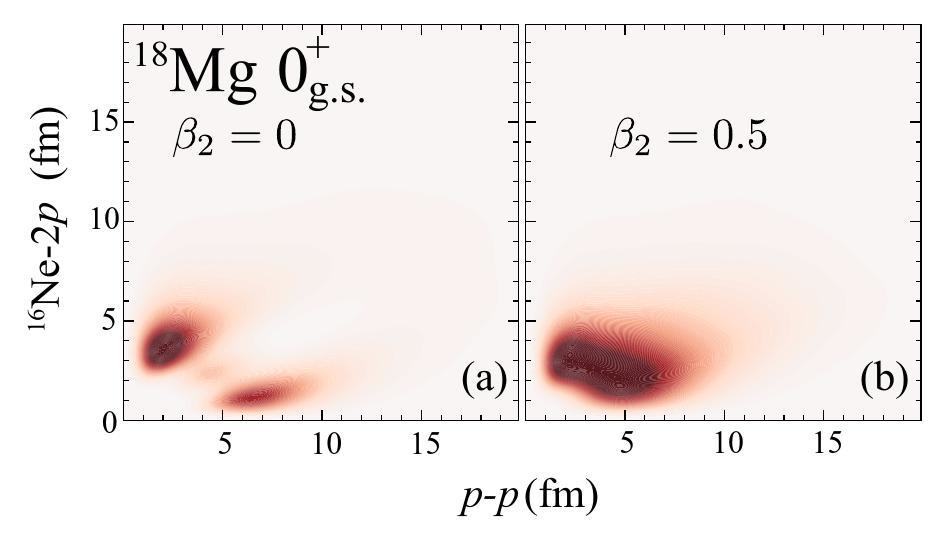
The properties of the related nucleus, ¹⁷Na, have also attracted considerable attention due to limited experimental data availability. Energy spectra have been calculated in several studies to predict the decay scheme of ¹⁷Na [71, 72]. In addition, to assess the effect of deformation on structural characteristics and decay properties, we computed the energy spectrum of ¹⁷Na and the 2p density distributions of the ¹⁸Mg ground state as functions of the quadrupole deformation parameter β₂ (refer to Figs. 4 and 5). The analysis of the spectral evolution of ¹⁷Na reveals a gap between the s and d orbitals with increasing deformation. This gap is also observed as the (K, ${\mathcal{l}}_x\mathrm{,}{\mathcal{l}}_y\mathrm{,}S$) = (4,0,0,0) and (4,1,1,1) configurations decreases from a spherical shape to a prolate deformation in the ground state of ¹⁸Mg. Consequently, this results in a change in the primary structure of ¹⁸Mg, as shown in Fig. 5. Notably, considerable deformation (β₂ = 0.5) represents uniform density distribution.

Fig. 4Full-screen View

Calculated spectrum of ¹⁷Na as a function of quadrupole deformation β₂

Fig. 5Full-screen View

(Color online) Ground-state density distributions of ¹⁸Mg with (a) spherical and (b) β₂ = 0.5 deformations

Decay properties of ¹⁸Mg

The internal configurations and spectroscopic details of ¹⁸Mg and its adjacent nuclei have been reported previously. An intriguing aspect to further examine is the influence of these properties on the decay dynamics and mechanisms. For this purpose, we employed a time-dependent framework to evolve the initial wave function across extensive spatial and temporal scales, as shown in Fig. 6.

Fig. 6Full-screen View

(Color online) Time evolution of the ground state of ¹⁸Mg with a quadrupole deformation β₂ = 0.3. Density distributions of two emitted protons are shown in Jacobi-Y (left) and -T (right) coordinates for four different time slices

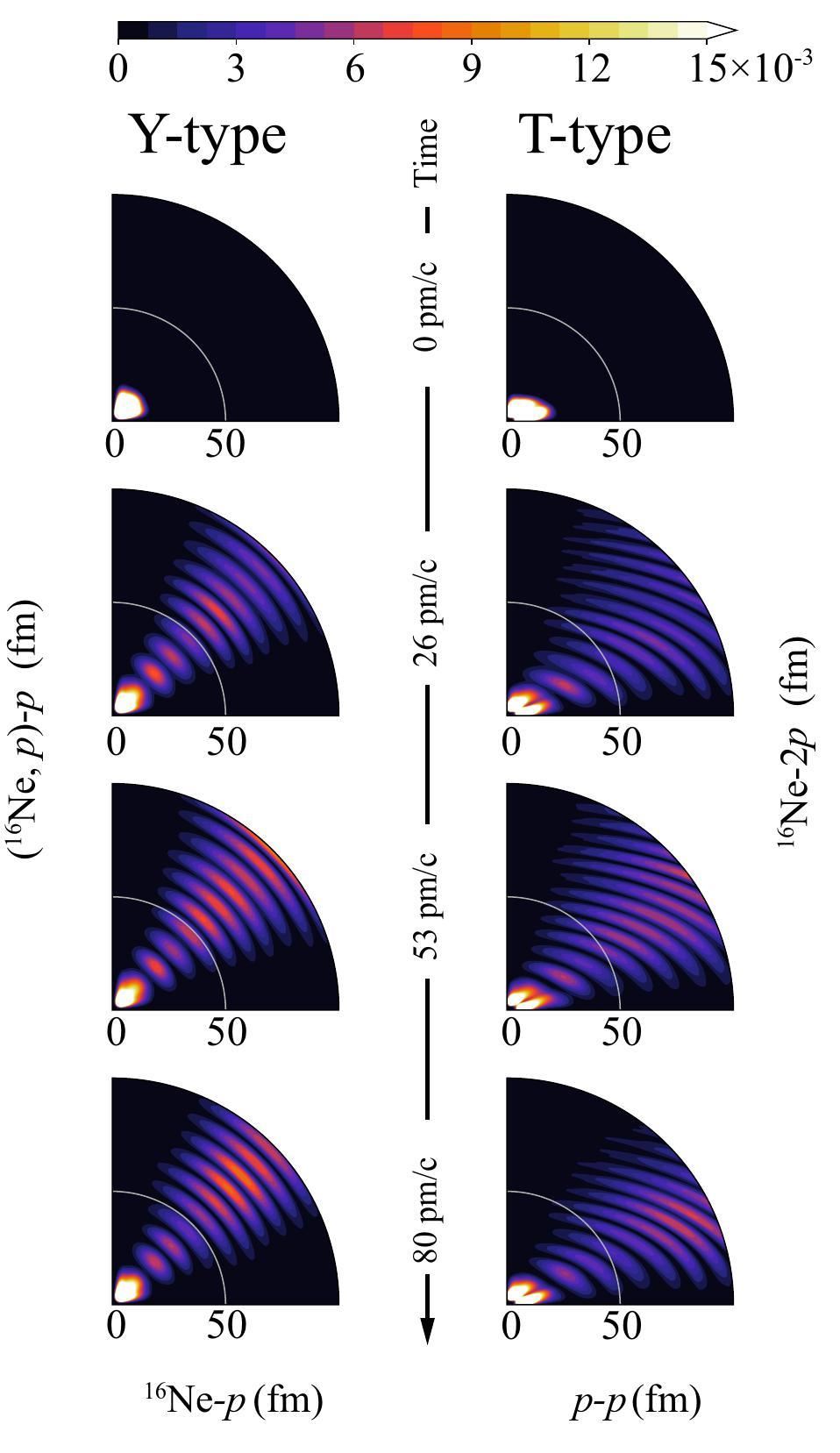
Initially (t = 0), most of the ¹⁸Mg ground-state wave function was confined within the nuclear boundary, forming the discussed diproton and cigar-like structures. However, the density evolution within the Jacobi-T coordinate reveals the merging of these structures during the tunneling phase; a dynamic distinct from the decay behavior observed in the p-shell nucleus ⁶Be [61] but similar to that of the sd-shell nucleus ¹²O [73]. This similarity is attributed to the substantial s-wave component and relatively large decay energy/width characteristic of the ¹⁸Mg ground state. Concurrently, in the decay process, the distance between ¹⁶Ne and a proton remains similar to the increasing separation in the (¹⁶Ne,p)–p configuration, as observed in the density evolution depicted in the Jacobi-Y coordinate shown in Fig. 6. This observation suggests that, despite the energetic feasibility of single-proton decay for the ¹⁸Mg ground state, simultaneous two-proton emission is the most probable decay mode.

The correlations between protons emitted from the ground state of ¹⁸Mg are shown in Fig. 7. Given the notably wide decay widths associated with light–mass systems, the energy or angular distributions cannot easily reveal distinct patterns that could differentiate between decay mechanisms. Specifically, for ¹⁸Mg, the energy correlation of the T-type is almost uniform, which is attributed to the substantial s-wave component within the ground-state wave function, as previously discussed. Meanwhile, the Y-type energy correlation attains a noticeable peak around $E_{\text{core-p}}/Q_{\text{2p}}$, further supporting the likelihood of a simultaneous 2p emission, rather than a sequential decay process.

Fig. 7Full-screen View

(Color online) Asymptotic energy (a), angular (b), and two-dimensional correlations of two emitted protons from the ground state of ¹⁸Mg with β₂ deformation of 0.3 in Jacobi-T (left) and -Y (right) coordinates, respectively. Q_2p is the total decay energy

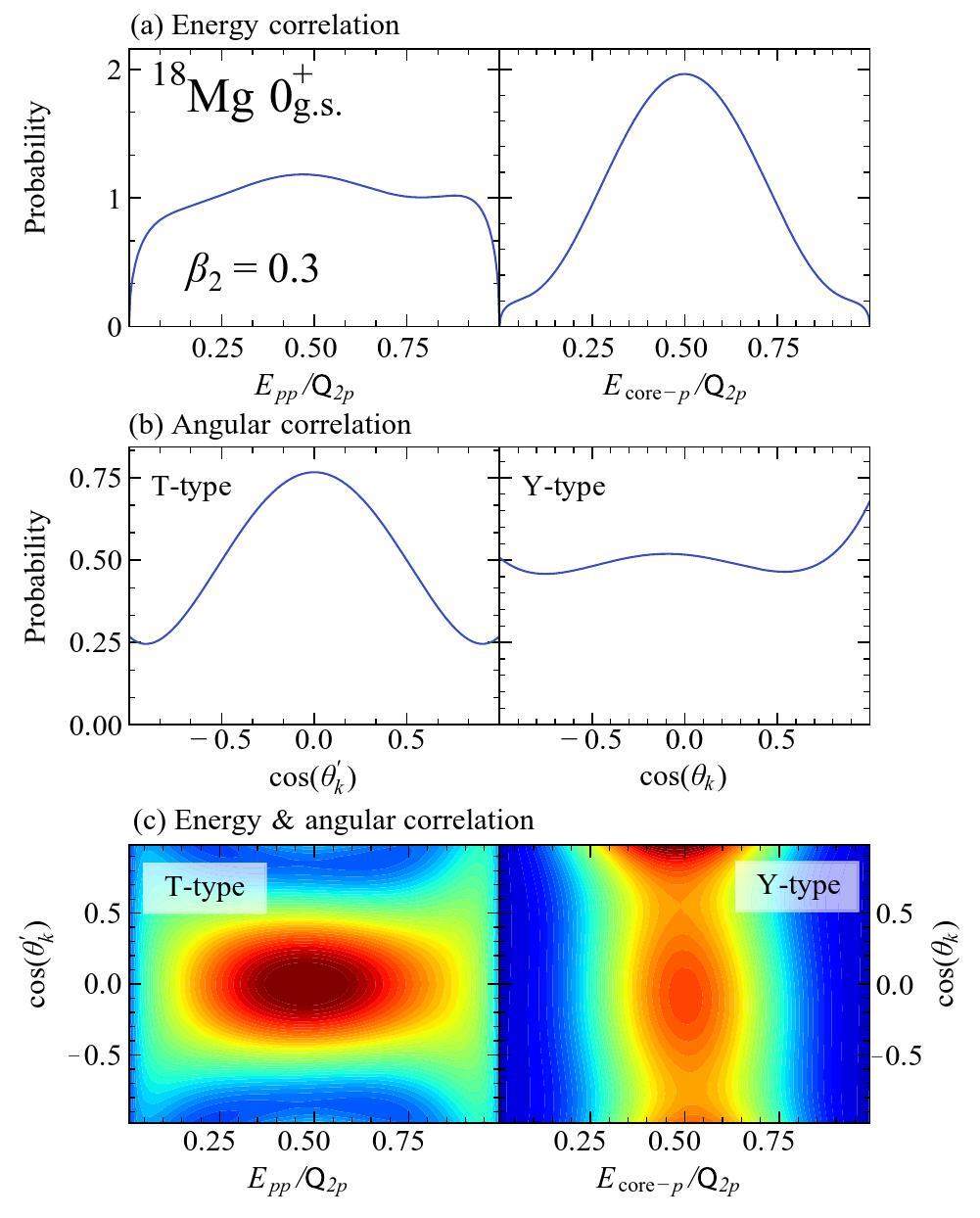
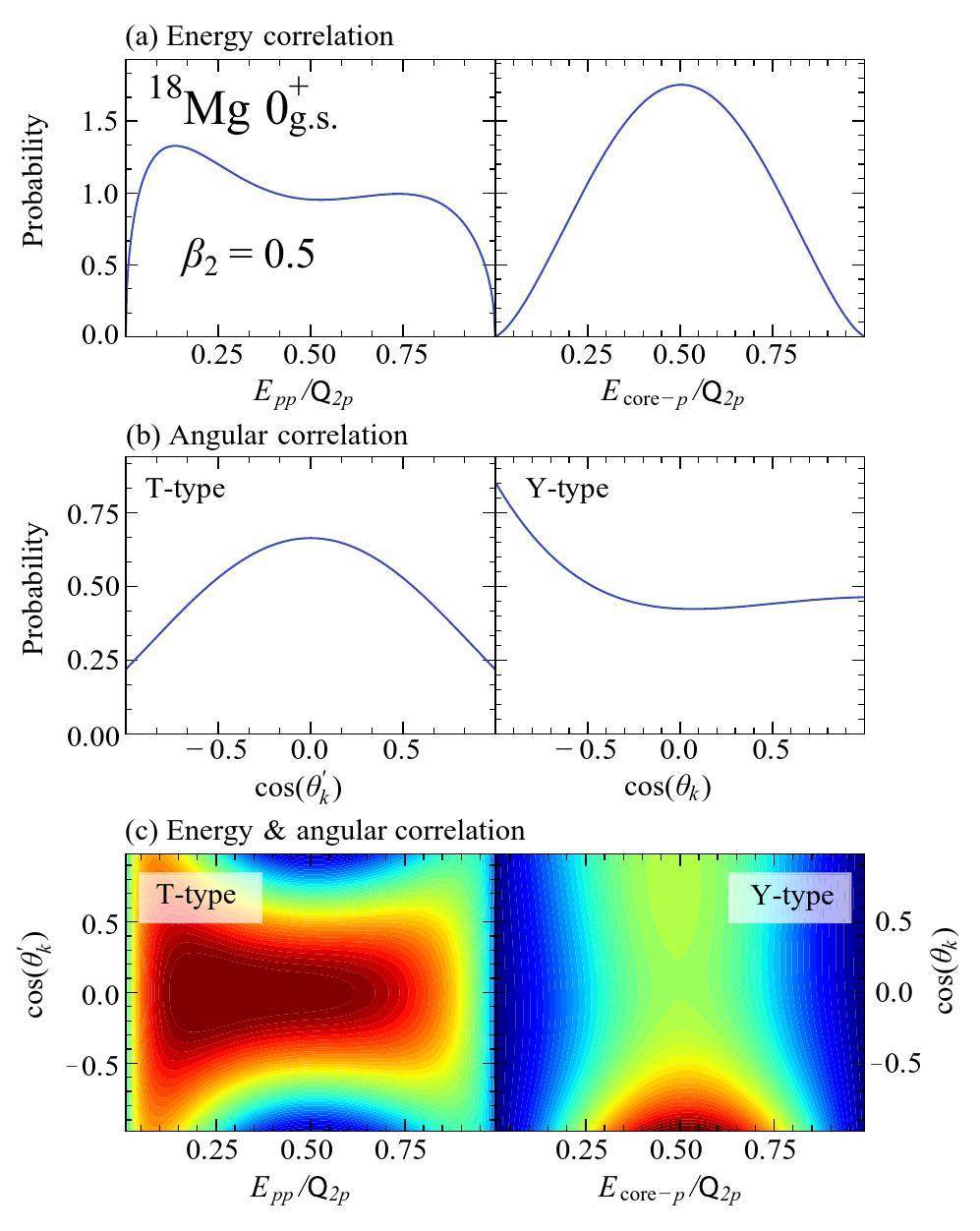
Furthermore, we investigated the effect of deformation on the asymptotic correlations of ¹⁸Mg, as shown in Figs. 7 and 8. When the quadrupole deformation β₂ changes from 0 to 0.3, the asymptotic correlation is slightly affected. However, the T-type energy correlation and Y-type angular correlation are significantly changed for β₂ = 0.5. This is in accordance with the change in the internal structure/configuration as deformation increases. In particular, enhanced peaks are observed in the small E_pp and largeθk regions (see Fig. 8), which might indicate a diproton emission, although the density of the valence proton inside the nucleus is uniformly distributed for β₂ = 0.5 (see Fig. 5). Given that nucleon–nucleon correlation can be directly measured, further experimental investigations are required.

Fig. 8Full-screen View

(Color online) Similar to Fig. 6 but for the β₂ deformation of 0.5