Production cross sections of isotopes with heavy and superheavy in ⁴⁸Ca-induced reactions

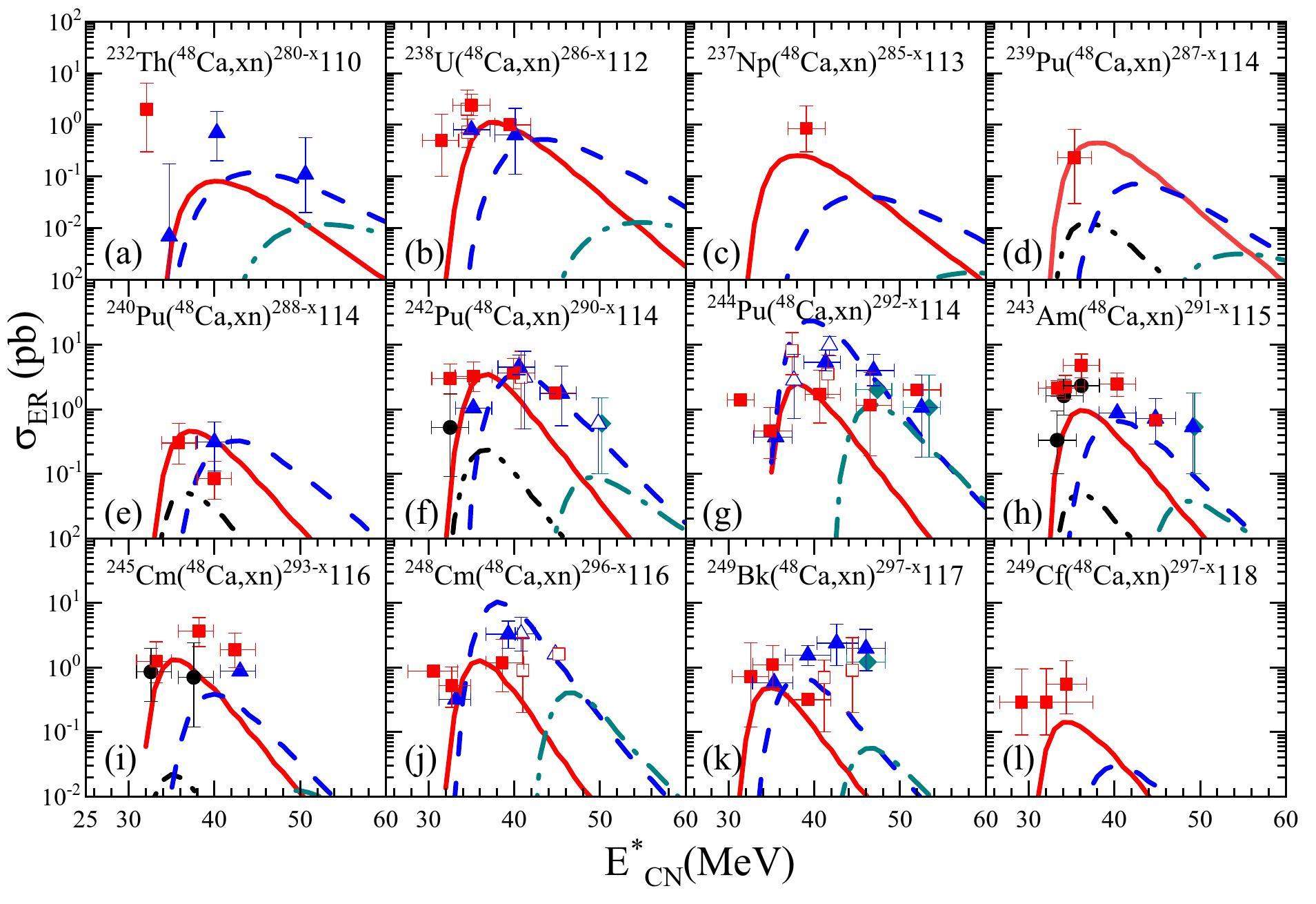
To ensure the reliability of our calculations, we ensured that all the reaction systems for the various projectile–target combinations were calculated using the same set of models and parameters. Fig. 1 shows the results for the synthesis of superheavy elements with charge numbers Z=110-118 through different xn channels in ⁴⁸Ca-induced reactions comprising ²³²Th(⁴⁸Ca,xn)^280-x110 [130, 131], ²³⁸U(⁴⁸Ca,xn)^286-x112 [12, 25, 132-134], ²³⁷Np(⁴⁸Ca,xn)^285-x113 [135, 12], ²³⁹Pu(⁴⁸Ca,xn)^287-x114 [32], ²⁴⁰Pu(⁴⁸Ca,xn)^288-x114 [32, 97], ²⁴²Pu(⁴⁸Ca,xn)^290-x114 [132, 136, 19, 12], ²⁴⁴Pu(⁴⁸Ca,xn)^292-x114 [132, 137, 37, 28, 20, 12], ²⁴³Am(⁴⁸Ca,xn)^291-x115 [23, 12, 99], ²⁴⁵Cm(⁴⁸Ca,xn)^293-x116 [137, 37, 12], ²⁴⁸Cm(⁴⁸Ca,xn)^296-x116 [132, 37, 26, 12], ²⁴⁹Bk(⁴⁸Ca,xn)^297-x117 [138, 139, 30, 12], and ²⁴⁹Cf(⁴⁸Ca,xn)^297-x118 [37, 138, 12]. The lines indicate the theoretical calculation results and the symbols, the experimental data. The calculated excitation functions for different xn channels are compared with the corresponding experimental data. There is good consistency between our calculated ERCSs and the experimental values for most evaporation channels, especially for the 3n and 4n channels. Meanwhile, we observe that for the reactions ²³⁸U(⁴⁸Ca,xn)^286-x112, ²³⁷Np(⁴⁸Ca,xn)^285-x113, ²³⁹Pu(⁴⁸Ca,xn)^287-x114, ²⁴⁰Pu(⁴⁸Ca,xn)^288-x114, ²⁴³Am (⁴⁸Ca,xn)^291-x115, ²⁴⁵Cm(⁴⁸Ca,xn)^293-x116, and ²⁴⁹Cf(⁴⁸Ca,xn)^297-x118, the maximum theoretical and experimental values of ${\sigma }_{\text{ER}}$ occur in the 3n channel, while for the reactions ²³²Th(⁴⁸Ca,xn)^280-x110, ²⁴²Pu(⁴⁸Ca,xn)^290-x114, ²⁴⁴Pu(⁴⁸Ca,xn)^292-x114, ²⁴⁸Cm(⁴⁸Ca,xn)^296-x116, and ²⁴⁹Bk(⁴⁸Ca,xn)^297-x117, they occur in the 4n channel. In addition, the position of the maximum ERCS in the 3n and 4n channels depends on the behavior of the fusion probability P_CN as the excitation energy increases. Although our current theoretical models for the synthesis of superheavy nuclei yield good results and accurately reproduce some experimentally measured evaporation residue cross sections, it is important to note that merely reproducing experimental results does not necessarily imply a complete understanding of the mechanisms involved in superheavy nuclei formation. Therefore, further theoretical investigations are necessary to deepen our understanding of superheavy nuclei synthesis processes.

Fig. 1Full-screen View

(Color online) The calculated ERCSs compared with the available experimental data for the reactions ⁴⁸Ca+²³²Th [130, 131], ⁴⁸Ca+²³⁸U [12, 25, 132-134], ⁴⁸Ca+²³⁷Np [135, 12], ⁴⁸Ca+²³⁹Pu [32], ⁴⁸Ca+²⁴⁰Pu [32, 97], ⁴⁸Ca+²⁴²Pu [132, 136, 19, 12], ⁴⁸Ca+²⁴⁴Pu [132, 137, 37, 28, 20, 12], ⁴⁸Ca+²⁴³Am [23, 12, 99], ⁴⁸Ca+²⁴⁵Cm [137, 37, 12], ⁴⁸Ca+²⁴⁸Cm [132, 37, 26, 12], ⁴⁸Ca+²⁴⁹Bk [138, 139, 30, 12], and ⁴⁸Ca+²⁴⁹Cf [37, 138, 12]. The measured ERCSs of the 2n, 3n, 4n, and 5n channels are denoted by black circles, red squares, blue triangles, and dark cyan rhombi, respectively. The corresponding theoretical values are indicated by black double-dot dashed lines, red solid lines, blue dashed lines, and dark cyan dot-dashed lines, respectively. The solid symbols represent data from DGFRS and open symbols data from other sources (SHIP, BGS, TASCA, RILAC)

To further verify the reliability and applicability of the DNS model, we continued to use ⁴⁸Ca as a projectile for bombarding lanthanide target nuclei. The fusion-evaporation excitation functions of the ¹⁵⁴Gd(⁴⁸Ca,xn)^202-x84 [140], ¹⁵⁹Tb(⁴⁸Ca,xn)^207-x85 [140], ¹⁶²Dy(⁴⁸Ca,xn)^210-x86 [140], ¹⁶⁵Ho(⁴⁸Ca,xn)^223-x87 [140], ¹⁷²Yb(⁴⁸Ca,xn)^220-x90 [120], ¹⁷³Yb(⁴⁸Ca,xn)^221-x90 [120], and ¹⁷⁶Yb(⁴⁸Ca,xn)^224-x90 [120] reactions were calculated. Fig. 2 shows a comparison between the theoretical and corresponding experimental results for the seven reactions. The experimental data are denoted by red squares, blue triangles, dark cyan rhombi, and orange pentagrams, respectively, while the theoretical calculation results are represented by red solid lines (3n), blue dashed lines (4n), dark cyan dot-dashed lines (5n), orange double dot-dashed lines (4n+5n) (${\sigma }_{\text{ER}}={\sigma }_{\text{cap}}\times P_{\text{CN}}\times W_{\text{sur}}$), and black dashed lines with hollow circles (2n), red dashed lines with hollow squares (3n), blue dashed lines with hollow triangles (4n), dark cyan dashed lines with hollow rhombi (5n), and orange dash lines with hollow pentagrams (4n+5n) (${\sigma }_{\text{ER}}={\sigma }_{\text{cap}}\times W_{\text{sur}}$).

Fig. 2Full-screen View

(Color online) The calculated ERCSs compared with the available experimental data for the reactions ⁴⁸Ca+¹⁵⁴Gd [140], ⁴⁸Ca+¹⁵⁹Tb [140], ⁴⁸Ca+¹⁶²Dy [140], ⁴⁸Ca+¹⁶⁵Ho [140], ⁴⁸Ca+¹⁷²Yb [120], ⁴⁸Ca+¹⁷³Yb [120], and ⁴⁸Ca+¹⁷⁶Yb [120]. The measured ERCSs of the 3n, 4n, 5n, and 4n+5n channels are denoted by red squares, blue triangles, dark cyan rhombi, and orange pentagrams, respectively, while the theoretical calculation results are indicated by the red solid lines (3n), blue dashed lines (4n), dark cyan dot-dashed lines (5n), and orange double-dot dashed lines (4n+5n)(${\sigma }_{\text{ER}}={\sigma }_{\text{cap}}\times P_{\text{CN}}\times W_{\text{sur}}$), and the black dashed lines with hollow circles (2n), red dashed lines with hollow squares (3n), blue dashed lines with hollow triangles (4n), dark cyan dashed lines with hollow rhombi (5n), and orange dashed lines with hollow pentagrams (4n+5n) (${\sigma }_{\text{ER}}={\sigma }_{\text{cap}}\times W_{\text{sur}}$)

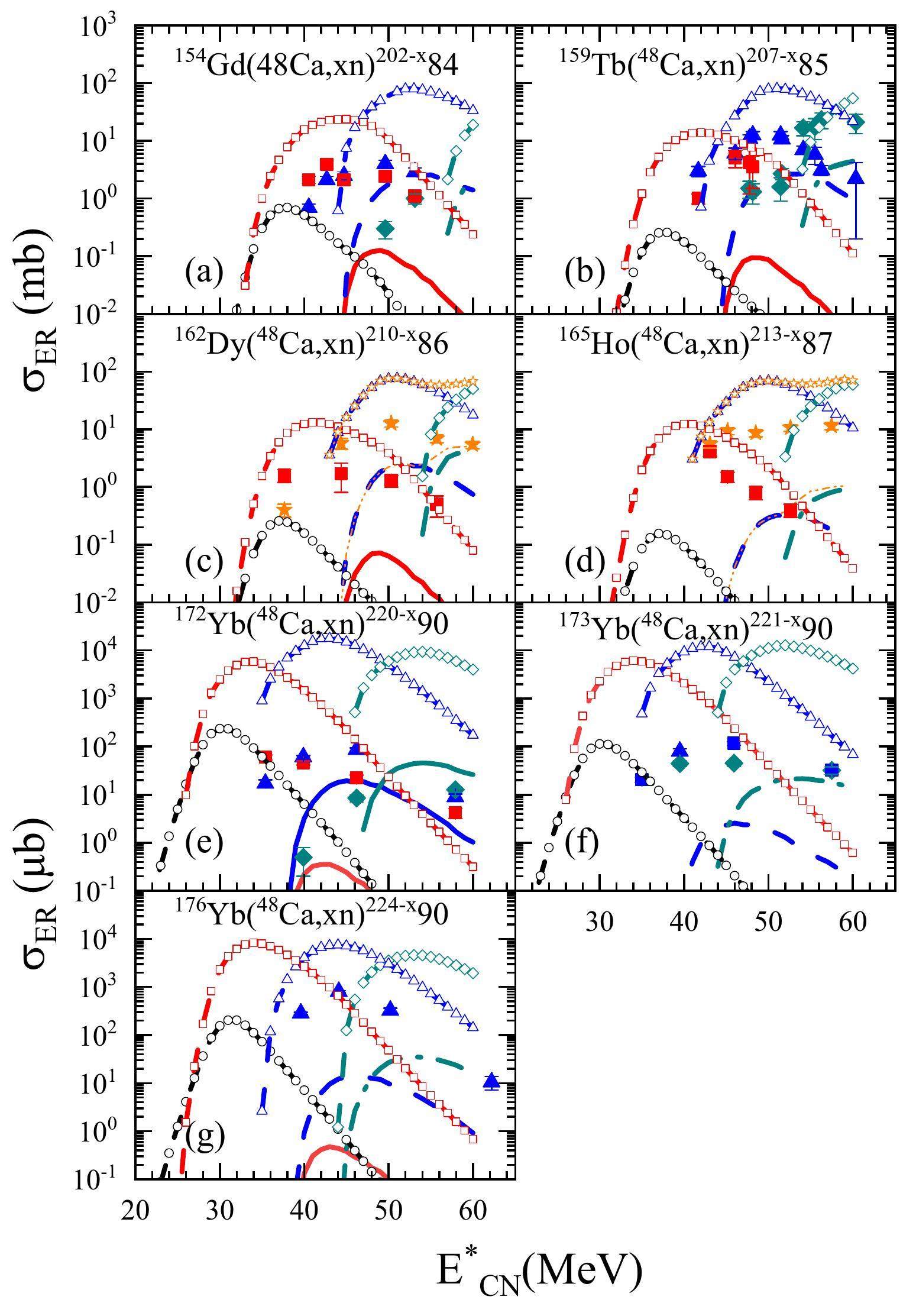
Although the theoretical calculation results for the 4n and 5n channels of ¹⁵⁴Gd(⁴⁸Ca,xn)^202-x84, ¹⁵⁹Tb(⁴⁸Ca,xn)^207-x85, and ¹⁷²Yb(⁴⁸Ca,xn)^220-x90 and the 5n channel of ¹⁷³Yb(⁴⁸Ca,xn)^221-x90 are systematically lower than the experimental values by 2-3 times, the experimental values and their variational trends with the excitation energy are still well reproduced. Despite the experimental values for the 3n channels of ¹⁵⁴Gd(⁴⁸Ca,xn)^202-x84, ¹⁵⁹Tb(⁴⁸Ca,xn)^207-x85, ¹⁶²Dy(⁴⁸Ca,xn)^210-x86, ¹⁶⁵Ho(⁴⁸Ca,xn)^223-x87, and ¹⁷²Yb(⁴⁸Ca,xn)^220-x90 and the 4n channels of ¹⁷³Yb(⁴⁸Ca,xn)^221-x90 and ¹⁷⁶Yb(⁴⁸Ca,xn)^224-x90 being larger than the theoretical values by about one to two orders of magnitude, the variational trends of the cross section with excitation energy are still reproduced. The results show that although the experimental values are systematically larger than the theoretical ones, the variational trend with the atomic number is in complete agreement with that of the experimental measurements. Therefore, our predicted cross sections may be the lower limits of the experimental detection range. A careful comparison of the measured cross sections with the calculated results in Fig. 1 and Fig. 2 reveals discrepancies in the theoretical calculations in certain evaporation channels. These differences mainly stem from the limitations of the theoretical models. In the existing DNS framework, the potential energy surface is crucial for determining the transition probabilities and microscopic state dimensions; however, its theoretical calculation is not entirely accurate. From Fig. 2, it is evident that the fusion probability P_CN reduces the cross section by 2–3 orders of magnitude. The numerical uncertainty of P_CN and its dependence on the excitation energy and entrance channel of the reaction are also uncertain [142]. Therefore, further investigation into the fusion mechanism is required. Note that our calculated survival probability is based on nuclear data such as the nuclear masses, neutron separation energies, and fission barriers (shell correction energies), which are usually extrapolated. Therefore, the accuracy of our method is closely dependent on the extrapolation accuracy [143, 144]. In particular, the precision of the fission barrier is crucial in calculating cross sections for superheavy nuclei synthesis. In hot fusion reactions, the compound nucleus emits three to four neutrons. Imprecise fission barrier heights can therefore cause calculation errors in the neutron decay width and the fission width to (xn) de-excitation cascade ratio at each step to accumulate, leading to increased calculation errors in the synthesis cross section [145]. These uncertainties limit the accuracy of the evaporation residue cross section. We will study these effects in our future work.

Production of Fl and Lv neutron-deficient isotopes in xn evaporation channels

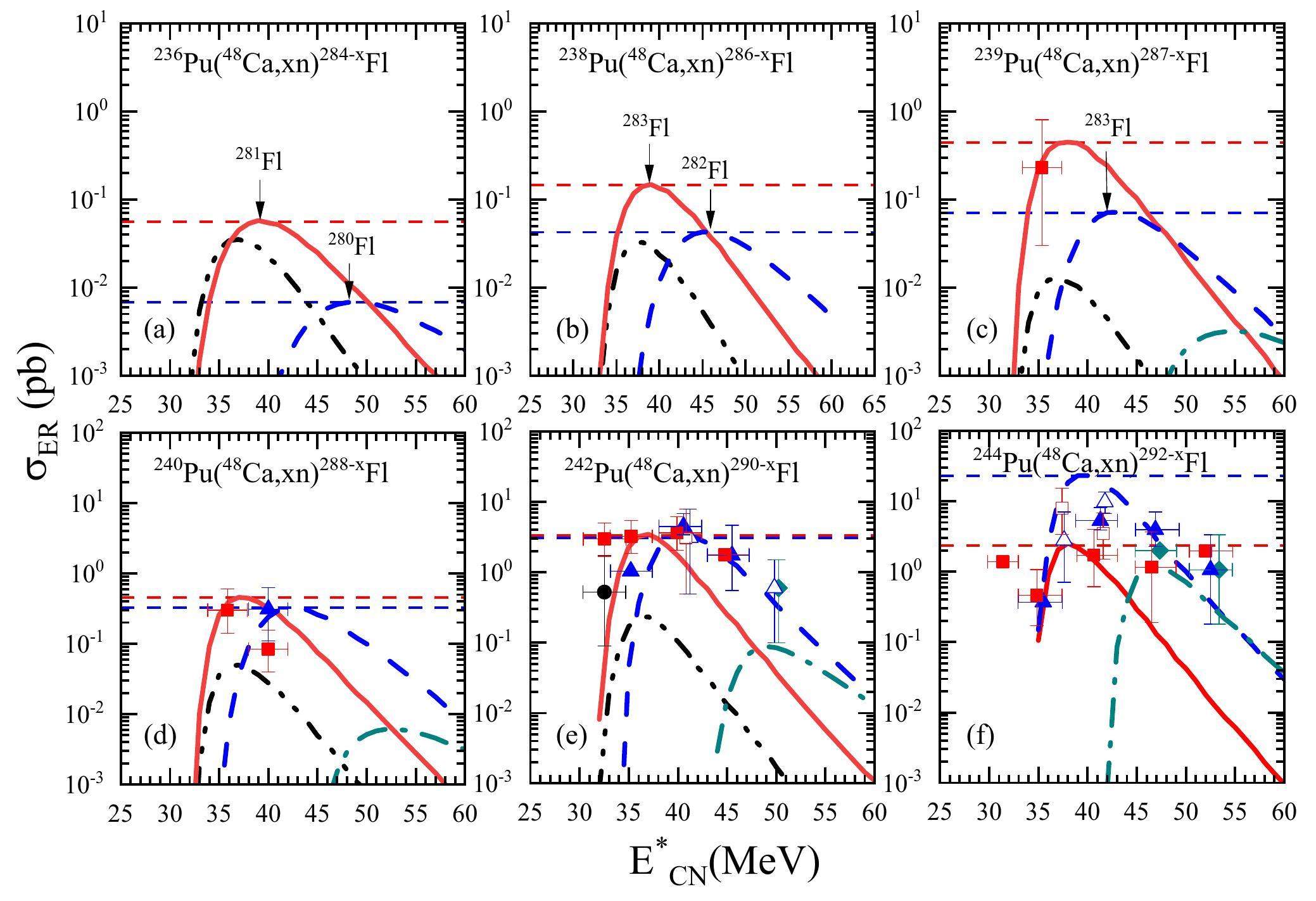
To investigate the possibility of synthesizing new neutron-deficient superheavy isotopes, we calculated the cross sections for the production of unknown Fl and Lv neutron-deficient isotopes in fusion reactions in which a ⁴⁸Ca beam is used to bombard Pu and Cm actinide targets. The excitation functions corresponding to the emission of 3 and 4 neutrons are shown in Fig. 3. In the ⁴⁸Ca+²³⁶Pu reaction, the maximum value of ${\sigma }_{3n}$ (0.058 pb) $E_{\text{CN}}^{*}$=39 MeV is approximately one order of magnitude greater than that of ${\sigma }_{4n}$ (0.007 pb) at $E_{\text{CN}}^{*}$=46 MeV. The maximum values of the 3n and 4n channels for the ⁴⁸Ca+²³⁸Pu reaction are 0.149 and 0.043 pb, respectively. The maximum ERCS of the 4n channel for the ⁴⁸Ca+²³⁹Pu reaction is 0.072 pb at $E_{\text{CN}}^{*}$ = 43 MeV. The above reactions can lead to the production of ^281-283Fl, with ²⁸³Fl being the most probable isotope owing to the current experimental detection limit being greater than 0.1 pb [12].

Fig. 3Full-screen View

(Color online) The calculated ERCSs compared with the available experimental data for the reactions ⁴⁸Ca+²³⁶Pu, ⁴⁸Ca+²³⁸Pu,⁴⁸Ca+²³⁹Pu [32], ⁴⁸Ca+²⁴⁰Pu [32, 97], ⁴⁸Ca+²⁴²Pu [132, 136, 19, 12], and ⁴⁸Ca+²⁴⁴Pu [132, 137, 37, 28, 20, 12]. The measured ERCSs of the 2n, 3n, 4n, and 5n channels are denoted by black circles, red squares, blue triangles, and dark cyan rhombi, respectively. The theoretical ERCRs of the 2n, 3n, 4n, and 5n channels are indicated by black double-dot dashed lines, red solid lines, blue dashed lines, and dark cyan dot-dashed lines, respectively. The solid symbols denote data from DGFRS and open symbols data from other sources (SHIP, BGS, TASCA)

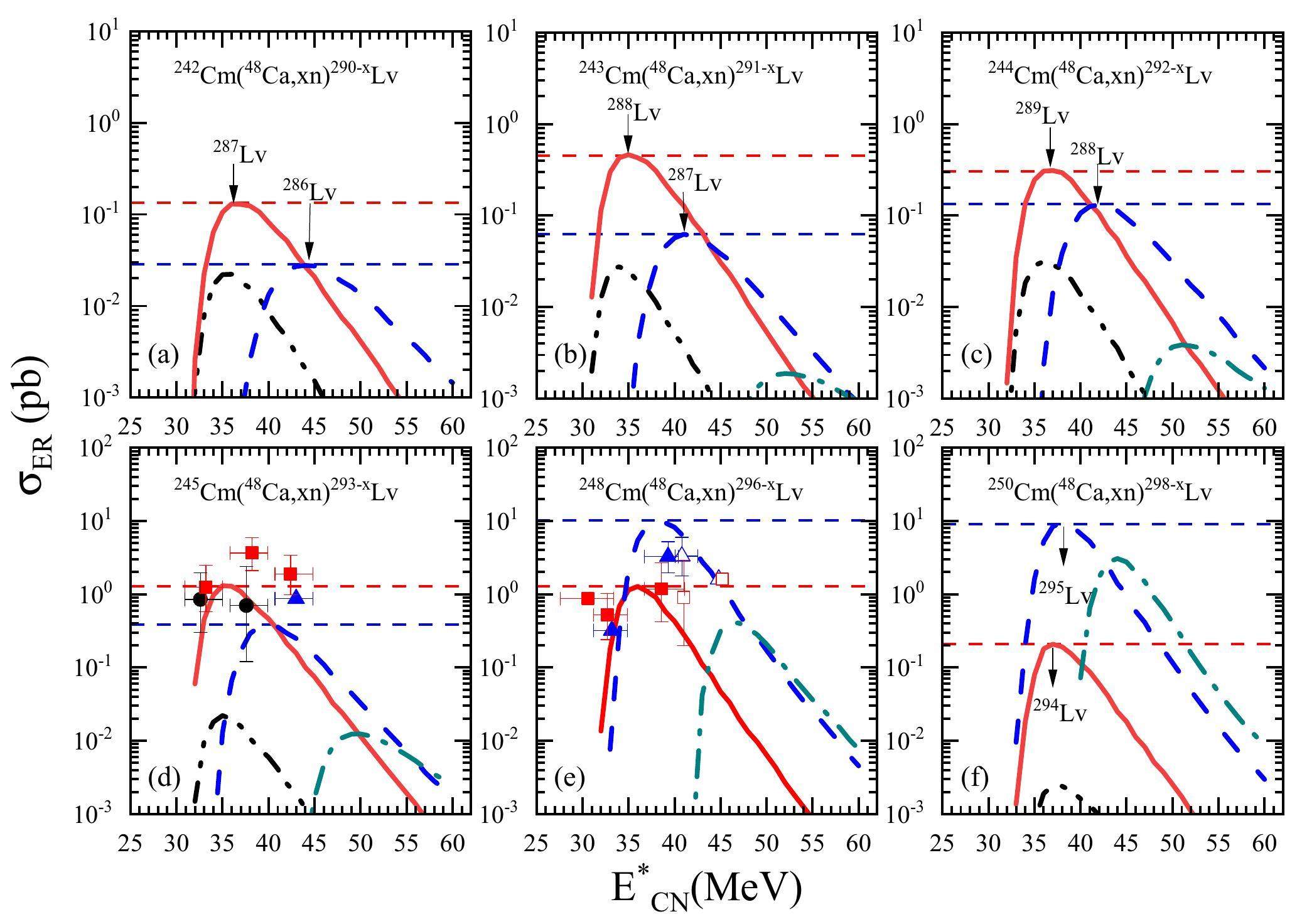
The isotopes ^{286,287,288,289,294,295}Lv can be produced in reactions in which ⁴⁸Ca projectile is used to bombard Cm targets with the mass numbers ^{242,243,244,250}Cm (Fig. 4). The production cross sections for the 3n and 4n channels are in the range of 0.03 pb–1  pb. Because the current experimental detection limit is greater than 0.1 pb [12], ²⁸⁷Lv(${\sigma }_{3n}=0.130$ pb),²⁸⁸Lv(${\sigma }_{3n}=0.462$ pb),²⁸⁹Lv(${\sigma }_{3n}=0.309$ pb),²⁸⁸Lv(${\sigma }_{4n}=0.132$ pb),²⁸⁸Lv(${\sigma }_{3n}=0.208$ pb), and ²⁸⁸Lv(${\sigma }_{4n}=9.522$ pb) are the most probable isotopes to be produced.

Fig. 4Full-screen View

(Color online) The calculated ERCSs compared with the available experimental data for the reactions ⁴⁸Ca+²⁴²Cm, ⁴⁸Ca+²⁴³Cm, ⁴⁸Ca+²⁴⁴Cm, ⁴⁸Ca+²⁴⁵Cm [137, 37, 12], ⁴⁸Ca+²⁴⁸Cm [132, 37, 26, 12], and ⁴⁸Ca+²⁵⁰Cm. The measured ERCSs of the 2n, 3n, 4n, and 5n channels are denoted by black circles, red squares, blue triangles, and dark cyan rhombi, respectively. The theoretical ERCRs of the 2n, 3n, 4n, and 5n channels are indicated by black double-dot dashed lines, red solid lines, blue dashed lines, and dark cyan dot-dashed lines, respectively. The solid symbols represent data from DGFRS and open symbols data from other sources (SHIP, BGS, TASCA)

In the DNS model, the isotope production trends are mainly determined by the fusion and survival probabilities. The increased internal fusion barrier as the neutron number of the target nucleus increases reduces the fusion probability. Figure 5 shows the Bn and Bf values for the 3n and 4n evaporation channels of the ⁴⁸Ca-induced reaction. The results indicate that when the target nucleus is odd, Bn(3n) > Bn(4n), whereas the opposite is true when the target nucleus is even. From the data, it can be observed that a smaller neutron separation energy and larger fission barrier (shell correction energy) are well correlated with a higher survival probability [7, 146]. The HIVAP code was employed in numerous studies in the previous century to investigate the values of fission barriers based on experimental data, including those from Darmstadt and Dubna. These studies revealed that as the proton number increases, the fission barrier is decreased by the Coulomb force. The emission of alpha particles by compound nuclei indicates the presence of a fission barrier. A sufficiently high fission barrier can protect the compound nucleus and prevent spontaneous fission. Within the energy range of $E_{\text{CN}}^{*}$=20–30 MeV, the shell correction in the ground state significantly enhances the survival probability of compound nuclei, thereby increasing the fission barrier. The survival probability of the compound system is mainly dependent on the continuous growth of the Coulomb force during the de-excitation process. In symmetric and asymmetric collision systems, the loss during the de-excitation process is determined by the fission barrier height in the compound nucleus. As the vibrational and spin levels increase, the larger level density ratio between the ground state and the saddle point results in a higher fission probability. This increase partially compensates for the decrease in fission probability by increasing the fission barrier. However, this compensatory effect only applies to spherical nuclei. In deformed nuclei in the ground state, the level density is collectively enhanced under both ground state and saddle point deformations. Because of the small difference between the ground state and saddle point deformation level densities, the survival probability against fission is hardly affected [146-153].

Fig. 5Full-screen View

(Color online) Neutron separation energies (black solid squares) and fission barriers (red crosses) predicted from FRDM1995 data for decaying nuclei produced by ⁴⁸Ca-induced reactions with the indicated targets for 3n and 4n emission

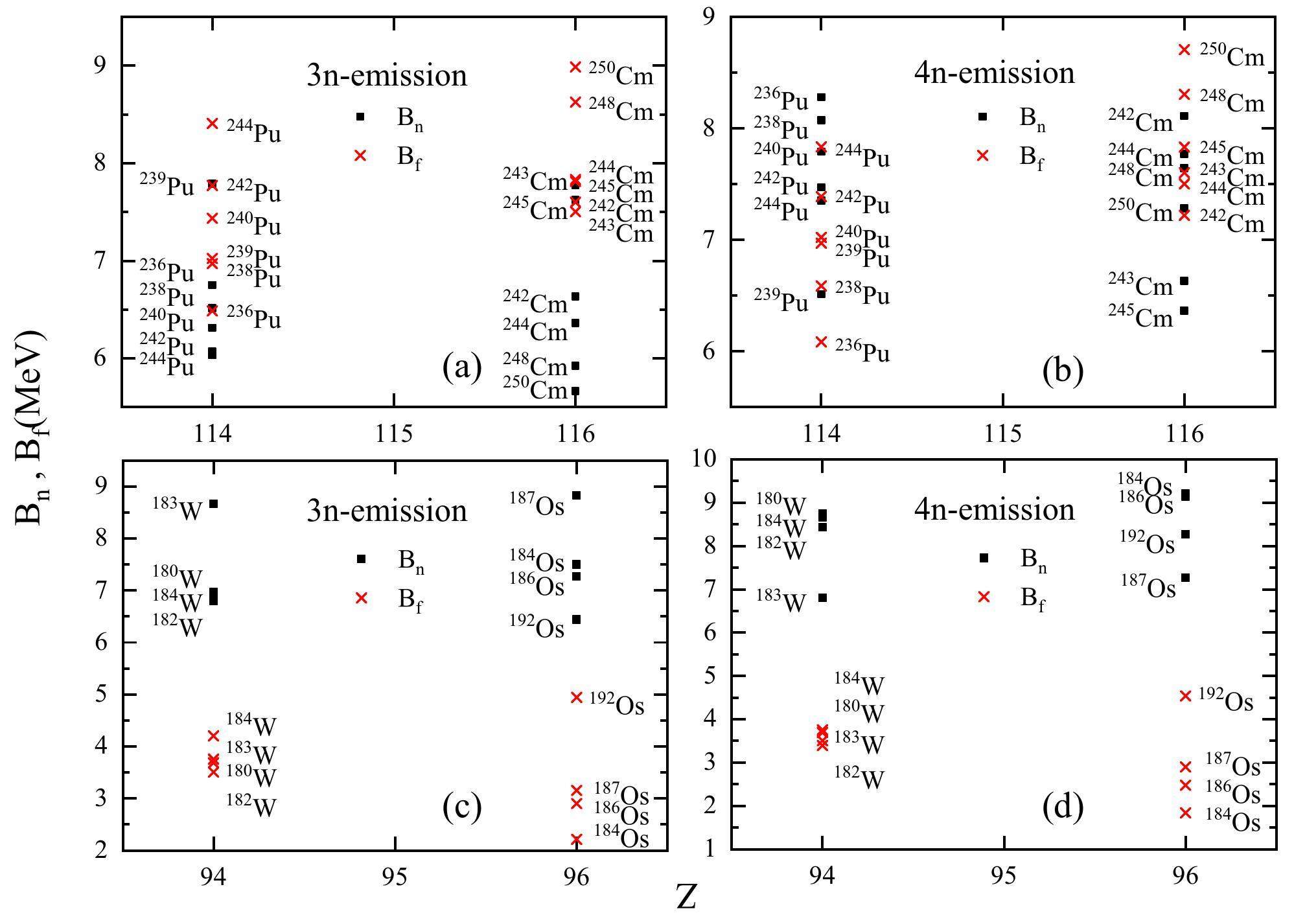
From Fig. 3, it can be seen that except for the 3n emission channel in the ⁴⁸Ca+²⁴⁴Pu reaction, the cross sections of the 3n and 4n channels in reactions with Pu isotopes generally increase with the neutron number. In most cases, the survival probability of the compound nucleus increases with the neutron number, reaches a maximum as the excitation energy increases, and then decreases. We note that in the calculation process for ⁴⁸Ca+^ACm reactions, P_CN is irregular and varies with the neutron number of the target nucleus. P_CN is mainly affected by the details of the driving potential, which are determined by the properties of each nucleus in the DNS model and their interactions. However, in most cases, the increase in W_sur with increasing proton number is not offset by the decrease in P_CN. This leads to an increase in the reaction cross section and a certain probability of producing new nuclides.

In recent years, attempts have been made to use theoretical models to predict new nuclei and interesting results have been obtained. Hong et al. [13] applied the DNS model to the ³⁶S+²⁴⁹Cf reaction and showed that 2-4 neutrons can be evaporated to produce the new neutron-deficient isotopes ^281-283Fl with a maximum cross section of 0.08–0.3 pb. In 2021, they used the ⁴⁸Ca+²⁴²Pu→²⁸³Fl+7n reaction and obtained a maximum cross section of 0.1 pb, indicating that the hot fusion reaction is superior to the cold fusion reaction [91]. Zhang et al. [92] also used the DNS model to predict relatively high cross sections in the ⁴⁸Ca+²⁴²Pu and ³⁶S+²⁴⁹Cf reactions. For the new isotopes ^281-283Fl, the ERCSs of the 2n, 3n, and 4n channels in the cold fusion reaction system (2.02, 36.16, and 6.17 pb, respectively) are larger than those of the 3n, 4n, and 5n channels in the hot fusion reaction system (0.29, 1.06, and 0.09 pb, respectively). In addition, Zagrebaev et al. [10] predicted that the cross sections of the 3n and 4n channels in the ⁴⁸Ca+²⁵⁰Cm reaction for the new Livermorium isotopes ^294,295Lv are approximately 1 pb.

Production of Pu and Cm neutron-deficient isotopes in xn evaporation channels

Some isotopes may be produced during the complete fusion reactions of ⁴⁸Ca + ^180,182,183W. Fig. 6 shows a comparison between the calculated ER cross sections for these four reactions and experimental data obtained from the available references [148](represented by the square points). The lines denote the calculated results where black, red, blue, and dark cyan correspond to the 2n, 3n, 4n, and 5n channels, respectively. The neutron-deficient isotopes ^224-227Pu, which have cross sections larger than 0.06 nb, can be produced. For the ⁴⁸Ca+¹⁸⁰W reaction, the 3n and 4n channels exhibit the maximum cross sections of 0.06 and 0.07 nb at the excitation energies of $E_{\text{CN}}^{*}$ = 48 and 60 MeV, respectively, resulting in the production of ^224,225Pu. In the ⁴⁸Ca + ¹⁸²W reaction, the maximum cross sections for the 3n and 4n channels are 0.18 and 0.24 nb at the excitation energies of $E_{\text{CN}}^{*}$ = 47 and 60 MeV, respectively, which leads to the production of ^226,227Pu. Furthermore, in the ⁴⁸Ca+¹⁸³W reaction, the 4n channel has a maximum cross section of 0.30 nb at the excitation energy of $E_{\text{CN}}^{*}$ = 58 MeV, leading to the production of ²²⁷Pu.

Fig. 6Full-screen View

(Color online) The calculated ERCSs compared with the available experimental data for the reactions ⁴⁸Ca+¹⁸⁰W, ⁴⁸Ca+¹⁸²W, ⁴⁸Ca+¹⁸³W, and ⁴⁸Ca+¹⁸⁴W [148]. The measured ERCSs of the 3n channel are denoted by solid red squares and theoretical ERCSs of the 2n, 3n, 4n, and 5n channels by black double-dot dashed lines, red solid lines, blue dashed lines, and dark cyan dot-dashed lines, respectively

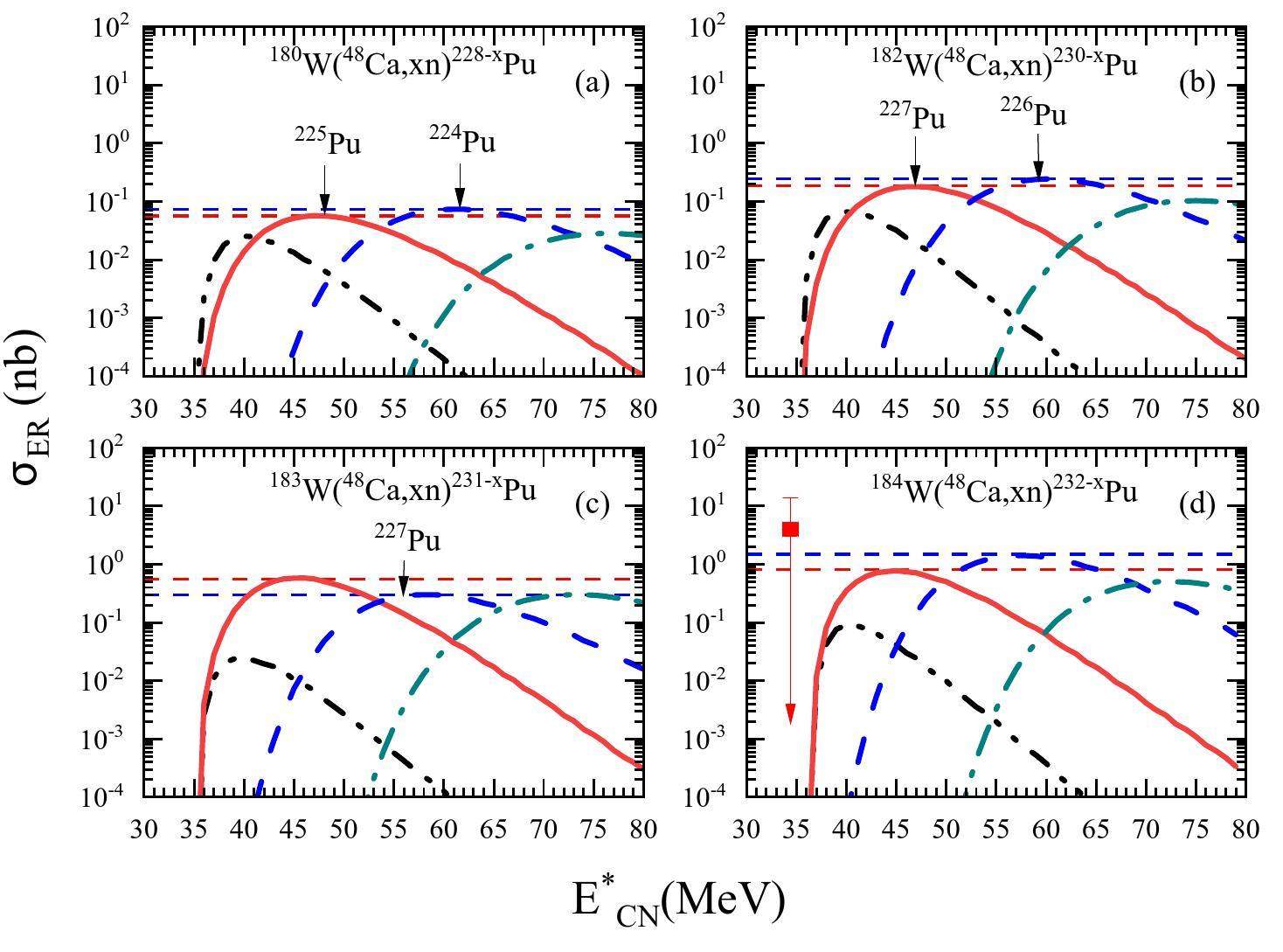
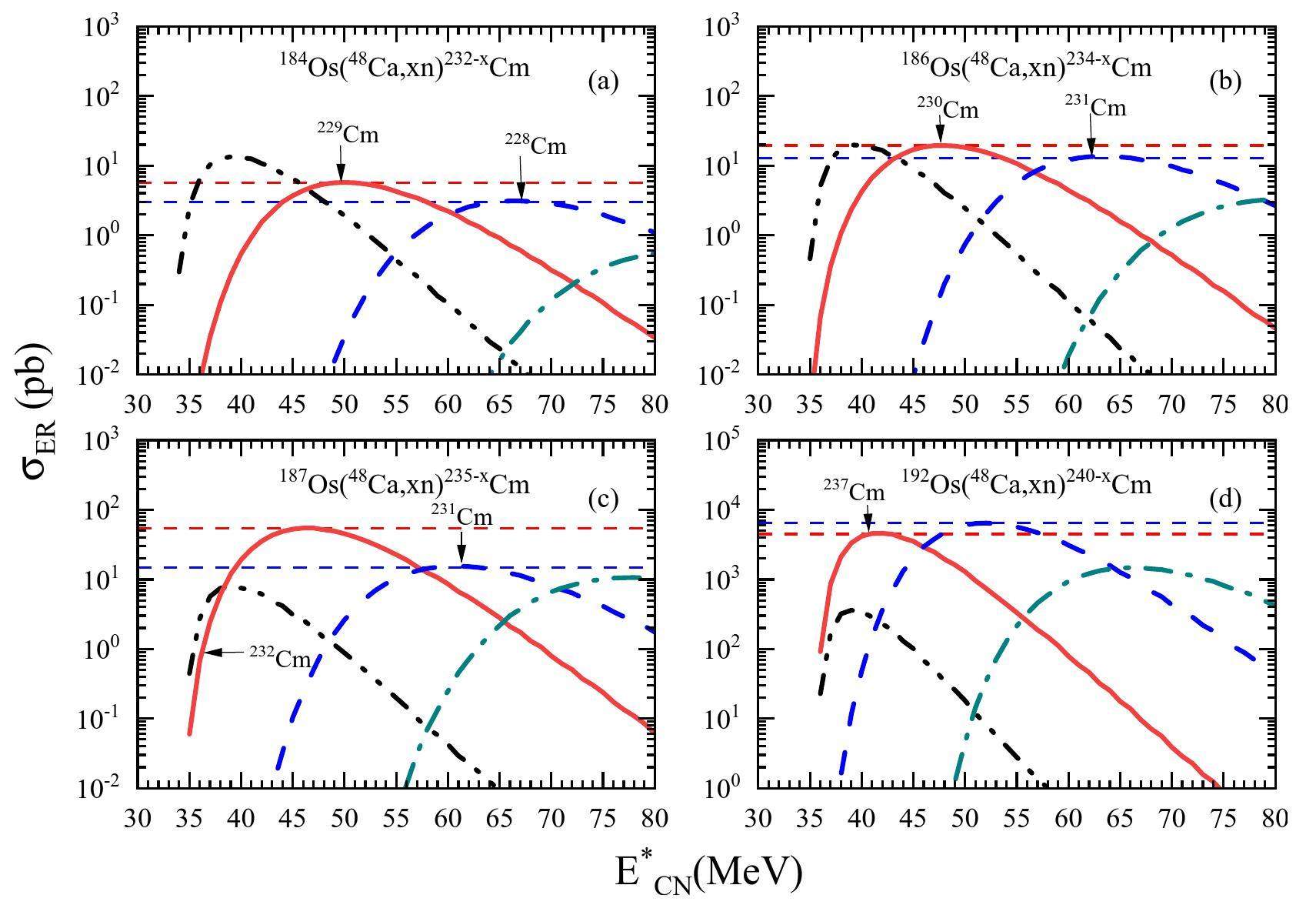
As shown in Fig. 7, the ⁴⁸Ca+¹⁸⁴Os reaction has the maximum cross sections of 5.73 and 1.96 pb for the 3n and 4n channels at the excitation energies of $E_{\text{CN}}^{*}$=50 and 60 MeV, respectively, resulting in the production of ^228,229Cm. At the excitation energies of $E_{\text{CN}}^{*}$=48 and 60 MeV, the ⁴⁸Ca+¹⁸⁶Os reaction has the maximum cross sections of 19.39 and 12.16 pb for 3n and 4n channels, respectively, which results in the production of ^231,230Cm. Additionally, the ⁴⁸Ca+¹⁸⁷Os reaction has the maximum cross sections of 54.79 and 15.44 pb for the 3n and 4n channels at the excitation energies of $E_{\text{CN}}^{*}$ = 46 and 60 MeV, respectively, which leads to the production of ^232,231Cm. Moreover, the ⁴⁸Ca+¹⁹²Os reaction shows a maximum cross section of 6.45 nb for the 4n channel at the excitation energy of $E_{\text{CN}}^{*}$ = 52 MeV, leading to the formation of ²³⁷Cm. For convenience, we summarize the data for the predicted new nuclei comprising the reaction systems, evaporation channels, target nuclei, maximum cross sections, and excitation energies in Table 1.

Fig. 7Full-screen View

(Color online) The evaporation residue cross sections of ⁴⁸Ca+^{184,186,187,192}Os at the 2n, 3n, 4n, and 5n channels are denoted by black double-dot dashed lines, red solid lines, blue dashed lines, and dark cyan dot-dashed lines, respectively

Typically, when actinide elements are produced in complete fusion reactions, the evaporation cross section increases with the mass number of the compound nucleus. This is evident when the 3n-4n evaporation channels in the reaction systems are compared, as shown in Fig. 6 and 7. Although P_CN decreases with increasing neutron number, the increase in W_sur overcompensates for the decrease in these reactions.