Introduction

Beam diagnostics are critical for understanding the characteristics of electron beams in accelerator facilities [1, 2]. Considering the development of free-electron lasers (FELs) and ultrafast electron diffraction (UED) facilities for example, the demand for highly precise beam diagnostics is continuously increasing[3-8], especially for the ultrafast exploration in pump-probe experiments. Moreover, noninvasive devices are favorable options that can provide real-time measurements and feedback, even bunch-by-bunch. Beam monitoring based on the TM₀₁₀ mode is a nondestructive method that has been utilized in many facilities owing to its many advantages, such as compactness, simple structure, and high sensitivity [9-11]. Because the TM₀₁₀ mode excited by the passing beam is related to many beam parameters, including the bunch charge, arrival time, bunch energy, and length[12, 13], this method has significant potential for measuring the four aforementioned parameters with a high resolution.

Regarding a cylindrical cavity, the amplitude of the TM₀₁₀ mode is proportional to the bunch charge. A resonant cavity can be employed for the bunch charge and arrival time measurements by precisely detecting the monopole mode, which is known as the cavity beam arrival time monitor (BAM) or the reference cavity of the cavity beam position monitor (CBPM)[14, 15]. This approach can achieve a high resolution and has been applied in many facilities [16-18]. The best resolution of the cavity BAM was reported ([16]) to be 13 fs at 250 pC, which was obtained at the Linac Coherent Light Source (LCLS) using a 2806 MHz cavity.

The bunch length is a key parameter of the beam longitudinal features. Many methods have been proposed to obtain the beam length [19-23]; however, only a few are nondestructive. Considering the development of FELs and UEDs, a noninvasive bunch-length monitor for short bunches is currently required, such as for those shorter than 1 ps. The TM₀₁₀ mode can be used for measuring the bunch length owing to the influence of the bunch length on the amplitude of the TM₀₁₀ mode [13, 24]. Compared to other techniques, this method has the potential for a high-resolution for measuring short bunches. It usually requires two TM₀₁₀ modes with different frequencies to measure the amplitudes of the beam longitudinal spectrum at two frequencies. For this technique, the beam energy, transverse offset, and longitudinal distribution all have an impact on the amplitude of the TM₀₁₀ mode, which may cause significant inaccuracies [25]. The errors caused by these factors will be carefully analyzed in this article.

The beam loss factor is also related to the beam energy [26, 27], indicating that the monopole mode may be used to measure the beam energy. Compared to techniques such as those using dipole magnets [28], measuring the bunch energy based on the TM₀₁₀ mode is compact and noninvasive. This technique demands two cavities with the same frequencies of the TM₀₁₀ modes to normalize the bunch length and charge; longer cavities can achieve a higher resolution. However, considering a limitation of this method, it can only be used for energy measurements of low-energy electron beams; therefore, it is particularly suitable for UEDs [5] and ultrafast electron microscopes (UEMs) [29].

Because the TM₀₁₀ mode is related to multiple parameters, the coupling effect must be limited when measuring a certain parameter. For the bunch length or energy measurements, the two cavities should be specifically designed to normalize the other parameters. A set of three cavities with different structures and frequencies of 1.902 GHz and 11.424 GHz is proposed for the diagnostics of the four beam parameters in this study. This design is expected to provide noninvasive measurements and save considerable space in accelerators compared to other beam diagnostic devices.

The relationship between each beam parameter and the TM₀₁₀ mode is theoretically analyzed in Sect. 2. Section 3 presents the simulation results of the different parameters and evaluation experiments. A design of three cavities for the diagnostics of the four beam parameters is presented in Sect. 4.

Theoretical basis of the TM₀₁₀ mode

When a relativistic electron beam moves along a cavity, the electromagnetic field of a series of eigenmodes is excited. Applying this theory, the voltage of a particular resonant mode excited in the cavity (V_exc) is represented as follows: $V_{\text{exc}}=k_{\text{loss}}q=\frac{\omega }{2}\left(\frac{R}{Q}\right)q,$ (1) where k_loss is the loss factor, ω is the resonant angular frequency of the mode, q is the bunch charge, and $\frac{R}{Q}$ is the normalized shunt impedance, which is a key factor for evaluating the beam loading effect. The monopole mode has the highest sensitivity of the resonant modes. Regarding the monopole mode of a pillbox cavity, $\frac{R}{Q}$ is calculated as follows: ${\left(\frac{R}{Q}\right)}_{010}=\frac{2J_0^2\left(\frac{j_{01}x}{d}\right)L{T}^2}{\omega {ϵ}_0\pi J_1^2\left(j_{01}\right)d^2}.$ (2) Here, x is the beam offset, d is the cavity radius, L is the length of the pillbox cavity, T is the transit time factor, Jn is the nth-order Bessel function, and j₀₁ is the 1st root. Notably, the $\frac{R}{Q}$ of the monopole mode of the pillbox is insensitive to the beam offset near the cavity center.

In principle, the loss factors of bunches passing through a cavity at a nonrelativistic velocity are lower than those at an ultrarelativistic velocity. The energy loss in the cavity should vanish when the velocity approaches 0. The influence of the bunch length must also be considered if the bunch length is not negligible with respect to the frequency of the TM₀₁₀ mode. Assuming a Gaussian bunch with an rms length ${\sigma }_{\text{s}}$ and velocity v=β c passing through a cylindrical pillbox, the line density is $\lambda (s)=\text{e}xp\left(-s^2/2{\sigma }_{\text{s}}^2\right)/\left(\sqrt{2\pi }{\sigma }_{\text{s}}\right)$. By integrating over all the particles in the bunch, the dependence of the beam loss factor on β and ${\sigma }_s$ can be expressed as follow:[26, 27]. $\frac{k_{010}\left(\beta \mathrm{,}{\sigma }_{\text{s}}\right)}{k_{010}\left(\mathrm{1,}{\sigma }_{\text{s}}\right)}=\exp \left(-\frac{{\omega }^2{\sigma }_{\text{s}}^2}{{\gamma }^2{\beta }^2{c}^2}\right){\left(\beta \frac{\sin \frac{j_{01}L}{2\beta d}}{\sin \frac{j_{01}L}{2d}}\right)}^2,$ (3) where c is the speed of light, and β and γ are the relativistic factors. Describing the beam length using the longitudinal time scale ${\sigma }_{\text{t}}={\sigma }_{\text{s}}/v$, the output voltage extracted from a coupling structure with an impedance Z can be expressed as follows: $V_{\text{out}}=\frac{\omega q}{2}\sqrt{\frac{Z}{Q_{\text{e}xt}}\left(\frac{R}{Q}\right)}\exp \left(-\frac{{\omega }^2{\sigma }_{\text{t}}^2}{2}\right)\left(\beta \frac{\sin \frac{j_{01}L}{2\beta d}}{\sin \frac{j_{01}L}{2d}}\right)$ (4) where $Q_{\text{ext}}$ is the external quality factor, which mainly depends on the coupling part. The $\frac{R}{Q}$ in Eq.(4) is solely determined by the cavity shape and is unrelated to $\beta$. As shown in Eq.(4), the output voltage is proportional to the bunch charge q, and related to the bunch length ${\sigma }_{\text{t}}$ and velocity β c. As the bunch length increases or the velocity decreases, the voltage decreases. The TM₀₁₀ mode can be used for the measurement of these parameters, but the coupling effect between the parameters should be taken seriously.

Regarding the measurement of the bunch charge, cavities with a low resonant frequency and short cavity length are preferred to reduce the influence of the bunch length and energy jitter, especially under conditions of a long bunch length or low energy.

V_out in Eq.(4) is proportional to $\exp \left(-\frac{{\omega }^2{\sigma }_{\text{t}}^2}{2}\right)$, indicating that two cavities with different frequencies can be used for measuring the bunch length, which can be determined by dividing the two ${\text{TM}}_{010}$ mode signals, simultaneously normalizing the bunch charge. Since V_out is also related to $\beta$, it may impact the bunch-length measurement. Regarding the ultrarelativistic case, V_out is independent of β. On the contrary, the energy jitter of the low energy beam will cause large errors in the accuracy of the beam length. The V_out can be rewritten as follows: $V_{\text{out}}=q\kappa \text{}\exp \left(-\frac{{\omega }^2{\sigma }_{\text{t}}^2}{2}\right)\sqrt{\frac{R}{Q}\left(\beta \right)},$ (5) where $\kappa =\frac{\omega }{2}\sqrt{\frac{Z}{Q_{\text{ext}}}}$, which is only determined by the cavity structure. Based on Eq.(5), by using two cavities with the same $\frac{R}{Q}\left(\beta \right)$, the effect of the bunch energy can be eliminated. The $\frac{R}{Q}$ depends only on the cavity shape and has no dependence on the material or surface condition of the cavity. Therefore, for the bunch length measurement, when the dimensions of the two cavities are proportional, the $\frac{R}{Q}$ values are the same but the frequencies differ. Additionally, the beam offset and longitudinal distribution can also cause errors, which will be simulated and analyzed in Sect. 3.

For measuring the bunch energy, the charge must be normalized; furthermore, the exponential term in Eq. (4), $\exp \left(-\frac{{\omega }^2{\sigma }_{\text{t}}^2}{2}\right)$, is also not negligible for long bunches. Therefore, two cavities with the same frequency but different L/d are required to eliminate the influence of the bunch length and charge when detecting the bunch energy. In this case, the dependence of the voltage amplitude on β is as follows: $V_{\text{out}}\propto \beta \frac{\sin \frac{j_{01}L}{2\beta d}}{\sin \frac{j_{01}L}{2d}}.$ (6)

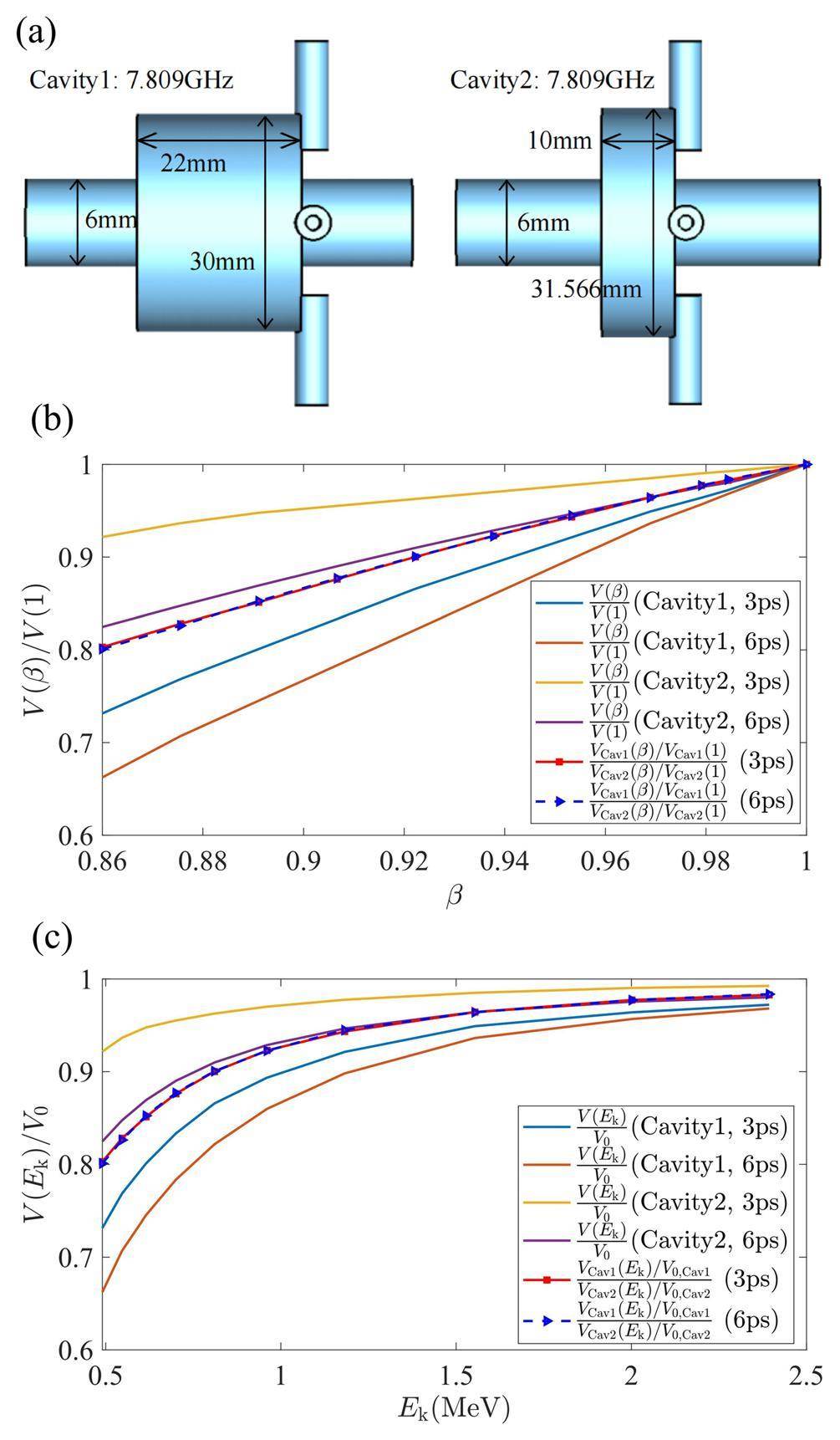
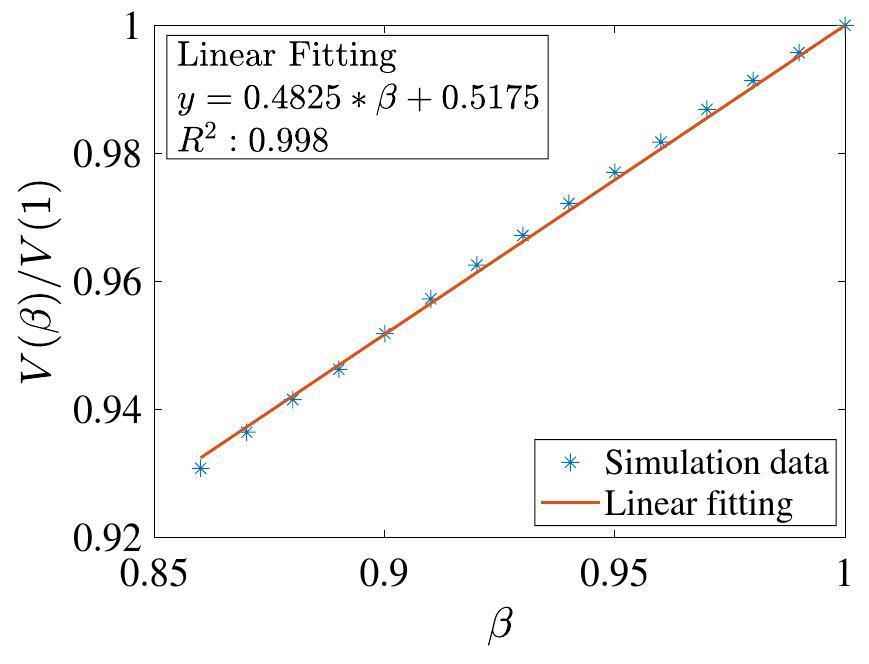
The variation in the amplitude of the TM₀₁₀ mode with β and the ratio of the cavity length L and radius d is shown in Fig. 1(a). Note, a nearly linear relationship between β and the voltage amplitude can be observed Fig. 1 when β>0.86 and L/d<2.

Fig. 1Full-screen View

(Color online) (a) Voltage amplitude deviations relative to the beam velocity $\beta c$ and L/d value of the pillbox. (b) Voltage amplitude dependence on the beam energy $E_{\text{k}}$ with different L/d values. The V₀ value on the Y-axis represents the voltage amplitude when the beam speed approaches c

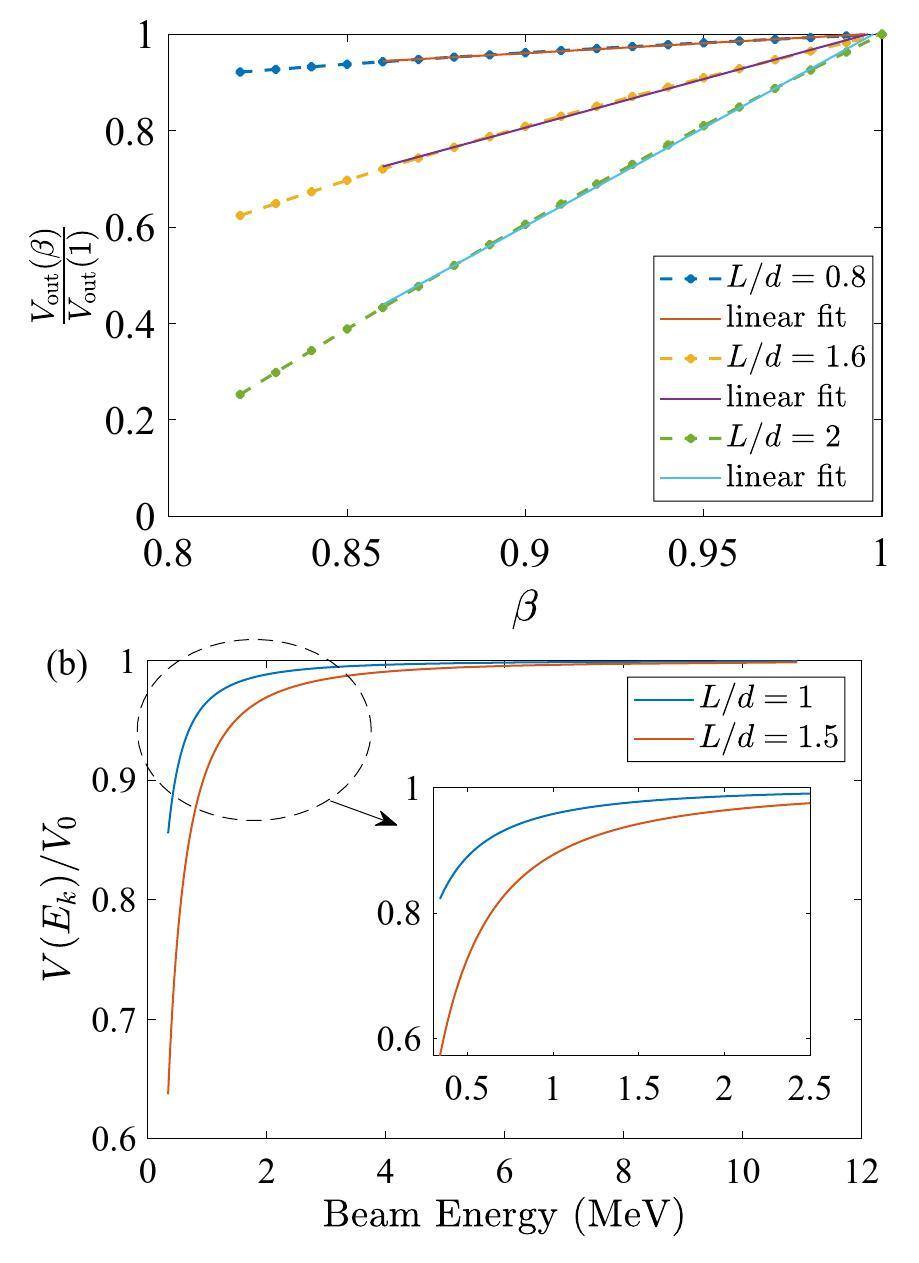
Compared to β, the beam energy E_k is a more commonly used parameter. The relationship between the beam energy and β is expressed by the following formula: $E_{\text{k}}=\left(\frac{1}{\sqrt{1-{\beta }^2}}-1\right)m_0{c}^2.$ (7) According to Eqs. (6) and (7), the relationship between the amplitude of the TM₀₁₀ mode and the beam energy $E_{\text{k}}$ is shown in Fig. 1(b). When the energy of the particle is above 5 MeV, the amplitude variations as the energy decreases can be ignored. The amplitude of the TM₀₁₀ mode begins to decrease when the energy is below 5 MeV and further rapidly decreases with a lower energy. Therefore, the TM₀₁₀ mode can be an effective tool to measure the low beam energy E_k, but it is not suitable for high-energy situations.

Simulation and test results of different parameters

3.1

Simulation and analysis of the cavity beam length monitor

3.1.1

Influence of the beam energy and the resolution analysis

Based on the discussion in Sect. 2, two cavities with proportional dimensions have the same $\frac{R}{Q}\left(\beta \right)$ values and the division of the two TM₀₁₀ mode signals can be employed to measure the bunch length, effectively mitigating the influence of the bunch charge and energy jitter. To verify the aforementioned analysis, two cavities were established in the CST software. The dimensions of the two models are shown in Fig. 2(a). The two cavities have the same shape, with a size ratio of 1:2. The frequencies of the two cavities were 7.912 GHz and 3.956 GHz; the simulated results of $\frac{R}{Q}$ with different $\beta$ values are shown in Fig. 2(b). The $\frac{R}{Q}(\beta )$ values of the two cavities are entirely identical.

Fig. 2Full-screen View

(Color online) (a) Two models built in CST; the dimensional ratio of the two cavities is 1:2 (b) $\frac{R}{Q}$ deviations of the two cavities with different $\beta$ values

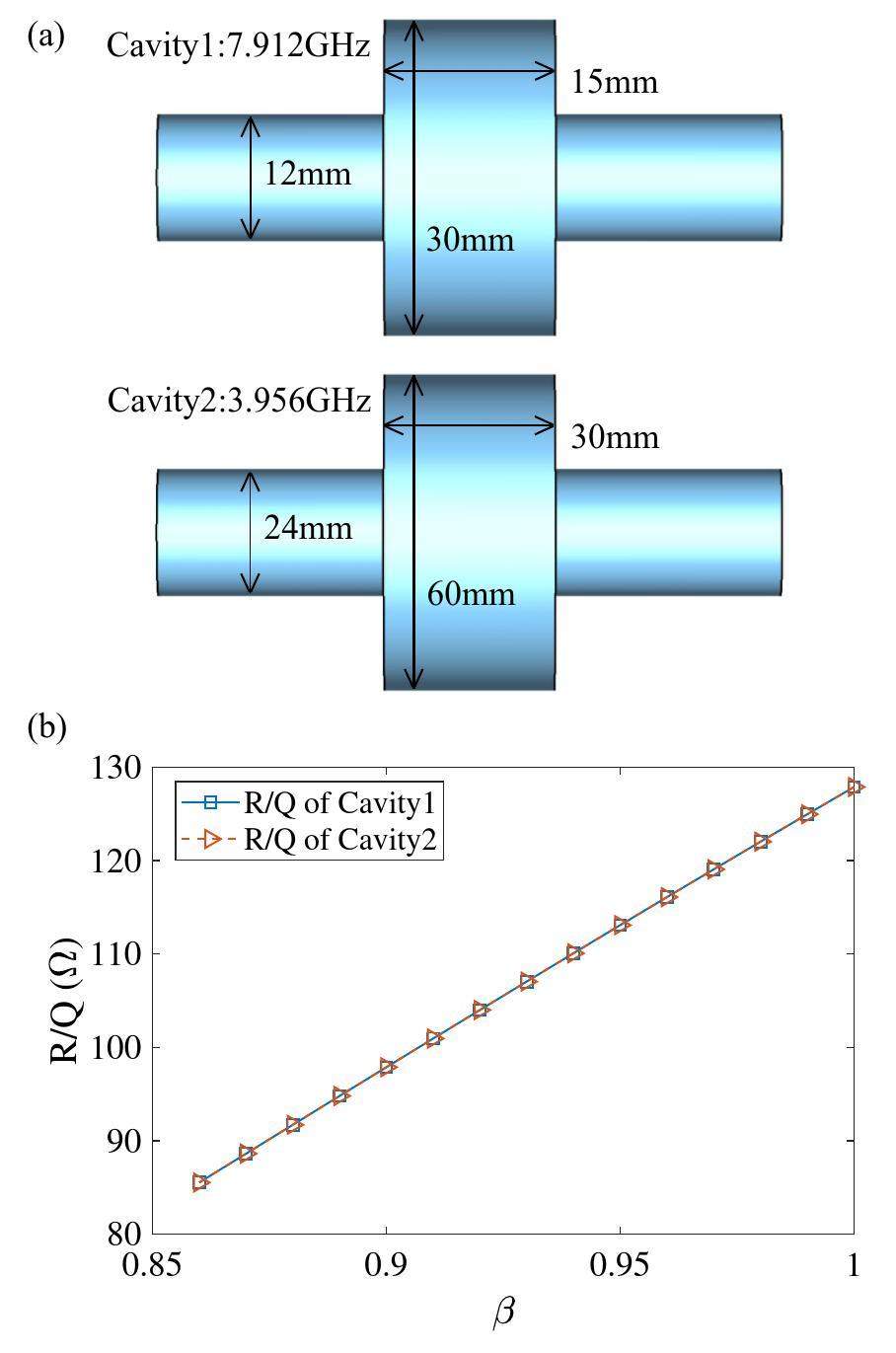
By cancelling the $\frac{R}{Q}(\beta )$ in Eq. (5), the bunch length measured by two TM₀₁₀ modes at different frequencies can be expressed as follows: ${\sigma }_{\text{t}}=\sqrt{\frac{2}{{\omega }_2^2-{\omega }_1^2}\ln \left(\frac{{\kappa }_2{V}_1}{{\kappa }_1{V}_2}\right)}.$ (8) The resolution $\text{Δ}{\sigma }_{\text{t}}$ of the detecting system can be derived from Eq. (8) as: $\text{Δ}{\sigma }_{\text{t}}=\frac{{10}^{-\text{SNR}/20}}{{\sigma }_{\text{t}}\left({\omega }_1^2-{\omega }_2^2\right)},$ (9) where SNR is the signal-to-noise ratio of the TM010 mode voltage measurement system. As shown in Eq. (9), the resolution of this method depends on the difference between the two frequencies and is inversely proportional to the beam length. However, when the bunch length was excessively long, the voltage amplitude rapidly decreased, resulting in a poor signal-to-noise ratio of the system, thus worsening the resolution. When the two frequencies were 5 and 10 GHz, a 106-fs resolution was achieved for a 1-ps bunch measurement with the SNR assumed to be 70 dB.

3.1.2

Influence of the transverse offset

The output voltage is proportional to the $\sqrt{\frac{R}{Q}}$ of the resonant mode. For a cylindrical cavity without the tube and coupling structure, Eq. (2) provides its $\frac{R}{Q}$ value of the TM₀₁₀ mode. Based on Eqs. (2) and (4), the voltage in a cylindrical cavity is proportional to $J_0\left(k_{\text{c}}^{01}x\right)$ and is maximized on the cavity axis. To study the influence of the beam transverse offset x, a closed pillbox with a radius of 20 mm was established in the CST software [30], and the simulation was evaluated using the eigenmode and wakefield solver. The theory and simulation results are demonstrated in Fig. 3, which are in good agreement.

Fig. 3Full-screen View

Normalized $\sqrt{R/Q}$ of the TM₀₁₀ mode in the pillbox cavity along the cavity diameter

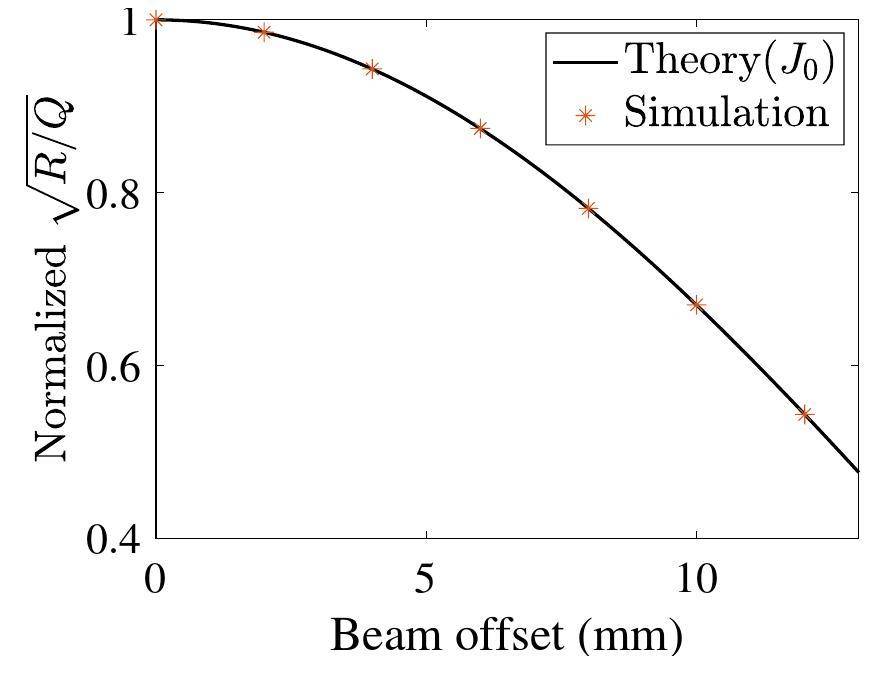
For cavities with tubes, the electric field intensity of the TM₀₁₀ mode along the cavity diameter is inconsistent with the J₀ function, especially for the pipe area. According to [31, 32], the $\frac{R}{Q}$ of a pillbox with a tube can be expressed as follows: $\frac{R}{Q}=\frac{{\left(V_{0}T\left(x\right)\right)}^2}{\omega U}=\frac{{\left(V_{0}T\left(0\right)I_0\left(Kx\right)\right)}^2}{\omega U}.$ (10) where $K=\frac{2\pi }{\gamma \beta \lambda }$, I₀ is the modified Bessel function, and T is the transit time factor. The effect of the transverse offset is included in the transit time factor, and the changes caused by the offset are negligible according to the properties of the $I_0\left(Kx\right)$ function. A model of the pillbox with a tube was also simulated with the eigenmode solver in CST, as shown in Fig. 4(a). The $\frac{R}{Q}$ values for different offsets on the z-axis were calculated considering the transit time factor, and the normalized results are presented in Fig. 4(b). The amplitude of the TM₀₁₀ mode of the pillbox with a tube can be considered invariant with respect to the beam offset compared with that of the closed cavity.

Fig. 4Full-screen View

(Color online) Pillbox with a tube in CST and normalized $\sqrt{R/Q}$ of the TM₀₁₀ mode of the pillbox with a tube

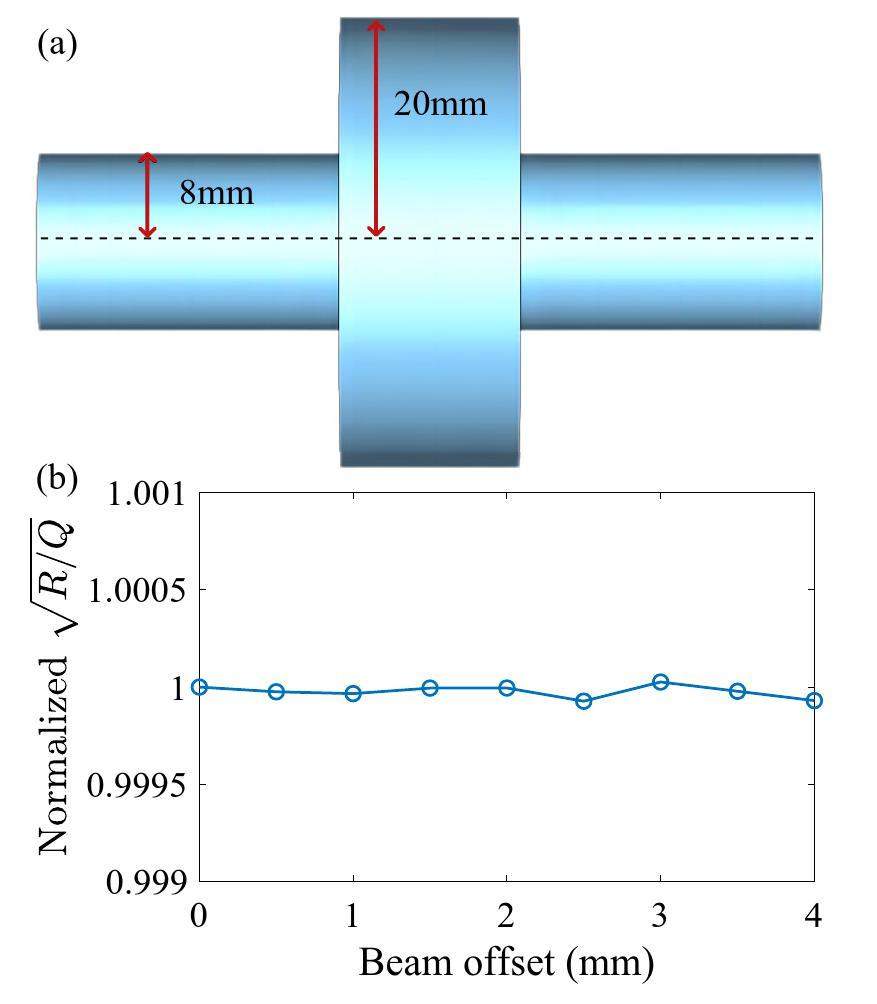
Coupling structures and cavity types, such as the reentrant type, can lead to noncylindrically symmetric structures of the cavity. In these cases, the beam offset effect no longer conforms to the aforementioned theoretical analysis. To study the influence, a simulation of the reentrant cavity monitor with different coupling ports was performed in the CST software. Figure 5 demonstrates the four cavities established for the simulation and the amplitude variation of the TM₀₁₀ modes. For the cavity with a single port, the beam offset had a significant impact on the output signal from the port; the change was approximately 1% with a 3 mm offset. For the four-port cavity, the amplitude variation owing to the transverse offset was less than 1.

Fig. 5Full-screen View

(Color online) Models of the reentrant cavities with different ports and the normalized $\sqrt{R/Q}$ variation of the TM₀₁₀ modes of the aforementioned models

3.1.3

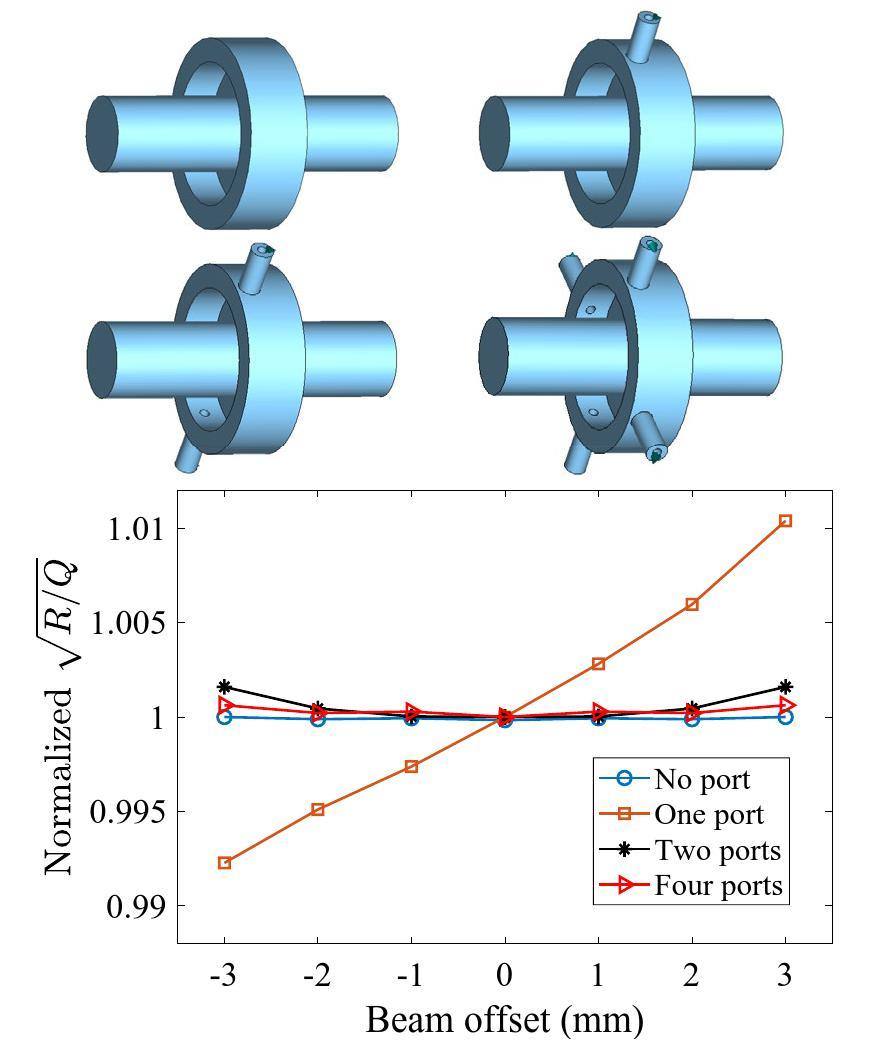
Influence of the beam longitudinal distribution

The measurement of the bunch length based on the TM₀₁₀ mode was achieved by evaluating the amplitudes of two frequencies of the longitudinal spectrum of the beam and should be independent of the distribution. Because the shape of the bunch is not Gaussian in an actual scenario, the influence of different distributions should be considered. For a bunch with a longitudinally symmetric distribution, the beam spectrum $F(\omega )$ expanded in the Taylor’s series can be written in the following form [13]: $\begin{array}{c}F\left(\omega \right)={\displaystyle {\int }_{-\infty }^{+\infty }}f\left(t\right)\cos \left(\omega t\right)\text{d}t\\ \approx {\displaystyle {\int }_{-t_0}^{+t_0}}f\left(t\right)\left(1-\frac{{\omega }^2{t}^2}{2}+\frac{{\omega }^4{t}^4}{24}+O\left({\omega }^6{t}^6\right)\right)\text{d}t\\ \le q\left(1-\frac{1}{2}{\omega }^2{\sigma }_{\text{t}}^2+\frac{\rho +3}{24}{\omega }^4{\sigma }_{\text{t}}^4\right),\end{array}$ (11) where f(t) is the beam longitudinal density function. ρ is the kurtosis, describing the tailedness of a distribution relative to a Gaussian distribution, and is 0 if f(t) is Gaussian. For ρ>0, the beam distribution is thin-tailed, and referred to as leptokurtic. For ρ<0, the distribution tends to be platykurtic, which is more realistic for electron beams. The probability densities of certain distributions with different kurtosis values are shown in Fig. 6. The difference between the spectra of the Gaussian and symmetric distributions with different kurtosis values can be described as follows: $\left|\frac{F\left(\omega \right)-F_{\text{G}}\left(\omega \right)}{F_{\text{G}}\left(\omega \right)}\right|=\frac{\left|\frac{\rho }{24}{\omega }^4{\sigma }_t^4\right|}{1-\frac{1}{2}{\omega }^2{\sigma }_{\text{t}}^2+\frac{3}{24}{\omega }^4{\sigma }_{\text{t}}^4}.$ (12)

Fig. 6Full-screen View

(Color online) Various symmetric distributions with different kurtosis values

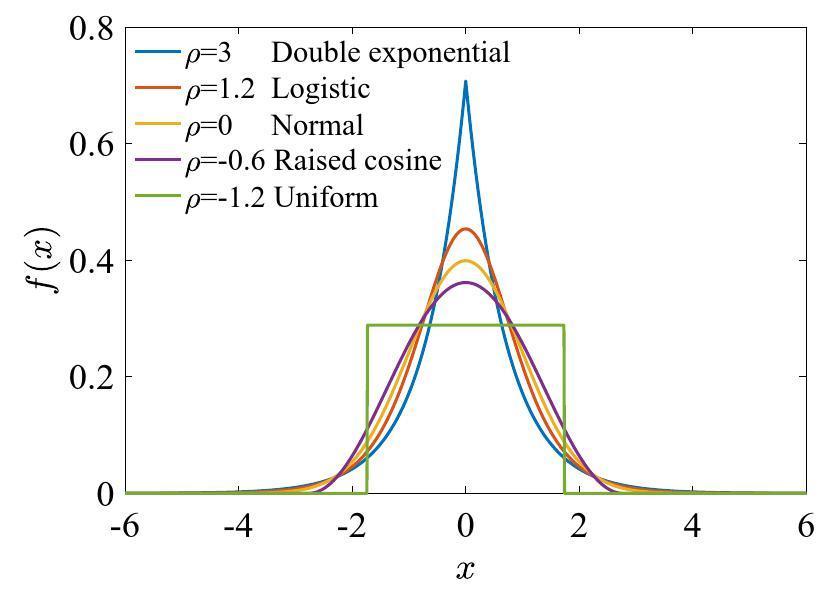
If the distribution of a longitudinally symmetric bunch is considered, in which the kurtosis significantly differs from that of the Gaussian distribution, such as the double exponential distribution (ρ=3), and if the error is limited to be within 1, the criterion of the beam length and frequency can be obtained as follows: $0<\omega {\sigma }_{\text{t}}<\mathrm{0.296.}$ (13) This is a rather strict criterion since the real shape of the bunch is usually between the Gaussian and rectangular distributions, 0<|ρ|>1.2.

In conclusion, the resolution in Eq.(9) is better with a higher frequency for short bunches, but the frequency is limited to ensure that the influence of different bunch shapes is negligible.

3.2

Simulation and analysis for low-energy measurement

3.2.1

Influence of the resonant frequency

As analyzed in Sect. 2, the TM₀₁₀ mode can be used for low-energy measurements. However, for a low energy, the bunch length and distribution may significantly vary owing to the space charge effects and low magnetic stiffness, which will affect the accuracy. The Eq. (4) can be rewritten as follows: $V_{\text{out}}\propto qF\left({\omega }_0\right)\left(\beta \frac{\sin \frac{j_{01}L}{2\beta d}}{\sin \frac{j_{01}L}{2d}}\right),$ (14) $F\left({\omega }_0\right)$ represents the component of the longitudinal beam spectrum at the cavity frequency ${\omega }_0$. Therefore, when using two cavities of the same frequency, both the beam charge and beam length can be normalized by dividing the TM₀₁₀ mode signals of the two cavities.

A simulation of two cavities was conducted in the CST software to validate the analysis. The two cavities were designed to have the same frequency but a different lengths, as shown in Fig. 7(a). Using the CST Wakefield solver, the voltage signals of the two cavities with different beam lengths and $\beta$ values were simulated. The amplitude dependence on $\beta$ are plotted in Fig. 7(b). The amplitude varies with $\beta$ at beam lengths of 3 and 6 ps, but the division of the signals of the two cavities is irrelevant to the beam length, and only depends on the energy. Generally, cavities with long lengths demonstrate a high dependence on $\beta$, and two cavities with the same frequency are required to obtain the beam energy. According to Eq. (7), the deviations in the amplitude of two cavities at different energies can be obtained, as illustrated in Fig. 7(c). the amplitude apparently decreases more rapidly at lower energies, aligning with the discussion in Sect. 2.

Fig. 7Full-screen View

(Color online) (a) Two models established in the CST with the same frequencies and different lengths. (b) Simulated amplitude deviations simulated with different $\beta$ values of the two cavities. (c) Simulated amplitude deviations at different beam energies obtained by the relationship between $E_{\text{k}}$ and $\beta$. The $V_0$ value on the Y-axis represents the voltage amplitude when the beam speed approaches $c$

3.2.2

Resolution analysis for low-energy measurement

The relationship between $\beta$ and the voltage can be approximated to be linear when β>0.86 and L/d<2, as indicated in Sect. 2. To normalize the beam charge and beam length, two cavities with the same frequency are required to measure the beam energy. The β parameter can be calculated from the two voltages of the TM₀₁₀ modes, which is expressed as follows: $\beta =a\times \frac{V_{\text{out}1}}{V_{\text{out}2}}+\left(1-a\right),$ (15) where a is the linear fitting coefficient that represents the sensitivity of the voltage signal to β, V_out is the normalized voltage, and β reaches 1 when the particle velocity is c. By obtaining the derivative of both sides of Eq. (15), the resolution of β can be obtained. ${\left(\frac{\text{Δ}\beta }{a}\right)}^2={\left(\frac{\text{Δ}{V}_{\text{out}1}}{V_{\text{out}1}}\right)}^2+{\left(\frac{\text{Δ}{V}_{\text{out}2}}{V_{\text{out}2}}\right)}^2$ (16) $\text{Δ}\beta =\sqrt{2}a\times \text{SNR}$ (17) By substituting the resolution of $\beta$ into the relationship between $E_{\text{k}}$ and $\beta$, as shown in Eq. (7), the expression for the resolution of $E_{\text{k}}$ can be derived as follows: $\text{Δ}E=\frac{\beta {\left(E_{\text{k}}+m_0{c}^2\right)}^3\text{Δ}\beta }{m_0^2{c}^4}.$ (18) Because Δ E is proportional to β and ${\left(E_{\text{k}}+m_0{c}^2\right)}^3$, the resolution rapidly deteriorates as the energy increases. Simulations based on our 4.76-GHz BAM pickup [33] were performed to apply the aforementioned analysis. The TM₀₁₀ mode dependence on β can be obtained by changing the velocity of the particles. Figure 8 presents the simulation results and the linear fitting equation. The ΔE values were calculated by using Eq. (18) and are summarized in Table 1, assuming that SNR is 70 dB, and the other low-frequency cavity is nearly independent of β and only used for charge normalization. The resolution can reach 3.17 keV at 0.5 MeV, but only 151.99 keV at 3 MeV.

Fig. 8Full-screen View

The TM₀₁₀ mode amplitude dependence on β of the 4.76 GHz pickup

Table 1Full-screen View

Simulation results of the beam energy resolution with the 4.76GHz pickup

$E_{\text{k}}$(MeV)	Resolution (keV)	Precision ()
0.5	3.17	6.34
1	11.52	11.52
2	55.02	27.51
3	151.99	50.66

Show more

3.3

Evaluation test of the bunch length and energy

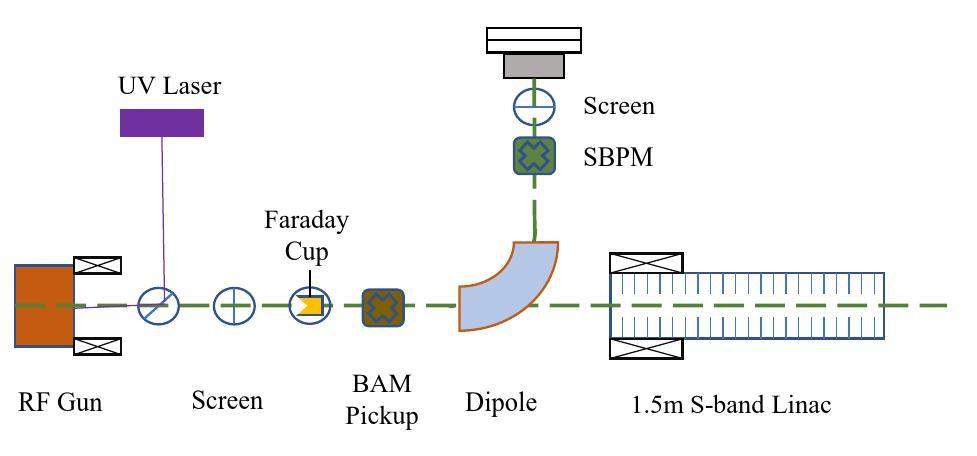
Evaluation experiments were performed based on a 4.76-GHz BAM pickup [33], which was installed after the RF gun in our test beamline of the Tsinghua Thomson scattering X-ray source facility [34], as seen in Fig. 9. The main beam parameters are summarized in Table 2.

Fig. 9Full-screen View

(Color online) Scheme of the test beamline

Table 2Full-screen View

Test beamline beam parameters

Parameters	Test beamline
Bunch charge (pC)	20-30
Laser pulse length (ps)	3
Electron energy (MeV)	0.5-3
Pulse repetition rate (Hz)	10

Show more

In the test, the beam energy ranged from 0.5 MeV to 3 MeV and the raw rf signals from the pickup were captured by a 20 GHz bandwidth oscilloscope. Because the variation in the bunch charge also affects the amplitude of the pickup, an adjacent Faraday cup was used to calibrate the charge information. The amplitude variation of the pickup with the energy is plotted in Fig. 10. The sensitivity is 130.54 mV/pC at an energy of 3 MeV, but when the energy is reduced to 0.5 MeV, the sensitivity is only 70.92 mV/pC, decreasing to 54%.

Fig. 10Full-screen View

(Color online) Measured data and simulated results of the 4.76 GHz pickup dependence on beam energy and length

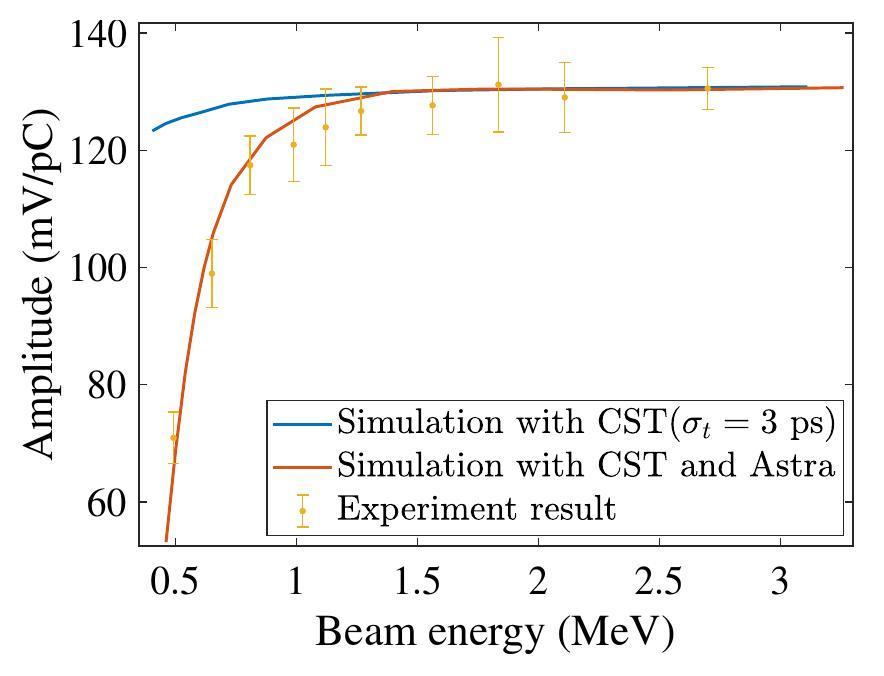
Figure 10 also presents the simulation results obtained in the CST with a beam length of 3 ps, which is the same as the laser pulse length. However, the simulated sensitivity is only reduced to 95% at 0.5 MeV, which is inconsistent with the experimental result. This occurred because the beam length increases at lower energies owing to the space charge force effects, which are not considered in the CST Wakefield solver. A simulation using Astra was performed with the space charge force activated, and the beam length at different energies was obtained. Subsequently, we imported the bunch energy and bunch-length parameters into CST to recalculate the amplitude of the pickup. As shown in Fig. 10, the experimental data and the simulation results obtained with the CST and Astra [35] are in good agreement.

A design of three cavities for the four-parameter measurement

Two cavities can be used for the bunch length or low-energy measurement. For the TM₀₁₀ mode in the cavity, a high frequency is sensitive to the beam length, and a long cavity length is sensitive to the beam energy, while the TM₀₁₀ mode with a low frequency and short length was used as the BAM monitor and for the charge normalization. A set of three cavities was designed to measure the beam charge, arrival time, beam length, and energy. Figure 11 presents the three cavities established in CST. The frequency of Cavity1 and Cavity2 was 1.904 GHz for both, but the cavity lengths were significantly different. The two cavities can be used to measure the beam energy with the beam length normalized. The frequency of Cavity3 increased to 11.424 GHz, and the sizes of Cavity3 and Cavity2 were proportional. Therefore, Cavity2 and Cavity3 can be used for measuring the beam length. Note, the three cavities were designed with four ports to reduce the influence of the beam offset.

Fig. 11Full-screen View

(Color online) Three cavities designed for measuring the four parameters

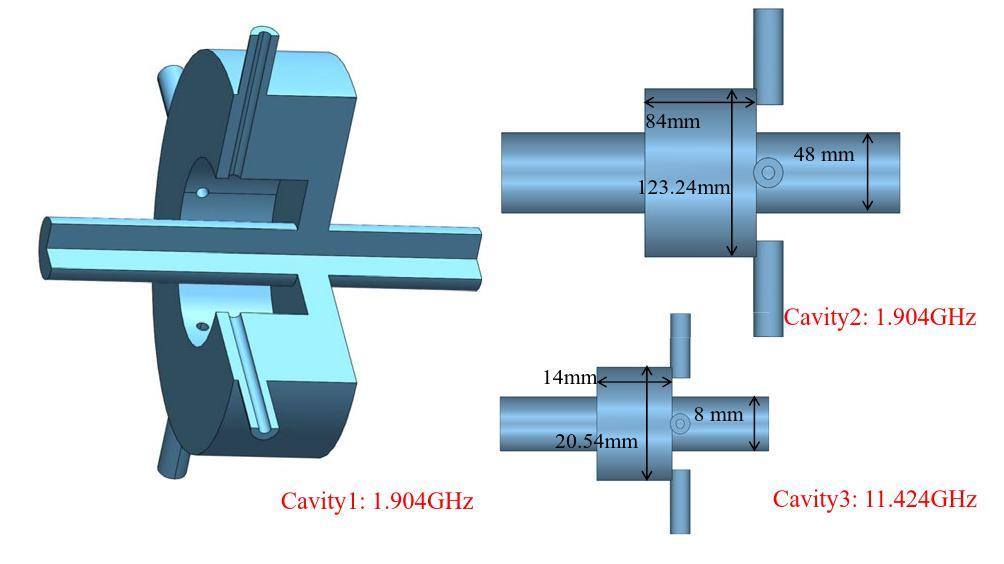
In the simulation, we found that increasing the length of the Cavity2 demonstrated a more apparent energy dependence, but the frequency of the TM₀₁₁ mode gradually approached that of the TM₀₁₀ mode. The long cavity length may also cause errors owing to the tilted incidence of the beam. The cavity length should be carefully chosen to avoid the effect of the TM₀₁₁ mode and the beam tilted incident. The final optimized dimensions and simulated rf parameters are summarized in Table 3.

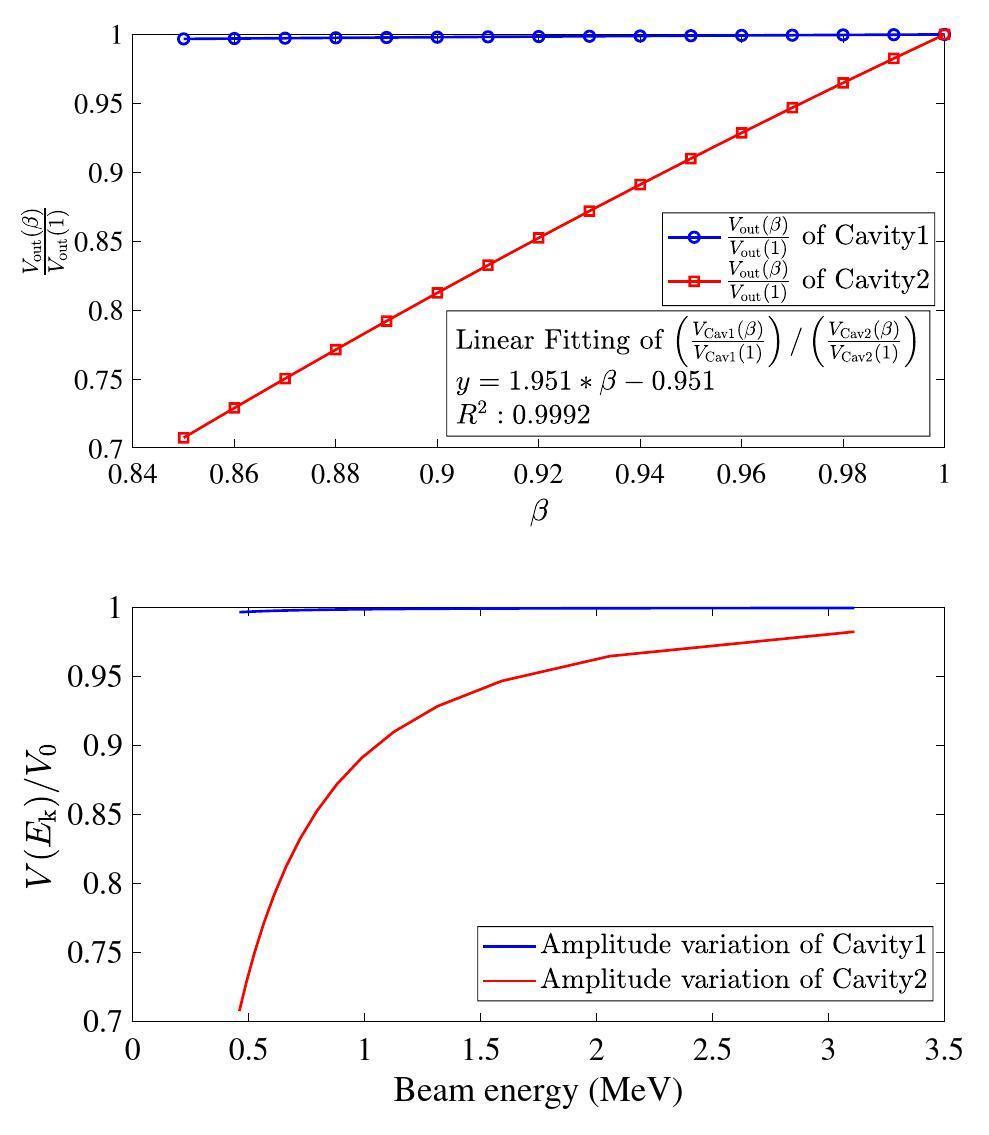
The amplitudes of the TM₀₁₀ modes in Cavity1 and Cavity2 were monitored while scanning the β values. As shown in Fig. 12, the voltage amplitude of Cavity1 was barely reduced compared to that of Cavity2. The ratio of the two normalized signals was proportional to β with a coefficient of 1.951. The energy measurement resolutions calculated by Eq. (18) are summarized in Table 4, with a 70 dB SNR. The theoretical resolution reached 0.70 keV at 0.5 MeV and decreased to 37.59 keV at 3 MeV.

Fig. 12Full-screen View

(Color online) (a) Simulated amplitude dependence on β of Cavity1 and Cavity2. (b) Simulated amplitude deviations at different beam energies of Cavity1 and Cavity2. The $V_0$ value on the Y-axis represents the voltage amplitude when the beam speed approaches c

The $\frac{R}{Q}$ values of the TM₀₁₀ modes in Cavity2 and Cavity3 were also simulated with different β values. As shown in Fig. 13(a), the $\frac{R}{Q}\left(\beta \right)$ value of the two cavities are consistent. For the bunch-length measurement, a parameter scan of the bunch length was applied in the simulation. The simulated amplitude deviations of Cavity2 and Cavity3 are shown in Fig. 13(b), which are consistent with the theoretical analysis. The maximum bunch length was 4.2 ps with a limit of Eq. (13). A simulation of the effect of the beam offset was also conducted for the two cavities, both containing four coupling ports. The results indicate that the TM₀₁₀ mode varies by less than 1, implying insensitivity to the beam offset. According to Eq. (9), the resolution can reach 63.13 fs at a bunch length of 1 ps bunch with an SNR of 70 dB.

Fig. 13Full-screen View

(a) $\frac{R}{Q}\left(\beta \right)$ of Cavity2 and Cavity3. (b) Simulated amplitude variations of the dual-cavity with the Gaussian distribution bunches

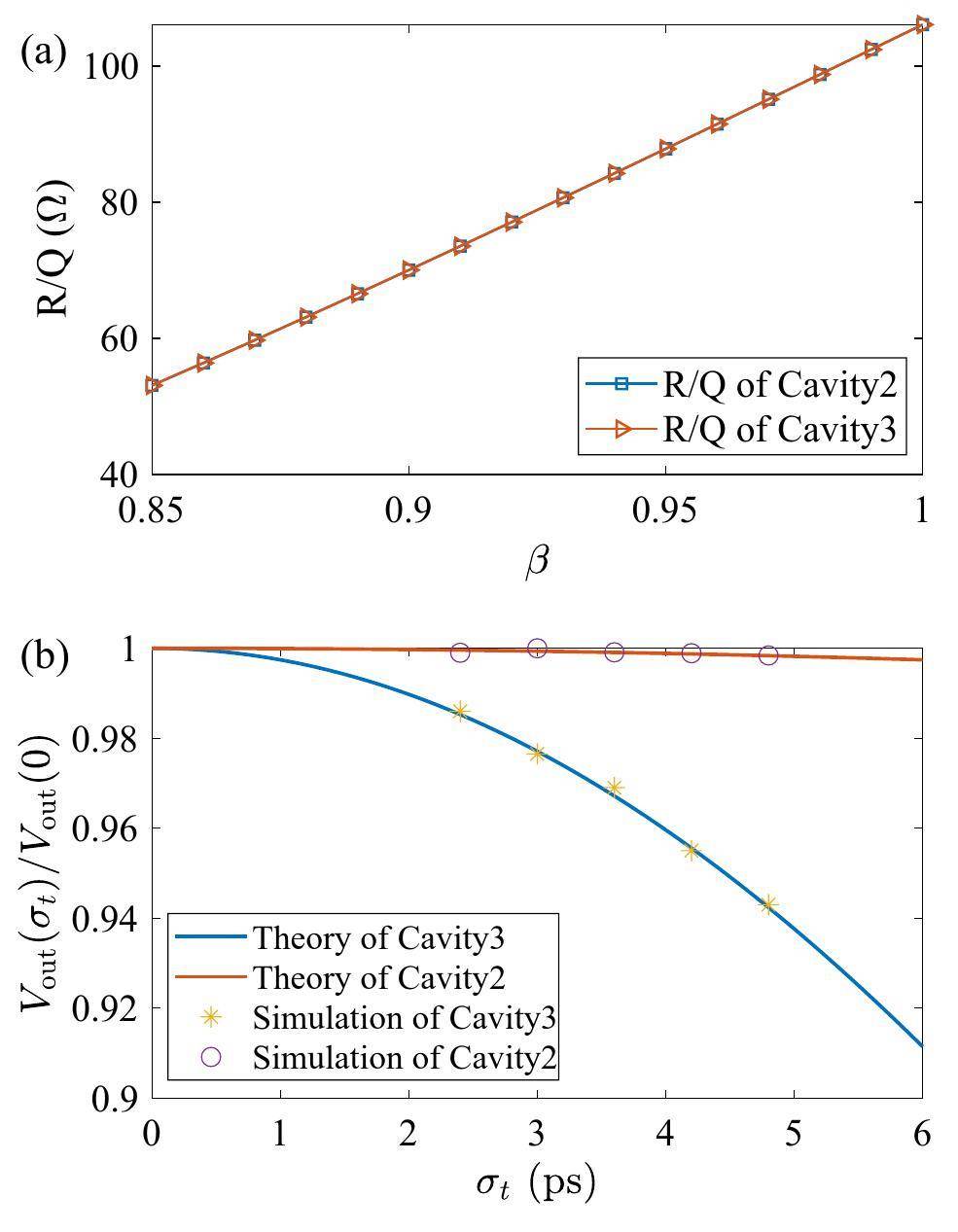
As shown in Fig. 12, the amplitude variation of Cavity1 was significantly small with β>0.86. The frequency of Cavity1 was 1.904 GHz, which is the same as that of Cavity2, which indicates that the amplitude of Cavity1 did not decrease when the bunch length was less than 6 ps. Therefore, Cavity1 can be used for monitoring the bunch charge and arrival time, as previously analyzed.

Summary

In this study, we analyzed beam diagnostics based on the TM₀₁₀ mode; the impacts of multiple beam parameters on the TM₀₁₀ mode were studied. The bunch length and energy measurements both require two TM₀₁₀ modes. Regarding the measurement of the bunch length, the errors caused by the beam energy, beam offset, and longitudinal distribution were thoroughly considered. For low-energy measurements, the amplitude of the TM₀₁₀ mode was nearly linear with β when β>0.86, and the bunch length was normalized with the same frequency of the two cavities. This method was used for low-energy measurements, achieving a high accuracy with a long cavity length. An evaluation test of the bunch length and energy was performed with a 4.76 GHz BAM pikcup. Finally, a set of three cavities with frequencies of 1.904 GHz and 11.424 GHz was proposed for measuring the four parameters, which reached a 63.13-fs resolution at 1 ps and a 1.56 precision at 0.5 MeV with a 70 dB SNR.