Introduction
China is planning to build a deep geological repository for high-level radioactive waste in the Beishan area of Gansu Province [1]. Gaomiaozi (GMZ) bentonite from Inner Mongolia was selected as an engineering barrier for the repository because of its high adsorption capacity, low permeability, good thermal conductivity, and abundant reserves [2-4]. It is a porous clay mineral with a layered structure consisting of tetrahedral-octahedral-tetrahedral sheets. Diffusion is the primary transport process of radionuclides through the bentonite barrier [5]. Anionic radionuclides with long half-lives, such as 129I-, 36Cl-,
Among diffusion parameters, the effective diffusion coefficient is a critical parameter in safety assessment. It is affected by many influencing factors, including porosity, the species diffusion coefficient in water, radionuclide concentration gradient, and tortuosity [8]. Numerous experiments have been conducted to identify certain influencing factors, including the compacted dry density, ionic strength, different types of bentonites, and temperature [9-12]. The relationship between these factors and radionuclide diffusion has been established. For example, the effective diffusion coefficient increases with a decreasing compacted dry density [13-18] and increasing ionic strength [10, 19-24]. Bentonites with a high montmorillonite content exhibit better radionuclide retardation owing to their low effective diffusion coefficient [7, 13, 20, 25]. Furthermore, the relationship between the effective diffusion coefficient and temperature has been described using the Arrhenius equation [20, 26]. Several numerical models, including the multi-porosity model [27, 28], integrated sorption and diffusion models [19], and pore-scale models [9, 29], have been used to predict the effective diffusion coefficient and analyze the impact of these influencing factors. These models have generated theoretical results that align with experimental results. However, few studies have reported quantitative metrics, such as the coefficient of determination (R2) or mean square error (MSE), to assess the models’ predictive accuracy.
Machine-learning methods can perform regression analysis and interpret non-linear relationships and multi-factor situations, making them valuable tools in engineering applications [30, 31]. Numerous studies have used machine-learning methods, such as artificial neural networks (ANNs) and gradient-boosting models, to estimate the chloride diffusion coefficient in cement [32]. The predictive accuracy can be increased by incorporating physical information into the model [33]. These studies implemented techniques such as Individual Conditional Expectation (ICE), Shapley Additive Explanations (SHAP), and Partial Dependence Plots (PDPs) to analyze the weight of the influencing factors on chloride diffusion [34]. Regression analysis has been used to predict the chloride diffusion coefficient, with input features ranging from 4 to 23 and experimental instances ranging from 72 to 843 [32, 34-37]. Recently, Light Gradient-Boosting (LightGBM) and ANN algorithms were developed to predict the effective diffusion coefficient of Re(VII) using pseudo-instances produced from a multi-porosity model. The ANN algorithm achieved an R2 of 0.97, whereas LightGBM achieved an R2 of 0.92 [27]. However, few studies have explained the correlation between the influencing factors and the effective diffusion coefficient of radionuclides using machine-learning models.
In this study, machine-learning models were employed to investigate the diffusion of several simulated radionuclide anions (
Materials and Methods
Materials
GMZ and Anji bentonite powders were obtained from Gaomiaozi, Inner Mongolia, and Anji, Zhejiang Province, respectively. The GMZ bentonite has a grain density of 2660 kg/m3, particle size (d50) of 7.1 μm, cation exchange capacity of 77.3 meq/100 g, and external surface area of 25.6 m2/g. The mineral composition is 74.5% montmorillonite, 12 wt% quartz, 7 wt% cristobalite, 4 wt% feldspar, 1 wt% calcite, and 1 wt% kaolinite [38]. In contrast, the Anji bentonite has a particle size (d50) of 11.6 μm, cation exchange capacity of 76 meq/100 g, and external surface area of 60.3 m2/g. The mineral composition is 46 wt% montmorillonite, 33 wt% quartz, 10 wt% orthoclase, 8 wt% microcline, and 3 wt% calcite [27].
Stock solutions of
Diffusion method
A through-diffusion method, which measures the diffusion parameters of ions through a specific thickness of porous materials, was applied to investigate the anion (
The bentonite powder was compacted into blocks (Φ 2.54 cm × 1.2 cm). Two stainless-steel filters (
The self-programmed Fitting for Diffusion Parameters software was used to calculate the rock capacity factor and effective diffusion coefficient by analyzing the accumulated mass as a function of time. The reliability of the two parameters was evaluated by examining the consistency between the calculated and experimental flux results.
Multi-porosity model
A multi-porosity model was established for the microstructure of montmorillonite because montmorillonite is the predominant mineral in bentonite. This model considers only the through-pores of compacted bentonite, where the total porosity (εtot) is subdivided into three components: diffuse double-layer porosity (εddl), interlayer porosity (εil), and free-layer porosity (εfree) [27, 39]. When compacted bentonite is saturated with an aqueous solution, the diffuse double-layer pores form transition zones from the surface of the bentonite particles to free pore water, containing a deficit of anions, water molecules, and an excess of cations. The interlayer pores contain cations and water molecules. Excess cations compensate for the charge deficit of the tetrahedral-octahedral-tetrahedral layers. By contrast, water molecules are arranged in layers [7]. Free-layer pores are spaces that comprise charge-balanced anions, cations, and water molecules.
Owing to the anionic exclusion effect, anionic radionuclides can barely enter the interlayer pores of bentonite. Therefore, the model assumes that the free-layer pores are the predominant diffusion paths, and the accessible porosity εacc is defined as
(1) At ρd≤1300 kg/m3,
• 0.119 kg H 2O/kg clay for one water layer at 1600 kg/m3≤ρd≤ 2000 kg/m3,
• 0.238 kg H2O/kg clay for two water layers at 1300 kg/m3 ≤ρd≤ 1600 kg/m3,
• 0.357 kg H2O/kg clay for three water layers at ρd≤1300 kg/m3.
The layer faction, xi, is approximately calculated as follows, where the subscript i denotes one, two, or three water layers [27, 39].
• At 1300kg/m3≤ρd≤1600kg/m3,
Database description and analysis
The training dataset was obtained from two sources. One is a dataset containing experimental instances from the JAEA-DDB (223 instances, 1989–2005) [42] and 15 publications (99 instances, 2006–2024), which are listed in Table S1 in the Supporting Information. The other database contained pseudo-instances produced using the multi-porosity model (15,000 instances) [27]. Table 1 summarizes the statistical information for the datasets. For the dataset collected from JAEA-DDB and the literature, only instances of anion diffusion in bentonite were chosen.
| Data source | Parameters | Mean | Min | Max | Std | Skw | |
|---|---|---|---|---|---|---|---|
| JAEA-DDB/Publications | Input | Rock capacity factor, α | 1.45 | 0.01 | 19.08 | 2.79 | 4.33 |
| Compacted dry density, ρd (kg/m3) | 1303.89 | 400 | 2000 | 326.16 | -0.38 | ||
| Species diffusion coefficient in water, logDw | -8.74 | -9.30 | -8.24 | 0.14 | -0.54 | ||
| Temperature, T (°C) | 29.38 | 12.00 | 90.00 | 15.36 | 2.18 | ||
| Mass ratio of montmorillonite, m | 0.78 | 0.33 | 1.00 | 0.18 | -1.08 | ||
| Ionic strength, I (mol/L) | 0.25 | 0.01 | 1.03 | 0.21 | 1.02 | ||
| Output | Effective diffusion coefficient, logDe | -10.25 | -12.60 | -9.17 | 0.72 | -1.02 | |
| Multi-porosity model | Input | External surface area, Aext (m2/g) | 69.20 | 10.00 | 129.98 | 34.5 | 0.03 |
| Mass ratio of montmorillonite, m | 0.65 | 0.30 | 1.00 | 0.20 | 0.00 | ||
| Ionic strength, I (mol/L) | 0.78 | 0.05 | 1.50 | 0.42 | -0.02 | ||
| Accessible porosity, εacc | 0.22 | 0.00 | 0.53 | 0.11 | 0.32 | ||
| Compacted dry density, ρd (kg/m3) | 1497 | 1000 | 2000 | 287 | 0.01 | ||
| Cementation factor, n | 2.71 | 2.00 | 3.40 | 0.40 | -0.03 | ||
| Fitting parameter, If | 0.85 | 0.70 | 1.00 | 0.09 | 0.01 | ||
| Species diffusion coefficient in water, |
-8.54 | -9.09 | -8.24 | 0.22 | -0.66 | ||
| Output | Effective diffusion coefficient, |
-10.51 | -19.73 | -8.88 | 0.88 | -1.93 |
Data pre-processing was performed using the Mahalanobis distance (MD) to remove outliers. MD is a distance measure used extensively in multivariate spaces. This accounts for the mean and covariance of the data. The cutoff point (di) is defined as [37]
The input features were the rock capacity factor, compacted dry density, mass ratio of montmorillonite, species diffusion coefficient in water, ionic strength, and temperature. The input features for the multi-porosity model dataset were the external surface area, mass ratio of montmorillonite, ionic strength, accessible porosity, compacted dry density, cementation factor, fitting parameter, and species diffusion coefficient in water. Among these features, the rock capacity factor indicates the ability of the bentonite barrier to impede radionuclide diffusion into the granite rock. If the rock capacity factor is less than the total porosity, it is equal to the accessible porosity. The external surface area, accessible porosity, and cementation factor indicate the bentonite characteristics, while the species diffusion coefficient in water indicates the radionuclide properties. The remaining features, such as the temperature, ionic strength, and compacted dry density, are parameters related to the experimental conditions. The effective diffusion coefficient is the only output feature.
The test dataset consisted of eight instances obtained from the diffusion of
Performance evaluation of the machine-learning model
The predictive accuracy was evaluated using R2 and MSE. These parameters were respectively calculated as follows:
Five-fold cross-validation (CV) was employed to mitigate overfitting, a situation characterized by high predictive performance in the training or validation datasets, but low accuracy in the test dataset, resulting in poor generalization and reduced robustness of the machine-learning model. In this approach, the dataset was randomly divided into five equally sized subsamples, with four subsamples used for training and one used for testing.
Results and discussion
Database distribution and characteristics
Figures 1a-f show the dependence of the effective diffusion coefficient on each input feature for the JAEA-DDB/publications dataset. The dependence of the multi-porosity model can be found in a previous study [27]. The histograms and kernel curves displayed on the top and right sides of each plot correspond to the distribution of the input features and effective diffusion coefficient. The shape of the curves is determined by the data point concentration; a high data point concentration results in a higher peak amplitude.
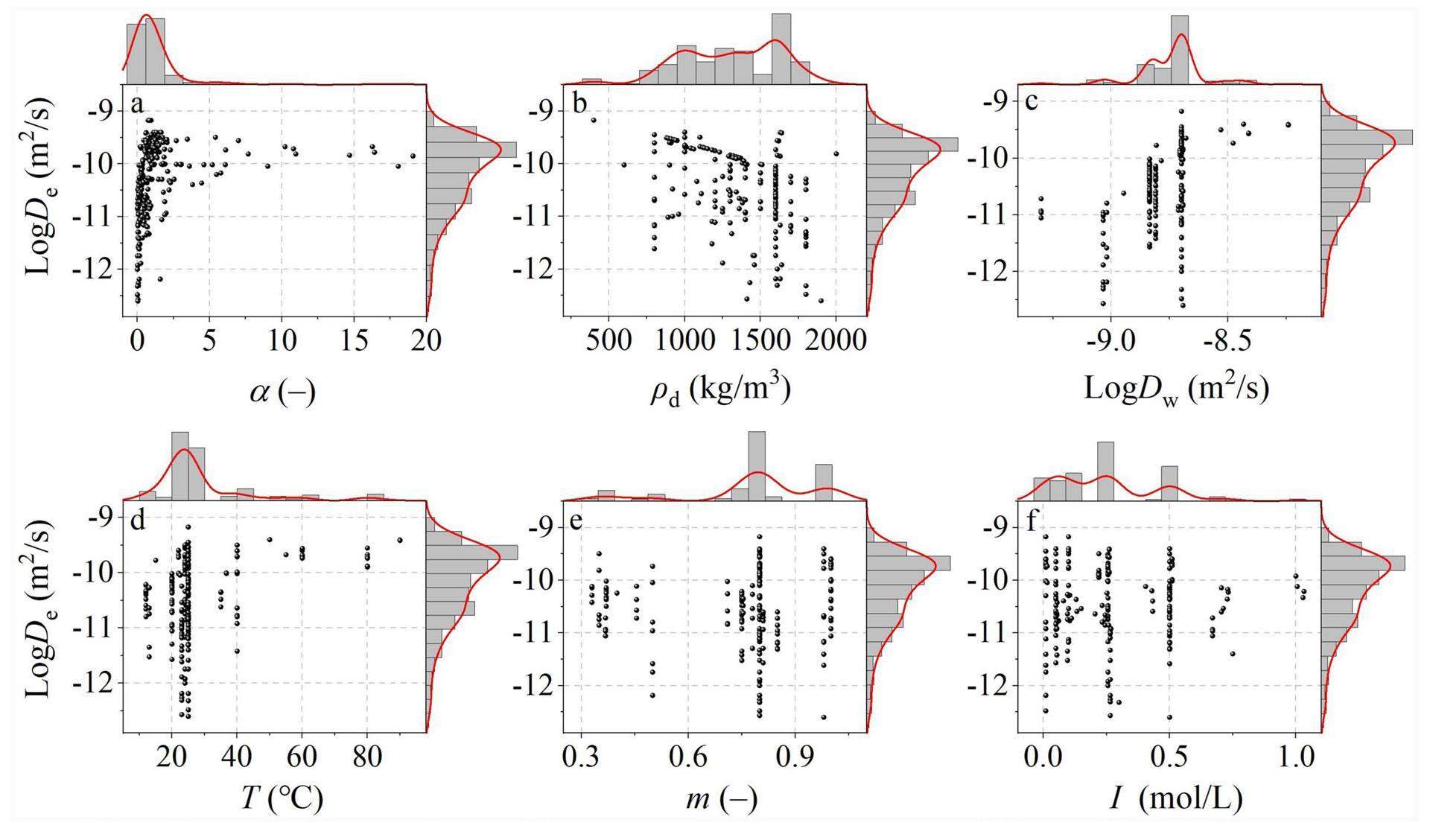
The rock capacity factor can be obtained directly using the through-diffusion method, or calculated as follows [27, 39]:
The effective diffusion coefficient increased with a decrease in the compacted dry density (Fig. 1b), which is consistent with previous experimental results [13-18]. It was not surprising that the effective diffusion coefficient increased with increasing species diffusion coefficient in water and temperature (Figs. 1c and d). This observed behavior can be attributed to adherence to two diffusion laws: one is known as Archie’s law, which can be expressed as
Measurement of diffusion parameters using the through-diffusion method
The through-diffusion method was used to determine the diffusion parameters of
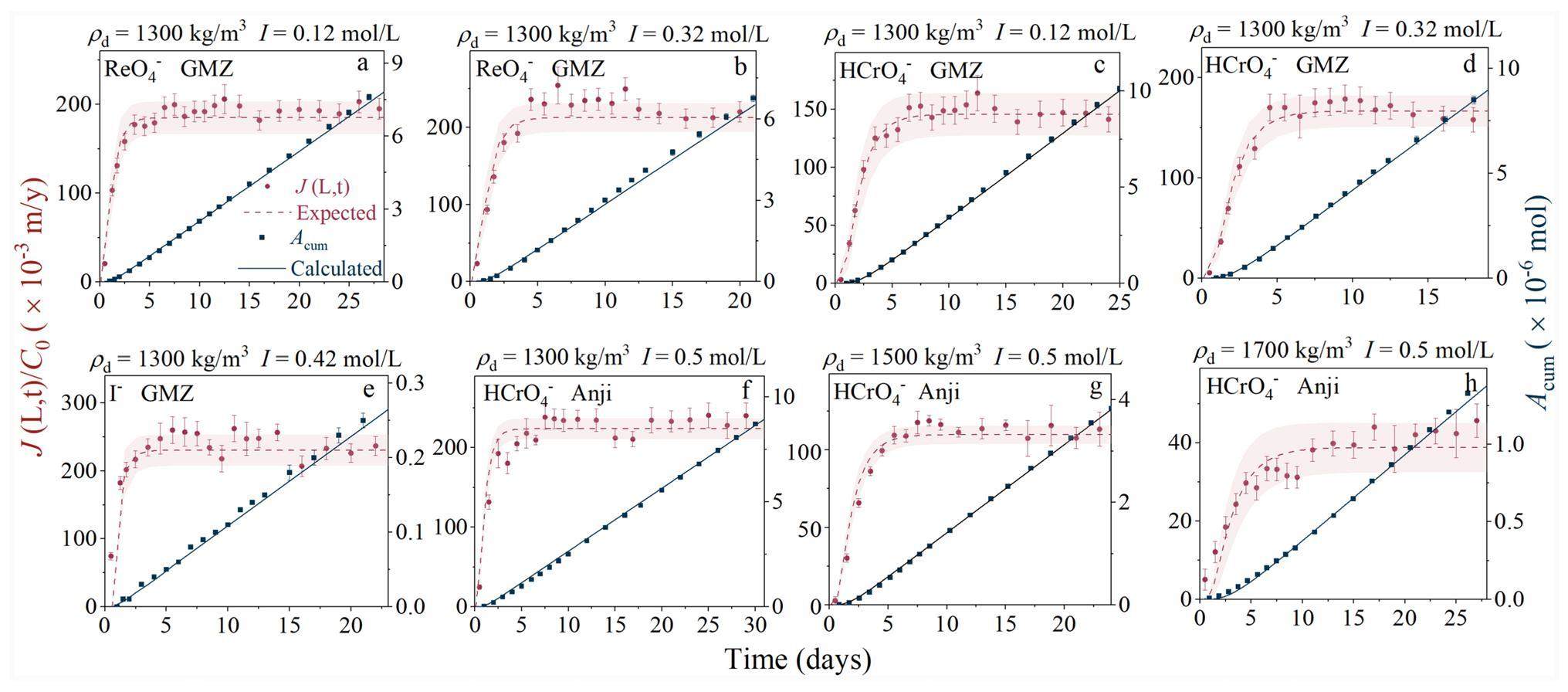
Table 2 lists the diffusion parameters of
| Clay | Anion | I (mol/L) | ρd (kg/m3) | C0 (× 10-3 mol/L) | De (× 10-11 m2/s) | α (-) | |
|---|---|---|---|---|---|---|---|
| GMZ | 0.12 | 1300 | 1.12 ± 0.05 | 7.1 ± 0.7 | 0.32 ± 0.04 | 0.51 | |
| 0.32 | 1300 | 1.12 ± 0.05 | 8.1 ± 0.7 | 0.40 ± 0.06 | 0.51 | ||
| 0.12 | 1300 | 2.14 ± 0.07 | 5.6 ± 0.7 | 0.46 ± 0.04 | 0.51 | ||
| 0.32 | 1300 | 2.14 ± 0.07 | 6.4 ± 0.6 | 0.50 ± 0.04 | 0.51 | ||
| I- | 0.42 | 1300 | 0.04±0.01 | 9.1 ± 0.7 | 0.30 ± 0.06 | 0.51 | |
| Anji | 0.50 | 1300 | 0.26 ± 0.01 | 7.1 ± 0.4 | 0.42 ± 0.04 | 0.54 | |
| 0.50 | 1500 | 0.27 ± 0.01 | 3.8 ± 0.2 | 0.35 ± 0.03 | 0.46 | ||
| 0.50 | 1700 | 0.26 ± 0.01 | 1.2 ± 0.2 | 0.22 ± 0.02 | 0.39 |
Prediction by the machine-learning algorithms
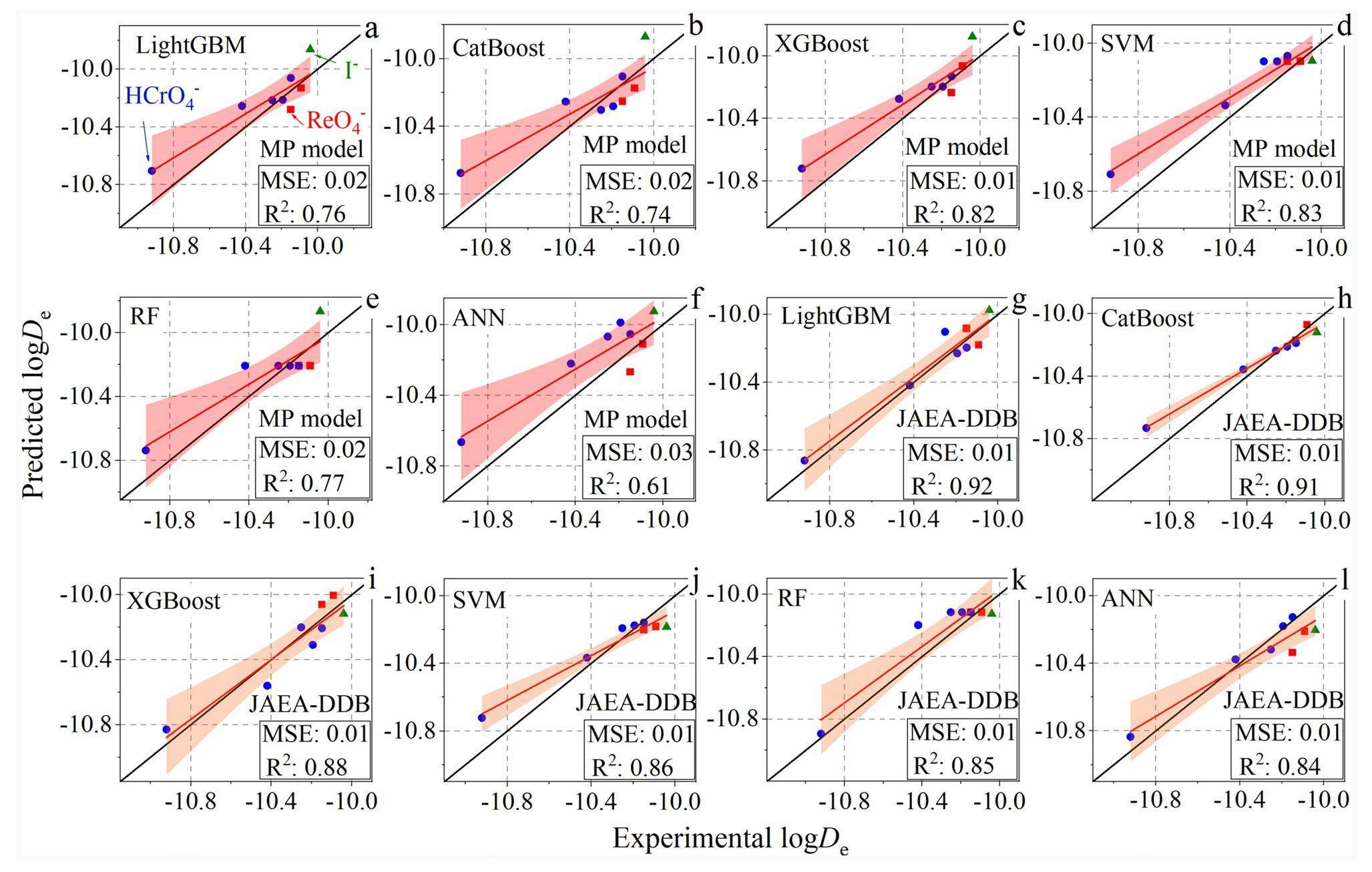
Six machine-learning algorithms, namely LightGBM, XGBoost, Catboost, ANN, RF, and SVM, were employed to predict the effective diffusion coefficient using two training datasets. One dataset comprised eight input features and 15,000 pseudo-instances produced by the multi-porosity model. The other dataset included six input features and 293 instances sourced from JAEA-DDB and 15 publications (Table 1). The datasets were divided into training and validation sets at a ratio of 4:1. The test dataset for the machine-learning models consisted of the experimental results listed in Table 2. LightGBM, XGBoost, Catboost, and RF are ensemble-learning algorithms, while ANN and SVM are traditional learning algorithms. Table 3 lists the mean values of the two performance metrics for the test datasets of the six machine-learning models using the five-fold cross-validation technique. LightGBM outperformed the other machine-learning models in terms of predictive performance, achieving the highest
| Algorithm | JAEA-DDB/Publications | Multi-porosity model | ||
|---|---|---|---|---|
| MSECV | MSECV | |||
| LightGBM | 0.87 | 0.01 | 0.74 | 0.02 |
| CatBoost | 0.85 | 0.01 | 0.73 | 0.02 |
| XGBoost | 0.73 | 0.02 | 0.75 | 0.02 |
| SVM | 0.72 | 0.02 | 0.78 | 0.02 |
| RF | 0.79 | 0.02 | 0.61 | 0.03 |
| ANN | 0.72 | 0.02 | 0.50 | 0.04 |
Hyperparameters, which are an integral part of machine-learning models, cannot be learned from the dataset. They were set prior to model training to control the models’ learning process. The grid search (GS) method was used to tune the hyperparameters. Reasonable settings for each hyperparameter were manually predefined. The model was iterated through each combination of the specified values. For the training datasets, the cross-validation method was used for guidance. After evaluating all combinations, the parameter combination with the best model performance was obtained. Table 4 summarizes the tuned hyperparameters for each machine-learning model.
| Algorithm | Parameter | Values | |
|---|---|---|---|
| Multi-porosity model | JAEA-DDB/publications | ||
| LightGBM | Num_boost_round | 10000 | 10000 |
| Max_depth | 2 | 1 | |
| Learning_rate | 0.001 | 0.05 | |
| Num_leaves | 30 | 30 | |
| Min_data_in_leaf | 21 | 14 | |
| Feature_fraction | 0.5 | 0.45 | |
| Boosting | gbdt | gbdt | |
| Bagging_freq | 30 | 4 | |
| Bagging_seed | 25 | 1 | |
| Bagging_fraction | 0.5 | 0.5 | |
| Lambda_l1 | 9 | 0.01 | |
| Lambda_l2 | 0 | 0.08 | |
| CatBoost | Iterations | 2000 | 200 |
| Depth | 11 | 7 | |
| Learning_rate | 0.01 | 0.48 | |
| Subsample | 0.70 | 0.81 | |
| Metric_period | 500 | 100 | |
| L2_leaf_reg | 39 | 0.97 | |
| Rsm | 0.4 | 0.4 | |
| Random_seed | 87 | 43 | |
| XGBoost | Num_boost_round | 1500 | 1000 |
| Max_depth | 3 | 10 | |
| Eta | 0.1 | 0.04 | |
| Gamma | 2 | 0.01 | |
| Lambda | 1 | 0.33 | |
| Subsample | 0.17 | 0.72 | |
| Min_child_weight | 7 | 12 | |
| Reg_alpha | 3 | 0.1 | |
| Booster | gbtree | gbtree | |
| Colsample_bytree | 0.8 | 0.2 | |
| SVM | Cache_size | 100 | 1 |
| Gamma | 0.001 | 0.01 | |
| Kernel | Rbf | Rbf | |
| C | 0.05 | 31 | |
| Epsilon | 0.01 | 0.44 | |
| RF | N_estimators | 3 | 21 |
| Max_depth | 4 | 1 | |
| Max_features | auto | auto | |
| Min_samples_split | 2 | 2 | |
| Min_samples_leaf | 4 | 0.15 | |
| Min_weight_fraction_leaf | 0.04 | 0.05 | |
| Random_state | 85 | 4 | |
| ANN | Epochs | 10000 | 10000 |
| Learning_rate | 0.005 | 0.005 | |
| Hidden layers | 3 | 3 | |
| Number of neurons | 64 | 100 | |
| Activation function | PReLU | PReLU | |
| Dropout | 0.2 | 0.2 | |
A comparison between the experimental and predicted effective diffusion coefficients is presented in Fig. 3, where the dots indicate the experimental data, the red lines represent the linear fit of the experimental data, and the shaded areas represent the 95% confidence interval. For the multi-porosity model, the predictive accuracy is ranked in descending order as SVM > XGBoost > RF > LightGBM > CatBoost > ANN (Figs. 3a-3f). The SVM outperformed the other machine-learning models in terms of predictive performance, with an MSE of 0.01 and R2 of 0.83. By contrast, when using the JAEA-DDB/publications dataset, the predictive accuracy is ranked in descending order as LightGBM > CatBoost > XGBoost > SVM > RF > ANN (Figs. 3g-3l). All gradient-boosting algorithms exhibited high performance, with R2 values above 0.88. LightGBM and XGBoost achieved similar predictive accuracies, with an MSE of 0.01 and R2 of 0.91. The JAEA-DDB/publications outperformed the multi-porosity model. This can be attributed to the complexity of the predictive tasks that involve predicting multiple species (
Shapley Additive Explanation and Feature Importance analyses
The Shapley Additive Explanation (SHAP) and Feature Importance (FI) methods are two widely used feature attribution methods that can identify the weight or significance of input features driving the predictions [34]. Although SHAP and FI analyses employ distinct techniques to characterize their importance, they can reflect the influence on the predicted output by ranking the importance of the input features [48]. In this study, they were applied to the LightGBM model using the JAEA-DDB/publications dataset, which yielded the highest predictive accuracy among the six machine-learning models. Higher SHAP and FI values for a feature indicate a greater impact on the effective diffusion coefficient. As can be seen in Fig. 4, the rock capacity factor and the compacted dry density are the top-two important input features for effective diffusion coefficient prediction. For the remaining four features, the FI analysis is ranked in descending order as follows: T >logDw > I > m, while the SHAP analysis ranked them as: ogDw≈T>m>I. The difference in the montmorillonite mass ratio ranking between the two analyses can be attributed to the underlying principles and assumptions of the two analysis technologies.
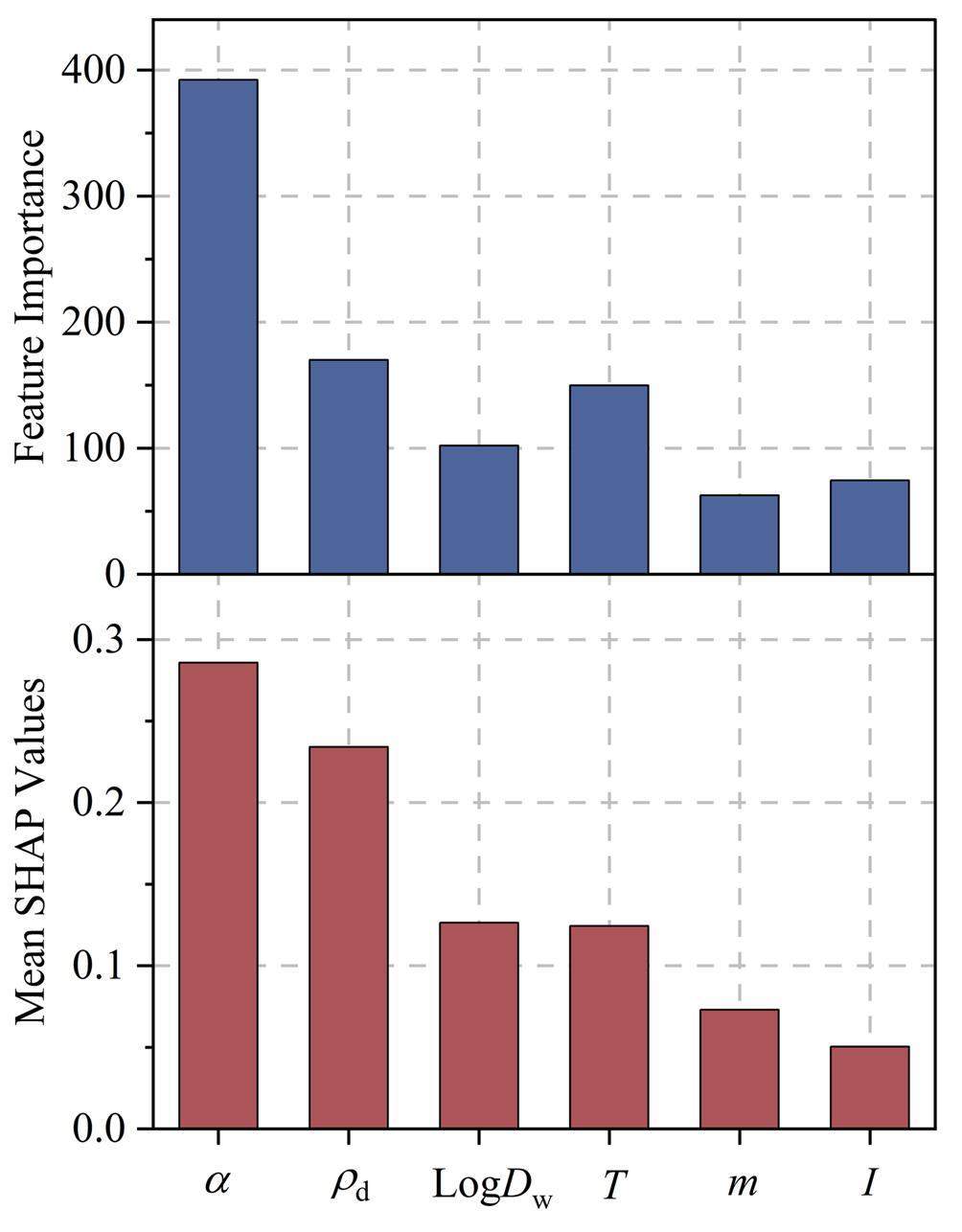
Ionic strength is closely associated with the electrical double layer located at the bentonite interface [9]. Although ionic strength had a limited effect on the effective diffusion coefficient prediction (Fig. 4), its influence on radionuclide diffusion has been investigated in previous experimental diffusion studies [9, 19, 24]. The effective diffusion coefficient increases in solutions with high salinity until the ionic strength exceeds 0.5 mol/L. This observation is explained by the minimum thickness of the electrical double layer, which results in negligible diffuse double-layer pores and a maximum width of free layer pores [9, 19, 24]. In addition, there is an ongoing debate on the effect of the electrical double layer on radionuclide diffusion [9, 49]. This can be explained by the small porosity proportion in the diffused double-layer pores [28]. It is worth noting that the weight of a feature relies on input features, instances, and algorithms. Further research is needed to clarify the importance of ionic strength in radionuclide diffusion.
Partial Dependence Plot analysis
Partial Dependence Plot (PDP) analysis indicates the ability to analyze the relationship between each input and output features [34]. These plots provide a quantitative assessment of the positive and negative effects of the six input features on the effective diffusion coefficient (Fig. 5). A feature with a strong impact on the output variable exhibits significant changes in the PDP curves, indicating a significant contribution to the model’s prediction. By contrast, a feature with little impact results in flat or nearly constant PDP curves.
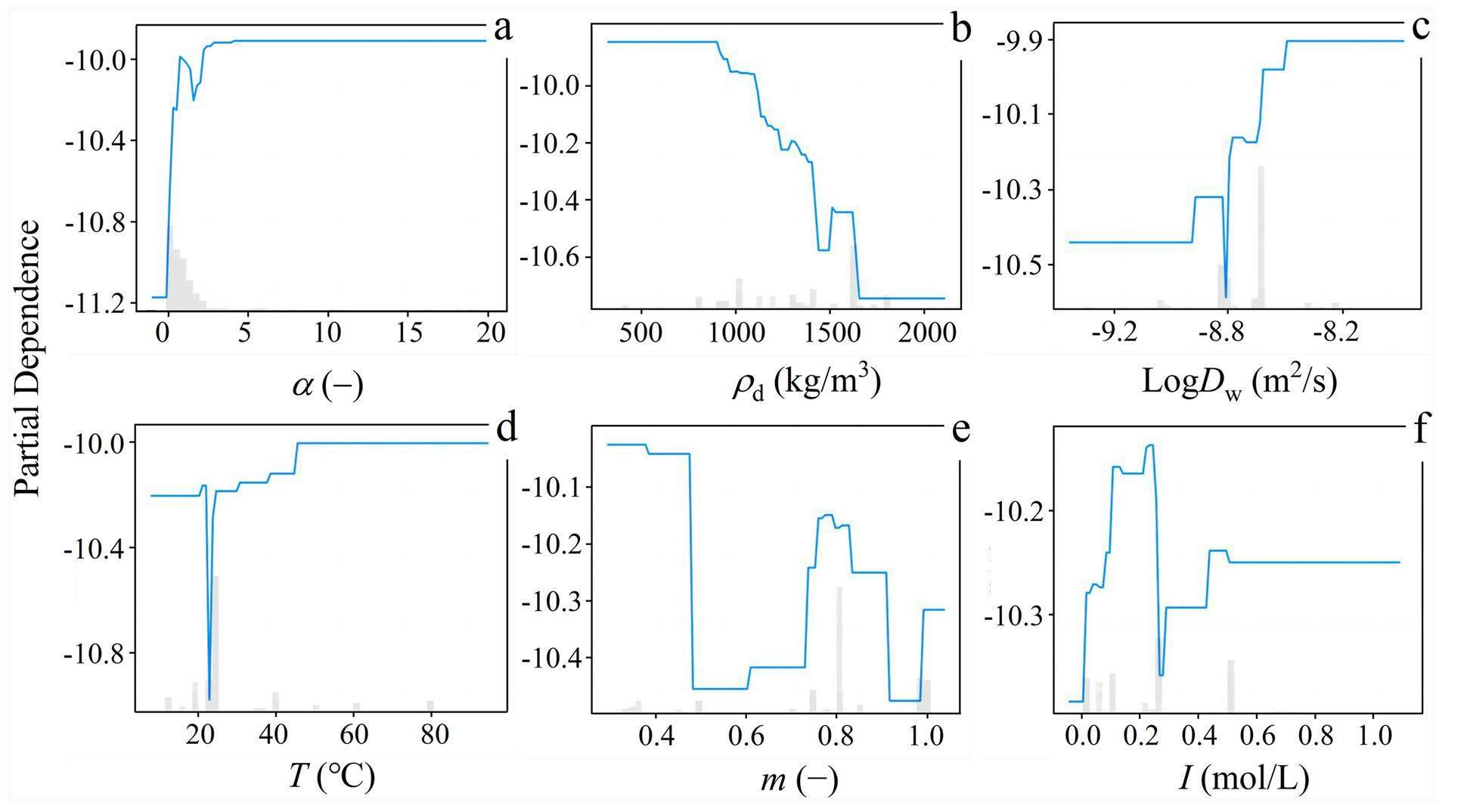
The rock capacity factor, species diffusion coefficient in water, ionic strength, and temperature positively impacted the effective diffusion coefficient, whereas the compacted dry density and montmorillonite mass ratio negatively impacted it. In other words, the effective diffusion coefficient increases with increasing species diffusion coefficient in water, temperature, and ionic strength, which is consistent with Archie’s law [39, 43], the Arrhenius equation [45], and previous experimental results [10, 19-24]. Conversely, the effective diffusion coefficient decreases in compacted bentonite with a high compacted dry density and high montmorillonite mass ratio, which is also consistent with previous experimental results [9, 13-15].
Among the input features, the rock capacity factor had the most significant influence on the effective diffusion coefficient, which is in agreement with the SHAP and FI analyses. An increase from 0.01 to 19.08 in the rock capacity factor resulted in a significant increase in the PDP value from -11.16 to -9.90, representing a substantial increase of approximately 11.3% (Fig. 5a). It is worth noting that the rock capacity factor of radionuclide anions should be lower than the total porosity if the anionic exclusion effect is considered [39, 43], indicating that some anionic instances with a rock capacity factor above the total porosity threshold should be removed from JAEA-DDB. Nonetheless, these instances were retained in this study for database integrity. The percentage increase in the PDP value is ranked in descending order as follows: α (11.3%) > T (8.8%) >
The compacted dry density had a negative impact, as an increase from 400 to 1700 kg/m3 led to a decrease in the PDP value from -9.85 to -10.74, corresponding to a decrease of approximately 9.0% (Fig. 5b). This finding is consistent with the results of previous studies [13-18]. Additionally, the montmorillonite mass ratio had a negative impact; an increase from 0.33 to 1.0 led to a decrease in the PDP value from -10.02 to -10.31, corresponding to a decrease of approximately 2.8% (Fig. 5e). This indicates that bentonite has a low montmorillonite mass ratio, such as the illite/smectite mixed-layer (I/S) (m = 0.33) and Kunigel V1 (m = 0.46-0.49) bentonites, and exhibits a higher effective diffusion coefficient, which is in agreement with the findings of previous studies [7, 9, 13, 16, 25]. Generally, bentonite barriers with a higher montmorillonite mass ratio exhibit better blocking abilities against radionuclides [5]. As can be seen in Figs. 5d and 5f, the predicted effective diffusion coefficient increases with increasing ionic strength and temperature. The effect becomes significant when the ionic strength and temperature range from 0.01 to 0.6 mol/L and from 22 to 60 ℃, respectively, which is consistent with the findings of previous studies [20, 26]. This indicates that the PDP analysis provides interpretability of the diffusion law and mechanism.
Conclusion
The effective diffusion coefficients of
(i) The training and validation datasets were obtained from two sources: experimental instances and pseudo-instances. The former outperformed the latter.
(ii) The Light Gradient-Boosting algorithm demonstrated a higher predictive accuracy than others machine-learning algorithms, achieving an MSE of 0.01 and R2 of 0.92, for the dataset obtained from the JAEA-DDB and 15 publications.
(iii) Analyses of the input features of the prediction using the Shapley Additive Explanation, Feature Importance, and Partial Dependence Plot methods revealed that the rock capacity factor and compacted dry density were the two most important features. The rock capacity factor had a positive influence, whereas the compacted dry density had a negative impact.
In this paper, a novel machine-learning model for radionuclide diffusion prediction with high accuracy is introduced and the diffusion mechanism is explored by ranking the influencing factors and analyzing the dependency of the effective diffusion coefficient on each influencing factor. This suggests that machine-learning algorithms can be powerful tools, offering a new paradigm for studying the diffusion of radioactive anions in bentonite barriers. Further research is necessary to evaluate the applicability of this method for improving machine-learning models by incorporating additional characteristic parameters of bentonite, complex chemical species, and a broader range of geochemical conditions related to high-level radioactive waste repositories.
China’s progress in radionuclide migration study over the past decade (2010–2021): Sorption, transport and radioactive colloid
. Chin. Chem. Lett. 33, 3405-3412 (2022). https://doi.org/10.1016/j.cclet.2022.02.054Recent progress in radionuclides adsorption by bentonite-based materials as ideal adsorbents and buffer/backfill materials
. Appl. Clay Sci. 232, 106796 (2023). https://doi.org/10.1016/j.clay.2022.106796Effect of synthetic water and cement solutions on the swelling pressure of compacted Gaomiaozi(GMZ) bentonite: The Beishan site case, Gansu, China
. Eng. Geol. 244, 66-74 (2018). https://doi.org/10.1016/j.enggeo.2018.08.002Investigation on gas migration behaviours in saturated compacted bentonite under rigid boundary conditions
. Acta Geotech. 17, 2517-2531 (2022). https://doi.org/10.1007/s11440-021-01424-1Fickian diffusion of radionuclides for engineered containment barriers: Diffusion coefficients, porosities, and complicating issues
. Eng. Geol. 152, 133-147 (2013). https://doi.org/10.1016/j.enggeo.2012.10.014Perturbation induced by EDTA on HDO, Br– and EuIII diffusion in a large-scale clay rock sample
. Appl. Clay Sci. 105–106, 142-149 (2015). https://doi.org/10.1016/j.clay.2014.12.004Modelling approaches for anion-exclusion in compacted Na-bentonite
. Geochim. Cosmochim. Acta. 75, 3698-3710 (2011). https://doi.org/10.1016/j.gca.2011.04.001Comprehensiveness of scenarios in the safety assessment of nuclear waste repositories
. Reliab. Eng. Syst. Saf. 188, 561-573 (2019). https://doi.org/10.1016/j.ress.2019.04.012Anion diffusion in compacted clays by pore-scale simulation and experiments
. Water Resour. Res. 56, 2019WR027037 (2020). https://doi.org/10.1029/2019wr027037Diffusion of HTO, 36Cl– and 125I– in upper toarcian argillite samples from tournemire: Effects of initial iodide concentration and ionic strength
. Appl. Geochem. 27, 1432-1441 (2012). https://doi.org/10.1016/j.apgeochem.2011.12.017Diffusion and sorption of Cs+, Na+, I– and HTO in compacted sodium montmorillonite as a function of porewater salinity: Integrated sorption and diffusion model
. Geochim. Cosmochim. Acta. 132, 75-93 (2014). https://doi.org/10.1016/j.gca.2014.02.004Diffusion of HTO, 36Cl– and 125I– in Opalinus Clay samples from Mont Terri
. J. Contam. Hydrol. 61, 73-83 (2003). https://doi.org/10.1016/S0169-7722(02)00114-6Combined tracer through-diffusion of HTO and 22Na through Na-montmorillonite with different bulk dry densities
. Appl. Geochem. 93, 158-166 (2018). https://doi.org/10.1016/j.apgeochem.2018.04.008Effects of dry density and exchangeable cations on the diffusion process of sodium ions in compacted montmorillonite
. Eng. Geol. 81, 246-254 (2005). https://doi.org/10.1016/j.enggeo.2005.06.010Anion diffusion pathways in bentonite clay compacted to different dry densities
. Appl. Clay Sci. 23, 69-76 (2003). https://doi.org/10.1016/s0169-1317(03)00088-7Effect of dry density on diffusion of some radionuclides in compacted sodium bentonite
. J. Nucl. Sci. Technol. 29, 872-882 (1992). https://doi.org/10.1080/18811248.1992.9731607Influence of dry density on HTO diffusion in GMZ bentonite
. J. Radioanal. Nucl. Chem. 292, 853-857 (2012). https://doi.org/10.1007/s10967-011-1523-yEffect of dry density on 125I diffusion in GMZ bentonite
. Sci. China Chem. 55, 1760-1764 (2012). https://doi.org/10.1007/s11426-012-4695-6Diffusion of tritiated water, 137Cs+, and 125I– in compacted Ca-montmorillonite: Experimental and modeling approaches
. Appl. Clay Sci. 211, 106176 (2021). https://doi.org/10.1016/j.clay.2021.106176Self-diffusion of water and its dependence on temperature and ionic strength in highly compacted montmorillonite, illite and kaolinite
. Appl. Geochem. 23, 3840-3851 (2008). https://doi.org/10.1016/j.apgeochem.2008.08.008Impact of the solution ionic strength on strontium diffusion through the Callovo-Oxfordian clayrocks: An experimental and modeling study
. Appl. Geochem. 61, 41-52 (2015). https://doi.org/10.1016/j.apgeochem.2015.05.011Modeling the ionic strength effect on diffusion in clay. The DR-A Experiment at Mont Terri
. ACS Earth Space Chem. 3, 442-451 (2019). https://doi.org/10.1021/acsearthspacechem.8b00192The effect of ionic strength on the diffusion of 125I in Gaomiaozi bentonite
. J. Radioanal. Nucl. Chem. 295, 1423-1430 (2013). https://doi.org/10.1007/s10967-012-2284-ySalt effects on Re(VII) and Se(IV) diffusion in bentonite
. Appl. Clay Sci. 141, 104-110 (2017). https://doi.org/10.1016/j.clay.2017.02.021Diffusion coefficients and accessible porosity for HTO and 36Cl in compacted FEBEX bentonite
. Appl. Clay Sci. 26, 65-73 (2004). https://doi.org/10.1016/j.clay.2003.09.012Diffusion mechanism of sodium ions in compacted montmorillonite under different NaCl concentration
. Phys. Chem. Earth. 33, 957-961 (2008). https://doi.org/10.1016/j.pce.2008.05.007Application of machine learning to study the effective diffusion coefficient of Re(VII) in compacted bentonite
. Appl. Clay Sci. 243, 107076 (2023). https://doi.org/10.1016/j.clay.2023.107076Porosity investigation of compacted bentonite using through-diffusion method and multi-porosity model
. Appl. Geochem. 146, 105480 (2022). https://doi.org/10.1016/j.apgeochem.2022.105480Cation diffusion in compacted clay: A pore-scale view
. Environ. Sci. Technol. 53, 1976-1984 (2019). https://doi.org/10.1021/acs.est.8b05755Novel algorithm for detection and identification of radioactive materials in an urban environment
. Nucl. Sci. Tech. 34, 154 (2023). https://doi.org/10.1007/s41365-023-01304-1Exceptional piezoelectricity, high thermal conductivity and stiffness and promising photocatalysis in two-dimensional MoSi2N4 family confirmed by first-principles
. Nano Energy. 82, 105716 (2021). https://doi.org/10.1016/j.nanoen.2020.105716Prediction of the chloride diffusivity of recycled aggregate concrete using artificial neural network
. Mater. Today Commun. 32, 104137 (2022). https://doi.org/10.1016/j.mtcomm.2022.104137An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications
. Comput Methods Appl Mech Eng. 362, 112790 (2020). https://doi.org/10.1016/j.cma.2019.112790Machine learning approach for investigating chloride diffusion coefficient of concrete containing supplementary cementitious materials
. Constr. Build. Mater. 328, 127103 (2022). https://doi.org/10.1016/j.conbuildmat.2022.127103Prediction of chloride diffusion in cement mortar using multi-gene genetic programming and multivariate adaptive regression splines
. Measurement. 112, 141-149 (2017). https://doi.org/10.1016/j.measurement.2017.08.031Developing an artificial neural network model to evaluate chloride diffusivity in high performance concrete
. HBRC J. 9, 15-21 (2013). https://doi.org/10.1016/j.hbrcj.2013.04.001A machine learning method for predicting the chloride migration coefficient of concrete
. Constr. Build. Mater. 348, 128566 (2022). https://doi.org/10.1016/j.conbuildmat.2022.128566Selection and basic properties of the buffer material for high-level radioactive waste repository in China
. Acta Geol. Sin–Engl. 82, 1050-1055 (2008). https://doi.org/10.1111/j.1755-6724.2008.tb00662.xInvestigation of Re(VII) diffusion in bentonite by through-diffusion and modeling techniques
. Appl. Clay Sci. 166, 223-229 (2018). https://doi.org/10.1016/j.clay.2018.08.023Porosity investigation of compacted bentonite using XRD profile modeling
. J. Contam. Hydrol. 128, 19-32 (2012). https://doi.org/10.1016/j.jconhyd.2011.10.005Ionic conductivity and diffusion at infinite dilution
. In: CRC Handbook of Chemistry and Physics. 83, 76-78 (2000).A modified version of Archie’s law to estimate effective diffusion coefficients of radionuclides in argillaceous rocks and its application in safety analysis studies
. Appl. Geochem. 59, 85-94 (2015). https://doi.org/10.1016/j.apgeochem.2015.04.002Diffusive transport in compacted mixtures of clay and crushed granite
. Radiochim. Acta. 65, 189-194 (1994). https://doi.org/10.1524/ract.1994.65.3.189Re(VII) diffusion in bentonite: Effect of organic compounds, pH and temperature
. Appl. Clay Sci. 127–128, 10-16 (2016). https://doi.org/10.1016/j.clay.2016.03.039Innovative modeling framework of chloride resistance of recycled aggregate concrete using ensemble-machine-learning methods
. Constr. Build. Mater. 337, 127613 (2022). https://doi.org/10.1016/j.conbuildmat.2022.127613Machine learning the nuclear mass
. Nucl. Sci. Tech. 32, 109 (2021). https://doi.org/10.1007/s41365-021-00956-1Decoding the nuclear symmetry energy event-by-event in heavy-ion collisions with machine learning
. Phys. Lett. B. 835, 137508 (2022). https://doi.org/10.1016/j.physletb.2022.137508Qing-Feng Li is an editorial board member for Nuclear Science and Techniques and was not involved in the editorial review, or the decision to publish this article. All authors declare that there are no competing interests.


