Although heavy-ion collisions generate strong magnetic fields, their direct measurement is a challenging task. A new observable, the baryon electric charge correlation, was recently found to be sensitive to the magnetic field strength and thus could be used as a magnetometer for heavy-ion collisions. Additionally, this observable may shed light on the equation of state and phase structure of quantum chromodynamics (QCD) under magnetic fields.

Determining and understanding the phase structure of quantum chromodynamics (QCD) is important in contemporary physics [1]. Owing to the confinement property of QCD, QCD matter at low temperatures and baryon densities is in the confined hadronic phase. To explore the deconfined phases, relativistic heavy-ion colliders have been constructed, such as the relativistic heavy-ion collider (RHIC) and Large Hadron Collider (LHC). These colliders can accelerate ions to relativistic energies and then make them collide to generate deconfined QCD matter in which quarks and gluons are the fundamental degrees of freedom. Such matter is usually referred to as quark-gluon plasma (QGP). Furthermore, relativistic heavy-ion collisions can generate very strong magnetic fields [2-4] because the moving ions form two strong transient electric currents that induce a strong magnetic field along the reaction plane. Several interesting physical effects can be induced by a strong magnetic field including the well-known chiral magnetic effect (CME), which is the induction of an electric current along the direction of a magnetic field if the QGP contains net chirality [5, 6]. This intriguing effect is crucial for detecting the possible parity violations of QCD in hot environments. Over the past 15 years, experimental efforts from both RHIC and LHC have focused on searching for the CME [7-12]. Moreover, the strong magnetic field introduces new dimensions into the QCD phase diagram, prompting questions regarding the phase structure of QCD on the temperature and magnetic field plane or on the baryon density and magnetic field plane. In this aspect, the magnetic catalysis of chiral symmetry breaking at low temperatures and inverse magnetic catalysis at temperatures near the QCD crossover temperature are perhaps the most interesting phenomena. Thus, magnetic fields can help us enrich and deepen our understanding of QCD matter [13-15].

However, despite theoretical calculations elucidating the strength of magnetic fields at the moment of collision, the complicated temporal evolution of the magnetic fields in the QGP hinders the estimation of the magnetic field strength in heavy-ion collisions [16-20]. Hence, the availability of observables capable of detecting the strength of magnetic fields is invaluable. Recently, H.-T. Ding et al. [21] proposed that the baryon electric charge correlation could serve as an observable. Employing lattice QCD, the authors calculated various correlations among conserved charges, revealing that the baryon electric charge correlation, denoted as ${\chi }_{11}^{\text{BQ}}$, is the most sensitive to the magnetic field, and thus can serve as a magnetometer for QCD.

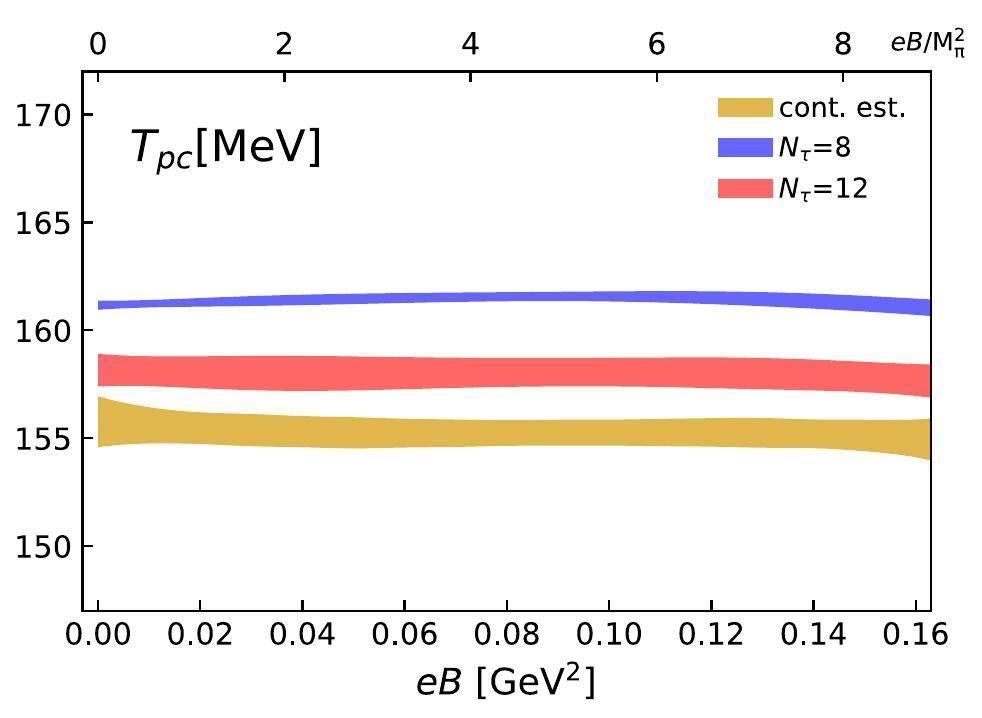
The absence of a sign problem is notable in lattice QCD simulations conducted under strong magnetic fields. However, the necessity of discretizing the magnetic field using integer values of the magnetic flux limits the magnetic-field strength of the simulation. Specifically, the maximum achievable strength is constrained by the square of the inverse lattice spacing, whereas the minimum achievable strength is limited by the square of the inverse spatial lattice size. This study employed the largest magnetic flux of six, thereby making the discretization error associated with the magnetic field negligible. Furthermore, the analysis of the conserved charge fluctuations relies on continuum estimates derived from lattices with temporal sizes (Nτ) of 8 and 12. The consistency between these continuum estimates for both ${\chi }_{11}^{\text{BQ}}$ and μ_Q/μ_B (the ratio of the electric and baryon chemical potentials) was established through additional lattice QCD calculations performed on Nτ = 16 lattices. Thus, the findings underscore the reliability of the continuum estimates based on Nτ= 8 and 12 lattices when applied to lattice QCD simulations in strong magnetic fields.

The fluctuations and correlations considered in this study are defined by ${\chi }_2^{\text{B}}=\frac{{\partial }^2\left(P/T^4\right)}{\partial {\widehat{\mu }}_B^2}\mathrm{,}{\chi }_2^{\text{Q}}=\frac{{\partial }^2\left(P/T^4\right)}{\partial {\widehat{\mu }}_Q^2}\mathrm{,}{\chi }^{\text{BQ}}=\frac{{\partial }^2\left(P/T^4\right)}{\partial {\widehat{\mu }}_B\partial {\widehat{\mu }}_Q}\mathrm{,}$ (1) evaluated at μB=μQ=0. Here, P denotes the total pressure of the system; T is the temperature; and ${\widehat{\mu }}_{B\mathrm{,}Q}={\mu }_{B\mathrm{,}Q}/T$. These quantities are generally functions of eB. However, the lattice simulations showed that the correlation ${\chi }_{11}^{\text{BQ}}$ exhibited the highest sensitivity. The result of ${\chi }_{11}^{\text{BQ}}$ normalized by its value at zero magnetic field along the crossover transition line is shown in Fig. 1. The crossover temperature must be examined, because these fluctuations and correlations exhibit critical behavior, leading to a peak near the crossover temperature [22-24]. A strong dependence on eB is observed; as eB grows from zero to 0.15 GeV², the ratio ${\chi }_{11}^{\text{BQ}}\left(eB\right)/{\chi }_{11}^{\text{BQ}}\left(0\right)$ approximately doubles. The crossover temperature also depends on eB; however, this dependence is very weak when eB<0.15 GeV², as shown in Fig. 2. The slowly decreasing behavior of Tpc versus eB is simply the inverse magnetic catalysis of the chiral phase transition which was discovered a decade ago in lattice simulations [25, 26].

Fig. 1Full-screen View

(Color online) The ratio ${\chi }_{11}^{\text{BQ}}\left(eB\right)/{\chi }_{11}^{\text{BQ}}\left(0\right)$ at the crossover temperature. The result from the HRG model (dashed line) is also shown Ref. [21]

Fig. 2Full-screen View

(Color online) Crossover temperature as a function of eB for $eB\lesssim 0.16$ GeV² Ref. [21]

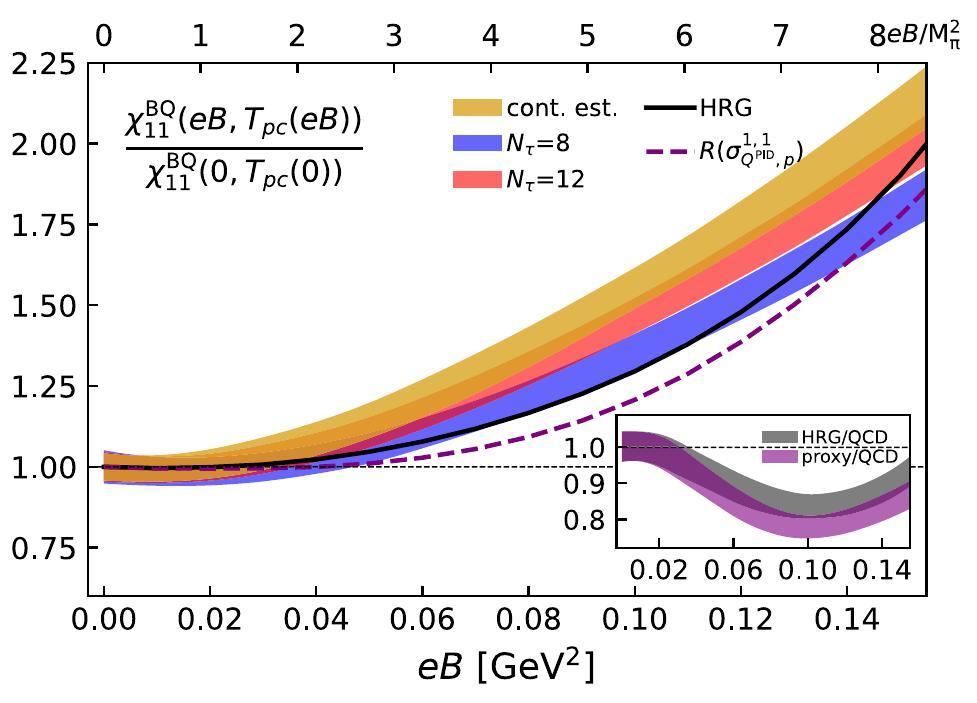
Additionally, Fig. 1 presents the results from the hadron resonance gas (HRG) model, which explain the lattice data in the studied eB window. This demonstrates that the behavior of ${\chi }_{11}^{\text{BQ}}\left(eB\right)/{\chi }_{11}^{\text{BQ}}\left(0\right)$ has a thermodynamic basis.

Several interesting consequences can arise from these results, as discussed in the following section.

First, a STAR Collaboration data analysis was recently performed primarily by a joint team of Fudan University, Brookhaven National Laboratory, University of California-Los Angles, and Institute of Modern Physics of Chinese Academy of Sciences, led by Jinhui Chen, Diyu Shen, Yu-Gang Ma, Aihong Tang, Gang Wang, Aditya Prasad Dash, Subhash Singha, and Dhananjaya Thakur. This analysis revealed a nontrivial sign change in the directed-flow splitting of charged hadrons, such as $\Delta v_1^p=v_1^p-v_1^{\overline{p}}$ and $\Delta v_1^{\pi }=v_1^{{\pi }^{+}}-v_1^{{\pi }^{-}}$, with increasing centrality [27, 28]. This strongly indicates the presence of magnetic fields. However, precisely extracting the strength of the magnetic field from v₁ splitting remains challenging, owing to the complex dynamic evolution of the hot medium and the magnetic field itself. This challenge stems largely from the absence of a robust model describing the coupled spacetime evolution of the hot medium and magnetic field. Now, the correlation ${\chi }_{11}^{\text{BQ}}$ emerges as a complementary observable, which provides a model-independent approach to quantify the magnetic field strength. This is because ${\chi }_{11}^{\text{BQ}}$ can be solely determined from the final-state hadron spectra (although, naturally, this approach remains subject to considerations, such as kinematic acceptance and detector corrections).

Second, the results show that the fluctuations ${\chi }_2^{\text{B}}$ and ${\chi }_2^{\text{Q}}$ exhibit a weaker dependence on the magnetic field within the studied parameter region. This is somewhat surprising, as the electric charge fluctuation is expected to be sensitive to electromagnetic fields. However, this behavior can be understood by considering the HRG model, which yields similar trends around the crossover temperature. Additionally, some insights can be gained from the high-temperature limit, where the system should predominantly consist of massless free quarks (and free gluons that do not interact with magnetic fields). In this scenario, as eB approaches zero, it can be shown that ${\chi }_2^{\text{B}}={\chi }_2^{\text{Q}}/2=1/3$ and ${\chi }_{11}^{\text{BQ}}=0$. Thus, when eB is turned on but remains weak (compared with the temperature), ${\chi }_{11}^{\text{BQ}}$ becomes sensitive to eB [29, 30].

Third, an intriguing insight is provided in Fig. 2 of Ref. [21], which illustrates the contributors to ${\chi }_2^{\text{B}}$, ${\chi }_2^{\text{Q}}$, and ${\chi }_{11}^{\text{BQ}}$. According to the HRG model, within the considered range of eB, the primary contribution to ${\chi }_2^{\text{Q}}$ stems from charged pions, whereas the largest contribution to ${\chi }_2^{\text{B}}$ originates from protons, although other hadrons also make significant contributions. However, in the case of ${\chi }_{11}^{\text{BQ}}$, protons dominate at $eB\lesssim 4m_{\pi }^2$, whereas doubly charged Δ(1232) baryons surpass protons at $eB\gtrsim 4m_{\pi }^2$. Because the proton contribution remains approximately constant with eB, the eB dependence of ${\chi }_{11}^{\text{BQ}}$ is primarily controlled by Δ(1232) baryons. This hinders the practical utilization of ${\chi }_{11}^{\text{BQ}}$ as a magnetometer in heavy-ion collisions, because Δ(1232) baryons are not directly measurable owing of their rapid decay into protons and pions. However, after accounting for such decays, the measurement of ${\chi }_{11}^{\text{BQ}}$ become quite reliable if a proxy for ${\chi }_{11}^{\text{BQ}}$ is constructed [21].

Finally, several interesting future directions were obtained. The lattice results for ${\chi }_2^{\text{B}}$, ${\chi }_2^{\text{Q}}$, and ${\chi }_{11}^{\text{BQ}}$ can be used to construct the equation of state of QCD matter under finite magnetic fields, small baryons, and electric chemical potentials. Higher-order fluctuations and correlations are necessary for determining a more precise equation of state or extending it to larger chemical potentials. Moreover, higher-order fluctuations and correlations are often considered as sensitive indicators of critical phenomena. Therefore, investigating the magnetic field dependence of these higher-order fluctuations and correlations near the crossover temperature is of considerable interest. Furthermore, the lattice results require the calculation of ${\chi }_{11}^{\text{BQ}}$ in other models that may complement the HRG model. Such studies can provide deeper insight into the magnetic field dependence of various fluctuations and correlations among conserved charges.