Physics opportunities of the nuclear excitation by electron capture process

INVITED REVIEW

Physics opportunities of the nuclear excitation by electron capture process

Yi Yang，

Han-Xu Zhang，

Yuan-Bin Wu，

Song Guo，

Xu Wang，

Chang-Bo Fu ，

Yang Sun，

Yu-Gang Ma

Nuclear Science and Techniques

Vol.36, No.8

Article number 146

Published in print Aug 2025

Available online 04 Jun 2025

DOI：10.1007/s41365-025-01717-0

CSTR：32136.14.NST.2025.08146

11800

Nuclear excitation by electron capture (NEEC) is a fundamental process in nuclear physics. Despite its theoretical framework established nearly half a century ago, the experimental confirmation of NEEC remains elusive because of significant technical challenges. A notable effort to validate NEEC experimentally involved the enhanced ^93mMo isomer-depletion experiment, which was ultimately hindered by substantial noise interference. This mini-review provides a brief historical overview of NEEC studies and explores the role of NEEC processes in astrophysical environments and laser-induced plasmas. Several platforms have been proposed to facilitate the observation of NEEC, including traditional cooling-storage rings, ion accelerators, and electron-beam ion traps. These approaches aim to enhance the nuclear excitation rate, thereby improving the signal-to-noise ratio. In addition, the employment of exotic vortex beams is discussed as a potential methodological approach to address these challenges.

NEECIsomerPlasmasAccelerator

Introduction

Nuclear excitation by electron capture (NEEC) involves a positively charged ion capturing a free electron, leading to the excitation of its nucleus. This intriguing process was first reported by Goldanskii and Namiot in 1976, who explored its potential for observation in the laser-generated plasma of ²³⁵U [1]. Originally referred to as inverse internal electron conversion, NEEC represents the inverse mechanism of internal conversion (IC) [2-4], as shown in Fig. 1.

Fig. 1

(Color online) Schematic diagrams of the NEEC (left) and IC (right) processes, which are inverse processes of each other

The NEEC process has a profound significance across various fields, including astrophysics and nuclear physics. For example, in astrophysical environments, this mechanism may influence nucleosynthesis. Elucidating nuclear mechanisms such as NEEC in astrophysical plasmas is essential to enhancing our understanding of the formation, evolution, and interactions of stellar bodies, galaxies, and other astronomical entities [5]. Furthermore, NEEC is expected to serve as an important method for nuclear isomer production with broad applications across various domains, including nuclear medical treatment [6, 7], nuclear batteries [8-10], nuclear clocks [11, 12], and nuclear lasers [13].

NEEC has been the subject of extensive theoretical analyses and experimental proposals since it was first reported nearly half a century ago, but it is yet to be confirmed experimentally. These efforts encompass a range of methodologies, including the use of cooling storage rings [14], ion accelerators [15-19], electron beam ion traps (EBIT) [20], and others based on laser-induced plasma [7, 21-23].

The primary challenge in detecting NEEC is the presence of substantial background noise. Pálffy et al. noted that by employing a Feshbach projection operator formalism to derive cross-sections of various processes during electron capture [24], including NEEC, dielectronic recombination (DR) [25], and radiative recombination (RR) [26], notable DR and RR processes generate signals that closely mimic those from NEEC, thereby introducing significant background noise in experiments [27, 28]. This issue is particularly evident in experiments involving the isomer ^93mMo, where a significant discrepancy exists between the theoretical predictions and experimental results. Signals initially attributed to NEEC were later suspected to have originated from other mechanisms [17, 18, 29-32].

In addition to the basic NEEC process, several other variants have been extensively explored in the literature. These include NEEC with X-rays (NEECX) [33], NEEC in excited ions (NEEC-EXI) [34, 35], and NEEC with vortex beams [36]. NEECX involves the capture of an electron into an excited atomic orbital rather than the ground state, followed by the emission of an X-ray photon [33]. This process facilitates coincidence measurements by simultaneously detecting the x- and γ-photons. On the other hand, NEEC-EXI is the process in which an electron is captured to an inner-shell vacancy in an atom that is already in an excited state [34].

NEEC with vortex electron beams introduces additional intriguing features into the study of NEEC. Vortex beams, distinguished by their helical wavefronts, carry an intrinsic orbital angular momentum (OAM) along the propagation direction [37-41]. This intrinsic OAM of vortex states introduces an additional degree of freedom compared with plane-wave states by introducing new selection rules for nuclear processes, offering novel opportunities in the study of nuclear excitation processes. Since the initial proposal concerning optical vortex beams in Ref. [42], optical vortices have garnered significant interest, leading to a plethora of remarkable achievements and applications. Vortex photons have been intensively studied in fields such as quantum communications, nonlinear optics, optical trapping, microscopy, nanotechnology, astrophysics, and manipulations of atomic transitions [37, 38, 43, 44]. In the context of NEEC, the use of electron vortex beams is expected to enhance the cross-section by up to four orders of magnitude [36].

In short, NEEC provides a quantum many-body platform that involves the interplay between atomic and nuclear systems. However, despite its fundamental nature, the process is not yet fully understood. In this mini-review, we begin with a historical overview of the theoretical work on NEEC, followed by an examination of the role of NEEC in astrophysical environments and laser-induced plasmas. In addition, the current status of NEEC studies using vortex beams and traditional accelerators is discussed. Finally, a brief summary of the proposed methods is presented.

Theoretical cross-section calculation of NEEC

In the theoretical treatment of the NEEC process, the capture of a free electron into a bound state by a positively charged ion is considered, which leads to the excitation of the nucleus. Typically, a γ-photon is emitted as follows. A Feynman diagram illustrating this process is presented in Fig. 2, involving two steps and three states. The initial state is represented by $| i 〉 = 〈 p m_{s}, I_{i} M_{I_{i}}, n_{k σ} = 0 〉$ , where p denotes the momentum of the free electron and ms is the spin in the z-direction. The nucleus is in its ground state with angular momentum Ii and z-component $M_{I_{i}}$ . The term $n_{k σ} = 0$ indicates the absence of photons. The intermediate state, $| d 〉 = | n l_{j_{d}}, I_{d} M_{I_{d}}, n_{k σ} = 0 〉$ , features the electron captured into the orbital $n l_{j_{d}}$ and the nucleus in the excited state $| I_{d}, M_{I_{d}} 〉$ , with no photons present. The final state, $| f 〉 = | n l_{j_{d}}, I_{i} M_{I_{i}}, n_{k σ} = 1 〉$ , depicts the electron remaining in the orbital $n l_{j_{d}}$ , the nucleus returned to its ground state $| I_{i}, m_{I_{i}} 〉$ , and the emission of photons, where $n_{k σ}$ is the number of photons with polarization $σ = \pm 1$ and wave vector k.

Fig. 2

The Feynman diagrams of the NEEC process. The “ⓔ” indicates that the electron is in an atomically bound state, while “e” denotes an electron in a continuum state. “N” represents the nucleus in its ground state, and “N^*” indicates the nucleus in an excited state

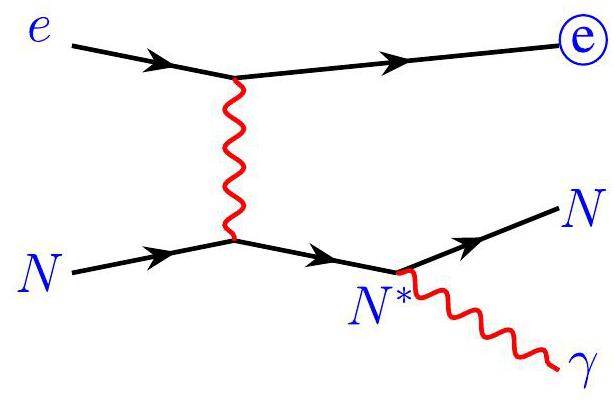
In this treatment, the nuclear excitation results from a time-dependent electromagnetic field acting on the nucleus. Typically, the influence of this field is minimal and can be effectively addressed using first-order quantum-mechanical perturbation theory. The excitation probability can be expressed in terms of the same nuclear matrix elements that govern radiative transitions between nuclear states. Detailed illustrations of the main physical features of this process are provided in Ref. [24]. In the following discussion, we present the mathematical results of the quantum-mechanical theory for the NEEC process.

The cross-sections of the NEEC process for a free electron with kinetic energy ε are expressed as follows: [24]: $σ_{i \to d \to f} = \frac{2 π^{2}}{p^{2}} \frac{A_{r}^{d \to f} Y_{n}^{i \to d}}{Γ} L (ε - ε_{0}),$ (1) where $p^{2} c^{2} = ε^{2} + 2 ε m_{e} c^{2}$ is the free-electron momentum. Given that NEEC is a resonant process, a Lorentz profile is essential. $L ((ε - ε_{0}) = \frac{Γ / 2 π}{{(ε - ε_{0})}^{2} + \frac{1}{4} Γ^{2}} .$ (2) The resonance energy ε₀ is determined by $ε_{0} = Δ E - E_{b}$ , where ΔE is the transition energy of the nucleus and Eb is the absolute value of the binding energy of the orbital $n l_{j_{d}}$ . The width of the excited level Γ is given by $Γ = A_{r}^{d \to f} + \frac{2 I_{d} + 1}{2 I_{i} + 1} Y_{n}^{i \to d},$ (3) which consists of the electron capture rate $Y_{n}^{i \to d}$ and photon emission rate $A_{r}^{d \to f}$ , representing the reaction rates for the excitation and de-excitation steps, respectively.

As previously noted, electromagnetic excitation involves the same nuclear matrix elements as the radiative transitions of the corresponding multipole order. Thus, for a given multipolarity $λ L$ with $λ = E / M$ , the photon emission rates Ar are determined by the reduced transition matrix elements as shown in Ref. [45]. $A_{r} = \frac{8 π (L + 1)}{L {[(2 L + 1)!!]}^{2}} \frac{ε^{2 L + 1}}{c} B ↓ (λ L, I_{d} \to I_{f}),$ (4) where $B ↓$ is the reduced nuclear transition probability for the decay. The electric (EL) and magnetic (ML) components of the electron capture rates Yn are given by Ref. [46] $\begin{array}{l} Y_{n}^{(E L)} = & \frac{4 π^{2} ρ_{i}}{{(2 L + 1)}^{2}} B ↑ (E L, I_{i} \to I_{d}) (2 j_{d} + 1) \\ \times \sum_{κ} | R_{L, κ_{d}, κ}^{(E)} |^{2} C {(j_{d} L j; \frac{1}{2} 0 \frac{1}{2})}^{2}, \end{array}$ (5) $\begin{array}{l} Y_{n}^{(M L)} = & \frac{4 π^{2} ρ_{i}}{L^{2} {(2 L + 1)}^{2}} B ↑ (M L, I_{i} \to I_{d}) (2 j_{d} + 1) \\ \times \sum_{κ} {| R_{L, κ_{d}, κ}^{(M)} |}^{2} (2 j + 1) {(κ_{d} + κ)}^{2} {(\begin{matrix} j_{d} & j & L \\ \frac{1}{2} & \frac{1}{2} & 0 \end{matrix})}^{2}, \end{array}$ (6) where ρi is the density of initial electronic states. The relation of reduced transition probability between the excitation $B ↑$ and decay $B ↓$ of the nuclear state is given by $B ↑ (λ L, I_{i} \to I_{d}) = \frac{2 I_{d} + 1}{2 I_{i} + 1} B ↓ (λ L, I_{d} \to I_{i})$ . Other parameters, including jd, j, and κ, are related to the electron orbital $n l_{j_{d}}$ . The radial integrals involved in these calculations are given by [46], $R_{L, κ_{d}, κ}^{(E)} = \int_{0}^{\infty} d r r^{- L + 1} (f_{n_{d} κ_{d}} f_{ε κ} + g_{n_{d} κ_{d}} g_{ε κ}),$ (7) $R_{L, κ_{d}, κ}^{(M)} = \int_{0}^{\infty} d r r^{- L + 1} (g_{n_{d} κ_{d}} f_{ε κ} + f_{n_{d} κ_{d}} g_{ε κ}),$ (8) where $f_{ε κ} (r)$ and $g_{ε κ} (r)$ in the integrals are the components of the partial-wave expansion of the continuum electronic wave function. $f_{n_{d} κ_{d}} (r)$ and $g_{n_{d} κ_{d}} (r)$ are the functions that represent the bound electronic states, and they can be computed using atomic codes such as GRASP92 and AMBiT.

NEEC in astrophysical environments

The NEEC process can significantly affect astrophysical plasmas by altering the proportion of nuclear isomers present, similar to the influence of other nuclear reactions [47]. Its effects may vary with the plasma temperature, which influences the electron energy distribution. Further research is required to clarify the role of NEEC in these environments and understand its potential impact on the behavior and evolution of astrophysical plasmas.

3.1

NEEC in astrophysical plasma

The role of NEEC in cosmic nucleosynthesis is poorly understood. Astrophysical nucleosynthesis calculations are dependent on accurate nuclear reaction rate inputs, and NEEC cross-sections could be critical for certain nuclear reactions within astrophysical plasmas. Considering that nucleosynthesis is a network of reactions, it is crucial to recognize that a single reaction rate can profoundly influence the astrophysical evolution. NEEC may significantly affect the production of isomers, thereby influencing nucleosynthesis processes.

A nuclear isomer is an excited state in which the structural effects within the nucleus inhibit its decay, potentially granting the isomeric state a longer lifetime than those of ordinary nuclear states. Known nuclear isomers exhibit a remarkable range of lifetimes, from 10¹⁵ years for ^180mTa—exceeding the widely accepted age of the universe—to as short as approximately 1 ns, as is commonly recognized [48, 49]. From the perspective of isomer types, while shape isomers, spin traps, and seniority isomers tend to be concentrated in narrow mass regions on the nuclear chart, K-isomers are more broadly distributed, particularly in heavy and well-deformed nuclei [50].

Isomers are noteworthy not only for their unique intrinsic properties but also for their potential practical applications. The energy density of conventional energy sources relies on chemical processes, and is fundamentally determined by the energy stored in chemical bonds—the so-called “chemical limit.” To overcome this limitation, it is necessary to explore the subatomic realm. Particularly interesting are nuclear isomers with half-lives of approximately one year or more. When energy is required, the reduction of the isomer population can be induced by providing the appropriate energy to excite the nucleus from the isomer to a higher state (referred to as the triggering level), and then allowing it to decay to the ground state via paths that bypass the isomer [51-53]. This process results in the release of energy on a much smaller time-scale than the natural decay of isomers. Among the proposed triggering processes, the triggering of long-lived nuclear isomeric states via coupling to the atomic shells in the NEEC process has attracted significant interest [14].

Low-lying triggering levels are desirable for obtaining a high-energy gain [54]. Identifying suitable triggering levels above the isomer is crucial to facilitate decay. For instance, most isomers, such as the 103.00 keV isomer in ⁸¹Se, predominantly transition to lower energy states, with transitions to the ground state occurring 99.949% of the time [55]. A sufficient connection to the ground state ensures that the destruction of the isomer does not deviate from the thermal equilibrium. Historically, the depletion of ^178m2Hf by low-energy (∼10 keV) photons was claimed by Collins et al. [56], but was subsequently refuted by more sensitive measurements [57, 58]. Thus, while an isomer with a long lifetime may prevent thermalization at low temperatures, in a hotter environment, thermally driven transitions through intermediate states can enable equilibration.

In addition, some isomers isolated from the ground state in the astrophysical sites where they are produced are not populated during the production of the nucleus. Thus, although some isomers play an influential role in astrophysical nucleosynthesis, most do not. This distinction leads to the definition of “astrophysical isomers” or “astromers” as nuclear isomers that have a significant influence in a specific astrophysical environment. Unlike their associated ground states, astromers behave differently and should be treated as separate species within nucleosynthesis networks. These networks may involve transitions that create and destroy these states [59].

In astronomical environments, the dynamics are governed by a multitude of microscopic processes, including electromagnetic processes such as ionization and RR, as well as nuclear reaction processes. The first two are crucial for maintaining charge balance and primarily occur between electrons and ions. Meanwhile, nuclear reaction processes may involve not only nuclei but also atoms, as seen in the case of NEEC. Cosmic plasmas are created through ionization, which can occur in several ways, including collisions of fast particles with atoms, photoionization by electromagnetic radiation, or electrical breakdown in strong electric fields. The charge state of the plasma is determined by the balance between ionization and recombination, with RR contributing significantly. Free electrons, abundant in astrophysical environments, are fundamental to the NEEC process. Thus, NEEC potentially plays a crucial role in nuclear excitation through electromagnetic interactions between electrons and ions during the recombination process.

Numerous nuclear interactions contribute to the production of elements during cosmic nucleosynthesis. Most of the hydrogen (H) and helium (He), along with a small amount of lithium (Li), were formed during the first 3 min following the Big Bang. This early element formation is a key aspect of Big Bang Nucleosynthesis [60-63], where the heavier elements required for the formation of complex matter, including organic matter and life, are predominantly produced through fusion processes. In addition, isotopes of elements heavier than iron (Fe) are primarily synthesized via neutron-capture processes (n-capture), including slow (s) and rapid (r) neutron-capture mechanisms. This is due to the strong Coulomb barrier that prevents their formation by fusion alone [60, 64-66].

The potential role of NEEC in the depletion or accumulation of isomeric states within highly charged ions in dense stellar plasmas, particularly in the context of the s-process, has attracted significant attention[47, 67-69]. During this process, a seed nucleus undergoes neutron capture to form an isotope with a higher atomic mass, followed by beta decay if it is unstable. Notably, nuclei along the s-process path tend to remain in isomeric states when the condition $τ_{β} ≪ τ_{n}$ is met, where $τ_{β}$ is the beta decay lifetime and τn is the timescale for capturing an extra neutron. Gan et al. have concluded that NEEC should play a significant role in depleting the isomeric states of ^58mCo, ^121mSb, and ^152mEu by providing an effective isomer-depletion channel [69].

Beyond affecting isomeric depletion, any nuclear reaction chain involving an intermediate isomeric state can be affected by the NEEC process. For example, consider the $A - i - B$ reaction sequence, where i represents an isomeric state. NEEC adds a new dimension by introducing an additional reaction step, $A - i - j - B$ , where $i - j$ symbolizes the NEEC-induced excitation of isomeric state i before it decays. This can potentially affect reactions such as ⁵⁷Co-^58m1Co(-^58m2Co)-⁵⁸Co [69].

NEEC is especially advantageous in extremely hot plasmas, which are better settings where NEEC can significantly influence nuclear reactions. This is because the reaction rate of NEEC increases as the charge states of ions increase [24]. Therefore, when performing astrophysical nucleosynthesis calculations, it is essential to incorporate NEEC rates (λNEEC) for ions with zero, one, or two initially bound electrons into the nuclear reaction rate inputs.

To put it succinctly, viewing nucleosynthesis as just a series of interconnected reactions may be too simplistic. Recognizing that a single reaction rate, including NEEC, can have a profound impact on astrophysical evolution is vital. NEEC can significantly affect both the accumulation and depletion of isomers, thereby playing a pivotal role in nucleosynthesis.

3.2

Nuclear structure models for $B (π L)$

In the NEEC process, identifying the NEEC rate is dependent on understanding the transition probabilities from the isomer to the triggering level [24]. These probabilities, which are crucial for evaluating the efficiency of triggering, is dependent on both the nuclear transition selection rules and the structural characteristics of the isomer and triggering level. If these transition probabilities have not been measured experimentally, they must be estimated using reliable nuclear structure model calculations.

For instance, in the case of the 21/2⁺ isomer in ⁹³Mo (with excitation energy Ex = 2.425 MeV and half-life $τ = 6.85$ h), the critical transition for triggering the isomer was identified as the E2 transition connecting the 21/2⁺ isomer to the upper 17/2⁺ level. Hasegawa et al. predicted that this level, lacking experimental data, would have a substantial transition probability of 3.5 W.u. through nuclear shell model calculations. Consequently, it was concluded that there was a substantial prospect for observing induced isomer de-excitation if the 17/2⁺ level as the triggering level can be properly populated [70]. Indeed, subsequent experimental and theoretical discussions [17, 31, 32, 71, 72] have relied significantly on this transition probability.

To adequately account for the structure of the isomers and triggering levels in discussions, theories aimed at calculating the NEEC cross-sections must incorporate dedicated nuclear structure models. This critical integration of NEEC theory with modern nuclear structure models, which would enable a microscopic description of the interaction between the nuclear and atomic levels, remains an unfulfilled need. Among existing modern structure models, the nuclear shell model is the preferred choice [73-75].

The shell model provides a powerful framework for detailed nuclear structure studies that are crucial for understanding nuclear isomers and their effects under various conditions. This is because theoretical states in these calculations must be eigenstates of basic quantum numbers, such as angular momentum, parity, and isospin, given that all nuclear transitions occur between the initial and final states with well-defined quantum numbers. Shell model calculations typically require significant computational resources. Thus, a minimal set of basis states that adequately captures the essential physics is sought. For nuclei that are neither heavy nor strongly deformed, only a limited number of single-particle states are used to define the low-energy structure. In such cases, the conventional spherical shell model can leverage the reduced basis to compute relevant quantities efficiently. Upon completion of these calculations, all levels, including isomers and triggering states and the transitions among them, are expected to be described consistently within the designated model spaces.

Except for nuclei near shell closures, the majority of nuclei on the nuclear chart exhibit are deformed, posing a significant challenge to the conventional spherical shell model because of the inevitable issue of dimensional explosion. Consequently, the exploration of nuclear structures in heavier, deformed nuclei—where most K-isomers are found—has predominantly relied on deformed mean-field approximations [76]. These models employ the concept of spontaneous symmetry breaking, where the angular momentum—a crucial quantum number for describing nuclear states—is not conserved in the calculations. Over the years, considerable efforts have been dedicated towards advancing beyond mean-field descriptions to develop shell models in which all excited states are exact eigenstates of the angular momentum. It has been emphasized that the angular momentum projection technique is an essential quantum-mechanical tool, with the projected shell model (PSM) [77] emerging as a practical model specifically tailored for the study of K-isomers.

Thus, for the microscopic study of nuclear isomeric states in general, and the NEEC process in particular, two distinct types of shell models are applicable, sharing the same conceptual framework but differing in their implementation. The first is the conventional shell model (CSM) that utilizes a spherical basis. The CSM calculation process is conceptually straightforward: it involves constructing a many-body configuration basis, selecting an appropriate Hamiltonian for this basis, and performing numerical diagonalization [78, 79]. Ideally, such calculations would yield a comprehensive excitation spectrum including low-energy collective states, isomers, and normal states. However, in practice, employing such a CSM to study arbitrarily heavy, deformed nuclei is impractical because of the huge dimensionality of the configuration space and related computational challenges. Even with current computational capabilities, standard CSM calculations are only feasible up to the mass-70 region, where the dimensions of the configuration space can approach one billion. For heavier mass regions, the general application of the CSM is untenable, and only a few selective calculations are possible for nuclei near closed shells.

In contrast, the PSM presents an unconventional approach [77] that significantly diverges from the CSM in both its implementation and targeted nuclei. The PSM utilizes angular momentum projection, which is an effective method for truncating the shell model space that would otherwise be unmanageably large [77]. This methodology—pioneered by Hara and Sun in their early work [80]—has undergone significant evolution over the years, and has been successfully employed in the nuclear spectroscopy of a wide range of isotopes on the nuclear chart [81, 82]. The representative calculations range from light [83] to heavy nuclei [84], and even extend to the superheavy mass region [85-87], thereby providing insights into the anticipated superheavy island of stability. Moreover, the PSM has been utilized in studies of nuclei exhibiting normal and super deformations [86, 87], and in advanced studies on exotic nuclear shapes, including the coexistence of reflection asymmetric and symmetric shapes, as detailed in Ref. [88].

Recently, the PSM has been noticeably expanded to include studies on nuclear-level density [89], marking a milestone where shell model calculations have addressed nuclear levels on the order of 10⁶ per MeV for the first time. Within the PSM framework, it is now feasible to simultaneously explore the properties of nuclear isomers and their associated triggering levels. This expansion may have far-reaching implications for the study of isomers in nuclear astrophysics, particularly in scenarios encountered in nucleosynthesis simulations involving the transmutation of nuclei via nuclear reactions and decays in thermally excited environments. In the absence of sufficient structural information on excited nuclear states, current nucleosynthesis calculations typically adopt one of two approaches to approximate nuclear transmutation rates [90]. The simpler approach neglects excited states and focuses solely on the ground-state properties of nuclei, as exemplified by discussions on neutrino luminosity via the Urca process [91, 92]. Alternatively, some models assume a thermal equilibrium population of excited states, with each state contributing to the overall rate of transmutation based on its thermal population probability [93]. However, as demonstrated by Misch et al. [59], depending on the specific astrophysical environment, nuclear isomers may challenge the validity of these conventional approaches. Notably, Wang et al. provided initial examples [94] demonstrating that the manifestation of isomer effects through the NEEC process is viable. This suggests the need for further investigation into appropriate astrophysical environments.

NEEC in Laser-induced Plasmas

The interactions between photons and matter remain a cornerstone of modern physics. The development of advanced laser technologies, particularly chirped pulse amplification (CPA) [95], has facilitated the creation of environments characterized by ultra-intense and ultra-short electromagnetic fields. When subjected to such fields, target atoms undergo ionization, leading to plasma formation. These plasmas possess electromagnetic fields significantly stronger than those produced by traditional magnetic systems. In such environments, the electrons and ions could be accelerated followed by a series of atomic and nuclear interactions [96-98]. The generated plasmas can achieve extremely high temperatures and densities, which can trigger a complex sequence of nuclear reactions, including the excitation, transformation, and decay of nuclei. Thus, intense laser-matter interaction produces plasmas containing free electrons and various ionic states [7, 19, 71, 99-103].

4.1

Laser-induced plasma

The invention of the laser in 1960 was a groundbreaking development, marking the first instance of coherent control over light. This milestone led to rapid advancements in laser technology, notably in the compression of laser pulse durations and the corresponding increase in peak intensities. The proposal and realization of CPA technology have significantly advanced these developments, bringing laser pulse durations into the femtosecond and even attosecond regimes, while dramatically enhancing laser intensities [95]. By 2023, three scientists received the Nobel Prize for their contributions to attosecond-pulse technology [104-106], underscoring the profound impact of this advancement. In contemporary settings, femtosecond laser pulses can achieve focused intensities as high as 10²² W/cm² in laboratory environments [107-109]. At such high intensities, the oscillating electric field of the laser significantly surpasses the internal electric field of atoms, quickly ionizing them into a plasma state. Consequently, the study of laser-plasma interactions has emerged as one of the most dynamic areas within the field of plasma physics [110].

The acceleration of electrons and ions driven by laser-plasma interactions provides an ideal experimental platform for investigating photon-nucleus and electron-nucleus reactions. These include photon excitation (PE) [111], Coulomb excitation (CE) [112-115], nuclear excitation by electronic transition (NEET) [116-120], electron bridge [12], and photonuclear reaction (γ, n) [7, 121, 122]. While both CE and NEET have been experimentally confirmed, NEET typically exhibits a much smaller cross-section than other processes. The dominant process or processes for nuclear excitation depend critically on specific laser parameters and plasma conditions [99, 123]. Therefore, meticulous calculations, simulations, and experimental investigations are necessary to determine whether NEEC or other competing nuclear excitation mechanisms predominate under particular experimental conditions.

4.2

Laser-ablated plasma

Laser ablation on a solid surface is a convenient method for plasma generation. The temperature and density of electrons within this plasma are highly sensitive to both position and time. By combining rough estimates of plasma density and temperature with the cross-sections of each relevant nuclear and electronic process, it is possible to approximate the rates of NEEC, NEET, nuclear excitation by inelastic electron scattering (NEIES), DR, and RR [22, 23, 102].

Subsequent studies have refined the determination of plasma conditions by simulating plasma dynamics from their generation to diffusion. Gunst et al. investigated NEEC processes in a cold, dense plasma environment induced by X-ray free-electron laser pulses irradiating an ⁹³mMo target [124]. Wu et al. investigated NEEC processes in a femtosecond laser-ablated plasma using a comparable target [72, 125]. Variations in laser parameters led to plasmas with different temperatures and densities, which were leveraged in these studies to identify optimal experimental setups for observing the NEEC process. In studies conducted by these researchers, it was emphasized that to effectively induce NEEC events while simultaneously minimizing background noise from processes such as RR and PE, the plasma temperature and density must be maintained at relatively low levels. For instance, laser intensities in the order of 10¹⁴–10¹⁶ W/cm² with energy ranges between 10 and 100 mJ are employed to generate plasma, resulting in a cold plasma where the thermal photon flux is insufficient to induce the PE of the nucleus, suppressing the NEIES process [72, 126, 127]. Concurrently, the nuclear energy gap should be appropriately low, on the order of several keV, which aligns with the region of cold plasma that corresponds to the highest density of electron energies. Examples include the 1.565 keV transition in ²⁰¹Hg, 1.642 keV transition in ¹⁹³Pt, 2.329 keV transition in ²⁰⁵Pb, and 4.821 keV transition in ¹⁵¹Sm, as listed in Ref. [128].

In cases where secondary X-rays are generated via inner-shell processes, such as those noted in Ref. [72], it must be ensured that the plasma density remains sufficiently low to maintain the stability of inner-shell vacancies, as higher densities would lead to rapid depletion of these vacancies due to RR processes.

Borisyuk et al. conducted an experiment focusing on the isomeric excitation of ²²⁹Th utilizing a Nd:YAG laser to ablate a Th:SiO₂ target containing 6.8% of ²²⁹Th [19]. They measured the energy levels and half-life of the generated ²²⁹Th isomer. Their theoretical calculations showed that nuclear excitation was induced by the NEEC process. However, the study did not provide detailed analyses to rule out other nuclear excitation mechanisms, leaving it unclear whether NEEC was indeed the dominant mechanism in this scenario.

4.3

Laser-heated cluster

The interaction between intense laser pulses and atom clusters offers a unique plasma environment that is well-suited for verifying NEEC [129]. Qi et al. proposed a method using laser-cluster interactions to excite ²²⁹Th from its ground state to its isomeric state [127]. Their calculations indicated that isomeric excitation was primarily driven by NEEC and NEIES. By adjusting the laser intensity, it was possible to continuously tune between NEEC and NEIES, providing an approach to confirm the NEEC.

Laser-heated clusters, although nanometer-sized plasmas, exhibit characteristics distinct from those of ablation plasma plumes. First, cluster nanoplasmas possess simpler plasma characteristics and dynamics, allowing more effective characterization. Second, they exhibit significantly higher electron densities, which highlight the importance of NEEC and NEIES over other mechanisms. To further isolate the NEEC, specific laser intensities can be employed to emphasize the NEEC while minimizing the contribution from the NEIES. Recently, Qi et al. demonstrated that the interaction between intense laser pulses and ²³⁵U clusters provides an ideal system in which the NEEC process accounts for over 99.9% of the nuclear isomeric excitation [126].

4.4

Pros and cons of using laser-ablated plasma

Here, we outline the advantages and disadvantages of verifying NEEC using laser-generated plasmas. The advantages include the following:

(i) Laser-generated plasmas provide a relatively well-controlled experimental environment in which plasma parameters, such as temperature, density, and composition, can be precisely adjusted and quantitatively measured, facilitating systematic investigations of NEEC under controlled environmental conditions.

(ii) The ability of laser-generated plasmas to achieve certain temperatures and densities increases the likelihood of NEEC occurrences, providing a suitable setting for the observation and study of this phenomenon.

(iii) Laser-generated plasma experiments enable the exploration of a wide energy range relevant to NEEC. This capability allows the investigation of various nuclear systems and energy regimes (e.g., 8 eV for ²²⁹Th, 76 eV for ²³⁵U, and 4.8 keV for ⁹³Mo) by adjusting laser parameters.

The disadvantages of employing laser-generated plasmas for investigating NEEC include the following:

(i) The lifespan of laser-generated plasmas is short because of rapid cooling and expansion, and restricts the temporal window available for NEEC occurrences, potentially limiting the experimental observation and analysis of the process.

(ii) Laser-generated plasmas allow multiple nuclear excitation mechanisms, such as NEEC, NEIES, NEET, and optical excitations. For instance, in cluster nanoplasmas, nuclear excitation predominantly arises from NEEC and NEIES, while in plasmas generated by more intense lasers, NEET may predominate. Therefore, detailed calculations are imperative to determine optimal laser parameters to emphasize NEEC over competing processes.

(iii) Interactions within a laser-plasma environment can introduce additional effects such as electron heating, ionization, and charge screening, each of which can influence nuclear excitation processes. Accurate simulations and accounting for these effects are necessary to approximate the actual conditions within the plasma.

NEEC Studies with Vortex Beams

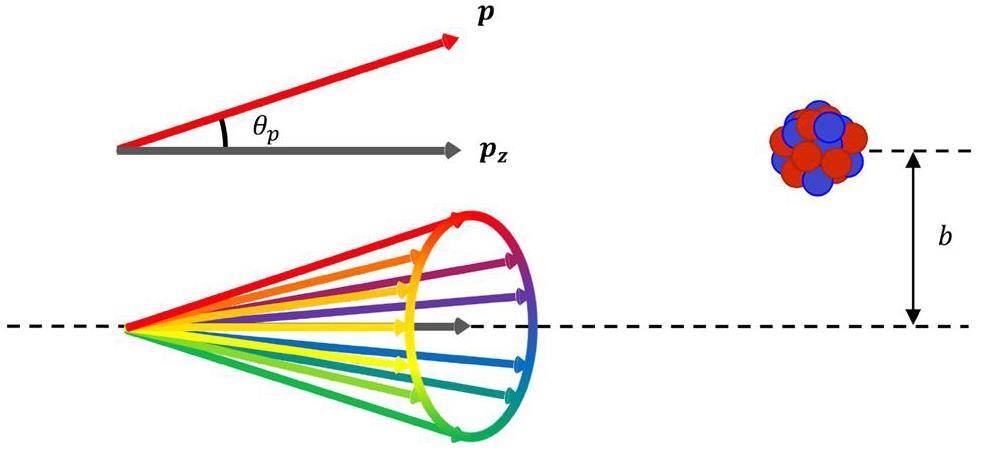
Vortex light beams (Fig. 3), first proposed in the 1990s [42], represent a transformative development in photonics. These beams are characterized by photons that carry not only intrinsic spin angular momentum but also OAM. The inclusion of intrinsic OAM introduces a new degree of freedom, distinguishing vortex states from traditional plane-wave states and inspiring the extensive exploration of novel phenomena in atomic and nuclear physics. For instance, theoretical studies on the photodisintegration of deuterons using twisted photons were discussed in Ref. [130, 131]. These studies examined the dependence of the photodisintegration cross-section on the impact parameter b, i.e., the distance between the target nucleus and vortex beam axis. These studies also identified the increased threshold energy required for the reaction, along with interesting features of selection rules for small-impact parameters. Similarly, hadron excitation induced by vortex photons was analyzed in Ref. [132]. More recently, theoretical studies on giant multipole resonances in nuclei induced by vortex γ-photons were presented in Ref. [133, 134]. These investigations highlight the potential for manipulating the excitation of giant multipole resonances by vortex γ-photons, facilitating transitions that are otherwise forbidden or enabling quasi-pure transitions, provided that the nucleus is precisely aligned with the vortex beam axis [133].

Fig. 3

(Color online) Composition of a vortex beam. A vortex beam is formed by the coherent superposition of plane waves arranged in a conical configuration. This arrangement gives rise to a helical phase structure and imparts orbital angular momentum to the beam. θp is the top angle of the cone, while b represents the impact parameter, defined as the perpendicular distance from the beam axis to the target

Recent advancements in fabricating phase masks with nanometer-level precision have enabled unprecedented control over the coherent superposition of matter waves, facilitating the generation of vortex beams with chiral wave-function spatial profiles that carry the OAM [135-139]. By imparting chirality to massive particles, vortex beams have been proposed as novel tools for studying [39-41, 44, 140] and even manipulating [138, 141-143] the structural properties of neutrons, protons, ions, and their associated particle and nuclear processes. Electron vortex beams—among the most extensively studied massive-particle vortex beams—have been experimentally realized using various techniques such as holographic gratings, phase plates, magnetic monopole fields, and chiral plasmonic near fields [39-41, 44, 135-137]. These beams achieved angular momenta as high as $1000 ℏ$ , demonstrating their potential for advanced applications.

The potential of vortex electrons to advance nuclear physics has been extensively discussed in Refs. [40, 41, 41, 143]. In particular, the possibility of manipulating nuclear excitation via vortex electrons has been studied theoretically in the context of NEEC [36].

The NEEC cross-section with a vortex electron beam is expressed as [36] $σ (E) = \frac{4 π^{2}}{p J_{z}} Y_{n} L (ε - ε_{0}),$ (9) where p is the momentum of the electron, Jz denotes the total incident current, and Yn is determined by mapping the vortex beam onto the partial-wave expansion of the continuum electron wavefunction. $\begin{matrix} Y_{n} = \frac{b^{2}}{4 π} \int_{0}^{2 π} \int_{0}^{2 π} \frac{d α_{p}}{2 π} \frac{d α_{k}}{2 π} e^{i m (α_{p} - α_{k})} Y (p, k) \\ \times_{0} F_{1} (2; u), \end{matrix}$ (10) where $| p_{⊥} | = | k_{⊥} | = ζ$ , αp, and αk are the polar angles of the momentum components spanning the interval $[0,2 π)$ , and m denotes the electron OAM. The notation $_{0} F_{1}$ represents the confluent hypergeometric limit function, and $u = - b^{2} ζ^{2} [1 - cos (α_{k} - α_{p})] / 2$ . For a nuclear transition of multipolarity $λ L$ , we have $\begin{array}{l} Y (p, k) = & \frac{16 π^{3} (2 J_{g} + 1)}{(2 J_{i} + 1) {(2 L + 1)}^{2}} \\ \times B ↑ (λ L) ρ_{i} \sum_{κ, m_{l}} \frac{Y_{b}}{2 l + 1} Y_{l m_{l}}^{*} (θ_{k}, ϕ_{k}) \\ \times Y_{l m_{l}} (θ_{p}, ϕ_{p}), \end{array}$ (11) where Ji and Jg are the angular momenta of the initial and final electron configuration of the ion, respectively. The term $Y_{l m_{l}}$ denotes the spherical harmonics characterized by quantum numbers l and ml, with $θ_{p} (θ_{k})$ and $ϕ_{p} (ϕ_{k})$ being the polar and azimuthal angles of the electron momentum $p (k)$ in the spherical coordinate system of the ion, respectively. Details of the integrals 𝒴b can be found in the Supplementary Material in Ref. [36].

The recombination orbital of the electron and nuclear transition multipolarity determine the selection rules governing the angular momentum components of the incoming electron participating in the NEEC process. For plane-wave electrons, the wave function has a fixed partial-wave expansion across all multipoles. However, vortex electrons can be intentionally shaped to enhance the NEEC efficiency [36]. By analyzing isomer depletion in ^93mMo and ^152mEu, representative of E2 and M1 nuclear transitions, respectively, Ref. [36] demonstrates that vortex electrons with a suitable opening angle and quantum number for the OAM, and precise control of the distance between the ion and electron vortex axis, could significantly alter the isomer-depletion rate. These results highlight new possibilities for the dynamical control of isomer depletion and other nuclear processes.

It is important to emphasize that the remarkable features observed in nuclear processes involving vortex photons and electrons rely on the highly precise positioning of the nucleus relative to the vortex axis, at a scale comparable to the photon wavelength or the inverse transverse momentum of the vortex particle. This behavior has also been observed in studies of vortex photon interactions with atomic systems [43, 44, 144-147]. However, the typical energy scale of nuclear processes, which ranges from keV to several MeV, makes achieving such precision a significant experimental challenge [41]. The use of cold neutron vortex beams may reduce these experimental challenges, allowing the exploration of the intriguing features of vortex particles in nuclear processes [41, 130, 148, 149]. Nonetheless, further research is required to develop methods that relax these stringent conditions while enabling the observation of these features, particularly in the context of the NEEC process. Advancements in this area would be crucial for applications of vortex particles in the manipulation of nuclear processes via the coupling of nuclear and electronic degrees of freedom.

NEEC Studies Based on Accelerators

Another approach for studying NEEC in laboratory settings involves the use of accelerators where high-energy beams of highly charged ions are generated.

6.1

By Using a Storage Ring

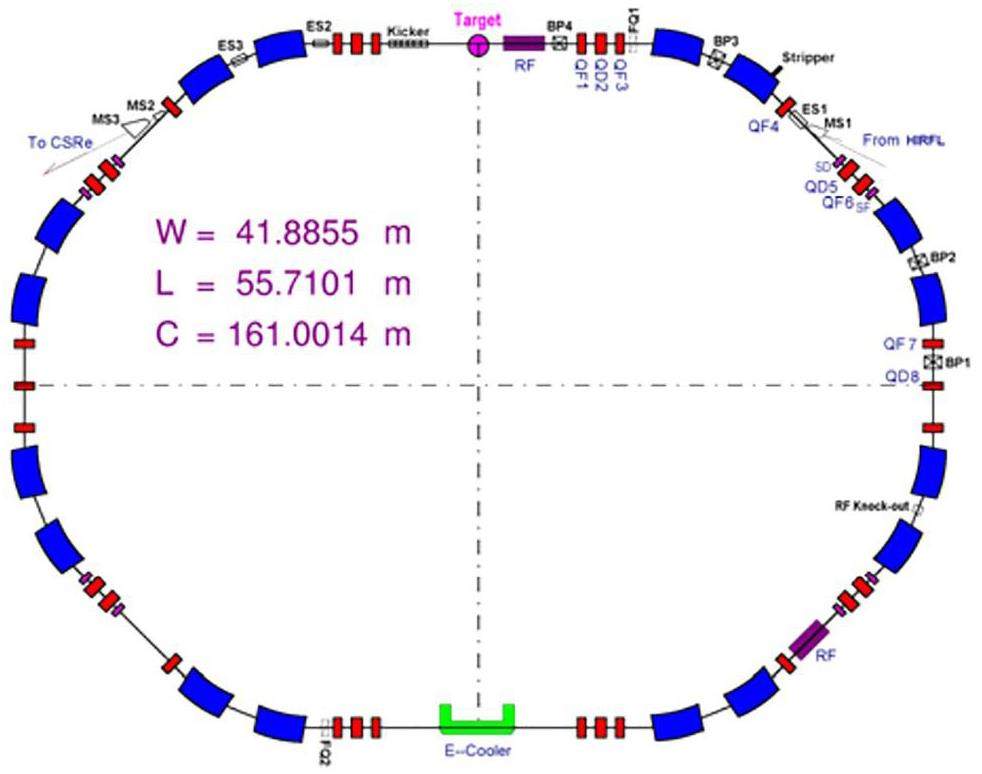
In a cooling storage ring, as illustrated in Fig. 4, a cooling electron beam is employed for ion-beam stability. This configuration facilitates electron-ion interaction experiments, which will enable the observation of the NEEC process. A heavy-ion storage ring provides an ideal experimental environment, in which relatively long-lived isomers interact with electron beams under controlled conditions, analogous to those in DR experiments [150-152].

Fig. 4

(Color online) The layout of the main cooler storage rings (CSRm) at Institute of Modern Physics, Lanzhou, China [153]

Palffy et al. proposed an experimental method for spatially separating photon emissions based on different timescales of the RR and NEEC processes, while also providing theoretical insights for enhancing the resonance strength of NEEC by introducing fast electronic X-ray decay [33]. In this approach, the RR process emits a photon within 10^-15 s, whereas the NEEC process emits the photon after the excited nucleus with time-scale of ns ~ μs. This temporal separation enables relatively pure confirmation of NEEC events through the detection of delayed photons.

A primary challenge in implementing this method is the efficient capture of excited isomers. Constructing a detector that encompasses the full circumference to capture all the emitted photons would be prohibitively expensive. Consequently, it is crucial to develop cost-effective techniques, such as coincidence detection, to enhance the efficiency of capturing these rare events [154]. As shown in Fig. 5, Yang et al. described the NEEC process that occurs within the interaction zone, where the circulating ion beam in the CSR interacts with an electron beam originally employed for beam stabilization. A photon detector array was positioned around the interaction zone, while ions—whose charge states were altered owing to the occurrence of NEEC or RR processes—were subsequently collected by a particle detector. The NEEC and RR events can be distinguished from each other by the emission time.

Fig. 5

(Color online) Proposed experimental layout for NEEC detection employing a storage ring

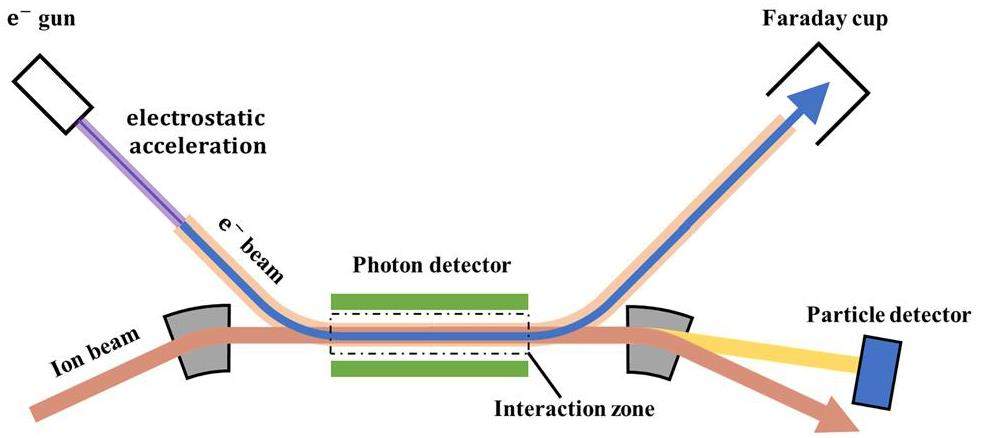
Adding another electron beam into storage rings, such as the High Intensity heavy-ion Accelerator Facility [155], holds significant promise for advancing NEEC experimental studies. This approach enables more precise and efficient detection methodologies, significantly expanding the range of isomers available for investigation compared with laser-induced plasma systems. The tunable energy of the electron beam offers enhanced control over resonance conditions, allowing access to a broader spectrum of nuclear energy levels.

6.2

By Using Ion Beams

When an ion beam is directed toward a solid target, the ions traverse the material and undergo continuous changes in direction and energy. Simultaneously, their excitation and ionization states may vary because of processes such as electron capture or loss [156-159]. Typically, as the velocity of ions decreases, their average charge state also diminishes. This variation depends significantly on the properties of the target material. During the stopping process, NEEC channels progressively close, beginning with outer orbitals and moving inward, as shown in Fig.6. For a given orbital, the resonance condition on energy is satisfied at a specific point during the stopping process. If the orbital is not firmly occupied, the corresponding NEEC channel can be activated during the stopping process.

Fig. 6

(Color online) Schematic diagram of nuclear excitation by electron capture in the ion-stopping process. Ek is the kinetic energy of a free electron in the centroid reference frame of the ion, while V denotes the potential energy of the electron orbitals

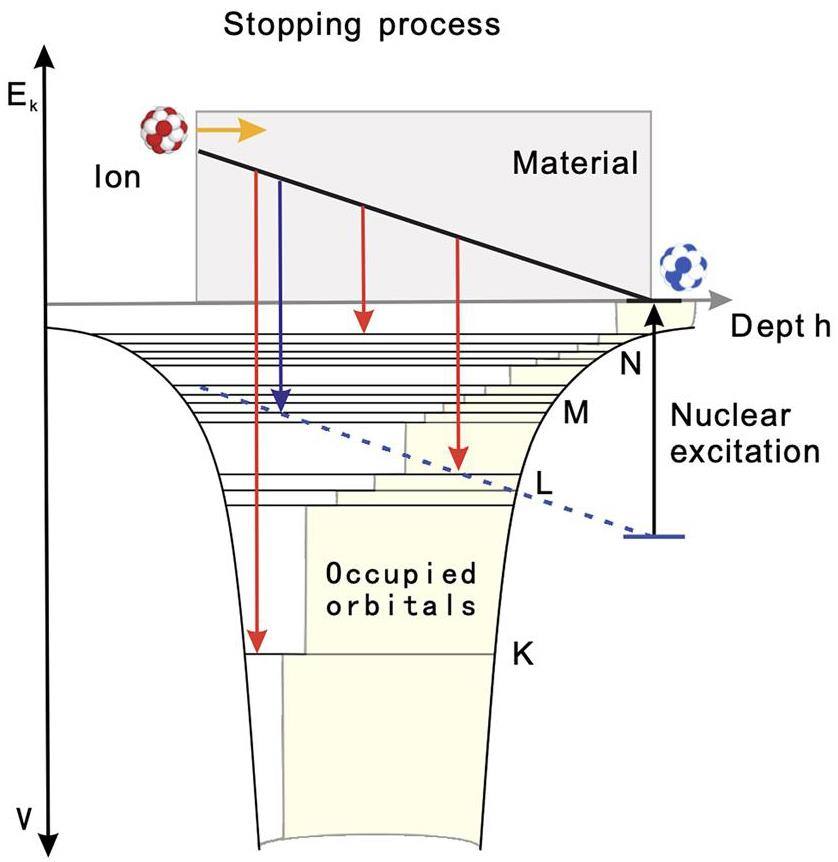
The number of active NEEC channels depends on the energy gap between the isomeric and triggering states. Therefore, the NEEC probability can vary significantly among different isomers. Based on theoretical predictions, several isomers have been proposed as candidates for experimental measurements. Among these, ^93mMo has attracted significant attention because of its favorable properties. This isomer has an excitation energy of 2425 keV, a half-life of 6.85 h, and spin and parity of 21/2⁺, as shown in Fig. 7a. A triggering state with 17/2⁺ lies just 4.8 keV above the isomeric state and has a half-life of 3.5 ns.

Fig. 7

(Color online) Structure of ⁹³Mo and the settings of two experiments. a) Level scheme of ⁹³Mo. b) The setting diagram of the experiment carried out at Argonne Laboratory in the United States. c) Schematic diagram of the experiment based on the Heavy Ion Research Facility in Lanzhou, China

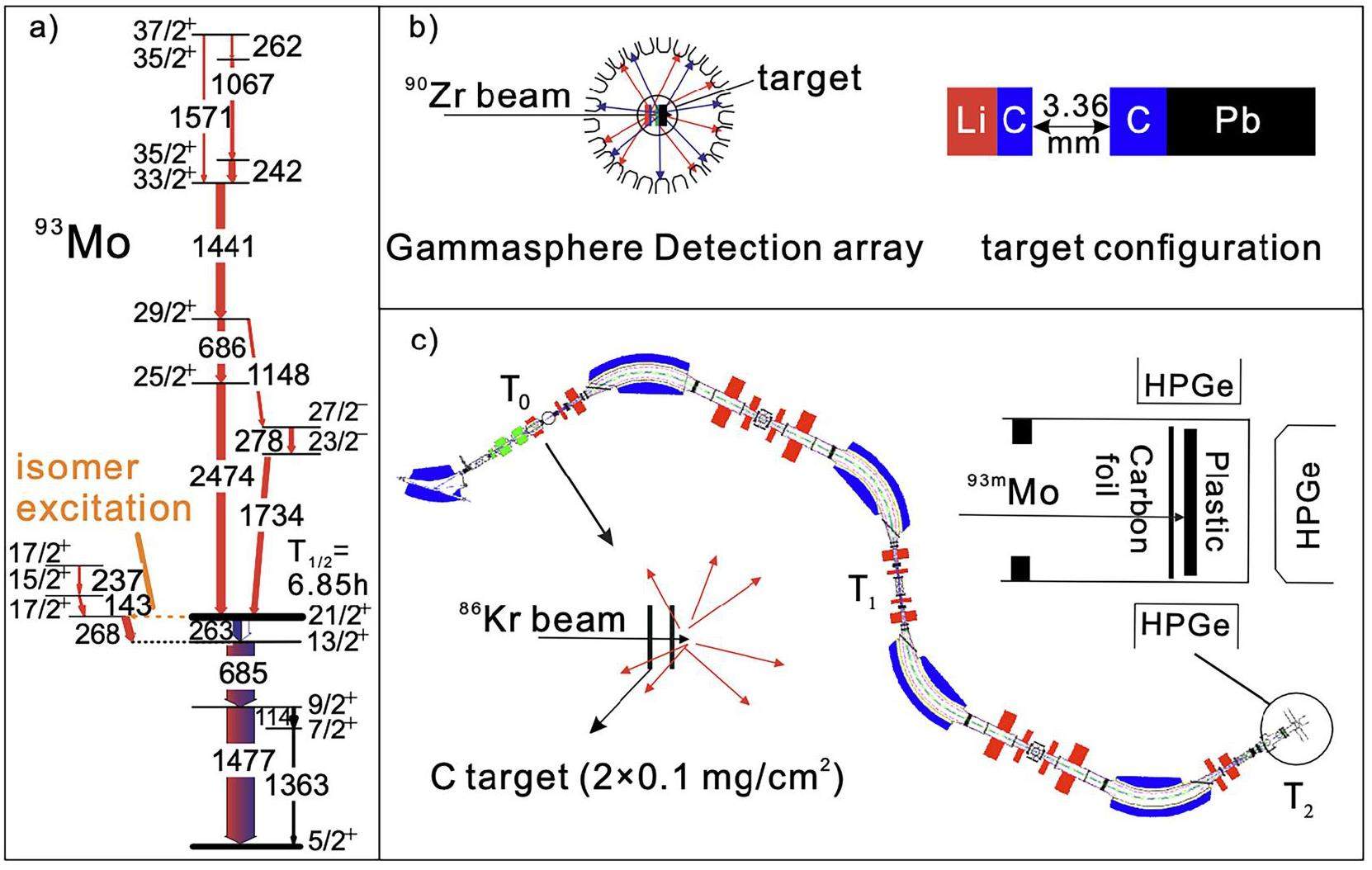
The first experimental observation of NEEC was reported by Chiara et al., with a probability of 0.010(3) for ^93mMo ions interacting with a carbon foil [17]. The measurements were conducted at the ATLAS facility at Argonne National Laboratory, utilizing the Gammasphere array to detect γ-rays, as shown in Fig.7b. In the experiment, ^93mMo ions were produced at the ⁷Li target bombarded by a ⁹⁰Zr beam with an energy of 840 MeV, implanted in a carbon foil located 3 mm away from the primary target, and finally stopped in the lead backing. The NEEC process was hypothesized to occur within the carbon foil, leading to the coincidence detection of γ-rays above the isomeric state and those below the triggering state. The γ-rays from states above the isomeric level exhibited Doppler shifts owing to the ionic motion, while those below the triggering state did not, as the ions stopped in the carbon and lead layers within a few picoseconds—a duration much shorter than the half-life of the triggering state.

From numerous triple- or higher-fold coincidence events, the coincidence between the 268 keV transition depopulating the triggering state and the transitions above the 21/2⁺ isomer was determined to be valid. Based on these results, a depletion probability of 0.010(3) was deduced. However, subsequent theoretical studies were unable to reproduce such a large probability; instead, they predicted a much smaller value of approximately 10^-11 [31].

Later, it was noted that the handling of the background in this experiment may have been overly idealized, potentially leading to an overestimation of the extracted NEEC probability. In a reply, Chiara et al. argued that the random coincidence could only contribute approximately 0.0008 to the reported probability, and the possible contamination of the reported spectra could be explained with some unpublished information [160].

To address the controversy surrounding the NEEC probability, another independent experiment was conducted at the Heavy Ion Research Facility in Lanzhou, as shown in Fig.7c [18]. In this experiment, an ⁸⁶Kr beam with an energy of 559 MeV was directed onto a carbon target positioned at T0 of the secondary radioactive ion-beam line (RIBLL) in Lanzhou. The resulting ^93mMo ions were transported by RIBLL to the detection station located at T2, and stopped in a plastic scintillator. The NEEC of ^93mMo ions was anticipated to occur during their deceleration in a 20μm-thick carbon foil located in front of the plastic scintillator. γ-rays emitted from the NEEC process and subsequent isomeric transitions were detected by five Compton-suppressed high-purity germanium detectors surrounding the plastic scintillator, while the prompt γ-rays from the primary fusion-evaporation reactions were emitted at T0 and did not contribute to the background of the measurement. The NEEC of ^93mMo was not observed in this experiment, with an upper limit of the NEEC probability of 2×10^-5.

However, the recoiling energy in the latter experiment was considerably lower, and the stopping materials differed between the two experiments. Consequently, the debate persists from both experimental and theoretical perspectives. Further experiments are required to provide conclusive evidence to resolve these discrepancies.

6.3

By Using Electron Beams

Because NEEC is a resonant process, the selection and preparation of appropriate energy levels and ion charge states are critical for its successful observation. An EBIT offers an alternative environment for these studies by providing a tunable electron beam and well-confined, highly charged ions.

In an EBIT, ions are confined within a narrow spatial region, primarily centered around the electron beam, as shown in Fig. 8. The electron-beam density ranged from approximately 10¹⁰ to 10¹² cm^-3. The equilibrium charge state of the ions can be controlled by adjusting key parameters such as the electron-beam energy, axial magnetic field, and the presence of neutral atoms in the trap region, as detailed in [161].

Fig. 8

(Color online) Setup structure of EBIT consisting of a cathode, permanent magnets, drift tubes, and an electron collector

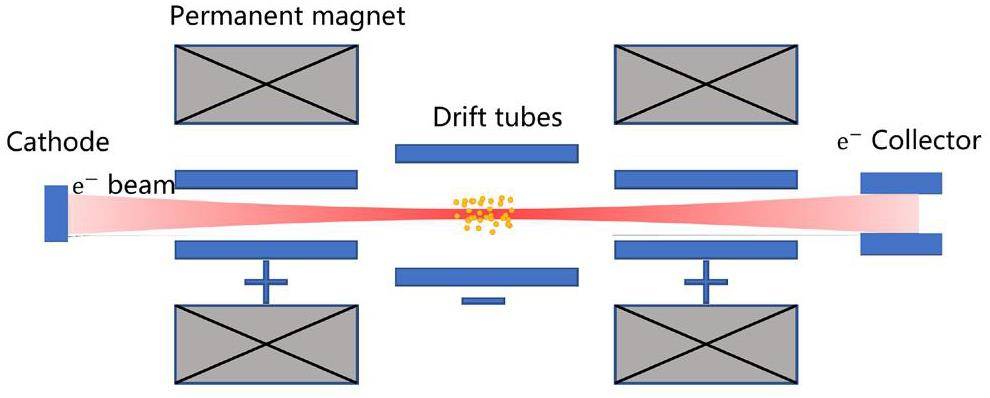
In Ref. [35], Ringuette conducted simulations of the NEEC process at the TITAN setup to excite ^129mSb ( $T_{1 / 2} = 17.7$ min) to a state 10 keV higher. However, careful selection of the ion charge state and atomic orbitals is necessary to overcome the challenges arising from switching the electron beam from charge-breeding energy to NEEC resonance energy. In Ref. [20], Wang et al. proposed a modified EBIT configuration that featured two electron guns with different energy settings: one is optimized to strip atoms to the high-charge states, while the other is tuned to meet the NEEC resonance conditions.

In the experimental setups proposed by these researchers, NEEC events were confirmed by detecting the photons emitted through an observation window around the drift tubes. As noted by Wang et al., the differentiation between NEEC events and background signals, particularly those from the RR process, relies primarily on their distinct angular distributions. Developing a more comprehensive approach for detection and discrimination, along with further optimization of experimental conditions, remains an active area of investigation.

The NEEC counting rate is significantly affected by the energy distribution of the electron beam in the EBIT [35]. In addition, it has been demonstrated that NEEC signals can be effectively distinguished from the RR background only when the experimental conditions, particularly the electron beam, are well defined [27].

Summary

The NEEC process, along with its inverse process of IC, represents a unique interaction that involves both atomic and nuclear structures. NEEC and IC are closely related to the excitation or de-excitation of nuclear isomeric states, with implications for technological applications and fundamental physics, including nuclear batteries, nuclear clocks, and nucleosynthesis in astrophysical environments.

Since its theoretical proposal in 1976, NEEC has attracted considerable attention from the scientific community. Several researchers in related fields have suggested that NEEC could play a significant role in astrophysical environments and plasma physics. In astrophysics, NEEC could extend the reaction chains of neutron-capture processes, potentially altering the isotopic abundances in stellar and cosmic contexts. In plasma environments, NEEC could influence the population balance of atomic nuclei and their associated isomers.

Nevertheless, despite its theoretical potential, experimental verification of NEEC has remained a formidable challenge. Key challenges include the high background noise inherent in experimental environments, whether in laser-induced plasmas or particle accelerators. In these settings, the NEEC cross-section is small compared to other competing electromagnetic interactions, such as CE and RR, complicating the task of isolating NEEC signals from substantial noise. Efforts to enhance NEEC rates and mitigate background interference continue to be an active research area.

In the selection of experimental setups and the design of experimental schemes, researchers such as Gunst, Wu, and Qi have explored optimal laser parameters and plasma properties to enable NEEC in laser-induced plasmas. They suspected that using low-energy-density lasers on solid targets to generate cold, low-density plasmas could effectively reduce noise and enhance the occurrence and detection of NEEC events. In plasma environments, the detection scheme for NEEC using X-rays tends to focus on nuclei or isomers with low gaps above, typically in the eV to keV range. However, researchers such as Pálffy, Chiara, Ringuette, and Wang have focused on demonstrating that precise energy control via electron or ion beams can improve the efficiency of NEEC, thereby reducing the influence of noise. They employ techniques such as storage rings, ion-beam interactions with solids, and electron-beam interactions with plasmas, which significantly expand the range of selectable nuclear energy levels. In particular, if dual electron beams are used in a storage ring or EBIT setup, the efficiency of reactions can be enhanced while maintaining the stability of the ion beam in the storage ring or plasmas in the EBIT. However, these methodologies require further refinement and development in future experimental setups.

In addition, it should be noted that owing to the inherent properties of nuclear transition selection rules, higher-order multipole transitions are typically suppressed, resulting in insufficient reaction cross-sections. Wang et al. introduced vertex beams into the study of NEEC and developed a theoretical framework for their application. Owing to the OAM carried by vortex beams, traditional selection rules are broken, enabling the occurrence of higher-order multipole transitions. Thus, the successful generation of high-intensity vortex beams in laboratory environments represents a significant breakthrough, potentially advancing the study of nuclear excitation processes.

Designing experiments that effectively eliminate background noise and enable the discovery of NEEC remain an active area of research. Successfully confirming NEEC would mark a significant breakthrough in our understanding of nuclear processes, paving the way for advancements in both fundamental research and practical applications.

References

V. Goldanskii, V. Namiot,

On the excitation of isomeric nuclear levels by laser radiation through inverse internal electron conversion

. Physics Letters B 62, 393 (1976). https://doi.org/10.1016/0370-2693(76)90665-1

Physics opportunities of the nuclear excitation by electron capture process

Introduction

Theoretical cross-section calculation of NEEC

NEEC in astrophysical environments

NEEC in astrophysical plasma

Nuclear structure models for B(πL)

NEEC in Laser-induced Plasmas

Laser-induced plasma

Laser-ablated plasma

Laser-heated cluster

Pros and cons of using laser-ablated plasma

NEEC Studies with Vortex Beams

NEEC Studies Based on Accelerators

By Using a Storage Ring

By Using Ion Beams

By Using Electron Beams

Summary

Nuclear structure models for $B (π L)$