Generation of the perturbed PFNS

The differential experimental data used in this method were sourced from the experimental nuclear reaction database (EXFOR), as reported in [39, 40]. These studies have reported the latest experimental data on the neutron-induced PFNS of ²³⁹Pu, covering 20 average incident energy points ranging from 1 to 20 MeV. Compared with the measurement results in the previous literature, this dataset has achieved breakthroughs in terms of accuracy, detailed uncertainty analysis, and thorough investigations of necessary corrections [39, 41].

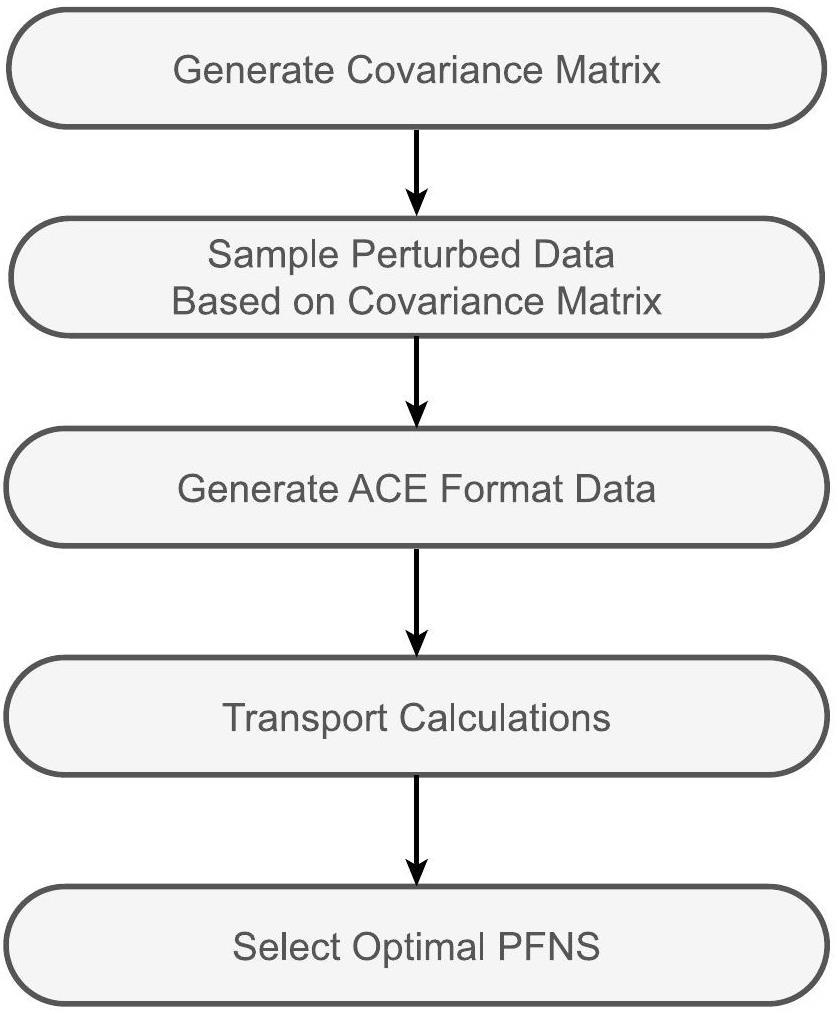
By utilizing the experimental uncertainty information, a perturbation of the data around the experimental measurements is proposed to generate a perturbed PFNS for transport code simulations. However, owing to the large number of data points, a gridded approach for generating points, in which candidate values are generated at each energy point based on the mean values and error bars, significantly slows the calculation process as the computational load grows exponentially with the number of data points. To reduce computational cost, this study introduces a sampling method that utilizes a covariance matrix to reduce the dimensionality of data variations. This obtains a relatively optimized PFNS with fewer simulation calculations, thereby improving computational efficiency.

The EXFOR database often includes experimental data accompanied by uncertainties; however, covariance data are not always available. To develop a method applicable to general scenarios, particularly in the absence of a reported covariance matrix, a correlation matrix was constructed based on the characteristics observed in the correlation matrix in [39, 40], and a covariance matrix was generated by combining the uncertainty information from the experiments. The correlation matrix diagram [39, 40] showed an extremely high correlation between the PFNS at different neutron incident energies. Therefore, assuming that the correlation between different data points in the PFNS spectrum decreases exponentially with the square of their distance, as shown in Eq. 2, a covariance matrix was constructed and used to perturb each data point of the PFNS spectrum at a single incident energy. $\begin{array}{c}{\text{cor}}_{ij}=e^{-\frac{d_{ij}^2}{2\sigma 2}}\\ d_{ij}=|i-dia{g}_j|\end{array}$ (2) where diagj represents the diagonal element coordinate in the jth row and i denotes the position of the ith element within the same jth row. The value of σ indicates the rate at which the correlation decreases as the distance increases. This assumption captures some of the patterns in the experimental data and effectively reduces the degrees of freedom for data perturbation.

To mitigate the impact of excessive uncertainty at low-energy points on the fitting function, data points were selected within an energy range consistent with those reported in the literature, specifically selecting points 100 keV for outgoing neutron energies. Based on the above description, the total uncertainty was used as the standard deviation, which is the square root of the variance. The correlation definition provided in Eq. 3 [42] was used to obtain the covariance matrix. From this definition, it was simple to derive Eq. 4. The covariance matrix was computed by combining the derived equation with the assumed correlation matrix. $\begin{array}{c}{\text{cor}}_{ij}=\frac{{\text{cov}}_{ij}}{\sqrt{{\text{cov}}_{ii}{\text{cov}}_{jj}}}\\ {\text{var}}_i={\text{cov}}_{ii}\end{array}$ (3) ${\text{cov}}_{ij}={\text{cor}}_{ij}\sqrt{{\text{cov}}_{ii}{\text{cov}}_{jj}}$ (4) where var denotes the variance vector, ${\text{cor}}_{ij}$ represents the element in the ith column and jth row of the correlation matrix, and ${\text{cov}}_{ij}$ represents the element in the ith column and jth row of the covariance matrix. Using the generated covariance matrix, the differential experimental data were perturbed, thereby producing PFNS discrete points proximal to the differential experimental data. As the new PFNS was obtained through sampling, it did not inherently possess the properties of a shaped spectrum. To address this, the Watt-Maxwellian function was employed to fit the perturbed data to generate a continuous, normalized, and non-negative PFNS. The fitting results are shown in Fig. 1.

Fig. 1Full-screen View

(Color Online) PFNS of ²³⁹Pu(n, f) for (a) perturbed data, shown by blue hollow triangles, in comparison to the literature values shown by red points [39], and (b) perturbed data, shown by blue points, along with the fitting result to the data

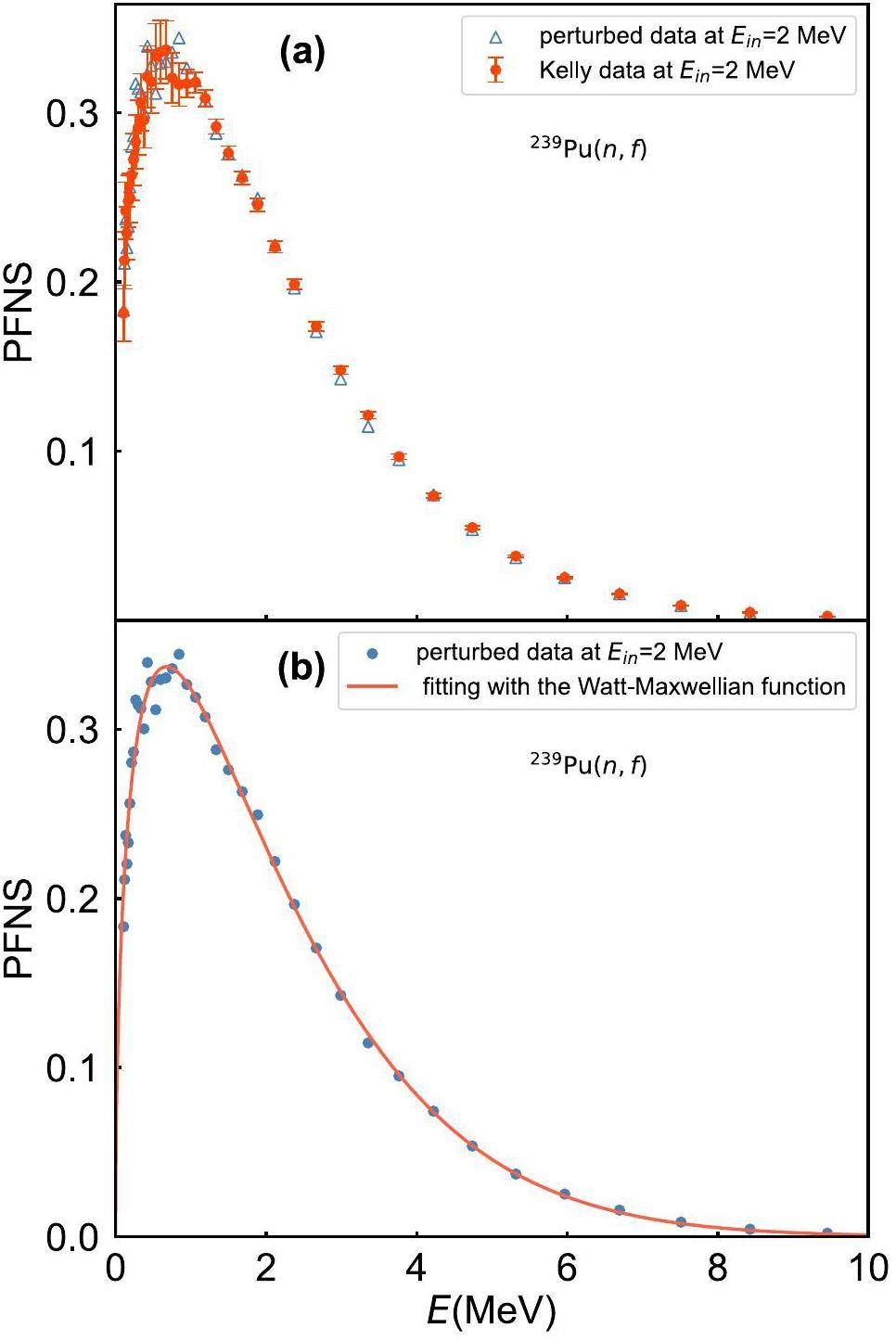
As depicted in Fig. 1, random sampling utilizing the covariance matrix effectively generated perturbed data proximal to the experimental data, and the Watt-Maxwellian function exhibited a robust fit to the perturbed data points. For a comprehensive set of PFNS encompassing various incident energies, a strong correlation across PFNS at different incident energies was achieved by selecting a uniform random number seed. This novel sampling and fitting methodology yielded a substantial number of continuous PFNS.

Using the perturbed data for transport calculations

To correlate differential data with integral data, transport calculations were used, taking differential data as the input and generating integral data as the output, which was then compared with the benchmarks. In this study, the Joint Monte Carlo transport (JMCT) code was utilized to perform criticality computations [43-45].

To optimize the PFNS, during transport calculations, except for the PFNS data, all other nuclear data were obtained from the ENDF/B-VIII.0 library [25]. To generate PFNS data suitable for utilization in this code, a nuclear data processing system (NJOY2016) was used to process the perturbed PFNS data, transforming them into the ACE format [46]. To facilitate subsequent comparisons with the results from ENDF/B-VIII.0, the same incident energy selections as those in ENDF/B-VIII.0 were adopted. As the experimental data did not perfectly align with this set of incident energies, linear interpolation was used to generate PFNS for various incident energies. As the range of the experimental incident energies was slightly narrower than that of ENDF/B-VIII.0, the PFNS was extrapolated for energies below the minimum experimental average incident energy of 1.54 MeV or above the maximum experimental incident energy of 19.59 MeV in ENDF/B-VIII.0. Specifically, a consistent approach of linear extrapolation, analogous to the aforementioned linear interpolation method, was used to predict PFNS at these incident energies.

Given that the differential experimental data employed in this study were limited to the incident energy range 1 MeV, the selection of fast neutron spectra was the most appropriate for this specific energy domain. To minimize the possible uncertainty in the transport process while covering as much of the experimental data region as possible, five criticality benchmarks with relatively simple geometric configurations were selected. Each of these benchmarks is characterized by a dominant “FAST” flux spectrum and is directly associated with the nuclide ²³⁹Pu. The benchmark cases employed in this study were Pu-Met-Fast-002, Pu-Met-Fast-003, Pu-Met-Fast-008, Pu-Met-Fast-009, and Pu-Met-Fast-010 [47, 48]. In the aforementioned benchmarks, Pu-Met-Fast-002 represents a bare experiment (20.1 at.% ²⁴⁰Pu), Pu-Met-Fast-003 represents an array of plutonium metal buttons in an unmoderated configuration, Pu-Met-Fast-008 represents an experiment involving a thorium reflector, Pu-Met-Fast-009 represents an aluminum reflected experiment, and Pu-Met-Fast-010 represents an experiment that utilizes a natural uranium reflector [49]. By utilizing these relatively simple criticality benchmark assemblies, which encompass diverse configurations, this study aimed to enhance the robustness of the constraints on differential data by integrating the experimental data. The input for the JMCT used computer aided design (CAD) modeling [45], and the models of these criticality benchmarks were constructed based on information sourced from the MIT Computational Reactor Physics Group [50].

All cases were executed using the same perturbed data, with each simulation using 10000 neutrons per cycle, 100 inactive cycles, and 1400 additional active cycles. The uncertainty of the calculated eigenvalue k_eff exhibited a slight variability depending on the device and input files; however, it consistently remained < 20 pcm. This value is notably smaller than the benchmark uncertainties.

Calculated $\delta k_{\text{eff}}$

To evaluate the quality of each perturbed PFNS, a comparative analysis was conducted between the eigenvalues k_eff derived from transport simulations for the five criticality benchmarks and their respective benchmark values. Specifically, the relative calculation-to-experimental ratio, denoted as $\frac{|C-E|}{E}$, was used to quantitatively assess the deviation between the calculated and benchmark k_eff values sourced from [47]. Notably, the benchmark k_eff values for these benchmark integral experiments were all 1.000. The relative difference between the calculated and experimental values is given by Eq. 5, where $k_{\text{eff,}b}^{\text{cal}}$ represents the calculated k_eff for the b-th criticality benchmark assembly, and $k_{\text{eff,}b}^{\text{ben}}$ represents the benchmark value of k_eff for the same assembly. Furthermore, the total relative difference was introduced, denoted by $\delta k_{\text{eff}}^{\text{tot}}$, which was defined as the average of $\delta k_{\text{eff,}b}$ calculated for all criticality benchmarks, as outlined in Eq. 6.

This approach enabled the identification of the most suitable perturbed PFNS that best captured the integral experimental behavior and achieved optimal results. $\delta k_{\text{eff,}b}=\frac{|k_{\text{eff,}b}^{\text{cal}}-k_{\text{eff,}b}^{\text{ben}}|}{k_{\text{eff,}b}^{\text{ben}}}$ (5) $\delta k_{\text{eff}}^{\text{tot}}=\frac{{\displaystyle {\sum }_b\delta k_{\text{eff,}b}}}{5}$ (6) To clarify the entire process of utilizing the integral experimental data to constrain the differential experimental data, a flowchart was created for the aforementioned method, which is presented in Fig. 2. By sampling from the covariance matrix, the perturbed PFNS were obtained that were distributed near the differential experimental data. These perturbed PFNS were then processed using the NJOY code to generate data in ACE format. For each set of perturbed PFNS, JMCT was employed to perform transport simulations on the five criticality benchmarks. Through extensive simulations, the perturbed PFNS were identified that not only exhibited the closest alignment with the benchmark values but also maintained close proximity to the original differential experimental data. This approach ensured a robust and reliable method for constraining differential experimental data using integral experimental information, ultimately enhancing the accuracy and applicability of differential experimental data.

Fig. 2Full-screen View

Flowchart of optimizing the differential PFNS process through the use of integral experiments

Calculation results from the generated covariance matrix

By following the steps shown in Fig. 2, a covariance matrix was initially generated based on Eq. 2, assuming that σ = 1. This assumption allowed the derivation of a correlation matrix that exhibited a relatively rapid decrease in the correlation between data points. By incorporating the uncertainty data provided in the experiment [40], the covariance matrix was obtained for this specific scenario. Subsequently, this covariance matrix was used to perform random sampling of the data points, thereby generating perturbed datasets. In this framework, 1,000 samplings were executed and the corresponding $\delta k_{\text{eff}}^{\text{tot}}$ values for each sampling were calculated. This process ultimately yielded a distribution of $\delta k_{\text{eff}}^{\text{tot}}$, as shown in Fig. 3.

Fig. 3Full-screen View

(Color Online) Assuming σ = 1.0, the distribution of $\delta k_{\text{eff}}^{\text{tot}}$ obtained by comparing the transport calculated results with the benchmark values is shown as follows: (a) a two-dimensional plot of $\delta k_{\text{eff}}^{\text{tot}}$ versus the sample number; (b) a histogram of the statistical distribution of $\delta k_{\text{eff}}^{\text{tot}}$. The red line represents a Gaussian function fit to the histogram in the range of $\delta k_{\text{eff}}^{\text{tot}}=0.002$ to 0.003, and the red solid line indicates the fitting range

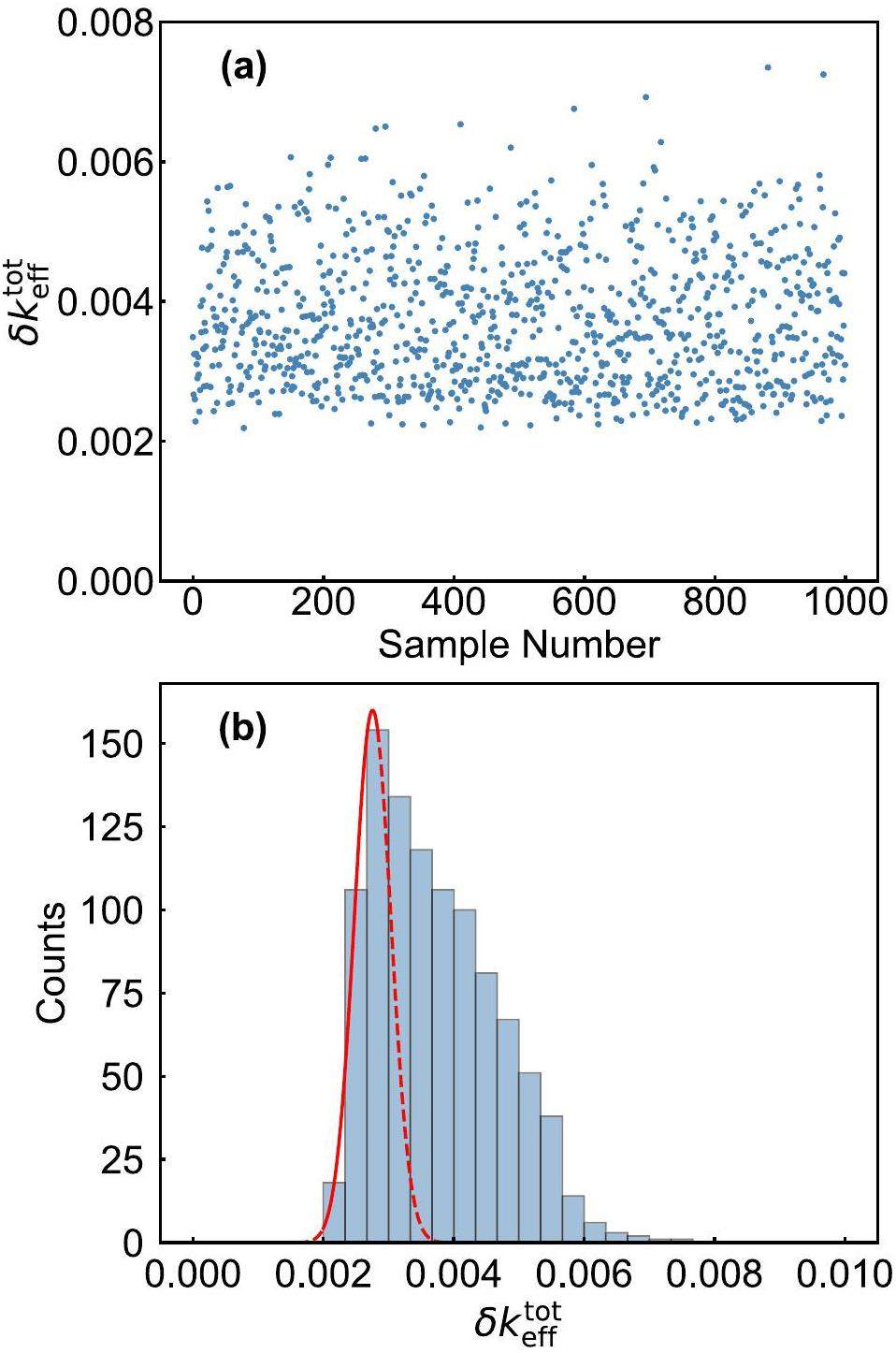
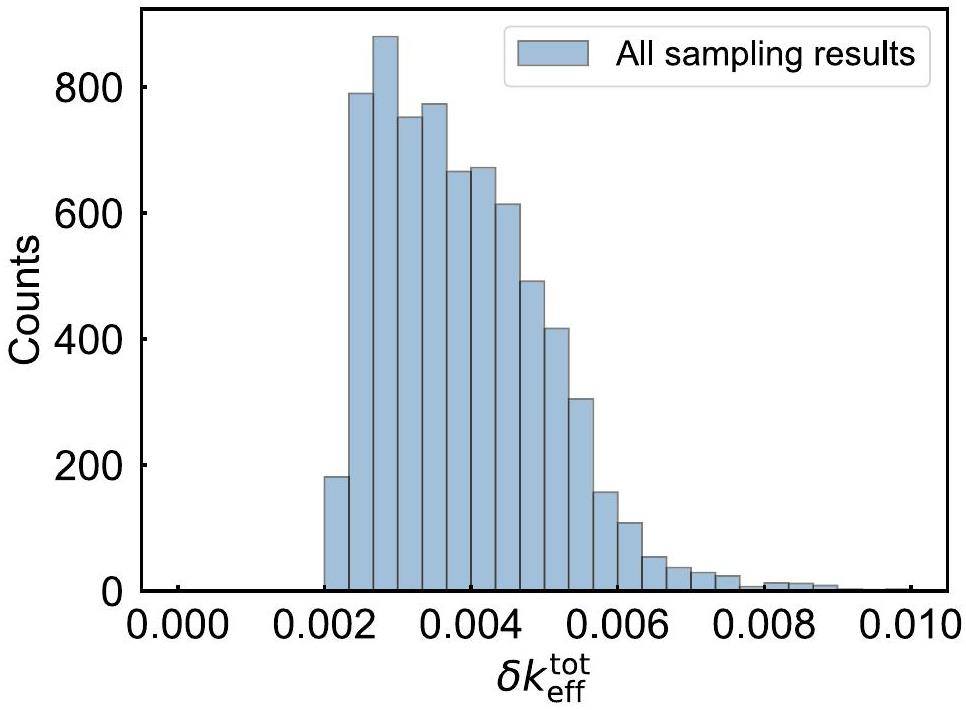
Figure 3(a) illustrates the effect of the PFNS sampled from the generated covariance data on the transport calculations. The scattered random distribution of points reflects the stochastic nature of the sampling process. It is evident that different PFNS lead to variations in the computed k_eff values, demonstrating that adjustments to the differential data within the error bands can affect the integral data. This further validates the effectiveness of constraining differential experiments through integral experiments. Figure 3(b) shows a histogram of the statistical distribution of $\delta k_{\text{eff}}^{\text{tot}}$, which shows a rapid decrease at both ends of the distribution. The red Gaussian function fitting line in Fig. 3(b) shows that as $\delta k_{\text{eff}}^{\text{tot}}$ decreased, its statistical distribution exhibited exponential decay. This suggests that the current sampling, with σ = 1.0, is statistically sufficient for obtaining the optimal value. Additionally, Fig. 3(b) shows that optimizing the calculation of k_eff by adjusting only the PFNS method ultimately leads to an optimal value of $\delta k_{\text{eff}}^{\text{tot}}$ of approximately 0.002. The optimal PFNS obtained through sampling corresponds to a $\delta k_{\text{eff}}^{\text{tot}}$ value of 0.00219. When the calculations were performed using the ENDF/B-VIII.0 library, the resulting $\delta k_{\text{eff}}^{\text{tot}}$ value was 0.00299. This comparison indicates that the PFNS that is perturbed using the latest experimental data performs better in integral experimental validation than the PFNS in the ENDF/B-VIII.0 library.

To broaden the scope of the parameter variation, different values for σ were selected in Eq. 2. By choosing distinct σ values, the rate of decrease in the correlation for the correlation matrix was altered, thereby generating different covariance matrices. In addition, σ = 0.1, 0.2, 0.5, 1.5, 2.0, and 5.0 were selected and the method detailed in Sect. 2 was used to generate the covariance matrices. Analogous to the case where σ = 1.0, $\delta k_{\text{eff}}^{\text{tot}}$ was computed for a range of σ values. Owing to variations in the covariance matrix, the distribution of the computed $\delta k_{\text{eff}}^{\text{tot}}$ also exhibited differences. For each value of σ, 1000 samples were taken, and $\delta k_{\text{eff}}^{\text{tot}}$ was calculated based on the perturbed PFNS generated by sampling, as shown in Fig. 4.

Fig. 4Full-screen View

(Color online) Distribution of $\delta k_{\text{eff}}^{\text{tot}}$ obtained by comparing the transport calculated results with the benchmark values under the following cases: (a) σ = 0.1; (b) σ = 0.2; (c) σ = 0.5; (d) σ = 1.5; (e) σ = 2.0; (f) σ = 5.0

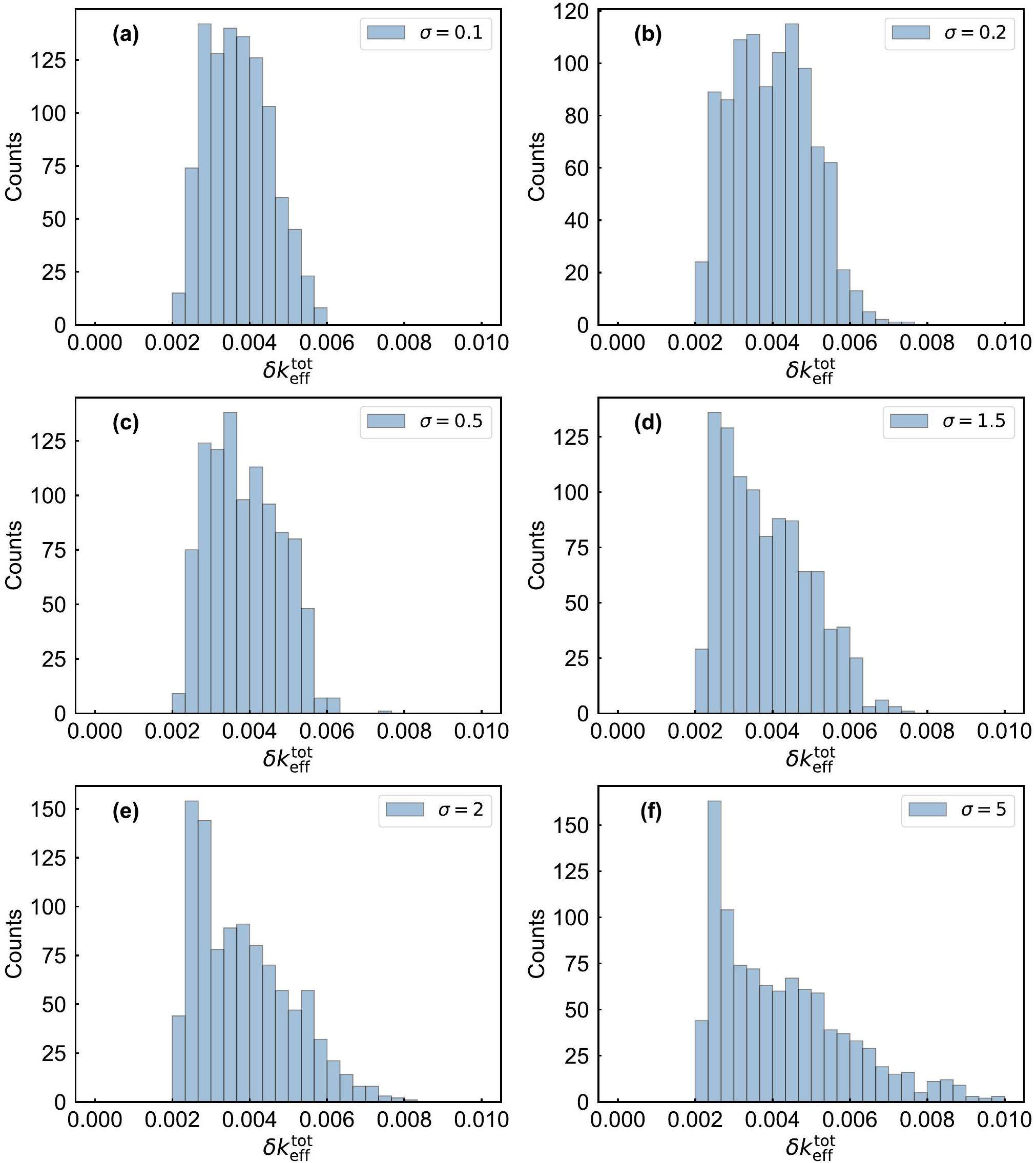
As illustrated in Fig. 4, although the distribution of $\delta k_{\text{eff}}^{\text{tot}}$ varied under different σ values, its main characteristics remained consistent as the distribution of $\delta k_{\text{eff}}^{\text{tot}}$ decreased rapidly at both ends. Notably, at the left end of the horizontal axis as shown in Fig. 4, all cases exhibited the same characteristics as when σ = 1.0, that is, as the value of $\delta k_{\text{eff}}^{\text{tot}}$ on the x axis in Fig. 4 decreased, its statistics decreased exponentially, converging to approximately 0.002. This indicates that the results obtained using a sample size of 1000 are sufficient to represent the distribution of $\delta k_{\text{eff}}^{\text{tot}}$. Although a larger sample size would yield results closer to the optimal value when sampling methods are used to obtain the best PFNS, the current sample size provided a satisfactory approximation.

The perturbed PFNS have been obtained for seven distinct σ values. The results were compiled together to use the statistical information from the entire sampling process. The overall distribution of $\delta k_{\text{eff}}^{\text{tot}}$ obtained from all sampling results is shown in Fig. 5. In the cases of the various σ values mentioned earlier, the distribution of $\delta k_{\text{eff}}^{\text{tot}}$ decreased rapidly at both ends and exhibited an exponentially decreasing trend at the low $\delta k_{\text{eff}}^{\text{tot}}$ end and converged to approximately 0.002. To synthesize the previous data, Fig. 5 naturally exhibits such characteristics in its distribution of $\delta k_{\text{eff}}^{\text{tot}}$. However, owing to improvements in the statistics and superposition of various σ cases, the statistical fluctuations of the distribution decreased, resulting in a more continuous distribution. The optimal $\delta k_{\text{eff}}^{\text{tot}}$ obtained for all perturbed PFNS generated using the method based on covariance matrix creation and sampling was 0.00210. This value is very close to the optimal $\delta k_{\text{eff}}^{\text{tot}}$ previously obtained by considering only the case where σ = 1.0, which also indicates a rapid decrease in $\delta k_{\text{eff}}^{\text{tot}}$ at the low $\delta k_{\text{eff}}^{\text{tot}}$ end.

Fig. 5Full-screen View

(Color online) Distribution of $\delta k_{\text{eff}}^{\text{tot}}$ across all sampling results, including those with σ = 0.1, 0.2, 0.5, 1.0, 1.5, 2.0 and 5.0, totaling 7000 samples

Calculation results from the experimental covariance matrix

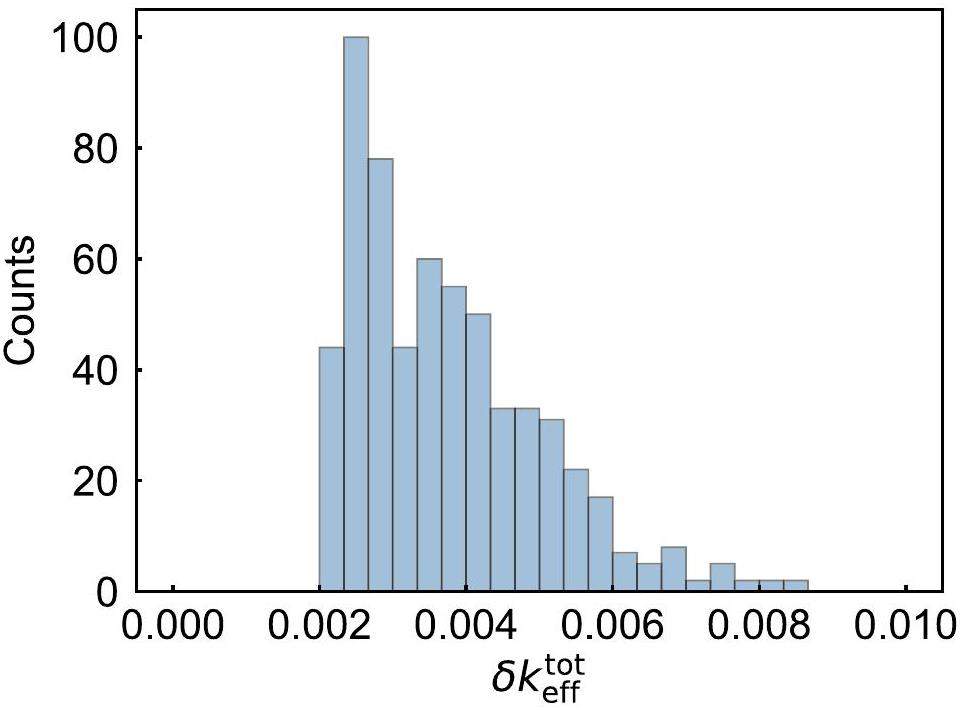
In recent years, with the growing emphasis on covariance data in experiments and evaluations, more experiments have begun to report covariance data. The experimental data used in this study included a reported covariance matrix [39, 40]. The reported covariance matrix from the experiment was used to generate a perturbed PFNS using the aforementioned sampling method. This specific method is consistent with that described in Sect. 2, with the only modification being the replacement of covariance matrix generation. 600 samplings were performed using the covariance data provided by the experiment and the $\delta k_{\text{eff}}^{\text{tot}}$ values were calculated based on each perturbed PFNS. The distribution of $\delta k_{\text{eff}}^{\text{tot}}$ calculated using the PFNS sampled based on the experimental covariance matrix is shown in Fig. 6. This distribution exhibited a relatively higher probability at lower $\delta k_{\text{eff}}^{\text{tot}}$ values, which is beneficial for achieving faster convergence to the optimal value of $\delta k_{\text{eff}}^{\text{tot}}$. The optimal PFNS obtained through this sampling method, utilizing the covariance matrix, was directly derived from the experiment, yielding a $\delta k_{\text{eff}}^{\text{tot}}$ of 0.00208, which was slightly better than previous results.

Fig. 6Full-screen View

(Color online) Distribution of $\delta k_{\text{eff}}^{\text{tot}}$ calculated using the perturbed PFNS sampled from the experimental covariance matrix

Discussion

Covariance matrices were generated for the differential data using two distinct methods. Method 1 involved constructing a correlation matrix and combining it with the experimental uncertainty information,. Method 2 directly utilized the covariance information provided by the experiment. The experimental data were perturbed near the error range through random sampling and the perturbed PFNS were used for transport calculations to conduct integral validation, thereby optimizing the differential PFNS.

Based on the results presented in Figs. 5 and 6, the distributions of $\delta k_{\text{eff}}^{\text{tot}}$ produced by the perturbed PFNS obtained using both methods exhibited rapid decreases at low $\delta k_{\text{eff}}^{\text{tot}}$ values. The optimal PFNS values converged using the two methods were not significantly different. The results are listed in Table 1, which demonstrates that the optimized PFNS obtained through the random sampling method performed better in integral experiments than the PFNS provided by ENDF/B-VIII.0. Furthermore, Figs. 5 and 6 show that, at the left end of the $\delta k_{\text{eff}}^{\text{tot}}$ distribution, it converged to a value near 0.002, rather than 0. This implies that merely adjusting the PFNS may not be sufficient to obtain a k_eff calculation value that is identical to the benchmark. However, a relatively better PFNS can still be obtained using this method.

Although methods 1 and 2 can optimize the PFNS to approach an optimal value, differences in the covariance matrix lead to varying convergence speeds of the data near this optimal value. The distribution characteristics near a low $\delta k_{\text{eff}}^{\text{tot}}$ can be described by comparing the ratios of the distributions obtained using methods 1 and 2. Specifically, the distribution generated by Method 2 was used as the standard and the distribution histograms of $\delta k_{\text{eff}}^{\text{tot}}$ were compared under different σ values in Method 1 with those in Fig. 6 by calculating their ratios. Specifically, after normalizing Fig. 3, Figs. 4(a)-(f) were used to calculate the ratios with the normalized histogram of Fig. 6 for each bin within the range of $\delta k_{\text{eff}}^{\text{tot}}=0.002\sim 0.008$ to obtain Fig. 7. The horizontal coordinates of the points indicated in Fig. 7 shows the center values of the bins.

Fig. 7Full-screen View

(Color Online) Ratios represent the comparison between the normalized distribution of $\delta k_{\text{eff}}^{\text{tot}}$ obtained under varying σ values using Method 1, and the normalized distribution of $\delta k_{\text{eff}}^{\text{tot}}$ calculated through covariance sampling derived from experimental data, denoted as Method 2. The red horizontal dashed line indicates a ratio of 1

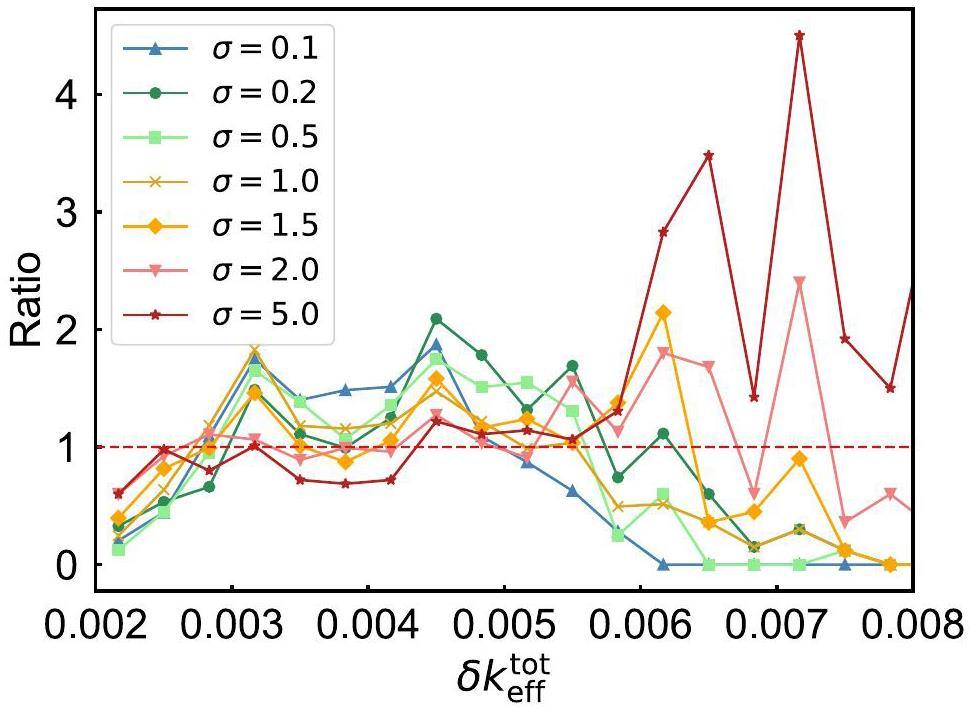
Figure 7 illustrates that, near the left end of the $\delta k_{\text{eff}}^{\text{tot}}$ distribution, the ratio of the distribution of $\delta k_{\text{eff}}^{\text{tot}}$ obtained from all samples in Method 1 to the distribution derived from Method 2 was < 1. This suggests that the covariance provided by the experimental data was more suitable for sampling to obtain the optimal PFNS. However, it should be noted that in cases where experimental covariance data are missing, Method 1, which constructs a correlation matrix combined with experimental uncertainty information to generate a covariance matrix for sampling, can also effectively approximate the optimal value. However, compared with Method 2, it exhibited a relatively lower efficiency near the optimal value. This observation aligns with the results presented in Table 1, demonstrating that Method 2 achieves a better PFNS with fewer sampling instances.

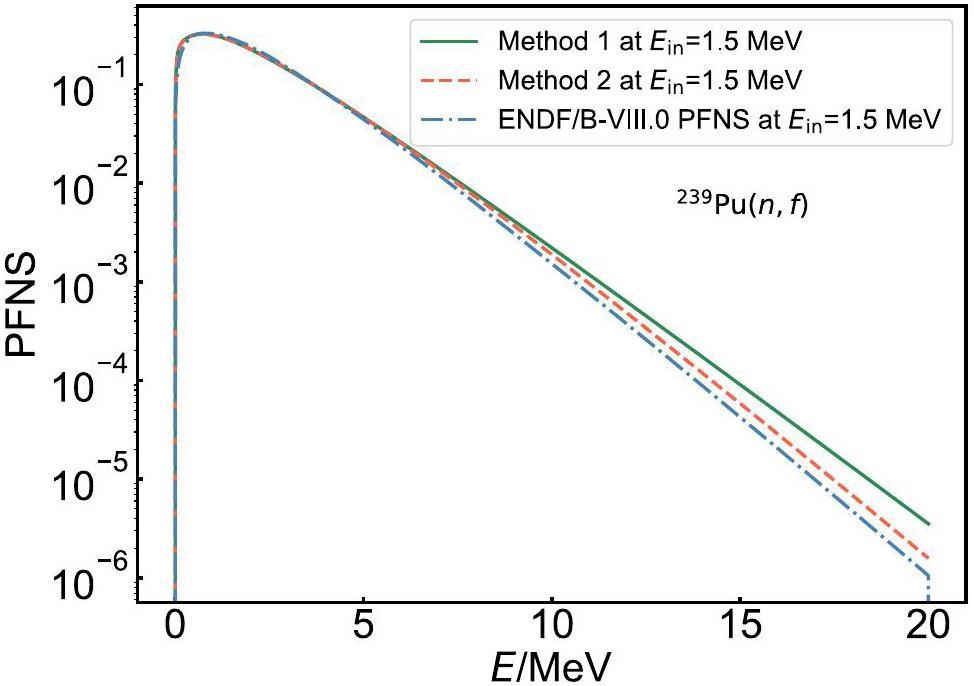
Figure 8 presents a comparison of the optimized PFNS results obtained using Methods 1 and 2 with ENDF/B-VIII.0, using an incident energy of 1.5 MeV as an example. The optimized PFNS exhibited slight variations from ENDF/B-VIII.0, and these variations contributed to the optimization of the integral experiment for calculating k_eff. As illustrated in Fig. 8, the method of utilizing integral experiments to constrain differential experiments demonstrates an effective adjustment of PFNS. Owing to the normalization of the spectrum, there is inevitably an interplay between the low- and high-count parts of the final energy spectrum, and the distribution in the low-count region is modulated by slight variations in the high-count region. The results show that the adjusted PFNS performs better in calculating the criticality benchmarks. Consequently, the adjustment to the PFNS is beneficial for the entire spectrum, as it aligns well with both the microscopic and integral experiments.

Fig. 8Full-screen View

(Color Online) Comparison of the optimized PFNS of ²³⁹Pu(n, f) results obtained using Methods 1 and 2 with ENDF/B-VIII.0, illustrated using an incident energy of 1.5 MeV as a representative example