Introduction

The field of research concerning the interactions of strong laser fields with atoms and molecules has reached a considerable degree of maturity [1-3]. Recently, projects for extremely high-intensity lasers have been proposed by the Shanghai Ultra Intensive Ultrafast Laser Facility [4, 5], the Extreme Light Infrastructure for Nuclear Physics [6, 7], and a Russian group [8]. Because of the enhancements envisaged for the near future, laser-driven nuclear physics has attracted increasing interest and extensive research has been performed on, for example, the impact of laser fields on α decay [9-19], proton emission [6, 20, 12], cluster radioactivity [12, 18], nuclear fission [12], nuclear fusion [21-23], and nuclear excitation [24-26]. Among these, significant attention has been paid to the α decay of nuclei under the influence of strong laser fields.

α decay is crucial in nuclear physics because it provides information on the nuclear structure [27-29] and facilitates the understanding of topics such as the nuclear transformation between the liquid state and cluster state [30, 31]. α radioactivity was first discovered by Rutherford in 1903. Following this discovery, many attempts were made to modify α decay rates by changing the temperature, pressure, and magnetic and gravitational fields [32, 33]. The changes in the decay constant were small and could be neglected. These interpretations may stem from Gamow’s explanation of quantum-mechanical tunneling [34], according to which α decay is correlated with the width through the potential. The distortions in the potential and changes in the decay energy modified by the above experiments were negligible and no effect was detected. The remarkable developments in laser technology provide an alternative method to explore and advance this study.

Lasers interact with matter through two fundamental mechanisms: single-photon and electromagnetic field interactions. The former is not feasible for nuclear processes because of the significant energy discrepancy between a single photon (on the order of 1 eV) and nuclear energy levels (on the order of 1 MeV). When the laser intensity is sufficiently high, the laser–matter interaction is predominantly governed by the electromagnetic field [3], which is believed to possess the potential to control nuclear systems. Thus, many studies have focused on the necessity of high-intensity lasers to modify decay processes [9-19]. According to Ref. [11], no significant modification of α decay is expected with the lasers currently available or those anticipated for the forthcoming years.

However, some recent studies have indicated the substantial effect of current laser intensities on α decay by solving the time-dependent Schrödinger equation within the oscillating Kramers–Henneberger frame [15-19]. Others suggest a small yet detectable influence at the current laser intensities or those that will be attained in the foreseeable future [9, 10, 12-14]. The inconsistencies in these findings highlight the ongoing debate and the lack of a clear consensus. Moreover, the temporal and angular effects and variation in the spatial shape of the laser field are intriguing for experiments; however, these remain ambiguous. In this study, we investigated the influence of extreme laser fields on nuclear α decay using the frozen Hartree–Fock (FHF) approach [35-37]. In contrast to the aforementioned approaches, it can compute the microscopic internuclear potential and deformation effects in a self-consistent manner [38-40]. Cluster radioactivity has been investigated since 1984 [41] as an intermediate process between α decay and spontaneous fission [42-44], and it has deepened our understanding of decay mechanics. Thus, it would also be interesting to study cluster radioactivity.

The remainder of this paper is organized as follows. Section 2 introduces the theoretical framework for laser-assisted particle decay using the FHF method. Section 3 presents and discusses the results. Finally, Section 4 presents the conclusions of this study.

Theoretical framework

Results

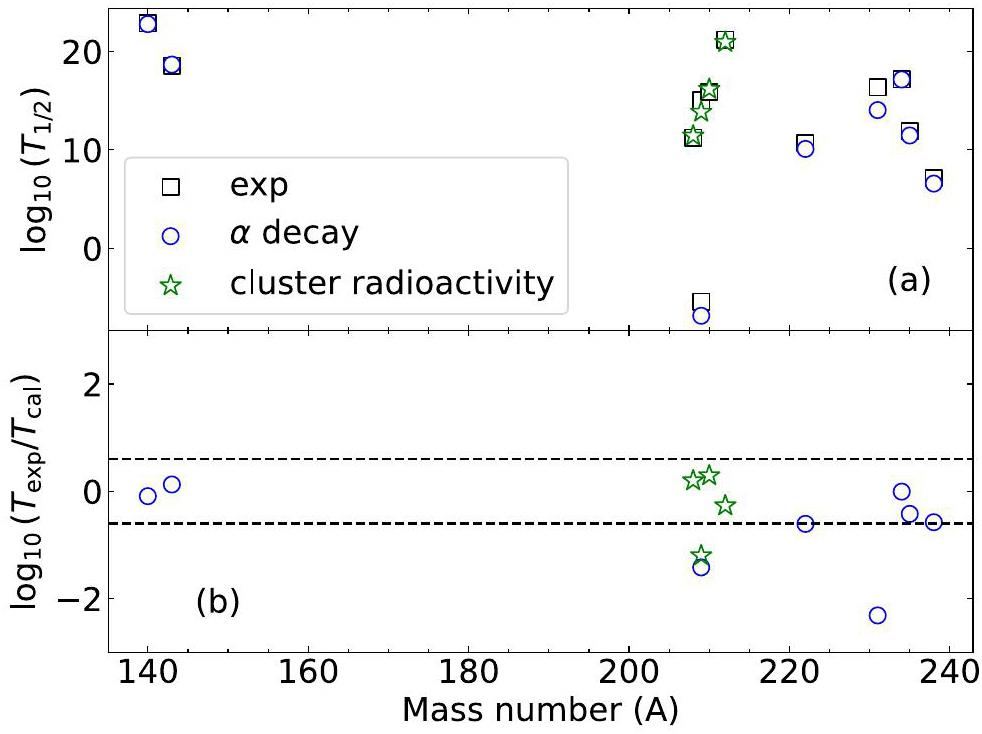
Figure 1(a) shows a comparison of the experimental and theoretical half-lives. The corresponding deviations between the logarithms of the experimental half-lives and the calculated values are shown in Fig. 1(b). The blue circles represent the calculated α decay of the ground-state parent nuclei ¹⁴⁴Nd, ²²⁶Ra, ²³⁸U, ²⁴²Cm, ¹⁴⁷Sm, ²¹³Po, ²³⁵U, and ²³⁹Pu. The green stars represent the calculated ¹⁴C cluster radioactivity of the ground-state parent nuclei, ^{222,223,224,226}Ra. It can be observed that the difference between the calculated values and experimental data is small. The values of log₁₀(T_exp/T_cal) for α decay and cluster radioactivity were generally within the range of approximately ±0.6. These values correspond to the values of the ratio T_exp/T_cal within the range of approximately 0.25–3.98. This demonstrates the reliability of our model for predicting half-lives. Detailed information regarding the experimental and calculated data is presented in Table 1.

Fig. 1Full-screen View

(Color online) (a) Experimental and calculated half-lives for different parent nuclei. The black squares represent the experimental data. The blue circles represent the calculated α decay half-lives of the ground state parent nuclei ¹⁴⁴Nd, ²²⁶Ra, ²³⁸U, ²⁴²Cm, ¹⁴⁷Sm, ²¹³Po, ²³⁵U, and ²³⁹Pu. The green stars represent the calculated ¹⁴C cluster radioactivity half-lives of the ground state parent nuclei ^{222,223,224,226}Ra. (b) The corresponding logarithms of hindrance factors (HF = T_exp/T_cal)

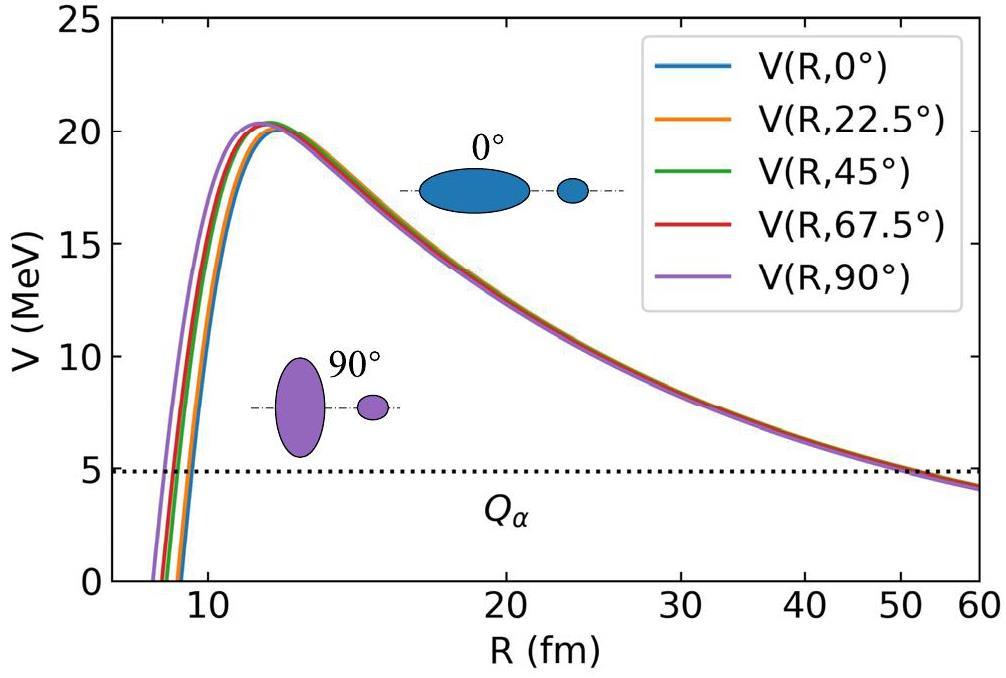
One typically assumes a spherical shape for the nuclei to simplify the calculation of α decay half-lives. However, nuclear deformation has been reported to significantly affect these calculations [50, 51]. Figure 2 shows the FHF potential of α+²²²Rn for selected orientations. Because the α particle is spherical, the differences in these potentials stem from the orientation of the daughter nucleus ²²²Rn. This shows that as the orientation rotates from the tip to the side, the Coulomb barrier increases and the nuclear part of the potential becomes shallower. This phenomenon can be attributed to the larger overlap of the nuclear density distribution in the tip orientation, which leads to a more pronounced effect on the nuclear potential. This also shows that the tunneling points differ by approximately 1 fm with varying orientations, resulting in an order-of-magnitude change in the penetration probability and subsequent alterations in α decay half-lives. In addition, the laser–nucleus interaction depends on the angle between the directions of the laser field and particle emission. It is inferred that nuclear deformation is a critical factor that should be incorporated into laser-assisted α decay and cluster radioactivity calculations.

Fig. 2Full-screen View

(Color online) Frozen Hartree–Fock potential for the α+²²²Rn system with different orientations of ²²²Rn. In particular, 0 and 90 represent tip and side orientation, respectively. Q_α is the experimental α-decay energy

To illustrate the influence of the laser field on the penetration process, a comparison of the laser-free internuclear potentials for the α+²²²Rn system with the two laser-assisted cases is shown in Fig. 3. For simplicity, only the tip-orientation case is presented. The laser field induces a downward shift in the Coulomb portion of the potential and an increase in the α-decay energy, whereas its impact on the nuclear portion remains negligible. This is not surprising, because the intense laser field of intensity 10³² W/cm² (10²⁹ W/cm²) is comparable to the Coulomb field strength from the daughter nucleus ²²²Rn at a distance of approximately 66 fm (371 fm). The Coulomb component is defeated by the nuclear component within the core. Therefore, the laser field alters the tunneling points by deforming the long-range Coulomb part of the potential and changing the energy of the emitted particles, thereby affecting the penetration probability.

Fig. 3Full-screen View

(Color online) Comparison between laser-free and laser-modified internuclear potentials for the α+²²²Rn system under two laser intensities, I = 10²⁹ W/cm² and 10³² W/cm². 0 represents the tip orientation of ²²²Rn. The solid line stands for the laser-modified case, and the dashed line stands for the laser-free case. The dotted line represents the α emission energy, where $Q_{\alpha }$ is the experimental α decay energy, and $Q_{\alpha }^{*}$ is the energy of the emitted α particle accelerated by the laser field

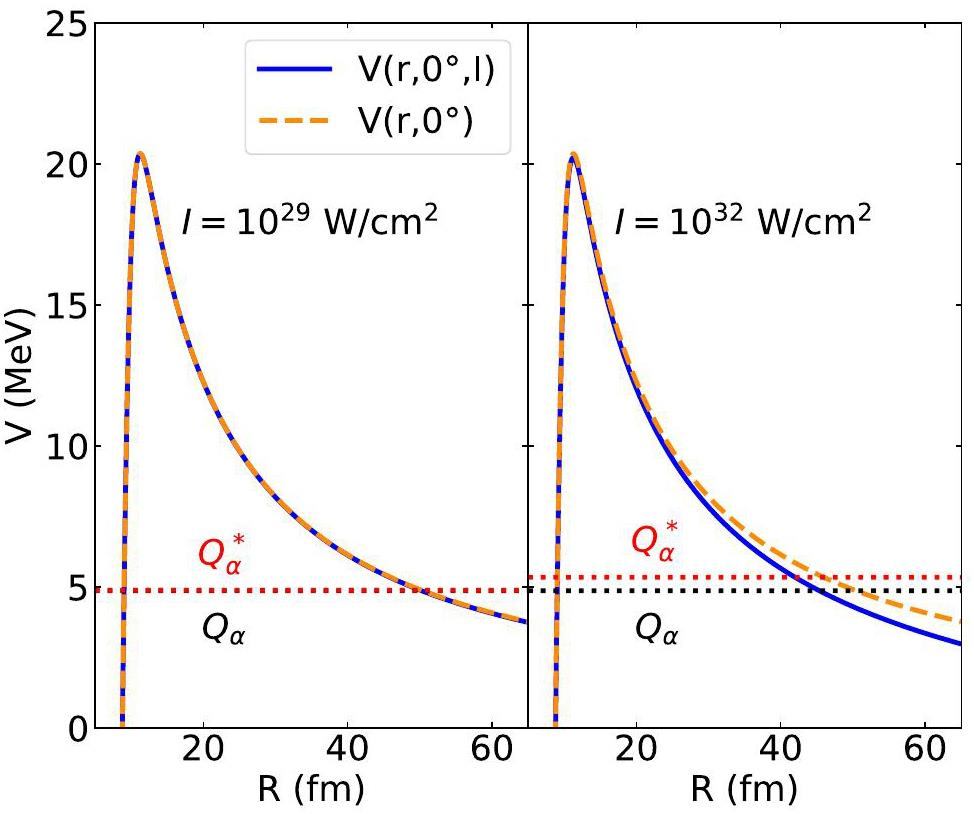
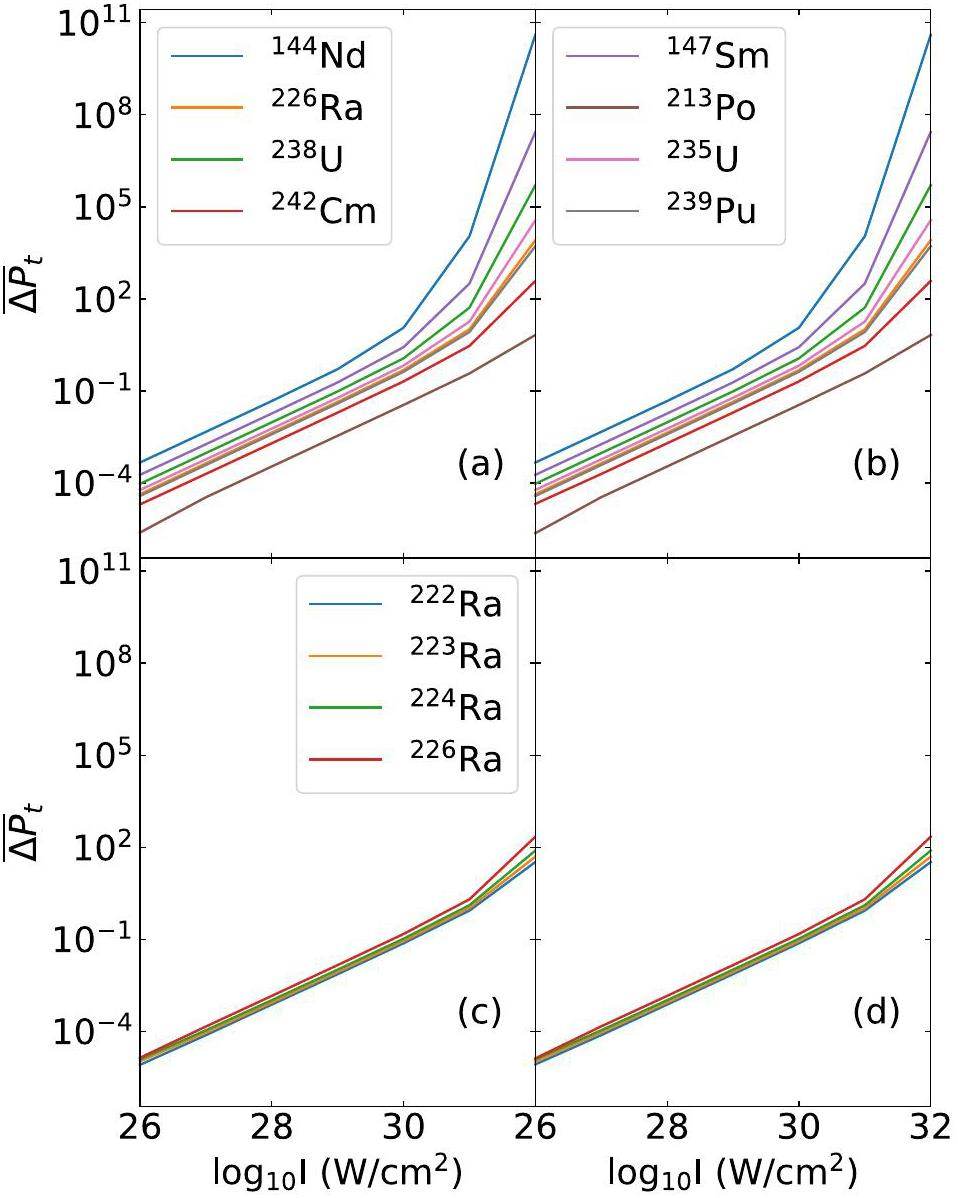
As shown in Fig. 3, the modification by the laser field becomes observable only when the intensity reaches 10³² W/cm². Given the current laser technology, no significant modifications in the half-lives were observed experimentally. Nevertheless, even subtle alterations in the potential or decay energy may give rise to discernible effects on the decay processes because tunneling is highly sensitive to the internuclear potential. This is illustrated in Fig. 4. The relative change in the penetration probability ΔP can reach 10^-3 within the accessible laser intensity. In Fig. 4, ΔP is obtained at the moment of the peak electric field strength with a fixed angle θ = 0°. ΔP and the laser intensity I are plotted on a logarithmic scale. As depicted in Fig. 4, the lower the decay energy a parent nucleus has, the greater the relative change in its penetration possibility across different nuclei. Evidently, the parent nucleus ¹⁴⁴Nd is susceptible to laser-induced modification. This stems from its relatively low α decay energy, which results in an extended tunneling path, thereby allowing the laser field to exert a prolonged influence on the decay process. At an intensity of 10²⁴ W/cm², the modification of the penetration possibility is on the order of 0.1% for ¹⁴⁴Nd, which is in agreement with Ref. [10, 12].

Fig. 4Full-screen View

(Color online) Relative change in penetration possibility $\text{Δ}P\left(t_0\mathrm{,}{\theta }_0\mathrm{,}I\right)$ for (a) α decay and (b) ¹⁴C cluster radioactivity at the moment t₀ of the peak electric field strength with a fixed angle θ₀ = 0°. The dashed line in (b) represents ΔP for α decay of parent nucleus ²²⁶Ra

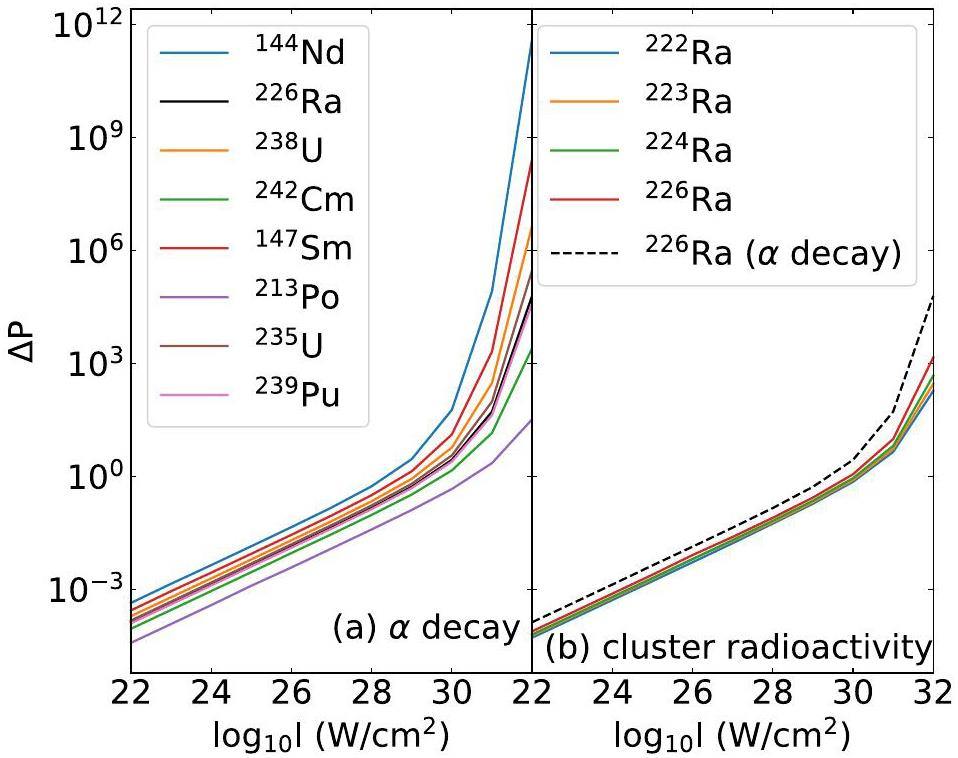
The laser-assisted α decay modifications for the even–even nuclei also show good agreement with the predictions in Ref. [13, 14]. The above calculations were conducted using the same approximations (dipole and quasistatic approximations) for the laser field and various internuclear potentials. Some studies [10-14] employed the phenomenological internuclear potentials, whereas this work utilized the microscopic potentials and considered nuclear deformation effects. Although the results are similar, the FHF method helps pursue a more microscopic understanding of laser-assisted α decay and cluster radioactivity in a self-consistent manner. In addition, in contrast to the modest impact of the laser field predicted by our model, several studies [15-19] have suggested a significant alteration in the alpha decay processes under current laser intensities. These calculations were obtained by solving the time-dependent Schrödinger equation within the oscillating Kramers–Henneberger frame. The critical assumption was the continuity of the laser field, whereas this study was based on the premise of a single laser pulse. This discrepancy in laser conditions resulted in substantial differences in the respective predictions. However, high-intensity continuous laser fields are unattainable. The potential for future technological advancements in continuous laser technology presents an intriguing area for exploration with the promise of inducing more pronounced modifications in α decay processes.

A comparison of ΔP between α decay and cluster radioactivity for the same parent nucleus, ²²⁶Ra, was made. As shown in Fig. 4(b), ΔP for α decay is larger than that for cluster radioactivity of any parent nucleus shown here. This can be illustrated by the sensitivity of tunneling to changes in potential and decay energy. It is known that the α (¹⁴C cluster) decay energies used here are approximately 5 MeV (30 MeV) and that the tunneling exit points for α (¹⁴C cluster) are approximately 60 fm (25 fm). This implies that the modifications of the laser field in the potential and decay energy for α decay have a larger impact on the decay processes and, subsequently, a higher relative change in the penetration possibility. In addition, ΔP exhibits linear dependence on the laser intensity, whereas the values of the slope change dramatically after 10³⁰ W/cm². This can be explained using Eq. (22) and Eq. (23) or Eq. (24). At relatively low intensities, ΔP is proportional to $\sqrt{I}$. Only for high intensities, the term ${\gamma }^{\left(2\right)}$ proportional to I is not negligible, leading to an inflection in the curves. It should be noted that the slope of ΔP versus intensity curve is steeper for the alpha decay at extreme intensities. This indicates a higher sensitivity of alpha decay to high laser intensities. Given the increased sensitivity, it is reasonable to extrapolate that the effect of laser acceleration on proton emission should be even more pronounced. Consequently, it is recommended that laser-accelerated proton emission be used as a diagnostic tool for assessing the impact of an intense laser field.

The aforementioned theoretical calculations were implemented at the peak laser electric field strength and a fixed angle θ = 0°. Figure 5 shows the linearly polarized laser electric field strength E and the relative modification of the penetration possibility ΔP at a fixed angle θ = 0° as a function of time. It is clear that time-dependent E_t and ΔP share a similar variation trend, which can be explained by Eq. (22) and Eq. (23). Theoretically, the laser promotion and suppression effects on the possibility of penetration can be observed throughout a laser pulse circle. However, the best time resolution of the experimental detector is of the order of nanoseconds, which is much larger than the current laser period (of the order of femtoseconds). This implies that we cannot observe a time-dependent alteration in ΔP, as shown in Fig. 5(b), but a time averaging result in practice. Therefore, it is necessary to consider the effect of the complete laser period on ΔP.

Fig. 5Full-screen View

(Color online) (a) Linearly polarized laser electric field strength E and (b) relative modification of penetration possibility $\text{Δ}P\left(t\mathrm{,}{\theta }_0\mathrm{,}{I}_0\right)$ at a fixed angle θ₀ = 0° as a function of time. The intensity I₀ is 10²⁶ W/cm² for the α+²²²Rn system

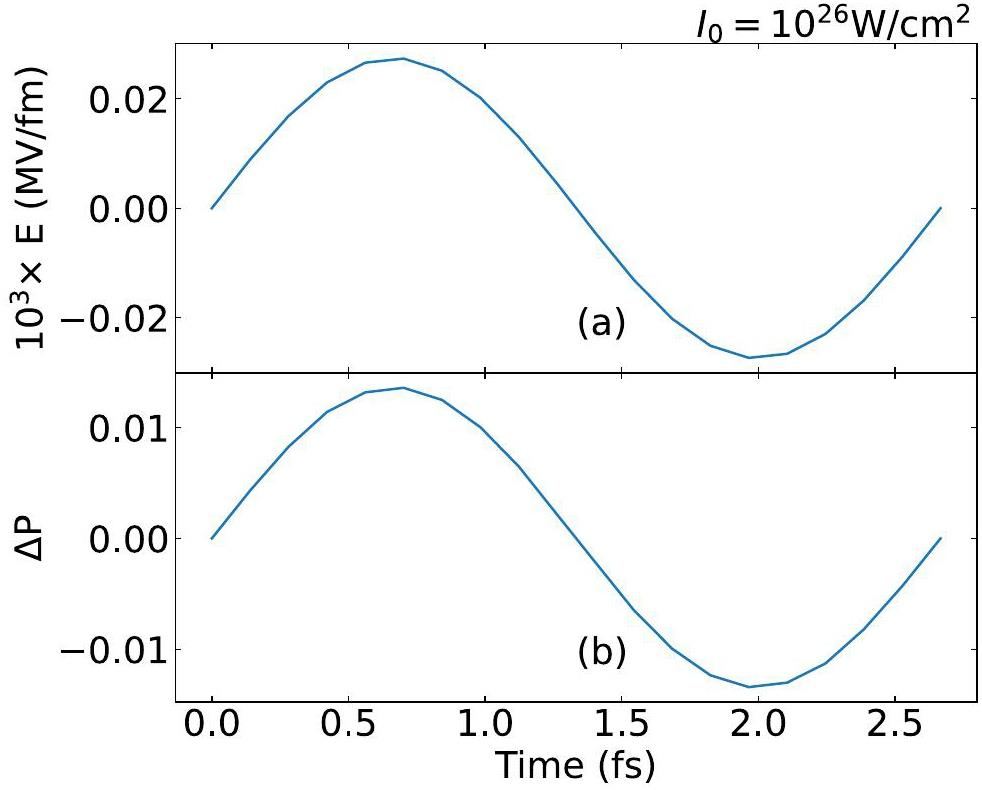
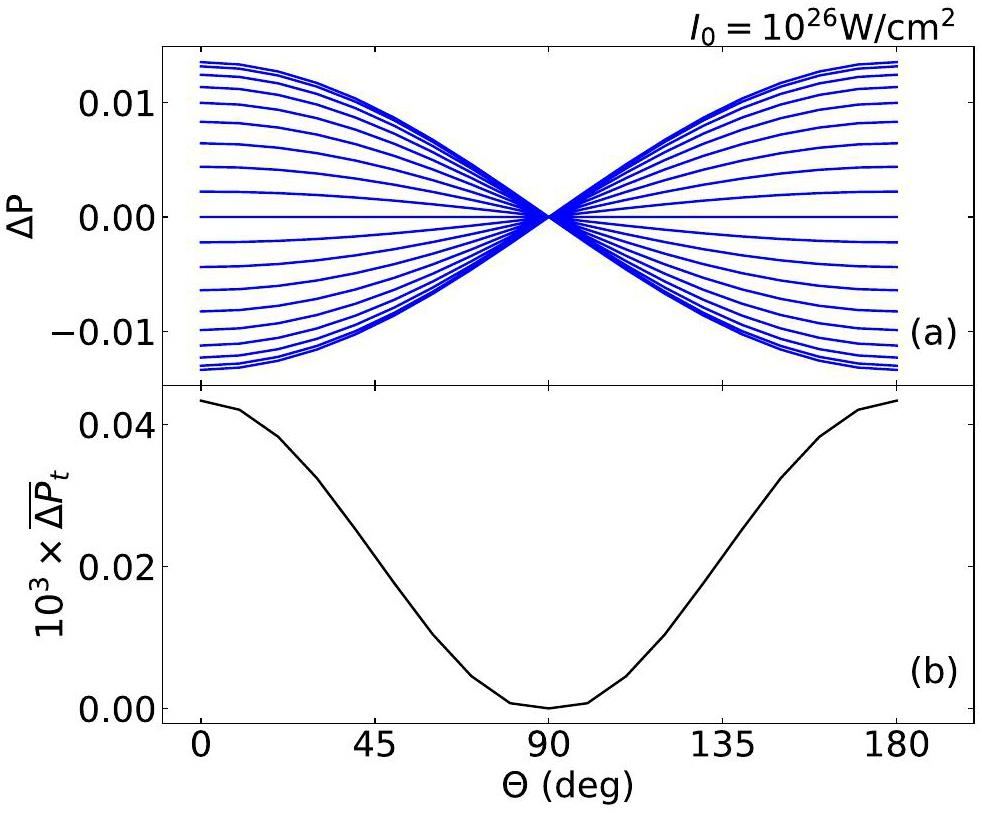
Figure 6(a) shows the correlation between ΔP and θ for a circular pulse. As illustrated in Eq. (23), ΔP exhibits a linear correlation with cosθ at some moment t. This explains the large variations in ΔP around 0 and 180 and the lack of modification along 90. Along one fixed angle, ΔP appears quite symmetric to be canceled by integrating over time. Thus, no net gain would remain for modification. Figure 6(b) shows the time-integrated modification ${\overline{\text{Δ}P}}_{\text{t}}$ as a function of angle θ. We can infer that some small asymmetries do exist such that a residual net gain remains. As can be observed in Eq. (23), the first equation, involving $\sin \left(\frac{2\pi c}{\lambda }t\right)$, cancels out over time, whereas the second equation remains positive throughout the laser period, contributing to the net gain. The time-integrated modifications are the strongest along 0 and 180, which are three orders of magnitude smaller than those before integration.

Fig. 6Full-screen View

(Color online) (a) Relative changes in penetration possibility $\text{Δ}P\left(t\mathrm{,}\theta \mathrm{,}{I}_0\right)$ as a function of angle θ seen from one pulse circle. Various curves depict the scenario at a specific moment t within the pulse cycle. (b) Time-integrated modification ${\overline{\text{Δ}P}}_{\text{t}}\left(\theta \mathrm{,}{I}_0\right)$ as a function of angle θ. θ represents the angle between the directions of the laser field and particle emission. Linear polarization is used here for system α+²²²Rn at the intensity of I₀ = 10²⁶ W/cm²

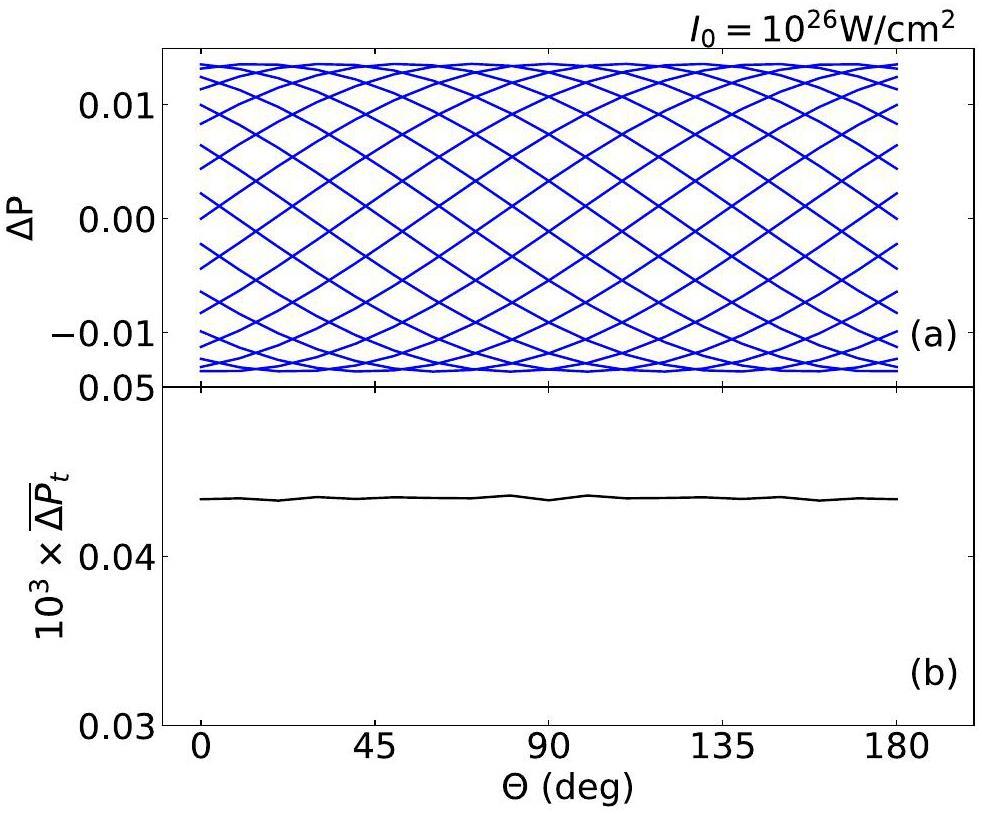
Some studies [59, 60] have explored the potential of elliptically polarized lasers to harness more information from strong-field atomic physics. Circular polarization, a specific manifestation of elliptical polarization, was considered. Figure 7(a) shows the correlation between ΔP and θ for a pulse circle with circular polarization. Unlike in the linearly polarized case, ΔP in the circular polarization arises from the superposition of sinθ and cosθ, leading to uniformly distributed modifications across all angles. The time-integrated results are presented in Fig. 7(b). It can be observed that the time-integrated modification ${\overline{\text{Δ}P}}_{\text{t}}$ is not affected by the angle between the directions of the laser field and particle emission, emphasizing the advantage of circular polarization in rendering the modification of the penetration possibility free from time averaging. This view coincides with that proposed by Qi et al. [10] who recommended using an elliptically polarized laser over a linearly polarized laser.

Fig. 7Full-screen View

(Color online) The same as Fig. 6 but for circular polarization

As was shown in Fig. 6, the linearly polarized laser results in angular anisotropy, with the most significant modifications along 0 and 180. A comparison of the time-integrated modification ${\overline{\text{Δ}P}}_{\text{t}}$ along 0 between linear and circular polarizations is shown in Fig. 8(a). Both exhibit consistent behavior. In other words, the time-integrated modification ${\overline{\text{Δ}P}}_{\text{t}}$ in circular polarization maintains the maximum value observed in linear polarization throughout the entire range of angles. This indicates that the primary distinction between the modifications induced by these two types of polarized lasers is associated with their angular distribution characteristics. Xiao et al. [14] indicated that it is important to consider angular integration because nuclei often appear as a population. The time- and angle-integrated modification ${\overline{\text{Δ}P}}_{\text{t}\theta }$ is represented in Fig. 8(b). Evidently, the modification of the circular polarization was several times larger than that of the linear polarization at the same intensity. It is preferable to employ a circularly polarized laser for a more significant modification.

Fig. 8Full-screen View

(Color online) (a) Time-integrated modification ${\overline{\Delta P}}_{\text{t}}\left(\theta =0°\mathrm{,}I\right)$ and (b) time- and angle-integrated modification ${\overline{\text{Δ}P}}_{\text{t}\theta }\left(I\right)$ using two polarization methods. The system is α+²²²Rn

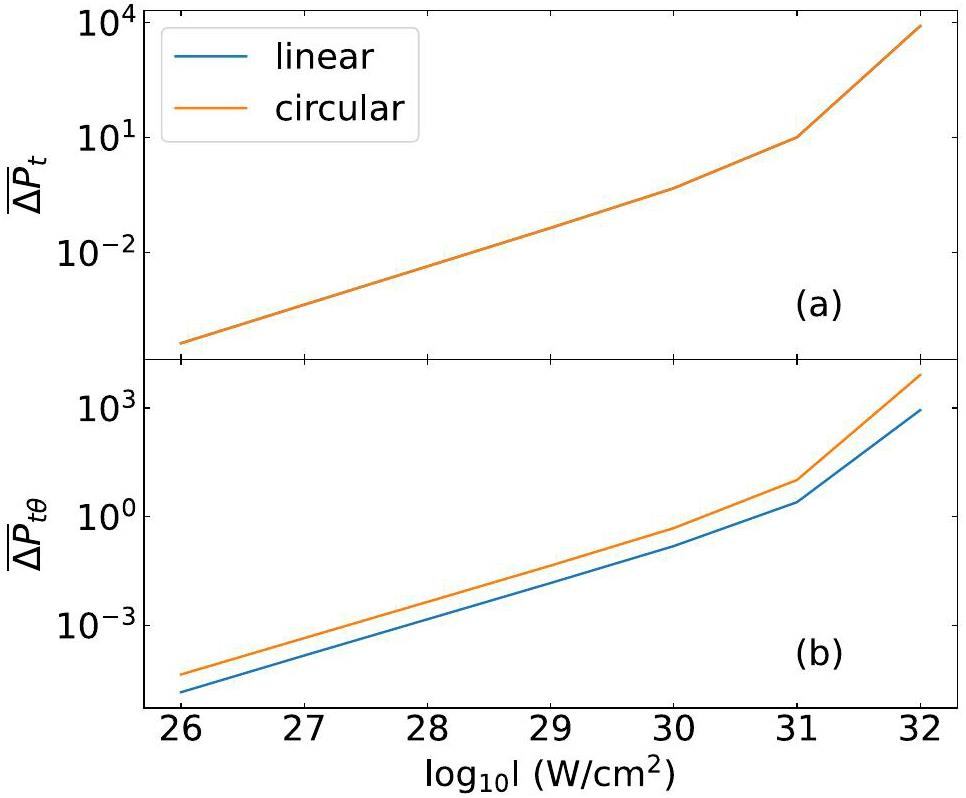
Figure 9 displays the time-integrated modification ${\overline{\text{Δ}P}}_{\text{t}}$ along 0 for (a) and (c) α decay and (b) and (d) ¹⁴C cluster radioactivity across different nuclei. The left and right panels refer to the linear and circular polarizations, respectively. Similar to Fig. 8(a), the two polarizations show the same behavior when the angle θ is fixed at 0. Among these nuclei, ¹⁴⁴Nd remains the parent nucleus that is the most susceptible to laser-induced modification, which is attributed to its relatively low decay energy. This modification attained a value of 0.1% at an intensity of 10²⁷ W/cm², which significantly exceeded the current laser intensity of 10²³ W/cm². A higher intensity of 10²⁸ W/cm² was required for ¹⁴C cluster radioactivity. Notably, additional physical effects are expected when the intensity approaches or surpasses the Schwinger critical field strength [61], whose corresponding laser intensity is 2.3×10²⁹ W/cm². The laser intensity I for circular polarization, where the time- and angle-integrated modification ${\overline{\text{Δ}P}}_{\text{t}\theta }$ reached an order of magnitude of 10^-3, is detailed in Table 2. These results are consistent with the scenario where θ = 0°. The modifications reached the order of 0.1% at an intensity of 10²⁷ W/cm² for α decay and 10²⁸ W/cm² for cluster radioactivity. Consequently, it is evident that laser-assisted α decay and ¹⁴C cluster radioactivity are not practically achievable with current technology.

Fig. 9Full-screen View

(Color online) Time-integrated modification ${\overline{\text{Δ}P}}_{\text{t}}\left(\theta =\mathrm{0,}I\right)$ for (a)(c) α decay and (b)(d) ¹⁴C cluster radioactivity. The left and right panels refer to the linear and circular polarization, respectively

Conclusion

In this study, we conducted a comprehensive microscopic analysis of the effects of extreme laser fields on α decay and cluster radioactivity. Our primary objective was to quantitatively assess the influence of intense laser fields, accounting for their temporal and angular effects, as well as variations in spatial structure. The theoretical framework is based on the Gamow model of quantum mechanical tunneling, whereas the FHF method provides a self-consistent description of the internuclear potential and nuclear deformation effects. The laser–nucleus interaction is represented by an electric field under the dipole approximation.

Our findings indicated that the laser field induced a downward shift in the Coulomb component of the potential and an increase in the decay energy. Given the high sensitivity of quantum tunneling to internuclear potential changes, even minor alterations in the potential or decay energy significantly affect the penetration probability. At an intensity of 10²⁴ W/cm², the modification in the penetration probability for the relevant nuclei reached approximately 0.1%, which is consistent with the results reported in Ref. [10].

The time- and angle-dependent modifications of penetration probability were analyzed using both linearly and circularly polarized lasers. In the case of linearly polarized lasers, the penetration probability exhibited its maximum modification at angles of 0 and 180, with no modification at 90. Conversely, circularly polarized lasers produced uniformly distributed modifications across all angles, and the angle-integrated modification induced by circular polarization was several times greater than that produced by linear polarization at the same intensity. Nevertheless, the modifications decreased by three orders of magnitude after temporal and angular integrations.

Finally, we compared the time- and angle-integrated modification of the penetration probability induced by circularly polarized lasers for both α decay and ¹⁴C cluster radioactivity across various nuclei. Among the studied nuclei, ¹⁴⁴Nd was the most susceptible to laser-induced modifications, primarily because of its relatively low decay energy. At an intensity of 10²⁷ W/cm², the modification of ${\overline{\text{Δ}P}}_{\text{t}\theta }$ for ¹⁴⁴Nd reached approximately 0.1%. However, this intensity far exceeds the currently achievable laser intensity of 10²³ W/cm², and the 0.1% modification remains below the detection threshold of the current measurement precision. The effect on the ¹⁴C cluster is weaker.

In conclusion, achieving observable laser-assisted α decay and ¹⁴C cluster radioactivity requires future advancements in laser technology to significantly enhance the intensity and experimental resolution. Consequently, expectations regarding the feasibility of laser-induced mechanisms for recycling nuclear radioactive waste should be carefully calibrated considering these technological constraints.