Introduction
Nuclear reactions at energies near the Coulomb barrier are effective for studying the interactions between the nuclear structure and dynamics. As more exotic weakly bound nuclei become accessible at new accelerator facilities, the measurement of reaction cross sections for weakly bound nuclear systems at sub-barrier energies is of great interest [1-3]. At present, it is found that in reactions involving these weakly bound nuclei, compared with theoretical calculations and tightly bound nuclei, complete fusion is significantly suppressed at energies above the Coulomb barrier and a remarkable enhancement at energies below the Coulomb barrier [4-8]. To investigate the breakup effects of weakly bound nuclei on the suppression of the complete fusion cross section, the study of the breakup reaction and mechanism of weakly bound nuclei is crucial importance [9-15].
Compared to a radioactive ion beam (RIB), the beam intensities of stable weakly bound nuclei such as 6,7Li and 9Be are orders of magnitude higher [16]. Several silicon detector arrays, such as EXPADES [17], GLORIA [18], and MITA [19], have recently been built to study the breakup mechanism induced by these stable weakly bound nuclei. Along with the identification of some breakup modes, the breakup effect of these nuclei on the fusion process has been preliminarily studied [20]. However, owing to the limited coverage angle of the previously mentioned detector arrays and the complexity of the breakup modes, it is challenging to detect rare breakup events and obtain the angular distribution of different breakup products.
In view of this fact, a new Silicon Telescopic Array for Reactions induced by Exotic nuclei (STARE), designed by the China Institute of Atomic Energy (CIAE), was employed for the coincidence measurement of charged fragments induced by weakly bound nuclei at energies around the Coulomb barrier. Compared with previous arrays [17-19], STARE incorporates more telescope detectors, providing larger solid-angle coverage and improved particle identification, which enables the detection of new breakup modes with small cross-sections. In addition, a specially designed frame allows both STARE and preamplifiers to be mounted directly inside the chamber, thereby simplifying the installation and reducing noise. The coincidence measurement of 6,7Li + 209Bi at Ebeam = 30, 40, 47 MeV was carried out successfully in the CIAE by STARE. In this study, the innovation features and performance of STARE, as well as the methods and preliminary results of the data analysis, are described in detail.
Description of the array
The STARE consists of eight telescope units, as shown in Fig. 1(a). Each telescope unit consists of (i) a double-sided silicon strip detector (DSSD) with a thickness of 40 μm for backward angles and 60 μm for forward angles, and (ii) a quadrant silicon detector (QSD) with a thickness of 1000 μm. To avoid the light charged particles not being clearly identified in the ΔE vs. E spectrum at forward angles due to their low energy loss in the DSSD, an additional QSD with a thickness of 300 μm was inserted between the DSSD and the 1000 μm thick QSD at forward angles. A brief description of this detector array is provided in Refs. [13, 21]. The eight telescope units surrounding the target were installed on a designed frame produced by 3D printing, which makes the array lighter and easy to be carried. The relative positions of the telescope units and the target are summarized in Table. 1. As shown in Fig. 1(b), the array covers polar angles θlab from 25° to 155°, and spans 301° in azimuthal angle, occupying 26.8% of the 4π sr. A larger number of telescope units provides larger solid angle coverage, greatly improving the coincidence detection efficiency compared with previous experiments [22-25].
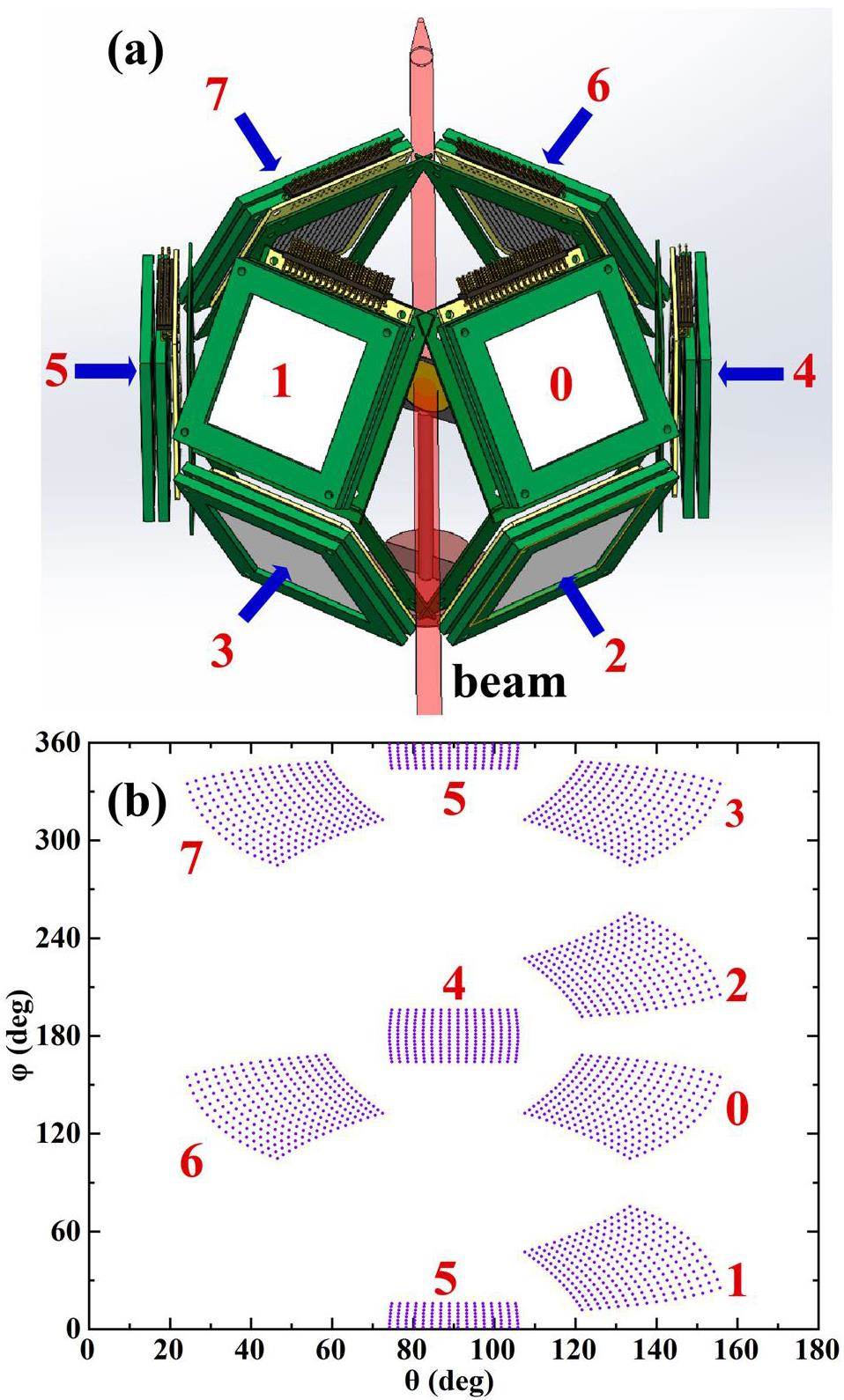
| Unit No. | Distance between unit and target (mm) | The angle of the center of each unit (θ, ϕ) |
|---|---|---|
| 0 | 70 | 132.1°, 139.2° |
| 1 | 70 | 132.1°, 40.8° |
| 2 | 70 | 132.1°, 220.8° |
| 3 | 70 | 132.1°, 319.2° |
| 4 | 82 | 90°, 180° |
| 5 | 82 | 90°, 0° |
| 6 | 70 | 47.9°, 139.2° |
| 7 | 70 | 47.9°, 319.2° |
A mylar foil with a thickness of 0.5 μm was installed in front of the telescope to stop low-energy electrons. As illustrated in Fig. 1(a), the compact structure enables the installation of the mylar foil and silicon detectors as close as possible to each other with the lowest energy loss and angular straggling. Moreover, the integrated preamplifiers designed by CIAE [26] were installed in close proximity to the detectors and positioned in the target chamber to reduce noise. To ensure stable operation of the preamplifiers, a cooling system is employed to dissipate the heat of the electronics and reduce the detector leakage current. Specifically, two brass rings are mounted on the top and bottom of the detector array, and all preamplifiers are fixed to these brass rings. During the experiments, the brass rings were cooled using a dedicated cooling system that provided a stable and low-temperature operating environment for the preamplifiers. These preamplifiers have been applied in several experiments and exhibit excellent and stable performance [27-34]. A specific photo is shown in Fig. 2.

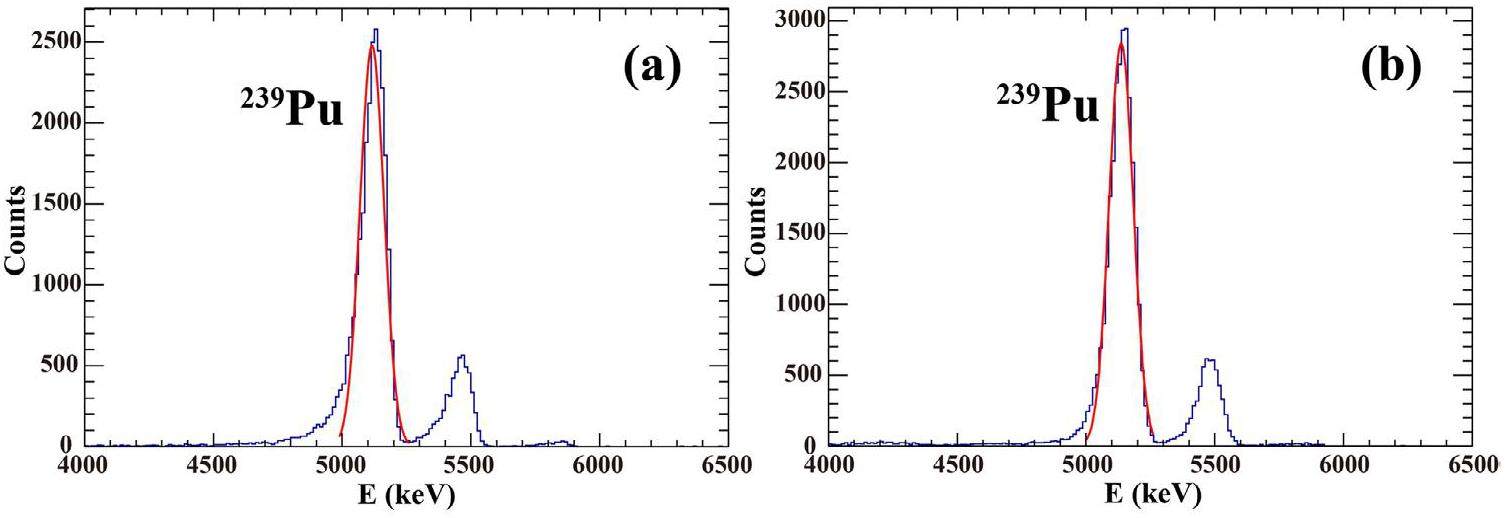
Silicon detectors are widely used owing to their high detection efficiency and good energy resolution [35]. In STARE, the kinetic energy of the particles was obtained from the energy signal of the pixel of the DSSDs, with a resolution of 100–150 keV FWHM for ~5 MeV α sources. To provide supporting evidence, Fig. 3 presents the energy spectra of the α sources measured using DSSDs of 40, 60 μm. The energy resolutions of the peaks corresponding to 239Pu were determined to be ~2.0%, ~1.8%, respectively. For the same α source, the energy resolution of the QSD is approximately 0.5%. The width of each strip of the DSSD was 3 mm, and the size of each pixel of the DSSD was 3 mm × 3 mm. Figure 1(b) shows the scattering angles of the centers of all DSSD pixels. We can infer that the angular resolution in the central region of each pixel of the DSSDs is approximately ±1.5°, with an improved resolution observed in the peripheral regions of the detector telescopes in the laboratory frame. Complete kinematic measurements can be performed with good energy and angular resolution, which are important for describing the breakup process.
Experiment
Coincident measurements with beams of 6,7Li were conducted at the HI-13 tandem accelerator of the CIAE. The beam energies at the center of the 209Bi target (210 μg/cm2 thick self-supporting) were approximately Ebeam = 30, 40, 47 MeV. A collimator with a diameter of 3 mm was positioned 30 cm upstream of the target, aligned along the beam axis, to precisely define the beam spot size and position. The target was fixed at the center of STARE with a normal angle of 70°relative to the beam line to minimize the dead area caused by the target frame. Four silicon detectors were installed at a distance of 250 mm from the center of the target for beam monitoring. To minimize the data collection rate during breakup measurements, the data were recorded when at least two pixels of the entire detector array were hit by particles in the multi-hit trigger mode.
Data analysis
Energy calibration
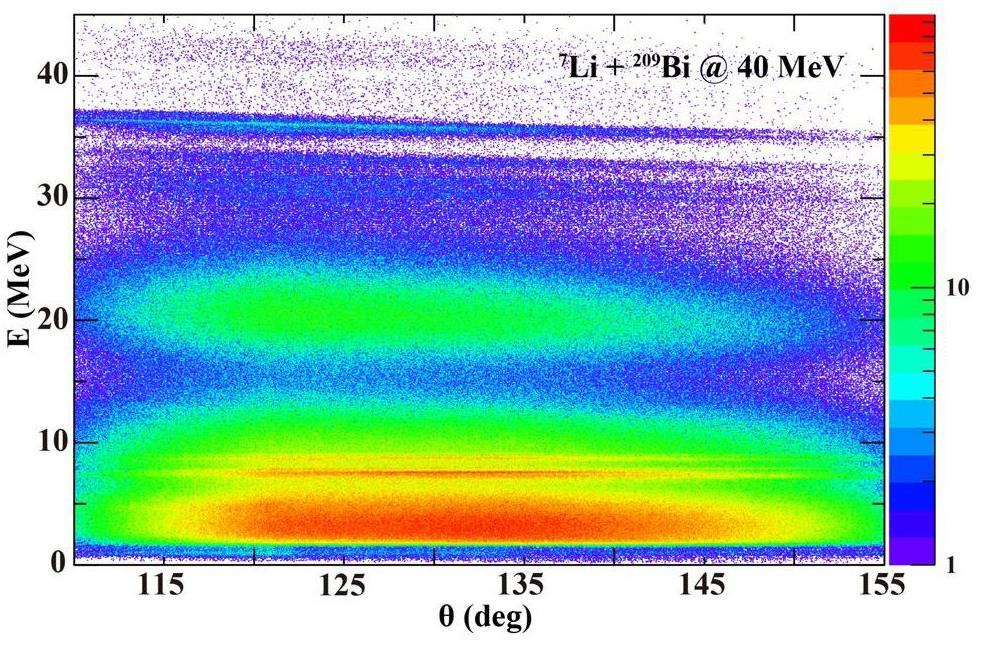
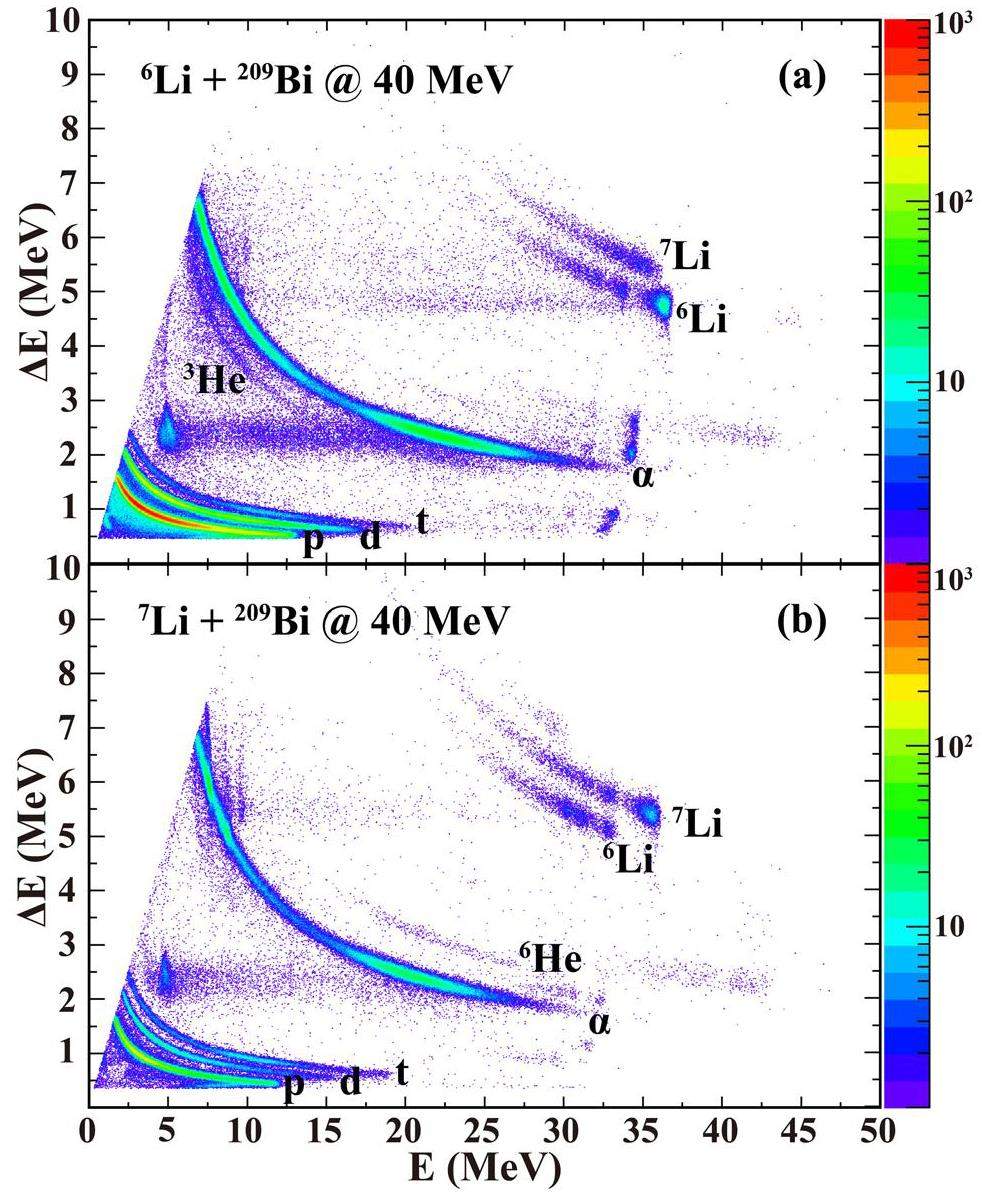
Energy calibration of the DSSDs was carried out using two α sources (239Pu, 241Am), and the α particles decayed from the products of the fusion reactions. Additionally, energy calibrations of the QSDs were performed by evaluating the deposited energies of the charged particles within the QSDs. This was achieved by subtracting the measured energy loss in the DSSDs from the expected particle energy, as determined by calculations using the reference for LISE++. In the experiment, the coordinate location of the DSSDs pixels was used to determine the scattering angle of the charged particles detected by the detectors. A typical energy-calibrated single spectrum for 7Li + 209Bi measured at Ebeam = 40 MeV is presented in Fig. 4, which shows elastic scattering events at ~36 MeV. For reactions in normal kinematics that produce two nuclei in the final state, such as elastic scattering or transfer, the energy of a projectile-like nucleus decreases monotonically with θ. The α lines between 5 and 10 MeV, as shown in Fig. 4, with energies independent of the angle, originate from the evaporation residues formed following complete fusion (CF) and incomplete fusion (ICF).
Removal of spurious events
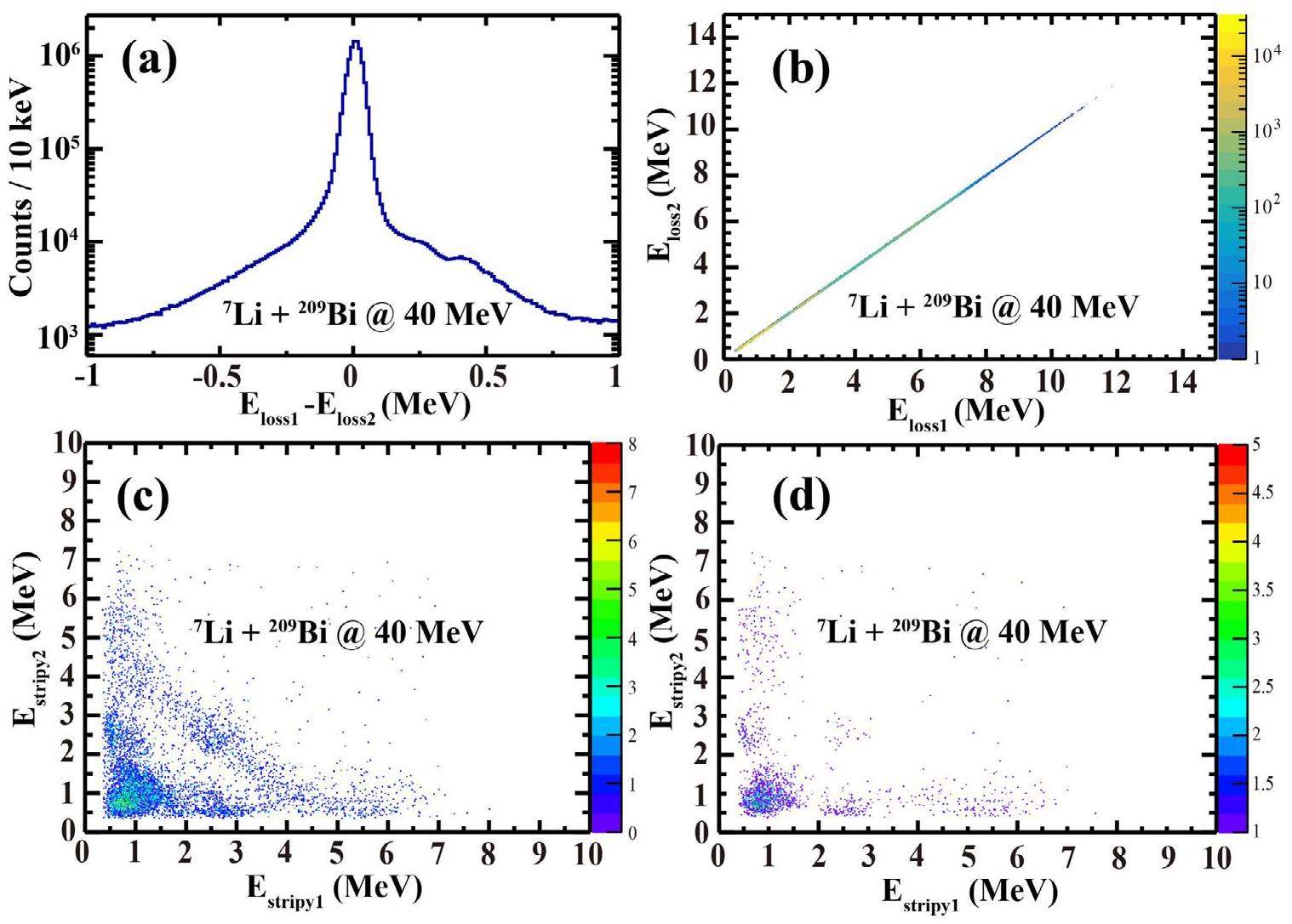
According to the principle of DSSDs, we used the energy signal output from both sides of the DSSDs (marked Eloss1, Eloss2, respectively) to select the correct events. As shown in Fig. 5(a), considering the statistics of events and the proportion of accidental coincidences, we select the events with Eloss1 - Eloss2 distributed within the σ (~100 keV) widening range as correct events. The two-dimensional spectrum Eloss1 vs. Eloss2 after screening is shown in Fig. 5(b). During the experiment, a large number of particles hit the inter-strips of the DSSDs, leading to a non-negligible number of accidental coincidence events (~3%). The two-dimensional spectra of the particles depositing energy in adjacent strips of the same DSSD before and after screening based on (a) are illustrated in Figs. 5(c) and (d). In Fig. 5(c), inter-strip events mainly originate from α, p, d, t particles distributed on the different lines
Typical two-dimensional particle identification spectra obtained from the same telescope unit are shown in Fig. 6. Owing to the excellent energy resolution of the detectors and statistics, the different masses (A = 1–7) and charges (Z = 1–3) produced by the different reaction channels can be clearly identified. In particular, the 3He and 6He bands can be observed in the experimental data of 6,7Li, which provides the possibility of observing new breakup modes. In Fig. 6(a), 7Li band can be observed. It is evident that 6Li picked up one neutron from the target; thus, 1n-pickup process induced by 6Li can occur. In Fig. 6(b), 6Li band can be observed. This is due to 1n-stripping of 7Li. The results show that 1n-stripping process is populated in the reactions of 7Li. The other light particles were analyzed in sections below.
Identification of breakup modes
During the breakup process, momentum conservation dictates that the total momentum of the fragments should remain zero in the center of mass frame of the projectile-like nucleus. Thus, fragments must travel in opposite directions in the center of the mass frame but may be emitted in any direction. As a result, we can filter out α particles from the breakup process, as shown in Fig. 7(a), from 6Li + 209Bi at Ebeam = 40 MeV, when a continuous distribution of energies with maximum and minimum energies is given by
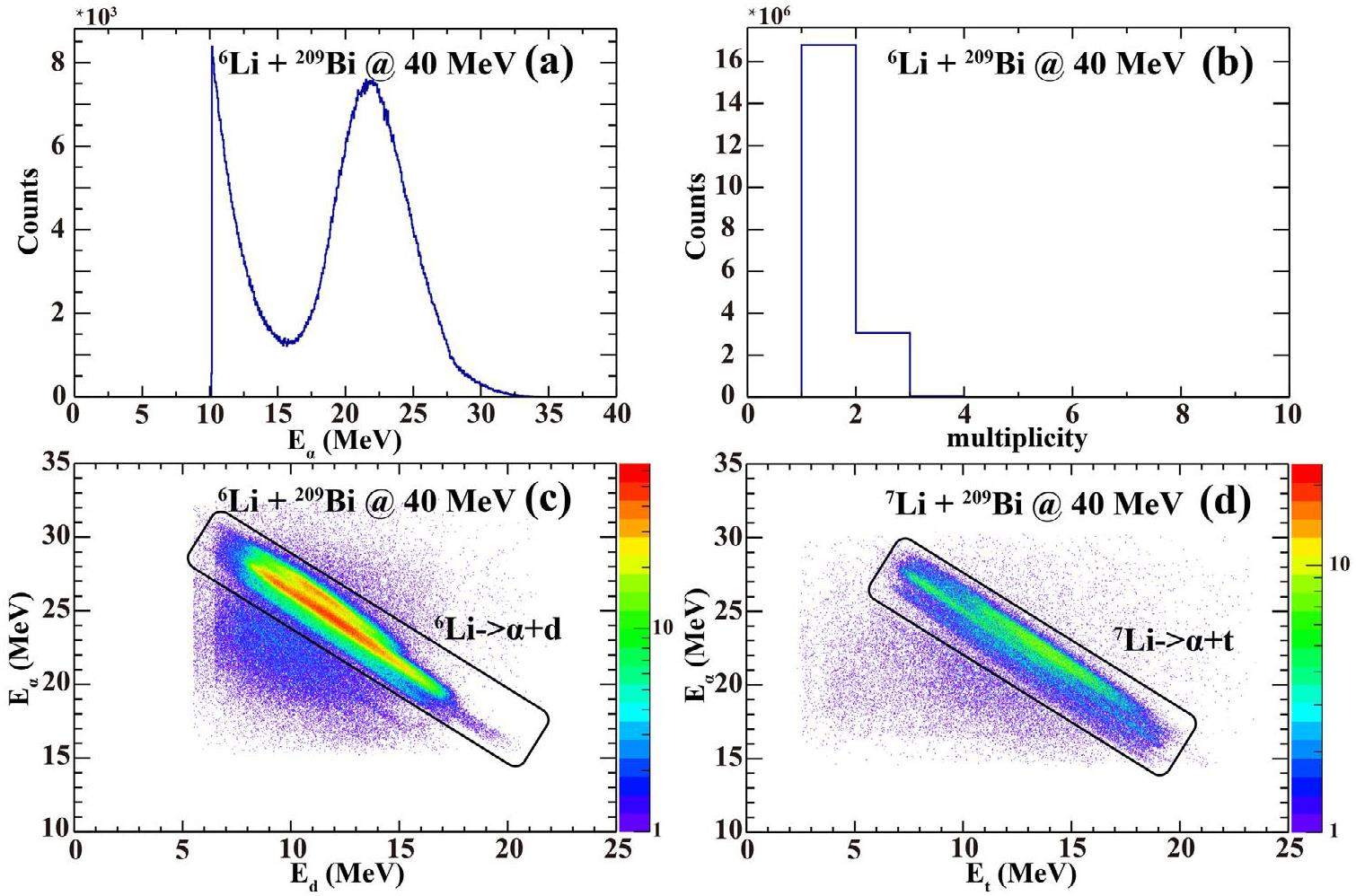
The correlations between the kinetic energies of the coincident fragments from the direct breakup mode of 6,7Li at Ebeam = 40 MeV are presented in Figs. 7(c) and (d). The band-like structures are immediately obvious, which suggests that these events have originated from the true 6Li → α + d and 7Li → α + t breakup processes. Other breakup events from different modes can be extracted in the same manner.
Based on the extracted breakup events, two-body dynamics calculations can be used to reconstruct the breakup reaction Q value to further understand the breakup mechanism. The energy change (Q value) in the reaction can be determined by Eq. (2):
The reconstructed Q spectra of all the breakup modes in the reactions of 6,7Li with 209Bi at Ebeam = 30, 40 and 47 MeV are shown in Fig. 8. Vertical dashed lines indicate the expected Qgg, which corresponds to the ground state of the target-like nucleus. In the reaction of 6Li, compared with the direct breakup mode (6Li → α + d), the breakup of 5Li into α + p after 1n-stripping seems to be the most dominant, as can also be verified in Refs. [23, 36, 37]. In addition, a new breakup mode, 7Li → α + t was observed for the first time by STARE with obvious Q value peaks, indicating the ground and excited states of 208Bi. We can observe that the relevance of the 7Li → α + t channel increases with beam energy. The discovery of 7Li → α + t breakup mode indicates that the 1n-pickup process cannot be ignored in the reaction of 6Li, which also provides an additional explanation for the origin of inclusive α particles [38, 39].
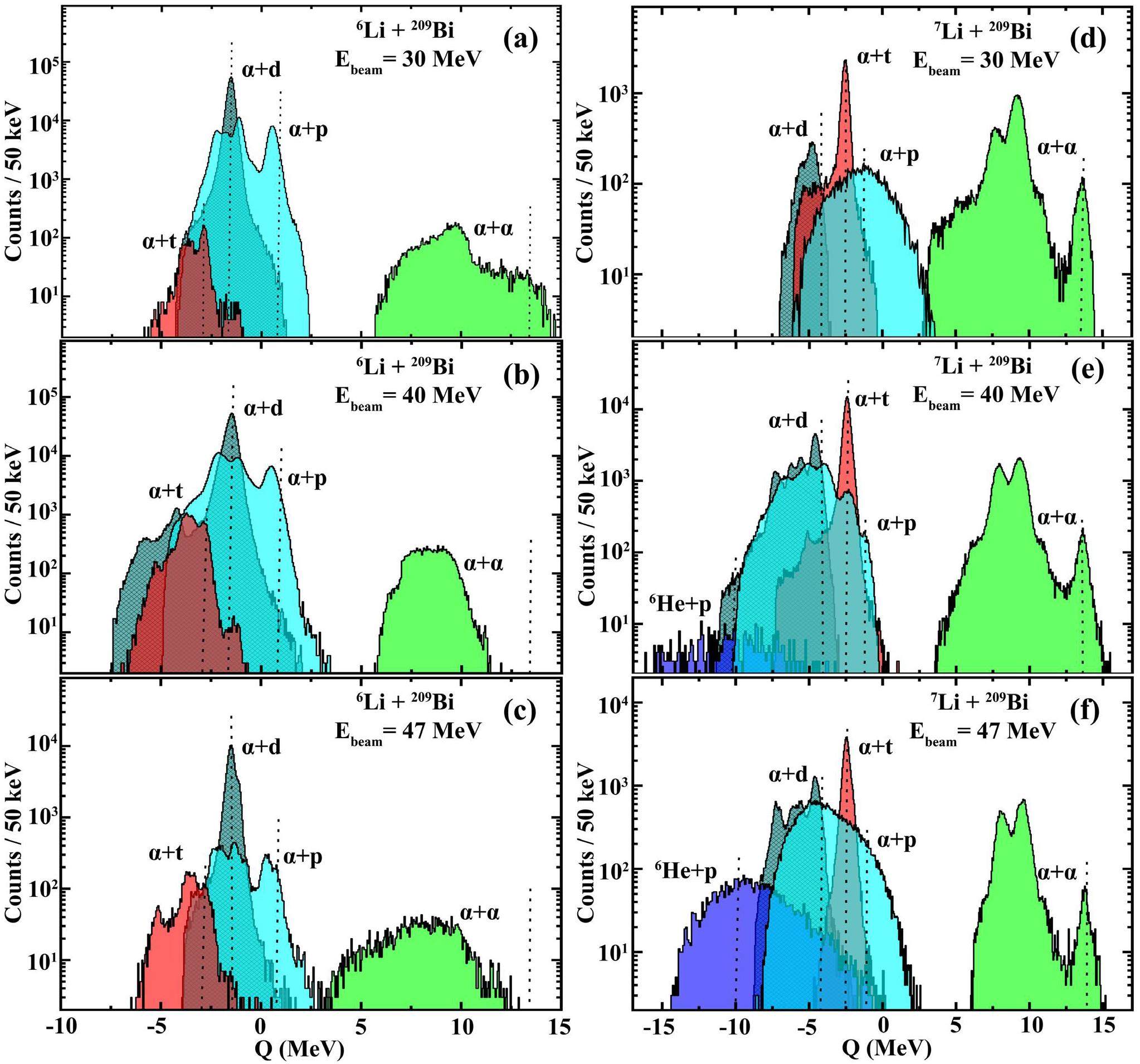
For the reaction 7Li + 209Bi, the breakup triggered by a 1p-pickup is the most probable channel for 7Li. The breakup after the production of 8Be into two α particles produces multiple peaks in the Q value spectra, including the ground state and two excited states of 208Pb. However, when the target is replaced by a medium-mass nucleus, conclusions may be inconsistent. In the 7Li + 93Nb system [40], α + t and α + d are dominant. When the beam energy was increased to 40, 47 MeV, despite a very high breakup threshold (~10 MeV), a significant number of 6He + p events were observed in 7Li + 209Bi system. The present exclusive measurement of 6He in coincidence with a proton that provides direct evidence of the 6He + p cluster configuration of 7Li is important for understanding the possible nuclear cluster structures of 7Li [41].
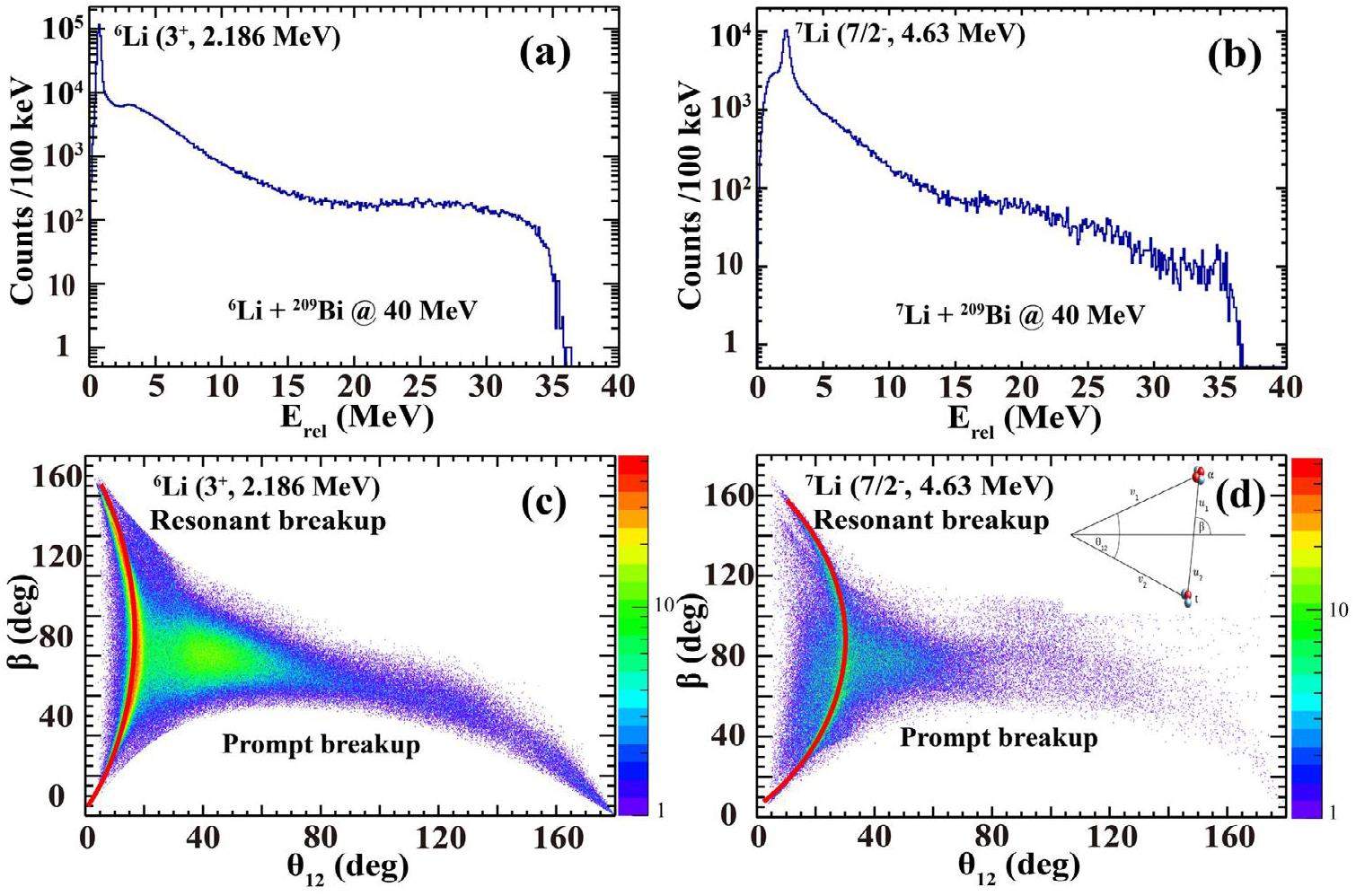
Prompt breakup vs. Reasonant breakup
In recent works [25, 36], the relative energy (Erel) of breakup fragments has been reported to provide significant information on the breakup time-scale and to allow a classification of the breakup process into prompt breakup or resonant breakup, which can be expressed in terms of the measured energies and masses of the fragments, and the measured opening angle of the fragments within the laboratory frame (
Summary
In this study, a new multilayer silicon telescope array was designed and manufactured to study the breakup reaction mechanisms induced by weakly bound nuclear systems at energies around the Coulomb barrier. In the new array, integrated preamplifiers are positioned near the detectors and operate continuously and stably in a low-temperature environment, which is very important for reducing noise. STARE with a large solid angle greatly improves the coincidence efficiency, making it possible to collect breakup events with very small cross-sections.
STARE has been successfully used to investigate the coincidence measurement of charged fragments in 6,7Li + 209Bi systems at Ebeam = 30, 40, 47 MeV. Owing to the powerful particle identification and energy resolution of STARE, different breakup modes can be clearly distinguished by two-body dynamics calculations, along with the observation of new breakup modes. Different breakup components (prompt breakup and resonant breakup) can be identified by the relative energy and angular correlation spectra, which are important for reproducing the breakup process of weakly bound nuclei. To facilitate the understanding of the breakup mechanisms of weakly bound nuclei and to elucidate the cluster structure within the projectile-like nucleus, the angular distributions of different breakup components are currently being pursued. Simultaneously, our collaborators are also trying to develop a theoretical framework for predicting these reactions. The details of this work are presented in a forthcoming paper.
Near-Barrier Fusion of the 6B + 58Ni Proton-Halo System
. Phys. Rev. Lett. 107,Recent developments in fusion and direct reactions with weakly bound nuclei
. Phys. Rep. 596, 1-86 (2015). https://doi.org/10.1016/j.physrep.2015.08.001Systematic study of reaction functions of weakly bound nuclei
. Phys. Rev. C 87,Small suppression of the complete fusion of the 6Li + 96Zr system at near-barrier energies
. Phys. Rev. C 91,Complete and incomplete fusion of 9Be + 169Tm, 187Re at near-barrier energies
. Phys. Rev. C 91,Coupling effects on the fusion of 6Li + 154Sm at energies slightly above the Coulomb barrier
. Phys. Rev. C 92,Negligible suppression of the complete fusion of 6,7Li on light targets, at energies above the barrier
. Phys. Rev. C 94,Fusion reactions in the 9Be + 197Au system above the Coulomb barrier
. Phys. Rev. C 100,Transfer and/or Breakup Modes in the 6He + 209Bi Reaction near the Coulomb Barrier
. Phys. Rev. Lett. 84, 5058-5061 (2000). https://doi.org/10.1103/PhysRevLett.84.5058Effect of breakup on the fusion of 6Li, 7Li, and 9Be with heavy nuclei
. Phys. Rev. C 70,Numerical assessment of post-prior equivalence for inclusive breakup reactions
. Phys. Rev. C 92,Comprehensive analysis of large α yields observed in 6Li-induced reactions
. Phys. Rev. C 95,Relative probabilities of breakup channels in reactions of 6,7Li with 209Bi at energies around and above the Coulomb barrier
. Chin. Phys. C 45 (2021). https://doi.org/10.1088/1674-1137/abe3eeBreakup of the proton halo nucleus 8B near barrier energies
. Nat. Commun 13, 7193 (2022). https://doi.org/10.1038/s41467-022-34767-8Further investigation on the fusion of 6Li with 209Bi target at near-barrier energies
. Chin. Phys. C 48 (2024). https://doi.org/10.1088/1674-1137/ad4264A powerful combination measurement for exploring the fusion reaction mechanisms induced by weakly bound nuclei
. Nucl. Instr. Methods Phys. Res. A 914, 64-68 (2019). https://doi.org/10.1016/j.nima.2018.05.067EXPADES: A new detection system for charged particles in experiments with RIBs
. Nucl. Instr. Methods Phys. Res. B 266, 4637-4642 (2008). https://doi.org/10.1016/j.nimb.2008.05.121GLORIA: A compact detector system for studying heavy ion reactions using radioactive beams
. Nucl. Instr. Methods Phys. Res. A 755, 69-77 (2014). https://doi.org/10.1016/j.nima.2014.04.002MITA: A Multilayer Ionization-chamber Telescope Array for low-energy reactions with exotic nuclei
. Eur. Phys. J. A 55, 1-11 (2019). https://doi.org/10.1140/epja/i2019-12765-7Breakup dynamics of weakly bound nuclei at energies around the Coulomb barrier
, Fundamental Research, https://doi.org/10.1016/j.fmre.2023.10.006The effects of beam drifts on elastic scattering measured by the large solid-angle covered detector array
. Nucl. Sci. Tech. 32, 14 (2021). https://doi.org/10.1007/s41365-021-00854-6Mechanisms and systematics of breakup in reactions of 9Be near-barrier energies
. Phys. Rev. C 81,Predominance of transfer in triggering breakup in sub-barrier reactions of 6,7Li with 144Sm, 207,208Pb, and 209Bi
. Phys. Rev. C 88,Resonant breakup of 6Li by 209Bi
. Phys. Lett. B 677, 139-144 (2009). https://doi.org/10.1016/j.physletb.2009.05.016Asymptotic and near-target direct breakup of 6Li and 7Li
. Phys. Rev. C 93,Compact 16-channel integrated charge-sensitive preamplifier module for silicon strip detectors
. Nucl. Sci. Tech. 31, 48 (2020). https://doi.org/10.1007/s41365-020-00755-0A detection system for charged-particle decay studies with a continuous-implantation method
. Nucl. Instr. Methods Phys. Res. A 804, 1-7 (2015). https://doi.org/10.1016/j.nima.2015.09.0390β-decay study of the Tz=−2 proton-rich nucleus 20Mg
. Phys. Rev. C 95,Observation of β-delayed two-proton emission in the decay of 22Si
. Phys. Lett. B 766, 312-316 (2017). https://doi.org/10.1016/j.physletb.2017.01.028Optical model potentials for 6He + 64Zn from 63Cu(7Li,6He)64Zn reactions
. Phys. Rev. C 95,Abnormal behavior of the optical potential for the halo nuclear system 6He + 209Bi
. Phys. Rev. C 96,Is the Dispersion Relation Applicable for Exotic Nuclear Systems? The Abnormal Threshold Anomaly in the 6He + 209Bi System
. Phys. Rev. Lett. 119,A detector setup for the measurement of angular distribution of heavy-ion elastic scattering with low energy on RIBLL
. Nucl. Sci. Tech. 28, 104 (2017). https://doi.org/10.1007/s41365-017-0249-0The calibration of elastic scattering angular distribution at low energies on HIRFL-RIBLL
. Nucl. Instr. Methods Phys. Res. A 846, 23-28 (2017). https://doi.org/10.1016/j.nima.2016.11.058Characterization of CIAE developed double-sided silicon strip detector for charged particles
. Nucl. Sci. Tech. 29, 73 (2018). https://doi.org/10.1007/s41365-018-0406-0Insights into the mechanisms and time-scales of breakup of 6,7Li
. Phys. Lett. B 695, 105-109 (2011). https://doi.org/10.1016/j.physletb.2010.11.007One-neutron stripping process in the 209Bi(6Li,5Li)210Bi* reaction
. Nucl. Sci. Tech. 35, 104 (2024). https://doi.org/10.1007/s41365-024-01462-wExclusive breakup of 6Li by 208Pb at Coulomb barrier energies
. Phys. Rev. C 67,Disentangling reaction mechanisms for α production in the 6Li + 209Bi reaction
. Phys. Rev. C 85,Probing transfer to unbound states of the ejectile with weakly bound 7Li on 93Nb
. Phys. Rev. C 93,Role of cluster structure in the breakup of 7Li
. Phys. Rev. C 97,The authors declare that they have no competing interests.

