Introduction

Atomic nuclei are self-bound quantum many-body systems, and a key goal in modern nuclear physics is to solve these systems using first principles. To achieve this, one can compute the ground-state and excited-state energies along with their corresponding wavefunctions, either in coordinate space or within a specific basis, such as the harmonic oscillator basis.

Methods in the coordinate space are typically represented by various Quantum Monte Carlo (QMC) techniques, including diffusion Monte Carlo (DMC) and the related Green’s function Monte Carlo (GFMC) [1-4]. These methods have proven to be successful in accurately determining the properties of light nuclei. However, a major obstacle of these methods is the Fermion sign problem: due to the antisymmetry property of the many-body wavefunction, the wavefunction necessarily contains both positive and negative amplitudes, which cannot be directly sampled using a probability distribution. Techniques such as the fixed-node approximation or constrained-path method are often employed to mitigate the sign problem [2, 4]. A key challenge in these methods is the requirement for a trial wavefunction that approximates the true wavefunction as closely as possible.

Configuration interaction (CI) methods, including the configuration interaction shell model (CISM) [5, 6] and no-core shell model (NCSM) [7, 8], provide direct and accurate frameworks for solving quantum many-body systems in basis space. However, the configuration space grows exponentially with the number of particles, making it computationally infeasible to store all the configurations in memory. To address this issue, one can truncate the configuration space using methods such as particle-hole truncation or ħω truncation. Despite these techniques, many configurations are still required to achieve converged results, which is impossible for large-dimension systems.

An alternative approach is the post-Hartree-Fock methods [9], which offers polynomial complexity. These include perturbative approaches, such as Many-Body Perturbation Theory (MBPT) [10-13], and non-perturbative approaches, such as the in-medium similarity renormalization group (IMSRG) [14-16] and Coupled Cluster (CC) [17, 18]. However, all of these approaches rely on truncation schemes, which may introduce inaccuracies, particularly in strongly correlated systems. Efforts to improve the accuracy by going to higher-order truncations [19, 20] are in progress. However, computational cost remains a significant challenge.

In 2009, Booth et al. developed a full configuration interaction quantum Monte Carlo method for quantum chemistry calculations [21]. This method samples wavefunctions in the configuration space, allowing the storage of only a small subset of important configurations that are often several orders of magnitude smaller than those in the full configuration space. Moreover, by utilizing signed walkers and walker annihilation, FCIQMC can avoid the Fermion sign problem and converge to the exact wavefunction without requiring prior knowledge of its nodal structure.

FCIQMC has been successfully applied to a range of systems [21-23], including both molecular and condensed matter systems, and has proven to be particularly effective for strongly correlated systems [24, 25]. Given its strengths, it shows promise for nuclear structure calculations. In this study, we developed a C++ code implementing FCIQMC, considering the symmetry properties of nuclear systems.

Several other quantum Monte Carlo methods also operate in configuration space, including the Monte Carlo shell model (MCSM) [26, 27], which constructs the basis by evolving in the auxiliary field and then diagonalizes the Hamiltonian using that basis; and the configuration interaction Monte Carlo (CIMC) [28, 29], which, despite its similar name to FCIQMC, uses a guiding wavefunction to perform a "fixed-node approximation" in configuration space. It is important to note that, although these methods share some similarities, they are fundamentally distinct from one another.

The remainder of this article is organized as follows: In Sect. 2, we introduce the theory and algorithm of FCIQMC and its enhanced variant. In Sect. 3, we present the benchmarking results with shell model calculations for Fe isotopes in the pf-shell and for an artificially constructed strongly correlated system. We also tested large-space calculations using examples of Mg isotopes in the full sdpf shell.

The Full configuration interaction quantum Monte Carlo

The CI method aims to solve the Schrödinger equation $\widehat{H}{\text{Ψ}}_0=E_0{\text{Ψ}}_0$ in configuration space. A configuration is a Slater determinant constructed on a single-particle basis. Considering a system of N particles with M single-particle orbitals, $a_i^{†}\left(i=\mathrm{1,}\mathrm{2,}\dots \mathrm{,}M\right)$, we can express all possible configurations as $|D_i\rangle =a_{i_1}^{†}{a}_{i_2}^{†}\dots a_{i_N}^{†}|0\rangle \mathrm{,}{i}_1<i_2<\dots <i_N\mathrm{,}$ (1) where $|0\rangle$ denotes the particle’s vacuum state. The Lanczos algorithm is powerful for diagonalizing Hamiltonians in the configuration space, as used in the computational codes of Bigstick [30] and kshell [31] to obtain the exact wavefunction, $\text{Ψ}={\displaystyle \sum _i}{C}_i|D_i\rangle \mathrm{.}$ (2) The dimensions of the full configuration space are of the order of $\left(\begin{array}{c}M\\ N\end{array}\right)$, which grows exponentially with the number of particles. This makes it impossible to store all the coefficients Ci in the memory when the system is large.

Instead, the FCIQMC method samples wavefunctions in the configuration space. To achieve this, we use the projection method instead of the diagonalization method to obtain the ground-state wavefunction Ψ₀ using the following operator: $\psi (\tau )=e^{-\tau \left(\widehat{H}-E_0\right)}\psi (\tau =0)\stackrel{\tau \to \infty }{\to }{\text{Ψ}}_0\mathrm{,}$ (3) where E₀ is the ground-state energy, and τ indicates the time evolution. In this process, excited states are projected, and only the ground state remains. This approach is achieved by the imaginary time Schrödinger equation as follows: $-\frac{\text{d}}{\text{d}\tau }\psi (\tau )=\left(\widehat{H}-E_0\right)\psi (\tau )\mathrm{.}$ (4) By expanding this differential equation in the configuration space, we obtain $-\frac{\text{d}{C}_i}{\text{d}\tau }={\displaystyle \sum _j}\left(H_{ij}-S{\delta }_{ij}\right)C_j\mathrm{.}$ (5) Here, we replace the ground-state energy E₀ with a self-adaptive shift S because the ground-state energy is unknown before the calculation. The method for adapting the shift S is explained later in this paper.

Similar to QMC methods in coordinate space, the coefficient Ci can be either positive or negative, making it impossible to sample them directly as a probability distribution. In the FCIQMC method, this issue is addressed by introducing the so-called walkers, which are distributed across various determinants. The number of walkers in $|D_i\rangle$ is denoted as Ni. Every walker is assigned a sign to represent negative coefficients, allowing Ni to be either positive or negative. The total number of walkers is given by: $N_w={\displaystyle \sum _i}\left|N_i\right|\mathrm{.}$ (6) We expect the walker number in a given determinant to be proportional to the corresponding expanded coefficients. Thus, the imaginary time Schrödinger equation is discretized as follows: $-\frac{\text{Δ}{N}_i}{\text{Δ}\tau }={\displaystyle \sum _j}\left(H_{ij}-S{\delta }_{ij}\right)N_j\mathrm{.}$ (7) A typical evolution of FCIQMC starts with a single determinant $|D_0\rangle$, which can be the Hartree-Fock ground state or a determinant with particles filling the lowest orbitals of the basis used. We begin the evolution with 10 walkers in $|D_0\rangle$ according to Eq. (7). The process of imaginary time evolution can be split into three periods: warm up, projection, and statistic.

During the warm-up period, we maintain a constant shift $S=\langle D_0\left|\widehat{H}\right|D_0\rangle >E_0$. The ground-state wavefunction grows with $\exp [-\left(E_0-S\right)\tau ]$, causing the total walker number to increase exponentially. Once the total waller number reached a certain number, we entered the projection period. During this period, the shift varied according to the total walker number. The goal was to maintain the total walker number at a constant level. The shift S was updated at A steps, as suggested in Ref. [21] $S(\tau )=S(\tau -A\text{Δ}\tau )-\frac{\zeta }{A\text{Δ}\tau }\ln \frac{N_w\left(\tau \right)}{N_w\left(\tau -A\text{Δ}\tau \right)}\mathrm{.}$ (8) In this study, we adapted the shift S every A = 10 steps and set $\zeta =0.1$ for all calculations.

When the imaginary time evolution reaches equilibrium, which means that the total walker number is almost stable, and the shift S fluctuates only slightly around the ground state, we begin the statistical period. We continued the equilibrium evolution for several steps and performed statistics to evaluate the ground-state energy. The shift parameter S can be used to evaluate the ground-state energy, and we can also use the local time energy: $E(\tau )=\frac{\langle D_0\left|\widehat{H}\right|\psi (\tau )\rangle }{\langle D_0|\psi (\tau )\rangle }={\displaystyle \sum _i}{H}_{0i}\frac{N_i\left(\tau \right)}{N_0\left(\tau \right)}\mathrm{,}$ (9) where $N_0\left(\tau \right)$ is the walker number in the $|D_0\rangle$ determinant and $H_{0i}$ is for $\langle D_0\left|\widehat{H}\right|D_i\rangle$.

The remaining challenge is the evolution of the imaginary time Schrödinger equation, Eq. (7) stably and effectively, which is key to the FCIQMC calculation. Every Δτ evolution is performed in the following three steps [21]:

The spawning step: For each walker in determinant $|D_i\rangle$, we select a connected $|D_j\rangle$ with a probability of p_gen(j|i) and attempt to spawn walkers into $|D_j\rangle$ with the following probability: $p_{\text{spawn}}\left(j|i\right)=\frac{\text{Δ}\tau \left|H_{ij}\right|}{p_{\text{gen}}\left(j|i\right)}\mathrm{.}$ (10) The sign of the newly spawned walker is opposite to $\text{sign}\left(H_{ij}{N}_i\right)$. Spawning walkers with probability $p_{\text{spawn}}\left(j|i\right)$ means that we spawn $\lfloor p_{\text{spawn}}\rfloor$ walkers with a probability of 1 and spawn one walker with a probability of $p_{\text{spawn}}-\lfloor p_{\text{spawn}}\rfloor$. Two determinants, $|D_i\rangle$ and $|D_j\rangle$ are said to be connected if $H_{ij}\ne 0$ and $j\ne i$. For a system with only one- and two-body interactions, there are two types of connected determinants: single and double excitations.

For a single excitation, we first select an occupied orbital (labeled a) from $|D_i\rangle$ with an equal probability of $1/N_a$ where Na is the number of occupied orbitals in $|D_i\rangle$. Next, we identify all unoccupied orbitals in $|D_i\rangle$ that have the same parity, spin projection m and isospin projection tz as those of the a orbital. From this set of unoccupied orbitals, we randomly selected one (labeled by b) with an equal probability of $1/N_b$ where Nb is the number of unoccupied orbitals. Then, $|D_j\rangle$ is constructed by removing the a orbital and adding the b orbital to $|D_i\rangle$. Finally, the generation probability p_gen(j|i) is determined as the product of the two probabilities, that is, equal to $1/\left(N_a{N}_b\right)$.

For double excitation, we first select two occupied orbitals labeled by a and b. Similar to the single excitation discussed above, each selection of a pair of occupied orbitals has an equal probability. Then, we identify all pairs of unoccupied orbitals that have the same parity, total spin projection m, and total isospin projection tz as those of the two-body state formed by the a and b orbitals. From this set of unoccupied orbital pairs, we randomly selected one pair with an equal probability. As in the single-excitation case, the generation probability p_gen(j|i) is determined by the product of the probabilities associated with selecting the pair of occupied orbitals and the pair of unoccupied orbitals.

In each spawning attempt, we performed either a single or double excitation chosen with probabilities p_single and $p_{\text{double}}=1-p_{\text{single}}$, respectively. The final p_gen is multiplied by p_single when a single excitation is chosen, or multiplied by p_double when a double excitation is chosen. In the present work, we used $P_{\text{single}}=1/2$ for all calculations. Our calculation indicates that this choice of probability assignment does not have a noticeable impact on the calculation outcomes.

Diagonal death/cloning step: For each walker in determinant $|D_i\rangle$, we calculate $p_{\text{death}}\left(i\right)=\text{Δ}\tau \left(H_{ii}-S\right)\mathrm{.}$ (11) If p_death(i) > 0, the walker dies with probability p_death(i). If p_death(i) < 0, the walker clones with a probability of -p_death(i).

The annihilation step: Collect all walkers in the same determinant (including the spawned walkers), and annihilate pairs of walkers with opposite signs until only walkers with the same sign remain in the determinant. This step is necessary to prevent exponential growth of walkers [21].

This algorithm can be easily extended to a Hamiltonian with three-body interactions, although we did not incorporated it in the present computational code. The only modification is that the spawning step should include triplet excitation.

The original FCIQMC [21], as described above, can work for some systems, but requires a minimum walker number that can be very large in certain cases. For example, with our code, we found that in sd and pf shells, the converged evolution requires a walker number that is almost equal to the dimension of a full configuration calculation which is due to the sign problem. During Monte Carlo evolution, some determinants may randomly acquire a small number of walkers with opposite signs to the main wavefunction [32]. These components of the wavefunction can spread in subsequent steps, which requires a large total walker number to adequately suppress them.

Deidre Cleland et al. showed that the walker number required for coverage can be dramatically reduced using initiator truncation [24]. In this method, one defines some important determinants as initiators and restricts non-initiator walkers from spawning to unoccupied determinants. In this way, we align the signs of the walkers in the small walker-number determinants with those in the large walker-number determinants, which helps to suppress the sign problem. This method is referred to as initiator FCIQMC (i-FCIQMC) [24]. The original Hamiltonian is truncated as follows: ${\tilde{H}}_{ij}=\{\begin{array}{ll}\mathrm{0,}\hfill & |D_j\rangle \text{ is not initiator and }{N}_i=\mathrm{0,}\hfill \\ H_{ij}\mathrm{,}\hfill & \text{otherwise}\mathrm{.}\hfill \end{array}$ (12) In our calculations, we define initiators using the determinants $|D_i\rangle$ with |Ni| > nα, where $n_{\alpha }$ is called the initiator threshold. This prescription approaches the original FCIQMC algorithm when the total walker number approaches infinity. In this study, we take an initiator threshold of $n_{\alpha }=3$.

Another improvement over the original FCIQMC method is the use of the floating-point walker number [33], which enhances the stability of the evolution and reduces the statistical error of the results. However, the floating-point walker approach can result in a large number of determinants being occupied by a small number of walkers. To reduce memory usage, a walker number cutoff N_occ was introduced [33]. In this method, if the walker number Ni is less than N_occ, it is either replaced by N_occ with a probability of $N_i/N_{\text{occ}}$ or removed with a probability of $1-N_i/N_{\text{occ}}$. The same procedure was applied to spawned walkers with a separate cutoff parameter κ. We use the floating-point walker number method in the present work, and we take N_occ = 1 and κ = 0.1 in all calculations.

The i-FCIQMC method can also be used to obtain excited states [34]. In this respect, several parallel imaginary-time evolutions were performed. After each Δτ evolution, we used the Gram-Schmidt orthogonalization to obtain the orthogonal components of the wavefunction.

Calculations and discussions

We first benchmarked our computations with the standard shell model calculations for the Fe isotopes with the pf-shell interaction GXPF1A [35] using the code kshell [31]. As a detailed example, the Monte Carlo evolution of ⁵⁶Fe is shown in Fig. 1. During the warm-up period, the total walker number increased rapidly. When the total walker number reaches the preset limit (it is 10⁷ in ⁵⁶Fe), the shift S starts to vary according to Eq. (8). In the present study, we made a small modification based on those in Ref. [24], which means that we do not apply initiator truncation in the warm-up period, whereas initiator truncation is used in the subsequent periods. With initiator truncation, the total walker number drops temporarily, but increases again. As time progresses, the system reaches equilibrium and the shift S should be stable around the expected ground-state energy. After that, we continued the evolution for a few more steps and performed statistical analysis to extract the ground-state energy. In the ⁵⁶Fe calculation, we used $\text{Δ}\tau =5\times {10}^{-4}\text{zs}$ for the evolution. The projection period was $3.5\text{zs}$ and the statistical period was $1.5\text{zs}$.

Fig. 1Full-screen View

Monte Carlo evolution in ⁵⁶Fe using the GXPF1A interaction. The upper panel shows the shift S and local-time energy E(τ) as a function of the imaginary time τ, compared with the standard shell model calculation. The lower panel shows the total walker number during the evolution

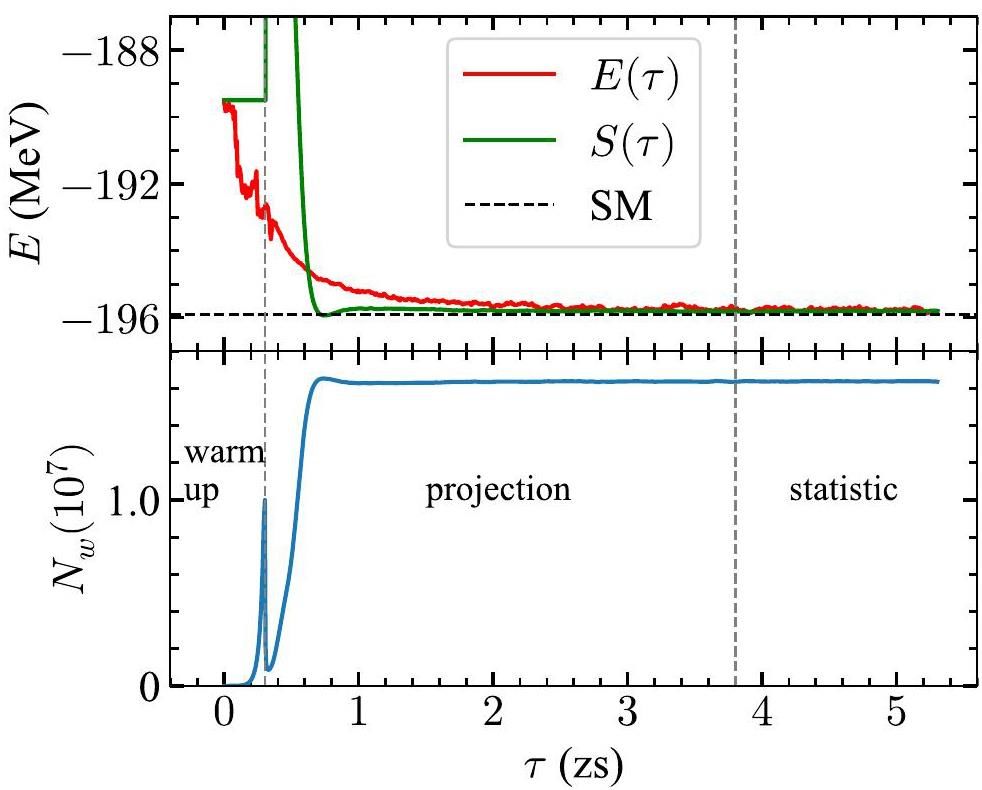
The equilibrium walker number and evolution time can vary across systems, and there is no fixed ratio between the equilibrium walker number and the preset warm-up limit. The time required for projection and statistical periods can also vary from system to system. The preset walker number and evolution time can be optimized through a trial run with a smaller walker number and empirical judgment.

Table 1 presents our i-FCIQMC calculations of the Fe isotopes with the GXPF1A interaction benchmarked with the standard shell model calculations with the same interaction. The i-FCIQMC calculations gave almost the same results as the full pf configuration SM calculations, demonstrating the validity of the i-FCIQMC applied to calculations of the nuclear structure. In Table 1, we also show the mean walker number in equilibrium, which is smaller than the dimension of the full configuration SM calculation. Using our current implementation, the i-FCIQMC method achieves these results with a memory requirement that is to 1-2 orders of magnitude smaller than that of the SM calculations.

FCIQMC is applicable to strongly correlated systems, whereas other methods do not work well. In Ref. [37], Horoi et al. demonstrated that for a strongly correlated system, the CC calculation may yield significantly unbound energies compared with the full configuration SM calculation. In Ref. [37], the correlations in ⁵⁶Ni were enhanced by decreasing the shell gap between 0f_7/2 and 1p_3/2 orbitals. The i-FCIQMC method was applied to the same systems and the results are shown in Fig. 2, along with the results from the CC methods, CISDTQ (configuration interaction singles, doubles, triplets, and quadruples), and full configuration SM. The calculated energies are relative to the reference energy of -203.800 MeV, which is consistent with Ref. [37]. The statistical uncertainties in the i-FCIQMC calculations were negligible and are therefore not displayed in the figure. We used approximately 10⁸ walkers for each state, which is the current limit of our computations.

Fig. 2Full-screen View

The computations of the ⁵⁶Ni ground-state energy using different methods, as a function of the shell-gap shift between 0f_7/2 and 1p_3/2 orbitals in the pf-shell GXPF1A interaction

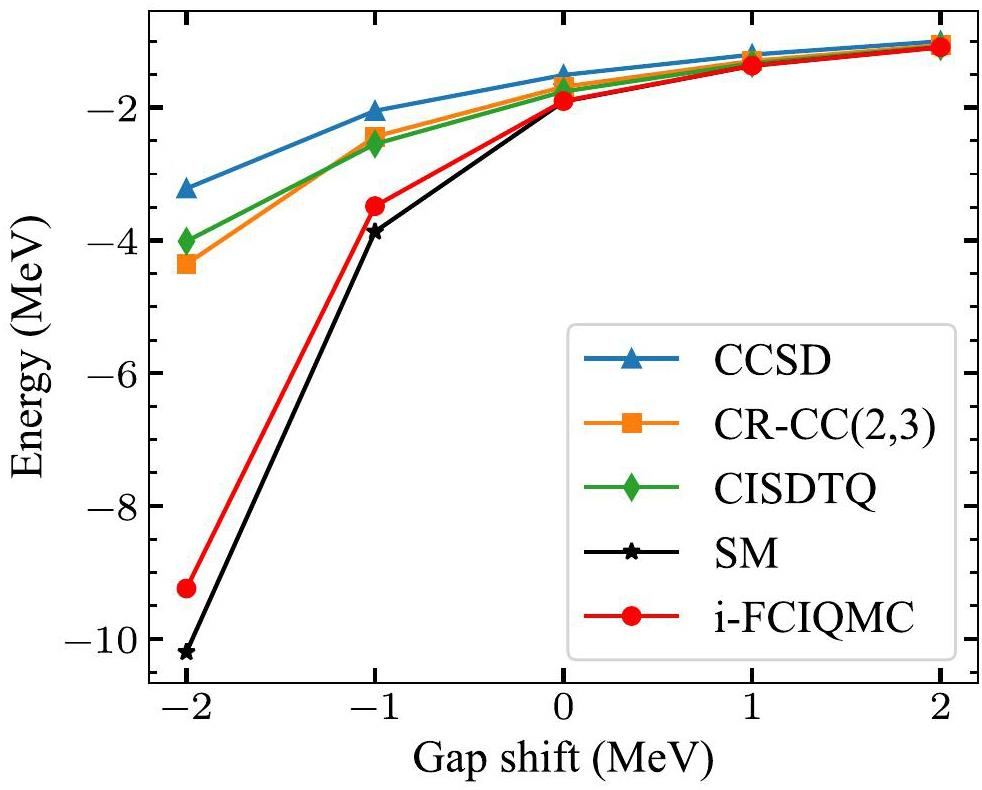
In the CC methods, the ground state is expressed as $\exp \left(\widehat{T}\right)|D_0\rangle$, where the cluster operator $\widehat{T}$ is defined as ${\widehat{T}}_1+{\widehat{T}}_2+{\widehat{T}}_3+\cdots$, and ${\widehat{T}}_n$ is the n-particle-n-hole (np-nh) component of $\widehat{T}$. In practice, $\widehat{T}$ is typically truncated to ${\widehat{T}}_1+{\widehat{T}}_2$, corresponding to the CCSD (CC singles and doubles) method. The completely renormalized (CR)-CC(2,3) method improves upon this by introducing a noniterative contribution from ${\widehat{T}}_3$, thereby including additional correlations [37-39]. As illustrated in Fig. 2, the i-FCIQMC results for ⁵⁶Ni are close to the exact solutions from the pf-shell full configuration SM calculations, even in the strongly correlated case (i.e., with $-2\text{MeV}$ shell-gap shift). In contrast, both CCSD and CR-CC(2,3) have lower bound energies, and CR-CC(2,3) calculations approximate the CISDTQ (aka SM with 4p-4h truncation), indicating that they cannot account for correlations beyond the 4p-4h level in these systems [37]. The i-FCIQMC method allows walkers to explore all possible determinants within the full configuration space, enabling them to capture high-order correlations that are inaccessible to CC methods.

We have went to a larger model space for the sdpf shell. Using the sdpf-mu interaction [40], we calculated Mg isotopes with a total walker number of $\approx {10}^8$. The results are presented in Fig. 3. Our present computing resources only allow us to perform the sdpf full configuration SM calculation for the light isotopes ^24,26Mg of the Mg chain. For heavier isotopes, the sdpf full configuration SM calculation exceeds the current computational capability. Therefore, we performed the SM calculation with a ħω truncation, in which a N truncation means that only the configurations with excitation energies $\le N$ are included in the SM calculation. In the present work, we truncated the configuration space with $2\hslash \omega$ and 4ħω, as shown in Fig. 3. (Note that 4ħω calculations of isotopes heavier than $34\text{Mg}$ remain beyond our current computational resources). We see that the SM calculations with the $2\hslash \omega$ truncation yield unbound results compared to other methods owing to the truncation error. The i-FCIQMC and SM calculations with 4ħω truncation provide similar results for the Mg isotopes and are also in good agreements with the full configuration SM calculations in ^24,26Mg.

Fig. 3Full-screen View

Ground-state energies of Mg isotopes, calculated with the i-FCIQMC, SM with $2\hslash \omega$ and 4ħω truncations, and SM with full sdpf configurations. The sdpf-mu interaction is used. The lower panel shows the dimensions required in the calculations. Currently, the dimension limit of SM calculation is 10¹¹ [41]

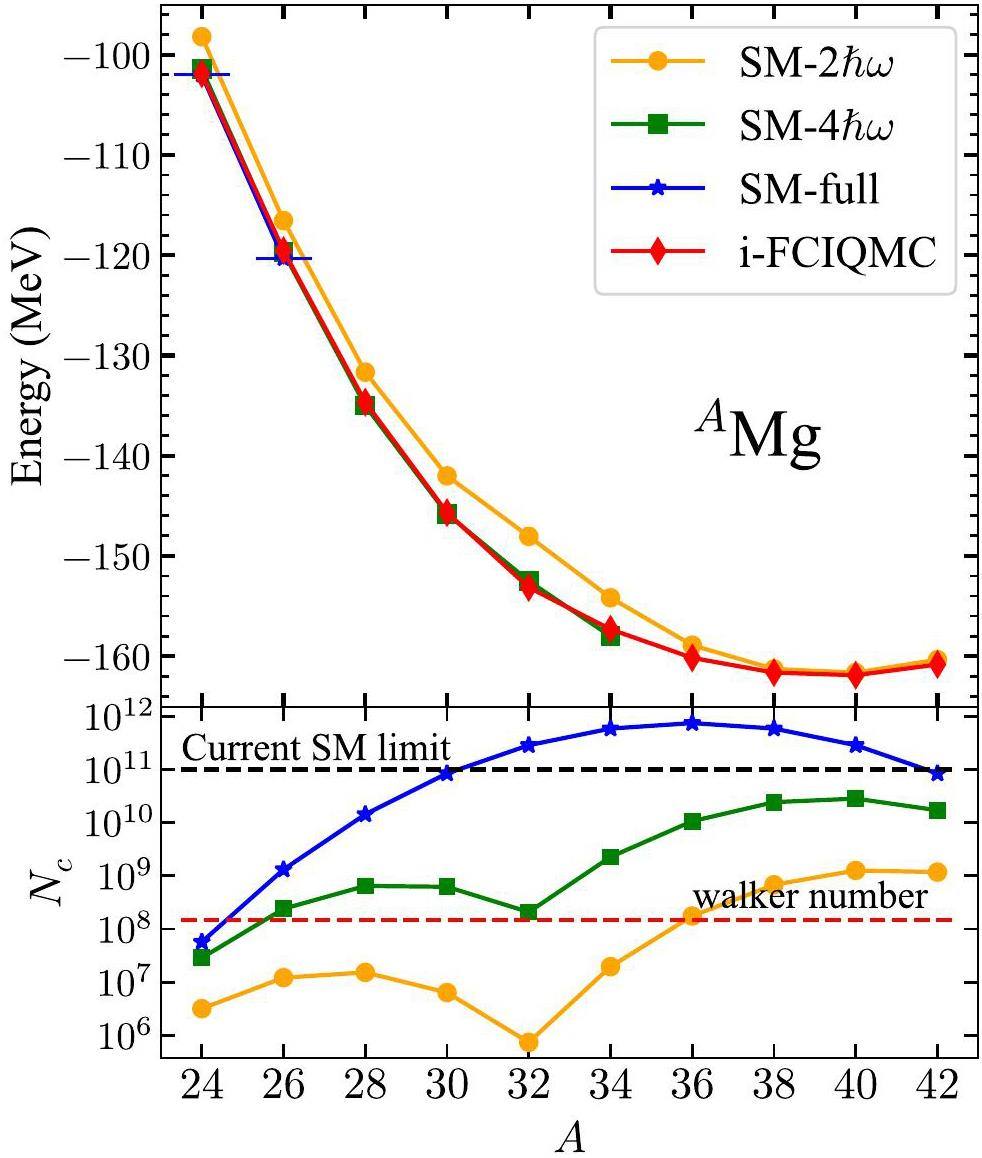
In i-FCIQMC calculations with approximately 10⁸ total walker number, only 10-20 GB of memory is required, demonstrating its significant potential for nuclear structure calculations in the configuration space. One of the major challenges in shell model calculations is the prohibitive memory cost in large model spaces. In contrast, i-FCIQMC requires a much smaller configuration space dimension compared to full configuration shell model calculations. Furthermore, unlike shell model calculations, i-FCIQMC does not require storing hundreds of Lanczos vectors, which significantly reduces the memory usage. The current i-FCIQMC implementation is parallelized using OpenMP, and MPI parallelization has been implemented for electron calculations [42]. In the future, we plan to further optimize the code with more efficient parallelization techniques, enabling the calculation of larger total walker numbers.

Summary

In this study, we applied the FCIQMC method to nuclear structure calculations and demonstrated its effectiveness in nuclear many-body systems. According to our code, the original FCIQMC method requires a large total walker number to converge, which makes it impractical for nuclear structure calculations. However, we showed that the initiator FCIQMC method performs well in these calculations.

Our i-FCIQMC computations were benchmarked with full configuration shell model calculations with a focus on Fe isotopes in the pf shell. The results confirmed the validity of our i-FCIQMC computations. For ⁵⁶Ni, using the shell-gap-shifted GXPF1A interaction, the i-FCIQMC method produced more accurate results than those obtained with Coupled Cluster calculations, highlighting its strength in handling strongly correlated systems. Additionally, we performed large-space calculations for Mg isotopes in the sdpf shell, demonstrating the capability of i-FCIQMC to calculate large-space many-body systems.