Transition energy

In general, the transition energy is determined by the momentum compaction factor $\alpha =\frac{1}{{\gamma }_{\text{tr}}{}^2}=\frac{1}{C}{\displaystyle {\int }_0^C}\frac{D\left(s\right)}{\rho \left(s\right)}\text{d}s\mathrm{,}$ (1) where C is the orbit length, $D(s)$ is the dispersion function, and $\rho (s)$ is the radius of orbit curvature, and s is the longitudinal coordinate. This is a characteristic of the lattice and remains constant regardless of the particle type. In the first order, the slip factor $\eta ={\eta }_0=1/{\gamma }_{\text{tr}}^2-1/{\gamma }^2$; thus, the frequency of the synchrotron oscillations ${\omega }_{\text{s}}\sim \eta$ tends to zero when the beam energy approaches the transition value. In this case, the adiabaticity of the longitudinal phase motion is violated, which leads to instabilities as well as the influence of nonlinear effects of higher orders of momentum spread δ. The introduction of modulation into the $D\left(s\right)$ or $\rho \left(s\right)$ function leads to variations in the momentum compaction factor and, consequently, the transition energy.

Superperiodic modulation

The equation for the dispersion function with biperiodic variable focusing [?] $\frac{{\text{d}}^{2}D}{\text{d}{s}^2}+\left[K(s)+\epsilon k(s)\right]D=\frac{1}{\rho (s)}\mathrm{,}$ (2) where $K\left(s\right)=\frac{e}{p}G\left(s\right)$, $\epsilon k\left(s\right)=\frac{e}{p}\text{Δ}G\left(s\right)$, $G\left(s\right)$ is the gradient of magneto-optical lenses, $\text{Δ}G\left(s\right)$ is the superperiodic gradient modulation. Here, is considered an additional perturbation to the regular one $\epsilon k\left(s\right)={\displaystyle {\sum }_{k=0}^{\infty }{g}_k}\cos (k\varphi )$, where gk is the k-th harmonic of the gradient modulation in the Fourier series expansion of the function. The solution for the superperiod momentum compaction factor is as follows for gradient modulation only: $\begin{array}{ll}{\alpha }_{\text{s}}=\hfill & \frac{1}{{\nu }^2}\left\{1+\frac{1}{4(1-kS/\nu )}{\left(\frac{\overline{R}}{\nu }\right)}^4\frac{g_k^2}{{\left[1-{\left(1-kS/\nu \right)}^2\right]}^2}\right\}\mathrm{,}\hfill \end{array}$ (3) where ${\overline{R}}_{\text{arc}}$ is the average value of the curvature, ν=νx is the betatron tune in horizontal plane on arc, S is the number of superperiods per arc length. Equation (3) considered without introducing curvature modulation, because of the possibility of introducing a variation in the transition energy into a stationary lattice. To increase the transition energy, it is necessary to reduce ${\alpha }_{\text{s}}=1/{\gamma }_{\text{tr,arc}}^2$, meaning that the expression under the sum sign must be negative, which is realizable under the condition $kS/{\nu }_{x\mathrm{,}\text{arc}}>1$.

First harmonic k=1 has a dominant influence, the condition is implemented for $S=\mathrm{4,}{\nu }_{x\mathrm{,}\text{arc}}=3$. Figure 1 shows 12 FODO cells per arc, 3 FODO cells are combined into one superperiod with complex transition energy ${\gamma }_{\text{tr,arc}}=i8$ [3]. Thus, an integer number of betatron oscillations on the arc forms tune, which is a multiple of 2π, so the arc has the property of a first-order achromat. Straight sections can correct tuning for an entire ring to avoid betatron resonances. Moreover, by choosing the ratio of the superperiod and tuning for the arc, second-order achromat properties can be achieved. Such a structure was first implemented at the KAON factory [4], and later at J-PARC [5], neutrino factory [6].

Fig. 1Full-screen View

(Color online) “Resonant” magneto-optic lattice with dispersion modulation and increased transition energy

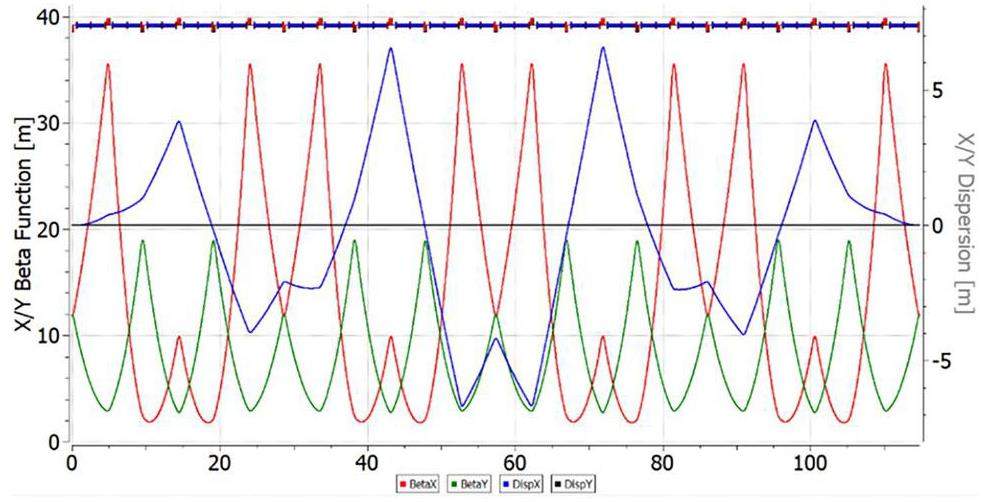
For structure where the missing magnet technique is used, for one reason or another it can be also implemented (Fig. 2), but the dispersion at the edge of the arc must be suppressed [7]. The transition energy for the entire ring with straight sections is achieve γ_tr = 15.

Fig. 2Full-screen View

(Color online) “Resonant” NICA magneto-optical adapted lattice with increased transition energy and missing magnet

Stochastic cooling

Let’s consider stochastic cooling using the approximate theory developed by D. Mohl [8, 9]. Based on the main findings, the cooling rate can be determined using the following expression: $\frac{1}{{\tau }_{\text{tr}\mathrm{,}\text{l}}}\text{=}\frac{W}{N}[\underset{\begin{array}{c}\text{coherent}\\ \text{effect(cooling)}\end{array}}{\underbrace{2g\cos \theta \left(1-1/M_{\text{pk}}^2\right)}}-\underset{\begin{array}{c}\text{incoherent}\\ \text{effect(heating)}\end{array}}{\underbrace{g^2\left(M_{\text{kp}}+U\right)}}]\mathrm{,}$ (6) where $W=f_{\text{max}}-f_{\text{min}}$ is the system bandwidth, N is the effective number of particles recalculated based on the ratio of orbit length to the beam length, along with the particle distribution, g is the fraction of observed sample error corrected per turn, U is the ratio of noise to signal, M_pk and M_kp are the mixing factors between the pickup-kicker and the kicker-pickup, respectively. Equation (6) in the absence of noise at $g=g_0=\frac{1-M_{\text{pk}}{}^2}{M_{\text{kp}}}$ reaches the maximum $\begin{array}{l}\frac{1}{{\tau }_{\text{tr}}}=\frac{W}{N}\frac{{\left(1-1/M_{\text{pk}}^2\right)}^2}{M_{\text{kp}}}\mathrm{,}\\ \frac{1}{{\tau }_{\text{l}}}=2\frac{W}{N}\frac{{\left(1-1/M_{\text{pk}}{}^2\right)}^2}{M_{\text{kp}}}\mathrm{.}\end{array}$ (7) The mixing coefficients are defined as $\begin{array}{l}{M}_{\text{pk}}=\frac{1}{2\left(f_{\max }+f_{\min }\right){\eta }_{\text{pk}}{T}_{\text{pk}}\frac{\text{Δ}p}{p}}\mathrm{,}\\ M_{\text{kp}}=\frac{1}{2\left(f_{\max }-f_{\min }\right){\eta }_{\text{kp}}{T}_{\text{kp}}\frac{\text{Δ}p}{p}}\mathrm{,}\end{array}$ (8) where ${\eta }_{\text{pk}}{T}_{\text{pk}}\delta$ and ${\eta }_{\text{kp}}{T}_{\text{kp}}\delta$ are the relative particle displacement times (mixing), η_pk and η_kp are the slip factor, as a first approximation ${\eta }_{\text{pk}}={\alpha }_{\text{pk}}-1/{\gamma }^2$, ${\eta }_{\text{kp}}={\alpha }_{\text{kp}}-1/{\gamma }^2$, α_pk and α_kp are the first-order of local momentum compaction factors, T_pk and T_kp are the absolute times between the pickup-kicker and kicker-pickup, respectively. The stochastic cooling times in Eq. (7) depends on the ratio of the effective particle density to the cooling system bandwidth and the properties of the magneto-optics and local momentum compaction factors α_pk, α_kp.

The maximum value of the frequency band is determined by the requirement that the “Schottky” beam bands do not overlap. In the simplest case, this can be expressed as $f_{\text{max}}<\frac{1}{{\eta }_{\text{pk}}{T}_{\text{pk}}\frac{\text{Δ}p}{p}}\mathrm{,}$ (9) thus, a mixing factor M_pk>1. Otherwise, the cooling efficiency would become zero. Thus, it is desirable to achieve the highest possible frequency band for a given number of particles. From an electronic point of view, modern technologies allow for the implementation of a 10 GHz frequency band [10]; however, their use is not always feasible owing to the large magnitude of the slip factor η_pk and momentum spread δ.

Equation (6) is derived for the coasted beam. The particle density of a single harmonic RF resonator is described by a Gaussian distribution: $\rho (s)=\frac{N_{\text{bunch}}}{{\sigma }_{\text{bunch}}\sqrt{2\pi }}\cdot e^{-\frac{s^2}{2{\sigma }_{\text{bunch}}^2}}\mathrm{,}$ (10) where s is the distance from the beam center, σ_bunch is the dispersion of the particle distribution, and N_bunch is the number of particles. Assuming that the cooling is at its minimum at the center (s=0), the effective particle number at orbit length $C_{\text{orb}}$ can be calculated as follows: $N=\frac{N_{\text{bunch}}}{4{\sigma }_{\text{bunch}}}\cdot C_{\text{orb}}\mathrm{.}$ (11) For a beam generated by a multi-harmonic barrier-type RF system, so-called “Barrier Bucket”, the particle distribution in the beam can be considered approximately uniform along its entire length. The effective particle number is determined by the simple ratio of the beam length to the total orbit length:

To summarize, the effective number of particles depends on their distribution and is determined by their form-factor $F_{\text{bunch}}=\sqrt{2\pi }÷4$ $N=N_{\text{bunch}}\cdot \frac{C_{\text{orb}}}{F_{\text{bunch}}\cdot {\sigma }_{\text{bunch}}}\mathrm{.}$ (12) For example, let us consider the case of NICA with maximal form factor F_bunch=4 with $C_{\text{orb}}=503.04$ m, σ_bunch=0.6 m, N_bunch=2.2⋅10⁹. Considering the accumulated FNAL [11] experience, the realistic values for the frequency band are f_max=8 GHz and f_min=2 GHz. For the NICA, f_max=4 GHz and f_min=2 GHz. With these parameters, the maximum achievable cooling rate was $1/{\tau }_{\text{tr}}=1/230$ s^-1.

Based on Eq. (8), asymptotic growth may occur in two scenarios:

1. slip-factor approaches the value $\eta \to \frac{1}{2\left(f_{\text{max}}+f_{\text{min}}\right)T_{\text{pk}}\delta }$, the beam Schottky spectrum becomes continuous and M_pk→1;

2. slip-factor approaches zero, mixing between the kicker to the pickup does not occur and M_kp→∞.

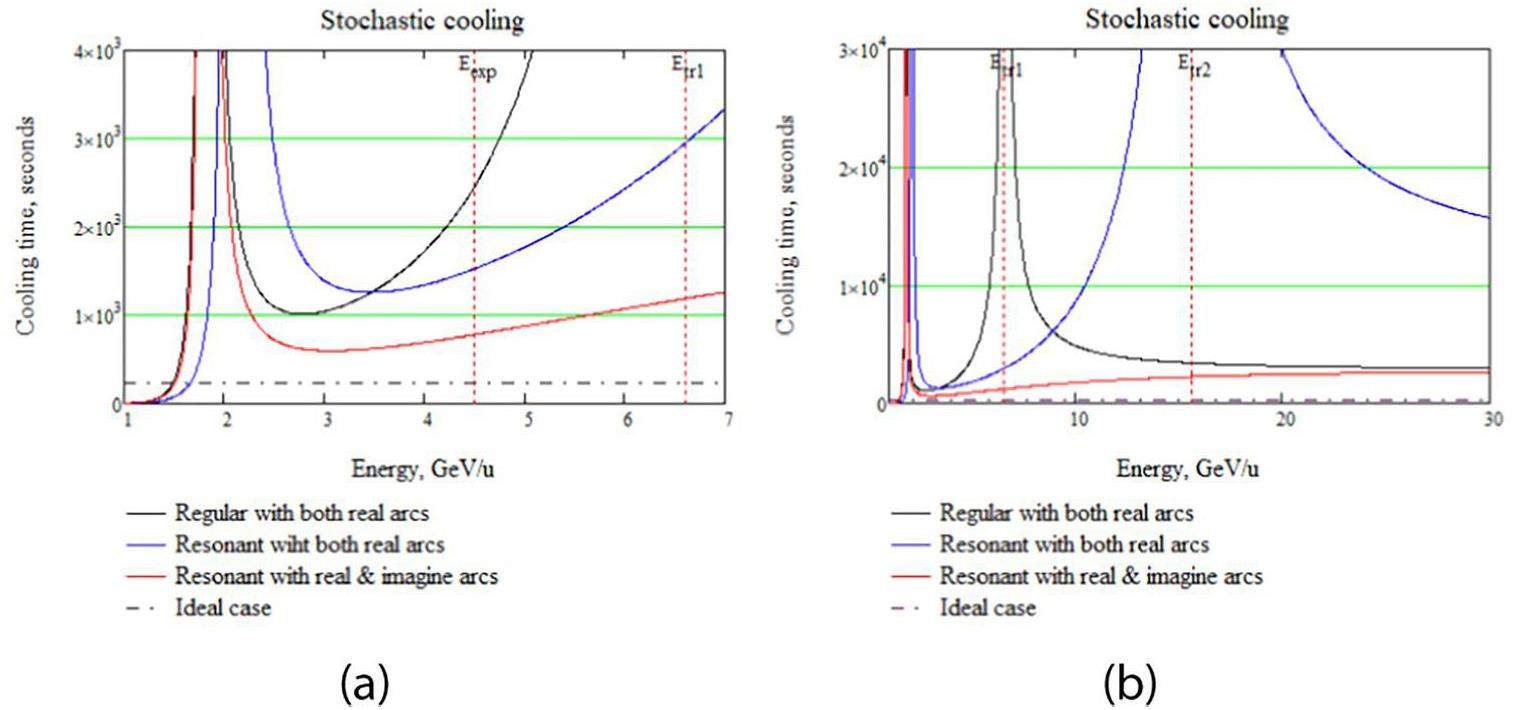
The efficiency of stochastic cooling depends on the properties of the magneto-optical structure. In classical “regular” lattices, transition energy is acquired through the horizontal frequency ${\gamma }_{\text{tr}}\approx {\nu }_x$ and slip-factor $\eta =1/{\gamma }_{\text{tr}}^2-1/{\gamma }^2$ can achieve zero. To avoid asymptotic growth, it is necessary to vary the slip factor, that is, γ_tr. This is possible in “resonant” lattice, where transition energy can be increased or even reach complex value. In more exotic case, can be used “combined” lattice thenη_pk (pickup-kicker) with real transition energy at one arc ${\eta }_{\text{pk}}=-1/{\gamma }_{\text{tr}}^2-1/{\gamma }^2$ (13) compensated by η_kp (kicker-pickup) with complex transition energy at another ${\eta }_{\text{kp}}=-1/{\gamma }_{tr}^2-1/{\gamma }^2$ (14) for the whole ring. This structure achieves the required ratio of mixing factors for a maximum cooling rate close to the ideal [12]. Let us delve deeper into the declared lattice in greater detail.

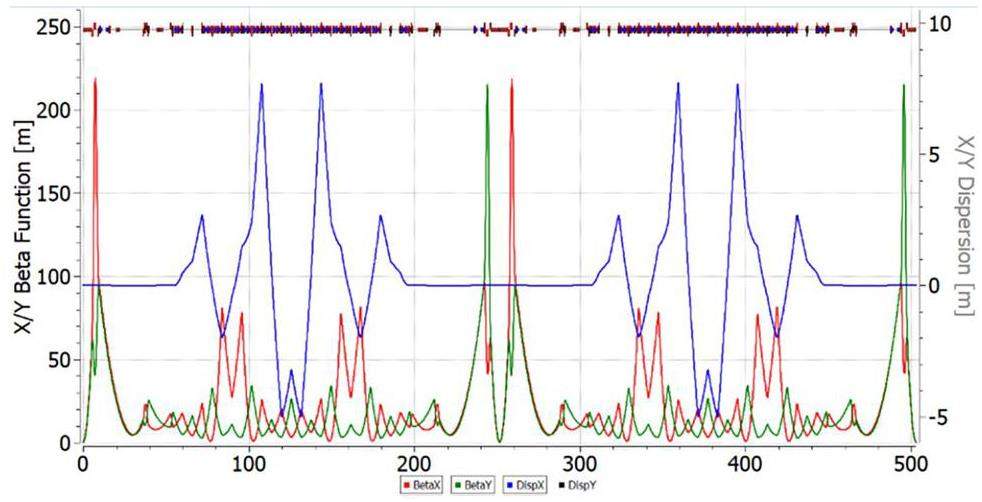
The behaviour of the β-functions and D the dispersion across the entire “regular” ring illustrates at Fig. 3 with γ_tr = 7. Straight sections, which remain constant in all lattices, are essential for analyzing the resonant characteristics of the entire structure. Their arrangement did not affect intrabeam scattering or transition energy. To suppress dispersion in the “regular” lattice, missing magnets technique implemented on both sides of the arc.

Fig. 3Full-screen View

(Color online) “Regular” FODO NICA magneto-optical lattice with missing magnets

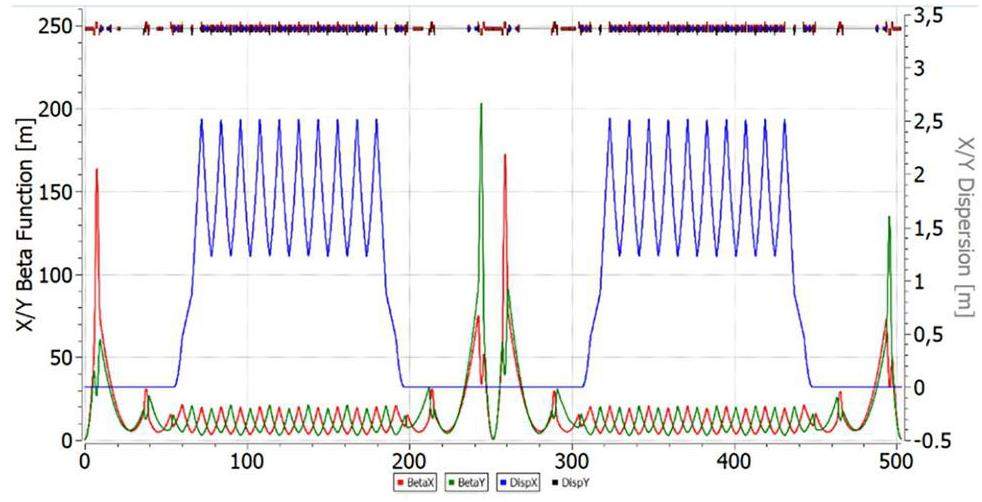
The “resonant” lattice is based on the principle of resonant modulation of the dispersion function and can be obtained from a “regular” one by introducing additional family of focusing quadrupoles. To suppress dispersion, two edge focusing quadrupoles on both sides of the arc or only two families of focusing quadrupoles on the arc can be used, when an integer number of betatron oscillations is reached.

The case of a “combined” lattice, one arc operates in a regular mode, while the other employs resonant modulation (Fig. 4). This choice was based on the principle of compensation, as described by Eqs. 13 and 14, which requires a greater modulation depth of the quadrupoles than in purely “resonant” lattice with increased transition energy.

Fig. 4Full-screen View

(Color online) “Combined” NICA magneto-optical lattice with real and complex transition energies in arcs

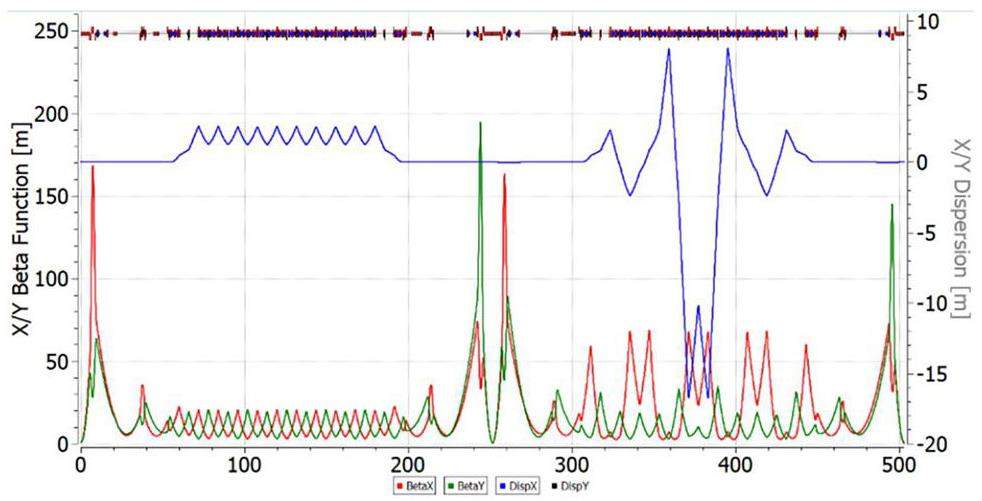
As illustrated in Fig. 5, “resonant” optics with increased transition energy up to γ_tr = 15, the second asymptotic is at higher energy compared to the “regular” lattice. In “combined” magneto-optics, the cooling efficiency is closer to the ideal value in a large energy range from 2.5 to 4.5 GeV/u, while in “regular” optics the cooling rate is almost two times lower at the most optimal point ~3 GeV/u. This behavior is explained by the absence of a second point of asymptotic growth.

Fig. 5Full-screen View

(Color online) The dependence of stochastic cooling time on the energy for various lattices. Energy range (a) 1-7, (b) 0–30 GeV per nucleon

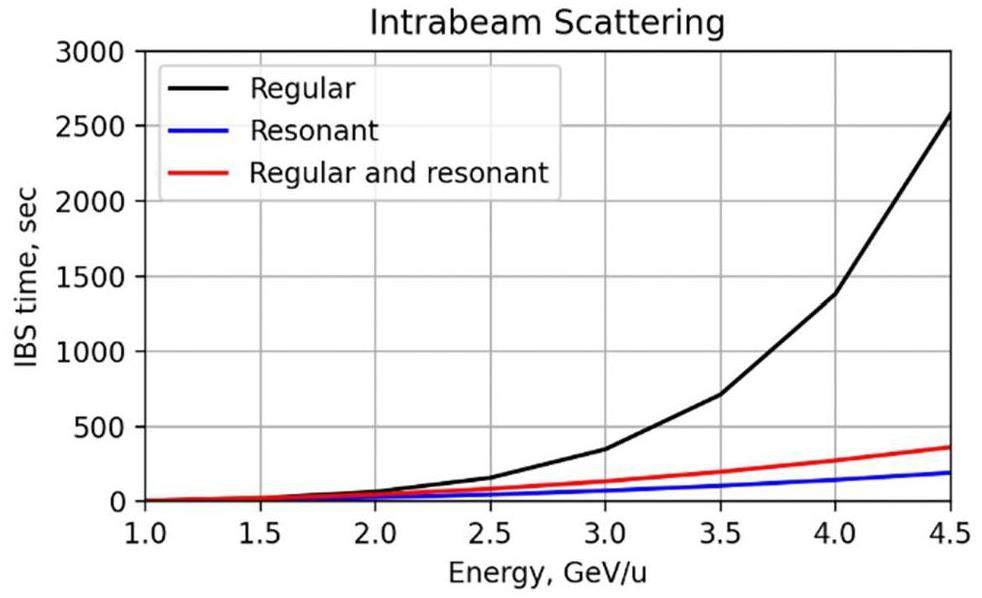
Intrabeam Scattering

Intrabeam scattering represents a fundamental limitation on the beam lifetime in the collider. Consequently, the selection of an appropriate cooling technique depends on comparing its characteristic timescales with the rate at which the beam is heated owing to intrabeam scattering. This is derived from the fundamental principles that govern the process $\begin{array}{ll}\frac{1}{{\tau }_{\text{IBS}}}=\frac{\sqrt{\pi }}{4}\frac{c{Z}^2{r}_{\text{p}}^2{L}_{\text{C}}}{A}\hfill & \cdot \frac{N}{C_{\text{orb}}}\cdot \frac{\langle {\beta }_x\rangle }{{\beta }^3{\gamma }^3{\epsilon }_x^{5/2}\langle \sqrt{{\beta }_x}\rangle }\times \hfill \\ \hfill & \times \left(\langle \frac{D_x^2+{\dot{D}}_x^2}{{\beta }_x^2}\rangle -\frac{1}{{\gamma }^2}\right)\hfill \end{array}$ (15)

Unlike stochastic cooling, the IBS rate increases as decreasing energy $1/{\gamma }^3$. In addition, the expressions in parentheses are proportional to the slip factor η. Therefore, it is expected that in optics with a value η close to zero, the heating rate should decrease. Figure 6 shows the dependences of the heating time constant in the three above-mentioned lattices calculated using MADX programs [13] for the parameters of the heavy ion beam ${}_{79}^{197}\text{Au}$ of the NICA collider with maximum luminosity ${10}^{27}{\text{cm}}^{-2}{\text{s}}^{-1}$. In the context of light nuclei, such as protons and deuterons, the IBS time significantly increases as the charge decreases. The corresponding IBS times for heavy and light beams are presented in Table 1 for beam intensities N_heavy = 2.2×10⁹ ppb and N_light = 1×10¹² ppb with a number of bunches n_bunch=22. Consequently, at the experimental energy, IBS times differ by approximately 10 times, so the issue of intrabeam scattering becomes critical for heavy-ion beams.

Fig. 6Full-screen View

(Color online) The dependence of the beam lifetime due to intrabeam scattering in “regular”, “resonant” and “combined” lattices on the beam energy for heavy ion beam

From the comparison of the IBS lifetime with the cooling time it can be concluded that in a regular lattice, stochastic cooling is able to balance intrabeam scattering in the energy range $W\ge 4.5\text{GeV/u}$. To apply stochastic cooling over the entire energy range, it is obvious that the luminosity of the beam at low energies must be sacrificed by increasing the emittance. In the resonant lattices, the IBS time was notably reduced. This is explained by the fact that the structure has a greater ratio $\langle \frac{D_x^2+{\dot{D}}_x^2}{{\beta }_x^2}\rangle$ between the dispersion and the beam β function than in the case of a regular function. Thus, for heavy ions, the configuration should be regular and minimally modulated. Electron cooling was used in the regular lattice to reduce the beam by 4.5 GeV/u [14, 15].