The continuous Bayesian probability method

In the CBP estimators, the residuals δ of R_C are treated as continuous variables and their posterior PDFs are derived from Bayesian theory. The estimated residuals, which are used to correct the theoretical models, can then be calculated from the posterior PDFs.

For continuous multivariate variables, given a set of features or variables $X_1\mathrm{,}{X}_2\mathrm{,}\dots ,X_m$ and a target variable Y, the posterior PDF can be expressed as $p\left(Y|X\right)=\frac{p\left(X_1|Y\right)p\left(X_2|Y\right)\cdots p\left(X_m|Y\right)p(Y)}{{\displaystyle \int }p\left(X_1|Y\right)p\left(X_2|Y\right)\cdots p\left(X_m|Y\right)p(Y)\text{d}Y}\mathrm{.}$ (1) The conditional PDF p(Xi|Y) represents the likelihood of observing events Xi given the occurrence of Y, whereas the prior PDF p(Y) denotes the frequency of occurrence for a given Y. The denominator in Eq. (1) acts as a normalization constant, ensuring that the posterior PDF p(Y|X) is integrated to unity.

According to Eq. (1), event Y represents the continuous residual δ. Events Xi correspond to the proton number Z_t and neutron number N_t of the target nucleus. It is assumed that Z_t and N_t are independent of other variables. Thus, the posterior PDF can be expressed as $p\left(\delta |Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)=\frac{p\left(Z_{\text{t}}|\delta \right)p\left(N_{\text{t}}|\delta \right)p(\delta )}{{\displaystyle \int }p\left(Z_{\text{t}}|\delta \right)p\left(N_{\text{t}}|\delta \right)p(\delta )\text{d}\delta }\mathrm{.}$ (2) The conditional PDFs $p\left(Z_{\text{t}}|\delta \right)$ and $p\left(N_{\text{t}}|\delta \right)$ in Eq. (2) can be derived using the following univariate Bayesian formula, $p\left(Z_{\text{t}}|\delta \right)=\frac{p\left(\delta |Z_{\text{t}}\right)p\left(Z_{\text{t}}\right)}{p(\delta )}\mathrm{,}$ (3) $p\left(N_{\text{t}}|\delta \right)=\frac{p\left(\delta |N_t\right)p\left(N_t\right)}{p(\delta )}\mathrm{.}$ (4) In Eqs. (3) and (4), the prior probability $p\left(Z_{\text{t}}\left(N_{\text{t}}\right)\right)$ was calculated from the occurrence frequencies of $Z_{\text{t}}\left(N_{\text{t}}\right)$ in the learning set. The likelihood PDFs p(δ|Z_t) and p(δ|N_t) are estimated using kernel density estimation (KDE). $p\left(\delta |Z_{\text{t}}\right)=\frac{1}{n_Z{h}_Z}{\displaystyle \sum _{i=1}^{n_Z}}K\left(\frac{\delta -{\delta }_i}{h_Z}\right)\mathrm{,}$ (5) $p\left(\delta |N_{\text{t}}\right)=\frac{1}{n_N{h}_N}{\displaystyle \sum _{i=1}^{n_N}}K\left(\frac{\delta -{\delta }_i}{h_N}\right)\mathrm{,}$ (6) where $h_{Z\left(N\right)}$ denotes the bandwidth parameter and $n_{Z\left(N\right)}$ represents the number of nuclei in the learning set that have the same $Z_{\text{t}}\left(N_{\text{t}}\right)$ as the target nucleus. Kernel function $K(t)$ is specified as a Gaussian kernel because the residuals follow a Gaussian distribution: $K(t)=\frac{1}{\sqrt{2\pi }}{\text{e}}^{-\frac{t^2}{2}}\mathrm{.}$ (7) Similarly, the prior PDF p(δ) can also be obtained using KDE, $p(\delta )=\frac{1}{n{h}_{\delta }}{\displaystyle \sum _{i=1}^n}K\left(\frac{\delta -{\delta }_i}{h_{\delta }}\right)\mathrm{,}$ (8) where hδ denotes the bandwidth parameter, and n is the total number of nuclei in the learning set. In Eqs. (5), (6), and (8), the individual residual δi is defined as ${\delta }_i=R_{\text{C}\mathrm{,}i}^{\text{exp}}-R_{\text{C}\mathrm{,}i}^{\text{th}}$. The values chosen for the bandwidth parameters hδ, hZ, and hN depend on several factors, including the range of δi, the size of the dataset, and the level of noise in the data.

When determining the likelihood PDF and prior PDF, a weight function is introduced to account for the local relationship between neighboring nuclei: $w\left(Z\mathrm{,}N;Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)=\text{exp}\left[-\frac{{\left(Z-Z_{\text{t}}\right)}^2+{\left(N-N_{\text{t}}\right)}^2}{\rho }\right]+\epsilon \mathrm{.}$ (9) Parameter ρ significantly affects the prediction performance and extrapolation range of the CBP estimator. Based on the distribution characteristics of the nuclei from the dataset on the nuclear chart, ρ=4 was selected for this study. Parameter ε affects the stability of the posterior PDF, and $\epsilon {=10}^{-10}$ was chosen to ensure a Gaussian distribution for $p\left(\delta |Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)$. The prior PDF and likelihood PDF with the applied weights are as follows: $p_{\text{wt}}\left(\delta \right)=\frac{1}{n{h}_{\delta }}{\displaystyle \sum _{i=1}^n}K\left(\frac{\delta -{\delta }_i}{h_{\delta }}\right)w\left(Z_i\mathrm{,}{N}_i;Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)\mathrm{,}$ (10) $p_{\text{wt}}\left(\delta |Z_{\text{t}}\right)=\frac{1}{n_Z{h}_Z}{\displaystyle \sum _{i=1}^{n_Z}}K\left(\frac{\delta -{\delta }_i}{h_Z}\right)w\left(Z_i\mathrm{,}{N}_i;Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)\mathrm{,}$ (11) $p_{\text{wt}}\left(\delta |N_{\text{t}}\right)=\frac{1}{n_N{h}_N}{\displaystyle \sum _{i=1}^{n_N}}K\left(\frac{\delta -{\delta }_i}{h_N}\right)w\left(Z_i\mathrm{,}{N}_i;Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)\mathrm{.}$ (12) The posterior PDF $p\left(\delta |Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)$ is obtained by combining Eqs. (2)-(12), and the expected value was used to determine the estimated residual of the target nucleus. ${\delta }^{\text{em}}\left(Z\mathrm{,}N\right)={\displaystyle \int }\delta p(\delta |Z\mathrm{,}N)\text{d}\delta \mathrm{.}$ (13) Ultimately, the refined nuclear charge radius is obtained by appending the estimated residual δ^em(Z, N) to the theoretical nuclear charge radius $R^{\text{th}}\left(Z\mathrm{,}N\right)$: $R_{\text{C}}^{\text{corr}}\left(Z\mathrm{,}N\right)=R_{\text{C}}^{\text{th}}\left(Z\mathrm{,}N\right)+{\delta }^{\text{em}}\left(Z\mathrm{,}N\right)\mathrm{.}$ (14)

Bayesian model averaging

Even after refinement by the CBP estimator, individual models often fail to comprehensively account for all physical phenomena, owing to their varying strengths and weaknesses in different regions of the nuclear chart. To consider the advantages of different models in the isotopic and isotonic chains, Bayesian model averaging (BMA) was introduced [86].

The BMA method is based on the Bayesian theorem, and assigns weights to each model by assessing its predictive performance. Specifically, given a set of K candidate models $M_1\mathrm{,}\dots \mathrm{,}{M}_K$, the BMA method calculates posterior probabilities based on the predictions for the benchmark nucleus from each model. These posterior probabilities serve as the weights for each model and are calculated as follows: $P\left(M_k|D\right)=\frac{P\left(D|M_k\right)P\left(M_k\right)}{{\displaystyle {\sum }_{i=1}^{K}P}\left(D|M_i\right)P\left(M_i\right)}\mathrm{.}$ (15) In this study, the six selected benchmark nuclei in dataset D were ⁴⁹K, ³⁸Ca, ¹⁰⁰Cd, ¹¹⁹Cd, ²⁰¹Po, and ²³³Ra, which were used to evaluate the accuracy of the models based on the entire nuclide chart. Residuals were obtained using three theoretical models: the HFB model with SLy4 parameterization, RHB model with PK1 parameter set, and semi-empirical liquid drop model. The prior probability $P\left(M_k\right)=1/K$ is related to the number of candidate models and the conditional probability $P\left(D|M_k\right)$ depends on the predictive performance of each theoretical model, $P\left(D|M_k\right)={\displaystyle \prod _j^J}\frac{1}{\sqrt{2\pi \mu }}\exp \left[-\frac{{\left({\delta }_{k\mathrm{,}j}^{\text{corr}}\right)}^2}{2{\mu }^2}\right]\mathrm{,}$ (16) where J denotes the total number of benchmark nuclei. The refined residuals ${\delta }_{k\mathrm{,}j}^{\text{corr}}$ for the j-th benchmark nucleus corresponding to the theoretical model Mk are defined as ${\delta }_{k\mathrm{,}j}^{\text{corr}}=R_{k\mathrm{,}j}^{\text{exp}}-R_{k\mathrm{,}j}^{\text{corr}}$. The parameter μ is used to normalize the values of ${\delta }_{k\mathrm{,}j}^{\text{corr}}$ and is defined by $\mu =\sqrt{\frac{1}{K\cdot J}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{j=1}^J}{\left({\delta }_{k\mathrm{,}j}^{\text{corr}}\right)}^2}\mathrm{.}$ (17) Finally, the average nuclear charge radius calculated using the BMA method is: $\overline{R}\left(Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)={\displaystyle \sum _{i=1}^K}{R}_{\text{C}\mathrm{,}i}^{\text{corr}}P\left(M_i|D\right)\mathrm{.}$ (18) The discrepancies between the corrected theoretical predictions and the experimental data for each model were assessed using the standard deviation σ_rms, defined as ${\sigma }_{\text{rms}}^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\left(R_{\text{C}\mathrm{,}i}^{\text{exp}}-R_{\text{C}\mathrm{,}i}^{\text{corr}}\right)}^2\mathrm{.}$ (19) In the CBP estimator, the prediction uncertainties are obtained from the posterior PDF. The one-sigma uncertainty ${\sigma }^{\text{em}}\left(Z\mathrm{,}N\right)$ of each model corresponding to a specific nucleus (Z,N) is defined as ${\sigma }^{\text{em}}\left(Z\mathrm{,}N\right)=\sqrt{{\displaystyle \int }{\left[\delta -{\delta }^{\text{em}}\left(Z\mathrm{,}N\right)\right]}^{2}p(\delta |Z\mathrm{,}N)\text{d}\delta }\mathrm{,}$ (20) and the uncertainty of the BMA is given by ${\sigma }^{{}^{\text{BMA}}}\left(Z\mathrm{,}N\right)={\displaystyle \sum _{i=1}^K}{\sigma }_i^{\text{em}}P\left(M_i|D\right)\mathrm{.}$ (21)

Global optimizations of the CBP estimator

The theoretical R_C values of 892 nuclei were calculated using three models, and the raw residuals ${\delta }^{\text{pre}}=R_{\text{C}}^{\text{exp}}-R_{\text{C}}^{\text{th}}$ for each nucleus were obtained. Subsequently, the CBP estimator was applied to refine the predictions of each model. According to Sect. 2, the posterior PDF $p\left(\delta |Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)$ of the target nucleus can be calculated by Eqs. (2)-(12). The refined charge radius $R_{\text{C}}^{\text{corr}}\left(Z_{\text{t}}\mathrm{,}{N}_{\text{t}}\right)$ was then obtained using Eqs. (13) and (14). The HFB and RHB models in this study were solved under the assumption of spherical symmetry. In the entire set, the majority of δ^pre is distributed within the range of -0.1 fm to 0.1 fm. For nuclei with identical proton or neutron numbers, the variation in δ^pre is typically limited to within 0.05 fm. Based on the distribution characteristics of δ^pre, the bandwidth parameters were selected as $h_{\delta }=\text{0}\text{.07}\text{fm}$, hZ=0.01, fm, and hN=0.02, fm. Table 1 presents the standard deviations σ_pre of the three theoretical models before optimization, and σ_post after optimization by the CBP estimator. The global optimization performance of the CBP estimator was evaluated using the improvement rate $\text{Δ}\sigma /{\sigma }_{\text{pre}}=\left({\sigma }_{\text{pre}}-{\sigma }_{\text{post}}\right)/{\sigma }_{\text{pre}}$.

As shown in Table 1, the standard deviations σ_pre for the spherical HFB, RHB, and semi-empirical formulas are approximately 0.04 fm. However, the deformed mean-field theories give a standard deviation of approximately 0.03 fm [41, 42]. After refining using the CBP estimator, the standard deviations σ_post for both spherical models are further reduced to approximately 0.016 fm, representing an improvement of approximately 60%. This improvement demonstrates the advantages of the CBP estimator. The CBP estimator can introduce deformation effects into the calculations of spherical theoretical models using statistics, thereby improving the description of R_C for deformed atomic nuclei.

To illustrate the progress achieved by the CBP method, Table 1 presents the optimization performance of the NBP method for comparison. The NBP method is a discrete Bayesian probabilistic approach that employs the k-means algorithm to determine the cluster centers δi, which are then used to refine the theoretical models. For the three models, the improvement rate of the CBP method is approximately 10% higher than that of the NBP method. This arises from the CBP estimator treating residuals as continuous variables and obtaining the estimated residual value δ^em by integrating the posterior PDF over the entire residual distribution, rather than using a discrete posterior probability, as in the NBP method. The CBP estimator accounts for all possible residual contributions, thereby achieving a higher degree of optimization and demonstrating a clear advantage.

To further illustrate the performance of the CBP estimator across the different models and regions, Fig. 1 presents the raw residuals (gray dots) from the HFB model, the RHB model and the semi-empirical formula, along with the corrected residuals (blue dots) after applying the CBP estimator. It is evident that after CBP optimization, the residuals for all three theoretical models were remarkably reduced across most regions. This improvement can be attributed to the CBP estimator framework. Based on the global description of theoretical models, the CBP estimator utilizes a statistical approach to further capture the local correlation effects among nuclei with identical proton or neutron numbers. The introduction of the weight function ensures that only nuclei in close proximity to the target nucleus on the nuclear chart significantly influence the prediction, thereby enhancing the sensitivity of the CBP estimator to local correlation effects. Therefore, the CBP estimator is more effective in regions where local correlations are stronger, and the distribution of δ^pre is more regular, such as regions with pronounced shell effects.

Fig. 1Full-screen View

　a The charge radii residuals $\delta =R_{\text{C}}^{\text{exp}}-R_{\text{C}}^{\text{th}}$ from the experimental data as a function of mass number A, The grey dots denote the raw results from the HFB calculations, and the blue dots denote the predicted residuals after the CBP refinements. b and c the same as a, but for the results from RHB model and Sheng’s formula, respectively

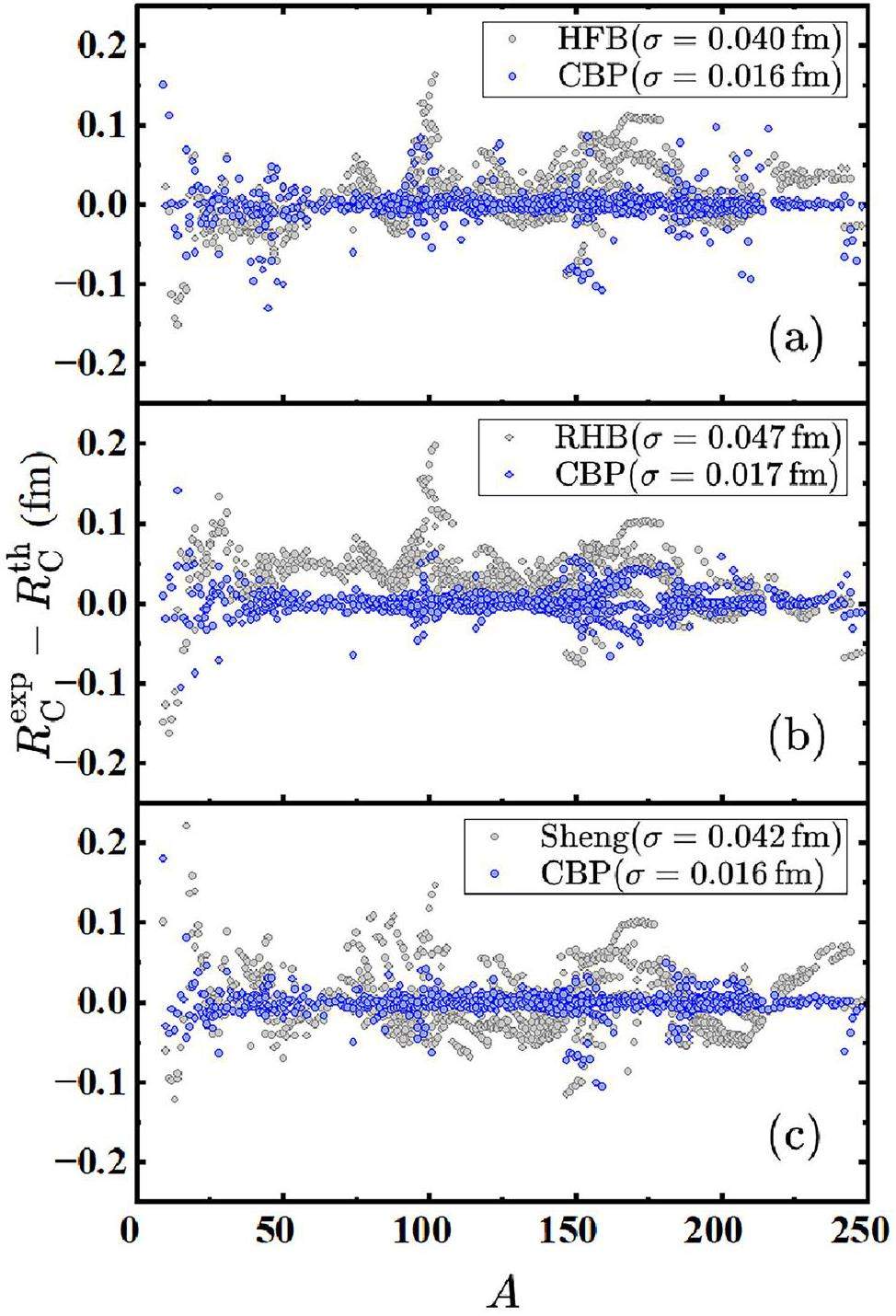
In regions 60<A<90, 120<A<140, and 215<A<240 in Fig. 1a; 45<A<90, 110<A<140, and 220<A<240 in Fig. 1b; and 80<A<95, 110<A<145, and 210<A<240 in Fig. 1c, where theoretical model predictions exhibit similar accuracy and the distribution of δ^pre is highly regular, the CBP estimator achieves substantial improvements, considerably reducing the residuals. In particular, for nuclei with mass numbers around A=100, A=150, and A=190, where proton-neutron residual interactions and other physical effects lead to large δ^pre, the CBP method markedly enhances the predictive accuracy by statistically accounting for these interactions and effects. However, for light nuclei, where δ^pre exhibits greater variability owing to relatively low nucleon numbers, the optimization effect of the CBP estimator is comparatively limited. As more charge radii of light nuclei are precisely measured in experiments, the predictive performance of the CBP estimator for light nuclei can be further enhanced.

Extrapolating capabilities of the CBP estimator

Model extrapolation was essential for the acquisition of unknown data. In this section, we evaluate the extrapolation performance of the CBP estimator. The learning set comprised 790 nuclei with proton numbers Z > 3 from the 2004 charge radii compilation [11], while the validation set included 102 experimental charge radii added between 2004 and 2013. The bandwidth parameters $h_{\delta }$, hN, and hZ used in the extrapolation process are the same as those employed in the global optimization. The standard deviations σ_pre and σ_post for the learning and validation sets, both before and after applying the CBP estimator, are reported in Table 2 along with the optimization rate $\text{Δ}\sigma /{\sigma }_{\text{pre}}$.

According to Table 2, the standard deviations of R_C calculated using the HFB, RHB, and semi-empirical formulas are approximately 0.040 fm for both the learning and validation sets. This consistency indicates that the initial theoretical models possess considerable extrapolation capabilities, which are more beneficial for the CBP estimator in predicting unknown regions. After applying the CBP estimator, the standard deviations for all three models in the learning set decreased to less than 0.020 fm, achieving an improvement of approximately 60% compared to the initial results. In the validation set, the standard deviations were slightly greater than 0.020 fm, with improvement rates of approximately 45% for the three models. The steady improvement rates across both the learning and validation sets demonstrate the robust extrapolation capabilities of the CBP estimator.

The optimization rates for all three models in the validation set were lower than those in the learning set. This phenomenon can be explained by the CBP framework: the Bayesian formula accounts for statistical correlations among nuclei with the same proton and neutron numbers, whereas the weight function considers local relationships among neighboring nuclei. Most nuclei in the validation set were positioned near the drip line, where fewer neighboring nuclei were represented in the learning set, thereby diminishing the performance of the CBP estimator. As more R_C values were measured experimentally, the extrapolation ability of the CBP estimator was expected to improve significantly.

The results in Table 2 indicate that the CBP estimator demonstrates excellent extrapolation capabilities. The HFB, RHB and semi-empirical formulas provide the overall trends of R_C variations. By inheriting the advantages of theoretical models and incorporating local correlation characteristics between nuclei, the CBP estimator captures the physical effects that are not reflected in theoretical models, leading to reliable corrections of R_C. Consequently, for nuclei lacking experimental data, the CBP estimator can offer precise and robust predictions.

Comprehensively factoring in the results of different models using the BMA method

After optimization using the CBP estimator, specific models exhibited optimal predictive performance in distinct regions, especially for nuclei far from the β-stability line. This study introduces the BMA method to integrate these strengths. The BMA method assigns weights based on the predictive performance of different models for the benchmark nuclei. To balance the predictive discrepancies between the theoretical models across different regions of the nuclear chart, the benchmark nuclei selected for the BMA method were ⁴⁹K, ³⁸Ca, ¹⁰⁰Cd, ¹¹⁹Cd, ²⁰¹Po, and ²³³Ra, which cover a wide range of the nuclear chart, including from light nuclei to heavy nuclei, and from proton-rich regions to neutron-rich regions. These selected nuclei are located near the edges of the nuclear chart and are outside the 2013 charge radii compilation, making them particularly valuable for benchmarking extrapolation capabilities.

After obtaining the corrected residuals ${\delta }^{\text{corr}}=R_{\text{C}}^{\text{exp}}-R_{\text{C}}^{\text{corr}}$ for the benchmark nuclei, the weights for each model were calculated using the BMA method and the results are presented in Table 3. The HFB model exhibits superior predictive accuracy for benchmark nuclei, and is thus assigned higher weights. In contrast, the RHB model and semi-empirical formula are assigned lower weights owing to their lower predictive accuracies. The BMA method was applied to optimize the predictions for 102 validation nuclei. The standard deviation is 0.019 fm, which is lower than that of the individual model optimized by the CBP estimator, as shown in Table 2. Compared with the HFB model, the RHB model, and Sheng’s formula individually optimized using the CBP estimator, the introduction of the BMA method improves the accuracy by 9.5%, 24.0%, and 26.9%, respectively. This demonstrates that the BMA method effectively combines the strengths of the different models, further enhancing predictive accuracy.

Analysis of the trend of variation in charge radii within isotopic chains reveals many important and interesting physical phenomena. This study combines the CBP and BMA methods to predict the R_C of the Ca and Sr isotopic chains, illustrating the capability of this approach to capture the physical effects within the isotopic chains. The calcium isotopic chain serves as a distinctive nuclear system for investigating interactions between protons and neutrons inside the nucleus [91-93]. In the stable isotope region of the Ca chain, ⁴⁰Ca and ⁴⁸Ca both exhibit a large number of protons and neutrons, and their R_C values are nearly identical. Owing to the change in the nuclear structure associated with shell closure, a kink in R_C at N = 28 is observed. For 20 < N < 28, the trend of R_C follows a parabolic shape, and the odd-even staggering effect on R_C is particularly pronounced. For neutron-rich nuclei with N > 28, R_C exhibited a strong increase.

Figure 2a presents the predicted charge radii $\overline{R}$ (purple squares) for the Ca isotopic chain based on the combined CBP and BMA methods, along with uncertainty bands calculated from the corresponding error estimates. The experimental values $R_{\text{C}}^{\text{exp}}$ (gray circles) and initial results from the HFB model (blue squares) are also provided for comparison. The HFB model predicts an approximately linear relationship between R_C and the mass number, which deviates from the experimental results. After corrections using the CBP and BMA methods, the discrepancies between $\overline{R}$ and the experimental data were substantially reduced, providing an accurate description of the parabolic trend of R_C and kink at ⁴⁸Ca.

Fig. 2Full-screen View

a The theoretical and experimental charge radii R_C for Ca isotopes, with uncertainty bands included for the predictions refined by the CBP estimator. b Similar to a, but for Sr isotopes

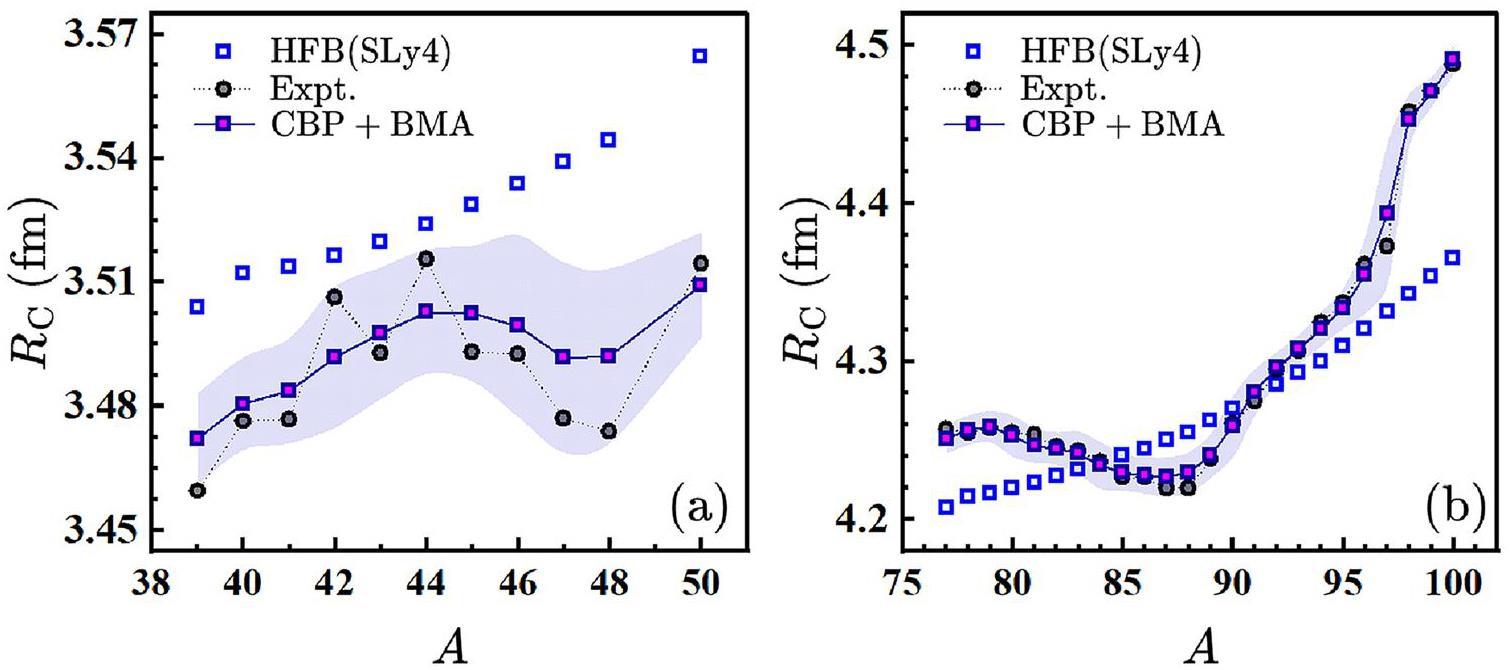
The experimental charge radii in Fig. 2a clearly show the shell effect and odd-even staggering. However, the odd-even staggering is diluted in the R_C predicted using the CBP estimator combined with the BMA method. This is because the calculation of the CBP estimator relies on nuclides with the same proton number Z or neutron number N, which leads to a weakening of the odd-even staggering effect. The introduction of the BMA method combines the results of the three models, further diluting the odd-even staggering effect.

In addition to Ca isotopes, the charge radii of Sr isotopes also exhibit prominent shell effects [94]. The Sr isotope chain extends from the valley of stability at ⁸⁸Sr, where isotopes show a spherical shape, to the strongly deformed isotopes on either side of the stability line. As the nucleus approached the neutron shell closure at N=50 from the neutron-deficient side, R_C gradually decreased. At N=50, it exhibited a kink, after which it began to increase. When N reached 60, a sudden increase in R_C was observed, corresponding to an experimental transition from a near-spherical shape to a strongly deformed configuration [95]. The refined predictions $\overline{R}$ of Sr isotopes obtained using the CBP estimator in conjunction with the BMA approach are shown in Fig. 2b. $\overline{R}$ was closely aligned with the experimental data, particularly for the kink of ⁸⁸Sr and the pronounced increase in R_C observed at ⁹⁸Sr.