Introduction

The nuclear mass or binding energy reflects complex nuclear forces that bind protons and neutrons together within a nucleus [1]. This fundamental quantity not only underlies nuclear stability [2] but also critically influences astrophysical phenomena, from nuclear reactions in stellar interiors [3] to the nucleosynthesis processes responsible for elemental production in the universe [4]. Consequently, the precise determination of nuclear masses is indispensable for advancing our understanding of nuclear structures [5] and has significant implications for nuclear astrophysics [6-8]. Thus, improved experimental precision and theoretical accuracy in nuclear mass evaluations not only deepens insights into fundamental research in nuclear physics [9] but also fosters progress in nuclear energy applications via both fusion and fission.

Global investments in rare isotope beam facilities–including the Heavy Ion Research Facility in Lanzhou (HIRFL) [10] and the High Intensity heavy-ion Accelerator Facility (HIAF) at Huizhou [11], China, the Facility for Rare Isotope Beams (FRIB) in the USA [12], the Radioactive Isotope Beam Factory (RIBF) at RIKEN, Japan [13], the Facility for Antiproton and Ion Research (FAIR) in Germany [14], the Rare isotope Accelerator complex for ON-line experiments (RAON) in Korea [15], and Isotope Separator and Accelerator in Canada (ISAC) [16]–have substantially advanced the production, identification, and investigation of nuclides far from the valley of stability. To date, experimental efforts have led to the identification of over 3300 nuclides [17], with mass measurements available for approximately 2500 of these [18-20]. By contrast, theoretical models predict the existence of approximately 7000–10000 nuclides [21, 22]. Given that the proton dripline has been established for isotopes with proton numbers $Z\gtrsim 90$ [23], whereas the neutron dripline has been delineated only up to Z=10 [24], it is anticipated that most unknown neutron-rich nuclei will remain experimentally inaccessible in the near future. Therefore, there is an urgent need for reliable theoretical predictions of the nuclear masses.

Extensive efforts have been devoted to reproducing measured nuclear masses and predicting those that are yet uncharted. Macroscopic-microscopic approaches exemplified by the finite-range droplet model (FRDM) [25] and the Weizsäcker-Skyrme (WS) model [26, 27] have achieved impressive accuracy in describing existing mass data; however, microscopic theories are widely accepted as offering superior predictive capabilities [28, 29]. In this context, density functional theory has emerged as a powerful framework for a unified description of nearly all nuclides across the nuclear chart [30-38]. Its relativistic extension, the covariant density functional theory (CDFT) [39], has been exceptionally successful in describing a variety of nuclear phenomena in both ground and excited states [39-48]. This success is largely attributable to the inherent advantages of CDFT, including the automatic incorporation of spin-orbit coupling [49, 50], natural explanation of pseudospin symmetry in the nucleon spectrum [51-53], spin symmetry in the antinucleon spectrum [53-55], and self-consistent treatment of nuclear magnetism [56, 57].

Within the framework of CDFT, the pairing correlations and continuum effects are taken into account self-consistently in the relativistic continuum Hartree-Bogoliubov (RCHB) theory [58, 59], making it capable of describing both stable and exotic nuclei [58, 60-65]. A pioneering application of RCHB theory is the construction of the first relativistic nuclear mass table incorporating continuum effects, in which the existence of 9035 bound nuclei with $8\le Z\le 120$ is predicted [22]. Notably, the inclusion of continuum effects is essential for extending the neutron dripline to a more neutron-rich region. Nonetheless, the accuracy of the RCHB mass table in reproducing experimental data is limited owing to the assumption of spherical symmetry within the theoretical framework.

Thus, it is natural to propose an upgraded mass table that incorporates not only continuum effects but also nuclear deformation degrees of freedom. This can be realized by employing the deformed extension of the RCHB theory, that is, the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) [66-69]. Axial deformation, pairing correlations, and continuum effects are considered microscopically and self-consistently in the DRHBc theory, which lays an important foundation for its great success [45, 70, 71]. In pursuit of a high-precision mass table [72], a point-coupling version of the DRHBc theory was developed [73, 74] for combination with the density functional PC-PK1 [75], which is probably the most successful density functional for describing nuclear masses [37, 44, 76]. The DRHBc mass table project, now in progress for over six years, has successfully completed the sectors for even-even [77] and even-Z [78] nuclei. Impressively, the root-mean-square (RMS) deviation of the DRHBc calculated masses from the latest Atomic Mass Evaluation (AME2020) data is approximately 1.5 MeV, positioning it among the most accurate density-functional descriptions for nuclear masses. Moreover, lots of relevant studies on halo phenomena [79-89], nuclear charge radii [90-92], shape evolution [93-96], shell structure [97-103], decay properties [104-107], and other topics [108-113] based on the DRHBc mass table underscore its value as a resource that extends far beyond a mere data repository [114].

In this work, inspired by the recent progress in nuclear mass measurements that provide new data beyond AME2020 or reduce the uncertainties of existing data, we further examined the predictive power of the DRHBc mass table using the new mass data. On the theoretical side, a new point-coupling density functional, PC-L3R, has recently been proposed, whose performance is even better than that of PC-PK1 in describing the masses of spherical nuclei [115]. Our second motivation is to test the accuracy of PC-L3R in describing the masses of deformed nuclei when combined with DRHBc theory. The remainder of this paper is organized as follows. The point-coupling DRHBc theory, relativistic density functionals PC-PK1 and PC-L3R, and numerical details are introduced in Sect. 2. DRHBc descriptions with PC-PK1 and PC-L3R for the new masses are presented and compared with those from other density functionals in Sect. 3. Finally, a summary is given in Sect. 4.

Theoretical framework

The point-coupling density functional theory starts from the Lagrangian density, $\begin{array}{c}\mathcal{L}=\overline{\psi }\left(i{\gamma }_{\mu }{\partial }^{\mu }-M\right)\psi -\frac{1}{2}{\alpha }_{\text{S}}\left(\overline{\psi }\psi \right)(\overline{\psi }\psi )-\frac{1}{2}{\alpha }_{\text{V}}\left(\overline{\psi }{\gamma }_{\mu }\psi \right)\left(\overline{\psi }{\gamma }^{\mu }\psi \right)\\ -\frac{1}{2}{\alpha }_{\text{TV}}\left(\overline{\psi }\overrightarrow{\tau }{\gamma }_{\mu }\psi \right)\left(\overline{\psi }\overrightarrow{\tau }{\gamma }^{\mu }\psi \right)-\frac{1}{2}{\alpha }_{\text{TS}}\left(\overline{\psi }\overrightarrow{\tau }\psi \right)(\overline{\psi }\overrightarrow{\tau }\psi )\\ -\frac{1}{3}{\beta }_{\text{S}}{\left(\overline{\psi }\psi \right)}^3-\frac{1}{4}{\gamma }_{\text{S}}{\left(\overline{\psi }\psi \right)}^4-\frac{1}{4}{\gamma }_{\text{V}}{\left[\left(\overline{\psi }{\gamma }_{\mu }\psi \right)\left(\overline{\psi }{\gamma }^{\mu }\psi \right)\right]}^2\\ -\frac{1}{2}{\delta }_{\text{S}}{\partial }_{\nu }\left(\overline{\psi }\psi \right){\partial }^{\nu }\left(\overline{\psi }\psi \right)-\frac{1}{2}{\delta }_{\text{V}}{\partial }_{\nu }\left(\overline{\psi }{\gamma }_{\mu }\psi \right){\partial }^{\nu }\left(\overline{\psi }{\gamma }^{\mu }\psi \right)\\ -\frac{1}{2}{\delta }_{\text{TV}}{\partial }_{\nu }\left(\overline{\psi }\overrightarrow{\tau }{\gamma }_{\mu }\psi \right){\partial }^{\nu }\left(\overline{\psi }\overrightarrow{\tau }{\gamma }^{\mu }\psi \right)\\ -\frac{1}{2}{\delta }_{\text{TS}}{\partial }_{\nu }\left(\overline{\psi }\overrightarrow{\tau }\psi \right){\partial }^{\nu }\left(\overline{\psi }\overrightarrow{\tau }\psi \right)\\ -\frac{1}{4}{F}^{\mu \nu }{F}_{\mu \nu }-e\overline{\psi }{\gamma }^{\mu }\frac{1-{\tau }_3}{2}{A}_{\mu }\psi \mathrm{,}\end{array}$ (1) where M is the nucleon mass, e the charge unit, and $A_{\mu }$ and $F_{\mu \nu }$ the four-vector potential and field strength tensor of the electromagnetic field, respectively. With the subscripts S, V, and T respectively standing for scalar, vector, and isovector, nine coupling constants, α_S, α_V, α_TV, β_S, γ_S, γ_V, δ_S, δ_V, and δ_TV, in the Lagrangian density of PC-PK1 and PC-L3R are listed in Table 1. As the isovector-scalar channels involving α_TS and δ_TS terms were found to be less helpful in improving the description of nuclear ground-state properties [116], they are not included in PC-PK1 and PC-L3R.

Starting from the Lagrangian density (1), the Hamiltonian can be derived via the quantization of the Dirac spinor field in the Bogoliubov quasiparticle space, and the energy functional can be constructed as its expectation with respect to the Bogoliubov ground state. The relativistic Hartree-Bogoliubov equation obtained by performing the variation of the energy density functional with respect to the generalized density matrix and neglecting the exchange terms reads $\left(\begin{array}{cc}{\widehat{h}}_{\text{D}}-\lambda & \widehat{\text{Δ}}\\ -{\widehat{\text{Δ}}}^{*}& -{\widehat{h}}_{\text{D}}^{*}+\lambda \end{array}\right)\left(\begin{array}{c}{U}_k\\ V_k\end{array}\right)=E_k\left(\begin{array}{c}{U}_k\\ V_k\end{array}\right)\mathrm{,}$ (2) where ${\widehat{h}}_{\text{D}}$ is the Dirac Hamiltonian, $\widehat{\text{Δ}}$ is the pairing field, λ is the Fermi surface, Ek is the quasiparticle energy, and Uk and Vk are quasiparticle wave functions. The Dirac Hamiltonian in coordinate space is $h_{\text{D}}\left(r\right)=\alpha \cdot p+V(r)+\beta [M+S(r)]\mathrm{,}$ (3) with the scalar $S(r)$ and vector $V(r)$ potentials, $\begin{array}{c}S(r)={\alpha }_{\text{S}}{\rho }_{\text{S}}+{\beta }_{\text{S}}{\rho }_{\text{S}}^2+{\gamma }_{\text{S}}{\rho }_{\text{S}}^3+{\delta }_{\text{S}}\text{Δ}{\rho }_{\text{S}}\mathrm{,}\\ V(r)={\alpha }_{\text{V}}{\rho }_{\text{V}}+{\gamma }_{\text{V}}{\rho }_{\text{V}}^3+{\delta }_{\text{V}}\text{Δ}{\rho }_{\text{V}}+e{A}^0+{\alpha }_{\text{TV}}{\tau }_3{\rho }_3\\ +{\delta }_{\text{TV}}{\tau }_3\text{Δ}{\rho }_3\mathrm{,}\end{array}$ (4) constructed by various densities, $\begin{array}{l}{\rho }_{\text{S}}\left(r\right)={\displaystyle \sum _{k>0}}{V}_k^{†}\left(r\right){\gamma }_0{V}_k\left(r\right)\mathrm{,}\\ {\rho }_{\text{V}}\left(r\right)={\displaystyle \sum _{k>0}}{V}_k^{†}\left(r\right)V_k\left(r\right)\mathrm{,}\\ {\rho }_3\left(r\right)={\displaystyle \sum _{k>0}}{V}_k^{†}\left(r\right){\tau }_3{V}_k\left(r\right)\mathrm{,}\end{array}$ (5) where the summation index k loops through the positive-energy quasiparticle states in the Fermi sea. Neglecting for simplicity spin and isospin degrees of freedom, the pairing potential reads $\text{Δ}\left(r_1\mathrm{,}{r}_2\right)=V^{pp}\left(r_1\mathrm{,}{r}_2\right)\kappa \left(r_1\mathrm{,}{r}_2\right)\mathrm{,}$ (6) where Vpp is the pairing interaction, and κ is the pairing tensor. A density-dependent interaction of zero range is adopted in the present DRHBc theory, $V^{pp}\left(r_1\mathrm{,}{r}_2\right)=V_0\frac{1}{2}\left(1-P^{\sigma }\right)\delta \left(r_1-r_2\right)\left(1-\frac{\rho \left(r_1\right)}{{\rho }_{\text{sat}}}\right)\mathrm{,}$ (7) where V₀ is the pairing strength, ρ_sat is the saturation density of nuclear matter, and $\frac{1}{2}\left(1-P^{\sigma }\right)$ projects onto the spin-zero S=0 component. Assuming axial symmetry and spatial reflection symmetry, one can expand nuclear densities and potentials in terms of even-order Legendre polynomials [117], $f(r)={\displaystyle \sum _l}{f}_l\left(r\right)P_l\left(\cos \theta \right)\mathrm{,}l=\mathrm{0,2,4,}\cdots \mathrm{,}$ (8) where the lth-order radial component is calculated by $f_l\left(r\right)=\frac{2l+1}{4\pi }{\displaystyle \int }\text{d}\text{Ω}f(r)P_l\left(\cos \theta \right)\mathrm{.}$ (9) After obtaining the self-consistent solution of the RHB Eq. (2), quantities including the total energy, RMS radius, and deformation parameter can be calculated from nuclear densities. The total energy is [59] $\begin{array}{c}{E}_{\text{RHB}}={\displaystyle \sum _{k>0}}\left(\lambda -E_k\right)v_k^2-E_{\text{pair}}\\ -{\displaystyle \int }{\text{d}}^{3}r(\frac{1}{2}{\alpha }_{\text{S}}{\rho }_{\text{S}}^2+\frac{1}{2}{\alpha }_{\text{V}}{\rho }_{\text{V}}^2+\frac{1}{2}{\alpha }_{\text{TV}}{\rho }_3^2\\ +\frac{2}{3}{\beta }_{\text{S}}{\rho }_{\text{S}}^3+\frac{3}{4}{\gamma }_{\text{S}}{\rho }_{\text{S}}^4+\frac{3}{4}{\gamma }_{\text{V}}{\rho }_{\text{V}}^4+\frac{1}{2}{\delta }_{\text{S}}{\rho }_{\text{S}}\text{Δ}{\rho }_{\text{S}}\\ +\frac{1}{2}{\delta }_{\text{V}}{\rho }_{\text{V}}\text{Δ}{\rho }_{\text{V}}+\frac{1}{2}{\delta }_{\text{TV}}{\rho }_3\text{Δ}{\rho }_3+\frac{1}{2}{\rho }_{p}e{A}^0)\\ +E_{\text{c}\text{.m}\text{.}}+E_{\text{rot}}\mathrm{,}\end{array}$ (10) where $v_k^2={\displaystyle \int }{\text{d}}^{3}r{V}_k^{†}\left(r\right)V_k\left(r\right)\mathrm{,}$ (11) and the pairing energy $E_{\text{pair}}=-\frac{1}{2}{\displaystyle \int }{\text{d}}^{3}r\kappa (r)\text{Δ}(r)\mathrm{.}$ (12) The center-of-mass (c.m.) correction energy is calculated as $E_{\text{c}\mathrm{.}\text{m}\mathrm{.}}=-\frac{1}{2MA}\langle {\widehat{P}}^2\rangle \mathrm{,}$ (13) with A the mass number and $\widehat{P}={\displaystyle {\sum }_i^A}{\widehat{p}}_i$ the total momentum in the c.m. frame. The rotational correction energy for a deformed nucleus from the cranking approximation reads $E_{\text{rot}}=-\frac{1}{2\mathcal{J}}\langle {\widehat{J}}^2\rangle \mathrm{,}$ (14) where $\widehat{J}={\displaystyle {\sum }_i^A}{\widehat{j}}_i$ is the total angular momentum and $\mathcal{J}$ is the moment of inertia that can be estimated using the Inglis-Belyaev formula [118]. The RMS radius is calculated as $R_{\text{RMS}}={\langle r^2\rangle }^{1/2}=\sqrt{\frac{{\displaystyle \int }{\text{d}}^{3}r\left[r^2{\rho }_{\text{V}}\left(r\right)\right]}{N}}\mathrm{,}$ (15) where ρ_V is the vector density and N denotes the corresponding particle number. The quadrupole deformation parameter is calculated as ${\beta }_2=\frac{4\pi \langle r^2{Y}_{20}\left(\text{Ω}\right)\rangle }{3N\langle r^2\rangle }\mathrm{,}$ (16) where Y is the spherical harmonic function.

The calculations in this study were performed using the same numerical details as those used to construct the DRHBc mass table [73, 74, 77]. Specifically, the pairing strength V₀=-325 MeV fm³, saturation density ρ_sat = 0.152 fm^-3, and pairing window was set to 100 MeV. The Dirac Woods-Saxon basis space was determined by an energy cutoff of $E_{\text{cut}}=300$ MeV and an angular momentum cutoff of $J_{\text{cut}}=\frac{23}{2}\hslash$. The Legendre expansion truncations in Eq. (8) are chosen as $l_{\text{max}}=6$ and 8 for the nuclei with $8\le Z\le 70$ and $71\le Z\le 100$, respectively. The blocking effects in odd-mass and odd-odd nuclei are included via an equal filling approximation [68, 74, 119].

Results and discussion

We have collected the newly measured masses of 296 nuclides from 40 references [120-159], published between 2021 and 2024 (subsequent to the release of AME2020) and summarized in Table 2. The sources and measurement methods for the new experimental data are presented in Table 3. The corresponding mass values in AME2020, which contained 241 experimentally measured values and 55 extrapolated empirical values (labeled #), are listed in Table 2 for comparison. The differences between the new data and the AME2020 values are also given in Table 2 and are scaled by colors in Fig. 1. The nuclides with only empirical values in AME2020 are highlighted by black squares in Fig. 1. Among these 296 mass data, 247 in AME2020 are consistent with new measurements with deviations smaller than 0.15 MeV. The RMS deviation between the new and AME2020 experimental data is σ=0.0984 MeV, and after including the empirical values in AME2020, σ becomes 0.1178 MeV.

Fig. 1Full-screen View

(Color online) The differences between the newly measured masses for 296 nuclides and the corresponding values in AME2020 [20] scaled by colors. The black squares represent nuclides for which AME2020 has only empirical mass values. The dark gray region shows the nuclides observed experimentally, and the light gray region shows the predicted nuclear landscape by the DRHBc mass table [77]

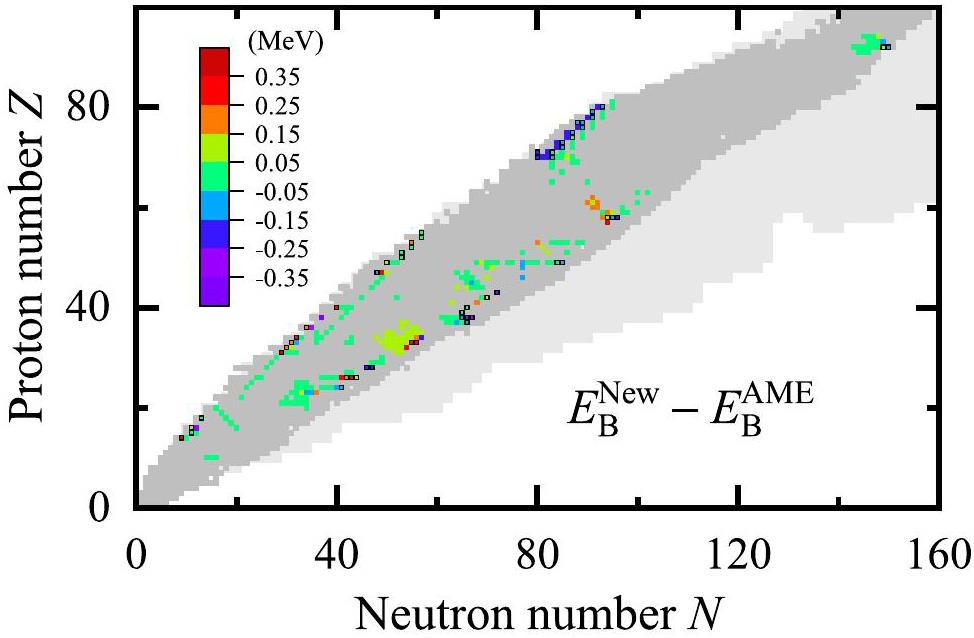
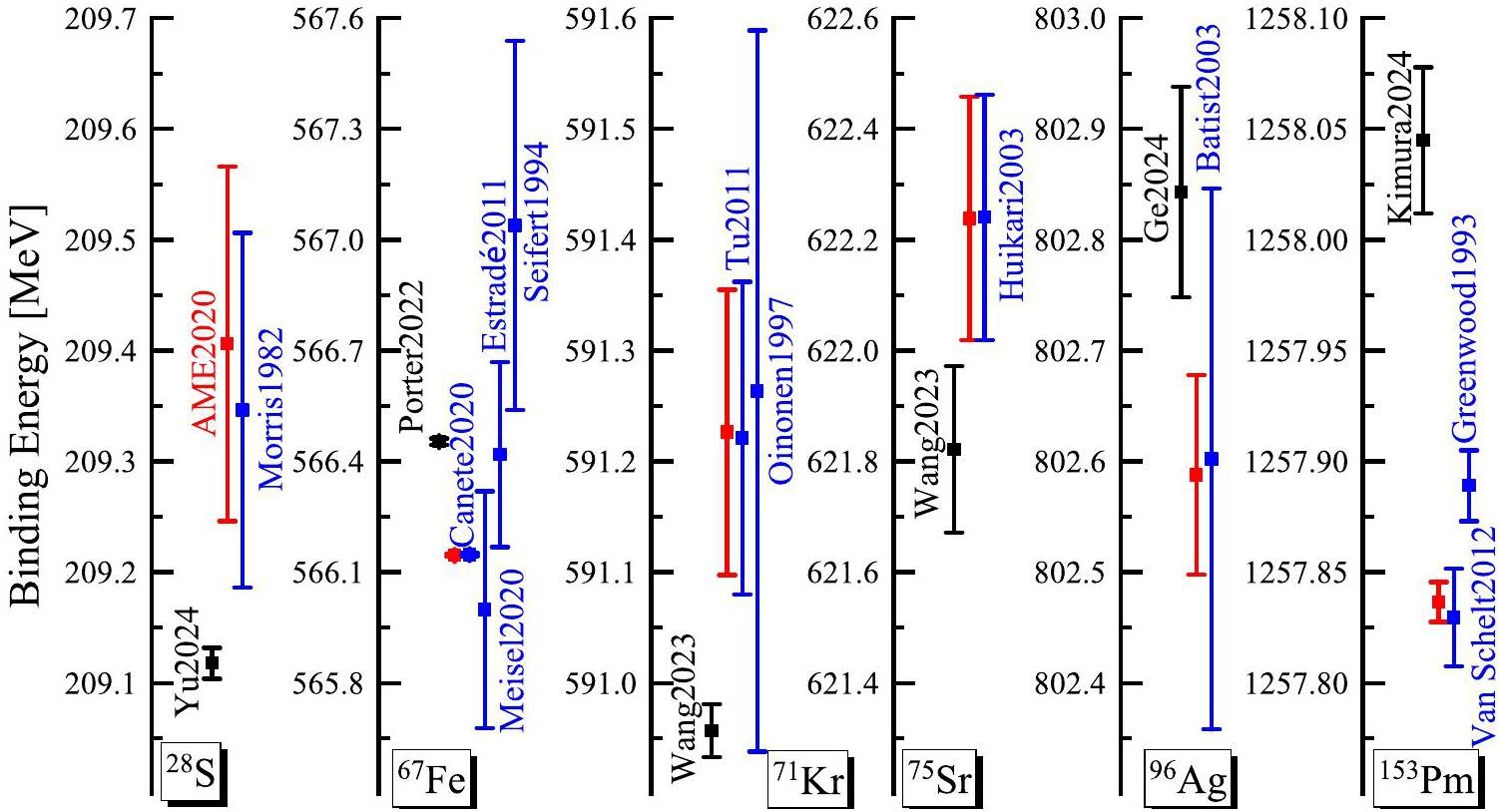
Most of the deviations between the new and AME2020 experimental data lie within experimental uncertainties. Nevertheless, even after considering the experimental uncertainties, disagreement still arises for 73 nuclides, which are labeled in bold in Table 2. Among these 73 data, the smallest difference, 0.00055 MeV, occurs between the upper bound of the new data and the lower bound of the AME2020 data for ¹¹¹Ag, while the largest one, 0.29516 MeV, occurs between the lower bound of the new data and the upper bound of the AME2020 data for ⁶⁷Fe. It is important to note that newly measured masses are not necessarily more accurate than those in previous evaluations. Systematic biases or experimental uncertainties may affect the measured values depending on the specific setup and techniques employed. Notably, for 23 nuclides, the central values of the newly reported masses deviated from those in AME2020 by more than 200 keV. Among the 23 nuclides exhibiting discrepancies exceeding 200 keV, 12 cases (²³Si, ⁷⁴Ni, ⁸⁶Ge, ⁸⁹As, ⁹¹Se, ⁷⁰Kr, ¹⁰⁴Sr, ¹⁰⁵Sr, ¹⁰⁹Nb, ⁷²Tc, ¹⁵¹La, and ¹⁵¹Yb) show overlapping uncertainty ranges between the new measurements and AME2020 values, indicating potential consistency within experimental uncertainties. For 5 nuclides (⁶⁹Fe, ⁶⁰Ga, ⁸⁸As, ⁶⁶Se, and ⁸⁰Zr), while the central value discrepancies also exceed 200 keV and uncertainty ranges do not overlap, the AME2020 masses are extrapolated values. Although such empirical estimates, based on trends in the mass surface and available experimental constraints, are often validated by subsequent measurements, deviations from true mass values may arise, for example, for nuclides exhibiting abrupt changes in shell structure. Finally, for 6 nuclides (²⁸S, ⁶⁷Fe, ⁷¹Kr, ⁷⁵Sr, ⁹⁶Ag, and ¹⁵³Pm), the central values differ by more than 200 keV, the uncertainty ranges do not overlap, and both the new and AME2020 masses are based on experimental data. The cases are compared in Fig. 2, along with earlier measurements referenced in AME2020. The observed discrepancies may arise from differences in the measurement techniques. For ²⁸S, its mass was derived from an indirect measurement in 1982 [160], whereas a recent result was obtained from a direct measurement using $B\rho$-defined isochronous mass spectrometry (Bρ-IMS) in 2024 [121]. For ⁶⁷Fe, AME2020 mainly adopted the ion trap data from 2020 [161], which fall within the uncertainty range of contemporaneous Bρ-time-of-flight (Bρ-TOF) measurements [162]. However, the 2022 result obtained using a multiple-reflection TOF mass spectrometer (MR-TOF-MS) [130] supports earlier data from the TOF isochronous spectrometer from 2011 [163] rather than that from 1994 [164]. For ⁷¹Kr, the AME2020 value was consistent with storage-ring IMS data [165]. While the new Bρ-IMS result from 2023 [133] shows deviations, it remains largely within the uncertainty range of the results inferred from the electron capture decay energy $Q_{\text{EC}}$ measurements [166]. For ⁷⁵Sr and ⁹⁶Ag, the AME2020 values are consistent with earlier estimates based on $Q_{\text{EC}}$ [167, 168], but deviate from recent measurements obtained via Bρ-IMS [133] and ion trap techniques [147], respectively. For ¹⁵³Pm, AME2020 primarily adopted ion trap data from 2012 [169]. Nonetheless, discrepancies were observed among the 2012 results, earlier estimates based on β^- decay energy from 1993 [170], and the latest measurement from MR-TOF-MS in 2024 [155]. Such discrepancies necessitate careful data evaluation and/or even further measurements. In this study, we adopt the newly measured masses for convenience in the following examination of the theoretical descriptions.

Fig. 2Full-screen View

The newly measured binding energies of ²⁸S, ⁶⁷Fe, ⁷¹Kr, ⁷⁵Sr, ⁹⁶Ag, and ¹⁵³Pm, in comparison with the AME2020 data and the previous data referenced in the AME

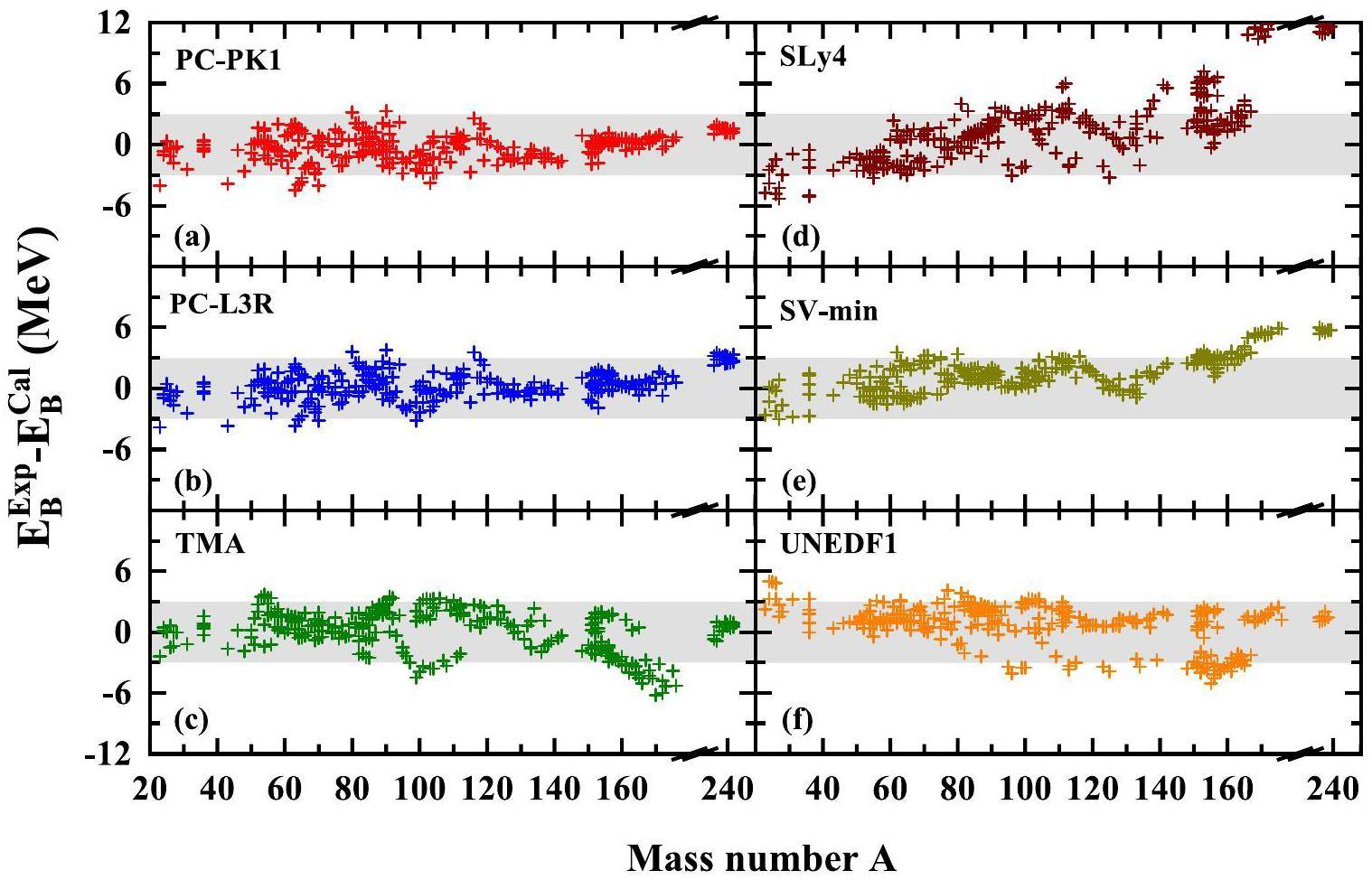
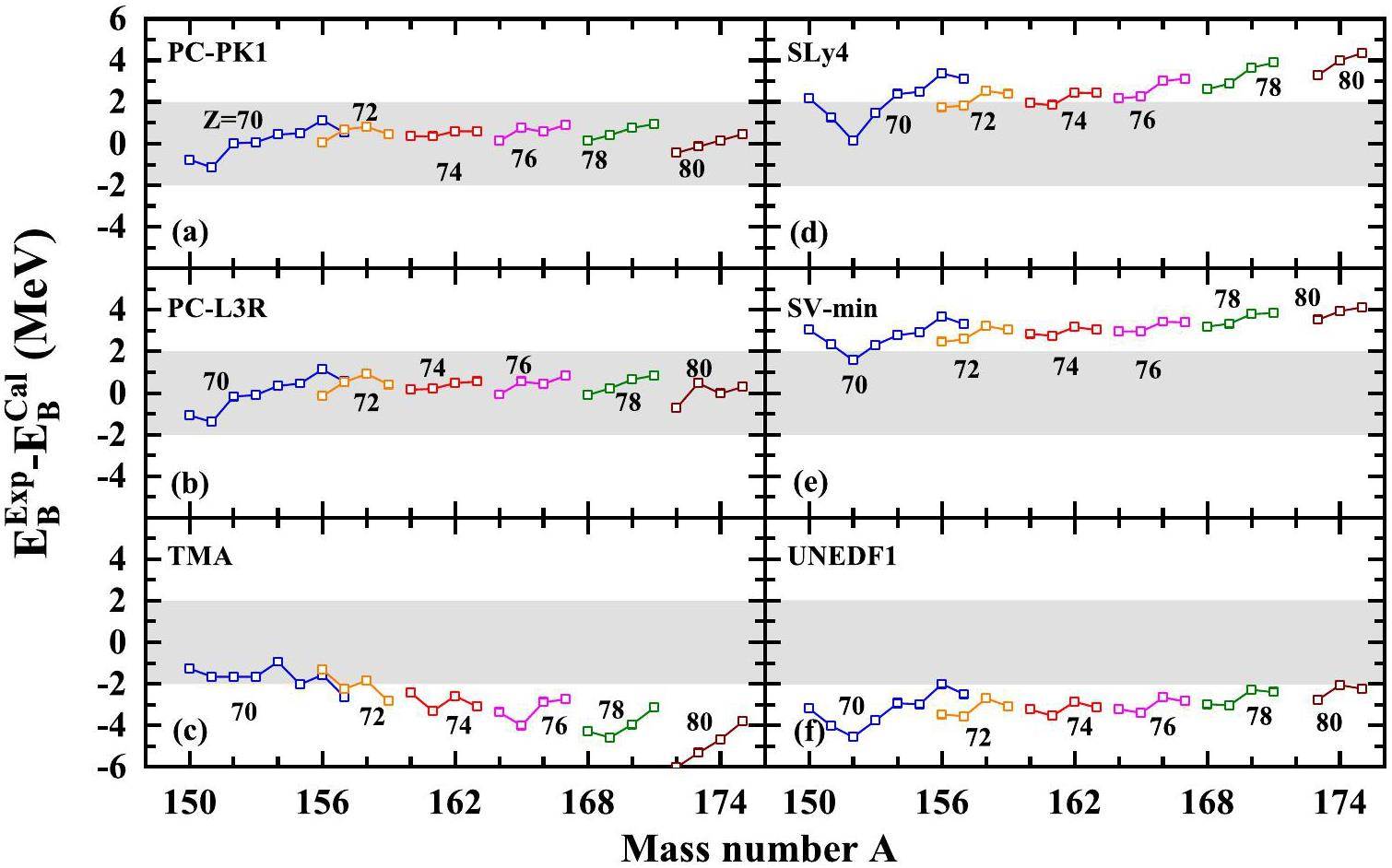
The DRHBc calculations for the 296 nuclides were performed with the density functionals PC-PK1 [75] and PC-L3R [115], and the deviations of the resulting nuclear masses from the experimental data are plotted in Figs. 3(a) and 3(b). For comparison, we also show the mass differences between the new data and the results from the relativistic mean-field plus Bardeen-Cooper-Schrieffer (RMF+BCS) calculations with TMA [32] and the non-relativistic Skyrme Hartree-Fock-Bogoliubov (HFB) calculations [171] with SLy4 [172], SV-min [173], and UNEDF1 [174], respectively, in Figs. 3(c)–(f), respectively. It can be seen that both the DRHBc calculations with PC-PK1 and PC-L3R reproduce the data fairly well within a deviation of 3 MeV, despite a few exceptions. The RMF+BCS calculations with TMA can achieve a similar level of accuracy for nuclides with A<150, but for heavier nuclides, an overestimation of up to 6 MeV arises. In contrast, the Skyrme HFB calculations with SLy4 significantly underestimated the data in the heavy-mass region, with deviations for several nuclides above 10 MeV. The results from the Skyrme HFB calculations with SV-min also exhibited a certain underestimation in the heavy mass region. Although the Skyrme HFB results with UNEDF1 improve the description in $A\gtrsim 170$, they apparently underestimate the masses of a few light and medium-mass nuclei and show significant overestimation at $A\approx 155$. The comparisons in Fig. 3 demonstrate that the descriptions of DRHBc using PC-PK1 and PC-L3R are qualitatively superior.

Fig. 3Full-screen View

(Color online) Mass differences between new data listed in Table 2 and the values from DRHBc calculations with density functionals PC-PK1 (a), PC-L3R (b), RMF+BCS calculations with density functional TMA [32] (c), as well as Skyrme HFB calculations [171] with density functionals SLy4 (d), SV-min (e) and UNEDF1 (f)

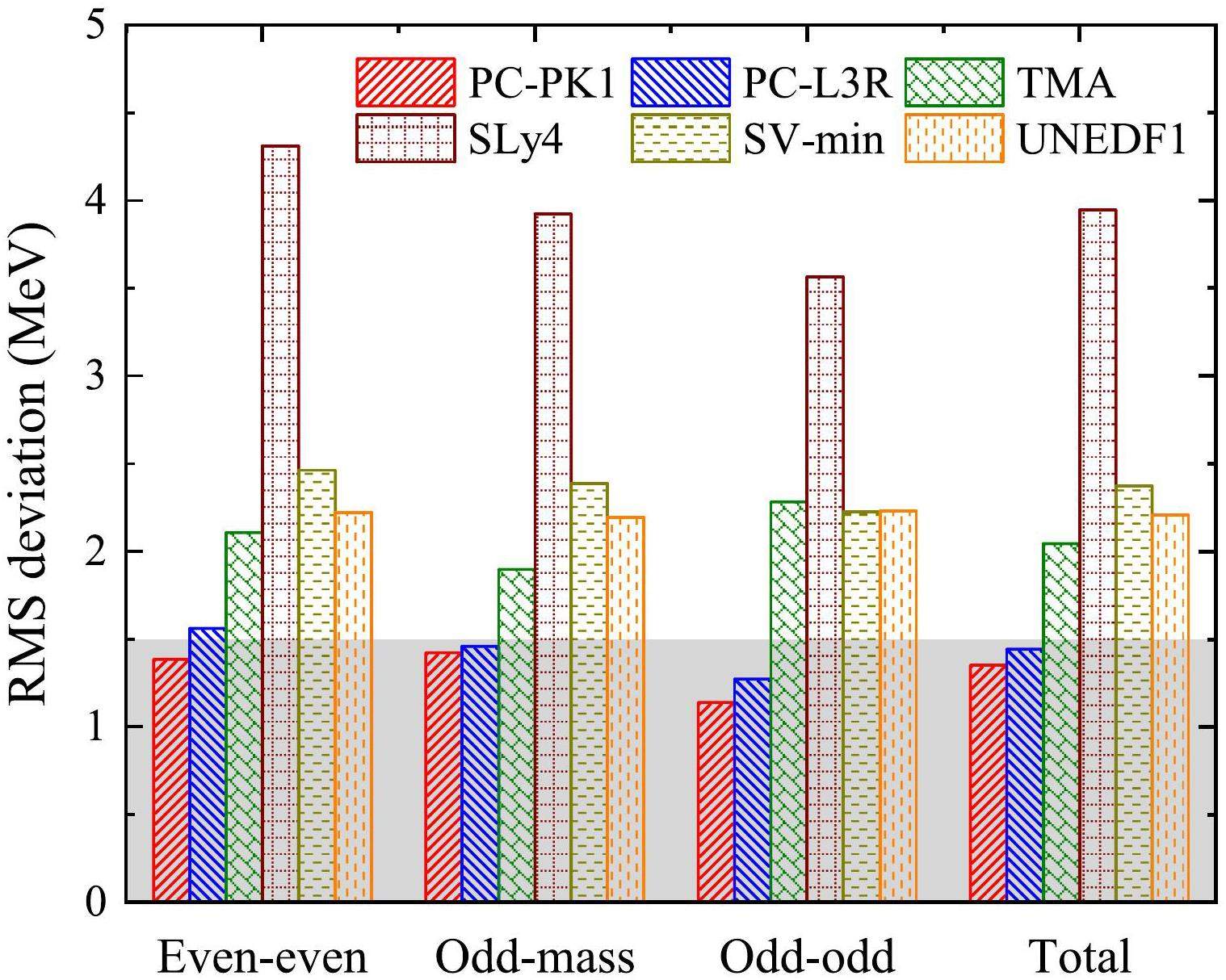
For further comparison, we show in Fig. 4 the RMS deviations between the 296 new mass data points and the above theoretical results. The RMS deviations for even-even, odd-mass, and odd-odd nuclei are also computed and presented separately in Fig. 4. It can be found that both the DRHBc descriptions with PC-PK1 and PC-L3R can achieve accuracies better than 1.5 MeV for all datasets, with the exception of DRHBc+PC-L3R for even-even nuclei. In contrast, the accuracies in the other four density functional descriptions were generally worse than 2 MeV. Overall, the odd-even effects on the accuracy are not very significant in the DRHBc results, with a slightly better description for odd-odd nuclei. However, this is not the case for the RMF+BCS description, which obviously deteriorates for odd-odd nuclei. Furthermore, DRHBc descriptions with PC-PK1 and PC-L3R for odd nuclei are expected to be improved by strictly incorporating nuclear magnetism [87]. Instead of self-consistent calculations, Skyrme HFB results for odd nuclei were obtained from interpolations using the masses and average pairing gaps of neighboring even-even nuclei [171]. As expected, the Skyrme HFB descriptions with SV-min and UNEDF1 showed marginal odd-even differences. In contrast, it seems strange that from even-even to odd-mass, and then to odd-odd nuclei, the SLy4 description gradually improves. It should also be noted that the number of mass data points here is not large enough to confirm whether the odd-even features observed in these theoretical results are common across the nuclear chart. Finally, the accuracies in describing the 296 new masses–1.35, 2.04, 3.95, 2.37, and 2.21 MeV for PC-PK1, TMA, SLy4, SV-min, and UNEDF1, respectively–are found to be generally consistent with those obtained for all available masses of even-Z nuclei: 1.43 MeV for PC-PK1, 2.06 MeV for TMA, 5.28 MeV for SLy4, 3.39 MeV for SV-min, and 1.93 MeV for UNEDF1 [78]. Moreover, even within the spherical RHB framework, PC-PK1 and PC-L3R are the only two relativistic density functionals that reproduce the experimental masses with RMS deviations below 8 MeV [22, 175]. Given the superiority of PC-PK1 and PC-L3R, a complete DRHBc mass table including both even-Z and odd-Z nuclei is desirable in the near future, and further large-scale DRHBc+PC-L3R calculations are worth pursuing.

Fig. 4Full-screen View

(Color online) The RMS deviations between the new mass data listed in Table 2 and different theoretical results. The RMS deviations for even-even, odd-mass and odd-odd nuclei are presented separately

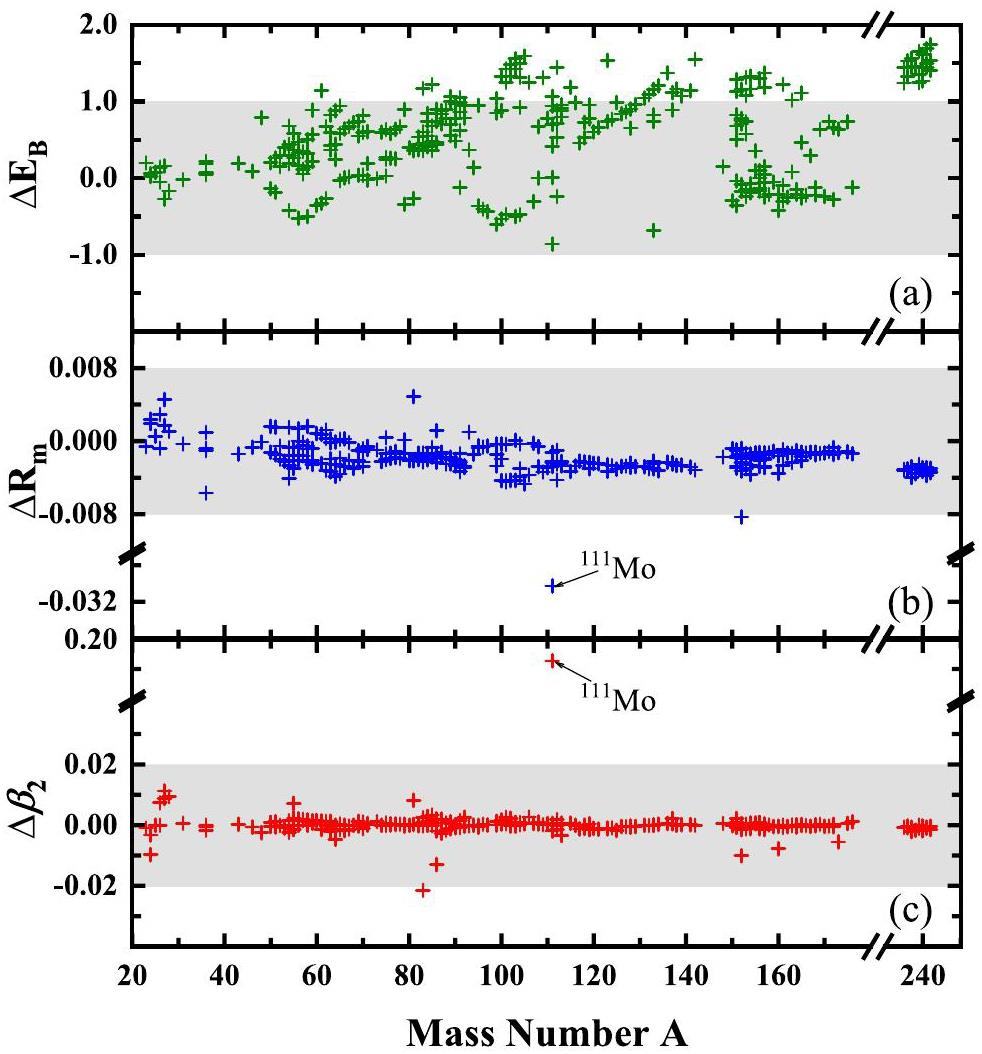
One can see from Fig. 3 that the superiority of PC-PK1 and PC-L3R is mainly due to the better description of nuclei with A>150 compared to other density functionals. Therefore, a detailed comparison of the isospin dependence of nuclear masses in this region is necessary. In Fig. 5, the mass differences between the theoretical and experimental values are presented for even-Z nuclei with $70\le Z\le 80$. If the masses of certain nuclei located in the middle of an isotopic chain were absent from the dataset of new measurements, we resorted to AME2020 for completeness. It can be found in Fig. 5 that only the accuracy of the DRHBc description in this region is always better than 2 MeV, whereas other density-functional descriptions show systematic deviations from the data. Furthermore, the DRHBc description along these isotopic chains is almost steady, with a slight, approximately linear isospin dependence, which is in contrast to many obvious staggering behaviors by other descriptions. Another feature, observed in Fig. 5 shows that the nucleus with N=82 and Z=70 is basically described as overbound compared to its neighboring isotopes. This is a well-known weakness of both nonrelativistic and relativistic density functional theories in describing magic nuclei [77]. From the above discussions, it can be concluded that DRHBc theory provides not only an overall high accuracy but also a robust description of isospin dependence for nuclear masses, and the results from PC-PK1 and PC-L3R are qualitatively similar.

Fig. 5Full-screen View

(Color online) Same as Fig. 3 but for the isotopic chains with Z=70, 72, 74, 76, 78, and 80

For a quantitative comparison, the differences between the DRHBc results for PC-PK1 and PC-L3R for binding energies $\text{Δ}{E}_{\text{B}}=E_{\text{B}}^{\text{PC}-\text{PK1}}-E_{\text{B}}^{\text{PC}-\text{L3R}}$, RMS matter radii $\text{Δ}{R}_{\text{m}}=R_{\text{m}}^{\text{PC}-\text{PK1}}-R_{\text{m}}^{\text{PC}-\text{L3R}}$, and quadrupole deformations $\text{Δ}{\beta }_2={\beta }_2^{\text{PC}-\text{PK1}}-{\beta }_2^{\text{PC}-\text{L3R}}$ are shown in Fig. 6. For the binding energies in Fig. 6(a), among these 296 nuclei, the $\text{Δ}{E}_{\text{B}}$ of 232 nuclei are located within -1.0 < ΔE_B < 1.0 MeV, whereas the $\text{Δ}{E}_{\text{B}}$ of 64 nuclei are located within 1.0 < ΔE_B < 2.0 MeV. Most values of $\text{Δ}{E}_{\text{B}}$ are positive, indicating that PC-PK1 generally describes these nuclei as being more bound than PC-L3R. The RMS matter radii shown in Fig. 6(b) reveal a clear trend of decreasing ΔR_m with increasing mass number A with only a few exceptions. Notably, the majority of ΔR_m values are negative, which is consistent with the general expectation that more strongly bound systems exhibit more compact density distributions. For most nuclei, ΔR_m values are confined within ± 0.008 fm, and two outliers emerge: one barely beyond -0.008 fm for ¹⁵²Pr and the other reaching -0.031 fm for ¹¹¹Mo. For the quadrupole deformation shown in Fig. 6(c), the Δβ₂ values in 291 nuclei are within 0.01, and almost all other nuclei show slightly larger values within 0.02, except for ⁸³Zr and ¹¹¹Mo. Δβ₂ for ⁸³Zr is only -0.021, whereas that for ¹¹¹Mo reaches 0.193, which corresponds to the large |ΔR_m| shown in Fig. 6(b).

Fig. 6Full-screen View

(Color online) Differences between the DRHBc results with PC-PK1 and PC-L3R for binding energies $\text{Δ}{E}_{\text{B}}=E_{\text{B}}^{\text{PC}-\text{PK1}}-E_B^{\text{PC}-\text{L3R}}$ (a), RMS matter radii $\text{Δ}{R}_{\text{m}}=R_{\text{m}}^{\text{PC}-\text{PK1}}-R_{\text{m}}^{\text{PC}-\text{L3R}}$ (b) and quadrupole deformations $\text{Δ}{\beta }_2={\beta }_2^{\text{PC}-\text{PK1}}-{\beta }_2^{\text{PC}-\text{L3R}}$ (c) as functions of mass number A

To understand the large deviations between the PC-PK1 and PC-L3R results for ¹¹¹Mo, in Fig. 7, the potential energy curves (PECs) of ¹¹¹Mo from the constrained calculations with PC-PK1 and PC-L3R are shown. For comparison, the corresponding results for the neighboring isotope ¹¹²Mo are also shown. The ground state is shown with the filled square (circle) from the calculations with PC-PK1 (PC-L3R). As demonstrated in Refs. [73-75], for PC-PK1, the rotational correction plays an important role in improving the mass description of the deformed nuclei. Therefore, the ground state, after including the rotational correction energy E_rot is also presented with an open symbol. Considering that the cranking approximation adopted to calculate E_rot in Eqs. (14) is not suitable for spherical and weakly deformed nuclei, we only calculate E_rot when |β₂|>0.05 and take it as zero when |β₂|<0.05. A more appropriate treatment for the correction energies in the nuclei with |β₂|<0.05 can be achieved using the collective Hamiltonian method [176] in future work.

Fig. 7Full-screen View

(Color online) Potential energy curves (PECs) of ¹¹¹Mo (a) and ¹¹²Mo (b) in constrained DRHBc calculations with PC-PK1 (red line) and PC-L3R (blue line). The ground state is shown with the filled square (circle) from the calculations with PC-PK1 (PC-L3R). For the case with |β₂|>0.05, the ground state after including the rotational correction energy $E_{\text{tot}}$ is shown with the open symbol. The green line represents the available data of $-E_{\text{B}}^{\text{Exp}}$

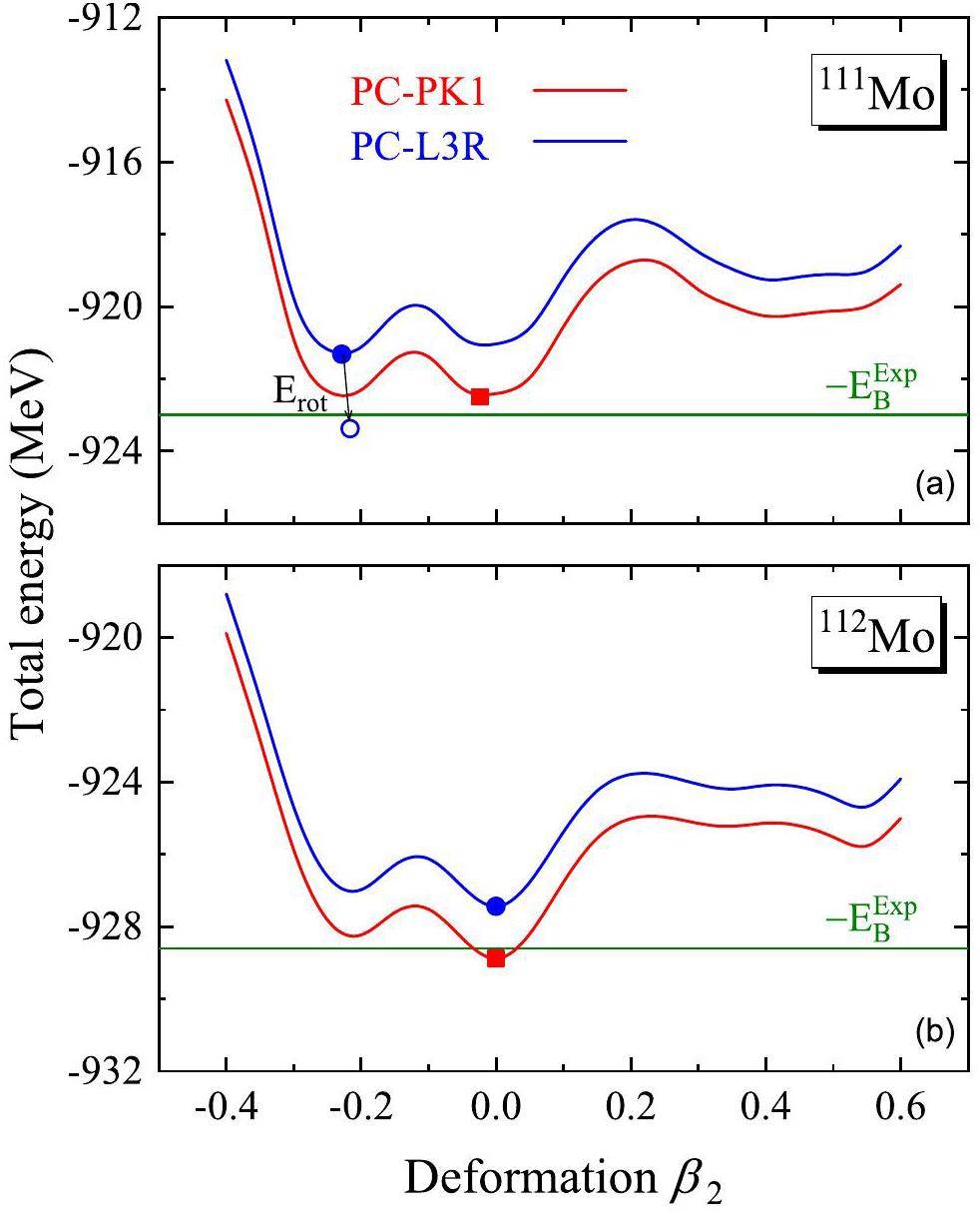
For ¹¹¹Mo in Fig. 7(a), in both PECs from the calculations with PC-PK1 and PC-L3R, there are three minima, that is, one near-spherical minimum and two well-deformed minima. In each curve, the difference between the oblate and near-spherical minima is within 0.25 MeV, whereas the excitation energy of the prolate minimum is approximately 2 MeV. The ground state from the PC-PK1 calculations is the near-spherical minimum with β₂=-0.024, whereas the ground state from the PC-L3R calculations is the oblate minimum with β₂=-0.216. This corresponds to the large $\text{Δ}{\beta }_2$ in Fig. 6(c). In addition, for the near-spherical ground state from PC-PK1, the rotational correction energy is taken as zero. For the well-deformed ground state from PC-L3R, the rotational correction energy is $E_{\text{r}ot}=-2.06$ MeV, and the result becomes more deeply bound than that from PC-PK1. Finally, the binding energies from the PC-PK1 and PC-L3R calculations are similar, both reproducing the experimental value for ¹¹¹Mo.

For ¹¹²Mo, the shape of the PEC is similar to that for ¹¹¹Mo, still exhibiting three minima. However, here the ground states from both PC-PK1 and PC-L3R are the spherical minima, while the excitation energies of the oblate and prolate minima are about 0.5 and 3 MeV, respectively. In both results from PC-PK1 and PC-L3R, the significant differences in deformations and the small differences in total energies indicate the shape coexistence in ^111,112Mo.

Summary

In this study, the newly measured masses for 296 nuclides from 40 references published between 2021 and 2024, subsequent to the release of the latest Atomic Mass Evaluation, were compiled. Although most of the new data are consistent with AME2020, for 73 nuclides, the deviations exceed the uncertainties. The new masses were calculated using the DRHBc theory with the PC-PK1 and PC-L3R density functionals and compared with the results from RMF+BCS calculations with TMA and Skyrme HFB calculations with SLy4, SV-min, and UNEDF1. The DRHBc calculations with both PC-PK1 and PC-L3R reproduce the data fairly well, with an RMS deviation below 1.5 MeV, demonstrating a clear advantage over other models in mass predictions. Taking the even-Z nuclei with $70\le Z\le 80$ as examples, the DRHBc calculations provide not only an overall high accuracy but also a robust description of the isospin dependence for nuclear masses. A quantitative comparison between PC-PK1 and PC-L3R results for the 296 nuclides shows that their differences in binding energies are generally below 1.0 MeV, those in RMS matter radii within 0.008 fm, and those in quadrupole deformations within 0.01. The largest discrepancies were found in ¹¹¹Mo, attributed to the competing oblate and near-spherical minima with similar energies in the potential energy curve. The significant differences in deformation and the small differences in energies between the two minima indicate the possible shape coexistence in ¹¹¹Mo and ¹¹²Mo.

These results strengthen confidence in the DRHBc predictions of nuclear masses. Continued progress would benefit from additional experimental mass measurements and establishment of a complete DRHBc mass table with PC-PK1. Moreover, large-scale DRHBc calculations using PC-L3R are highly promising. To further improve the mass description, the inclusion of triaxial deformation, rigorous treatment of nuclear magnetism, and beyond-mean-field extensions such as collective Hamiltonian approaches are being pursued within the DRHBc framework.