I. INTRODUCTION
An electric power source can be created by exposing a p–n junction to radioactive particles, such as alpha and beta sources. Becker and Kruppke (1937) observed that electron-hole pairs (EHPs) are produced in selenium semiconductor materials through cathode electron bombardment [1]. This phenomenon is called the electron-voltaic effect, which Ehrenberg and Billington studied. Rappaport (1953) found that isotope decay beta particles also produce EHPs in p–n junction devices and called this phenomenon the betavoltaic effect [2]. The concept of an alphavoltaic battery was proposed by Pfann and Roosbroeck in 1954 [3]. Thereafter, many studies investigated betavoltaic [4-14] and alphavoltaic [15] batteries.
Radiation sources used in previous studies on nuclear batteries include cathode electron tubes, artificial or natural radioisotopes, and particle accelerators. Research on nuclear batteries has mostly focused on solid, liquid, or gaseous radioisotopes from the earth. An interbedded epitaxial silicon betavoltaic based on an artificial radioisotope 63Ni was discussed through experiments and a MCNP5 simulation [11]. The theoretical maximum efficiencies of betavoltaics that utilize artificial radioisotopes 35S, 90S, and 90Y were studied by employing Monte Carlo codes, including Geant4, Penelope, and MCNPX [13]. A customized low-energy electron accelerator was used to characterize the performance of betavoltaics by varying the electron beam energy and electron beam flux [14]. In space, radioactive particles, such as protons, electrons, and helium particles, emit a large amount of energy. These particles have great potential as energy sources for nuclear batteries. However, little is known about the use of the energy of these space radiation particles.
This paper presents a concept of space radiation-voltaic batteries (SRVBs) based on various space radiation environments, including the earth radiation belt ( ERB), solar proton event ( SPE), and galactic cosmic rays ( GCRs). SRVBs convert the kinetic energy of particles in space directly into electric power. This study analyzes the energy deposition, structural optimization design, and output performance of SRVBs through the Monte Carlo toolkit Geant4 and theoretical formulas. The results demonstrate that SRVBs based on ERB and SPE are high-potential candidates for space power sources.
II. METHODS
A silicon p–n junction, which has low cost and mature processing technology, was used as the energy conversion unit (ECU) of SRVBs. The AE-8/AP-8 model in ERB and the data of SPE in 1972 were employed in this study. Due to the particles’ high-flux proportion, proton and helium particles were simulated in the radiation environment of GCR. The GCR model is CREME 86.
To ensure that the ECU is located in the area of maximum energy deposition, silicon film computation models combined with various space radiation environments were constructed (Fig. 1a). The transport of proton, electron, and helium particles in silicon semiconductor materials was then simulated with the use of the Monte Carlo toolkit Geant4 in the three space radiation environments. Based on the simulation results, SRVB computation models (Fig. 1b) were constructed. The study assumed that all energy deposited onto the ECU was used to produce EHPs despite the ECU radiation damage caused by high-energy particles.
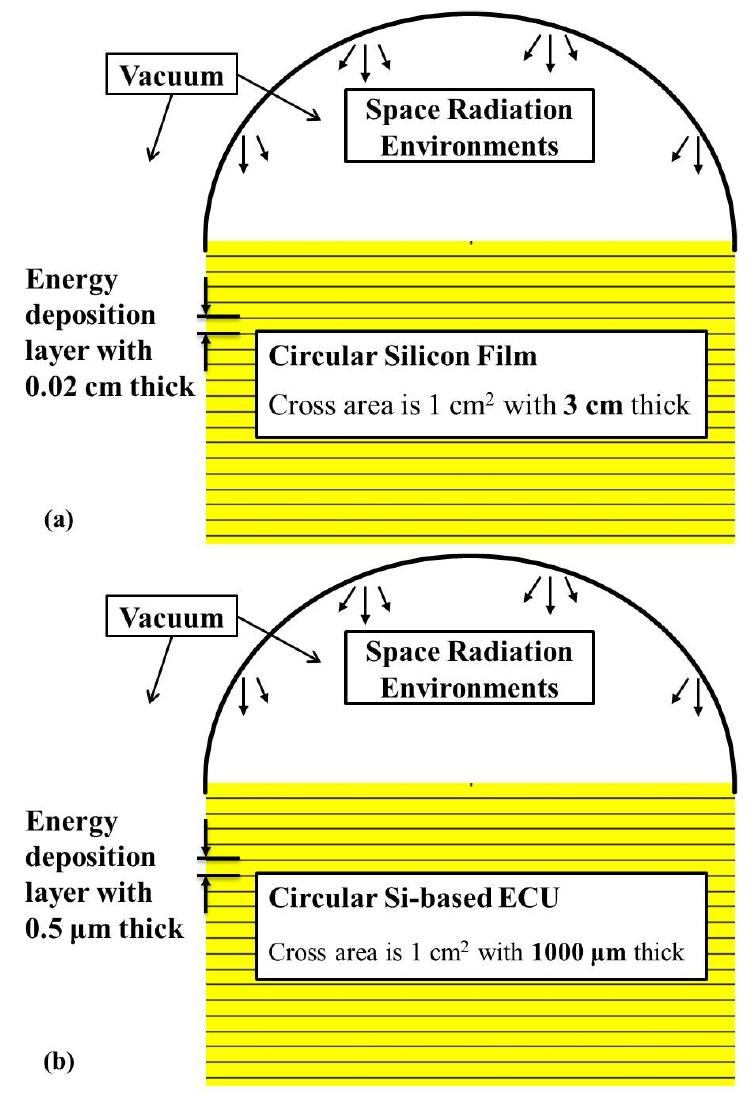
In SRVB computation models, the 1 000 μm thick Si-based ECU was segmented into 2 000 energy deposition layers of thickness 0.5 μm. One or several energy deposition layers in the incident surface of the Si-based ECU represent a heavily doped region, that is, the junction depth. Moreover, the other energy deposition layers represent a lightly doped substrate region.
The radiation-generated current density of the SRVB, that is, its short-circuit current density (JSC), was calculated by collecting EHPs from the energy deposition distribution on each layer of the ECUs based on ERB, SPE, and GCR. The collection ratio equation of EHPs can be written as follows [16]:
where CE(n) is the collection ratio of the EHPs of the nth energy deposition layer in the SRVB computation model, L is the minority carrier diffusion length (in μm), and xn is the distance between the position of the nth layer of Si and the depletion region (in μm). If the collection ratio of the electron hole pairs in the depletion region is 100%, JSC can be expressed as follows:
where q indicates the quantity of electric charge of an electron or a hole (in C), S indicates the cross section of the ECU (in cm2), Eehp is the average energy required to generate an EHP (in MeV; the Eehp of Si is 3.640×10-3 MeV), E(n) is the energy deposited onto the nth layer of the silicon ECU by particles in the three space radiation environments (in MeV), the subscript k is the number of types of particles, and Φk is the total flux of the kth type of particles (in cm-2s-1). In ERB, the fluxes of electron and proton particles are 4.6480×107 and 6.3873×107 cm-2s-1, respectively. In SPE, the flux of proton particles is 2.4506×1010 cm-2s-1. In GCR, the fluxes of proton and helium particles are 2.916 and 1.131 cm-2s-1, respectively.
With the use of MATLAB, other parameters of the SRVB were obtained according to empirical formulas. These parameters include the optimized doping concentration of the p-type (NA) and n-type regions (ND), open-circuit voltage (Voc), maximum power density (Pm), fill factor (FF), and conversion efficiency (η). The calculations made in the current study are similar to those in our other papers [9-11].
III. RESULTS AND DISCUSSION
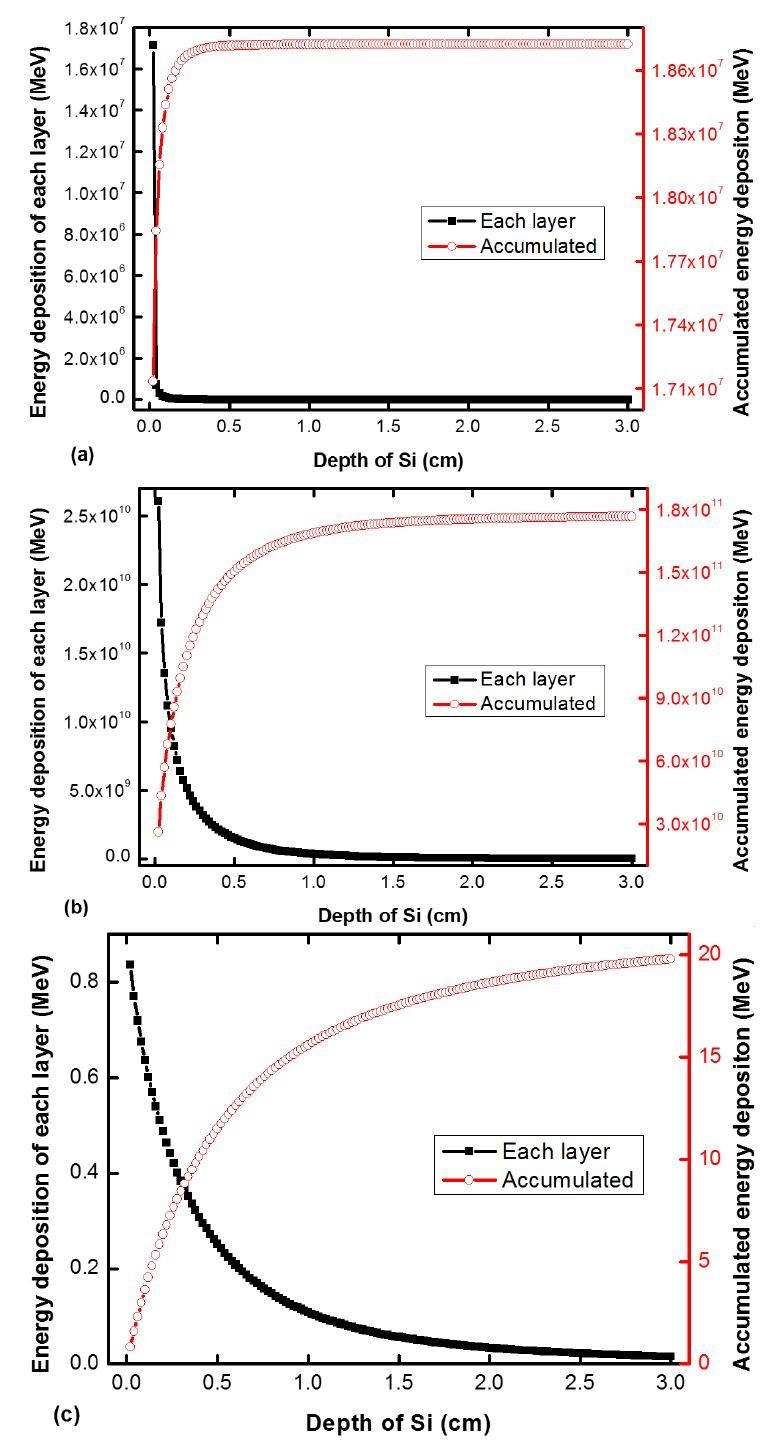
Figure 2 shows that the silicon film irradiated by ERB is the fastest one to achieve maximum accumulated energy deposition, whereas the film irradiated by GCR is the slowest one. Many particles in ERB are distributed primarily in the low-energy section, while many particles in GCR are distributed principally in the high-energy section. The energy spectrum of ERB is narrower than that of GCR. Thus, energy from ERB is more easily and quickly deposited onto the shallow part of the silicon film than that from GCR. However, energy deposition monotonically decreases as the depth in the silicon film in all space radiation environments increases. Consequently, the ECUs were designed to accept irradiation directly from ERB, SPE, and GCR (Fig. 1b). Energy deposition distribution in the ECU based on ERB, SPE, and GCR is obtained according to the SRVB computation model (Fig. 3). The trend of energy deposition distribution in the ECU is similar to that in the 3 cm-thick silicon film, as expected.
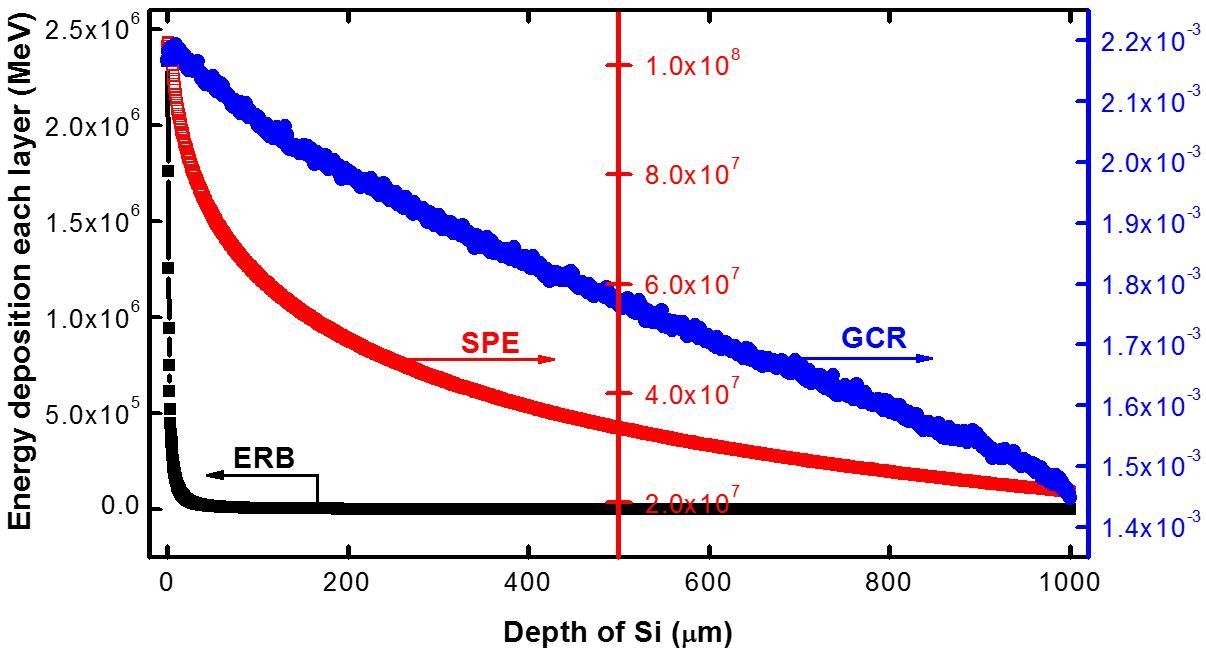
The conversion efficiency of the nuclear battery is associated with the flux of radiation particles. Generally, a high flux of particles increases battery efficiency. Optimization results (Table 1) show that the SRVBs in ERB and SPE have high maximum output power density. However, the maximum power density and conversion efficiency of the SRVB based on GCR are only 3.844×10-17 W/cm2 and 6.713×10-3%, respectively. The results show that the energy of GCR is difficult to collect and that, by contrast, SRVBs based on ERB and SPE are high-potential space power sources. In addition, the efficiencies of SRVBs based on ERB and GCR slowly decrease as the junction depth increases, whereas that of SRVB based on SPE gradually increases. This increase is associated with the energy deposition distribution in the ECU. This result suggests that the junction depth of SRVBs in ERB and GCR should be shallow and that of SRVB irradiated by SPE should be deep. The recommended junction depths of SRVBs based on ERB, SPE, and GCR are 0.5, 3.0, and 0.5 μm, respectively.
| Optimized parameters | Junction depth (μm) | NA(cm-3) | ND(cm-3) | JSC(Acm-2) | VOC(V) | Pm(Wcm-2) | FF (%) | η (%) |
|---|---|---|---|---|---|---|---|---|
| ERB | 0.5 | 4.467×1018 | 1.000×1016 | 7.299×10-7 | 0.3664 | 2.022×10-7 | 75.61 | 6.850 |
| 1.0 | 1.955×1018 | 8.913×1015 | 7.320×10-7 | 0.3642 | 2.013×10-7 | 75.51 | 6.819 | |
| 1.5 | 1.259×1018 | 8.913×1015 | 7.311×10-7 | 0.3634 | 2.005×10-7 | 75.47 | 6.792 | |
| 2.0 | 8.913×1017 | 7.943×1015 | 7.333×10-7 | 0.3615 | 1.998×10-7 | 75.38 | 6.768 | |
| 2.5 | 6.310×1017 | 7.943×1015 | 7.333×10-7 | 0.3605 | 1.992×10-7 | 75.34 | 6.747 | |
| 3.0 | 5.623×1017 | 7.943×1015 | 7.322×10-7 | 0.3602 | 1.986×10-7 | 75.32 | 6.727 | |
| SPE | 0.5 | 1.259×1019 | 8.913×1013 | 2.649×10-3 | 0.5191 | 1.112×10-3 | 80.86 | 8.947 |
| 1.0 | 5.623×1018 | 8.913×1013 | 2.650×10-3 | 0.5190 | 1.112×10-3 | 80.86 | 8.949 | |
| 1.5 | 3.548×1018 | 8.913×1013 | 2.651×10-3 | 0.5190 | 1.112×10-3 | 80.86 | 8.950 | |
| 2.0 | 2.512×1018 | 8.913×1013 | 2.651×10-3 | 0.5190 | 1.113×10-3 | 80.86 | 8.952 | |
| 2.5 | 1.778×1018 | 8.913×1013 | 2.652×10-3 | 0.5190 | 1.113×10-3 | 80.85 | 8.954 | |
| 3.0 | 1.413×1018 | 8.913×1013 | 2.653×10-3 | 0.5189 | 1.113×10-3 | 80.85 | 8.956 | |
| GCR | 0.5 | 1.000×1020 | 1.122×1015 | 8.659×10-14 | 0.001523 | 3.844×10-17 | 29.16 | 6.713×10-3 |
| 1.0 | 7.079×1019 | 1.122×1015 | 8.660×10-14 | 0.001522 | 3.843×10-17 | 29.16 | 6.711×10-3 | |
| 1.5 | 4.467×1019 | 1.122×1015 | 8.662×10-14 | 0.001521 | 3.842×10-17 | 29.16 | 6.709×10-3 | |
| 2.0 | 3.162×1019 | 1.122×1015 | 8.665×10-14 | 0.001520 | 3.841×10-17 | 29.17 | 6.707×10-3 | |
| 2.5 | 2.512×1019 | 1.122×1015 | 8.667×10-14 | 0.001519 | 3.840×10-17 | 29.17 | 6.706×10-3 | |
| 3.0 | 1.995×1019 | 1.122×1015 | 8.670×10-14 | 0.001518 | 3.839×10-17 | 29.17 | 6.704×10-3 |
In space, radiation particles may have low or high energies. These particles run in all directions. Therefore, thin ECUs have difficulties in absorbing all the energy of radiation particles. Table 2 shows that only a small amount of energy emitted by the space radiation environments, especially by GCR, is deposited onto the ECUs. Energy is mostly escaped from the other angle of the ECU, penetrated the ECU, or scattered from the surface of the ECU. Adding the number of ECUs and optimizing the structure of the ECU surface ensures that all energy from the space radiation environment could be deposited onto the ECU. Under these conditions, the maximum power density of SRVBs with the recommended junction depths based on ERB, SPE, and GCR are 8.371×10-7, 1.865×10-2, and 4.437×10-11 W/cm2, respectively.
| Space radiation environments | ERB | SPE | GCR |
|---|---|---|---|
| Total power (W) | 1.222×10-5 | 2.082×10-1 | 6.609×10-9 |
| Deposition in ECU (W) | 2.952×10-6 | 1.243×10-2 | 5.727×10-13 |
| Ratio to deposition in ECU (%) | 24.17 | 5.97 | 0.01 |
IV. CONCLUSIONS
In this paper, we propose SRVBs based on ERB, SPE, and GCR. The optimization output performance and corresponding parameter values of SRVBs at different junction depths were obtained at 300 K in ERB, SPE, and GCR. SRVBs in ERB and GCR should have shallow junction depths, whereas an SRVB irradiated by SPE should have a considerable junction depth. Calculation results suggest that SRVBs based on ERB and SPE are high-potential candidates for space power sources. To improve the conversion efficiency and service lifetime of SRVBs, wide band-gap semiconductor materials with high-radiation hardness, such as GaN and nano-semiconductors, may be used as alternatives in space power applications. However, further research is required to examine the dependence of SRVB output performance on temperature and radiation-induced damage. The results of this study could help raise awareness on the use of the energy from space raidiation particles and facilitate the research of SRVBs.


