I. INTRODUCTION
Output stability monitoring of medical LINAC is an important aspect of radiotherapy quality assurance. The daily/weekly check for output stability of medical LINAC currently in clinical practice was carried out according to the procedures of the International Atomic Energy Agency (IAEA) report No. 227 [1]. The dose difference of the iso-center point at different time was adopted to evaluate the output stability. However, with the clinical implementation of new dose measurement equipment, point dose showed the drawback that it could not reflect the planar dose output stability of the LINAC, so it had no statistical significance. This was definitely the case of Intensity-modulated Radiotherapy (IMRT), in which the planar dose evaluation for segment with small weight is of great importance. The gamma method introduced by Low Daniel A et al [2] was the most accepted approach and had been widely used by many groups [3-5]. In this paper, a modified evaluation method of the stability of medical LINAC was proposed. The gamma method was adopted to do planar dose verification and the output stability of LINAC was evaluated. This research was a part of Advanced/Accurate Radiotherapy System (ARTS) [6-12], in precision radiation treatment planning and quality assurance system project, developed by FDS Team [13-19].
II. MATERIALS AND METHODS
A. LINAC and MatriXX
The measurements were conducted using photon beam from XHA600D (SHINVA, China)(see Fig. 1(a)). The LINAC could produce 6 MV X-rays. Using the three-dimensional (3D) Blue Water Phantom (IBA, Germany), the maximum dose depth was detected to be 1.5 cm under water. The I’mRT MatriXX (IBA, Germany)(Fig. 1(b)) device consists of a two-dimensional (2D) array of ionization chambers. There are 1020 vented parallel plate ionization chambers on the array detector, arranged in 32 × 32 grid. The center-to-center distance of chamber is 7.62 mm, with an active area of 24 cm × 24 cm. The MatriXX was positioned using the LINAC field light. The beam buildup of MatriXX was about 3 mm. On the MatriXX surface, 30 cm × 30 cm RW3 Solid Water (Sun Nuclear, America) layers served as beam buildup with a thickness of 1.2 cm. The LINAC gantry angle was set to be 0 degree, and the source-to-surface distance (SSD) was 100 cm.

B. Calibration and measurement
1. Calibration
As recommended by international standards[1], under the radiation of SSD=100 cm and the field size is 10 cm × 10 cm, the temperature T=24.6°C, the pressure P=999.7Pa, the LINAC dosimeter should be modulated the output of 100 MU (MU: Monitoring Units) proportional to 100 cGy using the cylindrical ionization chamber with 0.125 cm3 air volume (PTW TM 31010 S/N03422) at the maximum dose depth (1.5 cm under the solid water for 6 MV photon).
The MatriXX was put under the measurement condition for 30 min in order to do the background correction. The solid water with 1.2 cm thickness was added to the surface (the device had a beam buildup of 3 mm). At each MU level, the average value was calculated for the center four pixels. The cylindrical ionization chamber was used to measure the absolute dose. After that the calibration scaling factor k was calculated and saved in the software of Omni I’m RT.
2. Data measurement
Under the radiation measurement condition (SSD=100 cm, field size: 10 cm × 10 cm), after LINAC warming up for 30 minutes (marked as period 1), different weight were irradiated on 1.2 cm solid water with 1 MU, 2 MU, 3 MU, 5 MU, 10 MU, 20 MU, 40 MU, 50 MU, 100 MU, respectively. The planar absolute/relative doses were obtained with MatriXX. For each MU level more than 10 planar doses were collected and the average planar doses were calculated, which was used as the reference data for gamma method. After keeping power on for 8 hours (marked as period 2), the same protocols were adopted and the average planar dose was used as the evaluated data.
With SSD=100 cm, 28 cm × 28 cm field size and 100 MU was preset, the active area of 24 cm × 24 cm (maximum field) was covered to investigate the beam uniformity of LINAC. The flatness and symmetry were key performance indicators of beam dose distribution. According to the International Electrotechnical Commission (IEC) standards, the flatness and symmetry of beam field should be within ±3%. 10 different X axis position and 10 different Y axis position were chosen to verify the flatness and symmetry of the maximum field. Table 1 showed that the flatness and symmetry of all positions were within ±3% and dose distribution was relatively uniform and there was no obvious noise point, which indicated that measured data obtained from MatriXX were reliable and could be used for dose verification.
| FLATNESS | SYMMETRY | |||
|---|---|---|---|---|
| X axis (%) | Y axis (%) | X axis (%) | Y axis (%) | |
| 1 | 102.70 | 101.97 | 100.78 | 100.51 |
| 2 | 102.72 | 101.99 | 100.78 | 100.49 |
| 3 | 102.72 | 101.99 | 100.84 | 100.54 |
| 5 | 102.72 | 102.00 | 100.81 | 100.51 |
| 6 | 102.72 | 102.00 | 100.80 | 100.52 |
| 7 | 102.69 | 101.97 | 100.77 | 100.46 |
| 8 | 102.71 | 101.95 | 100.80 | 100.49 |
| 9 | 102.69 | 101.97 | 100.79 | 100.48 |
| 10 | 102.70 | 101.92 | 100.77 | 100.51 |
C. Gamma (γ) method
The gamma method was mainly used to do the dose verification and analyze the difference between the reference data and the evaluated data. Expressed in formula, it could be read as:
ΔD: Dose difference between the reference data and evaluated data.
Δr: Spatial distance of the reference data and evaluated data.
δγ0: Distance to agreement tolerance, usually preset 3 mm/2 mm in clinical practice;
δD0: Dose difference tolerance, usually preset 5%/3% in clinical practice.
The pass-fail criteria for gamma index for certain point was as following:
when γ(r) ࣘ 1, pass,
when γ(r)>1, fail.
Then γ(r) values of all evaluated data consisted of thedistribution. If the value was less than or equal to 1, the point was considered to pass the verification. The pass rate was obtained through the pass points number divided by the total number of the evaluated data. If the pass rate was more than 95%, it represented the good agreement of two planar dose distributions [20, 21]. Since the resolution of the evaluated data was limited and gamma method required no less than 1 mm data resolution, we used the tool of Microsoft VC++ to realize the dose interpolation and dose comparison according to the formula (1) in this paper. The tolerance of 3%/3 mm was chosen. The flowchart of the program realization was just as Fig. 2.
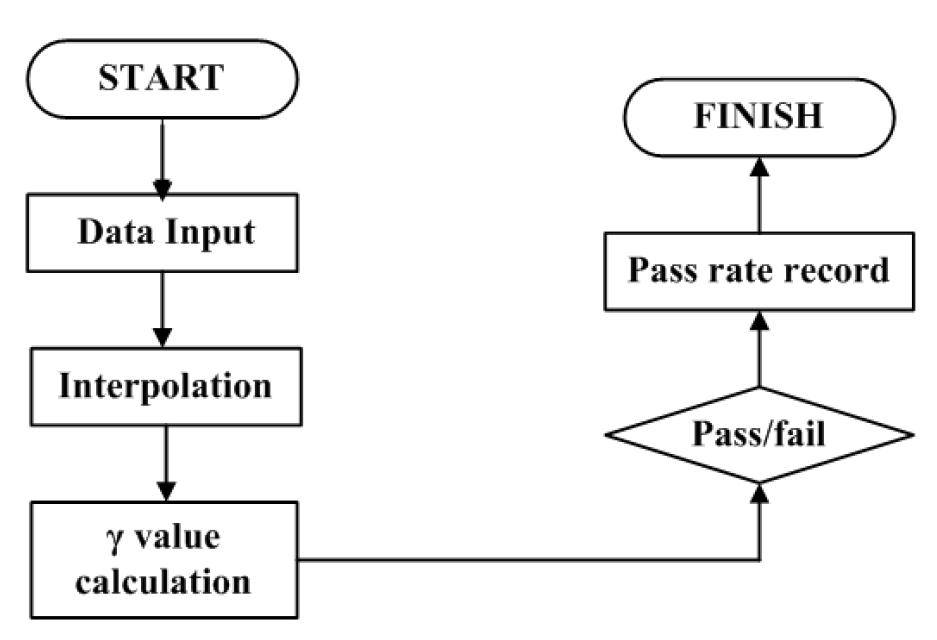
Step 1: input the data exported from Omni I’m RT with the format ".txt".
Step 2: interpolate the evaluated data making the data resolution from 32×32 to 320×320.
Step 3: calculate the value for each point in the evaluated data.
Step 4: record the pixel number with the value less than or equal to 1.
Step 5: calculate the pass rate of the evaluated data.
III. RESULTS
A. LINAC output stability for different MU level
Under the radiation condition of SSD=100 cm, 10 cm×10 cm field size, temperature T=24.6°C, pressure P=999.7 Pa, calibration factor ND=1.026, the 100 MU output of LINAC was modulated proportional to 100 cGy. The cylindrical ionization chamber ( "pinpoint" chamber) was adopted to measure the output dose at the position under 1.5 cm of solid water phantom. Table 2 showed the mean readout of 10 times and the output difference for each MU level.
| MUa | Data1 b(cGy) | Data2 c(cGy) | Error 1d(%) | Error 2e(%) | Δerrorf(%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| MAX | MIN | MEAN | MAX | MIN | MEAN | ||||
| 1 | 1.536 | 1.406 | 1.459 | 1.458 | 1.388 | 1.418 | 45.8 | 41.8 | 5.10 |
| 2 | 2.582 | 2.544 | 2.562 | 2.548 | 2.414 | 2.449 | 28.1 | 22.4 | 5.65 |
| 5 | 5.572 | 5.526 | 5.542 | 5.501 | 5.397 | 5.415 | 10.84 | 8.30 | 2.54 |
| 10 | 10.64 | 10.68 | 10.658 | 10.65 | 10.64 | 10.642 | 6.58 | 6.42 | 0.16 |
| 20 | 20.74 | 20.68 | 20.702 | 20.78 | 20.73 | 20.756 | 3.51 | 3.78 | 0.27 |
| 30 | 31.03 | 30.78 | 30.80 | 31.04 | 30.76 | 30.894 | 2.67 | 2.98 | 0.30 |
| 50 | 50.92 | 50.84 | 50.89 | 51 | 50.93 | 50.97 | 1.78 | 1.94 | 0.16 |
| 80 | 81.16 | 80.04 | 80.9 | 81.06 | 81.19 | 81.1 | 1.125 | 1.375 | 0.25 |
| 100 | 101.3 | 101 | 101.16 | 101 | 101 | 101 | 1.16 | 1.0 | 0.16 |
After MatriXX calibrated, the planar relative dose signal could be collected using the movie mode (collected time = 500 ms) and exported as document with the format ".txt". The scaling factor k gained from absolute dose calibration was multiplied by the relative dose distribution, then we could get the planar absolute dose. The planar dose obtained at period 1 was input into the gamma method program as the reference data while the data at period 2 as the Evaluated Data. Later the pass rate was calculated. Table 3 showed the absolute dose comparison results of two different periods for each MU gradient, and pass means that the dose distribution was similar or thought to be the same, while fail representing there was obvious difference between two dose distributions. The 3%/3 mm tolerance was chosen in this study.
| MU | Pass rate (%) | Pass/Fail |
|---|---|---|
| 1 | 20.83 | Fail |
| 2 | 39.06 | Fail |
| 5 | 64.37 | Fail |
| 10 | 93.03 | Pass |
| 20 | 95.84 | Pass |
| 30 | 97.59 | Pass |
| 50 | 95.32 | Pass |
| 80 | 95.97 | Pass |
| 100 | 100 | Pass |
B. Segment with small MU
In clinical practice, segments were adopted for IMRT and every fraction dose was usually optimized to be several segments with different weight. In this paper the segment with small MU output stability of LINAC was investigated. As in the Table 4, although the measured data of relative dose for 2 MU showed good uniformity, when multiplied by the scaling factor k (0.29), the absolute dose distribution was obtained, then the relative error of output dose was calculated. [(24 × 0.29)-2]/2 × 100%=248%
| X | -4.191 | -3.429 | -2.667 | -1.905 | -1.143 | -0.381 | 0.38 | 1.142 | 1.904 | 2.666 | 3.428 | 4.19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y | ||||||||||||
| -4.191 | 23 | 24 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 14 | 13 |
| -3.429 | 24 | 24 | 24 | 23 | 23 | 24 | 23 | 23 | 24 | 24 | 23 | 23 |
| -2.667 | 24 | 24 | 24 | 23 | 23 | 24 | 23 | 23 | 24 | 24 | 23 | 23 |
| -1.905 | 24 | 24 | 24 | 23 | 24 | 24 | 23 | 23 | 24 | 24 | 24 | 23 |
| -1.143 | 24 | 24 | 24 | 23 | 24 | 24 | 23 | 23 | 24 | 24 | 23 | 23 |
| -0.381 | 24 | 24 | 23 | 23 | 23 | 24 | 23 | 23 | 24 | 24 | 24 | 23 |
| 0.38 | 23 | 23 | 24 | 24 | 23 | 23 | 24 | 23 | 23 | 24 | 24 | 23 |
| 1.142 | 23 | 23 | 24 | 24 | 23 | 23 | 24 | 24 | 23 | 24 | 23 | 22 |
| 1.904 | 23 | 23 | 24 | 24 | 23 | 23 | 23 | 23 | 23 | 24 | 23 | 22 |
| 2.666 | 23 | 23 | 24 | 24 | 23 | 23 | 24 | 23 | 23 | 24 | 23 | 22 |
| 3.428 | 23 | 23 | 24 | 24 | 23 | 23 | 23 | 23 | 23 | 24 | 23 | 22 |
| 4.19 | 22 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 23 | 22 |
It was obvious that segment with small MU was fluctuated from the calibrated dose greatly. However, this was just the situation of small MU segment. From the results in Table 3 it could be concluded that when the segment with small weight the dose obtained failed the dose comparison, for example, 1 MU, 2 MU and 5 MU failed the comparison. When the segment weight was above 10 MU, the dose error was accepted.
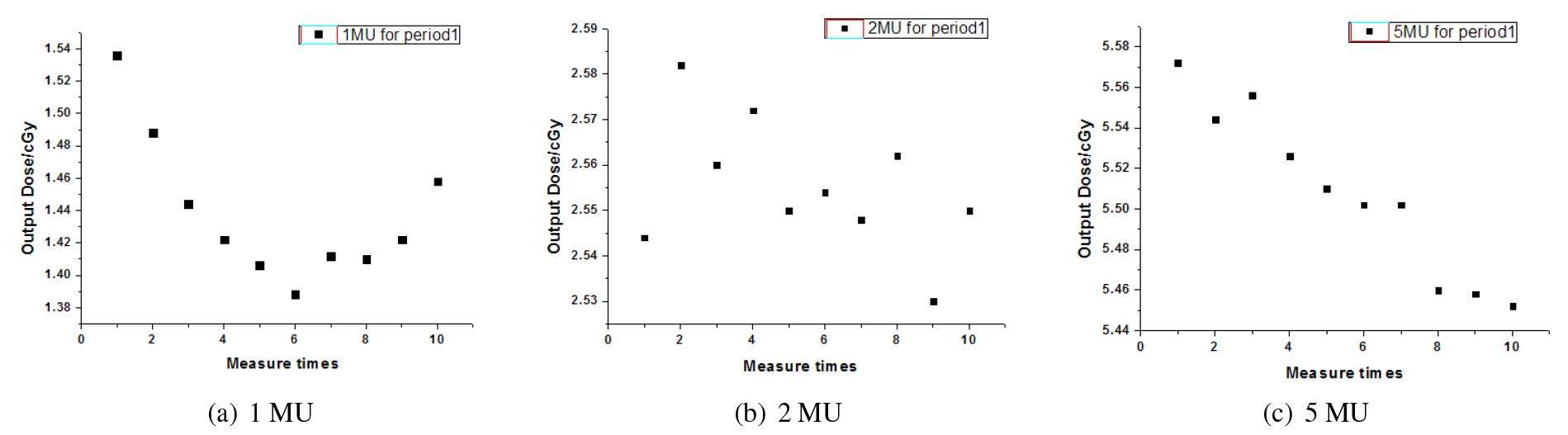
The readout data of cylindrical ionization chamber was used to verify the result, as in the Fig. 3, X axis represented the measure times and Y axis represented readout data. Period 1 was the time after LINAC warming up. It is obviously that the output weight fluctuated severely under 10 MU, and deviated from the calibrated data. The same trend of instability was also found at period 2. It inferred that small MU related to IMRT segment under 10 MU in reverse optimization should not be adopted in clinical.
IV. DISCUSSION AND CONCLUSION
An improved evaluation method of the output stability of medical LINAC based on planar dose combined with gamma method was proposed in this study. The dose in 10 cm × 10 cm field size was chosen to do the gamma analysis to avoid outside field dose interference.
The output stability analysis of medical LINAC using the tool of two-dimensional ionization chamber yielded similar results to that of using cylindrical ionization chamber. The results indicated that the method is feasible and efficient. Unlike the recommendation of IAEA-TRS277, in which the LINAC output stability is evaluated only when the weight was 100 MU, the method proposed in this study could not only be used to evaluate the LINAC output stability with point dose difference under any MU level, it could reflect the stability of certain planar dose with statistical meaning. The study also showed that when the segment weight was under 10 MU related to IMRT the output is instability and the error would be introduced.
The MatriXX measurement device has dose uniformity correction, especially for low dose, but the planar dose of small MU deviated from the real LINAC output dose distribution. The software of Omni I’m RT had gamma analysis and simple linear interpolation, however, we used Microsoft Visual C++ to realize bilinear interpolation method to obtain the evaluated data with high data resolution. The interpolated pixel data was calculated from the contribution of the pixels value around. In further study, the interpolation method precision would be compared, and long time (for example a year/month) output stability of LINAC should be investigated to get a better acknowledge of the LINAC performance.


