I. INTRODUCTION
The radiation protection of proton accelerators is a critical issue to the radiation safety of both the work personnel and the public [1-3]. One particular aspect of proton accelerators is the induced radioactivity, given that the intense primary proton beams, secondary neutron beams, and scattered particles can activate the materials of the accelerator components [4-8]. From the perspective of radiation safety, quantitatively evaluating the radioactivity induced by different materials is important. To estimate the induced radioactivity, a Monte Carlo simulation or some method of theoretical analysis[9] may be adopted.
FLUKA [10, 11] is a general-purpose Monte Carlo code that calculates the particle transport and their interactions with matter; it is applicable in an extended range of applications from proton and electron accelerator shielding to target design, calorimetry, activation, dosimetry, detector design, accelerator-driven systems, cosmic rays, neutrino physics, radiotherapy, and so on. FLUKA is widely used in estimating the induced radioactivity of the components of accelerators in the air of the tunnel or cooling water for the radiation protection of the personnel. Some benchmark experiments have been conducted to verify the accuracy of FLUKA in calculating the induced radioactivity of high-energy proton and electron accelerators [12-14]. However, studies that compare the FLUKA simulated results and experimental data of low-energy proton accelerators remain scarce.
Studying the induced radioactivity of low-energy proton accelerators is important, given the wide range of their applications. For example, medical proton accelerators that produce radioactive medicine have typical energy rates between 10 Mev and 18 MeV.
In the present study, the cross section of 63Cu (p, n) 63Zn and 65Cu (p, n) 65Zn in a Cu target at an 11 MeV proton accelerator was investigated through an activation experiment and a Monte Carlo simulation. Cu was chosen because it is a frequently used material in the structure of proton accelerators and is a relatively pure material compared with others. 63Zn and 65Zn, which are produced by the 63Cu (p, n) 63Zn and 65Cu (p, n) 65Zn reactions, respectively, were also investigated because they are two most important isotopes generated in the Cu target.
The measured results and the corresponding data simulated using FLUKA were compared to verify the accuracy of FLUKA at a low-energy range for proton accelerators.
II. METHODS
The activation analysis method, which originated in the 1930, is widely used in many fields[15-20]. The method is described in the subsequent sections.
Suppose a thin target sample with element N1 is placed in the homogeneous flux of a proton beam. The incidence protons result in nuclear reaction N1(p,n)N2. The cross section σ is expressed as
where λ is the decay constant of the activated nuclei; I is the current of the incident beam (i.e., incident particle counts in unit time s-1); nd is the nuclei number of the target with thickness d, cm-2, and nd is given by
where ρ is the target density in g/cm3; m is the atomic mass of the target material, and y is the quantity of the element.
In the experiment, Nirr is derived using the following formula:
where t1 is the cooling time after the irradiation ends, tdecay is the time during the activity measurement, and Ndecay is the number of decays measured in the radioactive nuclei.
III. EXPERIMENT
A. Target Properties
The Cu targets used in the experiment had the shape of a disc with a diameter of 1.7 cm and thickness of 30 μm, according to the precision requirements of the national standard. The major properties of the targets are listed in Table 1. Three Cu targets were used: one for the pre-test to identify the test procedures well and two for the cross section measurements, labeled as samples 1 and 2.
| Isotope | Atomic percent(%) | Daughter | Half-life |
|---|---|---|---|
| 63Cu | 69.345 | 63Zn | 38.47 min |
| 65Cu | 30.365 | 65Zn | 244.2 days |
B. Irradiation of the targets
The targets were irradiated using RDS 111-type proton cyclotron. The proton energy was 11 MeV, and the diameter of the beam spot was less than 2 mm. The range of the 11 MeV proton in copper was approximately 386.5 μm, which was much larger than the target thickness. The beam intensity was easy to adjust and measure using a Faraday cup, and was set as several μA during the experiment. The irradiation time for each sample was 4 s and was controlled by manually operating the control software of the accelerator.
Figure 1 shows that the beam was defined by a collimator. The incident beam intensity was measured with a Faraday cup mounted directly after the target. The stability of the beam intensity was monitored with a current integrator. The corresponding irradiation intensities for samples 1 and 2 were 2.66 and 3.02 μA, respectively.

C. Measurement of the induced radioactivity
After irradiation, the activated samples were placed in a separate low-background counting area and were measured using a hyperpure germanium detector. The energy resolution (FWHM) of this GEM70-S gamma spectrum detector was 1.90 keV@1332.5 keV. The energy spectrum data were obtained through 8192 channels of a digital spectrometer (DSPEC Plus). The entire system was calibrated using the virtual calibration software Gamma Vision 32 just before the measurement. The detection efficiencies for different photon energies are shown in Fig. 2.
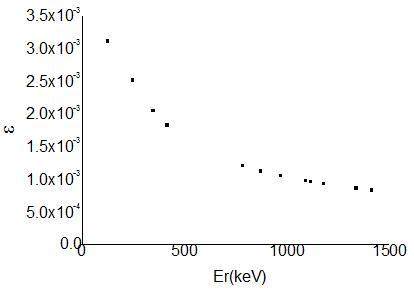
Given the statistical error requirement for the energy spectrum measurement, approximately 1.5 h was taken to measure the decay spectrum of 63Zn, and approximately 24 h for that of 65Zn. Another reason for this difference is because the half-life of 63Zn is shorter (38.5 minutes) than 65Zn (243.7 days). The activities of 63Zn and 65Zn at the stoppage time were obtained from the product of and Nirr, where Nirr is calculated using Eq. 3.
Table 2 lists the counting results, detection efficiency, and activities of 63Zn and 65Zn at the stoppage time and their corresponding errors for samples 1 and 2. The errors mainly originated from the statistical errors in counting.
| Photopeak (keV) | Counts | Efficiency (10-3) | Activity (Bq) | Errors (%) | ||
|---|---|---|---|---|---|---|
| Sample 1 | 63Zn | 669.62 | 12916 | 1.33 | 1.38 ×106 | 2.93 |
| 65Zn | 1115.55 | 17731 | 4.51 | 1.14 ×102 | 2.82 | |
| Sample 2 | 63Zn | 669.62 | 47398 | 1.33 | 1.50 ×106 | 2.62 |
| 65Zn | 1115.55 | 15410 | 3.64 | 1.23×102 | 2.86 |
IV. MONTE CARLO SIMULATION WITH FLUKA
The cross section data in FLUKA were partially obtained from experimental base of the American National Nuclear Data Center[10, 11]. The proton and neutron inelastic cross sections between 10 and 200 MeV were updated by fitting them to the experimental data. An accurate treatment of the cross-section energy dependence of all the charged particles independent of the step size was introduced at that stage through the fictitious-σ method. The present treatment for the hadron-nucleus cross section was based on a novel approach that combined experimental data, data-driven theoretical approaches, PDG fits, and phase-shift analysis when available.
To compare the measured cross section results and the corresponding data used in the FLUKA code, a detailed Monte Carlo simulation of the experiment was also conducted. The parameters in the simulation were the same as those in the experiment, such as beam energy, geometry, irradiation profile, and so on. The simulation was based on a detailed description of the experimental setup. The samples were defined using their actual size.
The full hadronic cascade was simulated in the experimental setup. Neutrons were transported down to thermal energies, and a threshold of 1 keV was applied to all other hadrons. A number of physical settings were activated; these settings included the request of PEANUT model at all energies, the treatment of coalescence, and the evaporation of heavy fragments. The activities of the radionuclides, 65Zn and 63Zn in the samples, at a certain cooling time were calculated using FLUKA. The cross sections of 65Cu (p, n) 65Zn and 63Cu (p, n) 63Zn used by FLUKA were then deduced using Eq. (1). The error of the cross section was mainly caused by the statistical error in the calculation of the activity, which was 0.1% and 0.2% for 65Zn and 63Zn, respectively. The relative uncertainties of the cross sections of 65Cu (p, n) 65Zn and 63Cu (p, n) 63Zn from the simulation were 0.1% and 0.2%, respectively.
V. RESULTS AND DISCUSSION
A. Uncertainty analysis of the cross section
To analyze the discrepancy between the measured cross section and that from the FLUKA simulation, a detailed uncertainty analysis was conducted on the measurement results. The uncertainty of the cross section data from the FLUKA simulation was mainly due to the statistical error in the calculation.
Equation 1 indicates that the uncertainty in the results originated from the errors in the quantities of the nuclei number of the target (nd), activity at stoppage time (Airr), beam intensity (I), and irradiation time (tirr). The formula is given as
where σ is the cross section, and σσ,
The uncertainties can be classified as follows:
a) Errors in the target manufacture These errors include the thickness, purity, and inhomogeneity of the thin copper foil. According to reference[21, 22], the difference between the quantity of 63Cu and that of 65Cu in natural Cu at different places is small and generally less than 0.2%. Therefore, the influence of isotope abundance can be neglected. Considering that the machining techniques of creating a 30 μm thick Cu target was very mature, the errors attributed to the purity and inhomogeneity of the thin copper foil in the manufacture were negligible compared with the errors of the target thickness.
Therefore, the uncertainty in the target manufacture originated mainly from the uncertainty of the thickness. According to the information provided by the manufacturer, the standard deviation of the thickness was 0.003 mm. The thickness of the Cu foils was 0.03 mm; hence,
b) Uncertainties in the irradiation period These uncertainties include errors of the proton beam energy, irradiation time, and beam intensity. The beam energy of RDS 111-type proton cyclotron was 11 MeV, and the uncertainty of the energy was found to be negligible according to the measurement results provided by the accelerator control department. As previously mentioned, the irradiation time for each sample was 4 s, and the error was estimated to be within 0.5 s. The error of the beam intensity was estimated to be 0.01 μA.
c) Uncertainties in the measurement of the induced radioactivity These uncertainties include errors of detection efficiency, counting time, and statistical errors in counting. The virtual calibration software Gamma Vision 32 description for the GEM70-S gamma spectrum detector shows that the uncertainty of the detection efficiency was lower than 2.5%. The uncertainty of the counting time was very small and negligible. The counting results were usually higher than 104 (i.e., the errors of the counting are less than 3% with a confidence interval of 99.7%). According to Eq. 2, the relative uncertainty of Nirr at the confidence interval of 99.7% is given by
where the uncertainty of the decay constant and counting time are neglected.
The activity at the stoppage time of irradiation Airr can be derived using the following formula:
The relative uncertainty of Airr can then be calculated by
The results for the relative uncertainty of Airr are shown in Table 2. The uncertainties of the measured cross section were obtained from the preceding discussion. The results are listed in Table 3.
| 63Cu(p,n)63Zn | 65Cu(p,n)65Zn | |
|---|---|---|
| Sample 1 | 391±63 | 674±108 |
| Sample 2 | 375±60 | 640±102 |
| Average | 383±4 | 657±72 |
| FLUKA | 302±5 | 658±15 |
B. Comparison of cross sections
Table 3 shows a summary comparison of the experimental results, FLUKA simulation results, and some other published data based on different calculation models[22-25] of the cross sections of 63Cu (p, n) 63Zn and 65Cu (p, n) 65Zn reactions. The uncertainties of the results were discussed in detail in the previous sections.
Both the average cross sections and FLUKA simulation are within the range of the various results of several references, where they are obtained from theoretical calculations. For the reaction of 65Cu (p, n) 65Zn, the difference between the cross sections from the experiment and FLUKA simulation was only 1.36%. However, for the reaction 63Cu (p, n) 63Zn, the cross section measured in this work was 25.41% higher than that in the FLUKA simulation.
VI. CONCLUSIONS
Induced radioactivity is one of the essential problems in the radiation protection of proton accelerators. The accuracy of estimating induced radioactivity relies on the precision of the cross section data. Therefore, verifying the related cross section data through simulation and experiment is important, given that the data for low-energy protons are limited. In this work, the cross sections of the reactions of 65Cu (p, n) 65Zn and 63Cu (p, n) 63Zn were studied using both the activation analysis method with irradiation experiment and the detailed Monte Carlo simulation with the FLUKA code. The uncertainties of the results were also analyzed in detail.
The cross sections obtained in this work through both the experiment and simulation are within the range of results of published papers, which were mainly based on theoretical calculations. A slight difference of 1.36% was observed between the cross section of the reaction of 65Cu (p,n) 65Zn from the experiment and that from FLUKA simulation. However, the data obtained through the experiment was 25.4% higher than that of the FLUKA simulation. Given that the benchmark for the FLUKA code at low-energy proton accelerators is limited, the work in this paper provides a reference in this field.


