I. INTRODUCTION
A. Spectrum unfolding problem of multi-sphere neutron spectrometer
Multi-sphere neutron spectrometer, also called Bonner sphere neutron spectrometer [1], was proposed by Bramblett in 1960. Because it has a lot of advantages such as wide neutron energy range covering from thermal neutrons to high energy neutrons, simple response functions, almost isotropic and high sensitivity, multi-sphere neutron spectrometer is widely used in radiation protection applications [2].
Multi-sphere neutron spectrometer mainly consists of a series of different radius polyethylene spheres, with a thermal neutron detector placed in the center of each polyethylene sphere. Different size spheres have different neutron slowing down abilities and different neutron fluence response functions. As the radius increasing, the peaks of the response functions gradually move to high energy area. These response functions can be obtained by using Monte Carlo simulation.
For a given multi-sphere neutron spectrometer, the relationship between neutron spectrum, response functions and detector readings can be expressed by the following mathematical equation [4]:
where Ri(E) represents response function; Φ(E) represents neutron spectrum; Ni represents detector reading; εi represents measurement uncertainty; i represents detector number; n represents quantity of detectors.
This equation shows the spectrum unfolding principle of multi-sphere neutron spectrometer. Without considering εi, the spectrum unfolding problem is solving neutron spectrum Φ(E) under the condition of given response functions Ri(E) and detector readings Ni. Mathematically, the response functions Ri(E) are given in discrete form at many energy groups, and it is not possible to get a continuous function Φ(E) depending on Ri(E) and several detector readings. Therefore, Φ(E) is solved in discrete form with the whole energy range divided into many energy groups as response functions Ri(E), and neutron fluence at each energy group is to be solved. Then the integral equation is rewritten to discrete matrix form as follows:
where Rij(E) represents response matrix; Φj represents neutron spectrum in discrete form; j represents energy group number; m represents the quantity of energy groups.
By now, the spectrum unfolding problem is abstracted to a linear equation group solving problem. There are n equations but m unknown numbers. Unfortunately, the quantity of detectors n is far less than the quantity of energy groups m normally, such as no more than 10 detectors only, but 100 energy groups for the accuracy requirement. With less equations but more unknown numbers, mathematically this linear equation group has many solutions, but there is only one actual neutron spectrum. So it is hard to solve this problem by using common numerical methods.
B. Spectrum unfolding using genetic algorithms
Genetic algorithms [5] simulate the natural biological evolution process, depending on the theory of survival of the fittest, using group search technology, to search for the global optimal solution. Genetic algorithms, which are very suitable for optimization problems, have the characteristics of global optimization and probabilistic search, ensuring that the search space evolves into the state that includes or approaches to the optimal solution. For specific question, there is search space generation t. Depending on the fitness evaluations, some solutions are selected, while some are eliminated, followed by code space genetic operators such as crossover and mutation which simulate chromosome genetic manipulations. At last search space generation t+1 is generated and the process will be repeated from the beginning until the optimal solution is obtained. The process of genetic algorithms is shown as follows:
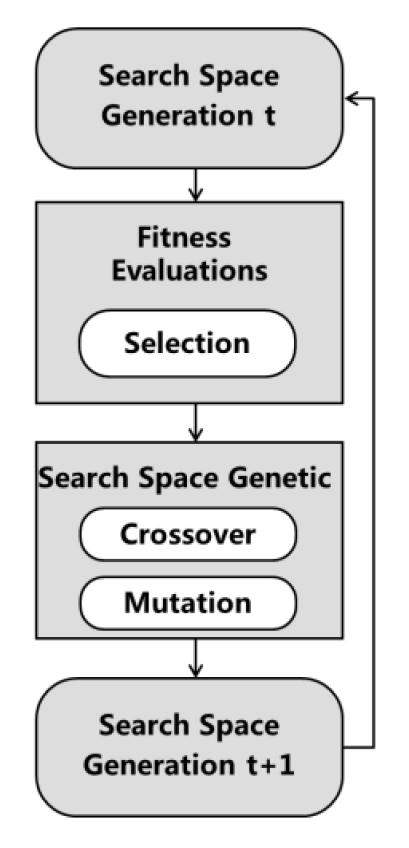
Considering these above characteristics, genetic algorithms are especially suitable for the kind of problems searching for the optimal solution without enough known conditions, so that they were chosen to unfold the neutron spectrum. Freeman developed the genetic algorithm unfolding code UMRGA [6] using multi-seed averaging technique and monoenergetic peak reward technique. UMRGA was tested with the data provided by EURADOS which contains 8 different radius spheres and 47 energy groups. Mukherjee developed BONDI-97 [7] genetic algorithm spectrum unfolding tool operating on Microsoft EXCEL. This paper presented a new spectrum unfolding code using genetic algorithm with combination of several processing strategies including proper fitness function selection, elitism and pseudo-parallel. The unfolding code, which was verified by typical spectra tests and actual experiment, can be successfully applied to multi-sphere neutron spectrometer MNS IL100 which contains 9 different radius spheres and 100 energy groups.
II. METHODS
A. Coding and decoding
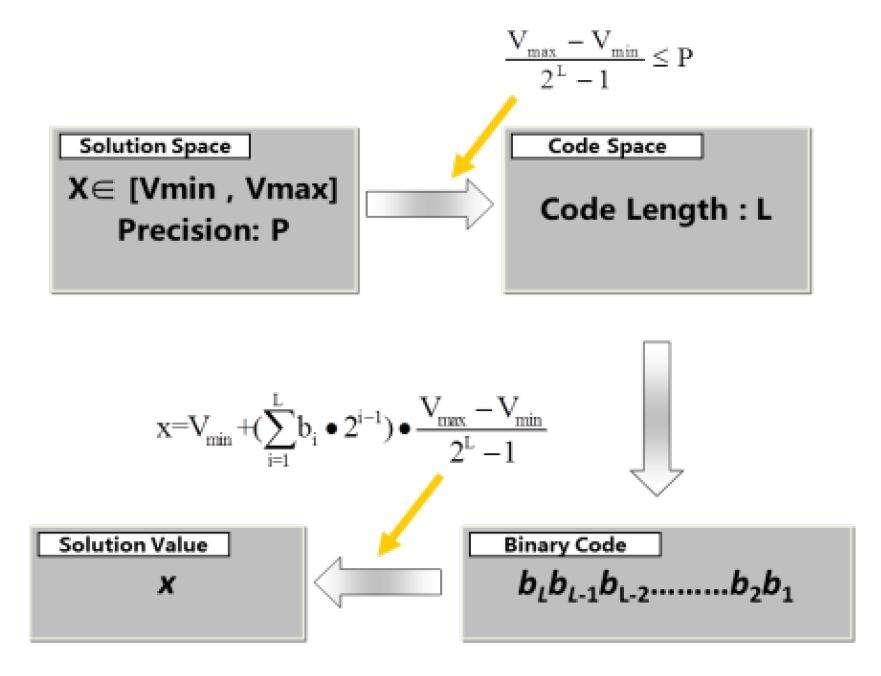
Binary codes are used here to represent solutions. Each binary code represents one solution. As genetic algorithms are executed in search space which contains many solutions, there should be many binary codes to represent the whole search space.
If the maximum possible value and the minimum possible value are defined as Vmax and Vmin, and the precision is P, then the binary code length L can be determined by the following formula:
The binary codes can be translated to the real solution values by using the following equation:
It is known that the minimum possible value of neutron flux is zero. Determining the maximum possible value is very important because it will affect the precision and the code length which will determine the workload and solving efficiency. For each energy group and detector pair, supposing that the detector reading is only generated from this energy group, the maximum possible value at this group is determined:
There are n detectors, so n maximum possible values for each group can be calculated by Eq.(5), while the real maximum possible value at this group is the minimum of these n values:
Because if there is any solution value beyond the minimum of these n values, the detector readings calculated by Eq. 2 will exceed the real detector readings.
The binary codes can be generated randomly for and only for the original search space. This means the algorithms do not need preset spectrum. Then the coding and decoding process can be described as the following figure:
B. Fitness functions, selection, crossover and mutation
The following two equations are used here as fitness functions to evaluate solutions:
where
Firstly the expected detector readings
Code space genetic operators crossover and mutation, which simulate chromosome genetic manipulations chiasmata and variation, are the methods for generating new solutions. One-point crossover and bit mutation [8] are used here.
C. Elitism replacement scheme
Elitism [9, 10] replacement scheme here is used to ensure the convergence. The scheme is that after the evolution process of current generation completed, the best solution of next generation will be compared with the best solution of current generation. If the best solution of next generation is better than the best solution of current generation, the elitism replacement scheme will be skipped, otherwise, the best solution of current generation will be forced to be saved into next generation to replace the worst solution of next generation. This scheme will prevent the best solution from being eliminated through the selection operation which will significantly improve the performance of genetic algorithms [10].
D. Pseudo-parallel strategy
Pseudo-parallel strategy is used to inhibit premature convergence. Premature convergence means that solution process converges to local optimal solution instead of global optimal solution prematurely. In parallel genetic algorithms, the search space will be divided into a number of sub search spaces. The basic genetic algorithms are executed in these sub search spaces independently. After one generation evolution processes of every sub search spaces completed, some information will be exchanged between these sub search spaces, so that the population diversity will be preserved to inhibit premature convergence. The "pseudo-parallel" means it is parallel logically but serial physically, with the parallel algorithm being implemented in a serial way. The island model [9] is applied here as information exchange method. For each sub search space, one swap-in sub search space and one swap-out sub search space are selected randomly. The worst solution of the swap-in sub search space will be replaced by the best solution of current sub search space, and the worst solution of the current sub search space will be replaced by the best solution of the swap-out sub search space.
III. RESULTS
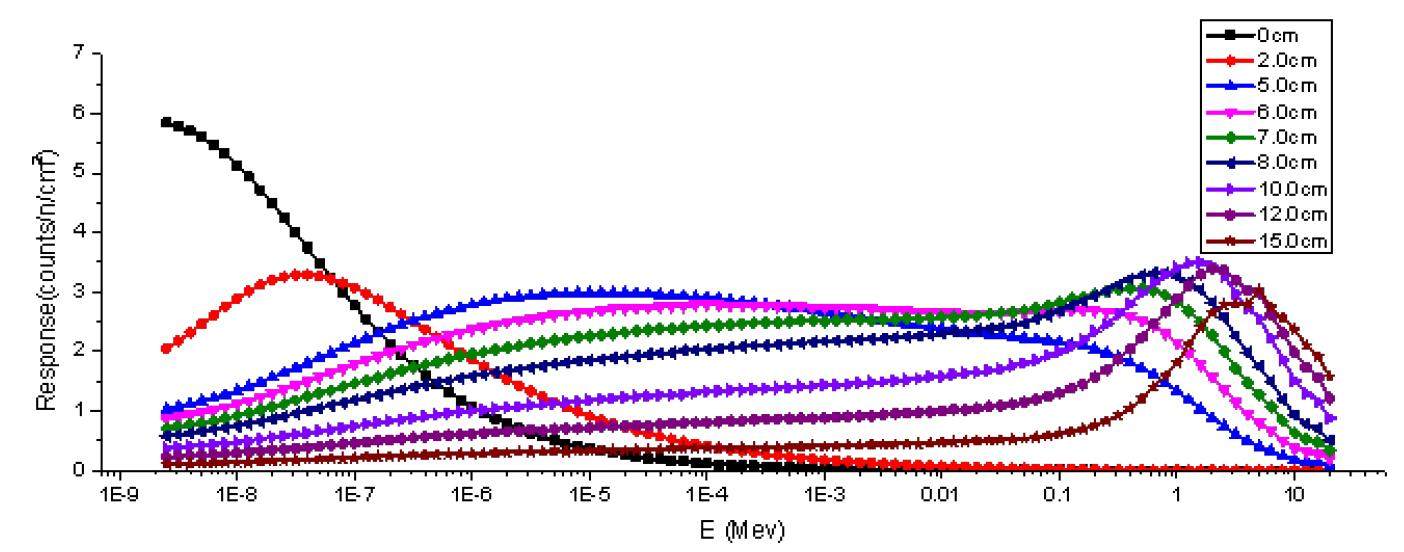
According to the algorithm mentioned above, a spectrum unfolding code was developed with different strategies and different fitness functions. Code verification and validation depended on the multi-sphere neutron spectrometer MNS IL100 developed by Tsinghua University. Firstly the energy response functions should be calculated. The whole energy range was divided into 100 energy groups in logarithmic coordinates. MCNP-4C was used to calculate the response functions of 9 different radius spheres which are 0, 2, 5, 6, 7, 8, 10, 12 and 15 cm. These 9 energy response function curves are shown in Fig. 3.
A. Simulation tests
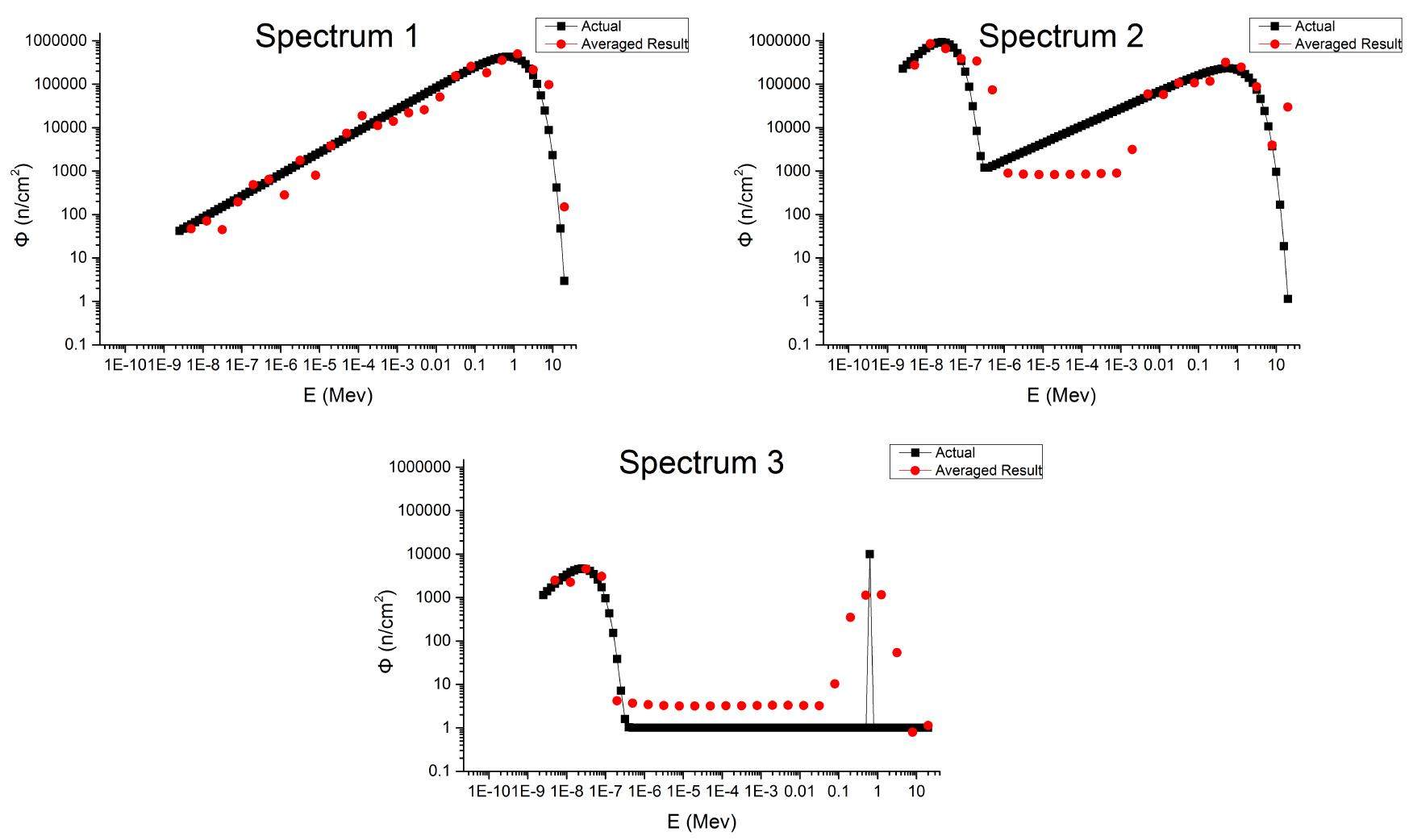
Figure 4 shows three typical neutron spectra used in simulation tests which are combinations of several differential fluence spectra mentioned in reference [6].
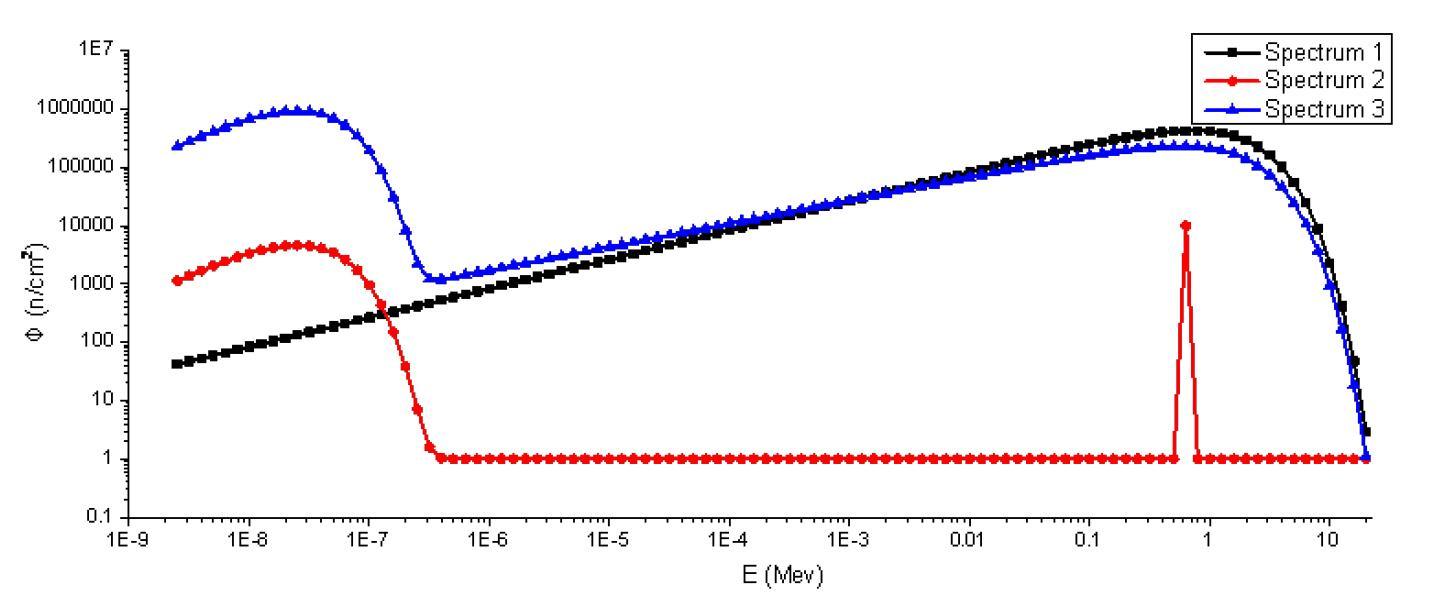
1. 252Cf spontaneous fast fission spectrum.
2. Combination of thermal Maxwellian spectrum, monoenergetic neutron beams spectrum and uniform distribution spectrum.
3. Combination of thermal Maxwellian spectrum and 252Cf spontaneous fast fission spectrum.
Four kinds of genetic algorithms were tested and compared here:
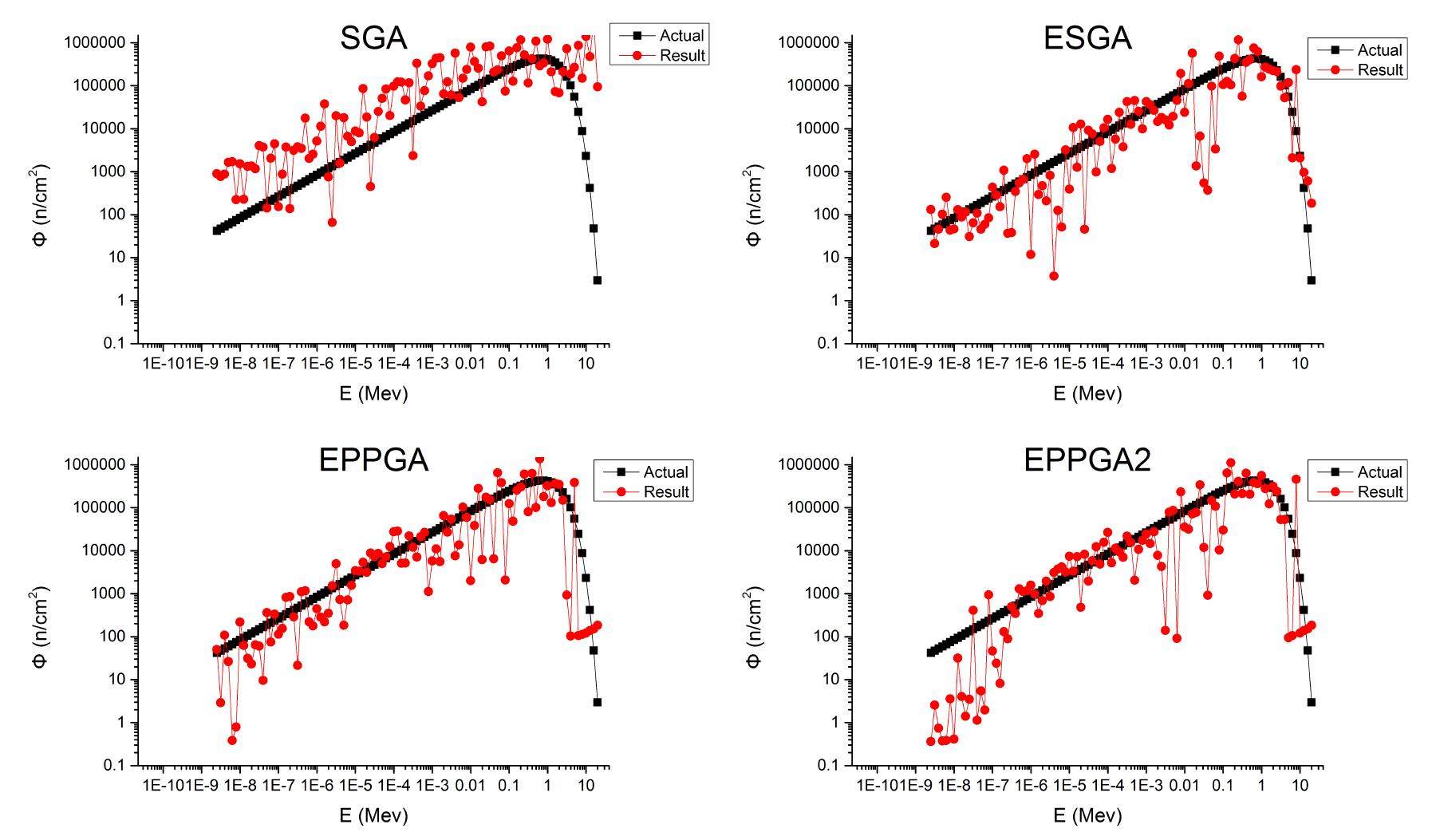
1. Simple genetic algorithm (SGA): Elitism replacement scheme and pseudo-parallel strategy are not applied to SGA. Eq.(7) is used as fitness function here. The population size is 2000, crossover rate is 0.06, mutation rate is 0.004, code length is 1000 and iteration number is 10 000.
2. Simple genetic algorithm with elitism (ESGA): Elitism replacement scheme is added to ESGA based on SGA.
3. Pseudo-parallel genetic algorithm with elitism (EPPGA): Pseudo-parallel strategy is added to EPPGA based on ESGA. The subpopulation size is 100, subpopulation number is 20, so that the total population size can keep consistent with ESGA.
4. Pseudo-parallel genetic algorithm with elitism and different fitness functions (EPPGA2): Eq. 8 is used as fitness function in EPPGA2 to replace Eq. 7 in EPPGA.
Equation 2 was used to calculate the detector readings with these spectra, then the detector readings were inputted into the spectrum unfolding code to solve the spectra. The following two functions were used to evaluate the performances of the unfolding code with different kinds of genetic algorithms.
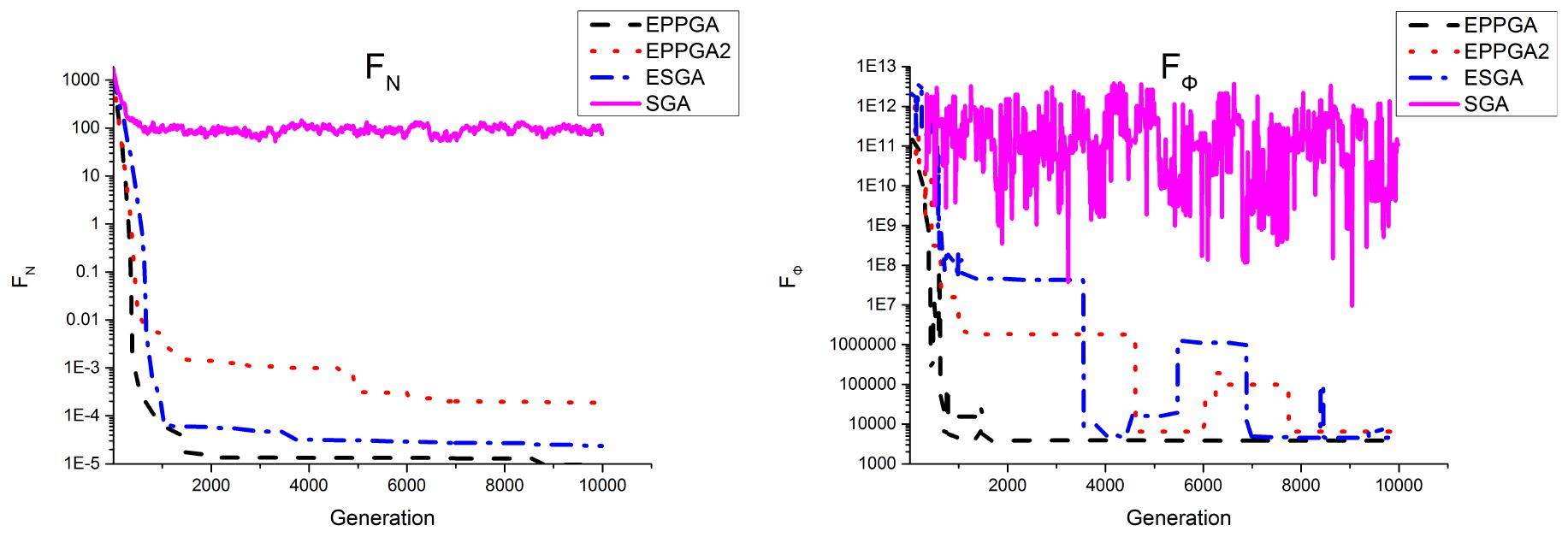
Figure 5 shows the calculation results of different genetic algorithms with spectrum 1. It is shown that result of EPPGA is the best one although the advantages are not very obvious. However, the performance comparison of different genetic algorithms with spectrum 1 depending on the convergence curves of FN and FΦ, which are shown in Fig. 6, proves that the convergence rate and convergence precision of EPPGA are much better than the other three genetic algorithms.
Considering the large scale fluctuations of the original result, these original 100 values at 100 energy groups are averaged to 25 values at 25 energy groups. The averaged results of the three typical neutron spectra using EPPGA are shown in Fig. 7.
B. Actual 252Cf spectrum measurement
The MNS IL100 and the spectrum unfolding code were used in actual experiment of 252Cf neutron source spectrum measurement. Fig. 8 shows the function curve of the standard spectrum of 252Cf [11] and the original 100 values calculation result by using EPPGA.
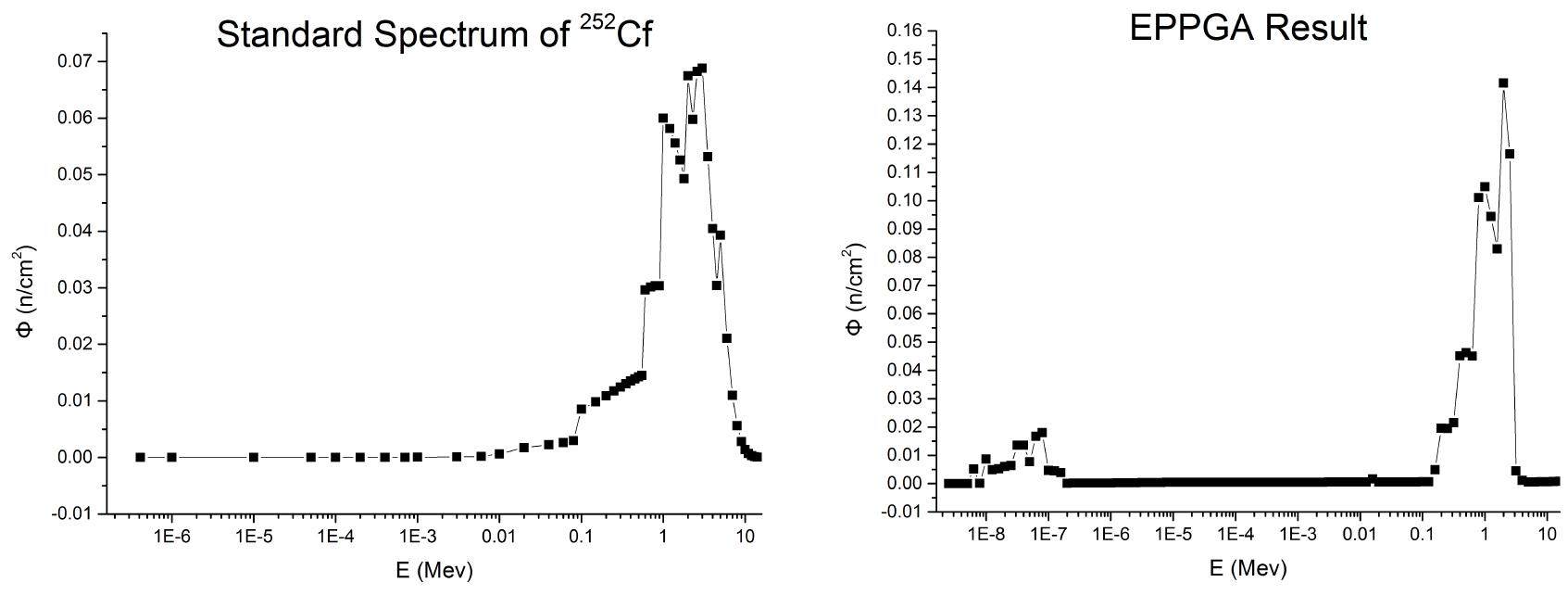
Figure 8 shows that from 0.1 MeV to 10.0 MeV, the calculation result is in good agreement with the 252Cf standard neutron spectrum, however, there are some distributions in low energy area which does not appear in standard neutron spectrum. Actually this is the thermal neutrons generated from the original neutrons which are slowed down after the effect of scattering from wall.
IV. CONCLUSIONS
It can be concluded that the EPPGA calculation results of simulation tests with several typical neutron spectra match up with the expected results, and the EPPGA calculation result of actual experiment is in good agreement with the 252Cf standard neutron spectrum, verifying that by determining effective search space and proper fitness function, and by using the elitism replacement scheme and the pseudo-parallel strategy, the genetic algorithms were applied to spectrum unfolding problem successfully. However, the calculation results of simulation tests have large scale fluctuations. This is because the algorithms search direction depends on the fitness evaluations. While despite the smoothness of the iteration results, the fitness function used here only focused on the degrees of closeness between the calculation results and the optimal result, which led the results to be not smooth. Smoothness ensuring part is being considered to be added to the fitness function, but there is no theory for reference about determining its form and weight. The future work will focus on the construction of the smoothness ensuring part.
Nuclear Decay Data for Dosimetric Calculations
. ICRP Publication 107. Ann. ICRP 38 (3).
