Introduction

Limitations of the nuclear landscape [1, 2] have always been an intriguing topic. Exotic nuclear properties, for example, the shell evolution [3-6], 4n resonant state [7, 8], and 4p unbound state [9], emerge at the limits of nuclear stability. The discovery of new elements (nuclides) involves the following three problems: production, separation, and identification [10]. Because the nuclei are unstable and have relatively short half-lives, appropriate probes must be utilized. Characteristic decay modes [10, 11] are commonly employed as a probe to signal the existence of exotic nuclei. Therefore, investigating and predicting the dominant decay modes of the unknown nuclides is crucial. The nuclear binding energy and half-life are key parameters for determining the decay mode of a nucleus. The former measures the stability of nuclides by using energy criteria, and the latter describes the possibility of decay.

Both microscopic and macroscopic methods have been used to study the nuclear binding energy [12-16] and partial half-life of each decay channel, including α decay [17-19], β decay [20, 21], spontaneous fission [22, 23], protons emission [25] and neutron emission [24], etc. Microscopic theories begin with nucleon–nucleon interactions, which can be based on either realistic or phenomenological models. The macroscopic theory uses selected variables with physical considerations to construct semi-empirical formulas and fit the experimental data, and it entails the risk of overfitting and inappropriate parameters. In addition, exotic nuclei may significantly deviate from the general fitting and be identified as outliers. Decreasing the deviation between theoretical predictions and the observed results remains a critical issue.

With advances in computing and storage, efficacious machine learning algorithms with diverse applications have been proposed [26, 27], e.g., nuclear properties [28-30], fission yields [31-35], spectra decomposition [36], solving Schrödinger equation [37], and other nuclear techniques [38, 39]. As summarized in a recent colloquium, estimating the residuals of nuclear properties using machine learning algorithms is a powerful strategy [40]. A neural network has been used to compensate for the residuals of nuclear masses [41-43] and nuclear charge radii [44-46]; this has been achieved through structural optimization and careful selection of the input parameters with definite physical interpretations. The applicability of the decision tree (DT) has been verified via training and testing with residuals of the binding energies [47]. However, random forest (RF) [48] algorithm, developed from the DT algorithm, has not been tested for determining the nuclear mass or the partial half-life of a specific decay channel; in this regard, semi-empirical formulas have suggested several major components but with residuals. Machine learning algorithms can include possible features to realize the training for residuals, whereas RF, with bootstrap sampling, not only avoids overfitting but also considers the correlation between the data combinations and several features. Thus, RF exhibits increased robustness and is conducive to extrapolation. The amount of computation increasing in accordance with the number of trees in the forest and size of the dataset, as well as the difficulty of model interpretability, may limit its applications.

This study entailed the application of an RF machine learning algorithm to analyze the major decay modes of heavy and superheavy nuclei. The competition between α decay, β decay, and spontaneous fission (SF) of new elements, as well as the possible long-lived island in the superheavy region were examined.

Method

This study focused on the $Z⩾84$ and $N⩾128$ regions. The partial half-lives of the α decay, β^- decay, β⁺ decay, electron capture (EC), and SF were calculated using semi-empirical formulas, and the residuals of each formula were then trained using the RF algorithm. The minimum partial half-life of a mode corresponds to the dominant decay mode.

Results and Discussion

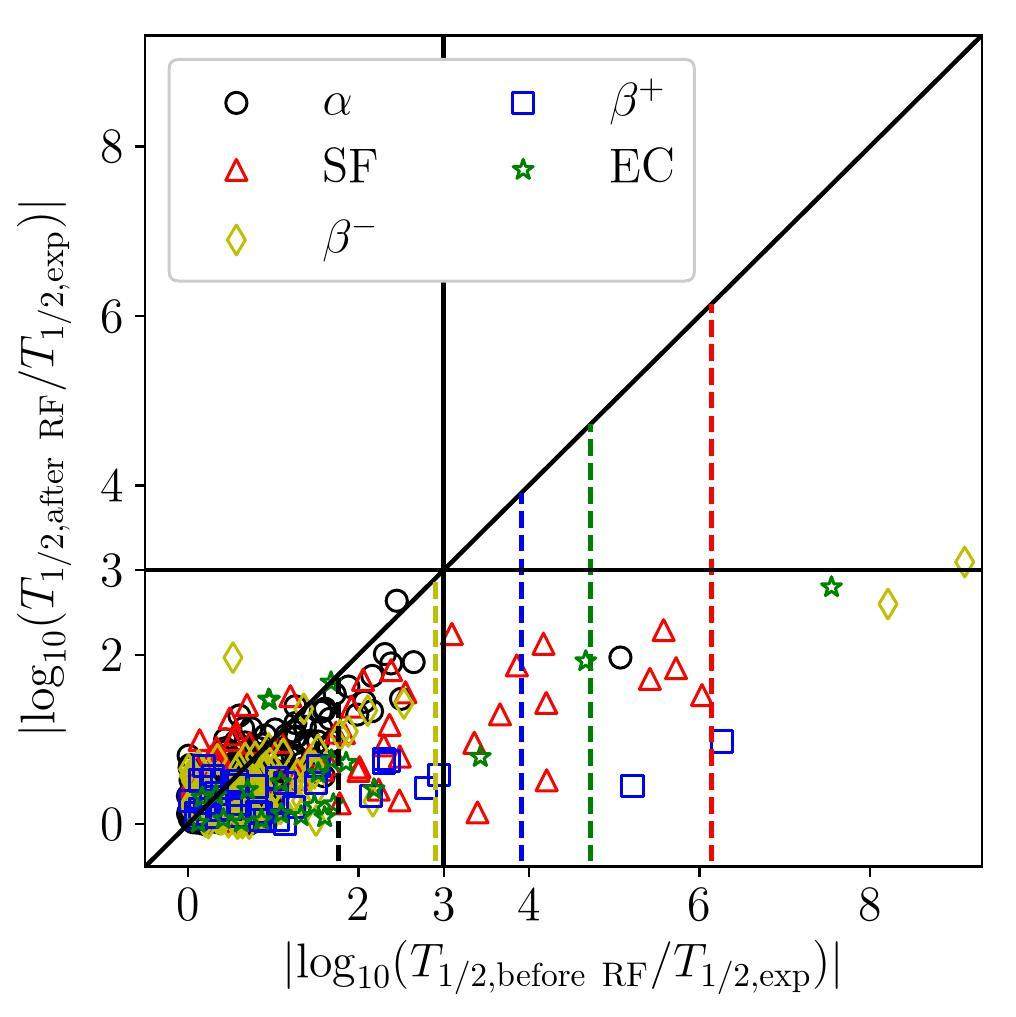
The residuals of the decay formulas of α decay, β^- decay, β⁺ decay, and EC were trained using the RF with features Z, N, A, the odevity of Z and N, and the decay energy. Because the decay energy cannot be defined for the SF, the fission barrier (FB) obtained from Ref. [61] was used to replace the decay energy in the feature set to consider the deformation effect. The number of leaves chosen for this study was 11, which was the same as that used for training the binding energy in this region in our previous study [62]. Fig. 1 compares the residuals of these decay formulas before and after RF training. Two conditions were assumed to determine the outliers: 1) located outside the dashed line with the corresponding color, which indicates that the scatter deviates by twice the RMSE from the experimental ${\text{log}}_{10}{T}_{1/2}$; and 2) the $\left|{\text{log}}_{10}\left(T_{1/\mathrm{2,}\text{cal}}/T_{1/\mathrm{2,}\text{exp}}\right)\right|$ value is larger than 3, which indicates that the calculated value is three times that of the magnitude of the experimental value. Thus, missing (adding) the outliers owing to the significantly large (small) RMSE can be avoided. After training, the biases of the outliers of these decay formulas were significantly reduced, and the RMSE of the formulas decreased (Table 1), as expected. The condition of the outlier is not too strict because the aim was not to maximally decrease the RMSE but to reach an appropriate scale wherein the dominant decay mode can be described. The same features and number of leaves of the RF were chosen in this study to train the residuals of the different decay formulas; this avoids overfitting while seeking an extremely small RMSE.

Fig. 1Full-screen View

(Color online) Comparison of the residuals of UDL (α decay), SF3 (SF), Eq. (3) (β^-, β⁺ and EC) before and after RF training. The dashed lines denote twice the RMSE of the corresponding formulas.

In total, 445 nuclides with measured partial half-lives and branch ratios of the five decay modes were obtained from NUBASE2020 [63]. The dominant decay modes and partial half-lives of the nuclides are illustrated in Fig. 2(a,b). A long-lived α decay valley from ${}_{88}^{226}$Ra₁₃₈ to ${}_{98}^{251}$Cf₁₅₃ lies between the narrow β⁺/EC decay band and the neutron-rich β^- region. The half-life of the nucleus decreases with increasing distance from this valley. The southwest was dominated by α decay, whereas the southeast was dominated by β^- decay. In the northwest, β⁺ decay and EC compete with α decay and lose after Z increases. In the northeast, α decay and SF compete with one other, and the region extending from the α valley appears to be dominated by the SF. Although the distribution of the dominant decay modes demonstrates a clear boundary, the minimum partial half-life was smooth.

Fig. 2Full-screen View

(Color online) Dominant decay mode (left panels) and minimum partial half-lives (right panels) of the α decay, β^- decay, β⁺ decay, EC, and SF. (a,b) Experimental data in NUBASE2020. (c–f) The results predicted through RF; WS4 [12] and UNEDF0 [13] denote the sources of predicted energies. Specifically, the FB is used to replace the decay energy to learn SF. The nuclides, for which the predicted partial half-life is longer than 10⁴ s, are marked by a star.

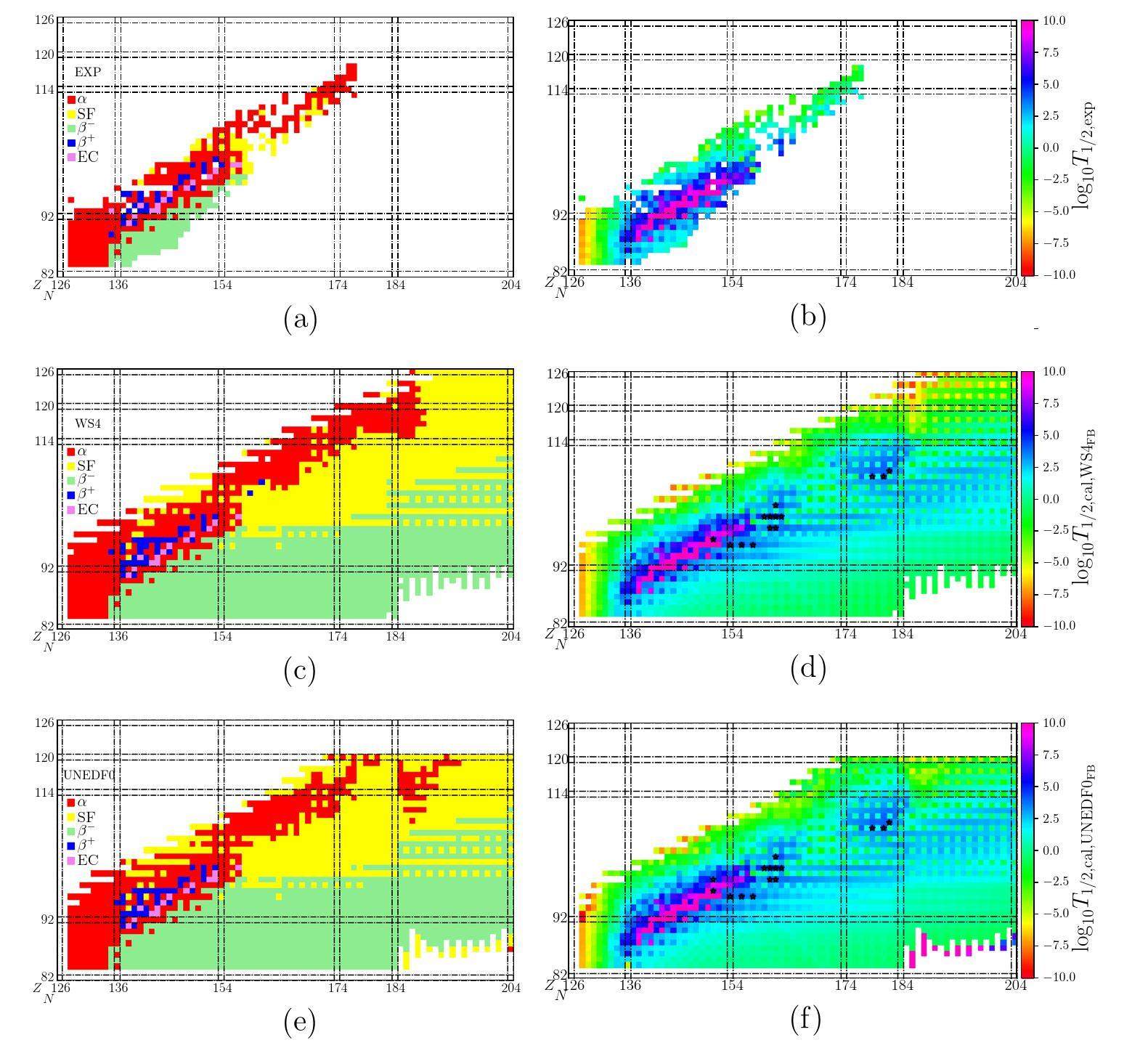
Among the 445 nuclides considered, 341 (104) nuclides had known (unknown) corresponding decay energies. The nuclides with unmeasured masses were calculated using WS4 [12] and UNEDF0 [13] to estimate the partial half-lives. The results of the RF are presented in Fig. 2(c–f). The calculated results sufficiently agree with the experimental results because the dominant decay mode is correctly described for 431 and 427 (96.9% and 96.0%) nuclei when the RMSE of ${\log }_{10}{T}_{1/2}$ of the dominant decay mode is 0.62 and 0.67, respectively. Nuclides, for which the dominant decay mode was inconsistently described, generally have two competitive decay modes. For example, the α and SF branch ratios of ²⁵⁵Rf, ²⁶²Db, and ²⁸⁶Fl were approximately 50%. Meanwhile, the liquid drop model trained by RF [62] was also applied to obtain the energies; the model afforded consistent results that are not presented herein.

The N-Z=48 chain, where the partial half-lives of the α decay, β decay, and SF are comparable, was used for a specific comparison. The results of the density-dependent cluster model within the anisotropic deformation-dependent surface diffuseness [64], Royer formula [66], modified Swiatecki’s formula [22], nuclear liquid drop model [23], and deformed self-consistent Hartree–Fock mean-field with Skyrme forces and pairing correlations [66] were compared with the experimental values; the results are presented in Table 2. The models afforded similar results and deduced a consistent dominant decay mode.

The accuracy of the obtained energy is crucial for half-life calculations. If the calculated energies of WS4 and UNEDF0 replace all the experimental energies, the number with a consistent decay mode compared to the experiment reduces to 72.6% and 64%, respectively, and the RMSE of log₁₀T_1/2 increases to 2.07 and 2.64. The difference in the results obtained using the energies of the two models is owing to the accuracy because the RMSE of the mass of WS4 is approximately 0.3 MeV [12], whereas that of UNEDF0 is approximately 1.45 MeV [13]. This also leads to differences during extrapolation. The consistency rate of the dominant decay mode between the energies calculated using these two models decreases from 82.2% to 66.2%. More accurate and precise measurements of the decay energy will aid in theoretical predictions. In addition, WS4 and UNEDF0 may lose their predictive power after training with machine learning. Training the WS4 and UNEDF0 binding energies with features Z, N, δ, and P, which sufficiently describe the residuals in Ref. [42], improves the energy description but decreases the consistency in the dominant decay mode by several percent, which is considerable compared to the 23.4% rate of the theoretical energies among all nuclides (104/445).

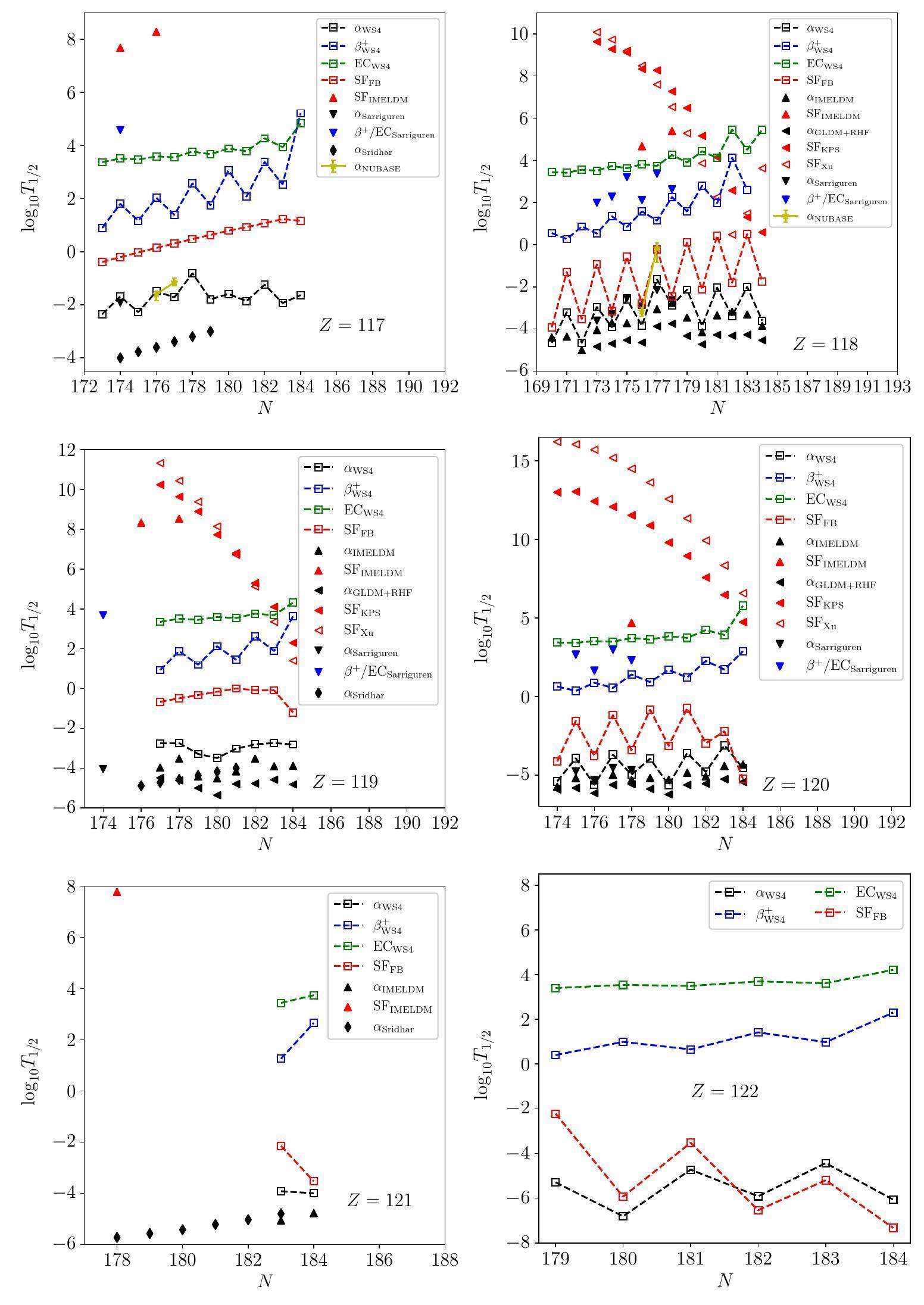
The SF is important for investigating the half-lives of superheavy nuclei. As shown in Fig. 2(c, e), the dominant decay mode of the unknown nuclides is determined in accordance with the competition between the SF, α decay, and β^- decay. The major competition is between the SF and β^- decay for neutron-rich nuclides, and between the SF and α decay for neutron-deficient nuclides. Existing experimental data demonstrates a long-lived α decay region from ${}_{88}^{226}{\text{Ra}}_{138}$ to ${}_{98}^{251}{\text{Cf}}_{153}$, lying between the β⁺ and β^- decay regions, and ending with the SF. The proposed models correctly describe this phenomenon. In the long-lived region, after N exceeds 154, the blue band shown in Fig. 2(d, f) indicates half-lives of approximately 10²–10⁷ s. At the southwest corner of Z=114 and N=184, nuclides in the circle have a longer half-life than those in the surrounding area. This is because of the high FB in this region, which leads to a longer $T_{1/\mathrm{2,}\text{SF}}$. Fig. 3 compares the evolution of FB and measured $T_{\text{1/2,SF}}$ along the mass number. The FB decreases with A before A=230 and subsequently behaves as a sinusoidal wave oscillating between 2 and 10 MeV. Apparently, an FB threshold exists, below which SF occurs. Nuclides with relatively long $T_{1/\mathrm{2,}\text{SF}}$ generally have small SF branch ratios. In addition, the FB of nuclides with SF branch ratios less than 1% were mostly higher than those with SF branch ratios greater than 1%, which implies that the higher the FB, the weaker the SF. However, considering only the nuclides with SF branch ratios of less than 1% or greater than 1%, the correspondence between FB and $T_{1/\mathrm{2,}\text{SF}}$ becomes significantly more complex.

Fig. 3Full-screen View

(Color online) Evolution of $T_{1/\mathrm{2,}\text{SF}}$ and FB along the mass number. The datasets are divided according to whether the corresponding $T_{1/\mathrm{2,}\text{SF}}$ is measured and whether the branch ratio (BR) of SF is less than 1%.

The nuclides with partial half-lives predicted to be longer than 10⁴ s are marked with stars in Figs. 2(d, f), which suggests ^250,252,254Cm, ^{260, 261}Es, ^261-264Md, and ²⁶⁵Lr for future measurements. No experimental value of the half-life of ²⁵⁰Cm was suggested in NUBASE2020 and was thus extrapolated in this study. In the NNDC, SF was shown to be the dominant decay mode, and its half-life was recommended to be 8300 years, which is relatively long. Although the calculations in this study underestimate the NNDC value, the long half-life and dominant decay mode are reproduced. In addition, the upper limit of the half-life of ²⁵²Cm was proposed to be two days in Ref. [65], which was not updated since then (1966), whereas the current study estimates a half-life of 1.43 days. No experimental half-lives were previously reported for ^{260, 261}Es, ^261-264Md, and ²⁶⁵Lr. However, their nearby isotopes have long half-lives, such as ²⁵⁷Es (7.7 days), ²⁶⁰Md (31.8 days), ²⁵⁹Md (1.6 h), ²⁵⁸Md (51.5 days), ²⁵⁷Md (5.52 h), and ²⁶⁶Lr (11 h). Moreover, the Es, Md, and Lr isotopes are located in the extension of the narrow long-lived region from ²²⁶Ra to ²⁵¹Cf, substantiating that the Es, Md, and Lr isotopes are candidates with long partial half-lives. Obtaining more measurements is also suggested; for example, the ²⁵²Cm data has not been updated for more than 50 years.

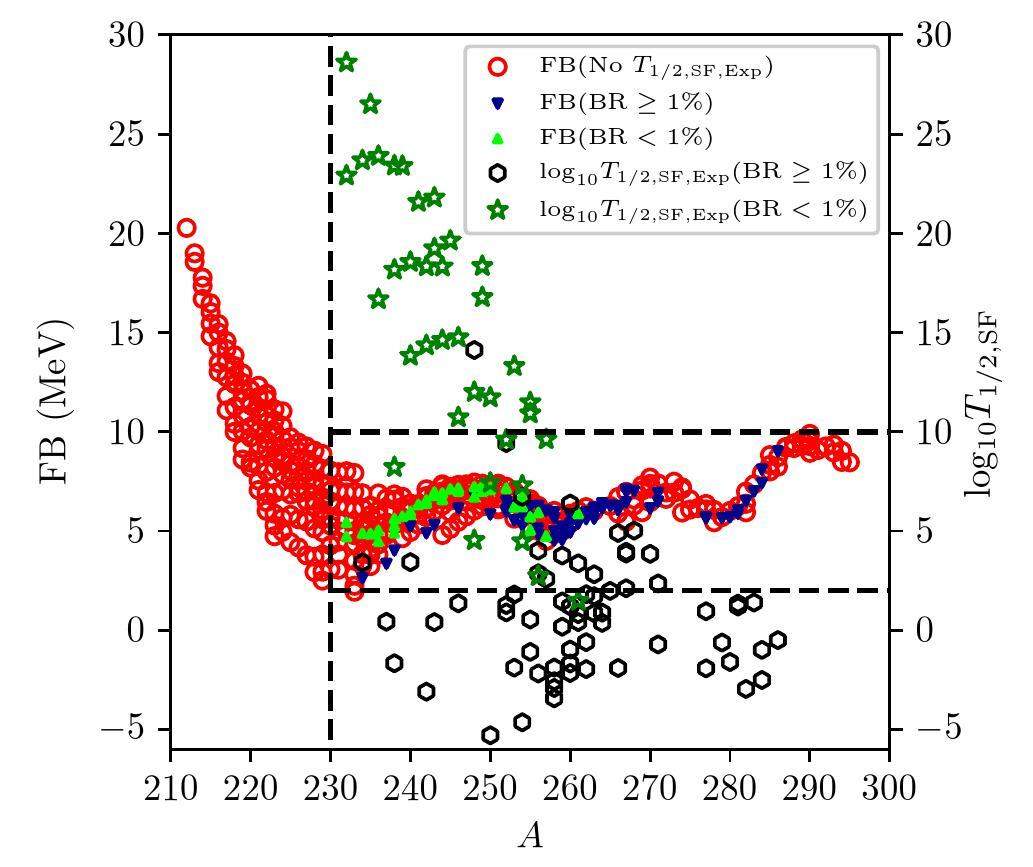
A comparison of all the possible decay channels is limited by the accurate description of each channel and the observed data; note, the SF mechanism remains unclear, such as its dependence on the FB or deformation. The effect of the quadrupole deformation parameter (ε₂) [15] on the half-life estimation was then investigated. If the FB is replaced with ε₂ during RF training, more nuclides are predicted to have longer half-lives. Further investigations should be conducted to understand the dominant factors that contribute to the half-life of SF. The FB combines the contributions of multipole deformations and thus presents a stronger quantum effect, as shown in Fig. 2(d, f), compared to ε₂. Fig. 3 demonstrates that the FB increases when Z is large; this indicates the competition between the FB and Coulomb repulsion in superheavy nuclides.

The extrapolation stops at the single-neutron (proton) and two-neutron (two-proton) drip lines. The UNEDF0 data set stops at Z=120. From the existing region to the neutron-deficient side, the α decay and SF are predicted to compete. On the neutron-rich side, the calculations predict the β^- decay as the dominant mode, whereas the SF competes for specific nuclides. The latest results of most theoretical calculations of the partial half-lives [17-20, 22, 23, 66-70] indicate that the α decay mode is dominant for new elements at $N⩽184$. As shown in Fig. 4, the partial half-lives of isotopes with Z=117–122 were predicted in this study and compared to the corresponding results in Refs. [18-20]. Although the partial half-lives of β⁺ decay and EC determined in this study were not longer than those indicated in Ref. [20], they remain approximately five orders of magnitude greater than that of α decay in this region, which does not change the dominant decay mode.

Fig. 4Full-screen View

(Color online) Comparison of the partial half-lives of isotopes with Z=117–122. IMELDM is extracted from Ref. [18], GLDM+RHF, KPS, and Xu are extracted from [19], Sarriguren is extracted from Ref. [20], Sridhar is extracted from Ref. [69].

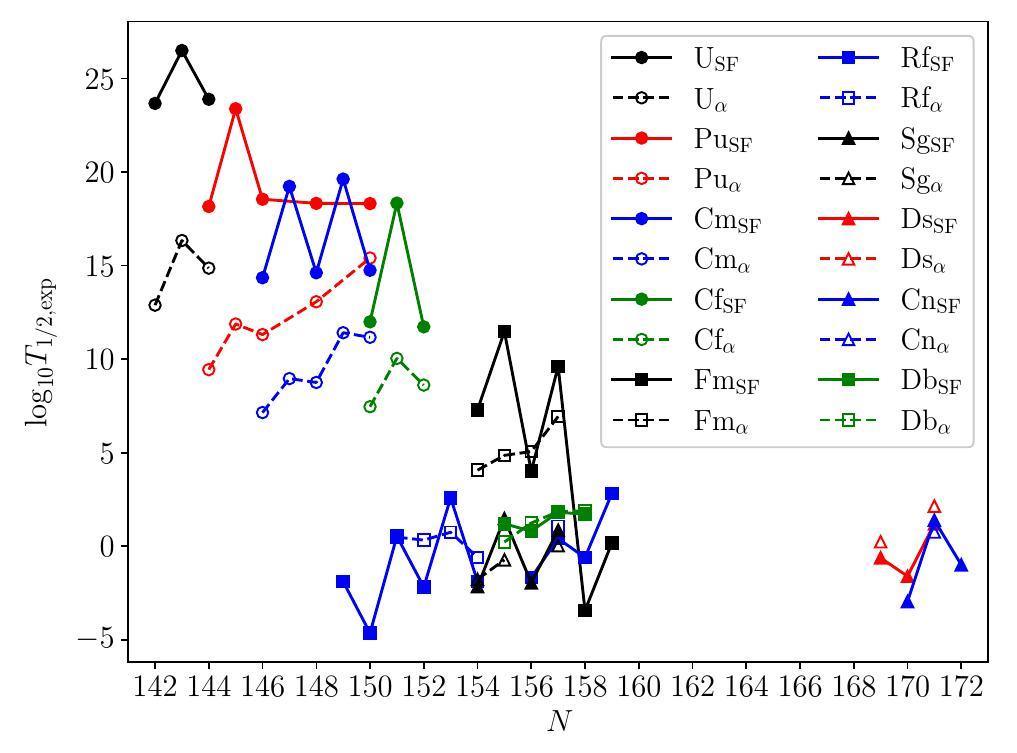
The T_{1/2, α} values predicted in this study were longer than those indicated in Refs. [18-20]; this does not change the dominant decay mode of odd-Z isotopes but enhances the competition of SF in even-Z isotopes. Furthermore, the prediction in this study demonstrated a strong odd–even staggering of T_{1/2, SF} of even-Z isotopes. In other words, the T_{1/2, SF} value of even–even nuclei is several times shorter than its two isotopic neighbors, which differs from the weak or unpredicted odd–even staggering effect obtained by other SF models shown in Fig. 4. Notably, all measured T_{1/2, SF} values of the even-Z isotopes demonstrate such odd–even staggering. Fig. 5 illustrates $T_{1/\mathrm{2,}\text{SF}}$ and T_{1/2, α} of isotopes with Z⩾92. For example, when Z is small in the U, Pu, Cm, and Cf isotopes, SF is not competitive with the α decay because the Coulomb repulsion is not sufficiently strong. However, when Z is large, the Coulomb repulsion increases, and this odd–even staggering makes the SF competitive with the α decay in the even–even nuclides. Thus, α decay is suggested to be a key signal detected for Z=119 and 121 isotopes, whereas the SF should also be considered for even-N isotopes of Z=120 and 122. Moreover, odd–even staggering also exists in odd-Z isotopes, which can only be verified by ^260-263Db because the data are limited. Therefore, the odd–even staggering of odd-Z isotopes was not predicted in this study. The DNS model predicted the σ_ER value of hundreds of FB for the 3n or 2n channels producing ${}^{293}{119}_{174}$ on the ²⁴³Am target [71], which can be examined for the new facilities of CAFE2 and SHANS2 in Lanzhou [72]. Given the odd–even effect of partial half-lives, nuclide candidates for new superheavy elements still require an analysis based on the cross-section and partial half-life.

Fig. 5Full-screen View

(Color online) Odd–even staggering of $T_{\text{1/2,SF}}$ of U, Pu, Cm, Cf, Fm, Rf, Sg, Ds, Cn, and Db isotopes and comparison with T_{1/2, α}.

Summary

In this study, the decay modes of superheavy nuclei were investigated using the RF algorithm. The partial half-lives of α decay, β^- decay, β⁺ decay, as well as EC, and SF were studied and compared. The dominance of α decay in the neutron-deficient region was relatively evident. β^- decay is predicted to be dominant in the neutron-rich regions. The SF contributes to a long-lived circle at the southwest corner of Z=114 and N=184. A more accurate and precise measurement of the nuclear mass and decay energy can improve the prediction of the decay mode. The odd–even effect of the SF was observed in even-Z nuclides. Combined with the strong Coulomb repulsion, the SF and α decay became competitive in even–even nuclides. Thus, the α decay is suggested to be a key probe of isotopes with Z=119 and 121, whereas the competition of SF should be considered in even–even isotopes with Z=120 and 122.

^{250, 252, 254}Cm, ^{260, 261}Es, ^261-264Md, and ²⁶⁵Lr with half-lives predicted to be longer than 10⁴ s were suggested for future measurements. The SF, influenced by the fission barrier and Coulomb repulsion, leads to a long-lived region during extrapolation. The results of this study indicate that research regarding SF, especially beyond ²⁸⁶Fl, which is currently the heaviest nuclide with a significant SF branch ratio, is critical for performing studies on new facilities, such as CAFE2 and SHANS2 in Lanzhou.