Introduction
As a crucial device for synchrotron radiation (SR) beamlines, the double-crystal monochromator (DCM) is a complex and precise optical system with multiple integrated factors [1-3]. The transmission performance of DCM depends closely on the thermophysical properties of the crystal and the thermal treatment technology [4-6]. The first aspect involves the coefficients of thermal expansion and thermal conductivity of the crystal, and the second is related to clamping, cooling, and deformation correction technologies for crystals. The performance of a monochromator is susceptible to thermal deformation; thus, the cooling technology is tightly linked to the performance improvement of the monochromator.
The design of crystal cooling schemes relies on finite element analysis (FEA). With the development of computer technology, the thermal analysis of Synchrotron Radiation monochromators has reached a higher level than experimental measurements of thermal deformation [7-10]. A common method for measuring the thermal deformation is to obtain the surface slope error using the difference between the full width at half maximum (FWHM) of the measured and theoretical rocking curves [11, 12]. It is simple and easy to implement; however, the FWHM of the rocking curve is a convolution of multiple factors, such as thermal deformation, bandwidth, angular divergence, and detection system, and cannot be directly deconvoluted to obtain the thermal deformation without loss of details. Other synchrotron radiation light source facilities have developed new measurement methods [13, 14], where the resolution is limited by the amount of data, or processing is difficult. In addition to direct deformation measurements, the temperature field can indirectly determine thermal deformation. However, conventional temperature sensors, such as thermocouples and thermal resistance sensors, fail in strong radiation environments. Infrared radiation thermometers can measure the temperature distributions on the surfaces of common objects, excluding silicon material, as it is transparent to the infrared band [15]. In addition, the resolution of infrared radiation thermometers fails to meet the requirements for characterizing crystal thermal deformation.
For an ideal working monochromator, the excellent initial lattice flatness of the first crystal should be maintained under high-power beam irradiation to match the lattice plane of the second crystal perfectly. Scientists at synchrotron radiation facilities have systematically studied the crystal materials, cooling structures, and coolants to achieve this goal [16-20]. Some crystal cooling techniques, such as the cryogenic cooling of liquid nitrogen, have positively suppressed crystal surface deformation. This method is employed in almost all third-generation synchrotron radiation facilities [4, 11, 21, 22]. These studies effectively addressed the basic survival problem of DCM in commission under high heat loads and made many experiments achievable with high-power synchrotron radiation [23, 24].
However, as mentioned above, in the design process of cooling systems, characterization of the DCM lags behind computer simulations in terms of precision. This implies that FEA results were validated experimentally only to a certain extent. In the absence of high-resolution, real-time feedback, the simulation is detached from the real surface of the operating crystal, which changes owing to vibrations, operating hours, and adjustments of other conditions during operation. In other words, the cooling solutions provided by current computer simulations may not be optimal, and existing experimental methods provide no valid feedback. The actual operation poses the possibility of uneven cooling owing to the distribution of coolant channels and the possibility of undercooling in some cases and overcooling in others, attributed to a fixed cooling temperature. Although these effects may not be apparent at present, the progressively severe working conditions of monochromators, driven by advancements in advanced light sources and increasing beam power density, underscore the need for continual improvements in cooling schemes. High-resolution, real-time measurements are crucial in enhancing the performance [25, 26].
Recently, we proposed a method to simply and effectively address the challenges in high-resolution and high-efficiency characterization of monochromators. Using an orthogonal analyzer crystal and a 2D detector, the angular divergence and energy bandwidth of the SR beam can be decoupled [27]. This decoupling allows the DuMond diagram to transition from phase space to real space. In this study, we used a Si(333) analyzer crystal to measure the DuMond diagram of DCM under varying incident powers and confirmed that the DuMond diagram of DCM changed from a parallelogram to a willow-leaf shape owing to thermal deformation. Additionally, we acquired the lattice deformation profile of the first crystal by analyzing the willow-leaf DuMond diagram and estimated the saturation intensity curve of the DCM using a hyperbolic tangent function analogous to the magnetization equation.
Theory
DuMond is a geometric method that qualitatively or semi-quantitatively illustrates the crystal diffraction characteristics of X-rays [28-30]. In principle, it can also be used to characterize the thermal deformation of monochromator crystals [31]. However, conventional experimental method is inefficient and has low precision when obtaining the DuMond diagram. This process involves multiple scans of the rocking curves of the DCM using an analyzer crystal with a specific wavelength and then stitching these curves together [32].
Angular divergence-bandwidth coupling and DuMond diagram of a monochromatic x-ray
According to X-ray dynamical diffraction theory [33], a coupling relationship exists between the beam divergence and bandwidth. Even when the incident white beam is perfectly parallel, the diffracted beam exhibits a certain bandwidth. Similarly, even when the incident divergent beam is perfectly monochromatic, the diffraction beam has an angular divergence limited by the Darwin width. For an SR beam with vertical and horizontal angular divergences, the beam’s cross-section from the DCM forms a rectangle with a specific energy bandwidth. For example, for a crystal placed horizontally in DCM, photons of different energies and angles do not have a specific distribution in the horizontal direction, and the photon distribution in the vertical direction is characterized by the top region comprising lower-energy photons with high diffraction angles and the bottom region comprising higher-energy photons with low diffraction angles. However, because of the dynamic diffraction theory, the exact values of the two coupling quantities, energy, and angle of the photon cannot be quantitatively determined simultaneously. This phenomenon impedes further improvement in measurement accuracy with rocking curves, typically obtained in the presence of divergence-bandwidth coupling.
To decouple the angular divergence and beam bandwidth, a DuMond diagram is used to replace the direct beam after the monochromator [29, 32]. The DuMond diagram was transformed from phase space to real space using a new experimental setup containing an analyzer orthogonal to the DCM and a 2D detector. A DuMond diagram can be imaged directly on a detector by diffracting the beam after DCM horizontally, resulting in a specific location distribution of photons with different energies and horizontal divergence angles [27]. In the rectangular cross-section of the beam, the vertical axis allows accurate determination of the vertical divergence angle, and the horizontal axis is used to determine the energy accurately. After decoupling the divergence bandwidth, a DuMond diagram imaged in real space can characterize a monochromator with high precision.
The diffraction lattice planes and probe energies were considered. The DuMond diagram is based on the relationship between the diffraction angle θ and wavelength λ in the Bragg formula for X-rays. At equal wavelengths, higher indices, such as 333 and 555, had narrower Darwin widths and gentler slopes than the lower index of 111. For example, for the diffractions of Si(111), (333), and (555) with energies of 18 keV, the Darwin widths were
Considering the integrated aspects of the experimental implementation, detection, and precision, we chose an index of 333 and an energy of 18 keV. The 333 diffraction has an energy resolution of 1/14.5 of the 111 diffraction, which can improve the resolution by more than one order of magnitude. Because synchrotron radiation has a broad spectrum, the λ and λ/3 components corresponding to the indices 111 and 333 exist simultaneously in the DCM beam. The measurements were obtained with 333 diffractions at 18 keV, whereas the monochromator crystal Si(111) was operated at 6 keV.
DuMond diagram of an ideal working DCM
DCM with two identical Si crystals is commonly used in synchrotron radiation beamlines. The first crystal diffracts the incident white beam at a certain wavelength and bandwidth to the second crystal. The second crystal diffracts the monochromatic beam to maintain the original direction of the incoming beam, which is insusceptible to diffraction angle variation. Ideally, the two perfect crystals with equal indices are flat and symmetric, and the DuMond diagrams of the DCM are parallelograms (whether detuned or not).
In the next section, we briefly describe the detuning phenomenon of two flat crystals to distinguish it from the thermal deformation case. The intensity of the beam exiting the DCM was maximized when the diffraction planes of the two crystals were perfectly parallel. Any deviation from the parallel state is known as detuning and is quantified by the deviation angle from the parallel position, the detuning angle. Assuming a slight detuning angle α between the two crystals without thermal deformation, the DCM beam intensity at a particular energy E is proportional to the following factors [34]:
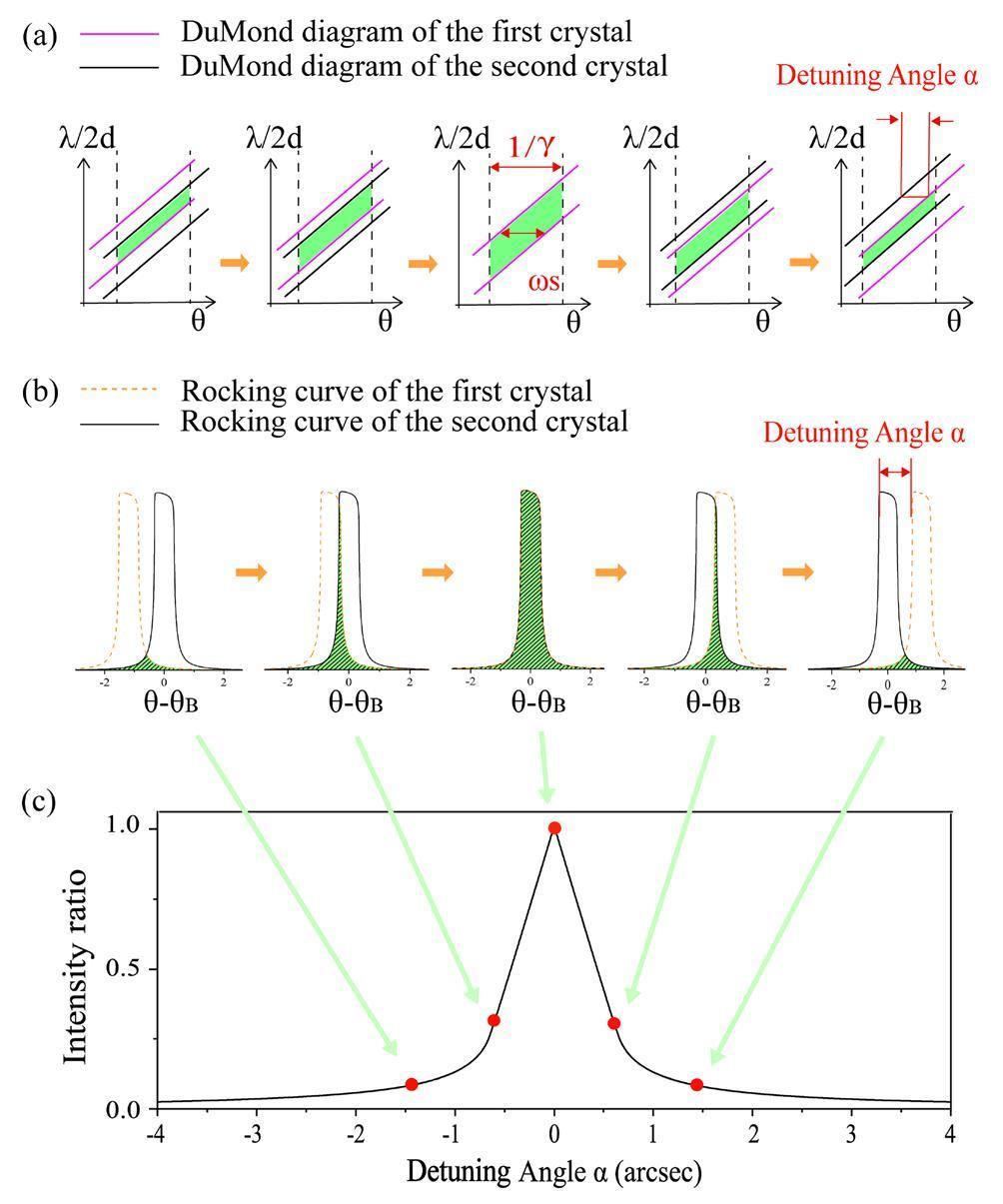
In addition to the total beam intensity, geometrically representing the diffraction process using DuMond diagrams is more intuitive. We began with a condition without thermal deformation, as illustrated in Fig. 1(a), which shows a DuMond diagram of an ideal DCM. The two vertical black dotted lines indicate the angular divergence range of the incident synchrotron radiation (the divergence angle of the bending magnet light source was approximately 1/γ). The red and black oblique lines indicate the dynamic diffraction bands (DuMond diagram) of the first and second crystals, respectively, and α is the detuning angle between the two crystals. The colored area is the overlapping part of the DuMond diagrams of the two crystals, the DuMond diagram of DCM. It depicts how the diffraction beam varies with the detuning angle: as the detuning angle α increases, the horizontal width of the DuMond diagram narrows, and the photon intensity decreases. Figure 1(b) shows the θ-I sectional profile of the DuMond diagram (with the intensity axis I perpendicular to the surface of the paper), that is, the rocking curves of the first and second crystals. Here, the colored area represents the overlapping part of the two rocking curves corresponding to the beam intensity. α is the detuning angle between the two crystals, which varies as the rocking curve of the first crystal translates, whereas the rocking curve of the second crystal remains fixed. Figure 1(c) shows the relationship between the beam intensity and detuning angle α, which is obtained from the overlapping areas of the two rocking curves at different detuning angles in Fig. 1(b). When the two crystals were parallel (α=0), their rocking curves completely overlapped when the beam intensity reached its maximum value. As the absolute value of the detuning angle α increased, the overlapping area of the two rocking curves and the beam intensity decreased.
Figure 1 illustrates the primary principles of the measurement method reported in this study. It is essential to emphasize that although this may appear similar to scanning rocking curves, there are distinctions between the two methods owing to the experiments. Compared with scanning rocking curve, the θ-I-sectional profile of the DuMond diagram was obtained by removing the divergence-bandwidth coupled photons from the beam. In addition, the latter is directly obtained in one image without rotating the monochromator; therefore, the incident power density and thermal deformation do not vary.
DuMond diagram of a DCM with deformed crystal
Under ideal conditions without thermal deformation, regardless of the detuning angle, the lattice planes of the two crystals were flat. In real operation, the first crystal of the DCM is irradiated with a high-power white beam, which causes lattice deformation and expansion. The beam incident on the second crystal is already monochromatic; thus, its heat power is negligible [7]. The deformation can be interpreted as follows. The crystal surface is divided into numerous flat minute-area cells along the beam footprint, with one microfacet of the first crystal and one microfacet of the second crystal constituting a microfacet pair. The total intensity of the beam exiting the DCM is the sum of the intensities of all microfacet pairs. The detuning angles α are identical for every microfacet pair without thermal deformation. When the first crystal surface undergoes thermal lattice deformation, the normals of microfacets at different positions x on the first crystal are tilted by different angles Δα, whereas the normal direction of each microfacet on the second crystal remains constant. The detuning angle between a pair of microfacets is
Then Eq. (2), and Eq. (3) can be rewritten as follows:
As shown in Fig. 1(a), DuMond diagrams of ideal DCM are always parallelograms. The sequence of parallelogram DuMond diagrams shows the detuning phenomenon on the timescale introduced by rotating the adjustable crystal. This is significantly different from the distorted DuMond diagrams that show the spatial distribution of the detuning phenomenon induced by thermal deformation. Similarly, Fig. 2(a) shows DuMond diagrams representing the diffraction process of a deformed crystal. For a point light source, the diffraction-angle range of the flat crystal is limited only by the angular divergence of the light source, as shown in the upper right diagram in Fig. 2(a). However, the diffraction angle range of the deformed crystal is bounded by both the source angular divergence and angular deformation of the crystal surface, as shown in the upper left diagram of Fig. 2(a). It is necessary to consider the physical meaning when two such crystals comprise a DCM. To unify the angle ranges of the two DuMond diagrams, the transverse axis of the actual diffraction angle θ is replaced by the light-source divergence angle θ′, as illustrated in the lower diagrams of Fig. 2(a). Beams with different divergence angles were incident on the microfacets of the first crystal, which had different local deformation angles Δα. These deformation angles change the actual diffraction angle of the first crystal and introduce local offsets into the DuMond diagram. The DuMond diagram of the DCM with a macroscopic detuning angle α0=0 is shown on the lower left and the DuMond diagram of the DCM with a small macroscopic detuning angle α0is shown on the lower right. Comparing to Fig. 1(a), the DuMond diagram of the DCM with a deformed crystal undergoes a significant distortion in shape and shifts its position as the macroscopic detuning angle of the DCM varies.
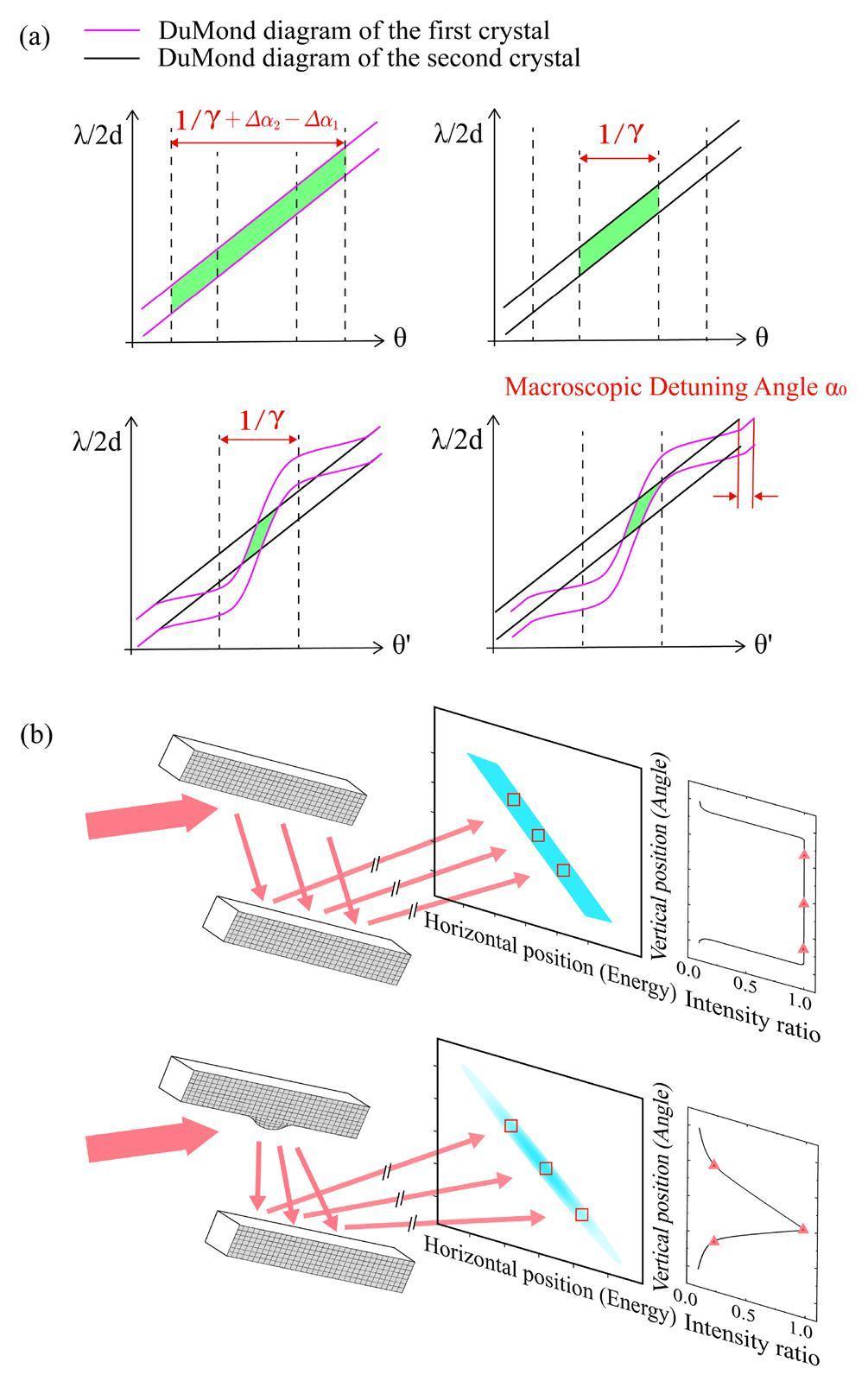
The experimental configuration allowed us to directly observe the DuMond diagrams of the monochromator under the operational conditions. As shown in Fig. 2(b), the upper figure illustrates a DCM crystal without thermal deformation, whereas the lower figure depicts a DCM crystal with thermal deformation. The beam underwent sequential longitudinal diffraction by the two crystals and subsequent horizontal diffraction by a downstream analyzer (omitted in the figure). The resulting image on the 2D detector was a divergence-bandwidth-decoupled light spot corresponding to the DuMond diagram of the DCM. The ordinate represents the vertical divergent angle of the beam exiting the DCM, the abscissa represents the energy distribution of the beam decoupled by the analyzer crystal, and the color shades represent the photon intensity. Without thermal deformation, the DuMond diagram appears as a parallelogram of uniform color. With thermal deformation, the DuMond diagram assumed a willow-leaf shape with an uneven color distribution. The distortion of the DuMond diagram can be quantified by the intensity loss, as illustrated by the rightmost integral intensity curve in Fig. 2(b). After eliminating the energy effects through horizontal integration, only the two-dimensional correspondence between the longitudinal divergence angle and the intensity was retained. The rightmost integration curve corresponds to the intensities of microfacet pairs at different longitudinal positions on the crystal surface. For a certain α0, the output intensity of a pair of microfacets is directly related to the deformation angle Δα. The central width of the willow-leaf-like DuMond diagram was comparable to that of the parallelogram DuMond diagram and progressively diminished as the position moved away from the central region. Meanwhile, both ends of the rightmost integral intensity curve show a decline.
Experiment
Synchrotron radiation from a bent magnet is uniform in the horizontal direction; for our analysis, we assume that the cooling effect of the first crystal is also horizontally uniform [35]. In this context, the 1D crystal profile along the propagation direction of the beam is sufficient to characterize the crystal thermal deformation. Utilizing the special machine time for commissioning a new beamline of the SSRF [36], we established a measurement system with an orthogonal analyzer crystal at BL09B. The behavior of the lattice deformation of the first crystal versus the increase in the ring current can be observed.
Experimental configuration, instruments, and parameters
An energy of 6 keV was selected as the operating energy of DCM Si(111), where the Bragg angle was 19.24, and the energy of the Si 333 diffraction was 18 keV. The experimental setup is illustrated in Fig. 3. With the light source as the origin point, the white light slit, DCM, and beryllium window were located at locations of 18.2 m, 21 m, and 38 m, respectively. The analyzer crystal Si(333) was at a distance of 39 m from the light source and was orthogonal to the crystals inside the DCM. The 2D detector is at a distance of 0.5 m from the analyzer crystal, and the dynamic range of the detector is 12 bits. The white beam is radiated to the DCM, and the monochromatic beam after the DCM is diffracted horizontally and decoupled by the analyzer Si(333), removing the energy-angle coupled photons that cannot satisfy both the energy and angle criteria. The initial beam with a rectangular cross-section was transformed into a tilted DuMond spot on the 2D detector monitor. The tilt angle, fixed at 45, is consistent because of the fixed and identical index planes for the horizontal and vertical diffraction.

The opening size of the white light slit is 3.15 mm × 1.75 mm (H × V). The horizontal and vertical dimensions of the incident white beam arriving at the front of the DCM are 3.63 mm and 2.02 mm, respectively. The first crystal had dimensions of 50 mm × 70 mm × 15 mm (L × W × H) and was indirectly water-cooled at a temperature of 25 ℃ at a flow rate of 0.9 L/min. After exiting the beryllium window and traveling 1.5 m in the atmosphere, the 6 keV component of the beam decayed to 1.7% of its initial intensity, whereas the 18 keV component remains at 85.7% of its initial intensity. Therefore, it can be concluded that the photons arriving at the 2D detector were 18 keV reflected by the 333.
In this study, a series of DuMond diagrams were obtained under different ring currents using the above experimental configuration. The correspondence between the ring current and the power density of the light source and that of the first crystal surface is shown in Table 1. The calculation was performed using Spectral [37].
| Ring current (mA) | Peak power density of source (W/mrad2) | Total power at crystal surface (W) | Peak power density at crystal surface (W/mm2) |
|---|---|---|---|
| 8.3 | 3.0 | 0.402 | 0.020 |
| 9.9 | 3.6 | 0.482 | 0.023 |
| 19.8 | 7.2 | 0.964 | 0.047 |
| 48.3 | 17.5 | 2.352 | 0.113 |
| 85.7 | 31.0 | 4.174 | 0.201 |
| 94.4 | 34.1 | 4.598 | 0.222 |
| 148.2 | 53.6 | 7.223 | 0.348 |
| 170.9 | 61.8 | 8.712 | 0.420 |
| 197.5 | 71.4 | 9.738 | 0.469 |
| 220.3 | 79.7 | 10.727 | 0.517 |
Experimental procedure and results
To compare and demonstrate the distortion of the DuMond diagram, we observed DuMond diagrams at a low storage ring current (9.9 mA) measured with 333 diffraction and 18 keV and DuMond diagrams at a high storage ring current (220.3 mA) measured with 111 diffraction and 6 keV. The DCM of BL09B is equipped with a precision rotation mechanism consisting of a motor and piezoelectric device on the first crystal, which can alter the macroscopic detuning angle α0 between the two crystals by rotating the first crystal.
Figure 4 shows the DuMond diagrams of the DCM decoupled by an orthogonal analyzer, sampled at an exposure time of 500 ms. The ordinate and abscissa represent the original vertical angle distribution and the wavelength of the beam from the DCM, respectively. Both axes are expressed in detector pixels, and the brightness of the spot indicates the beam intensity. Fig. 4(a) and 4(b) show the measurement results for indices 111 and 333, respectively, at different macroscopic detuning angles α0. Figure 4(a) and 4(b) show that when the detuning angle α0=0, the DuMond diagram has the maximum intensity and full width at half maximum (FWHM), regardless of whether the indexes are 111 or 333. The light spot intensity and transverse size decreased as the detuning angle increased. It is also worth emphasizing that all the measured spots had the basic shape of a parallelogram in either case. This result can be interpreted as follows: at a low current, the heat load on the crystal is marginal, and the detected thermal deformation is not significant, even if we used a Si 333 analyzer. At a high current, the heat load on the crystal was high, and the thermal deformation on the crystal surface was significant. However, the basic shape of the observed DuMond diagram remains a parallelogram owing to the low sensitivity of the diffraction index 111.

To verify whether the willow-leaf-like distortion of the DuMond diagram was due to thermal lattice deformation, we maintained a higher ring current of 220.3 mA and measured DuMond diagrams with 333 diffractions. Figure 4(c) shows the willow-leaf-like DuMond diagrams at different macroscopic detuning angles α0, which were altered by rotating the first crystal forward and reverse. The brightest position in the spot corresponds to the minimum detuning angle
Figure 4(d) shows the DuMond diagrams obtained when DCM was operated under different storage ring currents. The beam was held in each state for a period to ensure that all samples were in an equivalent operating condition, except for the ring current. As the ring current increased to 85.7 mA, the DuMond diagram showed a distinct nonuniform intensity distribution: the spot intensity was higher in the middle and lower at both ends in both the energy and angle directions. As the ring current increases to 148.2 mA, the DuMond diagram transforms from a uniform parallelogram to a willow-leaf shape with narrow ends. This suggests that the spatial detuning phenomenon characterized by the local deformation angle Δα(x) is a consequence of the heat load on the DCM. In addition, the presence of local light or dark points in the figure can be attributed to crystal defects. These points do not vary with increasing current but can be eliminated by varying the position of the crystal surface receiving light during the measurement.
Data analysis and discussion
The distortion in the DuMond diagram originates from the local deformation angle Δα(x). Thus, the thermal deformation profile of the first crystal can be obtained by quantitatively analyzing the willow-leaf DuMond diagram. We consider a DuMond diagram with α0=0 in Fig. 4(c) as an example to illustrate data processing briefly.
Assuming that the light is a point source, the coordinates of the spot on the detector can be backtracked to the footprint coordinates on the first crystal surface using geometric optical tracing. It can be theoretically determined that the vertical footprint size of the first crystal is 6.07 mm. The pixel size of the 2D detector is 7.4 μm, which corresponds to 11.9 μm on the first crystal surface, considering the angular divergence of the beam and the distance between the detector and the monochromator. Figure 5(a) shows the contour plot of the DuMond diagram with α0=0 shown in Fig. 4(c) after the ordinate is converted. The measured size of the light footprint on the first crystal surface in the vertical direction is 5.9 mm.
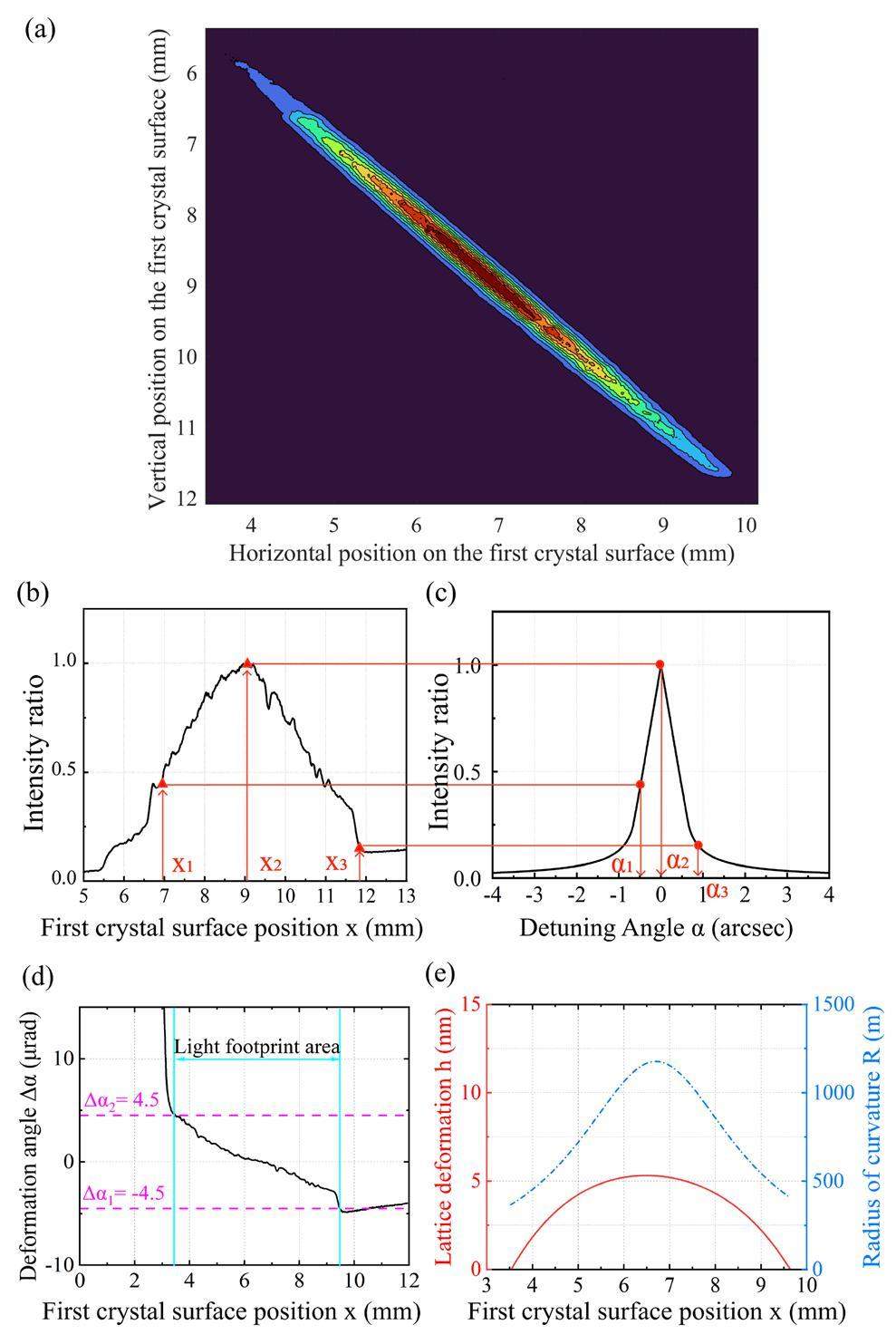
Figure 5(b) shows the relative intensity I(x) at various positions x in the vertical direction within the light footprint of the first crystal. It is derived from Fig. 5(a) by removing the background intensity, transversely integrating it, and normalizing it based on the maximum intensity. The maximum relative standard deviation resulting from the statistical fluctuation in the photon number was 2.6%. In Fig. 5(c), the relative intensity I(α) with different detuning angles α is presented and calculated in the same manner as that shown in Fig. 2(c)). The deformation angle Δα(x) on the first crystal surface was determined by substituting the measured intensity distribution I(x) at different locations into the calculated intensity distribution I(α) at different detuning angles. For example, the detuning angles at the positions x1, x2 and x3 are Δα(x1)=α1, Δα(x2)=α2, Δα(x3)=α3, respectively. The deformation angle distribution Δα(x) on the first crystal surface is shown in Fig. 5(d).
In geometric measurements, a common indirect representation method uses normal direction information [38]. The deformation angle distribution Δα(x) characterizes the deformed surface of the first crystal. Integrating Δα(x) over x yields the height h(x) of the deformation profile on the first crystal surface, as indicated by the solid red line on the left axis in Fig. 5(e). The maximum relative standard deviation was 4.2%, and the maximum standard deviation was 0.1nm. It should be noted that the zero value of height h(x) in Fig. 5(e) shows the initial point of the integration. Value of the point is an artificially set relative zero value. By fitting the deformation height h(x) once and then differentiating the fitting result with respect to x twice, the reciprocal of the absolute value of the differential result is the radius of curvature R(x) on the first crystal surface, which is indicated by the blue dotted line on the right axis in Fig. 5(e). There are inflection points but no extreme points on either side of the radius curve because the operando optics method can only measure deformations within the light footprint, and the extreme points may have been outside the range of the light footprint.
We now focus on the thermal deformation at different ring currents. We dealt with the observations using the above method for ring currents 8.3 mA, 19.8 mA, 48.3 mA, 85.7 mA, 94.4 mA, 148.2 mA, 170.9 mA, and 197.5 mA. Figure 6(a) shows the surface morphology of the first crystal after irradiation with X-ray beams with different ring currents. The vertical coordinates represent the deformation height, the transverse coordinates represent the light footprint coordinates on the first crystal surface, and the oblique coordinates represent the total incident power.
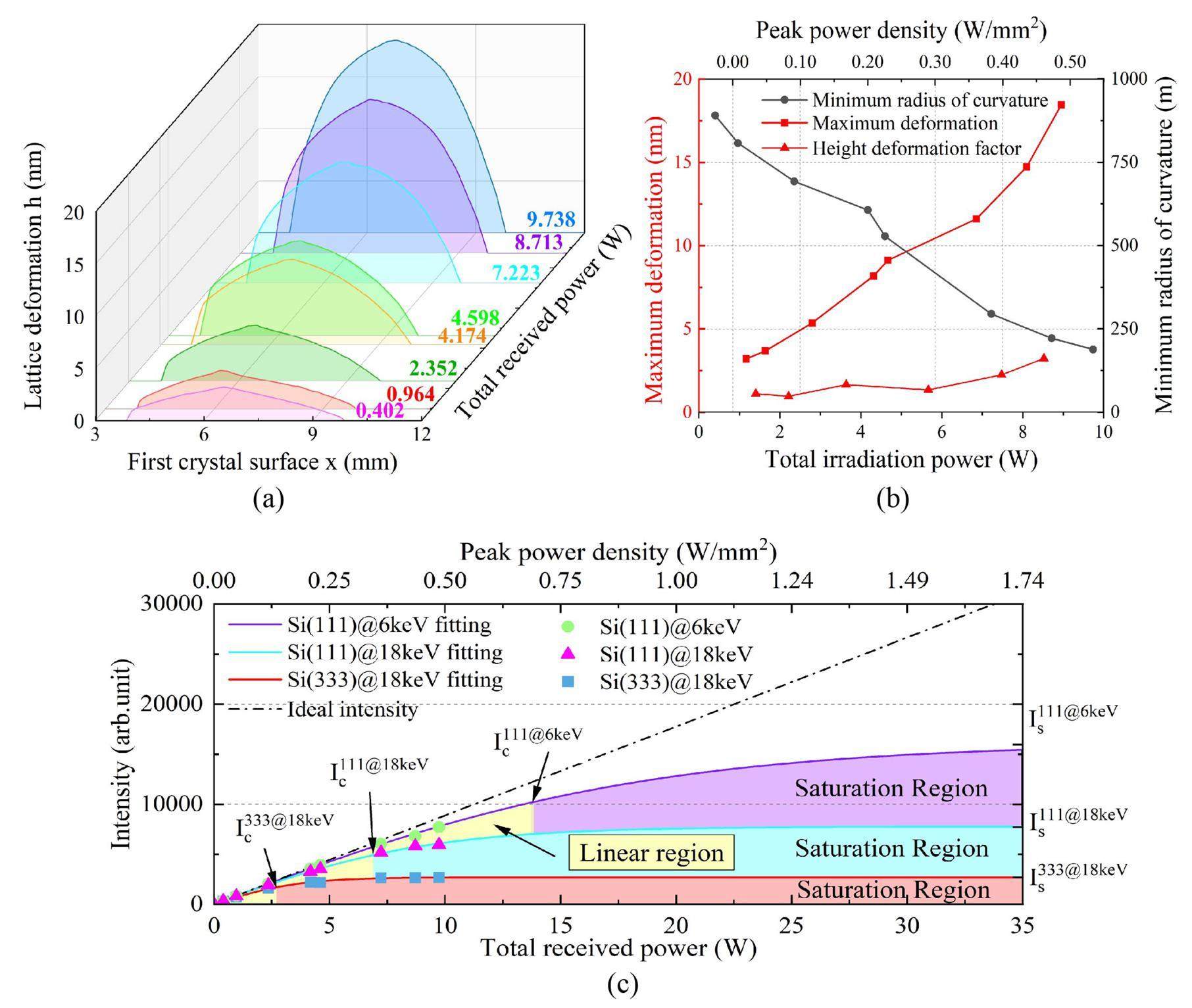
Figure 6(b) shows the variations in the maximum deformation height, height deformation factor, and radius of curvature at the center of the light footprint with incident power and power density. With increasing incident power and power density, the maximum height of the lattice deformation increases from 3.2 nm to 18.5 nm, and the radius-of-curvature at the profile center decreases from 891 m to 188 m. Theoretically, the maximum deformation should be proportional to the total absorbed power at this temperature range of the silicon crystal. However, the experimental results did not linearize the relationship between the measured maximum deformation and incident power. With increasing incident power and power density, the deformation factor of the maximum deformation increases by three times from 1.1 nm/W to 3.2 nm/W. This implies a decrease in the actual cooling effect of the system.
The intensity of the beam exiting an ideal monochromator is directly proportional to that of the incident beam. Nevertheless, with increasing incident power, thermal effects disturb the normal operation of the optics. Typically, cooling serves as a background function to ensure proper operation of the monochromator, whereas thermal deformation measurements evaluate the cooling technology. These measurements are not typically presented as direct characterization indicators, making it essential to establish a connection between thermal deformation and monochromator performance.
In this study, the more sensitive 333 diffraction was utilized to diagnose thermal deformation, whereas monochromators generally operated at lower indices in applications. For this reason, it is important to consider the performance of Si(111) diffraction. Figure 6(c) illustrates the variation in the DCM output beam intensity at the BL09B beamline. The black dashed line represents the ideal output intensity of 18 keV photons in Si(333) diffraction without thermal deformation. The blue rectangular scatter plot depicts the measured output intensity of the 18 keV photons in Si(333) diffraction. The inferred beam intensity of Si(111) diffraction at 18 keV is shown as a green circular scatter plot, and that at 6 keV is shown as a magenta triangular scatter plot. The curves of intensity I(α) at different detuning angles for Si(111)@18 keV and Si(111)@6 keV can be calculated in the same manner as shown in Fig. 1(b) and 1(c). The output beam intensity of the Si(111) diffraction can then be inversely inferred by incorporating the measured deformation angle Δα(x) into the calculated intensity curves I(α). As the incident power increased, the actual measured Si(333) diffracted output beam intensity of 18 keV tended to saturate significantly, and the calculated Si(111) diffracted output beam intensities of 6 keV and 18 keV deviated from the proportional straight line.
The saturation of the output intensity can be demonstrated intuitively by a preliminary fitting of the experimental data using the hyperbolic tangent function
Referring to the definition of the time constant, we consider (1-1/e) times the saturation intensity as the critical point for evaluating the cooling limit of the monochromator or the maximum input power that the monochromator can withstand using certain cooling technology. Before reaching the critical intensity, Ic=(1-1/e)Is, the crystal can be considered to be in an operating condition with efficient heat treatment, and the output intensity increases linearly with the input intensity. The thermal treatment effect is poor when the output beam exceeds the critical intensity. Even if the incident power is continuously increased, the increase in the output beam intensity is quite limited. Thermal deformation of the monochromator crystal limits the intensity growth; however, we can expand the linear working region of the monochromator by improving its working conditions. For a certain diffraction crystal plane and light wavelength, for example, the critical point can be shifted backward by optimizing the heat-treatment design and reducing the temperature gradient on the crystal surface.
Conclusion
Compared to computer simulations, there is a need for high-precision inspection techniques for thermal lattice deformation, which is one of the underlying factors affecting the performance of monochromators. In this paper, we present a new method for efficiently characterizing the thermal lattice deformation of monochromator crystals under service conditions, report nanometer-scale thermal lattice deformation profiles of an indirectly water-cooled DCM at a bent magnet beamline, and predict the performance of the monochromator under this cooling condition at higher incident power. The method presented in this report has nanoscale resolution, with a measurement time of only a few hundred milliseconds while the DCM is in operation. These features make it possible to monitor the thermal deformation of the monochromator in real time without interrupting downstream experiments. Furthermore, these results and future measurements at higher power densities and different cooling systems provide solid constraints for computer simulations of thermal treatment design and serve as an anchor for combining simulation calculations with actual operations.
Monochromators for X-ray synchrotron radiation
. Phys. Rep. 152, 1-71 (1987). https://doi.org/10.1016/0370-1573(87)90080-9A double-crystal monochromator for the photon-factory wiggler beamline
. Nucl. Instrum. Meth. Phys. Sect. A 246, 368-372 (1986). https://doi.org/10.1016/0168-9002(86)90110-5Performance of a cryogenically cooled monochromator for an in vacuum undulator beamline
. J. Synchrotron. Rad. 10, 313-319 (2003). https://doi.org/10.1107/S0909049503012135A water-cooled monochromator for the B16 Test beamline at the Diamond Light Source: Capabilities and performance characterization
. J. Synchrotron Rad. 26, 253-262 (2019). https://doi.org/10.1107/S1600577518014662Cryo-cooled silicon crystal monochromators: A study of power load, temperature, and deformation
. J. Synchrotron Rad. 29, 377-385 (2022). https://doi.org/10.1107/S160057752200039XThermal deformation of cryogenically cooled silicon crystals under intense X-ray beams: Measurement and finite-element predictions of the surface shape
. J. Synchrotron Rad. 20, 567-580 (2013). https://doi.org/10.1107/S0909049513009436Thermal bump removal of a crystal monochromator by designing an optimal shape
. Nucl. Instrum. Meth. Phys. Res. Sect. A 710, 155-160 (2013). https://doi.org/10.1016/j.nima.2012.11.041Expected thermal deformation and wavefront preservation of cryogenic Si monochromator for Cornell ERL beamlines
. J. Synchrotron Rad. 21, 366-375 (2014). https://doi.org/10.1107/S1600577514000514Design simulations of a horizontally deflecting high-heat-load monochromator
. J. Synchrotron Rad. 28, 91-103 (2021). https://doi.org/10.1107/S1600577520014009Performance limits of indirectly cryogenically cooled silicon monochromators–experimental results for APS
. J. Synchrotron Rad. 8, 22-25 (2001). https://doi.org/10.1107/S0909049500013868Performance of a silicon monochromator under high heat load
. J. Synchrotron Rad. 21, 315-324 (2014). https://doi.org/10.1107/S1600577513033158In situ visualization of thermal distortions of synchrotron radiation optics
. Nucl. Instrum. Meth. Phys. Res. Sect. A 576, 422-429 (2007). https://doi.org/10.1016/j.nima.2007.02.110Heat bump on a monochromator crystal measured with X-ray grating interferometry
. J. Synchrotron Rad. 20, 300-305 (2013). https://doi.org/10.1107/S0909049513001817Infrared properties of high-purity silicon
. Opt. Lett. 45, 4935 (2020). https://doi.org/10.1364/OL.393847Potential of cryogenic silicon and germanium X-ray monochromators for use with large synchrotron heat loads
. Nucl. Instrum. Meth. Phys. Res. Sect. A 246, 434-436 (1986). https://doi.org/10.1016/0168-9002(86)90126-9Microchannel water cooling of silicon X-ray monochromator crystals
. Rev. Sci. Instrum. 63, 433-436 (1992). https://doi.org/10.1063/1.1142722High heat load Diamond monochromator project at ESRF
, in SRI 2009, 10th International Conference on Radiation Instrumentation, pp. 229–232, (Large surface-area diamond (111) crystal plates for applications in high-heat-load wavefront-preserving X-ray crystal optics
. J. Synchrotron Rad. 23, 1118-1123 (2016). https://doi.org/10.1107/S1600577516011796Recent experiments with liquid gallium cooling of crystal diffraction optics a)
. Rev. Sci. Instrum. 63, 1746-1754 (1992). https://doi.org/10.1063/1.1143334Liquid nitrogen-cooled Si crystal monochromator: X-ray, focusing on a controlled heat load
. J. Phys. Conf. Ser. 425, 052008 (2013). https://doi.org/10.1088/1742-6596/425/5/052008A double-crystal X-ray monochromator for the SpLine diffraction and absorption synchrotron bending magnet beamline at ESRF
. J. Phys. Conf. Ser. 425, 052005 (2013). https://doi.org/10.1088/1742-6596/425/5/052005reduced the thermal deformation of InSb crystals using double-bounce HHRMs in the TPS tender X-ray absorption spectroscopy beamline
. J. Synchrotron Rad. 28, 1202-1209 (2021). https://doi.org/10.1107/S1600577521003994New challenges in beamline instrumentation for ESRF upgrade program phase II
. J. Synchrotron Rad. 21, 986-995 (2014). https://doi.org/10.1107/S1600577514015951Review of fully coherent free electron lasers
. Nucl. Sci. Tech. 29, 160 (2018). https://doi.org/10.1007/s41365-018-0490-1Theoretical analysis of the background intensity distribution in X-ray Birefringence Imaging using synchrotron bending-magnet radiation
. J. Appl. Phys. 117, 164902 (2015). https://doi.org/10.1063/1.4918925Historical development of cryogenically cooled monochromators for third-generation synchrotron radiation sources
. J. Synchrotron Rad. 7, 53-60 (2000). https://doi.org/10.1107/S0909049500000650Theory of the use of more than two successive X-ray crystal reflections to obtain increased resolving power
. Phys. Rev. 52, 872-883 (1937). https://doi.org/10.1103/PhysRev.52.872X-ray optics and monochromators for synchrotron radiation
. J. Appl. Phys. 48, 1576-1584 (1977). https://doi.org/10.1063/1.323836Characteristics of multicrystal monfiguration X-ray diffraction and application in characterizing synchrotron beamline bandwidth
. Acta Phys. Sin. 69, 104101 (2020). https://doi.org/10.7498/aps.69.20200165Simple, high-resolution method for measurement of natural relative energy bandwidth of Si(111) double-crystal monochromators
. Nucl. Instrum. Meth. Phys. Res. Sect. A 983, 164526 (2020). https://doi.org/10.1016/j.nima.2020.164526Dynamic diffraction of X-Rays by perfect crystals
. Rev. Mod. Phys. 36, 681-717 (1964). https://doi.org/10.1103/RevModPhys.36.681ShadowOui: A new visual environment for X-ray optics and synchrotron beamline simulations
. J. Synchrotron Rad. 23, 1357-1367 (2016). https://doi.org/10.1107/S1600577516013837The design of the test beamline at SSRF
, in Proceedings of the 13th international conference on synchrotron radiation instrumentation, – SRI2018, p. 060040, (SPECTRA: Synchrotron radiation calculation code
. J. Synchrotron Rad. 8, 1221-1228 (2001). https://doi.org/10.1107/S090904950101425XImprovements in the accuracy and the repeatability of long trace profiler measurements
. Appl. Opt. 38, 5468 (1999). https://doi.org/10.1364/AO.38.005468The authors declare that they have no competing interests.


