Radon migration theory

The one-dimensional steady-state convective and diffusive migrations of radon in porous media can be described as follows: $D\frac{{\partial }^{2}C}{\partial x^2}-\frac{v}{\eta }\frac{\partial C}{\partial x}-\lambda C+\frac{\alpha }{\eta }=\mathrm{0,}$ (1) where C is the radon concentration, Bq m^-3, x is the vertical depth of the porous medium, m, D is the diffusion coefficient of radon in the porous medium, m² s^-1, v is the superficial velocity in the porous medium, m s^-1, η is the porosity, %, α is the free radon production rate, Bq m^-3 s^-1, and λ is the decay constant of radon-222, that is, 2.1×10^-6 s^-1 [27].

The boundary conditions in Eq. (1) are $C(0)=C_a$ and ${\partial C/\partial x|}_{x=h}=0$ at the top and bottom of the porous medium, respectively (Fig. 1). The radon concentration in the boundary air is significantly lower than that in the porous medium; therefore, Ca=0 Bq m^-3 can be assumed. The analytical solution to Eq. (1) is $C(x)=\frac{\alpha }{\lambda n}\left(\begin{array}{l}1+\frac{{\text{e}}^{\frac{x\left(v+\sqrt{4D\lambda {\eta }^2+v^2}\right)}{2D\eta }}\left(v-\sqrt{4D\lambda {\eta }^2+v^2}\right)}{\left(\sqrt{4D\lambda {\eta }^2+v^2}A1+vA1+\sqrt{4D\lambda {\eta }^2+v^2}-v\right)}\hfill \\ -\frac{{\text{e}}^{\frac{x\left(v-\sqrt{4D\lambda {\eta }^2+v^2}\right)}{2D\eta }}\left(v+\sqrt{4D\lambda {\eta }^2+v^2}\right)}{\left(\sqrt{4D\lambda {\eta }^2+v^2}A2-vA2+\sqrt{4D\lambda {\eta }^2+v^2}+v\right)}\hfill \end{array}\right)\mathrm{,}$ (2) $A1={\text{e}}^{2h\frac{\sqrt{4D\lambda {\eta }^2+v^2}}{2D\eta }}\mathrm{,}$ (3) $A2={\text{e}}^{-2h\frac{\sqrt{4D\lambda {\eta }^2+v^2}}{2D\eta }}\mathrm{.}$ (4) The radon exhalation rate can then be theoretically deduced as follows: $E_{\text{a}-\text{c}}\left(x\right)=2\alpha \left(\begin{array}{l}\frac{{\text{e}}^{\frac{x\left(v-\sqrt{4D\lambda {\eta }^2+v^2}\right)}{2D\eta }}}{\sqrt{4D\lambda {\eta }^2+v^2}A2-vA2+\sqrt{4D\lambda {\eta }^2+v^2}+v}\hfill \\ -\frac{{\text{e}}^{\frac{x\left(v+\sqrt{4D\lambda {\eta }^2+v^2}\right)}{2D\eta }}}{\sqrt{4D\lambda {\eta }^2+v^2}A1+vA1+\sqrt{4D\lambda {\eta }^2+v^2}-v}\hfill \end{array}\right)+v{C}_{\text{b}}\mathrm{,}$ (5) where E_a-c is the initial radon exhalation rate, which comprises diffusion and convection, Bq m^-2 s^-1, and C_b is the radon concentration at the porous medium-air interface, Bq m^-3.

Fig. 1Full-screen View

One-dimensional model of radon diffusion in porous media

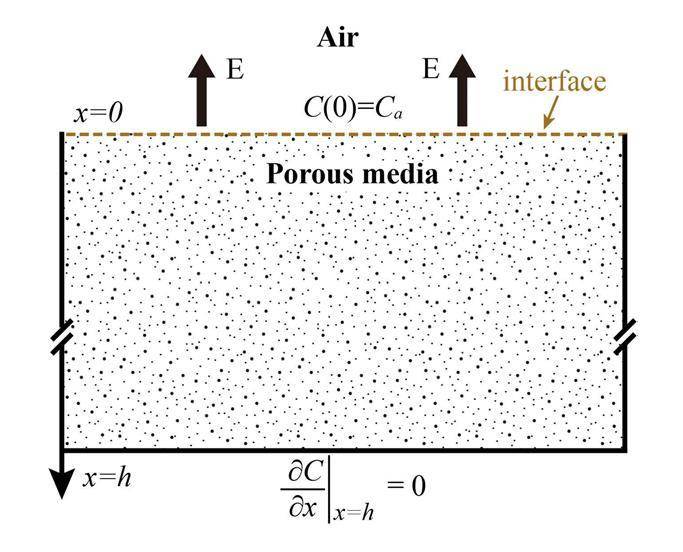
For v = 0 m s^-1, E_a-c becomes E_a, which is the initial radon exhalation rate for diffusion because of the assumption of no convection inside the porous medium.

In-situ measurement parameters

The radon exhalation rate was measured in the field on the surface of a uranium tailing pond located in southern China. A 1-kg sample of uranium mill tailings was collected within the 0–0.4 m depth range and mixed to obtain the following particle size distributions: <0.15 mm (10%), 0.15–0.3 mm (15%), 0.3–0.45 mm (24%), 0.45–1 mm (49%), and >1 mm (2%). After sample drying, the measured particle density was 2500±150 kg m^-3 based on the drained weight method. The mass radon production rate was (7.18±0.26) × 10⁻⁴ Bq kg⁻¹ s⁻¹, as determined by laboratory tests [27, 28] under dry conditions.

A schematic of the flow-through measurement process is shown in Fig. 2. The inlet of the accumulation chamber was connected to the atmosphere via a vent tube. The outlet of the chamber was connected to a flow meter, desiccants, a radon detector (RAD7 from Durridge Company Inc., USA), and a pump used to regulate the flow rate.

Fig. 2Full-screen View

(Color online) (a) In-situ flow-through measurement device and (b)system connection diagram

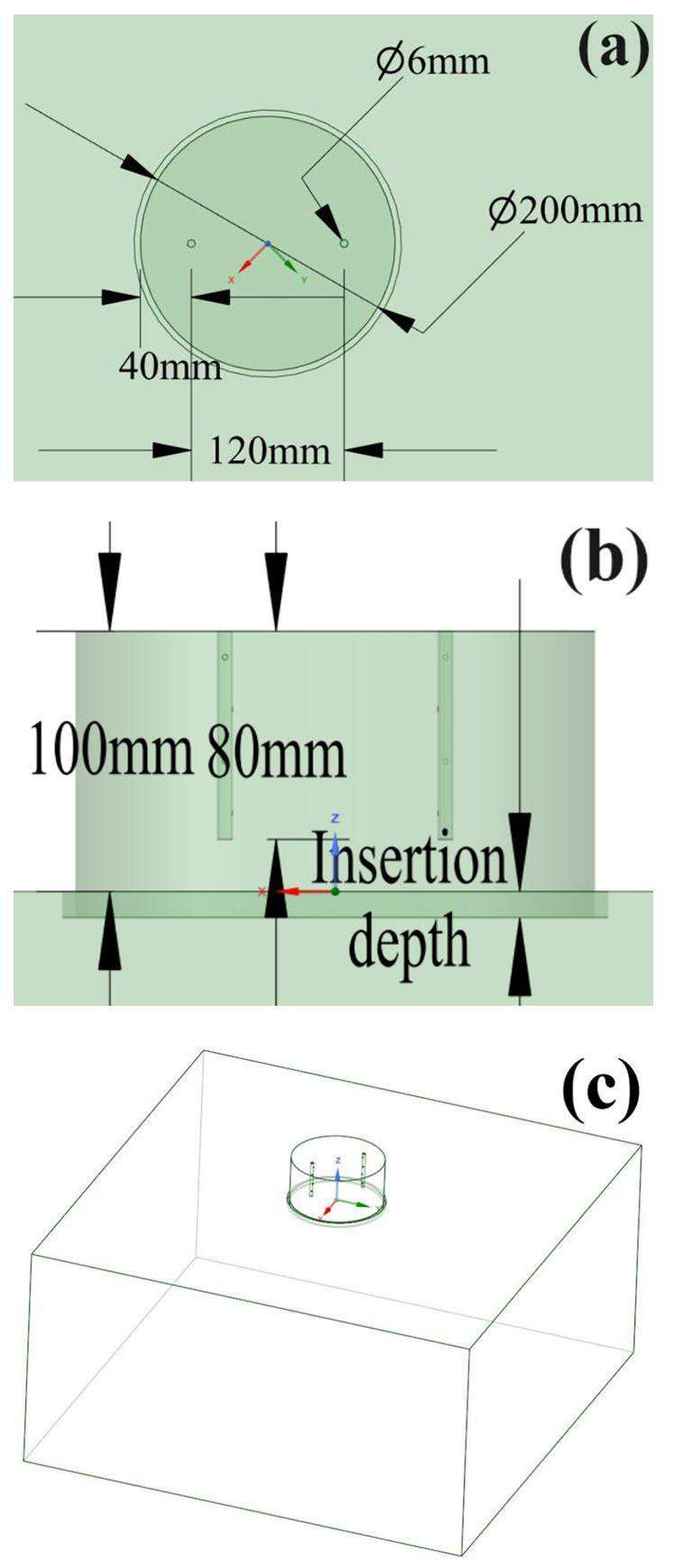
In the experiment, two cylindrical chambers with an inner diameter of Ø20 cm and a wall thickness of 5 mm were prepared. The heights of the two chambers were 11 and 13 cm, with insertion depths of 1 and 3 cm, respectively, suggesting that the effective height inside both chambers was 10 cm. The effect of the flow rate (0.5/1/2 L min^-1) on the radon exhalation rate was also considered. The RAD7 radon detector was calibrated at the Radon Laboratory of the University of South China prior to the experiment.

A digital flow meter (MF4008 of Siargo Ltd., USA) and differential pressure meter (RS-YC-4G-4, Shandong Renke Control Technology Co., Ltd., China) were used to record the flow rate at the outlet of the chamber and the pressure difference between the inside and outside of the chamber, respectively. The soil temperature was 27±1.5 °C and the soil moisture was 12±2%. The soil moisture was monitored using soil sensors (Jinan Keyu Electronic Information Technology Co.). The RAD7 device was operated in the SNIFF mode with a cycle of 5 min for the closed-loop method and 3 min for the flow-through method. Sufficient time (approximately 30 min) was reserved for purification of the RAD7 device after each measurement.

The accuracy of the digital flow meter was ±1.5% of the full reading, with a resolution of 0.01 SLPM. The deviation between the two flow meters at the same flow rate was less than 1%. The accuracy of the digital differential pressure meter was ±3% of the full reading ±0.08 Pa at 25 ℃, with a resolution of 0.01 Pa. The accuracy of the soil sensors was ±0.5 ℃ for the temperature reading and ±2% for the moisture reading.

The increase in the radon concentration in the accumulation chamber can be described as follows: $V\frac{\text{d}C}{\text{d}t}=E{S}_{\text{a}}+Q_{\text{in}}{C}_0-Q_{\text{out}}C-{\lambda }_{\text{Rn}}VC-{\lambda }_{\text{b}}VC-{\lambda }_{\text{l}}VC\mathrm{,}$ (6) where t is the accumulation time, s, E is the radon exhalation rate, Bq m^-2 s^-1, S_a is the inner surface area covered by the chamber, m², Q_out and Q_in are the flow rates flowing out of and into the accumulation chamber, respectively, m³ s^-1, V is the volume of the chamber, m³, λ_b is the back-diffusion rate of radon in the chamber, s^-1, and λ_l is the leakage rate of radon in the chamber, s^-1. Moreover, λ_e is the effective decay constant, which is equal to the sum of the radon decay, back diffusion, and leakage rates (λ_e=λ +λ_b+λ_l) s^-1.

The boundary condition in Eq. (6) is C(0)=C₀. The solution of Eq. (6) is $C\left(t\right)=\frac{E{S}_{\text{a}}+Q_{\text{in}}{C}_0}{Q_{\text{out}}+{\lambda }_{\text{e}}V}\left(1-e^{-\frac{Q_{\text{out}}+{\lambda }_{\text{e}}V}{V}t}\right)+C_0{e}^{-\frac{Q_{\text{out}}+{\lambda }_{\text{e}}V}{V}t}\mathrm{.}$ (7) Once the radon concentration inside the accumulation chamber was stabilized, Eq. (7) became $C\left(t=\infty \right)=\frac{E{S}_{\text{a}}+Q_{\text{in}}{C}_0}{Q_{\text{out}}+{\lambda }_{\text{e}}V}\mathrm{.}$ (8) By replacing λ_eV and Q_inC₀ with 0 as an approximation, based on the assumptions of $E{S}_{\text{a}}\gg Q_{\text{in}}{C}_0$ and $Q_{\text{out}}{}_{\text{e}}V$ [14, 21], Eq. (8) becomes $C\left(t=\infty \right)=\frac{E{S}_{\text{a}}}{Q_{\text{out}}}\mathrm{.}$ (9) Eq. (7) can be simplified to a linear form when $\left(Q_{\text{out}}/V+{\lambda }_{\text{e}}\right)t$ is sufficiently low. $C(t)=\frac{E{S}_{\text{a}}+Q_{\text{in}}{C}_0}{V}t-C_0\left(\frac{Q_{\text{out}}}{V}+{\lambda }_{\text{e}}\right)t+C_0\mathrm{.}$ (10) For C₀ = 0 Bq m^-3, the linear fit solution in Eq. (6) is as follows: $C\left(t\right)=\frac{E{S}_{\text{a}}}{V}t\mathrm{.}$ (11) The linear duration of the increase in the radon concentration for the flow-through method was 1 min owing to the high gas exchange rate in the chamber (a volume of 3.1416 L for the chamber, and a flow rate between 0.5 and 2 L min^-1).

The exponential fit of Eq. (7) and the linear fit of Eq. (11) were applied during subsequent data processing to obtain the fitted radon exhalation rates of E_f-exp and E_f-lin, respectively, with the criterion R²>0.9. R² depends on the residual sum of squares (RSS) and total sum of squares (TSS), which can be calculated as $R=1-\frac{RSS}{TSS}=1-\frac{{\displaystyle \sum _{i=1}^n{\left(y_i-f_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}\mathrm{,}$ (12) where n is the total sum of the data points, yi is the actual data point, fi is the value obtained from the fitted curve, and $\overline{y}$ is the mean value of all data points.

The uncertainty of the radon exhalation rate can be determined as [29] $\sigma E=E\sqrt{{\left(\frac{\sigma A}{A}\right)}^2+{\left(\frac{\sigma B}{B}\right)}^2}\mathrm{,}$ (13) where σE is the uncertainty of the radon exhalation rate, E is calculated as $E=\left(A\times B\times V-Q_{\text{in}}{C}_0\right)/S_{\text{a}}$, and A (defined as $\frac{E{S}_{\text{a}}}{Q_{\text{out}}+{\lambda }_{\text{e}}V}$) and B (defined as $\frac{Q_{\text{out}}+{\lambda }_{\text{e}}V}{V}$), and their corresponding uncertainties σA and σB, respectively, can be obtained via exponential fitting. Because the measurement errors of V, S_a, and Q_in were sufficiently low to be ignored, their contributions to σE were not considered.

Geometric model

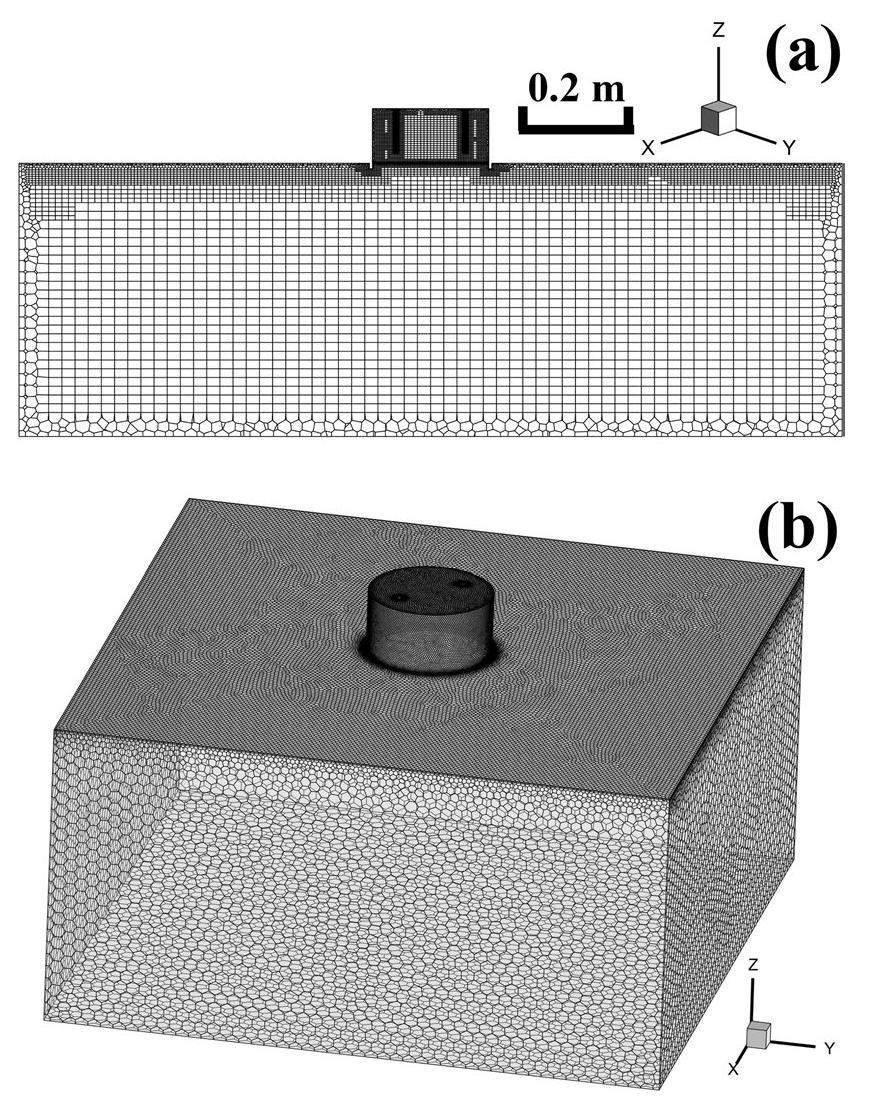
In the numerical simulation, the cylindrical accumulation chamber had a wall thickness of 5 mm, and the internal effective space of the chamber had a height and radius of 10 cm, as shown in Fig. 3. The two vent tubes (Ø6 mm) at the top of the chamber had a length of 8 cm, with four openings (Ø2 mm) in the walls of the tubes. Adjacent openings were spaced 2 cm apart and distributed at 90°, and the resultant confined jet improved the uniformity of the radon concentration inside the chamber. The dimensions of the radium-containing medium were 1 m (length) × 1 m (width) × 0.5 m (height).

Fig. 3Full-screen View

(Color online) Three-dimensional geometric model of the accumulation chamber: (a) Top view, (b) lateral view, and (c) overall view

To discretize the geometry, Fluent meshing was used to generate hybrid meshes that included polyhedral and hexahedral elements. The mesh was refined in regions where the radon concentration and gas flow changed rapidly (for example, the porous medium–air interface and vent tube), as shown in Fig. 4.

Fig. 4Full-screen View

(a) Sectional plane of the discrete mesh where vent tubes are included. (b) Discrete mesh (overall view)

Governing equations

The gas flows in the chamber and porous medium were assumed to be incompressible and followed the laws of mass and momentum conservation. According to the law of mass conservation, the mass-conservation equation can be expressed as follows: $\nabla \cdot \overrightarrow{u}=\mathrm{0,}$ (14) where $\overrightarrow{u}$ is the physical velocity vector, m s^-1.

Following the law of momentum conservation, the momentum-conservation equation can be expressed as follows [30]: $\frac{\partial {\rho }_{\text{a}}\overrightarrow{u}}{\partial t}+\nabla \cdot \left({\rho }_{\text{a}}\overrightarrow{u}\overrightarrow{u}\right)=-\nabla P+{\rho }_{\text{a}}\overrightarrow{g}+\nabla \cdot \left(\overline{\overline{\tau }}\right)-\overrightarrow{F}\mathrm{,}$ (15) where ρ_a is the density of air, kg m^-3, P is the static pressure, Pa, $\overrightarrow{g}$ is the gravitational vector, m s^-2, and $\overrightarrow{F}$ is the source term of the external body forces, N m^-3, which describes the viscosity of the porous medium and applies only to the porous zone. The laminar flow can be described as follows: $\overrightarrow{F}=\eta \overrightarrow{u}\frac{\mu }{K}\mathrm{,}$ (16) where K is the permeability, m², and μ is the dynamic viscosity, Pa s. The viscous stress tensor ($\overline{\overline{\tau }}$) is described as [31] $\overline{\overline{\tau }}=\left(\mu +{\mu }_{\text{t}}\right)\left(\nabla \overrightarrow{u}+\nabla {\overrightarrow{u}}^{\text{T}}\right)\mathrm{,}$ (17) where μ_t is the turbulent viscosity, m² s^-1, which is defined as [31] ${\mu }_{\text{t}}=\rho C_{\mu }\frac{k^2}{\epsilon }\mathrm{,}$ (18) where Cμ denotes a constant, k denotes the turbulent kinetic energy, m² s^-2, and ε is the turbulent dissipation rate, m² s^-3. The governing equation for radon migration can be expressed as $\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial x_{{}_i}^2}-u_i\frac{\partial C}{\partial x_i}+\frac{S_{\text{Rn}}}{\eta }\mathrm{,}$ (19) $u_i=\frac{K}{\eta \mu }\nabla P_i\mathrm{,}$ (20) where D is the radon diffusion coefficient, m² s^-1, ui denotes the physical velocity of convection along the x, y, and z directions, m s^-1, S_Rn denotes the source term, Bq m^-3 s^-1, and Pi denotes the gas pressure along the x, y, and z directions, Pa.

In a given porous medium, S_Rn is determined by the source and decay terms ($S_{\text{Rn}}=-\lambda \eta C+\alpha$), and D=D_m (D_m is the molecular diffusion coefficient of radon in air at 1.05e-×10^-5m² s^-1). In the accumulation chamber, the porosity was set to 1, S_Rn was determined by the decay term ($S_{\text{Rn}}=-\lambda \eta C$), and $D=D_{\text{m}}+D_{\text{t}}$ (D_t is the turbulent viscosity, m² s^-1, which is defined as $\frac{{\mu }_{\text{t}}}{{\rho }_{a}S{c}_{\text{t}}}$, where the turbulent Schmidt number (Sct) is 0.7 [32]).

Simulation parameters

The simulated scenarios involved controlling the insertion depth (H1/H3/H5 corresponding to insertion depths of 1/3/5 cm), flow rate (0.5/1/2 L min^-1), and permeability (1×10^-11/1×10^-10/1×10^-9 m²). The free radon production rate (α) can be obtained as [27] $\alpha =\lambda {\rho }_{\text{s}}{A}_{\text{Ra}}{E}_{\text{Rn}}\mathrm{,}$ (21) where α is the radon production rate, Bq m^-3 s^-1, ρ_s is the density of the porous medium, kg m^-3, A_Ra is the activity concentration of radium, Bq kg^-1, and E_Rn is the radon emission coefficient, which is dimensionless.

The radium activity concentrations in uranium mill tailings commonly range from less than 5 kBq kg^-1 to as high as 10 kBq kg^-1 [33], with an emission coefficient ranging from 0.1 to 0.35 [27], a dry bulk density of 1800±100 kg m^-3, and an average porosity of 0.4, as measured for the samples in the laboratory.

The diffusion coefficient is defined as [27] $D=\tau D_{\text{m}}\mathrm{,}$ (22) where τ is the tortuosity factor, 0.66 (dimensionless) [27, 34].

The calculated diffusion coefficient of radon was 6.93×10^-6m² s^-1. Laminar flow in a porous medium follows Darcy’s law, and permeability, which is an intrinsic property of porous media, can be defined using the Kozeny–Carman empirical equation [35]: $K=\frac{D_{\text{p}}^2}{180}\frac{{\eta }^3}{{\left(1-\eta \right)}^2}\mathrm{,}$ (23) where D_p is the average grain size, mm, and K is the permeability, m².

After sieving the tailing sand in the laboratory, D_p was determined as 0.5 mm on average. K was calculated as 2.47×10^-10 m².

Based on theoretical analysis and references, the determined bulk density was 1800± 100 kg m^-3, the radium activity concentration was 7500 Bq kg^-1, and the emission coefficient was 0.1. Considering the linear relationship between the radon exhalation rate and free radon production rate in Eq. (5), the determined radon production rate was 3 Bq m^-3 s^-1 in the simulations. Owing to the short duration (30 min) of the flow-through measurement and the low saturated radon concentration in the chamber contributing to a smaller back-diffusion effect than that of the closed-loop method, the determined radon diffusion coefficient was 6.93×10^-6m² s^-1. Because permeability is a key parameter representing the ability of gas to flow through a porous medium, the permeability ranges from 1×10^-11 m² to 1×10^-9 m², and the porosity is 0.4 based on references. The physical parameters for the simulations were ultimately determined, as listed in Table 1.

The finite volume method (FVM) was adopted for the numerical calculations. The $k-\epsilon$ turbulence model was used for the chamber zone owing to the confined jet from the four openings on the surface of the vent tube, whereas the laminar model was adopted for the porous medium. The empirical constants in the $k-\epsilon$ turbulence model equations [31] were as follows: Cμ=0.09, $C_{1\epsilon }=1.44$, $C_{2\epsilon }=1.92$, ${\sigma }_k=1.00$, and ${\sigma }_{\epsilon }=1.30$.

To simplify the model, the following assumptions were made: the porous medium was considered homogeneous, and the impacts of gravity and temperature were ignored.

For $Q_{\text{out}}{}_{\text{e}}V$ and t>4V/Q_out (t > 1500 s for Q_out=0.5 L min^-1) in Eq. (7), $e^{-t{Q}_{\text{out}}/V}$<1.9% indicates that the radon concentration in the chamber remained almost stable. A maximum duration of 1800 s was used in the subsequent simulations for the flow-through measurements.

Initial and boundary conditions

The initial radon concentration distribution in the porous medium was calculated prior to simulating the measurements, where the radon concentration at the porous medium–air interface was set to 0 Bq m^-3. The measurement was conducted in transient mode with an initial radon concentration of 0 Bq m^-3 at 0 s in the chamber. The detailed boundary settings are presented in Table 2.

Mesh independence

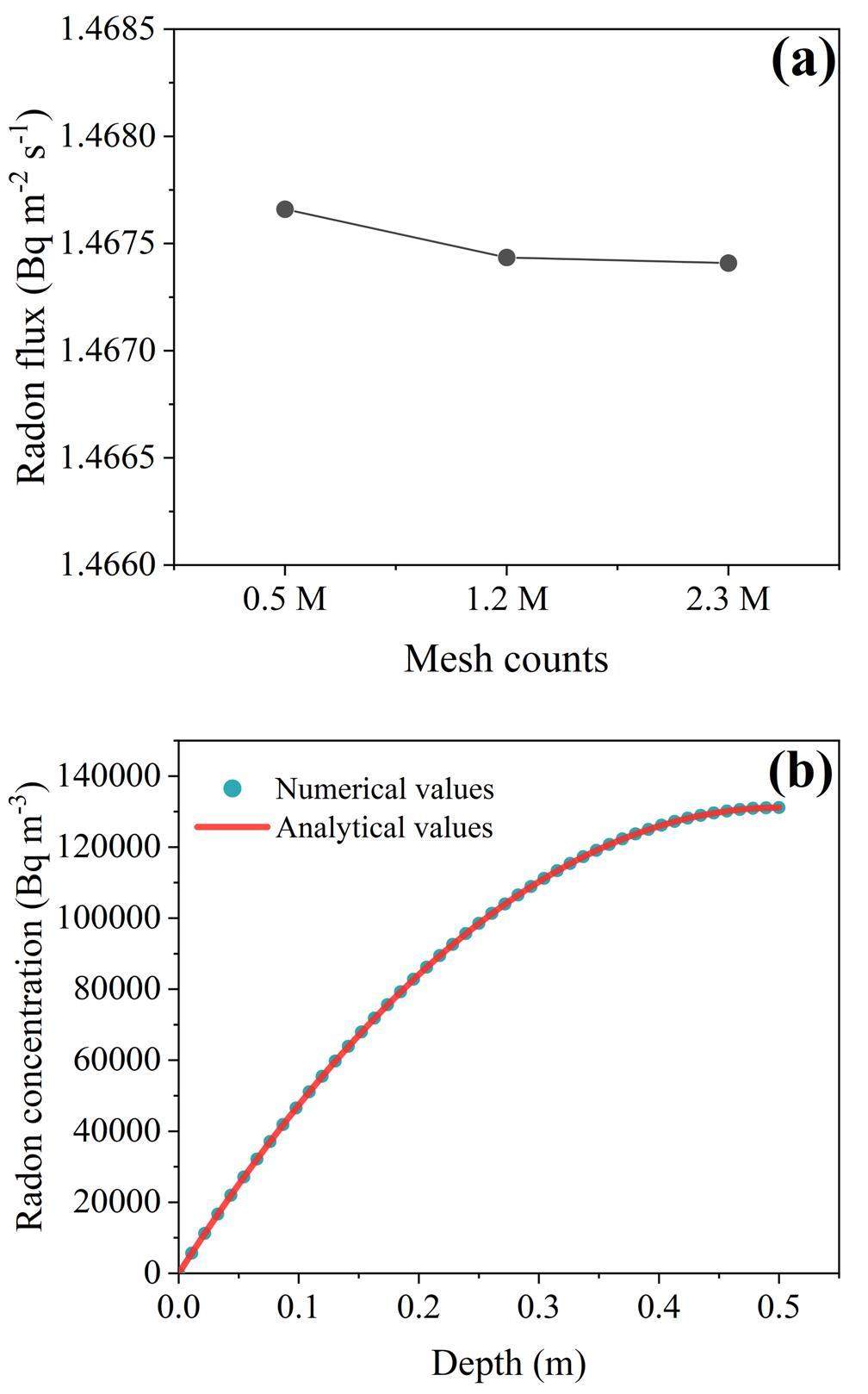
Coarse, medium, and refined (0.5 M, 1.2 M, and 2.3 M cells, respectively) hybrid meshes were generated for the geometric model. Subsequently, a mesh sensitivity analysis was conducted, as shown in Fig. 5. The radon exhalation rate approximately stabilized as the number of cells increased. The criterion for mesh discretization depends on minimizing the error between the numerical and theoretical results while reducing the calculation time. Thus, a medium mesh was used in subsequent simulations.

Fig. 5Full-screen View

(a) Mesh sensitivity analysis. (b) Comparison of the radon concentrations at different depths between the analytical and numerical solutions

The Reynolds number ranged from 89 to 517 according to the minimum (0.66 m s^-1) and maximum (3.8 m s^-1) velocities at the interface of the opening in the wall of the vent tube. By refining the mesh, the mesh sizes for the inlet, outlet, and openings of the tubes ranged from 0.12 to 0.3 mm, and y⁺ reached a maximum value of 3.6 for the tube wall and 2.5 for the chamber boundary, which ensured that rapid flow near the wall was captured.

The simulations were conducted using Ansys Fluent. The steady-state radon-concentration fields of the analytical and numerical solutions were compared before the transient simulations. The analytical and numerical radon concentrations at different depths were determined, and the difference was found to be less than 0.2%. A detailed comparison is presented in Fig. 5b.

The convergence condition was a residual of less than 10^-10 and a difference in the radon exhalation rate between two consecutive iterations of less than 10^-7.

In-situ measurement of the radon exhalation rate

Radon accumulation curves for the closed-loop and flow-through methods are shown in Fig. 6a and b, respectively. The radon exhalation rate was exponentially fitted using Eq. (7), and R² varied between 0.92 and 0.96, as shown in Fig. 6c. The radon concentration in the ambient air was monitored in all measurements, reaching 86 Bq m^-3 on average. The flow rates at the chamber inlet ranged from 3.5×10^-6 to 1.7×10^-5 m s^-1, as monitored using a digital flow meter.

Fig. 6Full-screen View

(Color online) Growth curves of the radon concentration for (a) the closed-loop method and (b) the flow-through method. Correlations between (c) the flow rate and fitted radon exhalation rate and between (d) the flow rate and negative pressure difference

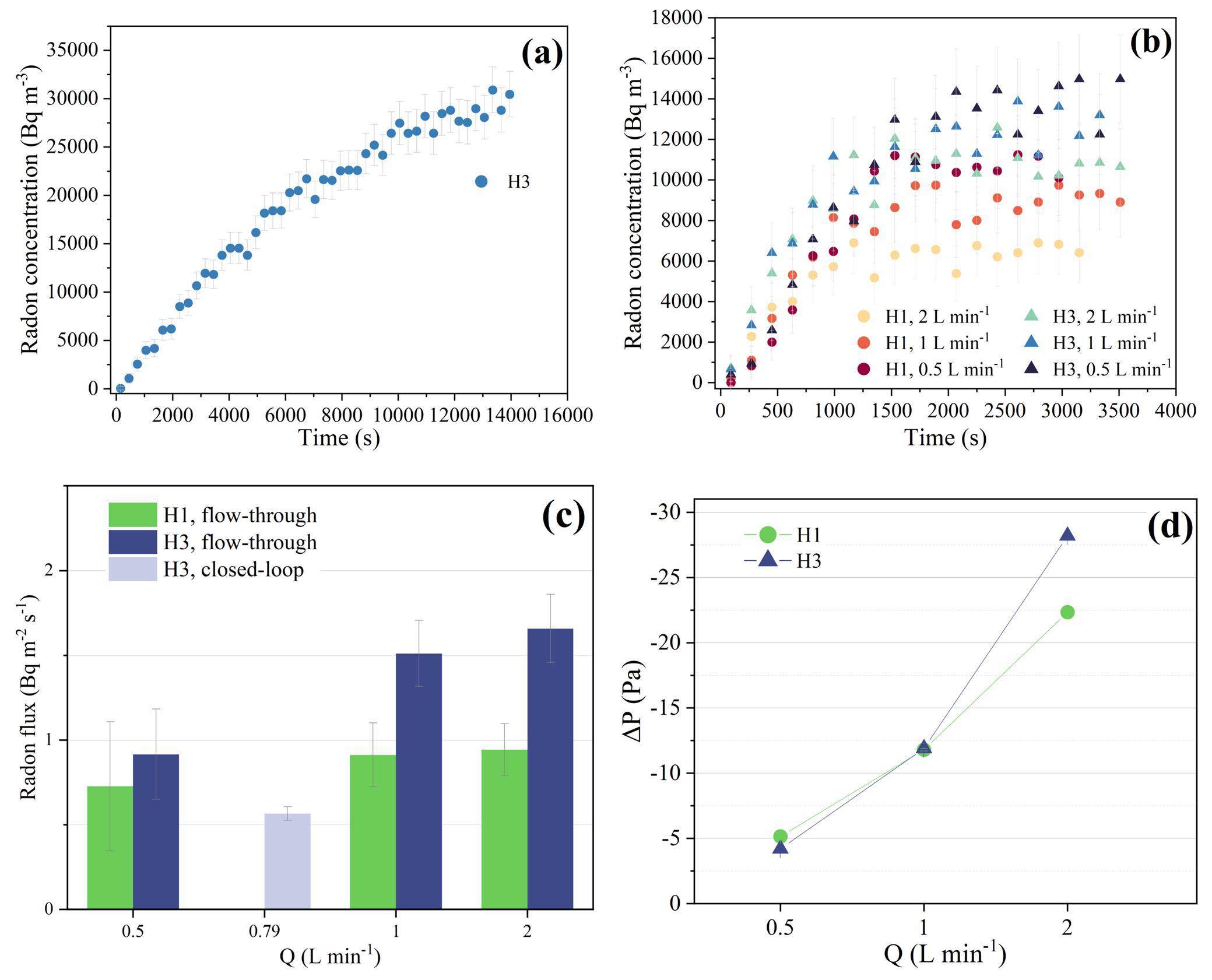
The radon exhalation rate measured using the flow-through method was higher than that measured using the closed-loop method and was positively correlated with the negative pressure difference and flow rate, that is, the higher the flow rate, the greater the radon exhalation rate or negative pressure difference, as shown in Fig. 6d. An increase of 161.88–293.2% (H3) was observed in the fitted radon exhalation rate determined using the flow-through method relative to that of the closed-loop method, with a slight increase at high flow rates between 1 and 2 L min^-1. The negative pressure in the chamber was affected by the variation in the flow rate, with the negative pressure difference increasing by 433.98% for H1 and 671.43% for H3 from 0.5 to 2 L min^-1.

Numerical simulation of the measurements via the flow-through method

5.2.1

Curve and linear fitting method

To comprehensively examine the impacts of the flow rate, insertion depth, and permeability of the porous medium on radon exhalation during the flow-through measurements, CFD-based techniques were employed to simulate the flow-through measurements at insertion depths of 1/3/5 cm, permeabilities of 1×10^-11/1×10^-10/1×10^-9 m², and flow rates of 0.5/1/2 L min^-1. The radon exhalation rate was obtained by applying exponential and linear fits, excluding the first 60 s of the data. The time ranges for exponential fitting were 60–600 s, 720 s, 900 s, 1020 s, 1200 s, 1500 s, and 1800 s, whereas those for linear fitting were 60–240 s, 360 s, 480 s, 600 s, 720 s, 840 s, 960 s, 1080 s, 1200 s, 1320 s, 1440 s, and 1560 s. A minimum duration of 60–600 s was considered for the exponential fitting because of the potential failure to fit data points with a shorter duration. The minimum duration of 60–240 s for linear fitting ensured that three-minute data points could be fitted after excluding the initial first minute of the data, as shown in Fig. 7.

Fig. 7Full-screen View

(Color online) Growth curves for the volume-averaged radon concentration in the chamber (1×10^-10 m², H1). The slope of the linear fit varies with increasing flow rate, whereas the radon exhalation rate of porous materials should remain constant in a specific environment

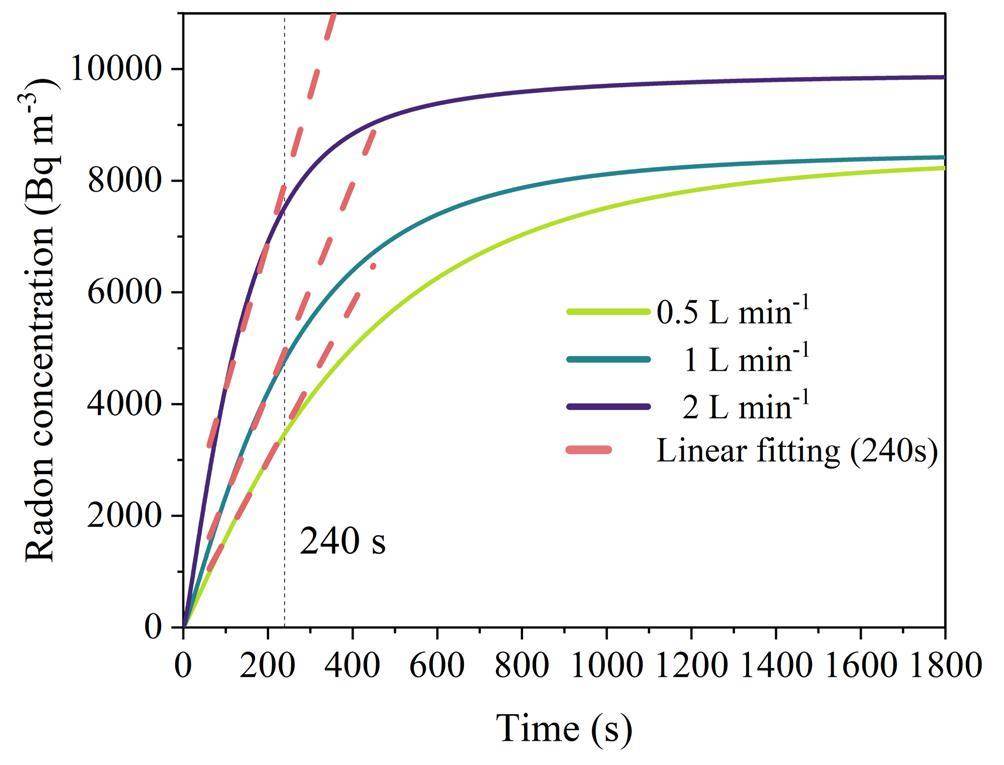
When a linear fit was applied, a short period of linear growth was observed in the flow-through measurements, as shown in Fig. 7. The slope of the linear fit at the same flow rate rapidly decreased with increasing time, whereas the slope differed for different flow rates. Therefore, a linear fit for the radon exhalation rate was not applicable to the flow-through measurements.

In addition, the radon accumulation in the chamber at 1800 s was close to saturation, and the steady-state radon concentrations were 8457.508, 8500.607, and 9714.73 Bq m^-3 at flow rates of 0.5, 1, and 2 L min^-1, respectively. The radon exhalation rates were calculated to be 3.93, 7.06, and 16.04 Bq m^-2 s^-1 using Eq. (9) and 1.89, 2.94, and 5.79 Bq m^-2 s^-1 using Eq. (8), respectively. The former values were significantly higher than the latter, suggesting that λ_eV in Eq. (8) cannot be ignored in the flow-through measurements because this term, rather than the negative value in the closed-loop method, can reach a positive value in view of the observed negative pressure difference in the field experiments. Therefore, calculating the radon exhalation rate using Eq. (9) is also inapplicable to flow-through measurements.

At $t>4V/\left(Q_{\text{out}}+{\lambda }_{\text{e}}V\right)$ in Eq. (7), $1-e^{-\left(Q_{\text{out}}+{\lambda }_{\text{e}}V\right)t/V}>0.981$ for Q_out=0.5 L min^-1 indicates that the radon accumulation in the chamber had almost reached saturation. Therefore, a duration of 60–1800 s for the radon exhalation rate curve fitting was considered in the subsequent investigation.

5.2.2

Effects of the permeability, insertion depth, and flow rate on radon exhalation

To investigate the effects of permeability, insertion depth, and flow rate on radon exhalation in the flow-through measurements, the fitted (exponential and linear fits), transient, and initial radon exhalation rates were compared for different time ranges. Both the insertion depth and flow rate affected the radon exhalation; however, the flow rate had a greater effect than the insertion depth, as shown in Fig. 8. With an increase in the flow rate from 0.5 to 2 L min^-1 at an insertion depth of 1 cm and a permeability of 1×10^-10 m², the curve-fitted radon exhalation rate (E_f-exp) increased by 305.68%, whereas it increased by 427.66% for an insertion depth of 5 cm. With an increase in the insertion depth from 1 to 5 cm at a flow rate of 0.5 L min^-1, E_f-exp increased by 97.99%, whereas it increased by 137.09% at a flow rate of 2 L min^-1. Both the increased flow rate and insertion depth contributed to the emission of radon at high concentrations, which contributed to an increase in the radon exhalation rate.

Fig. 8Full-screen View

(Color online) Radon exhalation rates for the fitted values (E_f-exp by curve fitting and E_f-lin by linear fitting) under various durations, transient values in the numerical simulation (E_n component, where E_n-d and E_n-c denote diffusion and convection, respectively), and analytical solution (E_a) (flow rate of 0.5/1/2 L min^-1, insertion depth of 1/3/5 cm, and permeability of 1×10^-10 m²)

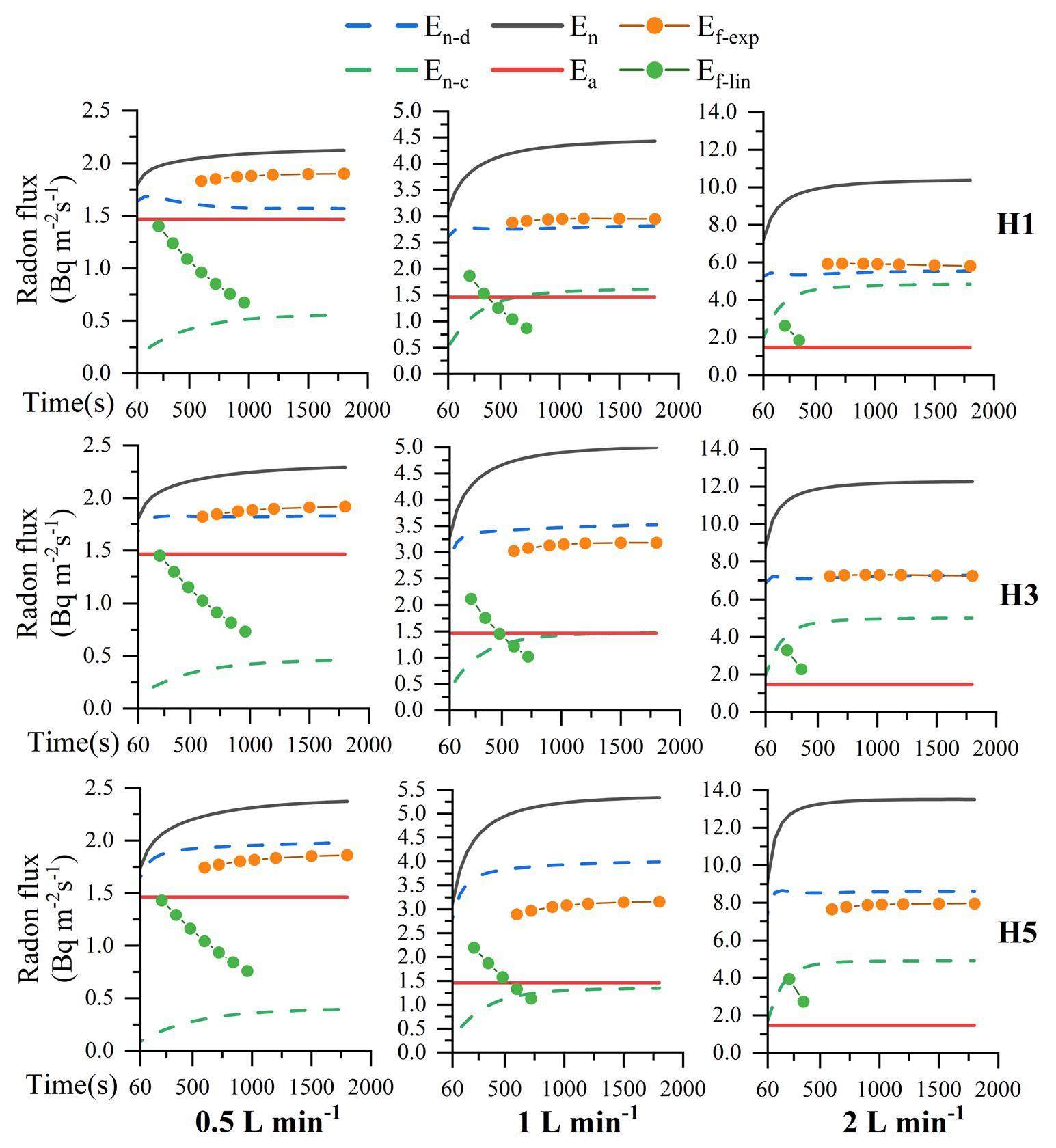
Similar trends were observed for the variation in permeability, as shown in Fig. 9. With an increase in the flow rate from 0.5 to 2 L min^-1 at an insertion depth of 1 cm and a permeability of 1×10^-11 m², E_f-exp increased by 135.66%, whereas it increased by 345.49% at a permeability of 1×10^-9 m². By increasing the permeability from 1×10^-11 to 1×10^-9 m² at a flow rate of 0.5 L min^-1, E_f-exp increased by 251.70%, whereas it increased by 640.99% at a flow rate of 2 L min^-1. The variation in the radon exhalation rate influenced by permeability could be conveniently simulated based on the assumptions of fixed porosity and radon diffusion coefficient. Changes in the permeability affect the ability of a porous medium to allow fluids to pass through. Higher permeability indicates lower fluid resistance, which promotes convective radon exhalation.

Fig. 9Full-screen View

Radon exhalation rates for the fitted values (E_f-exp by curve fitting and E_f-lin by linear fitting) under various durations, transient values in the numerical simulation (E_n component, where E_n-d and E_n-c denote diffusion and convection, respectively), and analytical solution (E_a) (flow rate of 0.5/1/2 L min^-1, insertion depth of 1 cm, and permeability of 1×10^-11/1×10^-10/1×10^-9 m²)

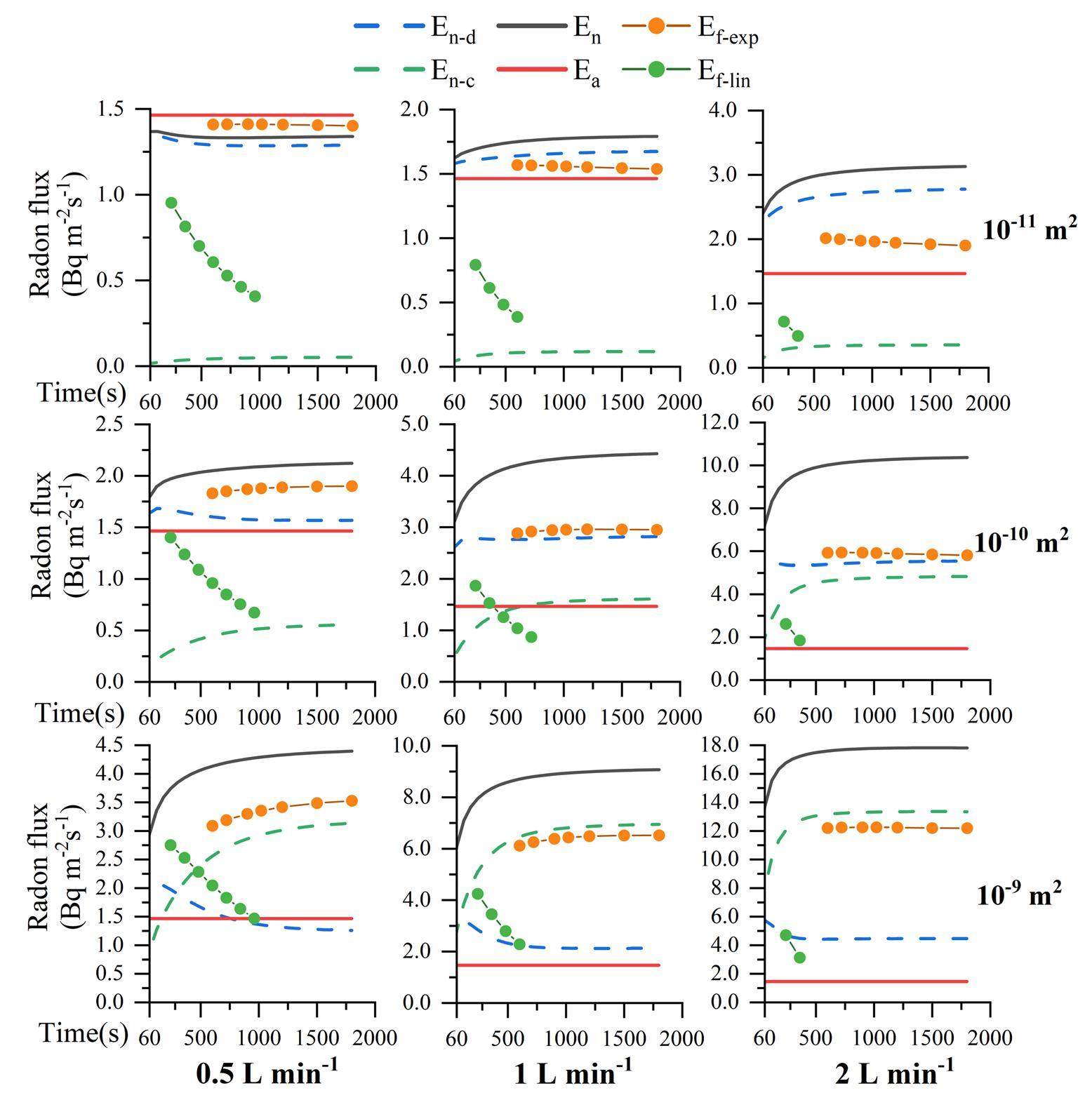
Both E_n-d and E_n-c gradually reached saturation after a certain period. In the case of a relatively low permeability (10^-11/10^-10m²), E_n-d was higher than E_n-c in most cases because the low permeability of the porous medium limited the radon at deeper layers from being drawn to the surface, and diffusive radon exhalation played a dominant role. In contrast, the case with higher permeability 1×10^-9 m² was dominated by convective radon exhalation. Moreover, the increased flow rate had a significant effect on E_n-d and E_n-c. Increasing the flow rate from 0.5 to 2 L min^-1 with a permeability of 1×10^-10 m² resulted in increases of 353.26% for E_n-d and 871.34% for E_n-c at H1, and 434.65% and 1243.71% for E_n-d and E_n-c, respectively, at H5. The larger the insertion depth of the chamber, the greater the impact of the increased flow rate on E_n-c than on E_n-d, where the high radon concentration around the insertion position is drawn to the surface and is responsible for the high convective radon exhalation rate.

For an insertion depth of 1 cm, a permeability of 1×10^-10/1×10^-9 m², and a flow rate of 0.5 L min^-1, the transient radon exhalation rate for diffusion (E_n-d) first decreased and then gradually stabilized over time. This is because radon accumulation in the chamber led to a decreased radon concentration gradient at the porous medium-air interface and inhibited diffusive radon exhalation. In contrast, the transient radon exhalation rate for convection (E_n-c) gradually increased over time and reached equilibrium because of the higher radon concentration at the porous medium–air interface induced by convective radon exhalation. As E_n-c was not negligible relative to E_n-d, the transient radon exhalation rate (E_n) was higher than the initial radon exhalation rate (E_a), and the difference increased with increasing permeability, flow rate, and insertion depth.

To quantify the effects of the permeability, insertion depth, and flow rate on the radon exhalation rate, E_n-c and E_n at 1800 s, E_f-exp for a duration of 1800 s, and E_f-lin for a duration of 240 s were extracted, as shown in Fig. 10. The effect of varying the permeability from 1×10^-11 to 1×10^-9 m² on E_n-c was significant, with increases of approximately 3750% and 6100% at 2 and 0.5 L min^-1, respectively. At an insertion depth of 1 cm, the permeability increased by approximately 251–650% for E_f-exp and E_f-lin, as shown in Fig. 10a. A flow rate ranging from 0.5 to 2 L min^-1 increased En-c by approximately 870%, whereas it increased by 75–340% for E_f-exp and E_f-lin, as shown in Fig. 10b. At 1 L min^-1, an insertion depth ranging from 1 to 5 cm resulted in a 58–162% increase in the radon exhalation rate, as shown in Fig. 10c.

Fig. 10Full-screen View

(Color online) Growth rates of the transient radon exhalation rate (E_n), transient exhalation rate for convection (E_n-c), fitted radon exhalation rate by curve fit (E_f-exp) and linear fit (E_f-lin) subject to variations in (a) the permeability (from 1×10^-11 to 1×10^-9 m² with a 1-cm insertion depth), (b) flow rate (from 0.5 to 2 L min^-1 with a 1-cm insertion depth), and (c) insertion depth (from 1 to 5 cm with 1 L min^-1)

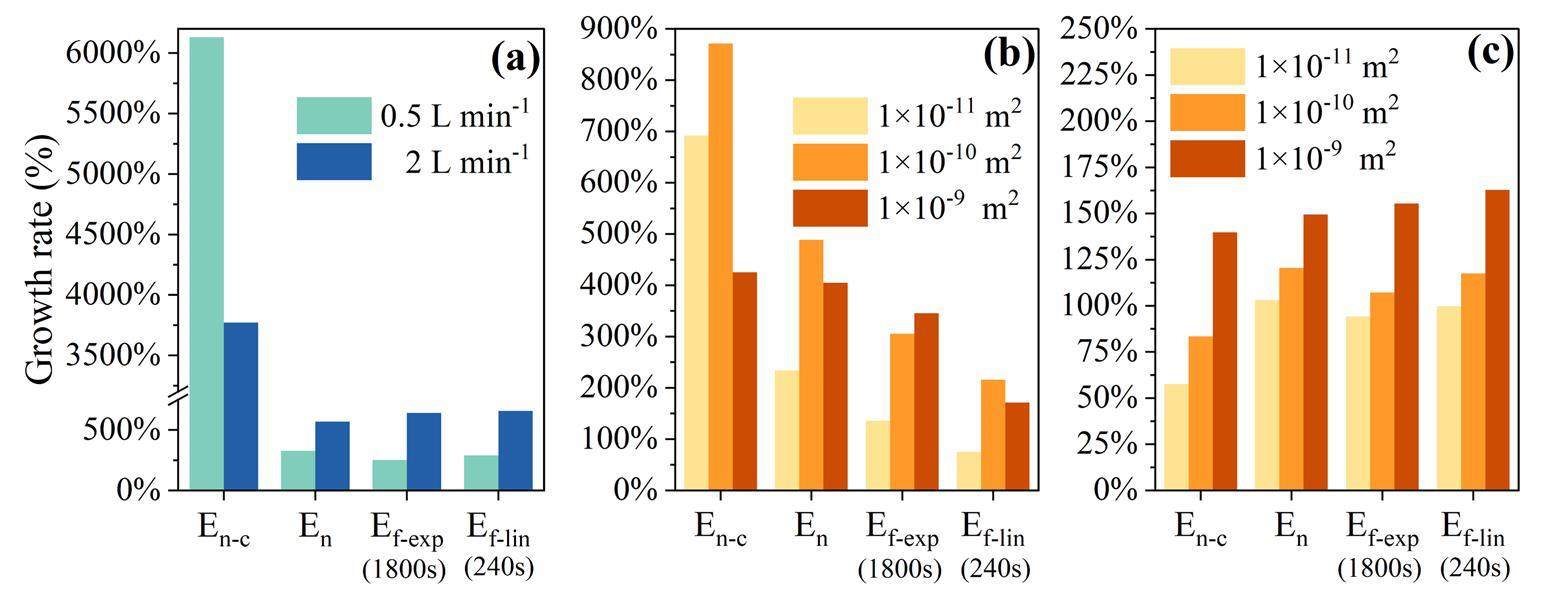
E_n-c increased with flow rate or permeability at a fixed insertion depth, as shown in Figs. 8 and 9. Excessive convective radon exhalation during flow-through measurements was mainly responsible for the considerably higher measured radon exhalation rates than the initial values, which reasonably explains the abnormally high radon exhalation rate in the field.

Correlation between E, Δ P, and Q

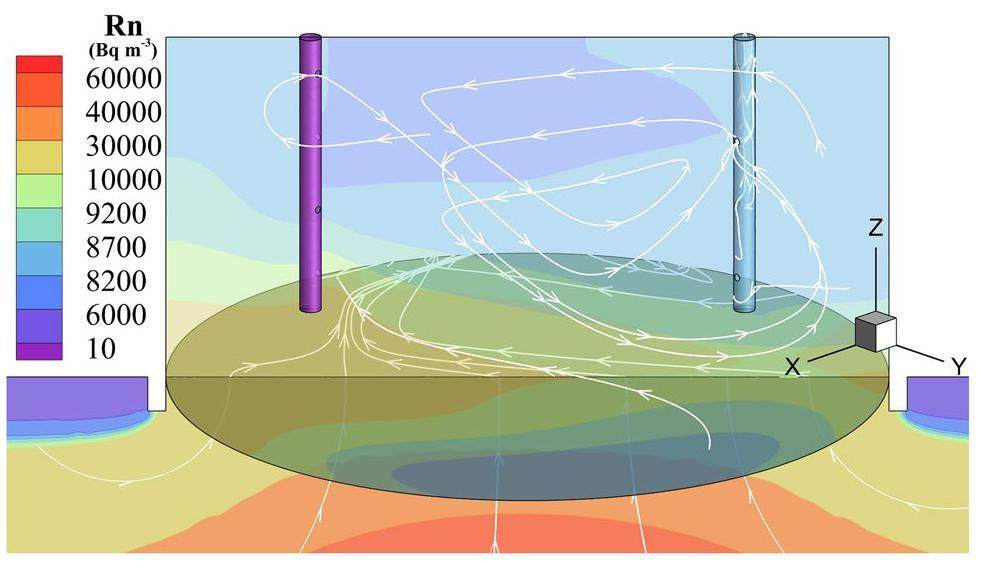
The previous line graphs revealed that both E_n-c and E_f-exp were greater than E_a under variations in permeability, flow rate, and insertion depth. Considering the negative pressure difference in the chamber observed in the field experiments, streamlines were obtained from the simulations, as shown in Fig. 11 (an insertion depth of 1 cm, permeability of 1×10^-10 m², and flow rate of 1 L min^-1 at 1800 s). The negative pressure difference in the chamber caused the gas outside the chamber to flow into the porous medium before entering the chamber, during which a high concentration of radon was transported into the chamber. This explains why E_f-exp was greater than E_a.

Fig. 11Full-screen View

(Color online) Streamlines inside the accumulation chamber and porous medium at 1800 s (1×10^-10 m², 1 L min^-1, H1). Owing to the negative pressure difference inside the chamber, the gas outside the chamber passes through the porous medium before entering the chamber. In this process, a high concentration of radon from deep is transported into the chamber, resulting in a higher cumulative radon concentration in the chamber

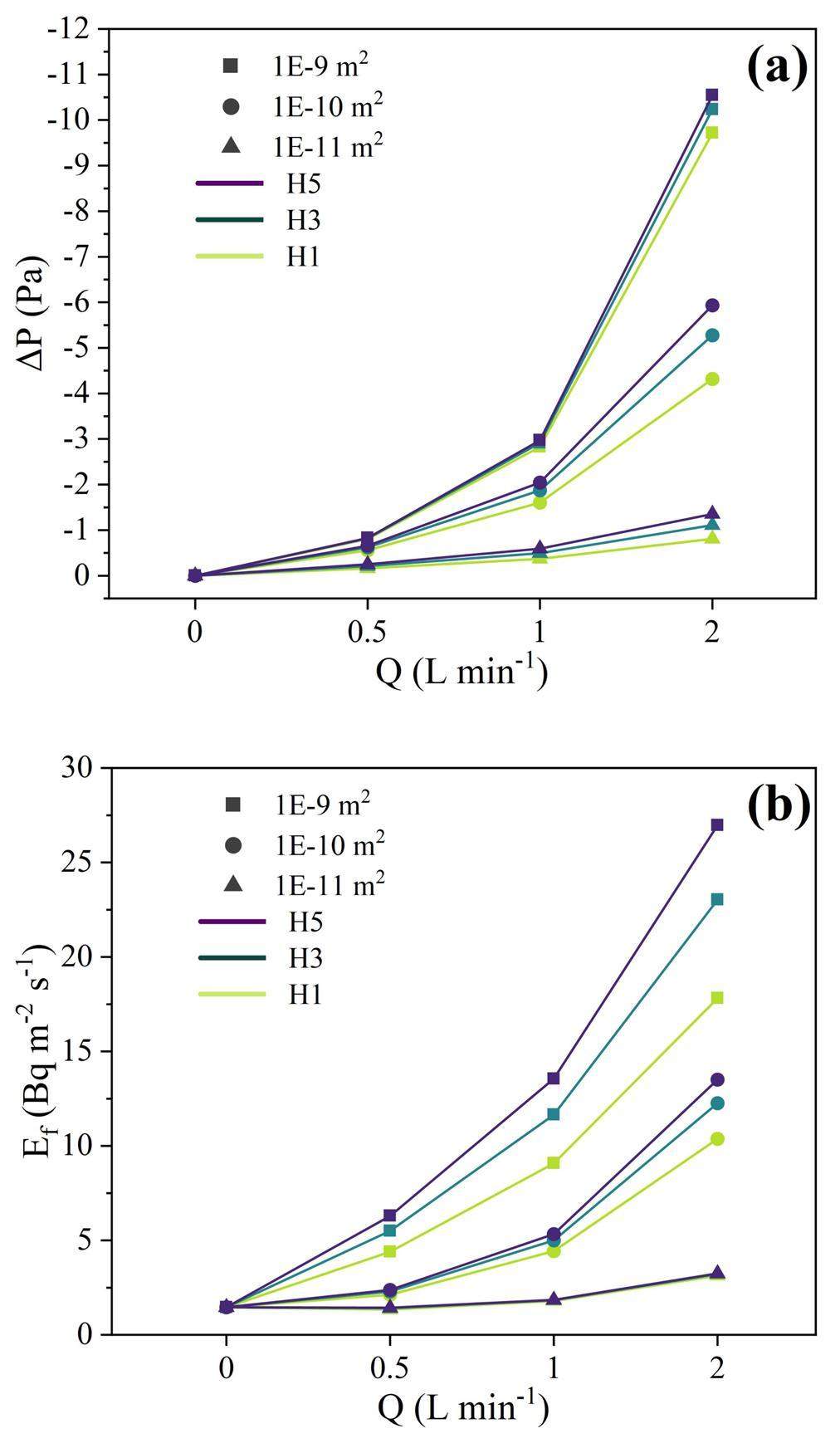
Furthermore, the correlations between the flow rate and negative pressure in the chamber and E_f-exp were obtained based on simulations, as shown in Figs. 12a and b, respectively, indicating positive relationships. At a high flow rate of 2 L min^-1, the negative pressure difference (Δ P) for a permeability of 1×10^-9 m² increased by 779.4% (H5) and 1202.67% (H1) when compared to that at a permeability of 1×10^-11 m². At a medium flow rate of 1 L min^-1, Δ P increased by 500.16% (H5) and 767.31% (H1) but increased by 332.92% (H5) and 495.74% (H1) at a low flow rate of 0.5 L min^-1. A comparable trend in the radon exhalation rate is shown in Fig. 12. At 2 L min^-1, E_f-exp at a permeability of 1×10^-9 m² increased by 640.99% (H1) and 1353.92% (H5) compared to that at a permeability of 1×10^-11 m². It increased by 229.44% (H1) and 699.46% (H5) at 1 L min^-1, whereas it increased by 251.70% (H1) and 335.21% (H5) at 0.5 L min^-1. Similarly, when the flow rate increased from 0.5 to 2 L min^-1 (H1), E_f-exp increased by 135.66% and 345.49% at permeabilities of 1×10^-11 and 1×10^-9 m², respectively. Clearly, permeability, flow rate, and negative differential pressure profoundly influence the radon exhalation rate.

Fig. 12Full-screen View

Correlations between (a) the flow rate and negative pressure difference and (b) the flow rate and curve-fitted radon exhalation rate (E_f-exp, 60–1800 s). In the steady state before the measurement (that is, Q=0 L min^-1), the pressure difference between the inside and outside of the chamber is 0 Pa, and the initial radon exhalation rate is 1.46 Bq m^-2 s^-1

The linear and nonlinear relationships between the negative pressure difference and the variables, that is, the insertion depth, permeability, and flow rate, can be represented using multivariate functions, as described by Eqs. (29) (R²=0.696) and (30) (R²=0.978): $\begin{array}{c}{P}_{\text{mf}}=-0.0541\times H\\ +3.3943\times {10}^9\times K,\\ -3.1994\times Q\end{array}$ (29) $\begin{array}{l}{P}_{\text{mf}}=-3.5591\times {10}^{-4}\times H^{0.0787}\times K^{-0.3551}\times Q^{1.7366}\hfill \end{array}\mathrm{,}$ (30) where P_mf is the fitted value from the multivariate functions, Pa, H is the insertion depth, 1/3/5 cm, K is the permeability, 1×10^-11/1×10^-10/1×10^-9 m², and Q is the flow rate, 0.5/1/2 L min^-1.

Similarly, the nonlinear relationships of E_f-exp with the insertion depth, permeability, and flow rate can be expressed using multivariate functions, as described by Eqs. (31) (R²=0.93) and (32) (R²=0.983): $\begin{array}{cc}\begin{array}{c}{E}_{\text{mf}}=1.4632+\left(1.959\times {10}^9\times K\times Q-0.0761\times H\right)\times H\\ +7.3055\times {10}^8\times K\\ +1.6846\times Q,\end{array}& ,\end{array}$ (31) $\begin{array}{cc}\begin{array}{c}{E}_{\text{mf}}=10676\times H^{\left(1.21\times {10}^8\times K\times Q-0.01\times H\right)}\\ \times K^{0.35579}\\ \times Q^{0.904},\end{array}& ,\end{array}$ (32) where E_mf is the fitted value from the multivariate functions, Bq m^-2 s^-1.

In the simulation with a permeability of 1×10^-11 m², E_f-exp decreased with increasing insertion depth, whereas for 1×10^-9 m², the correlation was positive. Interestingly, in the case of 1×10^-10 m², E_f-exp initially increased with increasing insertion depth before decreasing. This nuanced behavior was controlled by the terms $\left(1.959\times {10}^9\times K\times Q-0.0761\times H\right)$ in Eq. (31) and $\left(1.21\times {10}^8\times K\times Q-0.01\times H\right)$ in Eq. (32). A goodness of fit approaching 1 for the multivariate nonlinear fit suggests that the three variables, insertion depth, permeability, and flow rate, synergistically affect the negative pressure difference and radon exhalation rate. Additionally, the radon exhalation rate could be predicted and corrected using multivariate regressions.

Both the simulation and experimental results suggest consistent trends in the variations in the radon exhalation rates and negative pressure differences under certain insertion depths and flow rates. Deeper insertion of the chamber resulted in a significant increase in the negative pressure difference at a high flow rate of 2 L min^-1. This amplification of the negative pressure difference subsequently increased the radon exhalation rate. Therefore, the numerical method demonstrated reliability in revealing trends in the radon exhalation rates measured in the field.

Analysis of the variation in -λ_e

In Eq. (6), the term -λ_e can be interpreted as the radon dissipation inside the accumulation chamber, including radon decay, back-diffusion, and leakage. By applying an exponential fit to Eq. (7), the value of $\frac{Q_{\text{out}}}{V}+{\lambda }_{\text{e}}$ can be obtained to calculate the value of λ_e; the results are listed in Table 3. In previous analyses, certain relationships were observed between the negative pressure difference (or fitted radon exhalation rate) and permeability, insertion depth, and flow rate. The impact of these three factors on radon exhalation is also reflected in the variation in λ_e.

In most numerical simulations (except for H1, which involved a permeability of 10^-11 m² and a flow rate of 0.5 1×10^-11 m²), a positive value of -λ_e indicated the reverse process of radon dissipation, in which more radon flowed in and accumulated inside the chamber. In this process, the back-diffusion effect increases with the accumulation of high radon concentration in the chamber, reducing the increase in -λ_e. Specifically, by increasing the permeability from 10^-11 to 10^-9 m² with an insertion depth of H5, λ_e increased by 413.13% at 0.5 L min^-1 and by 37.01% at 2 L min^-1. When the flow rate increased from 0.5 to 2 L min^-1 with an insertion depth of H5, λ_e increased by 2347.43% for 10^-11 m² and by 210.26% for 10^-9 m². These data indicate that the term -λ_e had a positive value, and a higher permeability or flow rate caused a higher radon concentration in the chamber, as well as a nonnegligible back-diffusion effect at the porous medium-air interface, inhibiting the increase in λ_e.