Introduction

Recently, the contribution of one-neutron transfer reaction to the total reaction cross-section has been widely studied. Significant effort has been made to disentangle the phenomena of sequential or simultaneous two-neutron transfer reactions at above and below the Coulomb barrier energies [1-4].

To further strengthen/enlighten these phenomena, a series of experiments were performed by researchers at the Institute of Modern Physics, Chinese Academy of Sciences using loosely bound projectiles such as ^6,7Li and ⁹Be [5-8]. In these measurements, a stack of target-catcher assembly of appropriate thickness was irradiated using a preferred projectile beam of relevant energy to cover a wide energy range in a single irradiation. This method is highly efficient and accurate for determining the production cross-sections of residues with a half-life ranging from a few minutes to hundreds of days and decay via characteristic gamma-rays. A schematic diagram of the irradiation setup is shown in Fig. 1(top). These irradiated samples were subsequently transferred to a laboratory for offline-induced activity measurements of the characteristic gamma-rays. The detector dead time was maintained as low as possible (generally below 10%) to determine precise production cross-sections of the evaporation residues [9, 10]. Few hours after the irradiation, the samples had sufficiently high activity; therefore, a sample-to-detector distance of 5-8 cm is generally preferred, as shown in Fig. 1(bottom). In some cases, the isotopes of interest had longer half-lives; however, after a few days or weeks, the activity in the samples reduced. For nuclei with low activities, the samples must be measured as close as possible to the detector to increase the FEP efficiency. Our earlier publications contained detailed information of the experimental setup and analytical procedure [6-8].

Fig. 1Full-screen View

(Color online) (top) Schematic diagram of the online irradiation setup. (bottom) Laboratory view of the experimental setup for the simultaneous measurement of the irradiated stack of target-catcher (sample) assemblies for offline gamma-ray spectroscopy

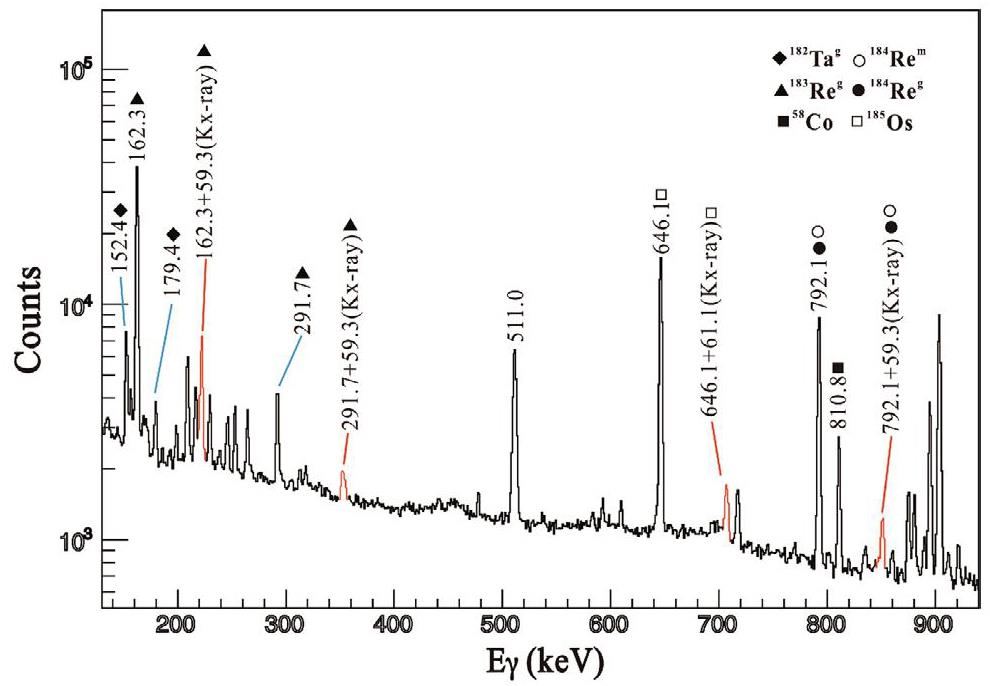
True coincidence summing (TCS) occurs in gamma-ray spectrometry when two or more cascade gamma-rays and/or X-rays are detected within the detector's resolving time. Within the timing resolution of the HPGe detector, the energy of these two gamma-rays/X-rays is deposited inside the detector's crystal [11-16], producing a single pulse that is equal to the total energy of the two individual photons. Summing in and out effects could occur as results of the addition of counts at the energy corresponding to the sum of two energies and the loss of counts from the two peaks, respectively. As shown in Fig. 2, because of the close proximity of the target-catcher (sample) assembly to the HPGe counting system, the sum peaks of the X-rays and fairly dominant γ-rays populated in ⁹Be+¹⁸¹Ta reactions were also detected and were clearly visible (the figure was adopted from our previous study [6]). The figure shows that at short sample-to-detector distance, the summing peak probability was significant and increased with decreasing target-to-detector distance; hence, for a precise/accurate determination of the FEP efficiency of these detectors, a summing peak coincidence correction was necessary. To overcome the constraints of true coincidence summing, the lack of standard mono-gamma-ray sources also encouraged the simulation of these detectors at short sample-to-detector distances. Thus, when the irradiated sample was measured very close to the HPGe detector, the calculated FEP efficiency might be inaccurate with multigamma-ray sources such as ⁶⁰Co, ¹³³Ba, and ¹⁵²Eu, where the decayed gamma-rays were emitted in cascade with other gamma-rays.

Fig. 2Full-screen View

Offline γ-ray spectrum for the ⁹Be+¹⁸¹Ta system at 46.8 MeV projectile energy measured 63 days after the activation with a measuring time of 48 h. For more information, please see Ref. [6]

Characterization of HPGe detector

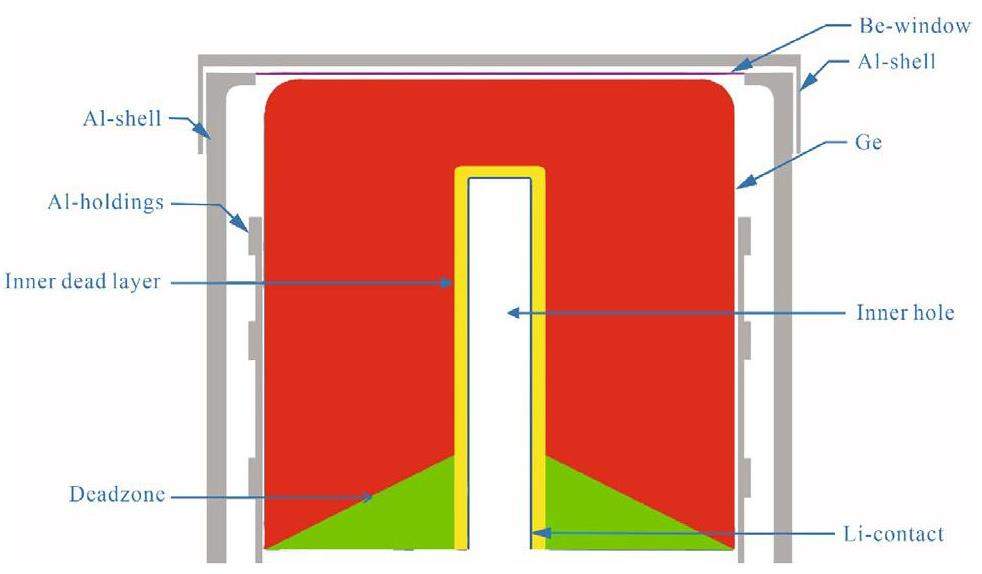
The detection of gamma-rays was performed using a coaxial n-type high-purity germanium detector (Model: EGC-70-230-R of Canberra) with 70% relative efficiency. A schematic diagram of the geometric configuration of the detector is shown in Fig. 3 and the details of the physical parameters are listed in Table 1. This HPGe detector has been used for more than a decade. The detector had a ~2.5 keV resolution for the ⁶⁰Co gamma-ray at 1332 keV. In general, coaxial HPGe detectors utilize two types of electrical contacts: diffused contacts, which consist of an n+ layer that serves as a positive electrode, and metal contacts, which is composed of a p+ layer that serves as a negative electrode. These detectors are divided into two types: n-type and p-type detectors. The diffused contacts are on the outside surfaces of p-type coaxial HPGe detectors, and the ion-implanted contacts are in the inner hole. The p-type detectors are less useful for gamma-rays below 40 keV [17] because the diffused contacts are thicker. However, the thinner metal contacts on the exterior layer of n-type coaxial detectors are usable down to 5 keV. In this study, a value of 0.3 μm was assigned to the outer dead layer composed of boron.

Fig. 3Full-screen View

(Color online) Labelled schematic diagram of the coaxial n-type HPGe detector. A boron-based outer dead layer was assigned a value of 0.3 μm in GEANT4 (not shown in the figure). (color online)

All the spectra were analyzed using digital pulse processor Pixie-16 modules by XIA LLC [18] with a 100 MHz sample rate. The signal from the preamplifier of the HPGe detector was directly fed into the digitizer. First, the efficiency of the detector was measured at a distance of 25 cm by counting standard point sources ⁶⁰Co, ¹³³Ba, ¹³⁷Cs, and ¹⁵²Eu with activities of 88, 118, 300.2, and 179.3 kBq, respectively. The samples were counted for a sufficient period of time to maintain a less than one percent statistical uncertainty.

GEANT4 [19-21] is a Monte Carlo simulation package [22-25] supported by the European Council for Nuclear Research (CERN) community. It has a very powerful toolkit for modeling detector geometry, tracking, hits, and phenomena of various physics processes possible for the passage of particles through matter. All possible physics processes, considering the interaction of gamma-rays with matter, were considered. Gamma-ray photons, electrons, and positrons are typically produced during the interaction of gamma-rays with detector substances [26, 27]. The most dominant interaction progressions for gamma-rays are the photoelectric effect, Compton scattering, and pair production. The configured set-up defined in the GEANT4 simulation is shown in Fig. 3. The geometry also included detector housings, including absorbing materials, aluminum end caps, and dead layers of the germanium crystal.

Most of the setup components were built into precise geometries. The original computer-aided design (CAD) of the setup was used as the foundation for the geometry description markup language (GDML) [28]. Characterizing a detector is challenging, particularly when its physical properties are obscured. Dead layer thickness is important in these estimations. The GEANT4 radioactive decay module can replicate efficiently the nuclide's entire decay path. The simulations used Livermore physics list [29] of low-energy electromagnetic processes. For each event, the energy deposited in the active area of the detector volume was gradually gathered. In the simulations, the event-wise data were used to analyze photo-peak efficiency and Compton scattering. The detector resolution was incorporated into the simulation results by redistributing the simulated data of each event with a random variable based on a Gaussian distribution of the standard deviation. The value of the insensitive zone was increased in steps of 1% to replicate the experimental spectrum and FEP efficiency. 10% insensitive zone of conical shape at the rear part of the Ge crystal was assumed in the simulations. A similar procedure was also performed in our previous study [30, 31].

Obtaining mono-energetic gamma-ray sources is challenging, and some require frequent replacement owing to their short half-lives, reducing their utility. Although multigamma-ray sources provide acceptable efficiency calibration, the calibration can be incorrect at tighter sample detector geometry due to coincidence summation effects. To simulate the efficiency, a model approach such as GEANT4 can be utilized. This method offers the advantage of replicating efficiency for a wide range of sample shapes and matrices without any coincidence-summing effects.

First, GEANT4 simulations were performed for point source geometry using the detector's dimensions provided by the manufacturer. In each simulation, 10⁶ particles were sampled to reduce statistical uncertainties. Figure 4 shows the experimental and GEANT4-simulated FEP efficiencies. The errors on peak areas and abundances were used to calculate the effective errors of the experimental efficiencies, as shown in the figure.

Fig. 4Full-screen View

(Color online) Experimental and GEANT4-simulated efficiency curves as functions of gamma-ray energy at a sample-to-detector distance of 25 cm. The solid lines represent the simulated efficiencies for various considerations of detector shell, shell+deadzone, and shell+deadzone+deadlayer

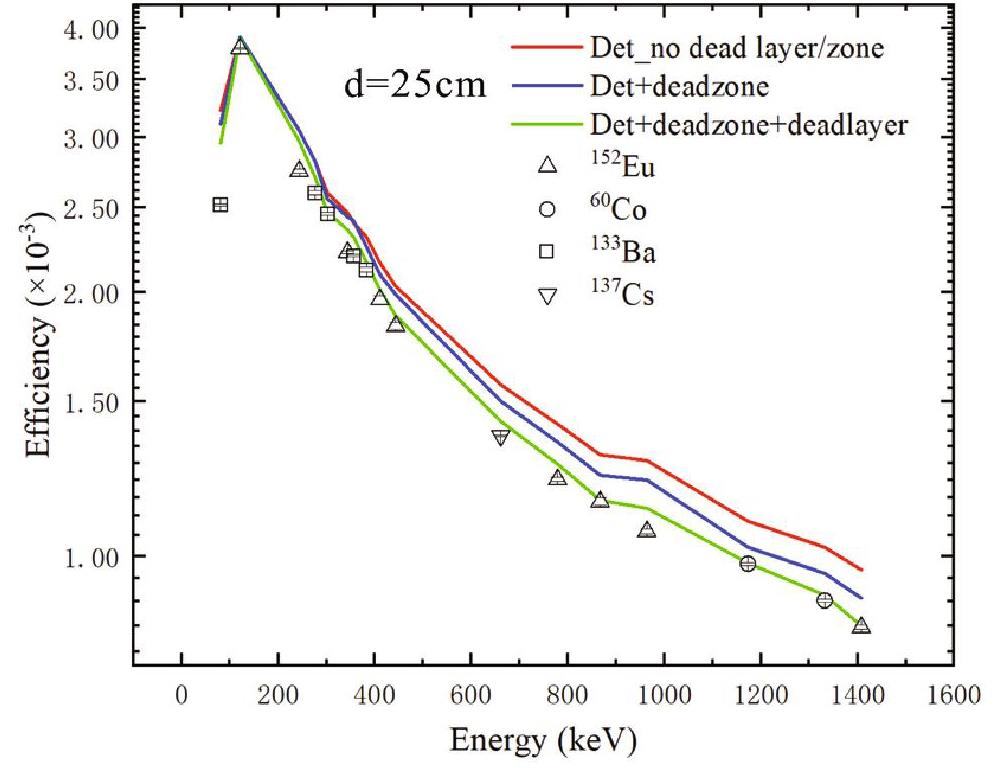
The simulated efficiencies were higher than the experimental efficiencies for all gamma-ray energies at a sample-to-detector distance of ~25 cm, indicating that the detector dimensions provided by the manufacturer were probably incorrect. The same effects were observed in several other measurements reported in the literature [11, 14, 32-35]. Similar to a previous study, we also increased the thickness of the inner dead layer by 0.2 mm in each step of the simulation to compare with the experimental FEP efficiency [36-44]. A considerable agreement was achieved at a total dead layer thickness of 2 mm and 10% dead zone in the Ge-crystal. Hence, simulating the experiment and estimating the physical parameters collected experimentally can be used to validate any experimental data or procedure. The method is highly beneficial in determining the detector's full energy peak (FEP) and total efficiency when it is difficult to perform owing to experimental constraints [45-52].

Calculation of Coincidence Summing Correction Factors

True coincidence summing becomes prominent at a short source-to-detector distance. At small distances, these effects result in an erroneous measurement of the activity of the source. Summing coincidence effects are independent of the source's count rate and are exclusively determined using the emission probabilities and detection efficiencies of cascade gamma-rays [53-55]. The magnitude of these adjustments increases significantly at short sample-to-detector distances owing to the higher likelihood of two gamma-rays reaching the detector simultaneously.

3.1

GEANT4 simulations

As discussed in Sect. 2, the detector geometry was initially optimized at a sample-to-detector distance of 25 cm. After achieving a satisfactory agreement between the experimental and simulated efficiencies for the optimized geometry, further simulations were conducted at various sample-to-detector distances considering the two physics definitions in GEANT4 of the mono-gamma-ray emitter for each gamma-ray and the ‘real-sources’ as ⁶⁰Co, ¹³³Ba, ¹³⁷Cs, and ¹⁵²Eu (including all gammas and X-rays in the decay scheme). Similar to Ref. [12], the summing coincidence correction factors k_TCS were computed by taking the ratios of efficiencies obtained using the two cases as $k_{\text{TCS}}=\frac{{ϵ}_{\text{mono}}}{{ϵ}_{\text{real}}^{\text{wc}}}$ (1) where ϵ_mono is the FEP efficiency in the case of the monoenergetic gamma-ray source and ${ϵ}_{\text{real}}^{\text{wc}}$ is the FEP efficiency without true coincidence summing corrections for that particular source.

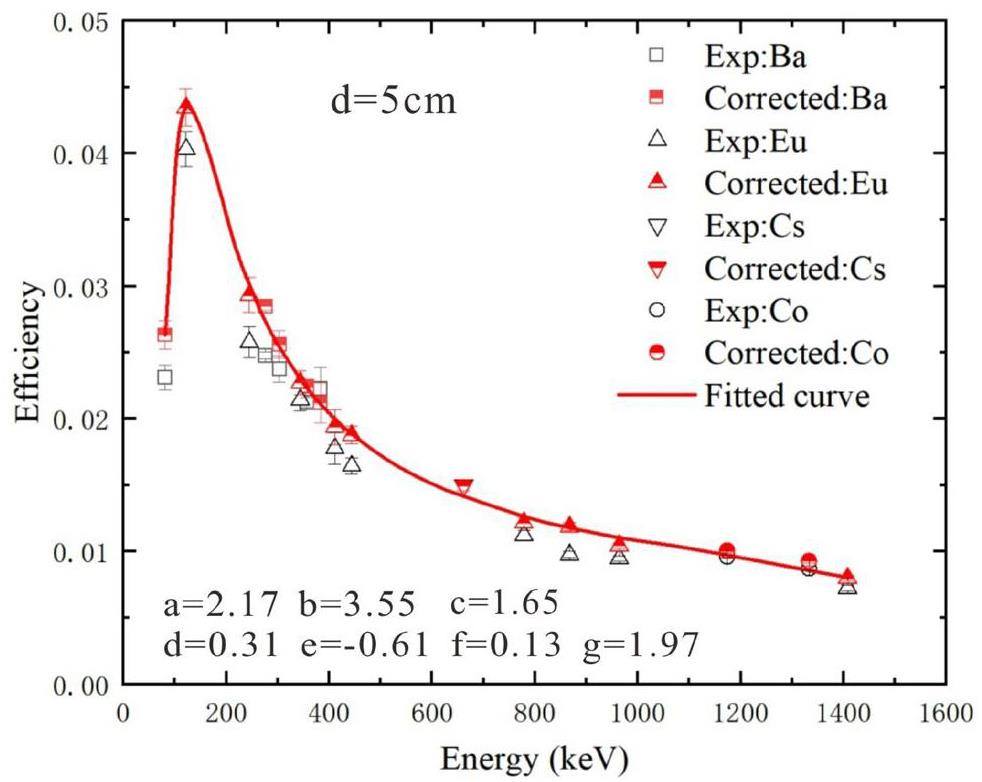
As simulations do not suffer from the true coincidence summing effect under the assumptions of a mono-energetic gamma-ray source, these summing coincidence correction factors were subsequently used to correct the experimental efficiencies. Table 2 presents the experimentally determined efficiencies for these sources at a source-to-detector distance of 5 cm, the corresponding summing coincidence correction factors (k_TCS), and corrected experimental efficiencies. These results are shown in Fig. 5. In line with the Radware package [56], the relationship between the FEP efficiency and the gamma-ray energy is typically described using a standard fitting function described as follows: ${ϵ}_{\gamma }=\exp {\left[{\left(a+bx+c{x}^2\right)}^{-g}+{\left(d+ey+f{y}^2\right)}^{-g}\right]}^{-1/g}$ (2) where $x=\log \left(\frac{E_{\gamma }}{E_1}\right)$, $y=\log \left(\frac{E_{\gamma }}{E_2}\right)$, E₁ = 100 keV, and E₂ = 1000 keV; the value of Eγ is expressed in keV. The seven parameters, denoted as a to g, were determined by fitting the data; their values are provided in Fig. 5.

Fig. 5Full-screen View

FEP efficiencies plotted against gamma-ray energy without (Exp: source/open symbol) and with (Corrected: source/ half-filled symbol) true summing coincidence correction for the ⁶⁰Co, ¹³³Ba, ¹³⁷Cs, and ¹⁵²Eu point sources at a sample-to-detector distance of d=5 cm. The efficiencies of gamma-rays from ⁶⁰Co, ¹³³Ba, and ¹⁵²Eu sources are indicated by circles, squares, and triangles, respectively. The fitting parameters for the corrected efficiency curve are also shown in the figure

Table 2Full-screen View

Experimental FEP efficiencies before and after the true summing coincidence corrections at a distance of 5 cm

Source	Eγ (keV)	Effi. (exp.) ϵti	kTCS	Corr. effi. (exp.) ϵti×kTCS
137Cs	661.66	0.01499	0.9977	0.01496
60Co	1173.23	0.00960	1.0464	0.01005
	1332.49	0.00871	1.0640	0.00927
	81.00	0.02313	1.1388	0.02634
	276.40	0.02478	1.1503	0.02850
133Ba	302.85	0.02375	1.0789	0.02562
	356.01	0.02124	1.0560	0.02243
	383.85	0.02229	0.9484	0.02121
	121.78	0.04032	1.0780	0.04347
	244.70	0.02578	1.1384	0.02935
	344.28	0.02144	1.0596	0.02272
	411.12	0.01777	1.0919	0.01940
152Eu	443.96	0.01644	1.1411	0.01876
	778.90	0.01121	1.0839	0.01215
	867.38	0.00975	1.2164	0.01186
	964.06	0.00947	1.1012	0.01043
	1408.01	0.00724	1.1029	0.00799

Show more

The values of summing coincidence correction factors were determined through GEANT4 simulations

Furthermore, the efficiencies obtained from GEANT4 are free of any true coincidence summation effects, allowing them to be employed at short sample-to-detector distances. There was a significant agreement between the simulated and experimental efficiencies after applying the summing coincidence corrections to the experimental data. Because of the high dead time of the detection system, using a strong source might not be appropriate for the accurate determination of the FEP efficiency of the HPGe detector in the experiment; however, using the developed model, the summing peak effect could be corrected at these short sample-to-detector distances, as shown in Fig. 5, using available standard gamma sources. After applying these appropriate correction factors, a new FEP efficiency curve was generated and the pertinent values for the specific detected gamma-rays were calculated. This facilitated in determining the accurate experimental cross-sections of the low-activity long-lived evaporation residues and the transfer reaction residues at short sample-to-detector distances.

Summing Peak Probability: Experiment vs. Simulations

The likelihood of detecting two gamma-rays concurrently decreased as the distance between the source and the detector increased. However, summation occurred to some extent at all source-to-detector distances. In practical terms, TCS losses diminish after a certain distance, which depends on the size of the detector. To investigate these effects, we compared the summing peak probabilities of the multigamma-ray sources (⁶⁰Co, ¹³³Ba, and ¹⁵²Eu) as functions of source-to-detector distance between the experimental and GEANT4-simulated spectra. We also determined the summing peak probability (SP) as a function of source-to-detector distance for the summing peak energy in the gamma-ray spectrum. The summing peak probability is expressed as $S_{\text{P}}=\frac{P{A}_{\text{A+B}}}{P{A}_{\text{B}}+P{A}_{\text{A+B}}}$ (4) where PA_A+B represents the efficiency-corrected peak area (PA) for summing coincidence energy and PA_B represents the peak area for the gamma-ray decaying to the ground state. A schematic diagram of the decay scheme is shown in the inset of Fig. 6.

Fig. 6Full-screen View

(Color online) Variation of summing peak probability pertaining to the coincidence gamma-ray decaying to the ground state as a function of source-to-detector distance. To simplify calculations, 121 keV & 1408 keV gamma-ray in ¹⁵²Eu, 81 keV & 356 keV gamma-ray in ¹³³Ba, and 1173 keV & 1332 keV gamma-ray in ⁶⁰Co were considered in coincidence in these nuclei

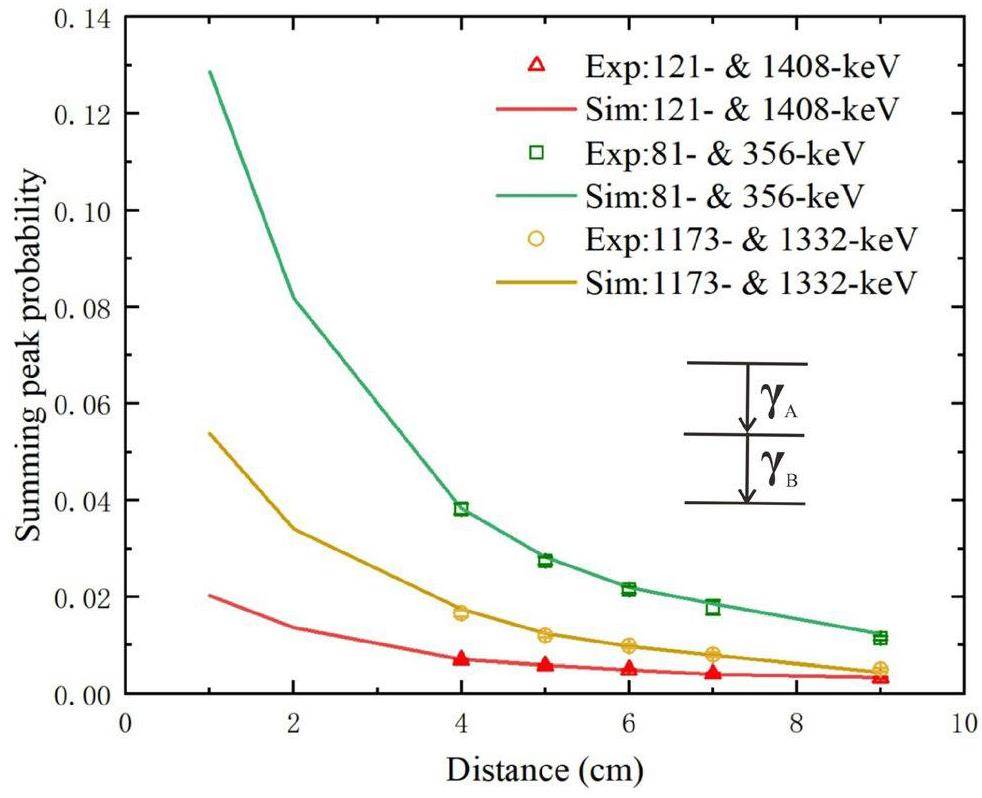
To simplify computations, only the coincident gamma-ray energies of 121&1408 keV in ¹⁵²Eu, 81&356 keV in ¹³³Ba, and 1173&1332 keV in ⁶⁰Co were evaluated. Figure 6 shows the simulated and experimental summing peak probabilities. Although the simulations were also performed for source-to-detector distances of 1, 2, and 3 cm, the experimental data is not available below the source-to-detector distance of 4 cm owing to the high deadtime of the measurement setup. The good agreement between the experimental and simulated summing peak probabilities shown in Fig. 6 indicates that simulated summing peak probabilities can be considered when data are unavailable for smaller distances due to experimental constraints.

Summary and Conclusions

This study was performed to optimize the HPGe detector parameters that our laboratory generally utilizes for gamma spectrometric measurements. A closed-end coaxial n-type HPGe detector with a 70% relative efficiency was used in this study. The summing effect in the HPGe detector was significant at shorter sample-to-detector distances, impacting the estimation of low cross-section residues in transfer reactions below the Coulomb barrier energies and measurement of radioactivity in environmental samples. Efficiency calibration of the detector was crucial in gamma-ray spectrometry to acquire quantitative information about the monitored nuclide. The FEP efficiency was significantly influenced by the entire volume of the detector rather than just its diameter or length. The detector's efficiency decreased as the dead layer thickness increased because of the gamma-ray attenuation in the dead layer and reduction of the active volume of the detector. GEANT4 has been recognized as a tool for generating simulated data for calculating summing coincidence correction factors for different gamma-rays of a specific source. The modeled detector geometry has a significant impact on the accuracy of GEANT4 simulations. Using optimized geometries of the HPGe detector at a distance of approximately 25 cm, where summing effects are negligible, the summing probability increased at smaller separations/distances between the source and detector's front surface. A consistent agreement between experimental and simulated efficiencies was observed at these distances. An analytical approach was also used to determine the coincidence correction coefficients for ⁶⁰Co, ¹³³Ba, and ¹⁵²Eu sources as functions of source-to-detector distance considering mono-energetic gamma-sources. When the sample-to-detector distance exceeded 9 cm, the correction factors for coincidence were minimal. Correction factors up to 1.615 at d=2 cm and 1.911 at d=1 cm were obtained for ¹⁵²Eu at 867 keV, which significantly impacted the FEP efficiency at these distances. Optimizing detectors' geometries is beneficial because after their dimensions are tuned using experimental efficiencies, they can be used to determine the efficiencies for various sample geometries without using gamma-ray standards.