Geometry and proton transport algorithm

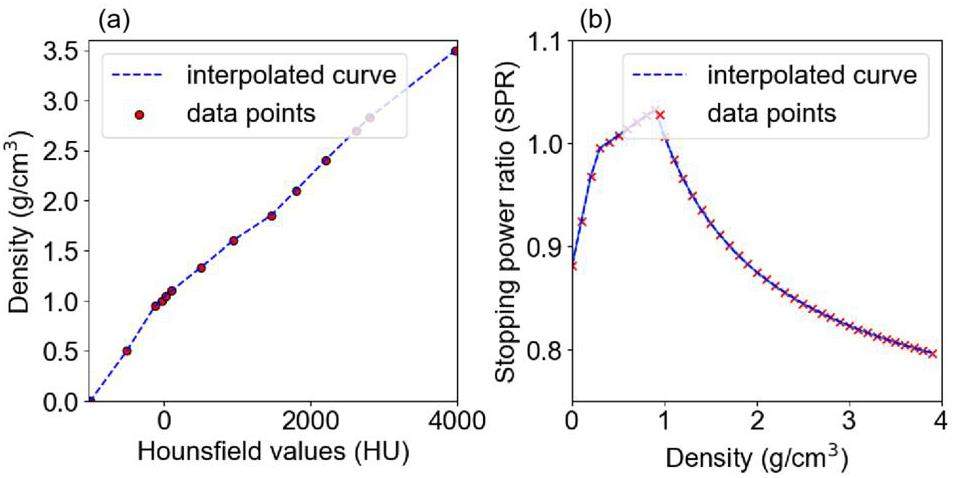
Serial CT images are routinely used for the planning and optimization of clinical treatment. First, standard calibration methods such as the Hounsfield unit (HU) look-up table are utilized to transform CT images into a three-dimensional density matrix ρ, as illustrated in Figure 1(a). Subsequently, regions of interest (ROI) are delineated using either threshold segmentation or artificial intelligence-based segmentation algorithms [39] to accurately represent tissues and organs with distinct material compositions. Furthermore, to determine the energy deposition at a specific step length Δs, we utilized the stopping power ratio (SPR) to rescale it to a step length in water, referred to as Δs_w, using Eq. (1). The SPR is related to the proton energy and material density. It can be determined by using a fitting formula [22], stoichiometric calibration [40], or artificial intelligence [41]. In this case, the first method was utilized, and a portion of the conversion curve (160 MeV) is shown in Figure 1(b). The geometric structure and processes employed enable the transport of protons within voxels. $\text{Δ}{s}_{\text{w}}=SPR\frac{\rho }{{\rho }_w}\text{Δ}s$ (1)

Fig. 1Full-screen View

(Color online) Material look-up table used in gMCAP: (a) Hounsfield value look-up table to determine density from CT images (for different CT machines, the curves are different), and (b) stopping power relative to water of different densities of material for 160 MeV protons

The transport of protons in the medium is influenced by both elastic and inelastic Coulomb collisions as well as elastic and inelastic nuclear interactions. Among these, numerous elastic Coulomb collisions occur, with almost 1×10⁶ instances per centimeter of the path [22]. Because of the impracticality of simulating these interactions individually, a Class II condensed history algorithm was employed for proton transport. A production threshold $T_{\text{e}}^{\text{min}}$ was established, which indicates the minimum energy required for ionization to occur and generate δ electrons. If the energy is below $T_{\text{e}}^{\text{min}}$, continuous energy loss occurs instead. Thus, reactions between protons and materials can be divided into two categories: continuous interactions (see Sect. 2.2) and discrete interactions, including ionization (see Sect. 2.3), elastic nuclear reactions (see Sect. 2.5.1), and inelastic nuclear reactions (see Sect. 2.5.2).

Protons are transported stepwise in the voxel geometry. One step Δs is defined by the minimum of three step sizes: (1) the distance to the closest voxel boundaries; (2) the user-defined maximum step size, which is set to 1 mm, or the residual range corresponding to 20% of the initial energy; and (3) the mean free path of each interaction, including ionization, elastic nuclear interaction, and inelastic interaction. The mean free path λ is defined by Eq. (2): $\lambda =-\log (\eta )\frac{1}{\text{Σ}}\mathrm{.}$ (2) Here, η is a random number between 0 and 1, and ∑ is the cross-section of each discrete interaction.

Continuous interactions

2.2.1

Energy loss algorithm

According to Zhang et al. [42], the energy loss (ΔE) of a geometric step Δs in a material is equal to the energy deposited in the step Δs_w in water. The proton's energy loss fluctuates around its mean energy loss $\overline{\text{Δ}E}$, and $\overline{\text{Δ}E}$ for a step is generally determined by integrating the restricted stopping power L_w, as shown in Eq. (3). L_w, which is consistent with $T_{\text{e}}^{\text{min}}$, is calculated using Geant4 [43] and is dependent on the proton energy T_p. Nevertheless, the process of obtaining the integral solution typically requires a significant amount of time, which is contingent upon the magnitude of the differential step size dx. $\text{Δ}{s}_{\text{w}}=-{\displaystyle {\int }_{T_{\text{p}}}^{T_{\text{p}}-\overline{\text{Δ}E}}}\frac{\text{d}{T}_{\text{p}}^{\text{'}}}{L_{\text{w}}\left(T_{\text{p}}^{\text{'}}\mathrm{,}{T}_{\text{e}}^{\text{min}}\right)}$ (3) Therefore, a proton Energy Range LookUp Table (ERLUT) is proposed to solve this issue. Initially, the L_w values of protons with various energies in water are determined. Subsequently, the L_w values of protons with varying energies are integrated to obtain their range in water. Finally, an ERLUT derived from the precise integration is acquired, as shown in Figure 2(a).

Fig. 2Full-screen View

(Color online) (a) The remaining range of protons with various energies (the ERLUT), (b) the cost time of protons with 200 MeV under different integration precisions, and (c) the CSDA range of protons with 200 MeV under different integration precisions

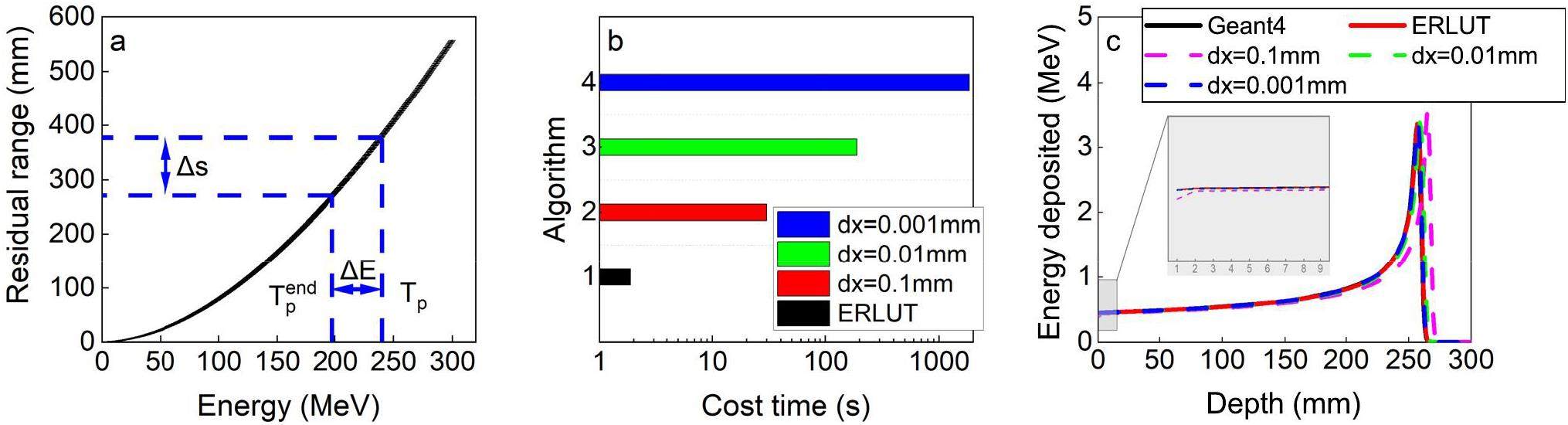
For a proton with initial energy T_p, the energy loss $\overline{\text{Δ}E}$ in step Δs can be obtained by interpolating the ERLUT twice. First, the remaining range corresponding to T_p is obtained via forward interpolation. The table is then inversely interpolated to obtain $T_{\text{p}}^{\text{end}}$ at the end of the step. The difference between the remaining ranges corresponding to T_p and $T_{\text{p}}^{\text{end}}$ is the step size Δs. Using this approach can not only save time but also ensure precision. Figures 2(b) and 2(c) show a comparison between the continuous slowing down approximation (CSDA) range and the calculation time for 200 MeV protons. The comparisons were performed under different integration precisions (dx) utilizing the ERLUT.

The energy straggling model was implemented to rectify the exact energy deposition of the protons within a single step. The energy deposition exhibits a Gaussian distribution with $\overline{\text{Δ}E}$ and a variation of σ, which is defined in Eq. 4. ${\sigma }^2=2\pi r_{\text{e}}^2{m}_{\text{e}}{n}_{\text{e}}\text{Δ}s\frac{\min \left(T_{\text{e}}^{\min }\mathrm{,}{T}_{\text{e}}^{\max }\right)}{{\beta }^2}\left(1-\frac{{\beta }^2}{2}\right)$ (4)

2.2.2

Multiple scattering model

Protons undergo elastic Coulomb collisions when they traverse matter, resulting in numerous small-angle deflections. These deflections can be simulated using a multiple scattering model. This study employs the multiple scattering theory proposed by Rossi and Greisen [44], which states that the deflection angle on the projection plane containing the initial track obeys a Gaussian distribution with σ as shown in Eqs. (5)-(6): $\sigma =\frac{1}{\sqrt{2}}\times \sqrt{\frac{1}{2}{E}_{\text{s}}^{2}t/p^2{\beta }^2},$ (5) $t\equiv \frac{\text{Δ}s}{X_0\left(\rho \right)}.$ (6) Here, p is the momentum of a proton, β is its velocity, Δs is the step length, and $X_0(\rho )$ is the radiation length of the material. According to Rossi and Greisen, the mean square angle of scattering is independent of the atomic number, and E_s is a constant parameter with the dimension of energy, given by Eq. (7): $E_s={\mu }_{\text{e}}{\left(4\pi 137\right)}^{\frac{1}{2}}=21\text{ MeV}.$ (7) Here, μ_e is the mass of the electron. Note that the value of E_s here differs from that of Fippel [22] because in Fippel's model, electrons are considered to slow down continuously.

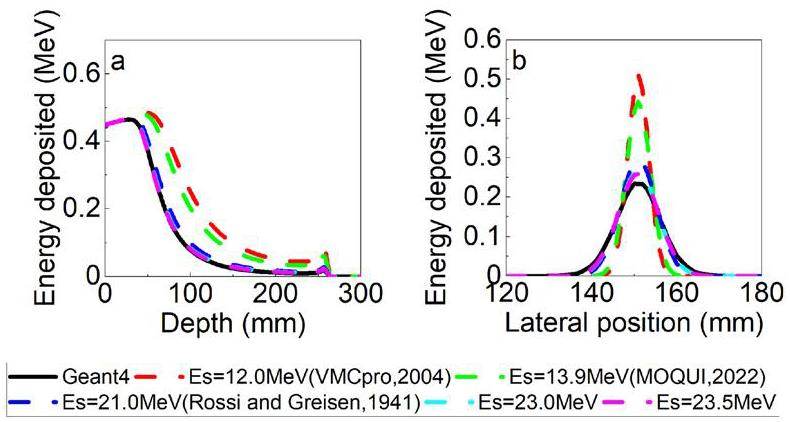
Within the gMCAP program of the registration-only electromagnetic interaction model, comparisons were made between the central axis depth dose (CADD) curve and the lateral dose distribution (LDD) at the peak position across various E_s values. The experimental results, illustrated in Figure 3, were compared with Geant4 simulations to identify the most appropriate Es value. After conducting the simulations, the energy parameter was refined by setting E_s to 23.5 MeV. This adjustment was implemented to maximize the precision of the electromagnetic process.

Fig. 3Full-screen View

(Color online) (a) Central axis depth dose curves and (b) lateral dose curves in the peak for different E_s values for a cube of water irradiated by 200 MeV protons

Ionization

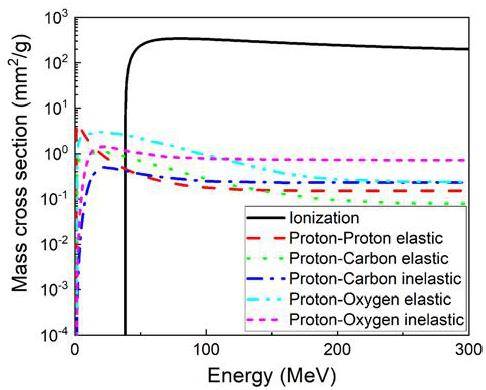
The ionization interactions between protons and matter are crucial for dose estimation. The cross-section for electromagnetic interactions is approximately two orders of magnitude larger than that for nuclear reactions. Taking G4_SKIN_ICRP as an example, which is composed of H (10%), C (20.4%), N (4.2%), O (64.5%), Na (0.2%), P (0.1%), S (0.2%), Cl (0.3%), K (0.1%). Figure 4 shows the cross-sectional data obtained from Geant4 scaled by mass density.

Fig. 4Full-screen View

(Color online) Cross-sectional data of discrete interactions in G4_SKIN_ICRP taken from Geant4

According to the two-body collision energy transfer relationship, the maximum energy $T_{\text{e}}^{\text{max}}$ transferred by a proton to a free electron is calculated using Eq. 8. $T_{\text{e}}^{\text{max}}=\frac{2m_{\text{e}}{\beta }^2{\gamma }^2}{1+2\gamma m_{\text{e}}/m_{\text{p}}+{\left(m_{\text{e}}/m_{\text{p}}\right)}^2}$ (8) Here, m_e and m_p are the electron and proton rest masses, respectively; the relativistic parameter $\gamma =\frac{T_{\text{p}}+m_{\text{p}}}{m_{\text{p}}}$; and ${\beta }^2=1-\frac{1}{{\gamma }^2}$. The differential macroscopic cross-section for ionization to produce a δ-electron is extracted from Geant4 using the class G4hIonisation with $T_{\text{e}}^{\text{min}}=81.5\text{ keV}$. This corresponds to a range of approximately 0.1 mm in water. The G4hIonisation class utilizes the following models:

• G4BetheBlochModel, valid for T_p >2 MeV

• G4BraggModel, valid for T_p <2 MeV

If an ionization event occurs during transport, a δ-electron is produced. The energy of the δ-electron is determined using a random sampling method with a probability distribution function [22]. Figure 5 shows the electron energy distribution produced by a 200 MeV proton.

Fig. 5Full-screen View

(Color online) The δ-electron energy distribution produced by a 200 MeV proton

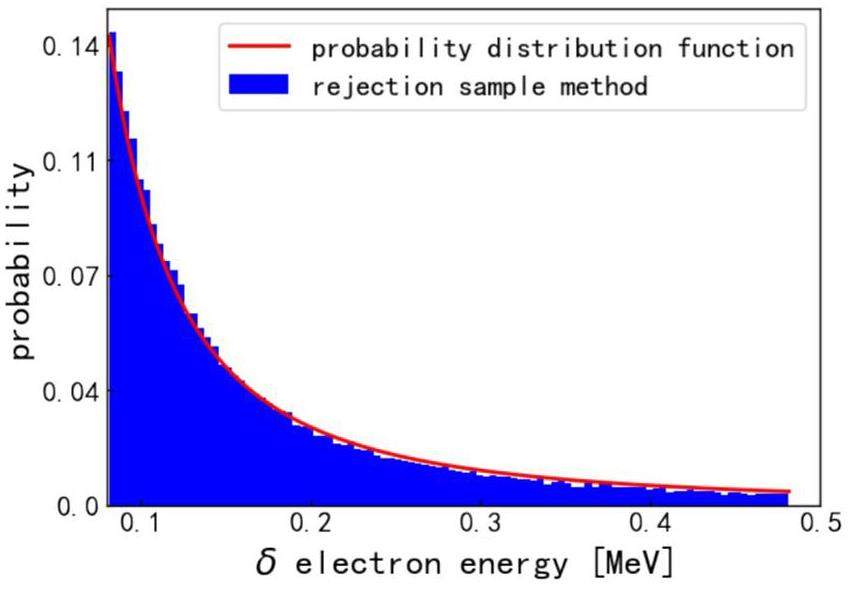
The scattering angular deflection of the proton during this process is ignored, as the mass of the proton is much larger than that of an electron, and its direction hardly changes during a collision. The δ-electrons deposit energy locally and cease to be transported.

Simplified nuclear reaction: APPROX model

The simplified APPROX model focuses on nuclear interactions between protons and H and O atoms, including elastic and inelastic reactions. In the APPROX model, soft tissue is presumed to undergo nuclear reactions similar to those in water. Assuming this, all tissues consist of H and O with a mass ratio of 1:8. Different tissues and organs exhibit variations in density.

The cross-sections of the three nuclear reactions were calculated using Geant4 and tabulated. The model proposed by Fippel and Soukup [22] was used to sample the energy and scattering angle of the nucleus. For the secondary particles, where secondary protons are stored in the stack for further transportation, other charged particles release energy locally, and long-range particles, such as photons and neutrons, deposit energy proportionally.

Refined nuclear reaction: REFINED model

Because human tissues contain atoms other than H and O, it is necessary to consider the nuclear reactions of these atoms. Particularly for middle-Z and high-Z atoms, such as P, Ca, Fe, and I, the normalized nuclear reaction cross-section with protons is significantly lower than that of O. Thus, employing the APPROX model to estimate the radiation dose to the bone may result in inaccuracies.

Consequently, a more advanced nuclear reaction model, REFINED, was developed in this study. It encompasses the nuclear interactions between protons and elements including H, C, N, O, Na, Mg, P, S, Cl, K, Ca, Fe, and I. Similarly, the cross-sections of protons with these atoms were obtained using Geant4. Next, the program was initialized to compute the cross-sections for various materials and each individual nuclear reaction. At the post-step point, the discrete interaction type was sampled and specific nuclear reaction procedures were executed.

GPU implementation

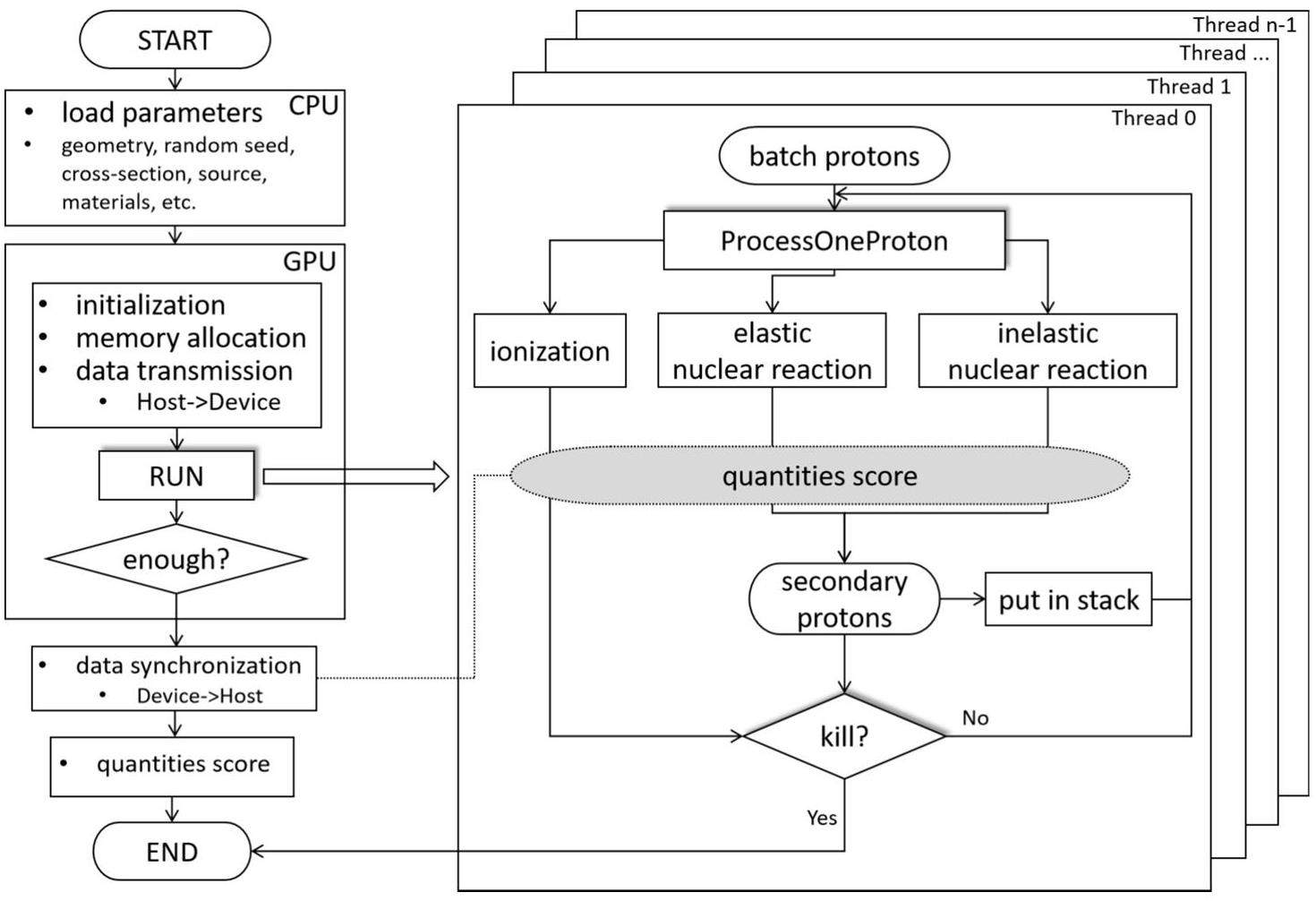
GPU parallel computing was implemented using CUDA v11.5, which supports programming in C/C++. When the program starts, the CPU initializes the cross-sectional data of the material, source information, geometric configuration, and random number seed. All these data are transferred from the CPU memory to the GPU global memory. After initialization, the primary and secondary protons are transported in batches, and each primary proton is transported using a GPU thread. Atomic addition is used to write the results to global memory to obtain the average dose of each voxel, thus avoiding memory conflicts and saving execution time.

The code employs a batch-based approach to compute statistical fluctuations, also known as statistical uncertainty. Typically, a single simulation consists of 10 batches. The calculation process is shown in Eq. 14, where v is the voxel, N is the number of batches, $X_i\left(v\right)$ is the physical quantity (dose or deposited energy) recorded by voxel v in the i-th batch, and $\overline{X}(v)$ is the average physical quantity within the voxel. $s(v)=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^N{\left(X_i\left(v\right)-\overline{X}\left(v\right)\right)}^2}}{N(N-1)}}$ (14) Before the program exits, it copies the results from the GPU to the CPU and outputs the data. The overall program architecture is illustrated in Figure 6.

Fig. 6Full-screen View

(Color online) The CPU-GPU coupling architecture diagram of the entire gMCAP

Validation and comparison

2.7.2

Homogeneous and heterogeneous phantoms

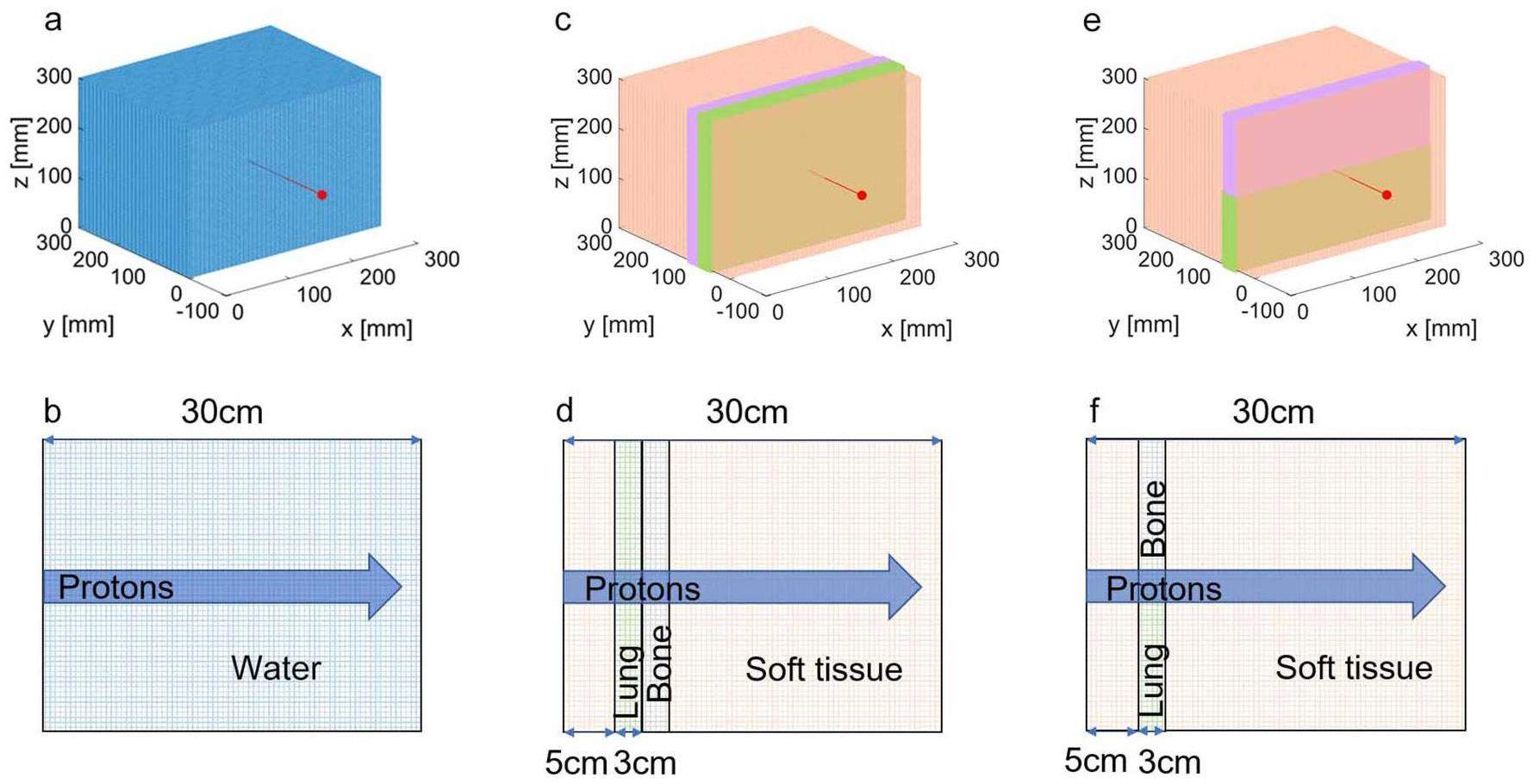
An extremely small proton beam was used to evaluate the stability of the gMCAP. The code was tested using three different phantoms: a uniform water phantom (WaterPhan), two standard heterogeneous phantoms (PhantomI and PhantomII) consisting of soft tissue, bone, and lung tissue. The voxel resolution for both the homogeneous and heterogeneous models was set to 1 mm×1 mm×1 mm, and the phantom size was 300 mm×300 mm×300 mm. In this experiment, proton beams with energies of 100 MeV, 150 MeV, and 200 MeV were employed to examine the water phantom. Additionally, a monoenergetic proton beam of 160 MeV was used to assess the heterogeneous phantom. Figure 7 illustrates a schematic of the source and geometry, as shown by Maneval et al. [31].

Fig. 7Full-screen View

(Color online) The homogeneous and heterogeneous phantoms and source: a-b show the schematic diagram of water, and c-f show the schematic diagram of the mixed model including soft tissue, lung tissue, and bone

2.7.3

Clinical cases based on patient treatment plans

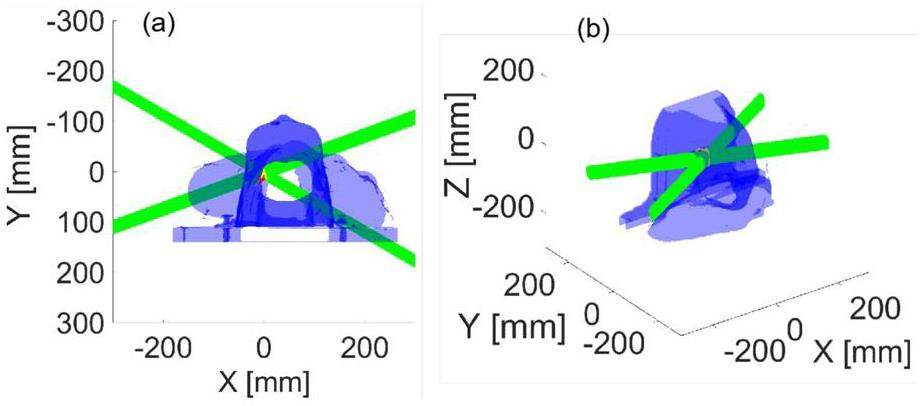
The suitability of the clinical case was evaluated using a dataset comprising head and neck CT data. The CT data were voxelized at a resolution of 0.875 mm×0.875 mm×3.000 mm, resulting in a total size of 512×512×79 voxels. Initially, a conversion process was applied to transform the HU values of the CT data into density values. Subsequently, the tissues were assigned. For the dose computation, the proton bixel width was set to 1 mm using the open-source treatment planning system matRad [46]. Information on 9651 rays from two irradiation fields was obtained. Figure 8 presents a schematic of the treatment plan in the laboratory coordinate system.

Fig. 8Full-screen View

(Color online) Schematic diagram of the treatment plan in the laboratory coordinate system: (a) top view, (b) 3D view

Moreover, in order to evaluate the impact of the two nuclear reaction models (APPROX and REFINED), proton beams with energies of 120 MeV, 140 MeV, and 180 MeV were utilized to irradiate the mandibular and tooth regions. These anatomical structures comprise tissues and organs that contain elements such as P and Ca. The dose distribution was recorded, and the relative deviations were analyzed using the two models.

Validation for discrete interactions

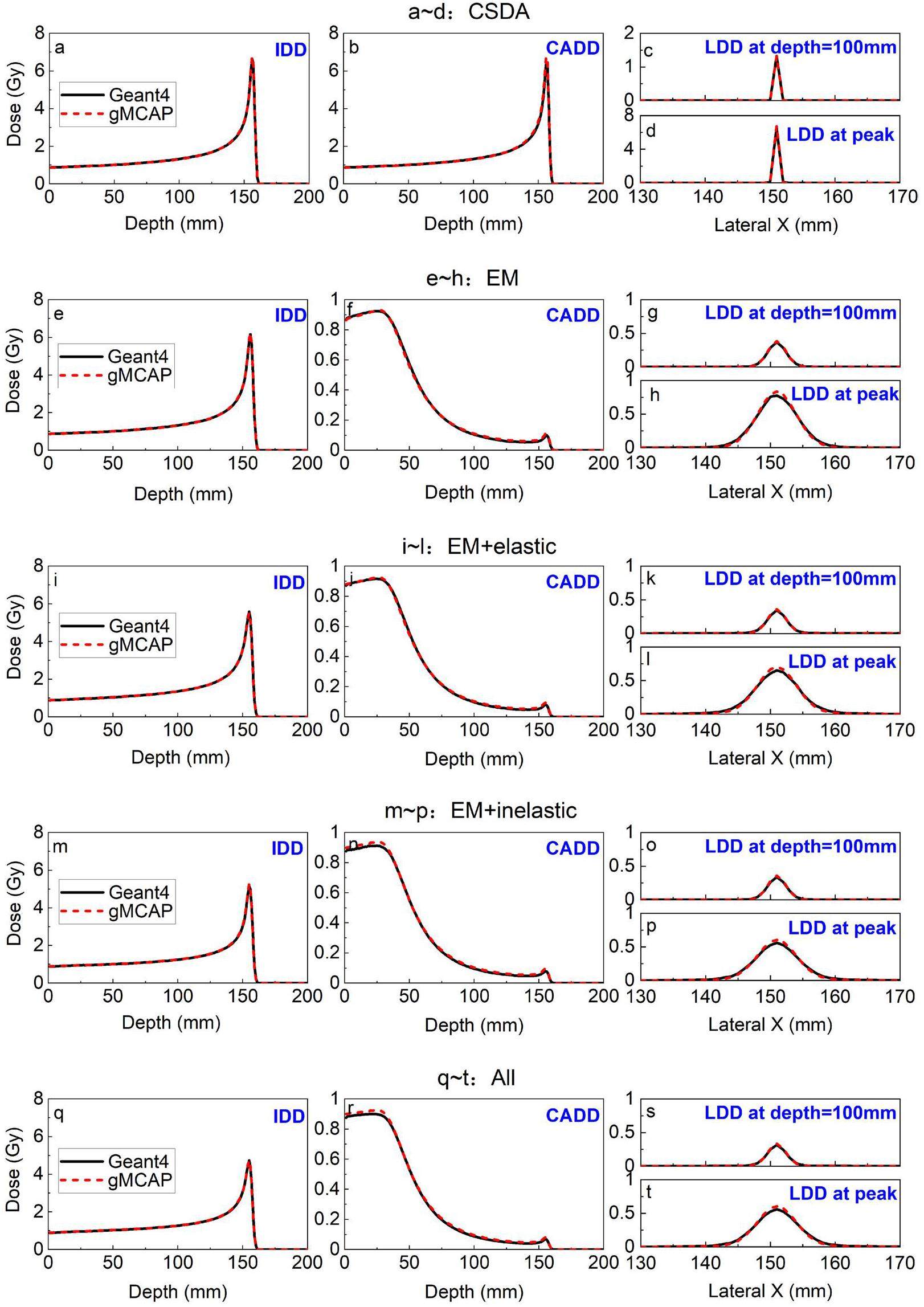
The discrete interaction was validated by comparing the dose distribution of a 150 MeV proton beam interacting with water using different physical models. In this study, the refined physical model, REFINED, of gMCAP was employed, whereas the well-studied simplified model, APPROX, was omitted because it has been extensively examined by previous researchers. Various physical models were tested separately, including CSDA, Electromagnetic Interactions (EM, which includes CSDA, Multiple Scattering, and Energy Straggling), Elastic Nuclear Interactions (EM + Elastic), Inelastic Nuclear Interactions (EM + Inelastic), and the complete set of physical models (All).

To verify the accuracy of the energy loss and angular deflection processes in each physical model, the integral depth dose (IDD), central axis depth dose (CADD), and lateral depth dose (LDD) at depth = 100 mm with LDD at the peak were examined and compared with the corresponding Geant4 results. The results, depicted in Fig. 9, demonstrate a strong agreement between gMCAP and Geant4, confirming the accuracy of the program's physical model. Notably, the LDD at the peak in gMCAP is slightly higher than that in Geant4. This discrepancy could be attributed to differences in the Multiple Scattering model being utilized. Despite the corrections made to this model in the present study, some deviations from Geant4 still exist. This discrepancy may be attributed to the exclusion of electron transport. However, it is important to emphasize that the level of inaccuracy is within an acceptable level. Further research on the transport model of secondary electrons will be conducted in the future.

Fig. 9Full-screen View

(Color online) Discrete interactions in water. The first column is the IDD curve, the second column is the CADD, and the third column is the LDD at depth = 100 mm and LDD at the peak. In the subgraph, (a)-(d) are the results of CSDA, (e)-(h) are the results of EM, (i)-(l) are the results of EM and Elastic interactions, (m)-(p) are the results of EM and Inelastic interactions, and (q)-(t) are the results of all interactions

Quantitative analysis

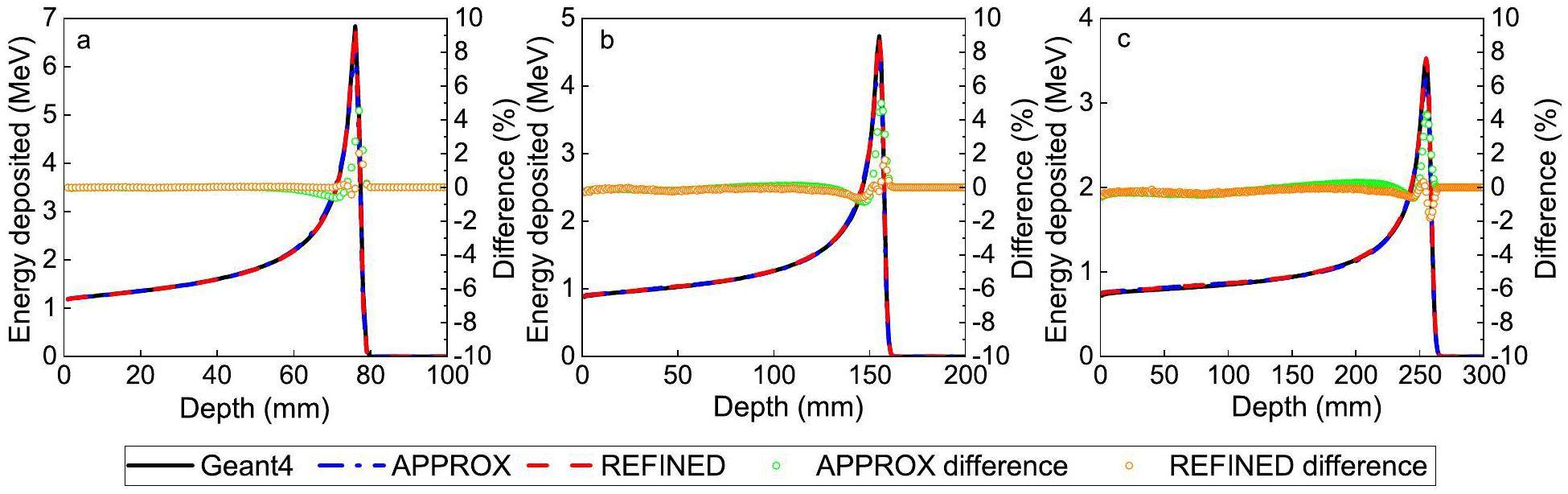
A quantitative analysis was conducted to compare the dose distributions of protons at different energy levels. This analysis involved the use of the APPROX and REFINED nuclear reaction models. The IDD curve was examined, as shown in Fig. 10. The results indicated that the disparity between the APPROX model and Geant4 was less than 5%. However, the REFINED model further reduced the overall deviation to 2%, with only a 1% deviation observed in the region beyond the distal fall-off area.

Fig. 10Full-screen View

(Color online) Integrated depth dose in water with primary proton energy of (a) 100 MeV, (b) 150 MeV, and (c) 200 MeV

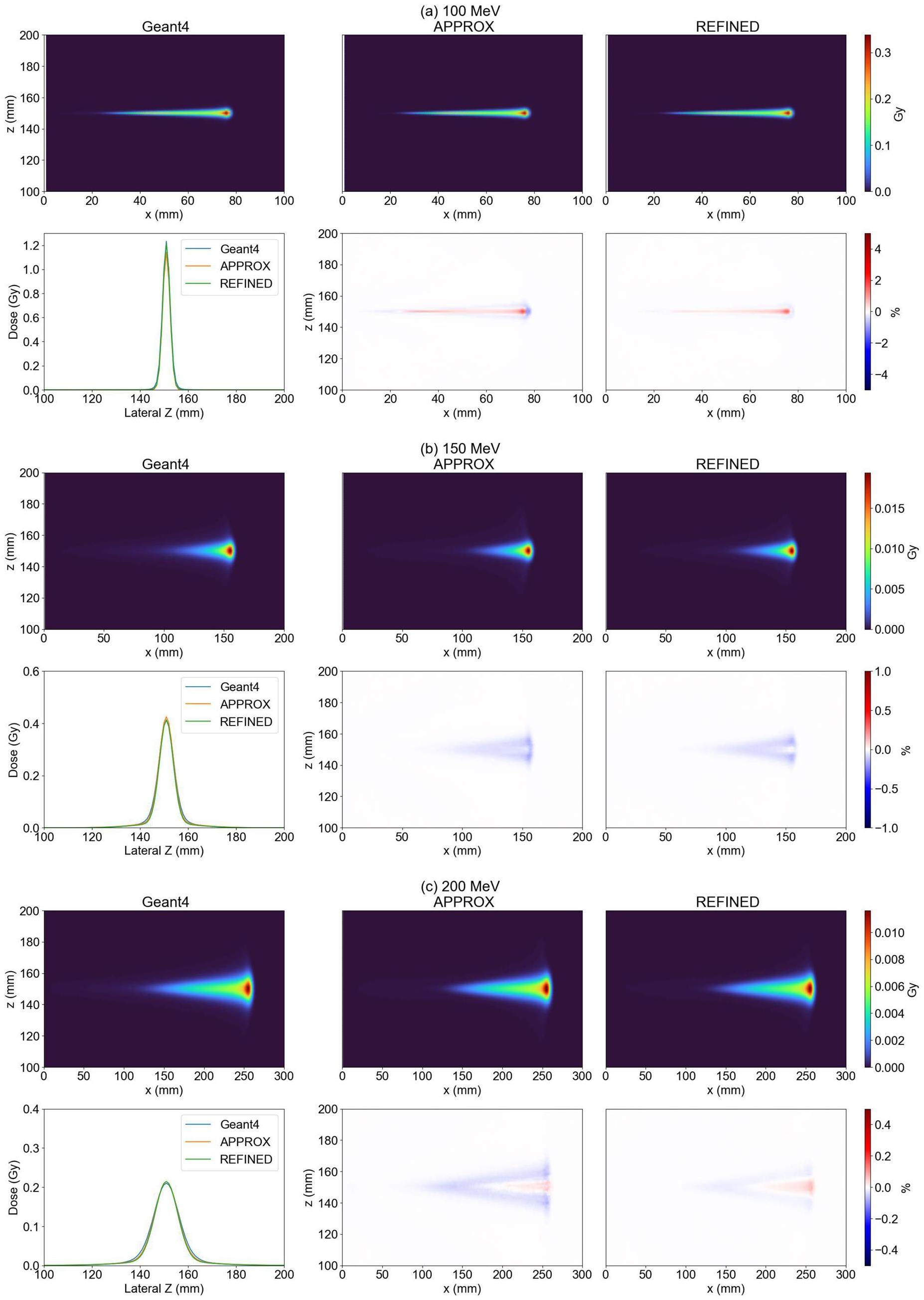
The analysis of the lateral distribution is presented in Fig. 11. The results demonstrate that the relative deviation between Geant4 and 90% of the data fell within 1%, indicating that the REFINED model exhibited better performance than the APPROX model.

Fig. 11Full-screen View

(Color online) Lateral dose distribution in water with primary proton energy of (a) 100 MeV, (b) 150 MeV, and (c) 200 MeV. The first row of each subfigure shows the dose distributions of Geant4, APPROX, and REFINED, respectively. The second row compares the lateral distributions at the peak, the relative error distributions between APPROX and Geant4, and the relative error distributions between REFINED and Geant4. The relative error is calculated as ${\text{error}}_i=\left({\text{dose}}_i^{\text{APPROX|REFINED}}-{\text{dose}}_i^{\text{Geant4}}\right)/\max \left({\text{dose}}^{\text{Geant4}}\right)$

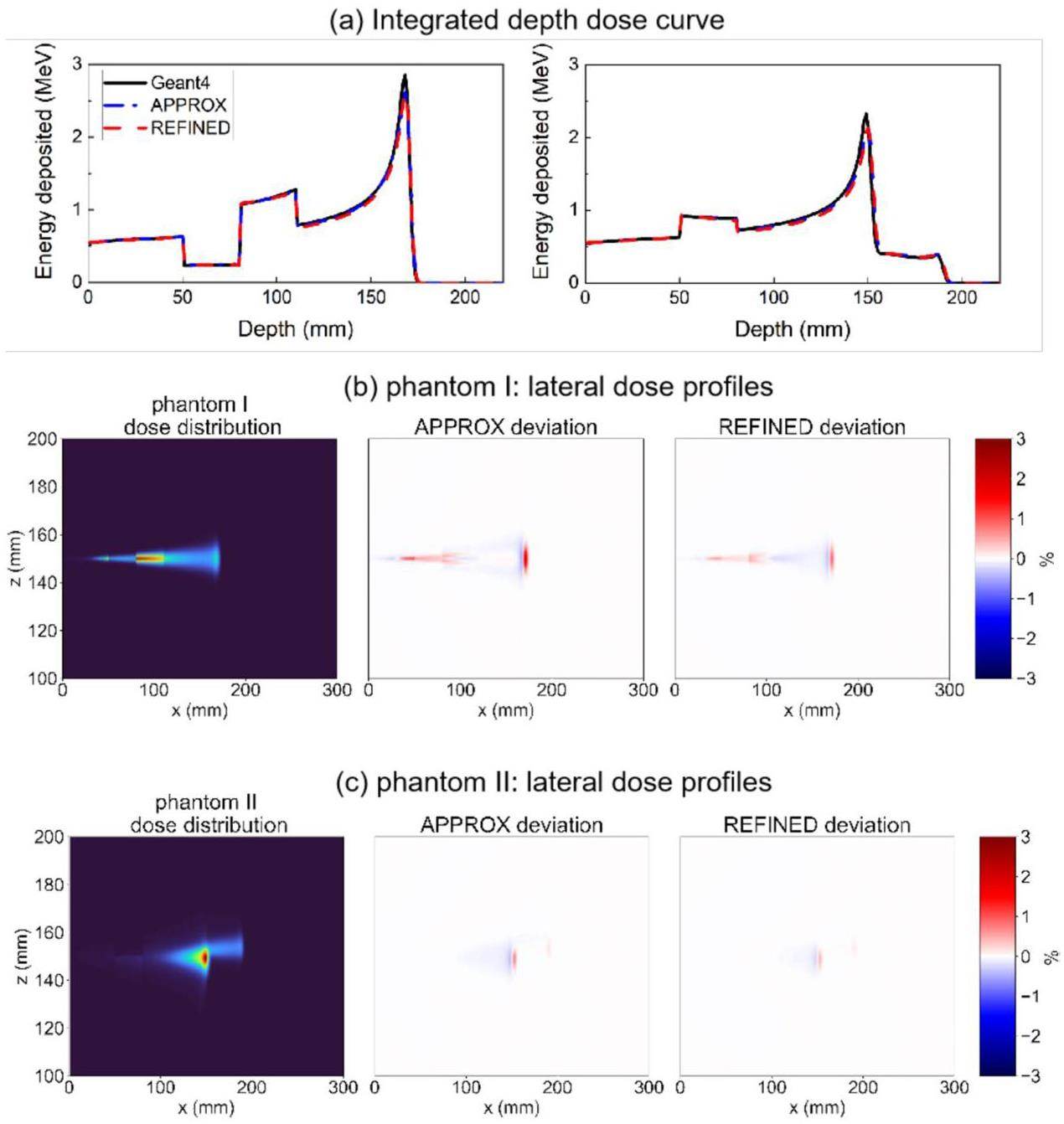
In addition, the heterogeneous model was used to evaluate the IDD curve and lateral dose profiles; the results are illustrated in Fig. 12. The results demonstrate good agreement between the dose distributions obtained from gMCAP and Geant4. Specifically, the relative deviation in the lateral dose profile was found to be within 3%. Notably, the REFINED model exhibited a reduced overall deviation compared to Geant4, in contrast to the APPROX model.

Fig. 12Full-screen View

(Color online) Integrated depth dose and lateral dose profile in heterogeneous model with primary proton energy of 160 MeV

The gamma passing rate, defined in [47], is a widely employed metric in radiotherapy for assessing the similarity of dose distribution maps. It considers voxels with doses greater than 10% of the maximal dose. The findings, presented in Table 1, indicate a high level of concurrence with the Geant4. The gamma passing rate of 2mm/2% exceeds 99%. Moreover, the REFINED model outperformed the APPROX model in terms of results.

Dose results of clinical cases

The dose outcomes for treatment plans targeting the head and neck region were compared. The dose distribution for the middle slice is shown in Fig. 13. The overall dose results closely match those of Geant4, with the relative deviation between gMCAP and Geant4 within 4%. Moreover, the gamma passing rates for both the APPROX and REFINED models were nearly identical at approximately 99%.

Fig. 13Full-screen View

(Color online) Dose distribution comparison of the head and neck treatment plan. The first row shows the dose distributions of Geant4, APPROX, and REFINED, respectively. The second row shows the integrated lateral dose distribution, the relative error distribution between APPROX and Geant4, and the relative error distribution between REFINED and Geant4. The third row shows the gamma index distribution of APPROX and REFINED compared to Geant4, respectively

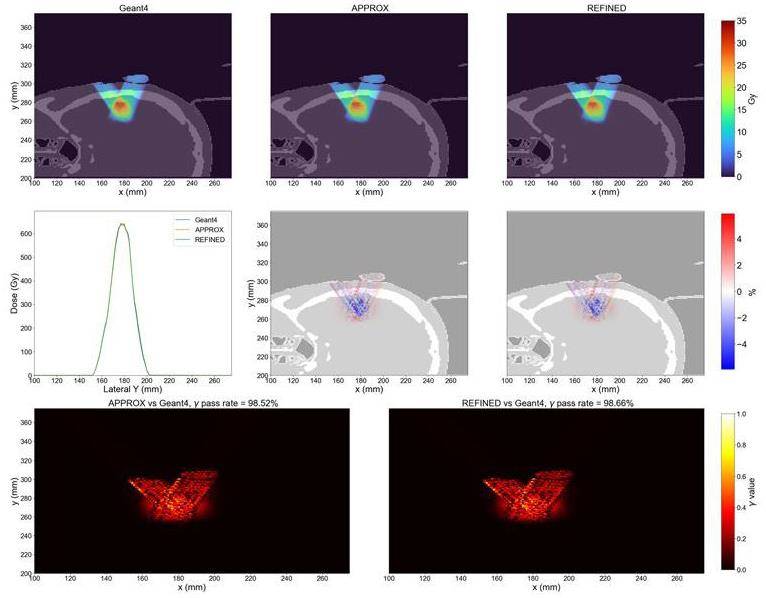
Furthermore, the dose outcomes along a line intersecting both beams and parallel to the y-axis were analyzed. The corresponding gamma values are also presented in the provided figure. This analysis provides additional insight into the agreement between gMCAP and Geant4 in terms of dose accuracy and conformity.

Efficiency gain

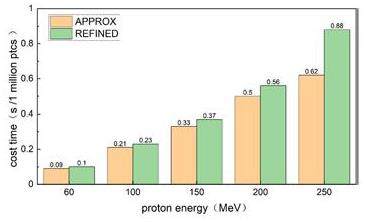
Compared to Geant4 running on a CPU for over 5 hours, gMCAP offers a significant reduction in runtime, completing the simulations within seconds. This translates to an efficiency gain of more than 1800 times in comparison to Geant4. The execution times for the two versions of gMCAP using the APPROX and REFINED models are summarized in Fig. 14. Using an NVIDIA GeForce RTX 4090 GPU, gMCAP achieved the transportation of one million particles in less than 1 second. Note that the REFINED model requires approximately 1.15 times more time than the APPROX model, with variations depending on the geometry and source type used in the simulations. These results highlight the efficiency and speed advantages of gMCAP for particle transport simulations.

Fig. 14Full-screen View

(Color online) Runtimes of gMCAP under different energies

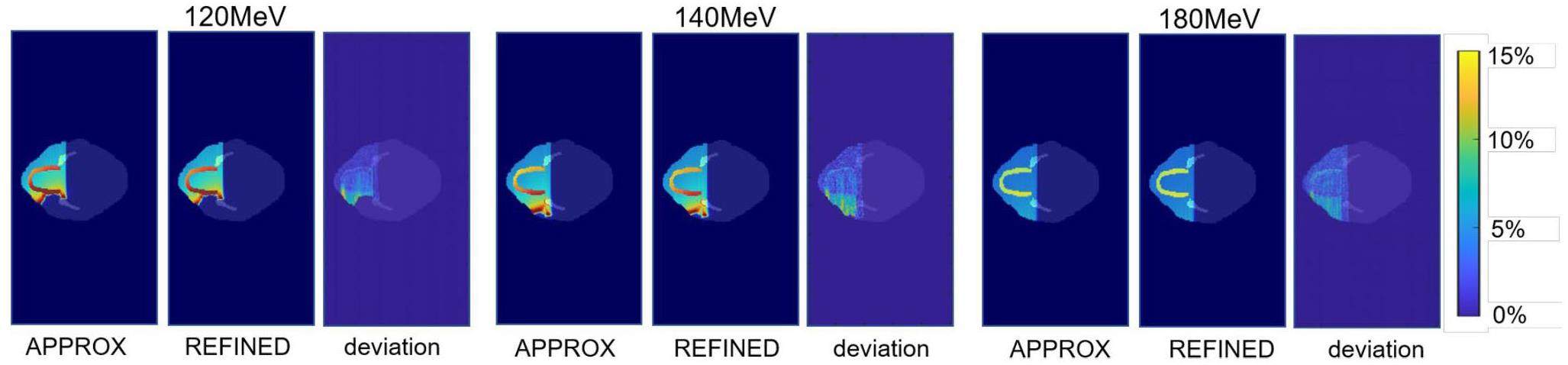
The impact of various nuclear models

Figure 15 shows the dose distribution and relative deviation of the two nuclear reaction models. Deviation primarily occurs in the teeth and downstream regions. The proton energies of 120 MeV, 140 MeV, and 180 MeV result in a maximum variance of approximately 15%. The primary explanation for this deviation is the ability of nuclear events to substantially alter the angular dispersion of secondary particles, primarily secondary protons. The tooth area comprises approximately 29% Ca and 14% P. The angular distribution of secondary protons generated through nuclear reactions differs from that produced by p-O nuclear reactions, leading to distinct energy and momentum distributions of the secondary protons downstream. The REFINED model incorporates the nuclear reactions of Z elements such as P and Ca, which rectify the angular distribution of secondary particles, leading to distinct downstream dose distributions.

Fig. 15Full-screen View

(Color online) Comparative analysis of the REFINED and APPROX models employing 120 MeV, 140 MeV, and 180 MeV protons for irradiating the mandibular area, respectively