General Description of the Simulink Model

The general structure of the model is based on a previously developed model [32]. The model was open-source on GitHub, where the exact implementation can be obtained. In this subsection, a brief introduction is provided to the major governing equations, constitutive relations, and changes made to the previous models. The important system parameters used in the MSRE model are summarized in Table 1.² The components of the coupled model are illustrated in Fig. 1.

Fig. 1Full-screen View

(Color online) Simplified diagram of the MSRE loop design. All the components and piping are included in the coupled model except for the drain tanks and frozen valves

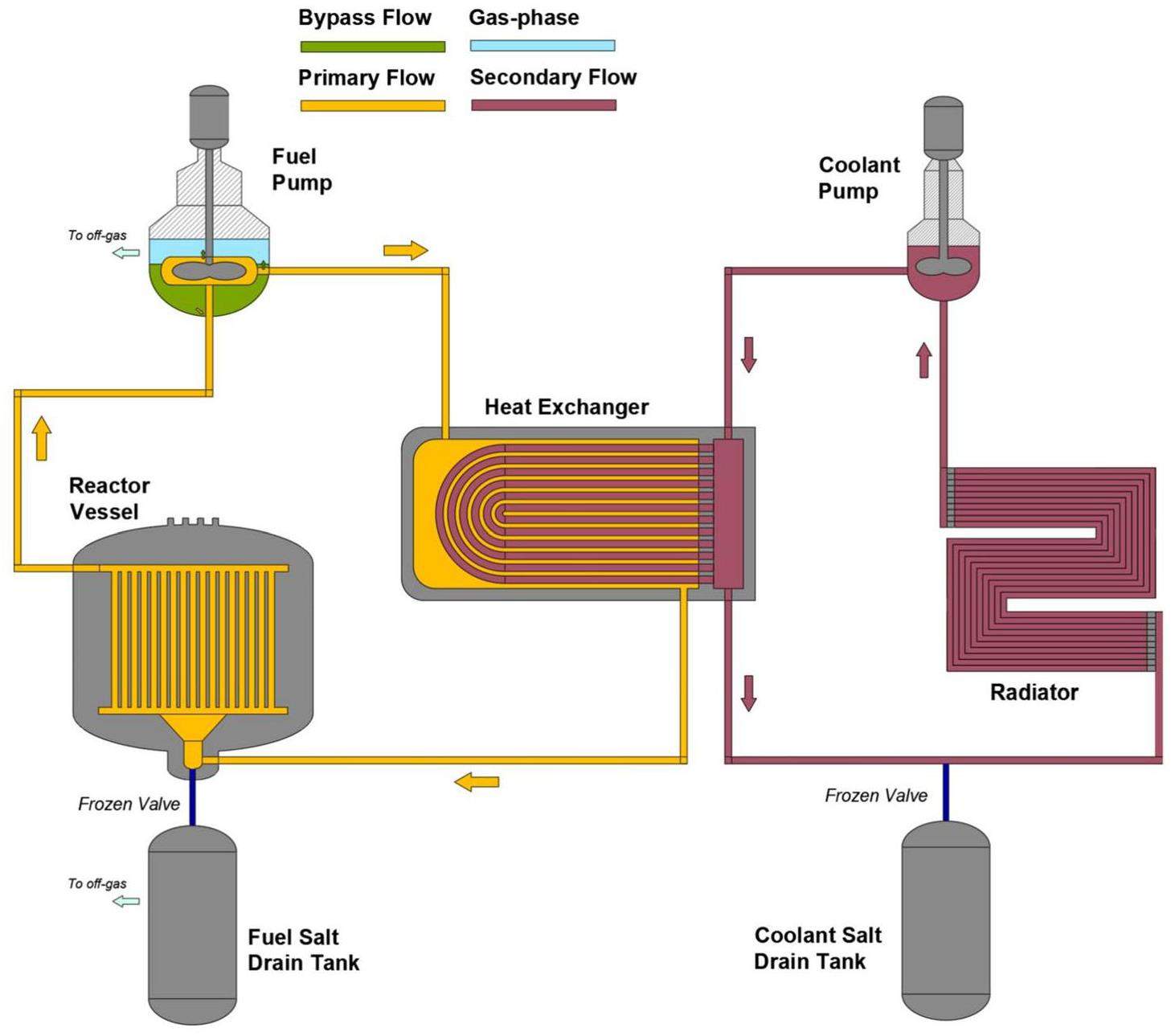
The Simscape toolbox in Simulink was used to provide building blocks for the thermal-hydraulics modeling of the reactor. Descriptions of the Simscape components are readily available in the Simulink/MATLAB documentation. Therefore, a detailed discussion of the individual components is omitted. The overall decay heat-generation rate was modeled using three decay heat-precursor groups with reference to the study by Pathirana et al. [63], and the heat generation in each lumped volume was explicitly calculated.

The transport models for xenon and void fractions were developed in a previous work [32]. The complex xenon and void-transfer processes in theMSRE pump bowl were modeled using semi-empirical equations. The diffusion of xenon inside the core graphite, transfer of xenon between the phases, and dissolution of entrained bubbles were described using theoretical and semi-empirical models. The xenon balance equations for a general lumped volume are as follows: $\begin{array}{c}\frac{\text{d}{C}_{\text{l,xe}}}{\text{d}t}=\frac{R_{\text{fission}}{\gamma }_{\text{xe}}}{\left(V_{\text{salt}}^{\text{core}}{N}_{\text{A}}\right)}+{\lambda }_I{C}_I-{\lambda }_{\text{xe}}{C}_{\text{l,xe}}\\ -{\varphi }_{\text{salt}}{\varsigma }_{\text{a}}{C}_{\text{l,xe}}-S_{\text{lgr}}-S_{\text{lb}}+\dot{V}\left(C_{\text{l,xe}}^{\text{in}}-C_{\text{l,xe}}^{\text{out}}\right)\mathrm{,}\end{array}$ (1) $\begin{array}{c}\frac{\text{d}{C}_{\text{b,xe}}}{\text{d}t}=-{\lambda }_{\text{xe}}{C}_{\text{b,xe}}-{\varphi }_{\text{salt}}{\varsigma }_{\text{a}}{C}_{\text{b,xe}}+S_{\text{lb}}\\ -S_{\text{bgr}}+\dot{V}\left(C_{\text{b,xe}}^{\text{in}}-C_{\text{b,xe}}^{\text{out}}\right)\mathrm{,}\end{array}$ (2) where S_lgr is the transfer term between the fuel salt and graphite, S_lb is the transfer term between the salt and bubbles, S_bgr is the transfer term between the bubbles and graphite, ς_a is the microscopic absorption cross section of xenon, R_fission is the fission rate, ϕ_salt is the average neutron flux in the fuel salt, and $\dot{V}$ is the volume flow rate of the fuel salt. The subscript l refers to quantities related to the salt, b denotes quantities related to the gas (bubbles), and gr is used to represent quantities related to the graphite. Outside the core, the direct fission generation, burnup, S_bgr, and S_lgr terms are zero, whereas the other terms remain the same. The diffusion of xenon inside the core graphite is calculated by numerically solving the following diffusion equation with the burnup and decay terms [74]: $\frac{\text{d}{C}_{\text{gr,xe}}}{\text{d}t}={\mathfrak{D}}_{\text{gr,xe}}{\nabla }^2{C}_{\text{gr,xe}}-\left(\lambda +\varphi {\varsigma }_a\right)C_{\text{gr,xe}}\mathrm{,}$ (3) $J_{\text{xe}}=-\epsilon {\mathfrak{D}}_{\text{gr,xe}}\nabla C_{\text{gr,xe}}\mathrm{,}$ (4) where $C_{\text{gr,xe}}$ is the phase-averaged xenon concentration, ε is the porosity of the graphite, and J_xe is the xenon mass flux at the outer boundary of the core graphite. The formation of each term is discussed in a previous publication [32].

The gas/void transport is based on volume conservation and the homogeneous equilibrium model. The gas and fuel salts were assumed to move at the same velocity. The solubility of the inert gas bubbles was considered using an algebraic model based on experimental data obtained during the MSRE [20, 32].

Modified Point-kinetics Equations, Core Nodes, and Feedback Effects

In the current model, the implementation of mPKEs and the calculation of reactivity feedback effects are modified in comparison with the previous study [32]. The modifications are discussed in this subsection. The neutronics and feedback parameters used for different fuel types are summarized in Table 2.

In MSRs, fuel salt circulates in the primary loop. Thus, the DNPs were transported out of the core. Thus, some of the delayed neutrons were lost during the transit time across the primary loop. Moreover, the physical and adjunct neutron fluxes and DNP-concentration profiles varied under the fuel-salt flow. Therefore, a modification of the point-kinetics equation derived for solid-fueled reactors is required. A rigorous derivation of mPKEs can be found in Dulla et al. [30, 85]. However, such a rigorous approach can only be realized by coupling a neutronics code to the system-analysis model, which significantly increases the simulation time. Instead, in the current study, the classical model by Kerlin et al. [28] is selected as the starting point. The model was developed during the MSRE and has been calibrated using various dynamics testing data obtained from the experiments. Therefore, even though this model was derived without considering the importance of DNP, it was in good agreement with the experiments. The original model proposed by Kerlin et al. [28] is $\frac{\text{d}n}{\text{d}t}=\frac{\rho -\beta }{\text{Λ}}n+{\displaystyle \sum _{i=1}^6}{\lambda }_i{C}_i+S\mathrm{,}$ (5) $\frac{\text{d}{C}_i\left(t\right)}{\text{d}t}=\frac{{\beta }_i}{\text{Λ}}n-{\lambda }_i{C}_i\left(t\right)-\frac{C_i\left(t\right)}{{\tau }_{\text{c}}}+\frac{C_i\left(t-{\tau }_l\right)e^{-{\lambda }_i{\tau }_l}}{{\tau }_{\text{c}}}\mathrm{.}$ (6) The last two terms in Eq. (6) correspond to the outflow and inflow of the DNPs at the reactor core. τ_l is the loop transit time outside the core and τ_c is the residence time within the core. The assumptions behind these equations are the instant mixing of DNPs inside the core and absence of precursor mixing outside the core.

In this study, Eq. (6) is replaced with a series of lumped conservation equations for DNPs. For each lumped volume, the following equation is solved: $\frac{\text{d}{C}_{i\mathrm{,}n}\left(t\right)}{\text{d}t}=\frac{{\beta }_i}{\text{Λ}}n-{\lambda }_i{C}_i\left(t\right)+\frac{\dot{V}{C}_{i\mathrm{,}\text{in}}\left(t\right)}{V_n}-\frac{\dot{V}{C}_{i\mathrm{,}\text{out}}\left(t\right)}{V_n}\mathrm{.}$ (7) If a sufficient number of lumped equations are included, Eq. (7) converges to Eq. (6). This implementation has three main advantages. First, Eq. (7) can be applied to both core and out-of-core nodes. It may be used with a neutronics code to derive the mPKEs using a quasistatic approach similar to that of Zanetti et al. [42] Second, by mapping the out-of-core node to each physical component and adding a correction factor to the outflow term, different mixing behaviors inside the corresponding physical components can be accounted for. Finally, the computer-memory requirement was significantly reduced by moving from Eq. (6) to Eq. (7). This is essential for applying the current coupled model to extended runs under low-flow conditions. In the current implementation, one core node and ten out-core nodes were used without exact mapping between the physical components and DNP nodes.

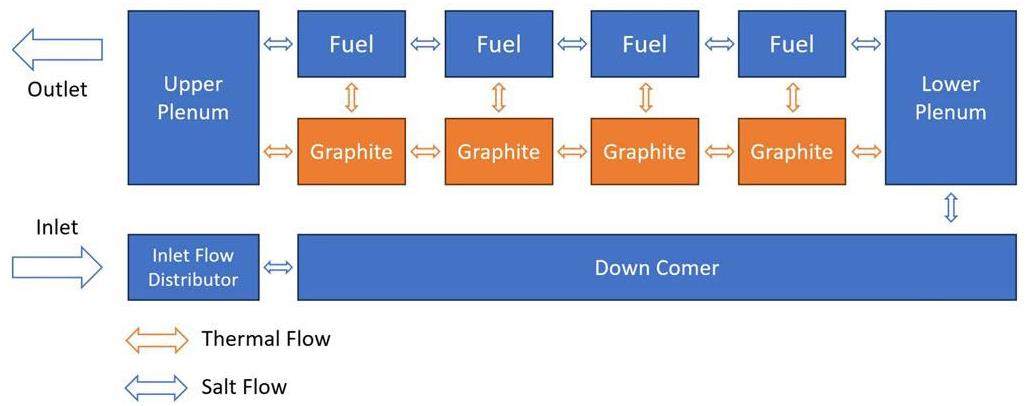
The thermal-hydraulics nodal diagram of the reactor is shown in Fig. 2, which includes the upper plenum, lower plenum, downcomer, inlet-flow distributor, and four linear core nodes. The axial heat conduction between the graphite nodes and plenums was included, whereas the radial conduction was neglected. The axial-power profile and nuclear-importance profile used to calculate the feedback effects were taken from Haubenreich et al. [80].

Fig. 2Full-screen View

Thermal-hydraulics nodal diagram of the MSRE core in the coupled model

Frequency Response

The frequency response of a dynamic system is its response to a sinusoidal input signal in the frequency domain. The different frequency responses of the system can be defined based on the selected input and output signals. The frequency response can be measured experimentally, which provides valuable information for controller design and stability analysis [86]. Moreover, frequency analysis is useful for the experimental determination of reactivity-related parameters [38, 86, 87]. During the MSRE operation, multiple dynamics-testing experiments were conducted to obtain the frequency responses of the reactor power to reactivity disturbances [33, 34]. These tests were conducted at different steady-state power levels for both ^235U and ^233U fuels.

Because the coupled MSRE model is highly nonlinear, the frequency response cannot be obtained from a derived transfer function, as in a linearized model. Numerical experiments are conducted to determine the frequency response of the coupled MSRE model. For each condition, the simulation was first run for three days to reach steady-state xenon distributions, while the reactor was maintained at a critical condition using a PI controller. The PI controller was disabled, the final reactivity insertion was recorded, and the steady-state solution was saved. Using the steady-state solution as the starting point, sinusoidal reactivity signals of different frequencies were introduced into the system, and the simulations were run for a minimum of ten cycles or 1500 s. The cross-power spectral density between the neutron density and reactivity signals was calculated and divided by the power spectral density of the reactivity signals. The outcome is a function in the frequency domain owing to the finite simulation time. The values of the signal frequencies form the frequency responses of the system.

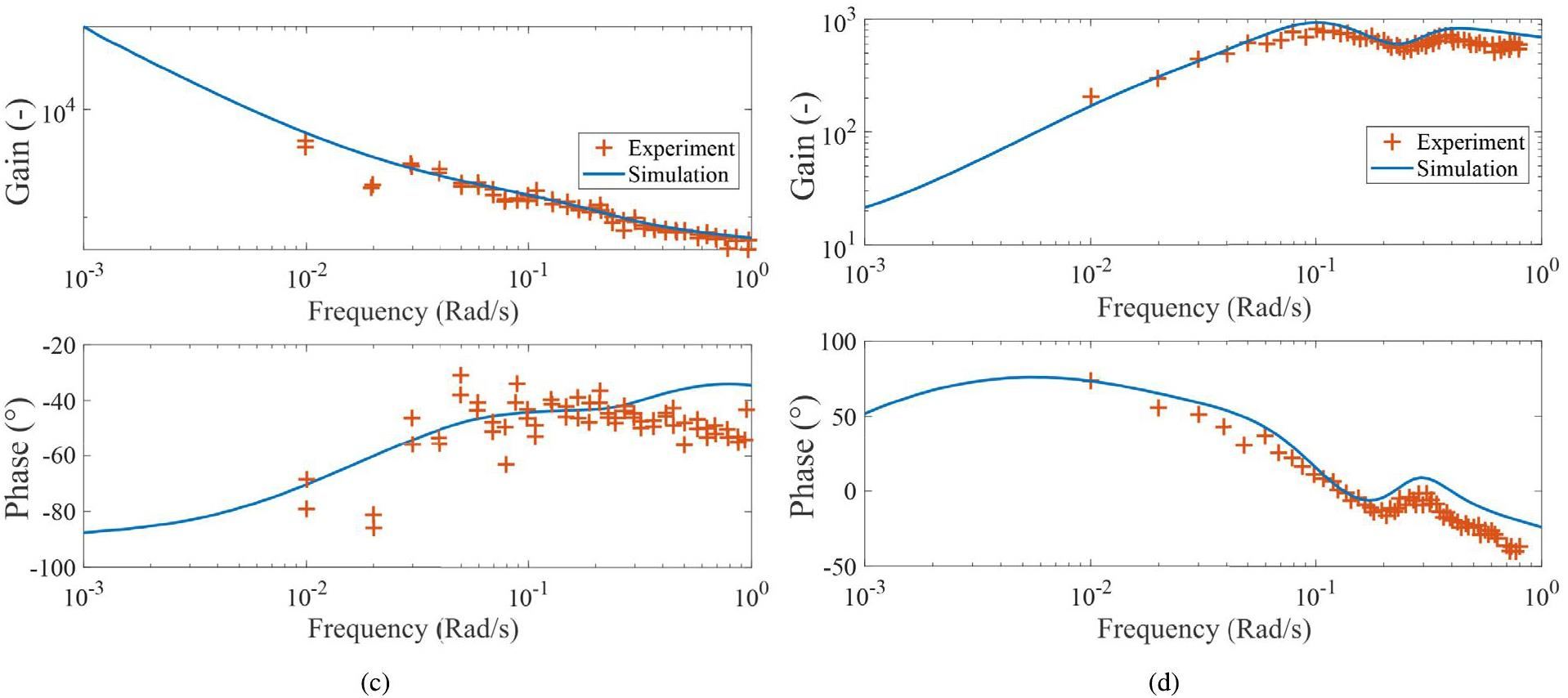
For the ^235U fuel, the simulated frequency responses at three different power levels are presented and compared with the experimental data [33] in Fig. 3 and Fig. 4. Different methods were used to obtain the frequency response in the dynamics-testing experiments. The results from the different methods are not distinguished in the current study, and the spread of data points may be considered as experimentally uncertain. Based on the results, a general agreement was reached between the simulation and experiment, which suggests that the coupled MSRE model can capture the reactor behavior under small reactivity disturbances. Cammi et al. [88], Guerrieri et al. [89], and Henderson and Ragan [90] performed theoretical analyses of circulating fuel reactors from a transfer-function perspective using mPKEs. The conclusions and equations from these studies are used to aid in further discussions on the results.

Fig. 3Full-screen View

Comparison of the power-to-reactivity frequency response from simulations and experiments at zero-power with ^235U fuel [35]

Fig. 4Full-screen View

Comparison of the power-to-reactivity frequency response from simulations and experiments at zero power with ^235U fuel [35]. (a) Frequency response at 2.5 MW; (b) Frequency response at 8 MW

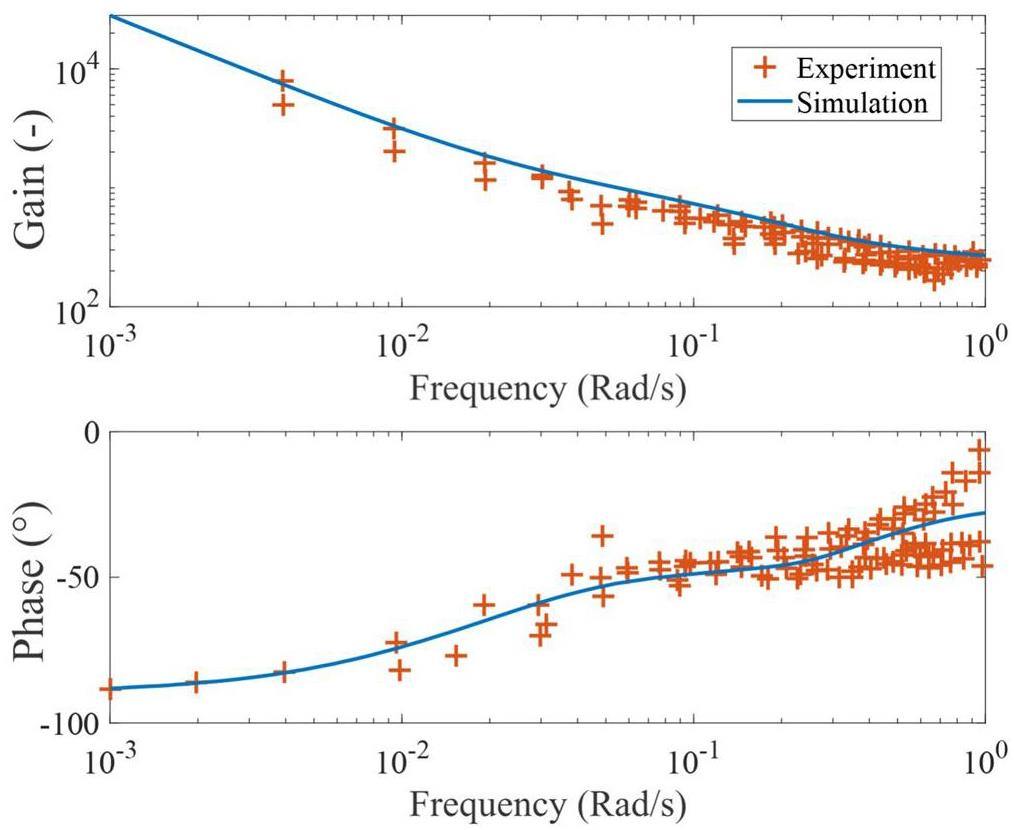
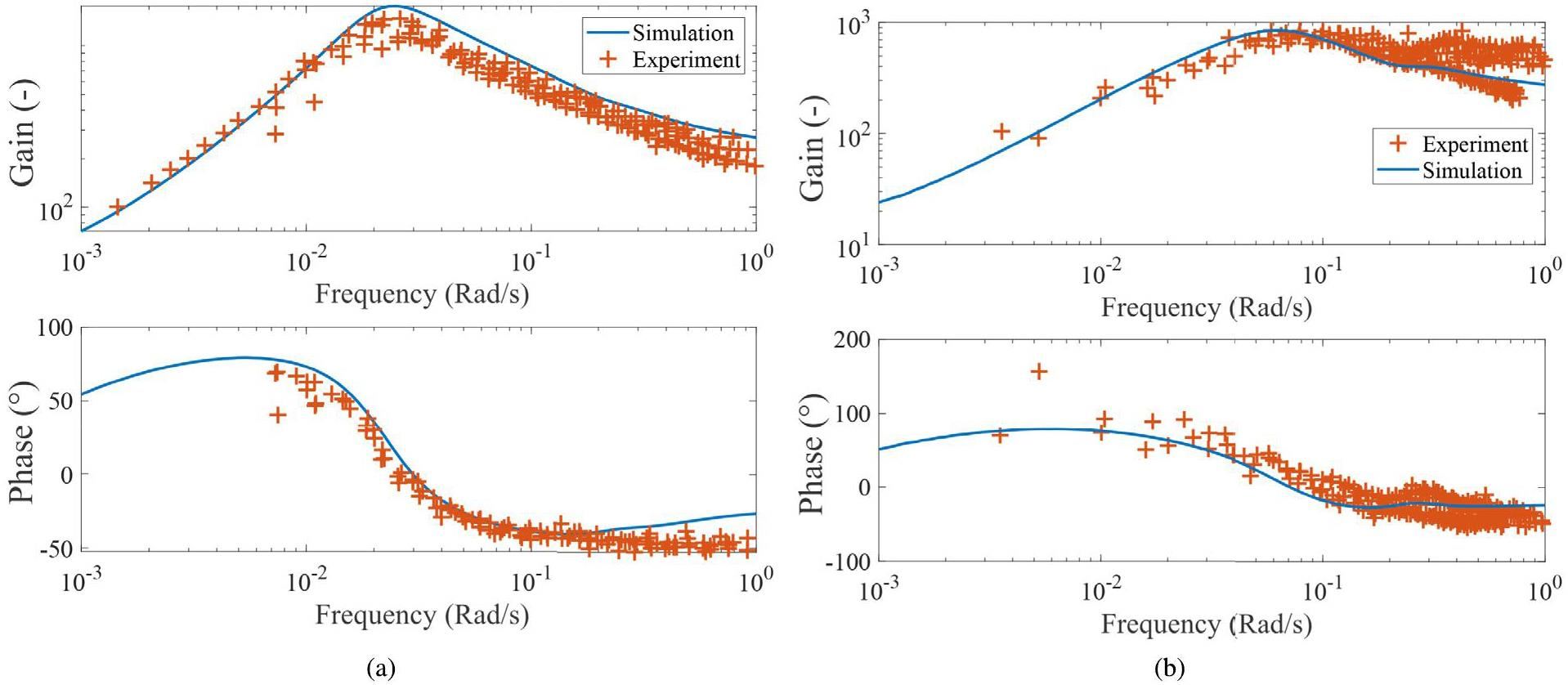
Figure 3 illustrates the reactor response at zero power. This condition is of special interest because the thermal and poisoning feedback effects are absent. For solid-fueled reactors, the frequency response at zero power is dominated by neutronics models. For MSRs, the flowrate in the reactor also plays a significant role. For low frequencies, the response of the reactor G(jw) is approximated by $G(jw)=\frac{\delta n}{n_0\delta \rho }\approx -\frac{j{w}_1}{w}\mathrm{,}\text{when}w\ll 1\text{rad/s}$ (8) $w_1=\frac{\beta }{\text{Λ}+{\displaystyle \sum }{\beta }_i\left[1+{\tau }_{\text{l}}\exp \left(-{\tau }_{\text{l}}{\lambda }_i\right)/{\tau }_{\text{c}}\right]/{\lambda }_i}\mathrm{.}$ (9) The result dictates a nearly linear decrease in the log-log plot of the gain, and a frequency lag starting from -90 degrees, as observed in Fig. 3. The agreement between the simulation, theory, and experiment at zero power provided strong confidence in the validity of the neutronics model adopted in this study.

When the reactor is powered, feedback effects from temperature and xenon poisoning occur, and the frequency response of the reactor is complicated. When considering only the thermal feedback with an averaged core temperature, the neutron-temperature feedback transfer function can be defined as $H^{\prime }\left(jw\right)=\frac{\delta {\rho }_{\text{t}}}{\delta n/n_0}\mathrm{,}$ (10) whereas the closed-loop transfer function $R(jw)$ is derived as $R(jw)=\frac{G(jw)}{1-G(jw)H^{\prime }(jw)}\mathrm{.}$ (11) Eq. (11) shows that when the magnitude of G(jw) is large, $R(jw)$ is dominated by H'(jw), which corresponds to the case at low frequencies. However, when G(jw) is small, the closed-loop function converges to G(jw), as expected for high-frequency disturbances, because the fluctuation ends before the system feedback can react. H'(jw) is proportional to the reactor power such that a higher reactor power stabilizes the reactor. Additionally, $H^{\prime }(jw)/P_0$ is dependent only on the thermal-hydraulics characteristics. Comparing Fig. 4a and b, the gain of the reactor at a higher power is dampened, as anticipated. Moreover, the phase difference at lower frequencies is positive rather than negative, as at zero power, which corresponds to a negative temperature-feedback coefficient in H'(jw). The simulation slightly overpredicts the gain at 2.5 MW, but satisfactorily predicts the gain at 8 MW. This reflects the imperfections in the thermal-hydraulics modeling employed in the current study.

Another characteristic of the frequency response can be observed by rearranging Eq. (11) as follows: $R(jw)={\left[1/G\left(jw\right)-H^{\prime }\left(jw\right)\right]}^{-1}\mathrm{.}$ (12) At low frequencies, the denominator converges to -H'(jw). As the frequency increases, the magnitude of $1/G(jw)$ increases, whereas the magnitude of H'(jw) decreases. A frequency exists at which the denominator is minimized, which is the natural or resonant frequency of the system. This resonance behavior is clearly observed in Fig. 4, where the reactor is the most unstable. Notably, the resonant behavior does not indicate instability. In general, a smaller gain at the resonant frequency and a larger bandwidth of the resonant peak are indicators of more stable systems [91]. Finally, in Fig. 4b and 5b, a dip is observed approximately at 0.23 rad/s, which corresponds to the out-of-core circulation time and delayed neutrons [59].

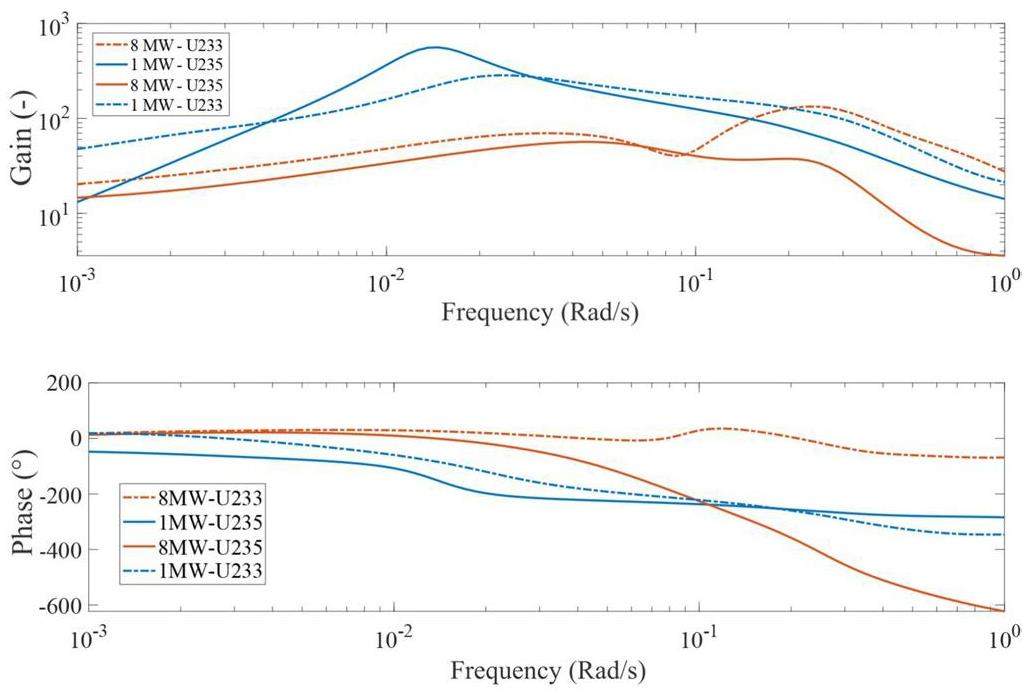
In Fig. 5, the frequency response for the ^233U fuel is shown, which possesses shapes similar to the frequency response for ^235U fuel. Again, good agreement is observed between the simulation and experiment. The gain of the reactor is generally increased for the ^233U fuel compared with the ^235U fuel, indicating that it is less stable. Moreover, a dip near 0.23 rad/s is again observed and is more prominent than that with the ^235U fuel.

Fig. 5Full-screen View

Comparison of the power-to-reactivity frequency response from simulations and experiments with ^233U fuel [33, 34]. (a) Frequency response at zero-power; (b) Frequency response at 8 MW

In Fig. 6, the frequency responses of core-outlet-temperature to rector-power from the simulations and experiments are presented. The frequency response obtained directly using the core-outlet temperatures deviated from the experimental data, especially at higher frequencies. The same problem was noted in the report by Steffy [34], in which the dynamic model used during MSRE could not capture the result. The larger deviation at higher frequencies suggests that the source of disagreement is the temperature measurement itself. Thermocouples were used during the MSRE for temperature measurements, which has non-negligible response times. The response time mainly originates from the thermal inertia and heat-transfer conditions in the measurement system. A heuristic transfer function between the thermocouple measurement and surrounding flow temperature is derived from the one-dimensional heat-conduction equation in the Appendix as follows: $\begin{array}{l}M(jw)=\frac{T_m\left(jw\right)}{T_{\infty }\left(jw\right)}\\ ={\left[\cosh \left(\sqrt{\frac{jw}{{\alpha }_{\text{th}}}}L\right)-\frac{k}{h}\sqrt{\frac{jw}{{\alpha }_{\text{th}}}}\sinh \left(\sqrt{\frac{jw}{{\alpha }_{\text{th}}}}L\right)\right]}^{-1}\mathrm{,}\end{array}$ (13) where h is the heat-transfer coefficient between the thermocouple wall and fuel salt, L is the characteristic length of the thermocouple, ${\alpha }_{\text{th}}$ is the thermal diffusivity of the thermocouple, and k is the thermal conductivity of the thermocouple. A transfer function was used to convert the true temperature signal at the core outlet into the measured temperature signal.

Fig. 6Full-screen View

Comparison of the temperature-to-power frequency response from simulations and experiments with ^233U fuel [34]

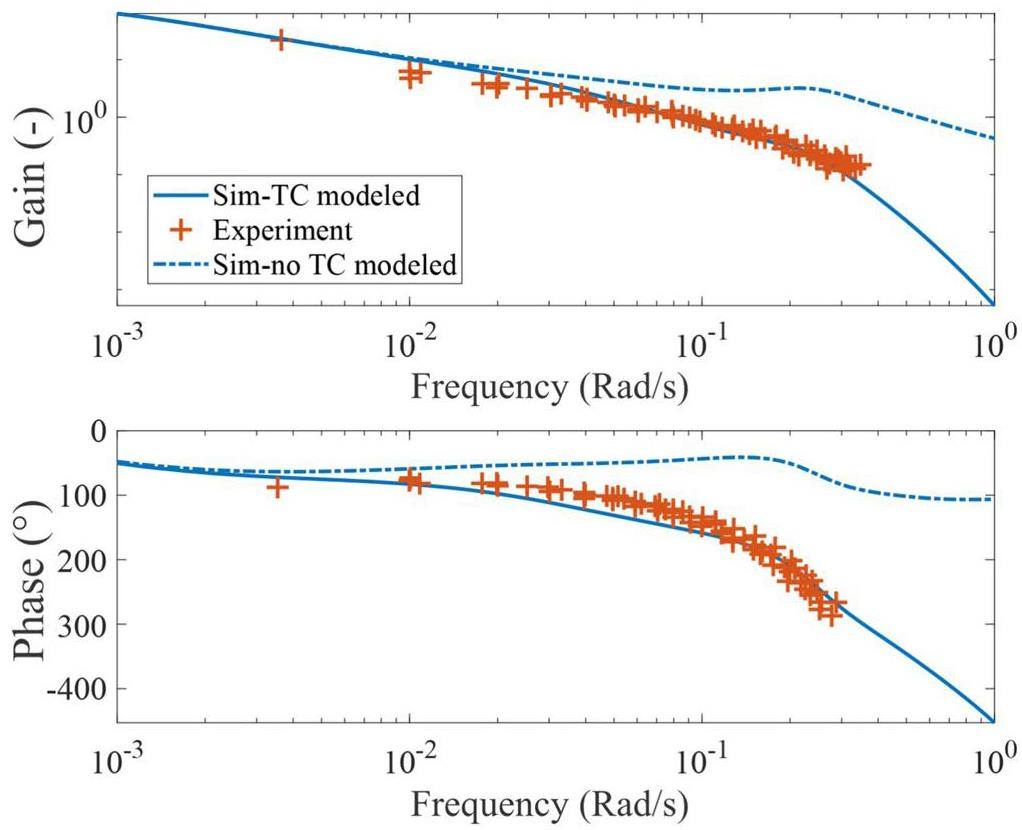
The thermocouple-sheath material used in the MSRE is Inconel, and the thermocouple is placed in the fuel salt using the so-called “INOR-8” lug [92]. The properties of Inconel 718 are used in Eq. (13). The heat-transfer coefficient is estimated using the following empirical correlation [93]: $h=\frac{0.683D_{\text{f}}R{e}^{0.466}P{r}^{1/3}}{2R_{\text{tc}}}\approx 6461.8\text{W/}\left({\text{m}}^{\text{2}}\cdot \text{K}\right)\mathrm{.}$ (14) Finally, the characteristic length used in the transfer function was 25.4 mm, which was the only nominal value used to approximate the thermal inertia of the measurement system. The solid lines in Fig. 6 show the simulations in which the thermocouple transfer function was applied. The good agreement between the experimental data and simulation results is remarkable, considering the great simplification made in the derivation of the transfer function.

In conclusion, the current coupled model can generally predict the frequency response of the MSRE at zero power and elevated power levels for both the ^235U and ^233U fuels. No significant difference was observed between the two fuel types in terms of system frequency responses. The good agreement at zero power validates the neutronics model. Moreover, the thermal-hydraulics modeling adopted in this study was validated using the temperature-to-power frequency response.

Transient Response

In the previous subsection, the system frequency responses obtained from the experiments and simulations were compared. Although the frequency response is a useful representation of system behavior, it does not have a direct link to the transient response of the reactor. In this subsection, the coupled model is validated against multiple transient experiments in the MSRE.

In the zero-power physics experiment of the MSRE, the transient responses during pump startup and pump coast-down are measured [38]. At zero power, feedback effects from thermal and fission product poisoning are absent, and the system response is dictated by the neutronics and hydraulics characteristics of the reactor system.

In the pump-startup experiment, the reactor was initially critical, whereas the pumps were idle. At the start of the experiment, the pumps were turned on and a salt flow was established. This procedure was reversed in the pump coast-down experiment. An automatic reactivity-control system was used to maintain the criticality of the reactor. The control-rod locations, pump speeds, and coolant flowrate were recorded. Unfortunately, the fuel-salt flowrate was not available. In the simulation, a hyperbolic tangent function was used to approximate the flowrate in the primary loop.

The simulations of the pump transients are compared with the experimental data in Fig. 7. Two simulation approaches are applied. In the first approach, depicted by the blue line, the reactor is assumed to remain perfectly at criticality, and the neutron density does not change. In the second approach, indicated by the purple line, a simple proportional controller is introduced as an approximation of the automatic control system employed in the MSRE. A sampling frequency of 40 Hz is used for the neutron-density measurement. The proportional parameter is set as -50 pcm percent neutron fraction. The maximum reactivity-change rate was limited to 25 pcm/s, matching the control-rod specifications in the MSRE [94].

Fig. 7Full-screen View

Comparison between the experiment and simulation of the pump transients [38]. The dash-dot line represents the relative flowrate in the primary loop (right axis). The solid lines correspond to the simulation results (left axis)

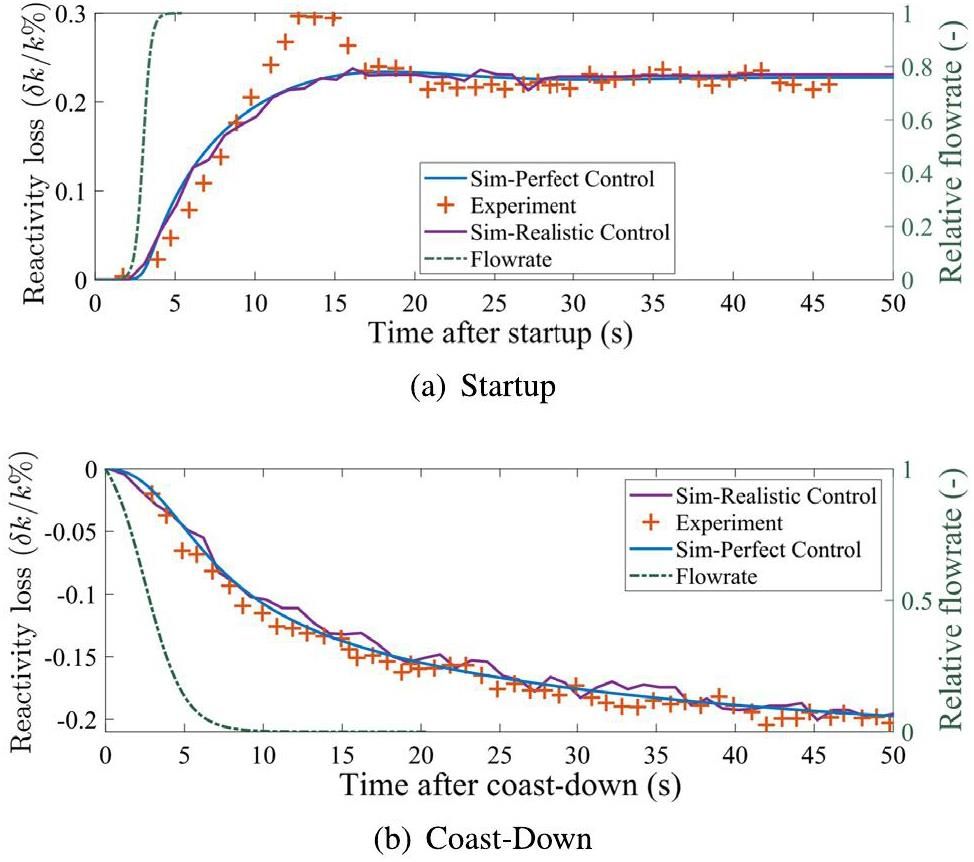
Figure 7a presents the simulation results for the pump-startup transient. Both simulation approaches predict the steady-state reactivity loss accurately but fail to predict the initial reactivity peak. The peak observed at approximately 15 s is related to the out-of-core circulation time. The simulation with the proportional controller exhibits the fluctuating behavior observed in the experiment, suggesting that such fluctuations may be related to the control system in the MSRE. Fig. 7(b) shows a comparison of the pump coast-down transient. Both simulation approaches capture the general trend of the reactivity change, whereas the PI controller helps reproduce short-period fluctuations.

Both simulation approaches failed to capture the reactivity peaks shown in Fig. 7(a), which requires further discussion. In studies by Guo et al. [45] and Shi et al.[52], the simulated reactivity loss also failed to match the reactivity peak. In these studies, mPKEs were used with a homogeneous DNP distribution in the core, as in the current study. In contrast, in the work by Fischer and Bureš [73], the mPKEs were solved together with 1D DNP-transport equations, and the delayed neutron-generation term was weighted using the steady-state adjunct flux and power profile. Consequently, a long-period fluctuating behavior in the startup transient is observed. Considering the differences in the models, the disagreement between the current simulation and experiment during the startup transient may be related to the homogeneous treatment of DNPs inside the core. This smears the sharp reintroduction of delayed neutrons to the core center, where neutron importance is highest.

Figure 8 shows the reactor power following a 19 pcm reactivity insertion at an initial power of 5 MW. The reactor power quickly increases after reactivity insertion in the first few seconds. Subsequently, as the temperature of the core increases, the feedback effect offsets the added reactivity. The net steady-state result shows a slight increase in reactor power. The simulation results generally agree with the experimental data. In the simulation, the initial power peak is slightly overestimated, and slow fluctuations in the power profile are not observed. Notably, during the experiments with the ^233U fuel, notable neutron noise is observed owing to the circulating bubbles. Circulating bubbles are considered as the major source of the observed fluctuations [34], which are not modeled in the current study.

Fig. 8Full-screen View

Comparison of the simulated and measured power transients following a 19.0 pcm reactivity insertion at 5 MW with ^233U fuel [34]

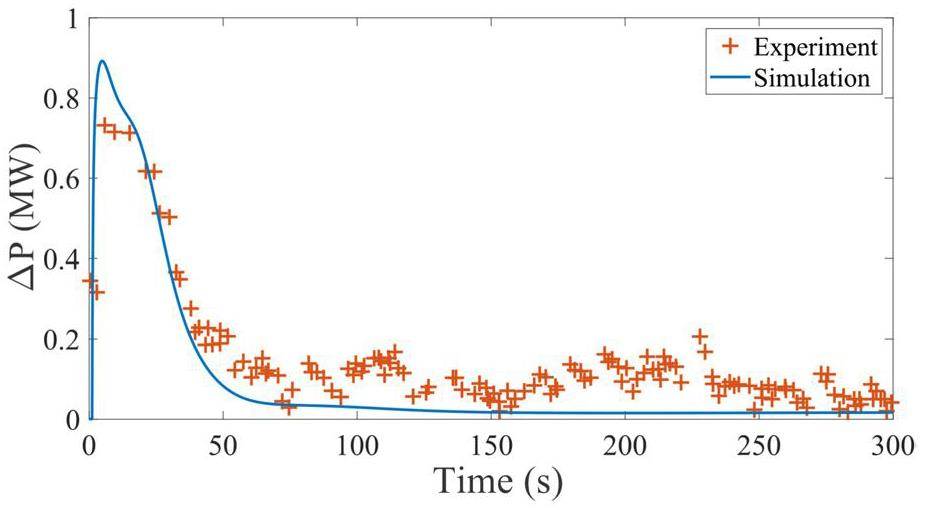
In conclusion, the current coupled model could predict the transient response of the MSRE under both zero-power and operational conditions. However, the mPKEs employed in the current study may require improvements to capture sharp transient behaviors and short-period fluctuations.

Power-to-flowrate and Void Frequency Reponses

In the previous section, the power-to-reactivity frequency response of the MSRE, which is of general interest in reactor control and stability analysis, was thoroughly investigated. In this section, two other types of frequency responses unique to MSRs are investigated.

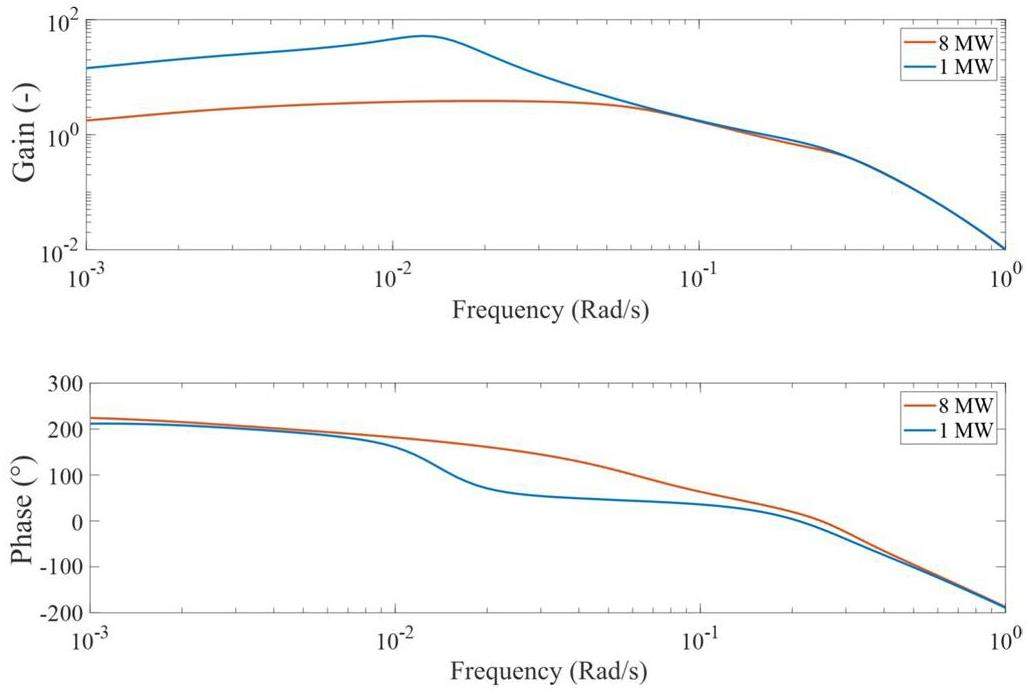
Figure 9 shows the power-to-flowrate frequency responses at different reactor-power levels and fuel types. The gain and flowrate are normalized to the operational parameters. The gain in Fig. 9 exhibits two peaks. The first peak corresponds to the resonant or natural frequency of the reactor, and is related to the heat transfer and thermal feedback of the reactor. The second peak is only observed at higher powers, which corresponds to the circulation of DNPs in the primary loop. The peak frequency is at approximately 0.23 rad/s, corresponding to the loop time of the reactor. The gain is larger at lower reactor powers, indicating reduced stability.

Fig. 9Full-screen View

Power-to-flowrate frequency responses of the MSRE

In Fig. 10, the power-to-core void-fraction frequency responses with the ^235U fuel are plotted at two different powers. The disturbance is initiated at the pump bowl by changing the entrained void fraction. The results show that the reactor is relatively insensitive to small disturbances in the circulating void fraction at 8 MW. Both lines are nearly identical at frequencies higher than 0.1 rad/s, corresponding to the timescale of the void-feedback effect. The frequency response at lower frequencies is also related to xenon removal and xenon poisoning in the reactor. This effect is comparable to that of the delayed neutron fraction when the reactor is powered. The reason that such a large reactivity effect is not reflected in the observed frequency response is the difference in the characteristic times. The change in xenon poisoning occurs within hours, whereas the change in the effective delayed neutron fraction has a timescale of seconds. The slow reactivity change associated with the circulating void fraction may be used for the shim control of MSRs.

Fig. 10Full-screen View

Power-to-core void-fraction frequency response of the MSRE

Plant Response During Unique Initiating Events

In this subsection, plant responses during two unique initiating events in MSRs are investigated. The first is a blockage in the off-gas system. When the off-gas system is blocked, xenon cannot be removed from the system and accumulates in the reactor. This results in a slow reduction in the reactivity. The second event is the loss of the circulating void fraction owing to a change in the condition of the pump bowl. During this event, the reactivity of the reactor first increases because of the removal of the core-void fraction. However, because the xenon removal is hindered by the removal of the void fraction, the reactivity decreases in the long term. The simulation of plant responses in these two unique scenarios was made possible by the xenon and void-transport capabilities of the coupled models.

Figure 11 shows the normalized power, core temperature, and xenon-poisoning levels following a blockage in the off-gas line at different powers. The blockage in the off-gas line prevents the removal of xenon from the pump bowl. The reactor power and core temperature slowly decrease as the xenon poisoning level increases after the initiating event. The reactor power is more stable when the reactor operates at a higher power, although the corresponding increases in xenon poisoning are larger. The operating temperature at 1 MW is slightly increased to separate the temperature lines. The temperature variation is more significant at 8 MW, compensating for the higher xenon-poisoning level. The temperature of the fuel increases as the fuel travels through the reactor, whereas the temperature of graphite is highest at the third node owing to the power-density profile. The large temperature variation at higher powers suggests that active control is required during this type of event to maintain a sufficient margin over the solidification temperature. However, limited intervention is required when the reactor is operating at a lower power.

Fig. 11Full-screen View

Plant response of the MSRE following a blockage in the off-gas line. In the upper figure, the dash-dot lines correspond to xenon poisoning, and the solid lines correspond to reactor power. In the lower figure, the solid lines correspond to temperatures of the fuel nodes, and the dashed lines correspond to temperatures of the graphite nodes

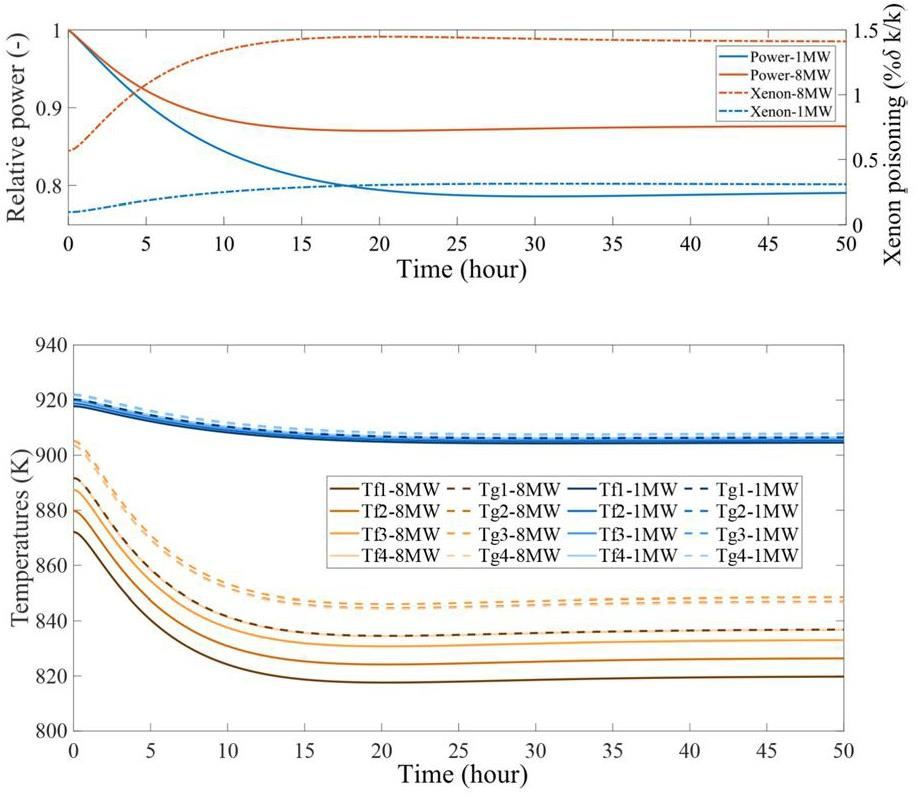
Figure 12 and Fig. 13 show the plant response following the loss of the circulating bubbles in the pump bowl. The responses during the first hour are presented in Fig. 12. The core void-fraction lines are almost identical during this event. The reactor power increases as the core void fraction decreases. The increase in reactivity due to the loss of the core void fraction is countered by the increase in the core temperature. At a higher reactor power, this thermal feedback occurs faster, and the resulting power peak is significantly lower. The xenon-poisoning level only slightly increases in the first hour and does not contribute significantly to the plant response.

Fig. 12Full-screen View

Plant response of the MSRE following the loss of circulating bubbles at the pump bowl in the first hour. In the upper figure, the dash-dot lines correspond to xenon poisoning, the solid lines correspond to reactor power, and the dashed lines correspond to the core void fraction. In the lower figure, the solid lines correspond to temperatures of the fuel nodes, and the dashed lines correspond to temperatures of the graphite nodes

Fig. 13Full-screen View

Plant response of the MSRE following the loss of circulating bubbles at the pump bowl from 1 h to 50 h. In the upper figure, the dash-dot lines correspond to xenon poisoning, the solid lines correspond to reactor power, and the dashed lines correspond to the core void fraction. In the lower figure, the solid lines correspond to temperatures of the fuel nodes, and the dashed lines correspond to temperatures of the graphite nodes

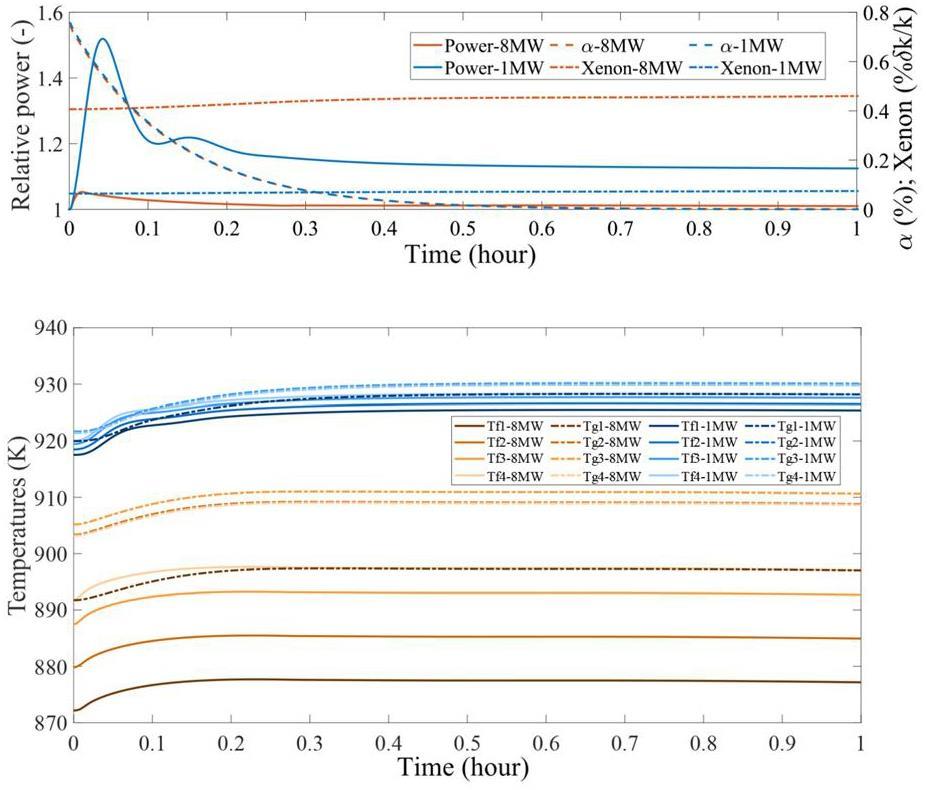
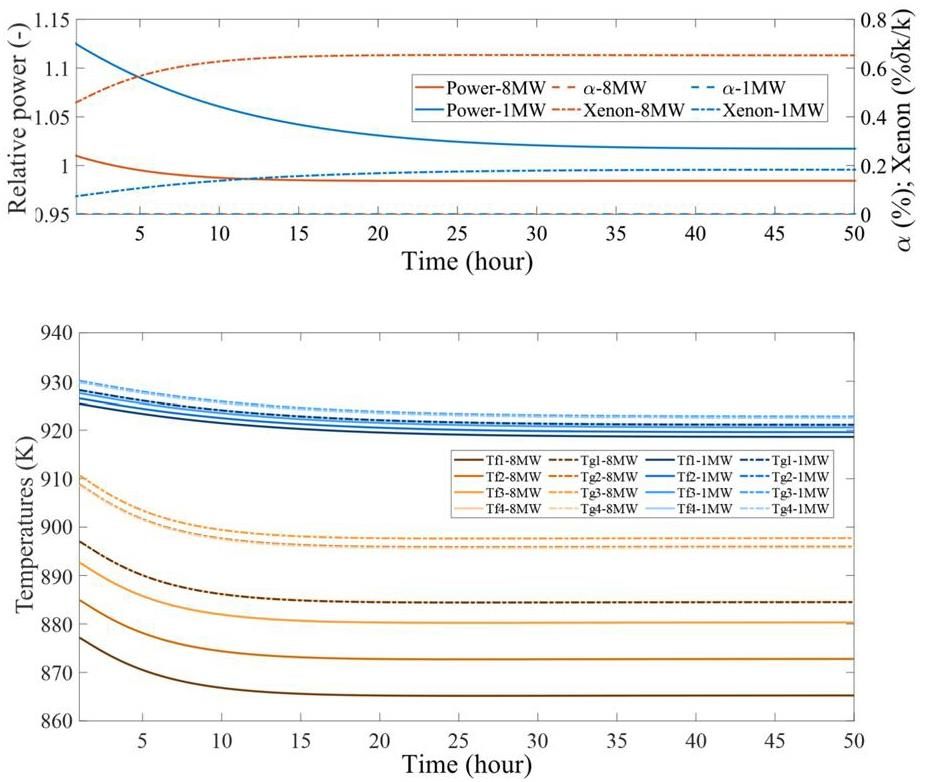
Figure 13 shows the plant response in the first 50 hours after the loss of the circulating void. The plant response during this period is solely controlled by the increase in xenon inventories owing to the absence of circulating bubbles. The plant reaches a steady-state within approximately 30 h. For the reactor at 8 MW, the final reactor power is slightly lower than that before the event, whereas the opposite is observed for the reactor at 1 MW. Notably, the loss of circulating bubbles does not lead to a complete loss of xenon removal because the spray in the pump bowl is still in operation.

Frequency-Response Sensitivity Study

In this subsection, a sensitivity study of various parameters of the power-to-reactivity frequency response is presented. Most of the frequency responses included in this subsection are obtained in a different manner from those in the other parts of the study. Instead of using sinusoidal reactivity signals with different frequencies in multiple simulations, a single band-limited white-noise signal is applied. The frequency response is obtained by dividing the cross-spectral power density by the spectral power density. This approach is analogous to the experimental method adopted in the dynamics-testing experiments during the MSRE [33].

The validity of the numerical method adopted in this study is illustrated in Fig. 14. In Fig. 14a, the frequency response obtained using the sinusoidal signals is compared with that obtained using the band-limited white-noise signal. The results obtained from both methods are identical at high frequencies. However, at lower frequencies, fluctuations are observed in the responses obtained using white noise. This fluctuation is due to insufficient sampling at lower frequencies. Fig. 14b illustrates the effect of the sample time ³. The fluctuating behavior is dampened when the sample time is reduced. Although they are not under the same conditions, the white noise shown in Fig. 14(a) is four times longer than that in Fig. 14b. Moreover, the extended sampling time significantly dampens the fluctuation at lower frequencies. In Fig. 14c, the effects of DNP nodes are presented. In terms of the frequency responses, no difference is observed between the uses of 20 and 10 nodes for out-of-core DNP transport.

Fig. 14Full-screen View

Effect of sample time and DNP nodes on simulated frequency responses. (a) Signal type; (b) Sample time; (c) DNP node

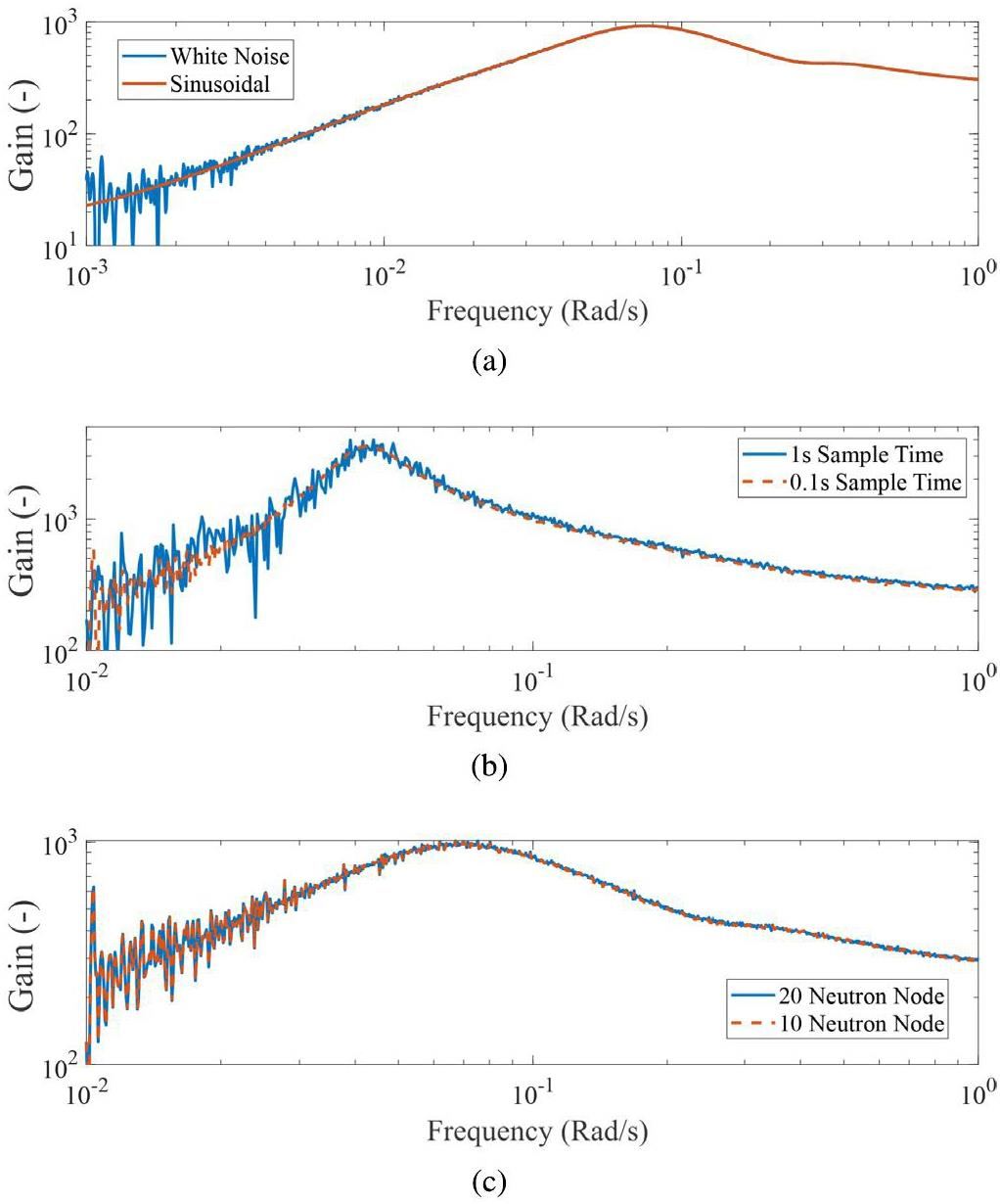
Figure 15 presents the effect of decay heat generation on the frequency response. In both the cases, the total reactor power is maintained at 8 MW. The decay heat model shifts the resonant peak slightly to a lower frequency while increasing the power-to-reactivity gain overall.

Fig. 15Full-screen View

Effect of decay heat generation on the power-to-reactivity frequency response at 8 MW

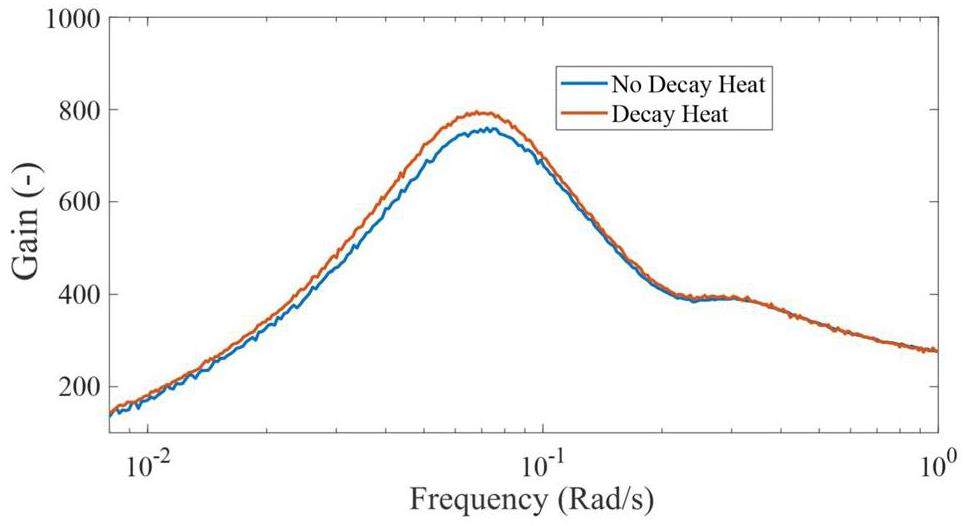
The effect of heat capacity on the frequency response is shown in Fig. 16. As shown in Fig. 16a and b, the heat capacities of the fuel salt and graphite significantly influence the frequency response of the reactor. Because most of the thermal power is deposited in the fuel salt, its heat capacity has a significant impact on the characteristic time of the thermal-feedback effect. A higher fuel–salt heat capacity shifts the resonance peak to the left and increases its magnitude. However, although a higher graphite heat capacity shifts the resonance peak to lower frequencies, it does not significantly change the height of the resonance peak. A relatively small effect on the coolant capacity is observed, as shown in Fig. 16c. The increase in the coolant heat capacity reduces the peak height and shifts the peak to higher frequencies. The change in the coolant heat capacity increases the overall heat capacity of the reactor, which tends to reinforce the oscillation. However, it improves the heat transfer at the heat exchanger and radiator, which should help suppress oscillations.

Fig. 16Full-screen View

Sensitivity study of different heat capacities on the simulated frequency response. (a) Fuel-salt capacity; (b) Coolant-salt capacity; (c) Graphite capacity

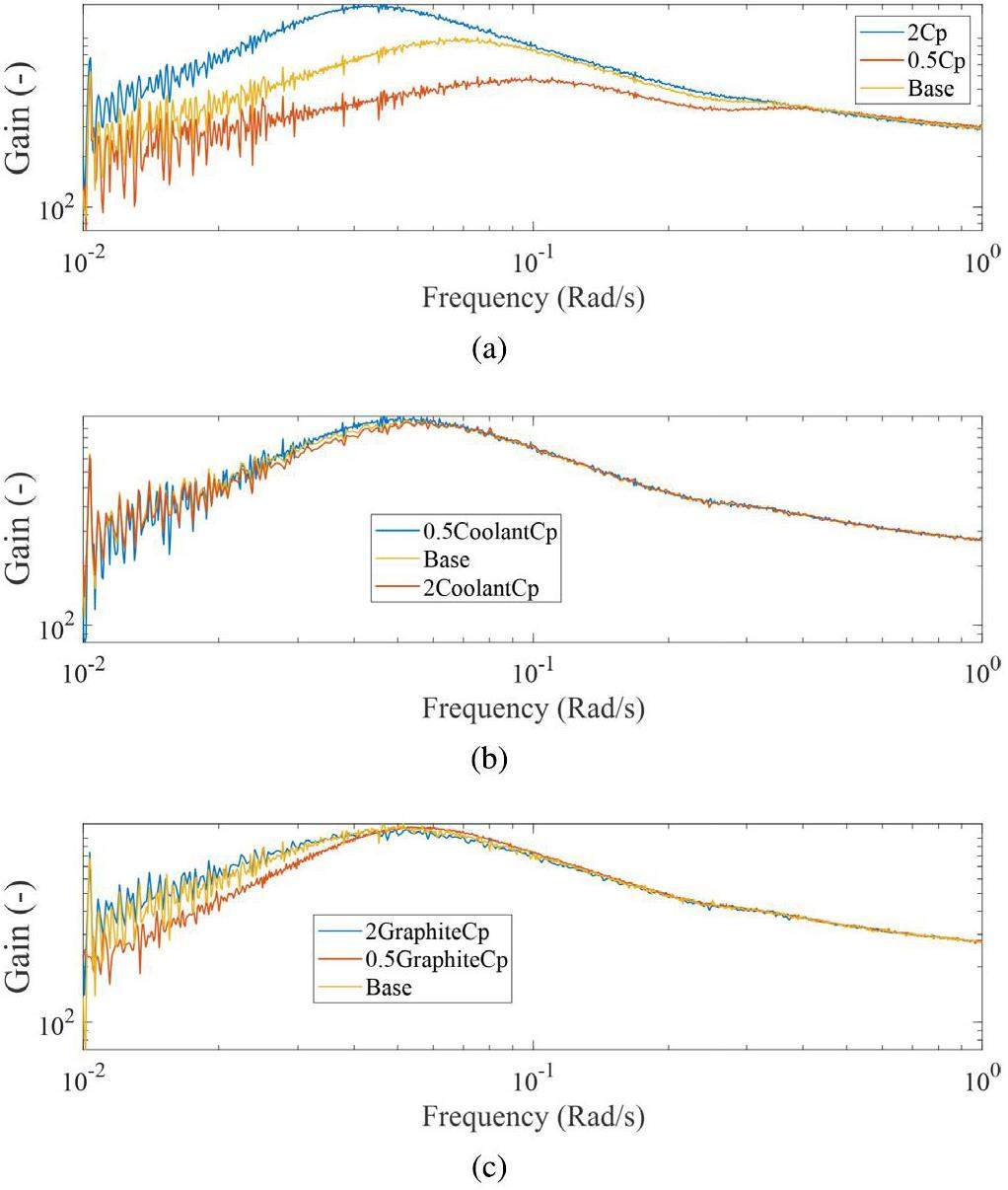
The effects of different heat-transfer coefficients are shown in Fig. 17. Figure 17a and b show that the salt–graphite and radiator heat-transfer coefficients have negligible effects on the frequency response. The temperature difference between the graphite and fuel salt is small, and only a limited fraction of the thermal power is deposited in the graphite. Moreover, heat transfer between the fuel and graphite involves heat conduction, and the convective heat-transfer coefficient is not the controlling parameter. Similarly, the heat transfer in the MSRE radiator is controlled by the flowrates, temperatures, and heat capacities of the coolant and airflow, whereas the heat-transfer coefficient is not a controlling parameter. However, in the study of the PHX, the overall heat-transfer coefficient varies. The improvement in heat transfer at the PHX dampens the resonance peak, as anticipated.

Fig. 17Full-screen View

Effect of different heat-transfer coefficients on the simulated frequency response. (a) Salt-graphite convection; (b) Radiator-air convection; (c) PHX overall

Figure 18 shows the effects of flowrates and fuel volume. A reduced fuel-salt flowrate leads to a reduction in the frequency response. The dominant effect of the reduced fuel flowrate is an increase in the effective delayed-neutron fraction, which helps to slow down the transient response of the reactor, corresponding to an overall dampening in the higher-frequency region, as shown in Fig. 18a. From Fig. 18b, the coolant flowrate has a limited effect on the plant responses in the considered range, suggesting that the heat transfer in the secondary loop primarily depends on the air flow at the radiator. In Fig. 18c, the effect of fuel volume in the reactor core is inspected. This is of practical importance because different values of core-fuel volume have been reported in MSRE documents. Their results indicate that a higher core-fuel volume leads to a lower resonance peak. Two competing mechanisms are at work. An increase in the core-fuel volume leads to a higher effective delayed-neutron fraction owing to a longer core residence time, which helps stabilize the reactor. However, the total fuel heat capacity increases, which tends to enhance the oscillation behavior.

Fig. 18Full-screen View

Effect of selected plant parameters on the simulated frequency response. (a)Primary loop flowrate; (b) Coolant flowrate; (c) Core fuel volume

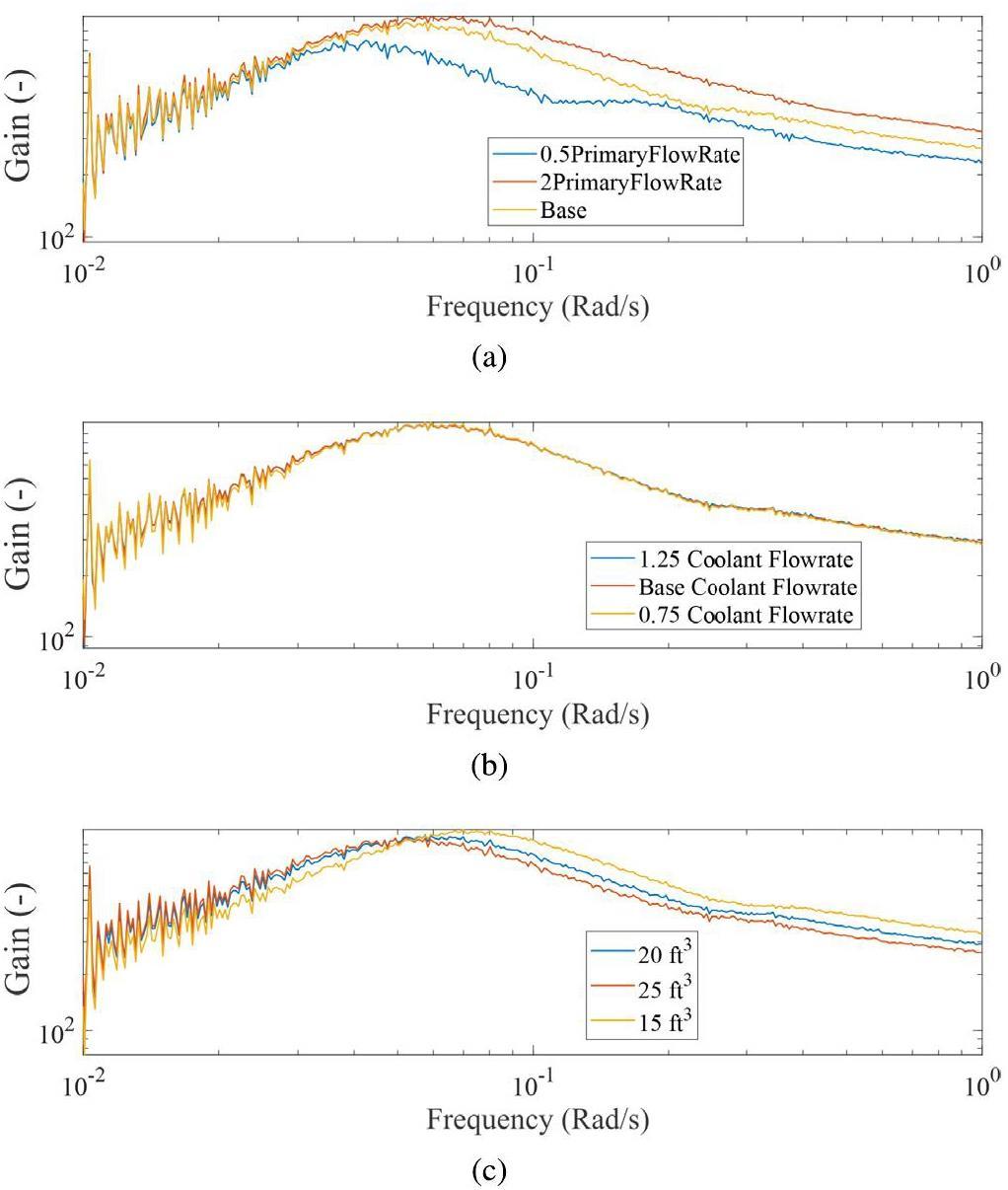
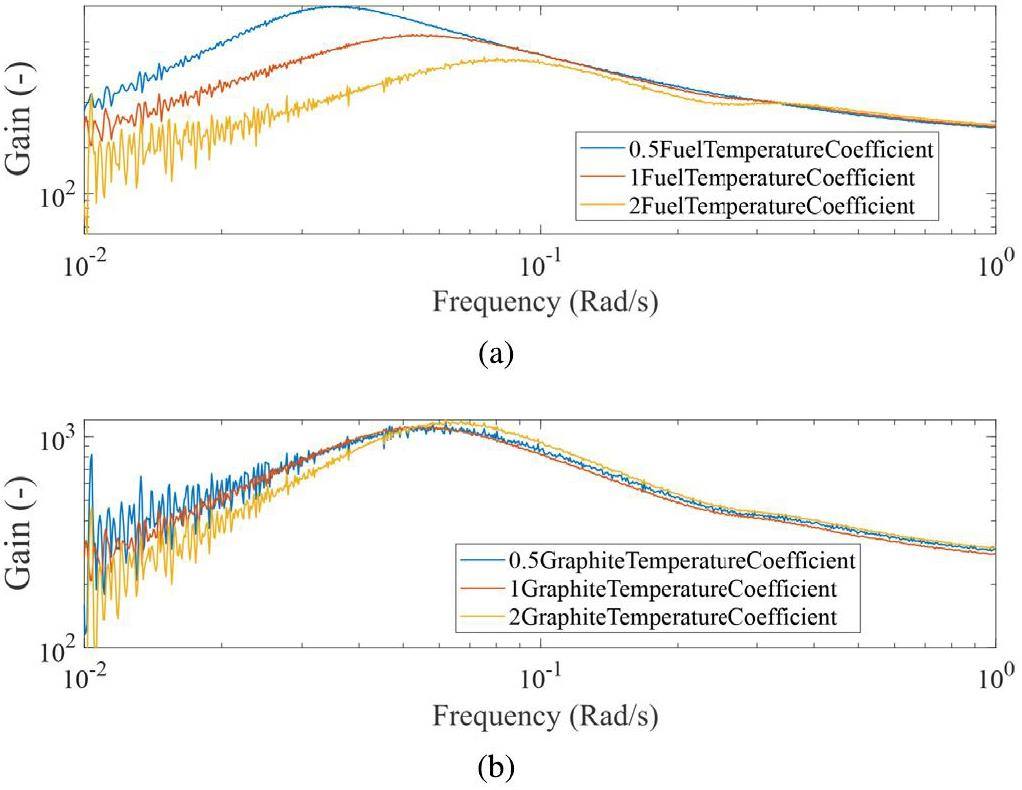
Figure 19 shows the effects of the temperature-feedback coefficients. Increases in the fuel and graphite temperature coefficients both reduce the gain at lower frequencies and shift the resonance peak to the right. The fuel temperature coefficient clearly has a stronger impact on the frequency response than the graphite temperature coefficient because of the direct deposition of fission power. Interestingly, an increase in the graphite temperature coefficient leads to a higher resonance peak, which may be related to the differences in the thermal response times of graphite and fuel salt.

Fig. 19Full-screen View

Effect of temperature-feedback coefficients on the simulated frequency response. (a) Fuel temperature; (b) Graphite temperature