Introduction

Conventional neutron sources, which include the isotope, accelerator, and reactor types, have played pivotal roles in advancing diverse scientific and technological domains such as materials science and nuclear physics [1]. Spallation neutron sources, which represent the forefront of this evolution, constitute a novel generation of high-intensity pulsed neutron sources. They have achieved neutron flux levels of approximately 10¹⁷ cm^-2s^-1 with short pulse widths. These attributes significantly enhance the precision of time-of-flight (TOF) measurements, which are a cornerstone of nuclear reactor design and nuclear astrophysics [2-5].

Despite these advancements, replicating high-neutron-flux conditions, which are crucial for understanding r-process nucleosynthesis [6], remains a formidable challenge. In the cosmic formation of heavy elements, neutron star mergers are the primary site of this process [7], whereas the contribution from supernovae explosions is still under debate [8]. These astrophysical events require specific conditions, including an intensive neutron flux ranging from 10²² to 10²⁸ cm^-2s^-1, a range that remains elusive in laboratory settings. This gap not only hinders our comprehensive understanding of these astrophysical phenomena but also limits advancements in related fields, such as nuclear physics and astrophysics. Therefore, the development of new methodologies capable of achieving these extreme conditions in a controlled environment is crucial.

The recent development of laser-driven high-intensity neutron sources has shown the potential to fill this gap owing to their exceptional temporal resolution and ability to achieve highly localized neutron beams (spatial resolution) [9, 10]. These sources employ various methodologies, including photoneutron production [11, 12] (10²¹ cm^-2s^-1), target normal sheath acceleration (TNSA) [13, 14] (10²⁴ cm^-2s^-1), and target compression via spherical shells (NIF) [15] (10³⁰ cm^-2s^-1). Although these methods offer advancements, the neutron flux from the laser-driven Z-pinch has the potential to surpass the current capabilities.

Z-pinch is a phenomenon in which an axial current flowing through a plasma generates a magnetic field. The interaction between this magnetic field and the current creates a radial Lorentz force, which radially compresses the plasma to a small volume [16]. Fusion and X-ray studies have also explored the potential of Z-pinch devices [17-20]. Recent studies have focused on augmenting laser-driven Z-pinch mechanics using nanowire arrays [21-23], which present notable intrigues. Nanowire arrays efficiently absorb the energy from a femtosecond petawatt laser, resulting in a high degree of ionization and intense X-ray generation [24, 25]. In addition, ions in the array are accelerated, triggering microscale fusion reactions [26].

Therefore, we performed a particle-in-cell (PIC) simulation and found that a femtosecond petawatt laser can pinch a single nanowire to more than 120 times its original density. It is referred to as a micropinch, owing to its small spatial scale and short duration. Simulations suggest that these micropinches can facilitate nuclear fusion reactions, leading to an intense, short-lived neutron pulse with an unprecedented flux of 10²⁷ cm^-2s^-1.

Simulation Setting

To investigate the neutron generation process in a Z-pinch setup, we employed full-dimensional kinetic simulations to reveal the ultrashort pinch process and the generation of neutrons using the PIC code Smilei [27]. The original nuclear reaction scheme [28, 29] was introduced in Smilei. Specifically, the cross-section for the reaction D + D→ n + ³He was integrated into the debugging version of Smilei. We improved the debugging version and corrected and checked the nuclear reaction cross-sections using a period boundary condition in a box [30]. In addition, we added the nuclear reaction D + T → n + ⁴He (data from [31]) to determine the potential for a higher-intensity neutron source.

In our simulation, the nanowire where Z-pinch was triggered was composed of deuterated polyethylene (CD₂). The particle number density of deuterium was set as $\rho =7.8\times {10}^{22}{\text{cm}}^{-3}$. Diameters of 300 and 500 nm were considered for varying wire lengths. The initial temperature of the particles was 300 Kelvin. The nanowire target was irradiated by 400 nm wavelength circularly polarized (CP) laser pulses of 30 or 60 fs full width at half maximum (FWHM) duration. The dimensionless amplitude of the laser field was a₀ = 10-40 ($a_0=eE/m_{\text{e}}c\omega$), where e and m_e are the electron charge and mass, E is the laser electric field, ω is the laser frequency, and c is the speed of light in vacuum. The focal spot size of the laser should be sufficiently large to cover an entire single nanowire. The typical focal-spot size was approximately 5 μm, reaching a peak intensity of ~5 × 10²¹ W/cm²(a₀ = 17). To avoid numerical heating, the size and number of cells were dynamically adjusted according to the volume of the nanowires. A typical cell size was set to 7.5 nm × 5 nm × 5 nm, with 27 macroparticles per cell. A small nanowire had 640 × 192 × 192 cells, corresponding to a cube of 4.8 μm × 0.96 μm × 0.96 μm, which was sufficiently large to hold the entire nanowire. The simulation boundaries were set to open conditions for both the fields and particles. Because field ionization is the dominant ionization process compared with that from Coulomb collisions between particles, collisional ionization was switched off to save simulation time. The binary collision between deuterium (tritium) was set, as nuclear reactions might occur.

Simulation Result

When irradiated with ultrashort high-intensity laser pulses, the atoms inside the wire undergo field ionization. The ionization process leads to a considerable potential difference on the surface of the nanowire. This potential disparity is balanced by the significant return current flowing across the nanowire's surface, maintaining quasi-neutrality. For an approximate estimation, we assumed that the electrons ionized from atoms within the nanowire were mostly distracted by the laser, corresponding to a total charge of $Q=1.3\times {10}^{-8}\text{C}$. The current can be calculated as $I=Q/t$, where t represents the FWHM duration of the laser, which is set to 60 fs. This estimated current of $2.2\times {10}^5\text{A}$ provides a starting point for further analysis of the Z-pinch dynamics.

We performed three-dimensional (3D) simulations to illustrate the laser-induced Z-pinch process. Figure 1 shows that the electrons are pulled out by the CP laser in the void (negative current represented in blue), whereas the positive current density is the return current of the electrons flowing in the opposite direction (positive current represented in red). The return current density reached $J{=10}^{15}-{10}^{16}{\text{A/cm}}^2$ (a cross section of 30 nm × 30 nm, $I_{\text{max}}\sim 1.4\times {10}^5\text{A}$), which is consistent with the estimation. Because of the extremely high current density, the induced magnetic field around the nanowire was also significant. The 2D image in Fig. 1 illustrates the transverse magnetic-field distribution in the simulation. The maximum field reached $B_y=1.0\times {10}^6\text{T}$, which exceeded the incident laser field (a₀ = 17, $B_y=4.6\times {10}^5\text{T}$). This quasi-static magnetic field exerted a $J\times B$ force on both the inner and outer currents (electrons) of the nanowire. The current on the inner surface of the nanowire was subjected to a force radially inward owing to the generated magnetic field, whereas the forces on the outer electrons of the nanowire were in opposite directions. Hence, the nanowire was compressed inward, whereas the electrons extracted from the nanowire were pushed outward.

Fig. 1Full-screen View

(Color online) 3D current density and 2D magnetic fields during the pinch simulation. In the 3D image, the red color represents positive current (max $J_x=1.4\times {10}^{16}{\text{A/cm}}^2$), whereas the blue color represents negative current. The 2D image illustrates the magnetic field (max $B_y=1.0\times {10}^6\text{T}$). The x-positive direction aligns with the laser propagation and the axial direction of the nanowire, whereas the y and z directions correspond to the radial directions of the nanowire

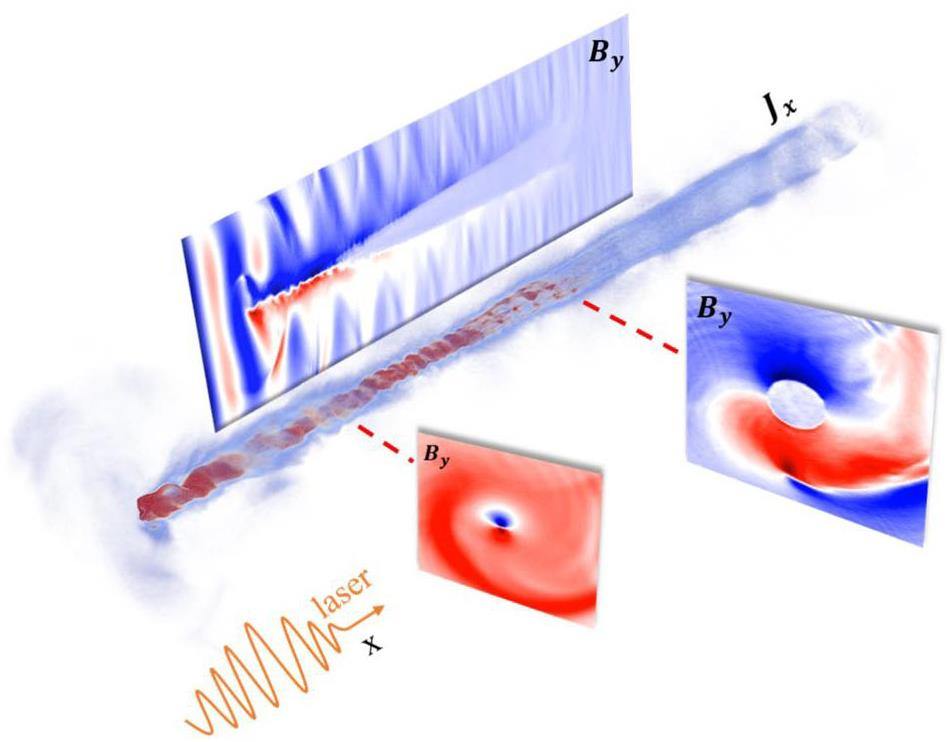
When the return electrons are pinched radially inward by the Lorentz force, they induce an electric field owing to charge separation. Deuterium ions are then drawn and pinched symmetrically inward from the surface by this electric field, resulting in a strong radial symmetry for the kinetic energy distribution of deuterium particles within the nanowire. In the following discussion, we estimated that the temperature of deuterium in the Z-pinch was 190 keV by comparing the ratios of the nuclear reaction rates. The electrons extracted from the nanowire (which were being pushed outward) also induced an electric field, drawing the surface deuterium outward and accelerating them. If the target is an array, the collisions between them are also significant for nuclear reactions because of their higher energies. Eventually, the pinched-inward ions are compressed near the center, creating a high-density zone (Fig. 2. The corresponding maximum energy density can reach an order of 1×10²⁴ MeV/cm³ (1×10¹² J/cm³) at approximately 54 fs, which is two orders of magnitude higher than that reported in our previous work [32].

Fig. 2Full-screen View

(Color online) Spatial and temporal profile of plasma density and energy density. The profile at 1.2 μm is shown from the top of the nanowire. The time-dependent variation of deuterium is depicted along the curve graph, specifically at the section indicated in blue, and red denotes electrons. The dotted lines denote the time-dependent variation of energy density. Sub-fig(2) demonstrates the deuterium number density after compression, which reaches a value of approximately 8×10²⁴ cm^-3

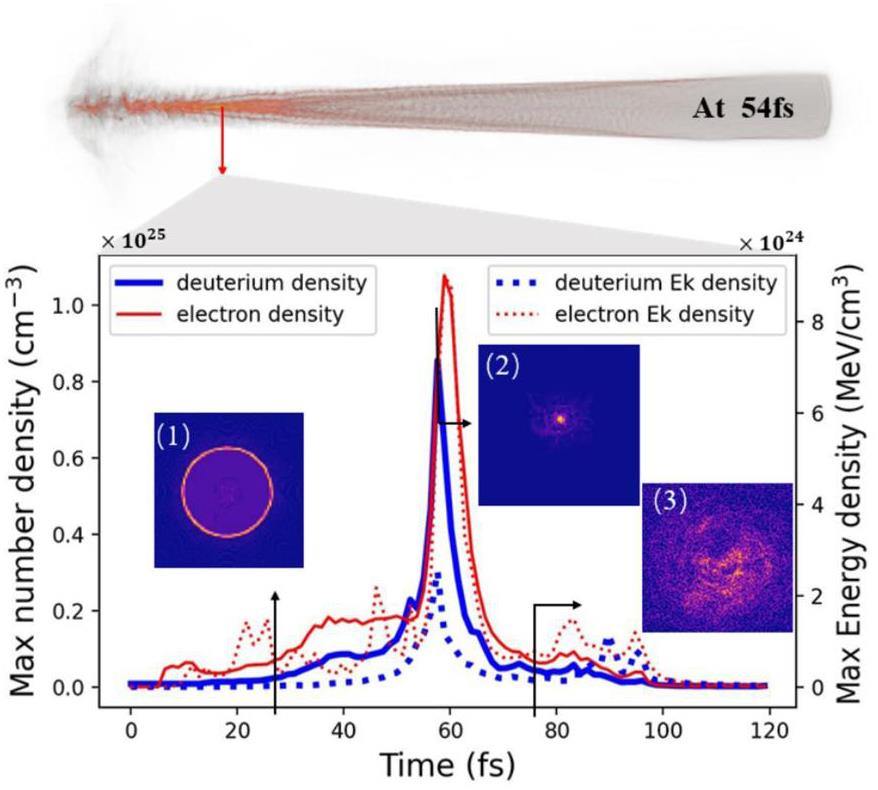
As shown in Fig. 2, compression occurred within approximately t_c=10 fs, and the maximum compression diameter was approximately D=30 nm. The maximum deuterium density exceeded ${\rho }_{\text{m}}=1\times {10}^{25}{\text{cm}}^{-3}$, that is, 120 times the initial ion density. The ion (proton or deuterium) radial flux reached approximately $1.0\times {10}^{34}{\text{cm}}^{-2}{\text{s}}^{-1}$ (${\rho }_{\text{m}}\pi D/t_{\text{c}}$), which is also of intense interest in laboratory nuclear astrophysics research [33-35]. Hence, nanowires can also serve as sources of other nuclear reactions, such as p + ¹¹B → 3α. These ions are concentrated within an extremely small volume of approximately 30 nm × 30 nm and cause intense nuclear reactions, including neutron production. For lasers with a₀ > 40, the maximum density of the nanowires increases slightly. For example, with a₀ = 150, a maximum density of $1.8\times {10}^{25}{\text{cm}}^{-3}$ is reached on the front of the wire, owing to an intense axial particle acceleration and the combined effect of the nanowire micro-pinch, which is long before the peak of the laser pulse. When the laser intensity increases, both the magnitude of the return current density and maximum ion density increase, but not indefinitely in our simulation. This would limit the number of nuclear reactions during the Z-pinch (Fig. 4(a)). This may be caused by instabilities [36], such as sausage or kink instabilities in the Z-pinch effect.

Figure 3 shows the number and density of nuclear reactions (D + D → n + ³He) generated by the Z-pinch. The propagation of the produced neutrons was not considered. At this point, the energetic ions collide in the densest vicinity. Because of the extremely high particle number density, the nuclear reactions primarily occur around the axis of the nanowire, as shown in Fig. 3(a). The neutron density resulting from D-D nuclear reactions is approximately of the order of 10¹⁸ cm^-3. This extremely short compression leads to a burst of reactions within femtoseconds, where the reaction rate is over 100/fs on such a small timescale, as shown in Fig. 3(b). If suitable nuclear reactions are available, the induced reaction exhibits ultrahigh peak flux and ultrashort pulse duration. From the simulations, we obtained neutrons with a narrow pulse width (30 fs) and small source surface area ($\pi 30\text{nm}\times 3000\text{nm}=2.8\times {10}^5{\text{nm}}^2$). The corresponding neutron (particle) flux reached 10²⁶ cm^-2s^-1.

Fig. 3Full-screen View

(Color online) (a) Longitudinal cross section of the accumulated neutron number density, where the blue curve is the distribution of neutrons along the Z-axis, which shows the spatial distribution where D-D nuclear reactions occur. The blue curve in (b) represents the number of nuclear reactions produced per femtosecond, whereas the red curve depicts the time evolution of the deuterium maximum density. The data in the figure have been normalized. The nanowire has a diameter of 300 nm and a length of 3.6 μm

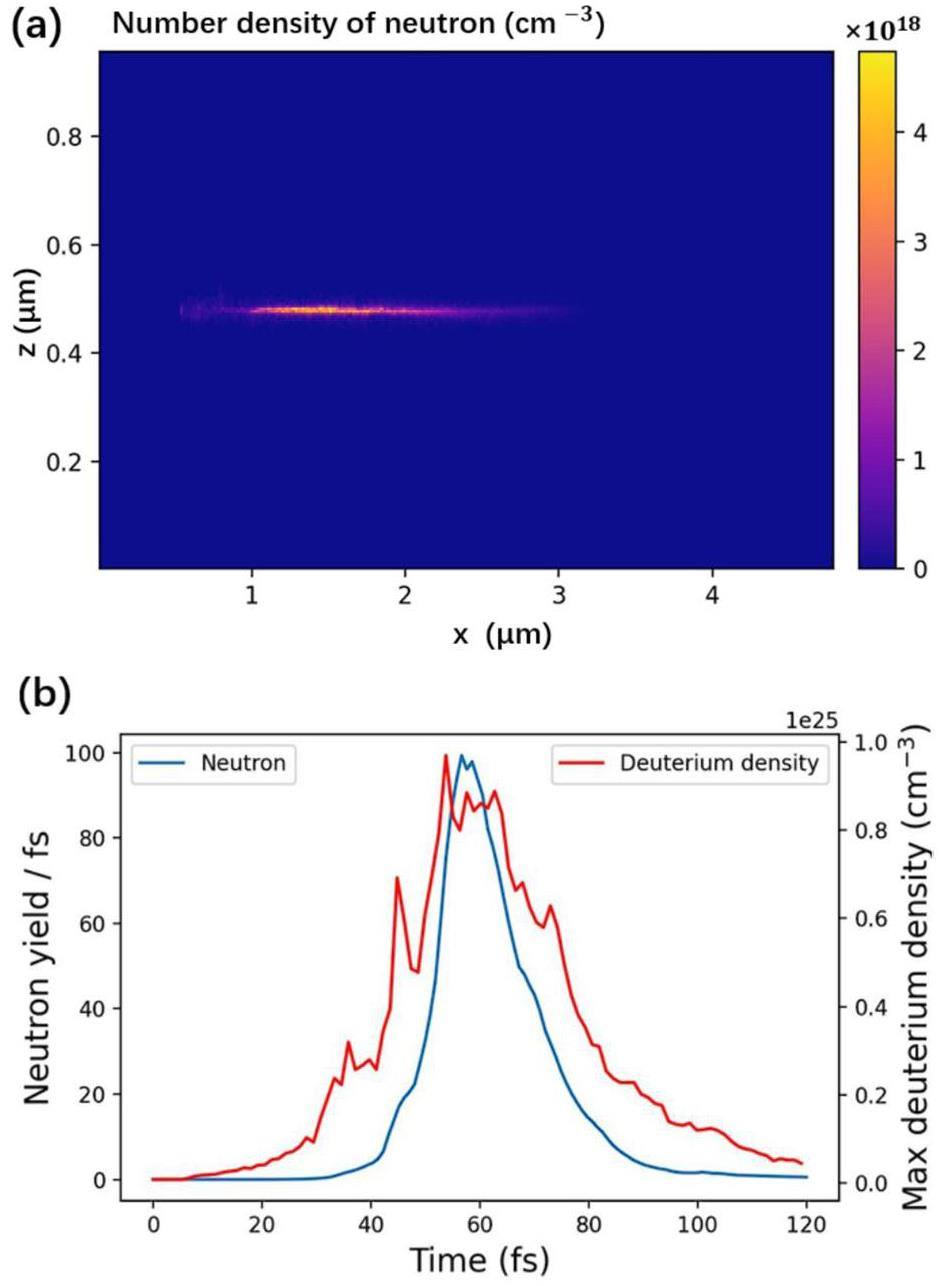
Figure 4(a) illustrates the relationship between the laser parameters (30 and 60 fs, circularly and linearly polarized, respectively) and the number of nuclear reactions generated by the Z-pinch. In addition, increasing the length efficiently enhances the number of nuclear reactions during the pinch phase. The diameter of the nanowire also affects the reaction rate. Under the same conditions, if normalized for the substance of material, the efficiency of nuclear reaction generation is the highest in the wire with a diameter of 500 nm, followed by that with a diameter of 300 nm. Both efficiencies were higher than those observed for the 200 nm and 800 nm wires.

Fig. 4Full-screen View

(Color online) (a) Relationship between the number of reactions in a nanowire with a diameter of 300 nm and a length of 3.6 μm and several laser intensities. The blue circle in the diagram represents a 60 fs pulse width circularly polarized laser, whereas the orange and green marks represent 30 fs pulse width circularly or linearly polarized lasers. The yellow range is the approximate range of nuclear reactions that we estimate can be generated by existing Z-pinch devices under the same substance of material conditions. The red star is one-tenth of the D-T reaction counts. (b) Number of fusions with various lengths. The red circle represents D-T fusion, and its yield is on the left. The blue square represents D-D fusion, and its yield is on the right

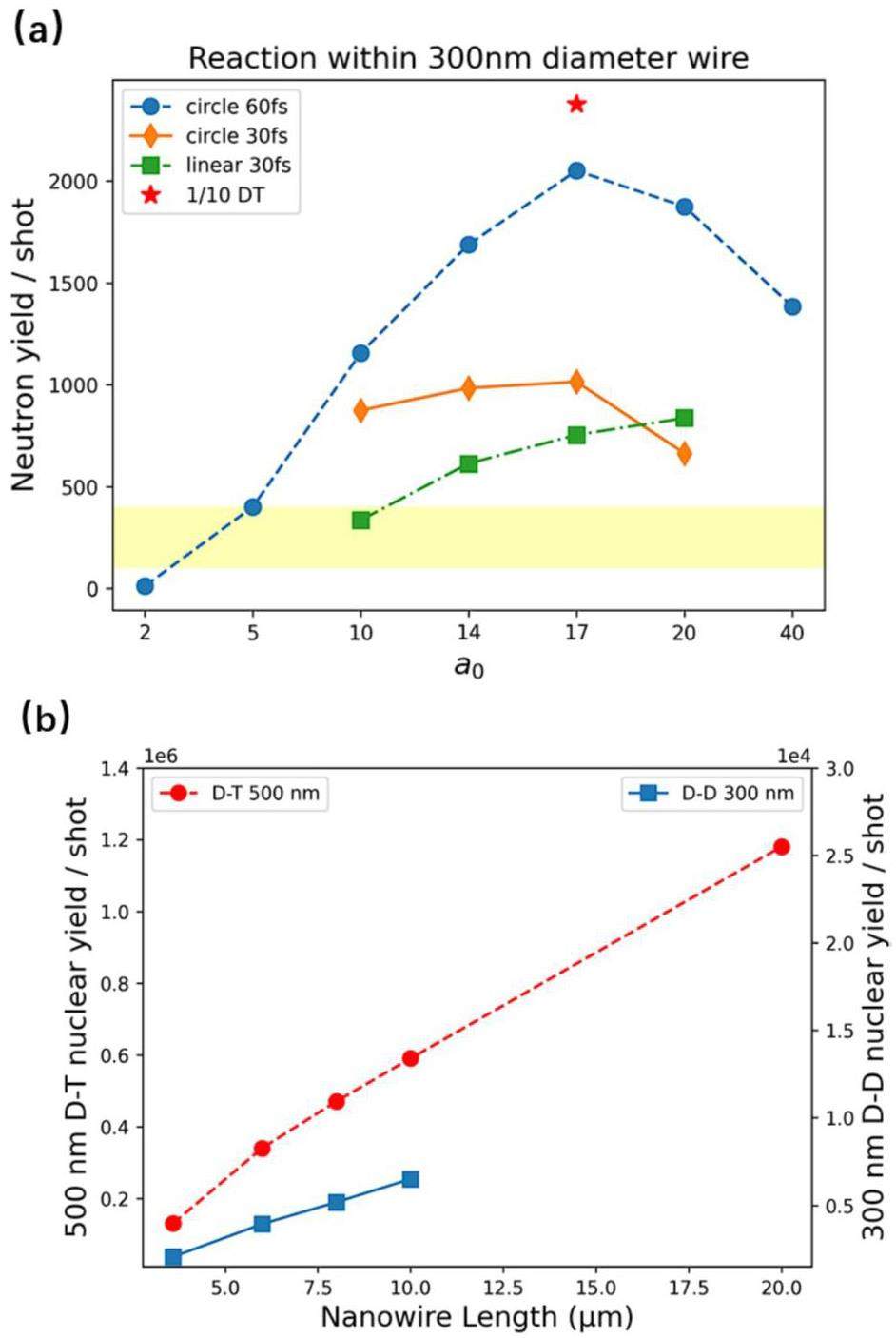
When the D-T system was considered, the fusion yield was found to be more than 10 times greater than that of the D-D system. Comparing the yields in the same system, the equivalent temperature [37] at which the nuclear reactions occurred in this nanowire was approximately 190 keV. The neutron flux could reach 10²⁷ cm^-2s^-1 in the D-T reaction system. Nanowires with a diameter of 500 nm and lengths of 6, 8, and 10 μm can generate 3.4 × 10⁵, 4.7 × 10⁵, and 5.9 × 10⁵ neutrons, respectively. Notably, this growth is almost linear with the length (because of the pulse width of the laser, it must be sufficiently long). More than 10⁶ neutrons can be generated within a single pulse if the length of the nanowire is increased to 20 μm, as shown in Fig. 4(b). Cascade reactions of D-D and D-T also occur within the system.

Conclusion

We conducted a study on the interaction between lasers and nanowires, with a particular focus on the Z-pinch effect. Notably, the deuterium density within the nanowire could exceed the initial density by more than 100 times. We analyzed the pinch density and current under different laser and nanowire parameters. The Z-pinch effect provides laser-driven nanowires with a short time scale and high spatial density environment for nuclear reactions to occur. It is thus suitable for use as a neutron source with the advantages of a small spatial scale (30 nm × 30 nm) and short pulse width (30 fs). This compression results in an extremely intense and short neutron pulse. The peak neutron flux reached 10²⁷ cm^-2s^-1. High-flux nuclear reaction (neutron) sources can be utilized for research on r processes [38]. The laser can not only pinch deuterium ions but also other particles as sources in nanowires. A typical example is a proton source. With a radial flux of approximately $1.0\times {10}^{34}{\text{cm}}^{-2}{\text{s}}^{-1}$, the proton source will provide a unique method for the two-proton capture reaction during the rp-process [39]. Future studies could utilize targets with different compositions to conduct further laboratory nuclear astrophysics research [40, 41], which could provide highly intense solutions.