Introduction
Shape coexistence in atomic nuclei has garnered significant attention in the field of nuclear physics and has become a prominent topic in contemporary research. This phenomenon refers to the presence of multiple distinct shapes within a single nucleus, where states with similar energies exhibit different deformations [1]. Understanding nuclear shapes is crucial for revealing the internal structure and properties of nuclei, providing tools for predicting and explaining nuclear behaviors, and advancing nuclear physics [2-6].
The study of nuclear shapes has a long history, with several foundational studies laying the groundwork for our current understanding. Early theoretical developments included Rainwater's 1950 paper [7], which first proposed the idea of nuclear deformation, and Bohr and Mottelson's collective model [8, 9], which provided a framework for describing rotational spectra in deformed nuclei. Arima and Horie's 1954 study [10] explored the role of configuration mixing in nuclear structure, while Nilsson's work [11] introduced a shell-model approach incorporating deformation effects. Around the same time, Morinaga's 1956 paper [12] specifically addressed the structure of 16O and explained the properties of its first excited state and ground state. He introduced the concept of multi-nucleon cross-shell excitation to describe the deformation characteristics, offering a new perspective on how nuclear shapes evolve. Further developments include Elliott's work in 1958 [13], which further developed the concept of SU(3) symmetry in nuclear deformation and highlighted the interplay between single-particle and collective motion. Over the past five decades, shape coexistence has evolved from a rare phenomenon to a common feature observed in many nuclei, highlighting its significance in nuclear structure research [14]. Recent experimental studies have revealed significant evidence of shape coexistence phenomena in neutron-deficient isotopes of lead and mercury. For instance, one study [15] specifically focuses on the 188Hg isotope, where theoretical predictions suggest the presence of shape coexistence.
These findings have led to increased theoretical investigations into nuclear shape coexistence, utilizing advanced experimental techniques such as tagging techniques at the University of Jyväskylä, Coulomb-excitation experiments at CERN, and relativistic energy-fragmentation experiments at GSI [16]. These experiments underscore the importance of understanding the mechanisms governing the evolution of nuclear shape. Building upon these experimental insights, theoretical investigations have played a pivotal role in elucidating the complexities of shape coexistence [17-19]. Previous studies have employed various theoretical frameworks, including macro-microscopic approaches and self-consistent models, to perform comprehensive calculations of nuclear ground-state masses and deformations across a wide range of nuclei [14]. Ref. [20] highlighted the presence of two distinct coexisting configurations, in platinum isotopes 176-186Pt, oblate and prolate, revealing the intricate shape evolution in this mass region. Therefore, shape coexistence in even-even 172-200Hg isotopes was comprehensively studied using the interacting boson model with configuration mixing [21]. Recently, using the Lublin-Strasbourg Drop (LSD) with Yukawa-Folded single-particle potential and the BCS pairing correction in a macro-microscopic model, Pomorski et al. provided the deformation PESs of nuclei near Z =82. Their study investigated the shape coexistence phenomenon in even-even isotopes of Pt, Hg, and Pb [22]. These studies revealed that nuclei in the vicinity of Hg exhibit a rich variety of shape coexistence phenomena, characterized by the interplay of spherical, oblate, and prolate configurations. Although significant progress has been made in understanding these features of heavier isotopes, lighter isotopes of Hg, Pt, and Pb have been relatively underexplored owing to the scarcity of experimental data [23]. To address this gap, further theoretical investigations are crucial, as they can illuminate the evolution of shape coexistence in these lighter isotopes. Such efforts would not only enhance our theoretical understanding but also provide valuable guidance for future experimental measurements, enabling better interpretation of the limited or ambiguous data that are currently available.
Despite its success, the BCS method [24], as well as the more refined Hartree-Fock-Bogolyubov (HFB) approach face limitations due to the small number of valence nucleons under the pairing correlation's influence [25-31]. These methods often fail to conserve particle numbers, leading to inaccuracies in describing higher-lying excited states [32]. Alternatives such as the shell model provide successful descriptions but are limited by the combinatorial growth of model space sizes, necessitating truncation schemes for heavy nuclei and often being constrained by computational resources [33]. Recent advancements in shell-model truncation techniques, such as the Monte Carlo shell model [34] and angular momentum-projected number-conserved BCS approach [35], have made significant progress in describing deformed nuclei in heavy mass regions, offering improved computational feasibility while maintaining accuracy.
The Exact solution to the standard pairing problem, first obtained by Richardson and now referred to as the Richardson-Gaudin method, offers a promising approach for the microscopic treatment of clustering in heavy nuclei [36-43]. This method is particularly suitable for handling the large model spaces and the pairing and shell effects necessary for accurately describing heavy nuclei [44-48]. In our previous work, the deformed mean-field plus pairing model within the Richardson-Gaudin method was used to explore the quantum phase transition around neutron number
The aim of the current study is to extend this line of inquiry by presenting a systematic study of PESs for even-even Pt, Hg, and Pb isotopes near Z=82. Our investigation leverages recent advancements in shape parametrization and adopted a macro-microscopic approach, integrating the LSD model with a Yukawa-Folded single-particle potential. The analysis focuses on the impact of pairing interactions on the shape coexistence of 170Pt, 172Hg, 174Pb nuclei, as well as 170-180Pt even-even isotopes.
Theoretical framework and numerical details
Deformed mean-field plus standard pairing model
The Hamiltonian of the deformed mean-field plus standard pairing model for either the proton or the neutron sector is given by
According to the Richardson-Gaudin method [36-43], the exact k-pair eigenstates of (1) with
If the value of x approaches twice the single-particle energy of a given level δ, i.e.,
The Fourier shape parametrization
Recent studies demonstrated that the developed Fourier parametrization of deformed nuclear shapes was highly effective in capturing the essential features of nuclear shapes, particularly up to the scission configuration [54, 22]. Current research indicated that combining this innovative Fourier shape parametrization with the LSD + Yukawa-Folded macro-microscopic potential-energy framework was exceptionally efficient [52, 53, 55, 56]. This work primarily adopted the macro-microscopic framework outlined in Refs. [52, 53], where the single-particle energies
The nuclear surface is expanded in terms of a Fourier series of dimensionless coordinates as follows:
Additionally, the non-axial deformation of nuclear shapes is described as follows, assuming that the surface cross-section at a given z-coordinate is elliptical with semi-axes a(z) and b(z):
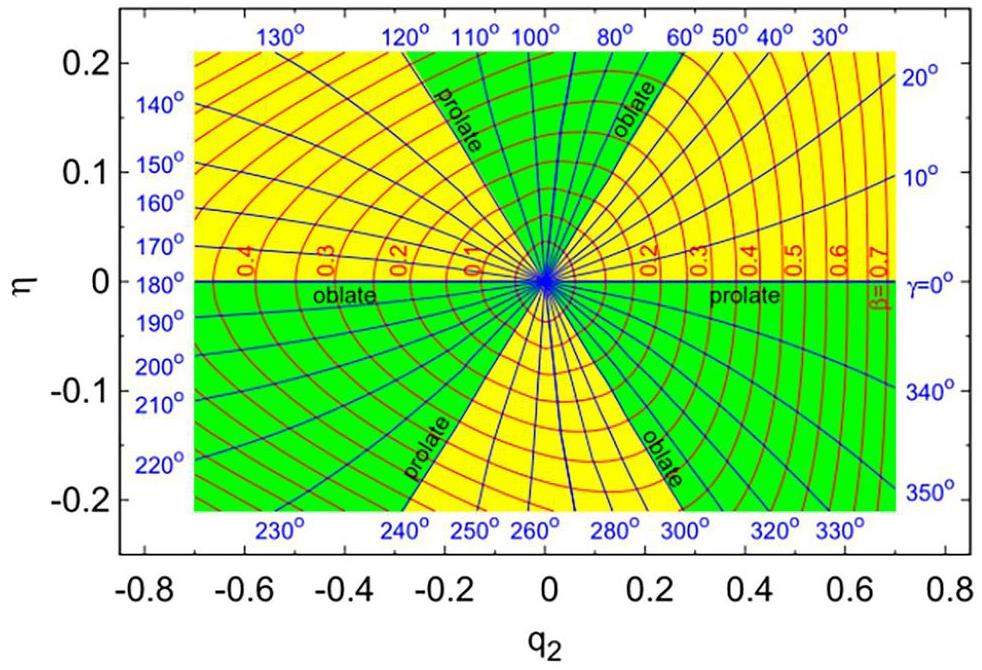
It is essential to stress that different points in the (β, γ), and (q2, η) planes can correspond to identical shapes when higher qn (n>2) degrees of freedom are neglected, differing only in the interchange of coordinate system axes. For example, the point
When analyzing potential energy landscapes that include triaxial degrees of freedom, it is crucial to avoid treating as distinct configurations points in the (q2, η) deformation plane that are merely rotational images of each other at
In this study, the dynamic process of nuclear fission will be described in the three-dimensional deformation space
The potential energy
This study calculated the PESs for the isotopes 170Pt, 172Hg, and 174Pb in a three-dimensional deformation space
To validate our results and further explored the efficacy of the exactly solvable pairing model, we also calculated the PESs for the isotopes considered under the BCS approximation. The pairing interaction was determined as the difference between the BCS energy [24] and the single-particle energy sum and the average pairing energy [64].
The average projected pairing energy, for a pairing window of width 2Ω, which is symmetric in energy with respect to the Fermi energy, is equal to
Influence of pairing interactions on the shape coexistence of 170Pt, 172Hg and 174Pb isotopes
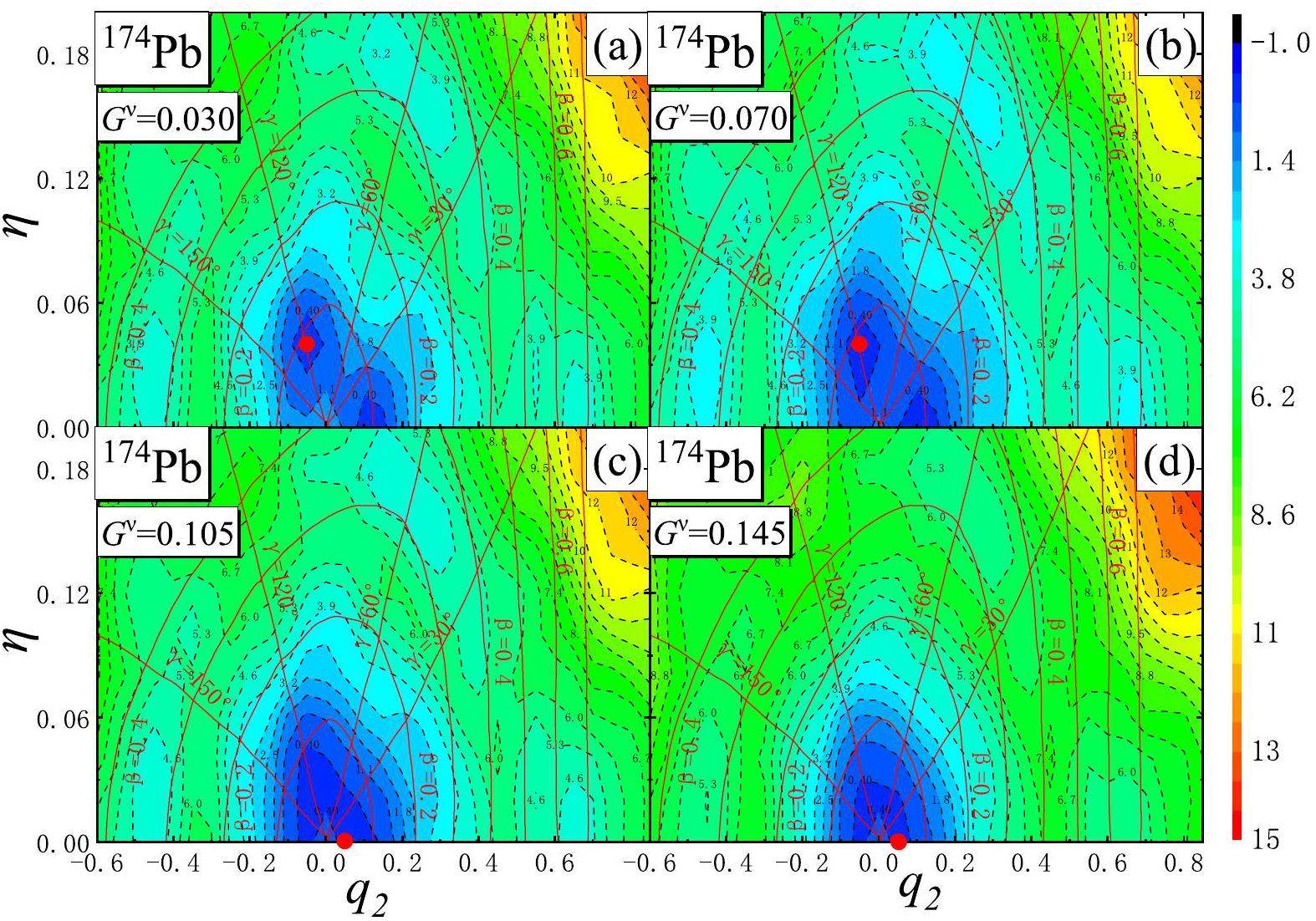
Figure 2 shows the PESs of 170Pt projected onto the (q2, η) plane for different pairing interaction strengths Gν (MeV), while the proton pairing interaction strength is fixed at Gπ = 0.100 MeV. Gν and Gπ represent the neutron and proton pairing interaction strengths (MeV), respectively. The energy is minimized in the q4 direction and q3 is set to 0 and normalized to zero energy at the ground-state value. The choice of Gν varying from 0.03 to 0.145 MeV, and Gπ = 0.100 MeV, were based on the fact that our calculations in the next section, when employing Gν = 0.145 MeV, and Gπ = 0.100 MeV, closely matched the experimental odd-even mass differences for the 171Pt to 180Pt isotopes. Therefore, this range was selected to study the effects of pairing strength variations on the shape coexistence. The red lines represent the corresponding (β,γ) coordinates, with γ coordinates distributed within 0≤γ≤180°. The β coordinate values are taken as 0.1, 0.2, 0.3 ..., etc.

In Figs. 2 (a)-(d), the PESs of 170Pt are shown for different values of the neutron pairing interaction strength Gν, while the proton pairing interaction strength is fixed at Gπ = 0.100 MeV. The values of Gν are: 0.030, 0.070, 0.105, and 0.145 MeV. It can be seen that the ground-state of the 170Pt isotope is located at (q2 ≈ 0.150,η = 0), indicating a prolate shape for different pairing strengths. The other minimum at (q2 ≈ -0.150,η = 0.04, γ=120°) illustrated in Fig. 2 is simply a reflection of the ground-state minimum.
It is noteworthy to highlight the existence of two distinct shape isomers in 170Pt with different pairing strengths. The first is an oblate shape isomer located at (q2 = -0.400, η = 0), with an energy approximately 3.900 MeV above the ground-state. The second is a triaxial shape isomer at (q2 ≈ 0.600, η ≈ 0.060 (γ ≈ 10°)), positioned around 4.0 MeV above the ground-state. These isomers represent the local minima on the potential energy surface that are separated from the ground-state by energy barriers, highlighting the complex deformation characteristics of the nucleus. With an increase in pairing strength, both shape isomers become shallower. When the pairing strength Gν reaches 0.145 MeV, the oblate isomer disappears (see Fig. 2(d)).
As shown in Figs. 3(a)-(d), the PESs for different pairing interaction strengths demonstrates the evolution of the triaxial minimum at (q2 = 0.150, η = 0.020) to the oblate minimum at (q2 = 0.100, η = 0.040) as the pairing interaction strength increases. The nucleus of 172Hg is nearly γ-unstable, with the energy difference between different points in the ground-state valley not exceeding approximately 0.4 MeV. Additionally, three shape isomers are visible in the (a)-(d) maps: a prolate isomer at (q2 ≈ 0.600, η = 0), E ≈ 5.0 MeV; a triaxial isomer at (q2 ≈ 0.400, η = 0.100), E ≈ 4.0 MeV, and oblate one at (q2 ≈ -0.45, η = 0), E ≈ 4.0 MeV. These local minima are separated by energy barriers of approximately 1 MeV in height. As the pairing strength increases, all shape isomers gradually become shallower. By Gν = 0.145 MeV and Gπ = 0.100 MeV (Fig. 3(d)), the triaxial isomer at (q2 ≈ 0.400, η = 0.100) disappeared.

The PESs of 174Pb, as presented in Figs. 4(a)-(d), reveal that a prolate ground-state (q2 ≈ 0.150, η = 0) (in Fig. 4(a)) tend to become spherical (in Fig. 4(d)) as the pairing interaction strength increases. The shape isomers observed here are particularly interesting: a prolate shape at (q2 = 0.600, η = 0, E ≈ 5.0 MeV and a slightly triaxial oblate shape at (q2 = 0.450, η = 0.020, E ≈ 3.9 MeV in Fig. 4(a), and (b), respectively. As the pairing strength increased, both shape isomers gradually became shallower. When Gν = 0.145, MeV, and Gπ = 0.100 MeV (Fig. 4(d)), they almost disappeard. Overall, regardless of pairing strength, there was no indication of robust shape coexistence in this nucleus.
Figures 5 illustrate the PESs projections of 170Pt, 172Hg, and 174Pb under realistic pairing interaction strengths, with Gν = 0.145 MeV, and Gπ = 0.100 MeV under both Exact and BCS pairing schemes.
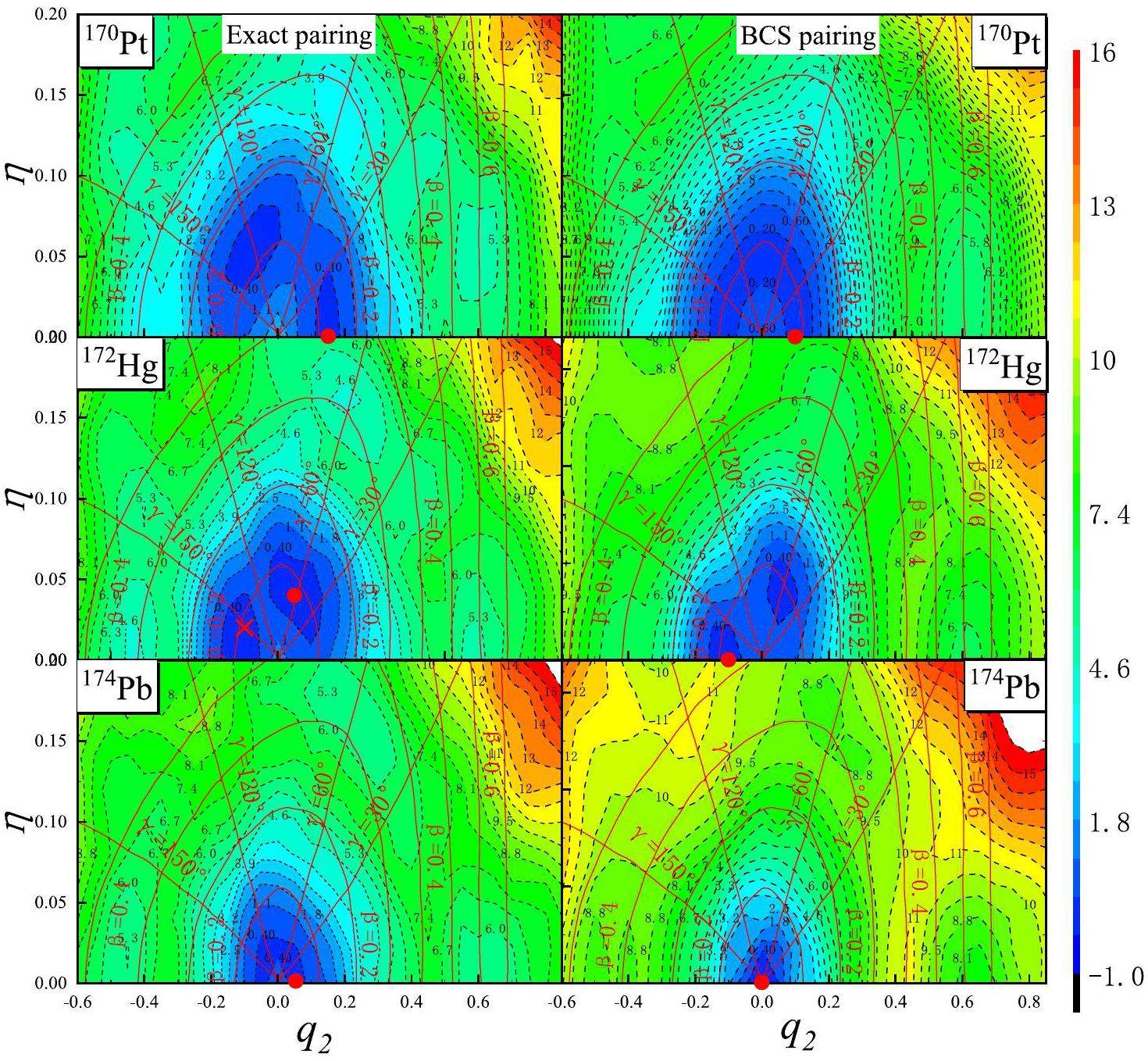
As shown in Fig. 5, the ground-state of 170Pt is prolate, located at (q2 = 0.15, η = 0) under both the Exact and BCS pairing schemes. However, BCS pairing exhibited a shallower depth for the prolate minimum compared with Exact pairing, indicating a less pronounced prolate ground-state. Furthermore, a triaxial isomer appeared at (q2 ≈ 0.600, η ≈ 0.060 (γ ≈ 10°)) under Exact pairing, whereas it was less distinguishable in the BCS case.
The ground-state of 172Hg (Fig. 5) is found at (q2 = 0.10, η ≈ 0.04) as an oblate minimum, with another minimum at (q2 ≈ -0.100, η ≈ 0.02), which exhibits γ-unstable deformation. The PES of 172Hg provides an excellent example of an almost γ-unstable nucleus. Under Exact pairing, this γ-unstable minimum is more symmetric, with clear reflections around γ=150°, γ=30°, and γ=90°. Under BCS pairing, the γ-unstable features are less prominent, and the oblate minimum becomes more dominant. Additionally, two shape isomers are visible under Exact pairing model: a prolate isomer at (q2 ≈ 0.600, η = 0), E ≈ 4.6 MeV, and an oblate one at (q2 ≈ -0.45, η = 0), E ≈ 4.6 MeV. However, these changes were not distinguishable in the BCS case.
As shown in Figs. 5(c), the ground-state shape of 174Pb tended to be spherical. The PES under Exact pairing revealed a nearly spherical configuration with minor prolate and oblate shape isomers. In contrast, BCS pairing resulted in a more pronounced spherical minimum and diminishes the depth of shape isomers.
In summary, as the number of protons increases, the ground-state transitions from prolate for 170Pt to the coexistence of γ-unstable and oblate for 172Hg, eventually approached a nearly spherical configuration for 174Pb. The comparison between Exact and BCS pairing demonstrates that BCS pairing tends to smooth out shape coexistence and reduce the depth of shape isomer, leading to less pronounced deformation features. The differences in results between Exact and BCS pairing may be attributed to the mean-field approximation in the BCS approach, which likely simplifies the treatment of pairing interactions. This approximation is thought to smooth out shape coexistence phenomena by suppressing pairing fluctuations, energy gaps, and shell effects, potentially leading to less pronounced deformation features.
Shape coexistence analysis in the Pt isotope chain
In this paper, we investigate the PESs of the even-even 170-180Pt isotopes using the exactly solvable deformed mean-field plus pairing model. Our analysis provides a comprehensive examination of the shape coexistence phenomena across these isotopes.
The pairing interaction strength, denoted as G, serves as the sole adjustable parameter within our model. It is typically determined either through empirical formulas or by fitting to experimental odd-even mass differences [65, 66]. In this study, we determined Gν by fitting the experimental odd-even mass differences for the 171-180Pt isotope chain and Gπ by fitting the experimental odd-even mass differences for the 174Pt to 178Pb isotonic chain. The odd-even mass differences are computed using the following expression:
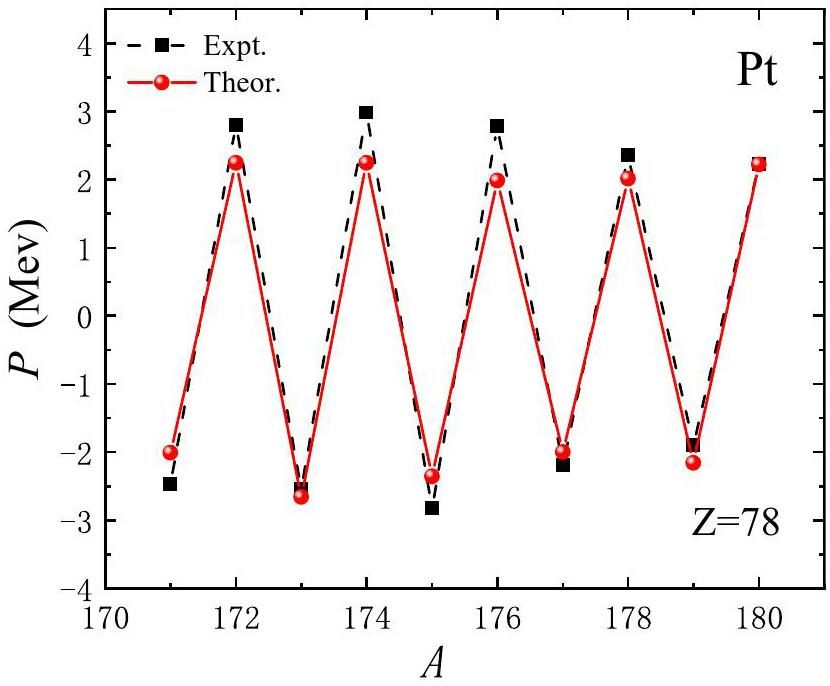
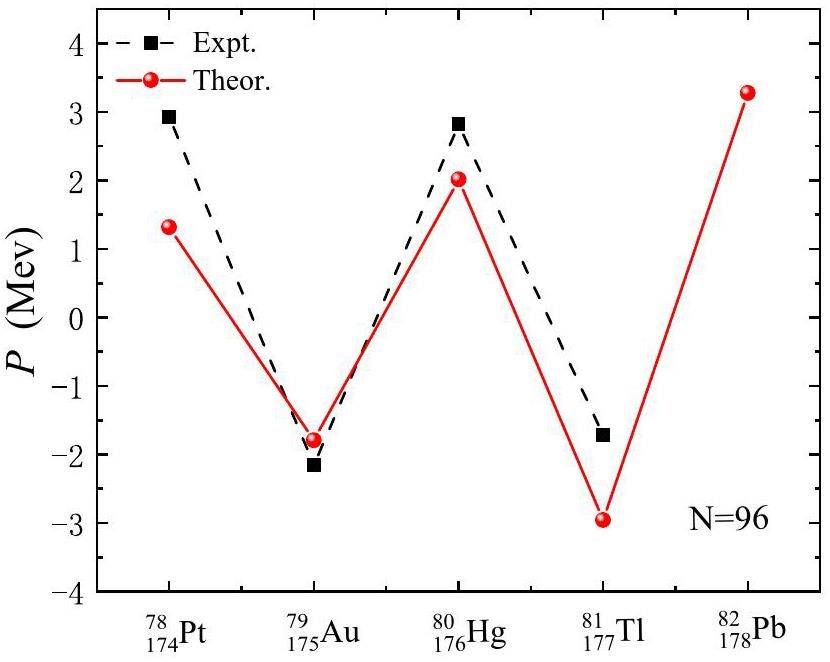
Next, we examine the PES of the 170-180Pt even-even isotopes under the determined pairing interaction strengths Gν=0.145 MeV and Gπ=0.100 MeV. Figure 8 shows the PES projected onto the (q2, η) plane. For 170Pt, the ground-state exhibited a prolate deformation at (q2=0.15, η=0). In contrast, for 172Pt, a more deformed minimum emerged, leading to the coexistence of a triaxial shape (γ≈30°) and a nearly prolate-deformed minimum at (γ≈120°), indicative of γ-instability due to the presence of multiple low-energy configurations at different γ values. The triaxial shape is even more pronounced in 174Pt, where the ground-state is triaxial with deformation parameters (q2=0.020, η=0.10, β≈0.2, γ≈90°) and a coexisting prolate minimum at (q2=0.15, η=0). In 176Pt a γ -unstable ground-state and a prolate minimum coexisted, but by 178Pt and 180Pt, a well-deformed prolate minimum quickly developed, becoming the most pronounced prolate ground-state at the mid-shell.
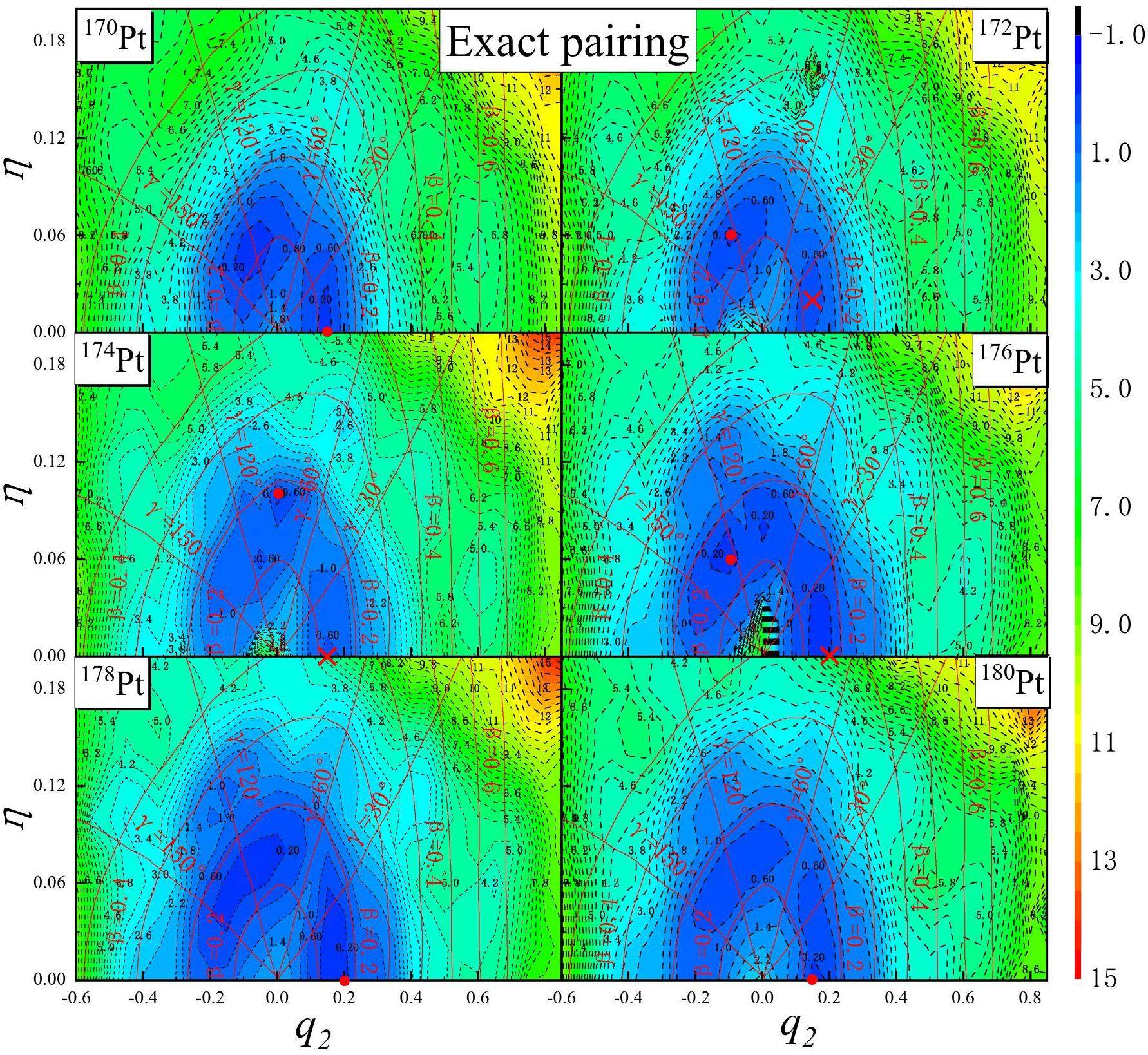
The findings of this study are broadly consistent with the results of Ref. [20], which studied the 172-194Pt isotopic chain in the framework of the interacting boson model and self-consistent HFB calculation using the Gogny-D1S interaction. Both studies identified shape coexistence in the 172-176Pt region, with γ-unstable minima and triaxial shapes in 174Pt. Additionally, both studies showed the dominance of prolate deformation in 178Pt, and 180Pt, with the prolate minimum becoming the most pronounced ground state at the mid-shell.
It is noteworthy that a triaxial shape isomer exists for 170-174Pt, characterized by (q2 ≈ 0.600, η ≈ 0.060 (γ ≈ 10°)), and positioned approximately 5.0 MeV above the ground-state. However, this triaxial shape isomer vanishes for 176-180Pt.
Conclusion
In this study, we systematically investigated the shape coexistence phenomenon in isotopes near the magic proton number of Z = 82, focusing specifically on the nuclei 170 Pt, 172 Hg, and 174Pb, as well as the Pt isotopic chain from 170Pt to 180Pt. Our analysis, using a macro-microscopic approach that combines the LSD model with a Yukawa-Folded potential and pairing corrections, revealed significant insights into the impact of pairing interactions on nuclear shape evolution.
The PES of 170Pt revealed a prolate ground-state with additional triaxial and oblate shape isomers. Both shape isomers become progressively shallower with increasing neutron pairing strength Gν, and the oblate isomer vanishes at Gν = 0.145 MeV, indicating a significant dependence of shape isomers on pairing strength. The ground-state deformation of 172Hg transitions from triaxial to oblate with increasing Gν, reflecting its nearly γ-unstable nature. Three shape isomers (prolate, triaxial, and oblate) were observed, with energy barriers separating these configurations. As Gν increased, the triaxial isomer disappeared at Gν = 0.145 MeV, demonstrating the impact of pairing interactions on shape stability. 174Pb exhibited a prolate ground-state that became increasingly spherical with stronger pairing interactions. While shape isomers are present at weaker pairing strengths, their prominence diminishes significantly, and robust shape coexistence was not observed in this nucleus.
For realistic pairing interaction, the ground-state shapes transition from prolate in 170Pt to a coexistence of γ-unstable and oblate shapes in 172Hg, ultimately approaching spherical symmetry in 174Pb. This progression highlights the interplay between proton number and pairing interactions in shaping nuclear deformation. The comparison between Exact and BCS pairing for realistic 170Pt, 172Hg, and 174Pb demonstrated that BCS pairing tends to smooth out shape coexistence and reduce the depth of shape isomers, leading to less pronounced deformation features.
These findings emphasize the critical role of pairing interactions in shaping nuclear deformation landscapes and shape coexistence, offering deeper insights into the structural evolution of nuclei near the mid-shell region. This study contributes valuable theoretical perspectives to the understanding of nuclear shape phenomena and the influence of pairing interactions on nuclear dynamics.
Based on the analysis of the PESs for the even-even 170-180Pt isotopes, the results show significant shape evolution across the isotopic chain. For 170Pt, the ground-state exhibited prolate deformation, with deformation parameters. However, for 172Pt, a more deformed minimum appears, leading to the coexistence of a triaxial shape and a nearly prolate-deformed minimum. The triaxial shape becomes even more pronounced in 174Pt, where the ground-state is triaxial with deformation parameters, coexisting with a prolate minimum. For 176Pt, a γ-unstable ground-state coexists with a prolate minimum. By 178Pt, and 180Pt, a well-deformed prolate minimum develops rapidly, becoming the most pronounced prolate ground-state in the mid-shell.
These results highlight the complex shape evolution in the Pt isotopes, with shape coexistence and γ-instability playing significant roles in the nuclear structure evolution, particularly around the mid-shell region where prolate deformation dominates.
Publisher's Note: Shape coexistence in atomic nuclei
. Rev. Mod. Phys. 83, 1467 (2011). https://doi.org/10.1103/RevModPhys.83.1655Imaging the initial condition of heavy-ion collisions and nuclear structure across the nuclide chart
. Nucl. Sci. Tech. 35, 220 (2024). https://doi.org/10.1007/s41365-024-01589-wNeutron skin and its effects in heavy-ion collisions
. Nucl. Sci. Tech. 35, 211 (2024). https://doi.org/10.1007/s41365-024-01584-1Random forest-based prediction of decay modes and half-lives of superheavy nuclei
. Nucl. Sci. Tech. 34, 204 (2023). https://doi.org/10.1007/s41365-023-01354-5Prediction of (n, 2n) reaction cross-sections of long-lived fission products based on tensor model
. Nucl. Sci. Tech. 35, 184 (2024). https://doi.org/10.1007/s41365-024-01556-5Shape Coexistence in Selenium Isotopes
. Nucl. Phys. Rev. 27, 2 (2010). https://doi.org/10.11804/NuclPhysRev.27.02.146Nuclear energy level argument for a spheroidal nuclear model
. Phys. Rev. 79, 432 (1950). https://doi.org/10.1103/PhysRev.79.432Collective and individual-particle aspects of nuclear structure
, Dan. Mat. Fys. Medd. 27, 16 (1953).Moments of Inertia of Rotating Nuclei
. Dan. Mat. Fys. Medd. 30, 1 (1955).Configuration mixing and magnetic moments of odd nuclei
. Prog. Theor. Phys. 12, 623 (1954). https://doi.org/10.1143/PTP.12.623Binding states of individual nucleons in strongly deformed nuclei
. Dan. Mat. Fys. Medd. 29, 16 (1955).Interpretation of some of the excited states of 4n self-conjugate
. Phys. Rev. 101, 254 (1956). https://doi.org/10.1103/PhysRev.101.254Collective motion in the nuclear shell model
. I. Classification schemes for states of mixed configurations. Proc. R. Soc. A 245, 128(1958). https://doi.org/10.1098/rspa.1958.0072Global Calculation of Nuclear Shape Isomers
. Phys. Rev. Lett. 103Shape coexistence in the neutron-deficient 188Hg investigated via lifetime measurements
. Phys. Rev. C. 102,In-beam spectroscopic studies of shape coexistence and collectivity in the neutron-deficient Z ≈ 82 nuclei
. J. Phys. G.43,Self-consistent mean-field models for nuclear structure
. Rev. Mod. Phys. 75, 121 (2003). https://doi.org/10.1103/RevModPhys.75.121Shape coexistence in the relativistic Hartree-Bogoliubov approach
. Phys. Rev. C. 65,Structure and α decay of superheavy nucleus 296Og
. Nucl. Phys. Rev. 40, 4 (2023). https://doi.org/10.11804/NuclPhysRev.40.2023059Shape evolution and shape coexistence in Pt isotopes: Comparing interacting boson model configuration mixing and Gogny mean-field energy surfaces
. Phys. Rev. C 98,Nuclear shape coexistence: A study of the even-even Hg isotopes using the interacting boson model with configuration mixing
. Phys. Rev. C 89,Shape isomers in Pt, Hg and Pb isotopes with N≤126
. Eur. Phys. J. A, 56, 107 (2020). https://doi.org/10.1140/epja/s10050-020-00115-xENSDEF
(2010), http://www.nndc.bnl.gov/ensdfTheory of Superconductivity
. Phys. Rev. 108, 1175 (1957). https://doi.org/10.1103/PhysRev.108.1175Possible analogy between the excitation spectra of nuclei and those of the superconducting metallic state
. Phys. Rev. 110, 4 (1958). https://doi.org/10.1103/PhysRev.110.936Effect of pairing correlations on nuclear properties
. Dan. Mat. Fys. Medd. 31, 11 (1959).Roles of tensor force and pairing correlation in two-proton radioactivity of halo nuclei
. Chin. Phys. C 47,Tensor force effect on two-proton radioactivity of 18Mg and 20Si
. Phys. Rev. C 110,Pairing effects on bubble nuclei
. Chin. Phys. Lett. 36,Effect of a tensor force on the proton bubble structure of 206Hg
. Phys. Rev. C 91,Effect of the reduced pairing interaction on α-decay half-lives of multi-quasiparticle isomeric states
. Phys. Rev. C 90,Accuracy of BCS-based approximations for pairing in small Fermi systems nuclei
. Phys. Rev. C. 78,Underlying structure of collective bands and self-organization in quantum systems
. Phys. Rev. Lett. 123,Nucleon-pair truncation of the shell model for medium-heavy nuclei
. Phys. Rev. C 106,A restricted class of exact eigenstates of the pairing-force Hamiltonian
. Phys. Lett. 3, 3277 (1963). https://doi.org/10.1016/0031-9163(63)90259-2Application to the exact theory of the pairing model to some even isotopes of lead
. Phys. Lett. 5, 82 (1963). https://doi.org/10.1016/S0375-9601(63)80039-0Exact eigenstates of the pairing-force Hamiltonian
. Nucl. Phys. 52, 221 (1964). https://doi.org/10.1016/0029-5582(64)90687-XPairing models of Pb206, Pb204 and Pb202
. Nucl. Phys. 52, 253 (1964). https://doi.org/10.1016/0029-5582(64)90690-XDiagonalization of a class of spin Hamiltonians
. Phys. J. 37, 1087 (1976).A particle-number-conserving solution to the generalized pairing problem
. Phys. Lett. B. 422, 1 (1998). https://doi.org/10.1016/S0370-2693(98)00034-3Electrostatic mapping of nuclear pairing
. Phys. Rev. Lett. 88,Colloquium: Exactly solvable Richardson-Gaudin models for many-body quantum systems
. Rev. Mod. Phys. 76, 643 (2004). https://doi.org/10.1103/RevModPhys.76.643Heine-Stieltjes correspondence and the polynomial approach to the standard pairing problem
. Phys. Rev. C 86,Gaudin models solver based on the correspondence between Bethe ansatz and ordinary differential equations
. Phys. Rev. B 83,Bethe ansatz and ordinary differential equation correspondence for degenerate Gaudin models
. Phys. Rev. B 85,Numerical algorithm for the standard pairing problem based on the Heine-Stieltjes correspondence and the polynomial approach
. Comp. Phys. Commun. 185, 2714 (2014). https://doi.org/10.1016/j.cpc.2014.05.023Exact solution of the pairing problem for spherical and deformed systems
. Phys. Rev. C 92, 051304(R) (2015). https://doi.org/10.1103/PhysRevC.92.051304Ground state phase transition in the Nilsson mean-field plus standard pairing model
. Phys. Rev. C 94,An iterative approach for the exact solution of the pairing Hamiltonian
. Comp. Phys. Comm. 275,Impact of pairing interactions on fission in the deformed mean-field plus standard pairing model
. Phys. Rev. C 104,Impact of the pairing interaction on fission of U isotopes
. Phys. Rev. C 107,Pairing effects on the fragment mass distribution of Th, U, Pu, and Cm isotopes
. Nucl. Sci. Tech. 34, 173 (2023). https://doi.org/10.1007/s41365-023-01316-xPerformance of the Fourier shape parametrization for the fission process
. Phys. Rev. C 95,Fission fragment mass yields of Th to Rf even-even nuclei
. Chin. Phys. C 45,Analysis of nuclear fission properties with the Langevin approach in Fourier shape parametrization
. Phys. Rev. C 103,The coupling of nuclear surface oscillations to the motion of individual nucleons
. Dan. Mat. Fys. Medd. 26, 14 (1952).Microscopic inertial functions for nuclei in the barium region
. Nucl. Phys. A 274, 151 (1976). https://doi.org/10.1016/0375-9474(76)90233-5Hexadecapole Nuclear Potential for Non-Axial Shapes
, Acta Phys. Pol. B 12, 1001 (1981). https://doi.org/10.1016/0003-4916(82)90273-1Data tables
. Atom. Data Nucl. Data Tables 98, 149 (2012). https://doi.org/10.1103/PhysRevC.79.064304Nuclear liquid-drop model and surface-curvature effects
. Phys. Rev. C 67,Shell effects in nuclear masses and deformation energies
. Nucl. Phys. A 95, 420 (1967). https://doi.org/10.1016/0375-9474(67)90510-6'Shells' in deformed nuclei
. Nucl. Phys. A 122, 1 (1968). https://doi.org/10.1016/0375-9474(68)90699-4On the nuclear structure and stability of heavy and superheavy elements
. Nucl. Phys. A. 95, 1 (1969). https://doi.org/10.1016/0375-9474(69)90809-4Projection techniques to approach the nuclear many-body problem
. Phys. Scr. 91,Pairing gaps from nuclear mean-field models
. Eur. Phys. J. A 8, 59 (2000). https://doi.org/10.1007/s10050-000-4504-zU. S. National Nuclear Data Center
: http://www.nndc.bnl.gov/The authors declare that they have no competing interests.