Introduction

An atomic nucleus, which contains valuable information regarding atomic structure, is a fundamental physical property [1]. Changes in atomic mass directly affect the nuclear stability and energy release during nuclear reactions [2]. The mass of a neutron-rich nucleus plays a crucial role in fast neutron capture (the r-process) during stellar nucleosynthesis. Thus, studying mass is essential to comprehensively understand the formation and evolution of elements in the universe [3-5]. Recently, the development of radioactive ion beam facilities has led to experimental measurements of more than 3000 ground state atomic masses [6, 7], with studies continuously expanding to both sides of the β stability line. In astrophysics, large amounts of data concerning the masses of neutron-rich or neutron-poor nuclei in regions far from the stability line are required. This is difficult to measure directly using the current technology. Therefore, several mass models have been proposed.

In 1935, Bethe and Weizsacker proposed the semiempirical BW mass formula [8-10] that predicts mass with an accuracy of approximately 3 MeV. In Ref. [11], nuclear binding energy is divided into two parts: a large and smooth component and a small and fluctuating component. The classical droplet model only accounts for a smooth trend and fails to consider the rapid fluctuation of the binding energy around the shell gap with a number of protons and neutrons. This suggests that important physical effects are absent in the classical mass model [12, 13]. To solve this problem, physicists have developed macroscopic-microscopic mass models. These models introduce shell correction terms such as the finite force range droplet model (FRDM) [14], Koura–Tachibana–Uno–Yamada (KTUY) [15], and Lublin–Strasbourg drop (LSD) [16], and micromass models such as the Hartree–Fock–Bogoliubov (HFB) approach [17, 18] and relativistic mean-field (RMF) theory [19]. The cited research is primarily based on the density functional theory (DFT) [20]. Although DFT is more complex, it exhibits superior extrapolation capabilities.

Kirson et al. added six physical terms as constraints to the mass model [21-27]. The obtained BW2 mass model was improved to some extent by addressing the problems of missing physics and overfitting that existed in early semiempirical mass formulations, thereby reducing the root mean square error (RMSD) [28] to 1.92 MeV. Machine learning has important applications in nuclear physics because of its ability to handle complex problems, such as predicting half-life, charge radius, and charge density [29-32]. By considering the α-decay energy and Garvey–Kelson relations (GKs) and applying the multiobjective optimization (MOO) method [13, 33, 34], Qian et al. significantly improved the theoretical accuracy of the BW2 model. Considering the isospin dependence, Bhagwat improved the liquid drop model to a model related to isospin and added fluctuation terms [35], which explained the binding energy of nucleons very well. Sequential least squares programming (SLSQP) [36] is a suitable algorithm for solving nonlinear optimization problems with constraints, because it can handle multiple constraints and nonlinear objective functions.

In this work, we studied an improved BW2 mass model with a higher-order term of symmetry energy [37] by employing certain algorithms, such as SLSQP. The mass models and algorithms are presented in Sect. 2. In Sect. 3, we test the generality of the SLSQP method using 200 sample mass formulae derived from randomly selected parameters of the E_isospin mass model. Finally, the conclusions are presented in Sect. 4.

Semiempirical Mass Formula

Discussion

The coefficients of the BW3 model are improved with less error between the calculated values and experimental data using the SLSQP algorithm [36]. Subsequently, the following constraints were incorporated to guarantee the physical viability of the program calculations:

1. The nuclide numbers should satisfy N≥8 and Z≥8.

2. After satisfying Condition 1, the specific binding energy of the remaining nuclides, $\frac{B_{\text{Th}}}{N+Z}$, is distributed in the range of 5 - 9 MeV.

The performance metrics of the model were evaluated using RMSD [28], which is defined as follows: $RMSD=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left(B_{{\text{Ex}}_i}-B_{{\text{Th}}_i}\right)}^2}}{n}}\mathrm{,}$ (18) where n represents the total number of nuclides involved in the calculation and $B_{{\text{Ex}}_i}$ and $B_{{\text{Th}}_i}$ are the current experimental and theoretical nuclide binding energies, respectively.

The modified coefficients corresponding to several algorithms are listed in Table 1. Different algorithms can lead to alterations in the weights of the terms within the model, as listed in table. The weights signify the degree to which each term affects the model and the symbols denote positive or negative corrections. The volume, surface, symmetry, Wigner, surface symmetry, pairing, higher-order correction, and curvature terms have high weights because of their significant influence on the mass model, whereas the Coulomb, Coulomb exchange, and shell effect terms [21-27] have low weights because of their relatively minor influence. In the plot, the horizontal coordinate represents the number of neutrons N, and the vertical coordinate represents the percentage of the relative error [12], which is defined as $\frac{\delta B}{B}(\%)=\frac{B_{\text{Ex}}-B_{\text{Th}}}{B_{\text{Ex}}}\times 100\%\mathrm{.}$ (19) The errors exhibit different trends for different nuclide regions under different algorithms. Figures 1a, 1b, and 1c. show a reduction in the overall error and a narrowing of the fluctuation range of the light and medium nuclide regions. In Fig. 1e and 1f, the fluctuation amplitude of the heavy nuclide regions increases, which leads to an increase in the fluctuation amplitude of the light nuclide regions, such that the total RMSD does not decrease or even deteriorate. SLSQP [36] exhibits greater advantages in reducing model errors when comparing performance metrics, such as $\frac{\delta B}{B}(\%)$ [12] and RMSD [28] of the mass model obtained using different algorithms. This is attributed to the reduced weights of the surface and curvature terms by SLSQP and the increased weights of Wigner, surface symmetry, pairing, and higher-order correction terms. The results also show that in Atomic Mass Evaluation (AME2020), the influence of the surface and curvature terms on the binding energy decrease, whereas that of the Wigner, surface symmetry, pairing, and higher-order correction terms on the overall effect increase. This also indicates that the mass model under SLSQP not only reduces the impact of the surface and curvature terms on the binding energy but also enhances the impact of the Wigner term on the overall effect, thereby improving its extrapolation ability [17, 18] and more accurately reflecting the contributions of different physical terms to the binding energy.

Fig. 1Full-screen View

(Color online) BW3 mass model relative error comparison using different algorithms, and its RMSD is shown in parentheses

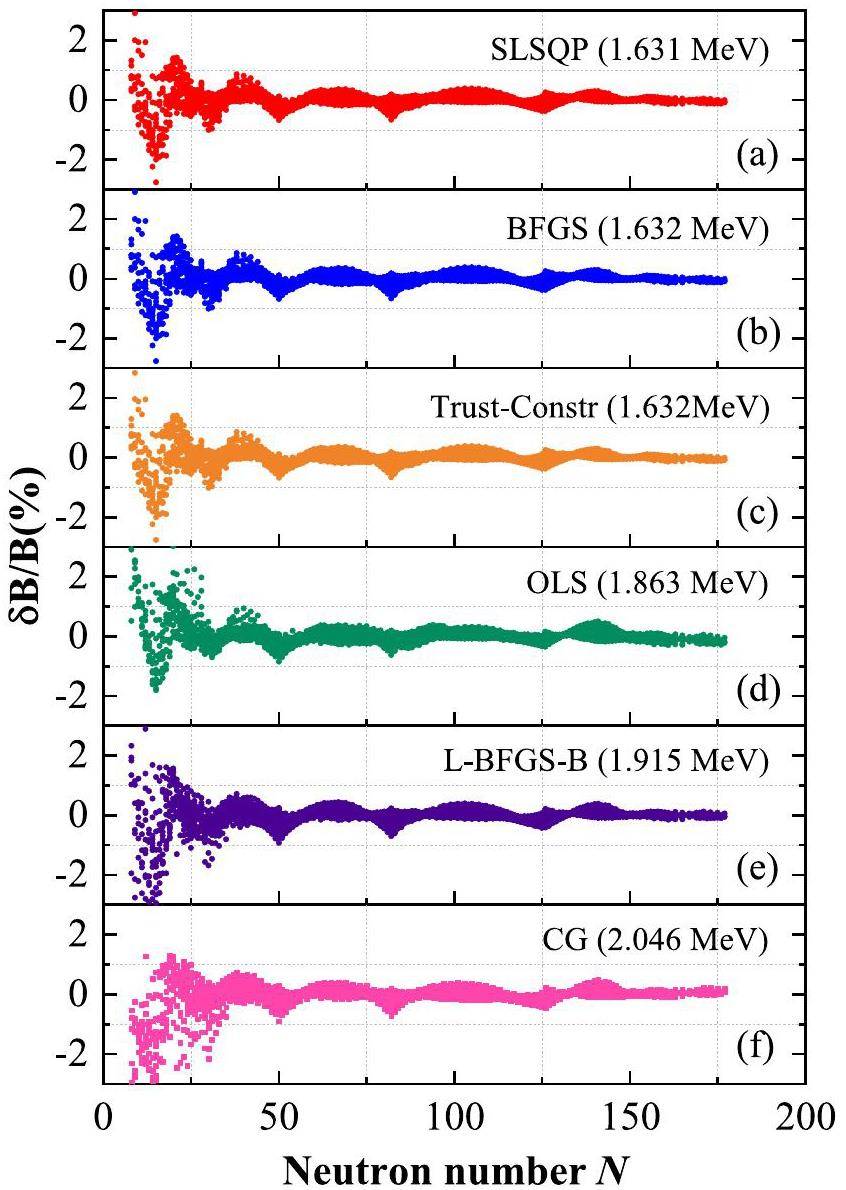
Figure 2 shows the relative error between the theoretical and experimental values of the BW3 mass model obtained by employing the SLSQP and OLS algorithms, where the x-axis represents the neutron number, the y-axis represents the atomic number, and the z-axis corresponds to the relative error percentage $\frac{\delta B}{B}(\%)$. In the figure, the fluctuations in the differences are more pronounced for the magic nuclei, particularly those nuclei in the vicinity of the doubly magic nuclei, which implies distinct interactions between the magic and nonmagic nuclei. The SLSQP improves the error near the doubly magic nuclei, captures the special interaction effects around the magic nuclei more accurately, and thus enhances the accuracy of the theoretical model.

Fig. 2Full-screen View

(Color online) BW3 mass model relative error comparison with SLSQP/OLS coefficients

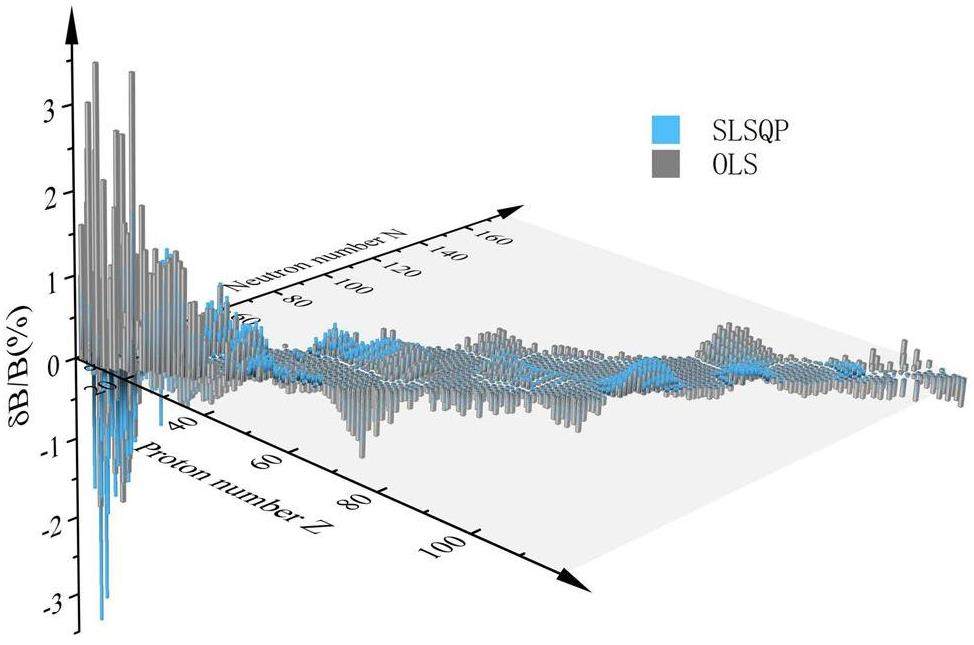
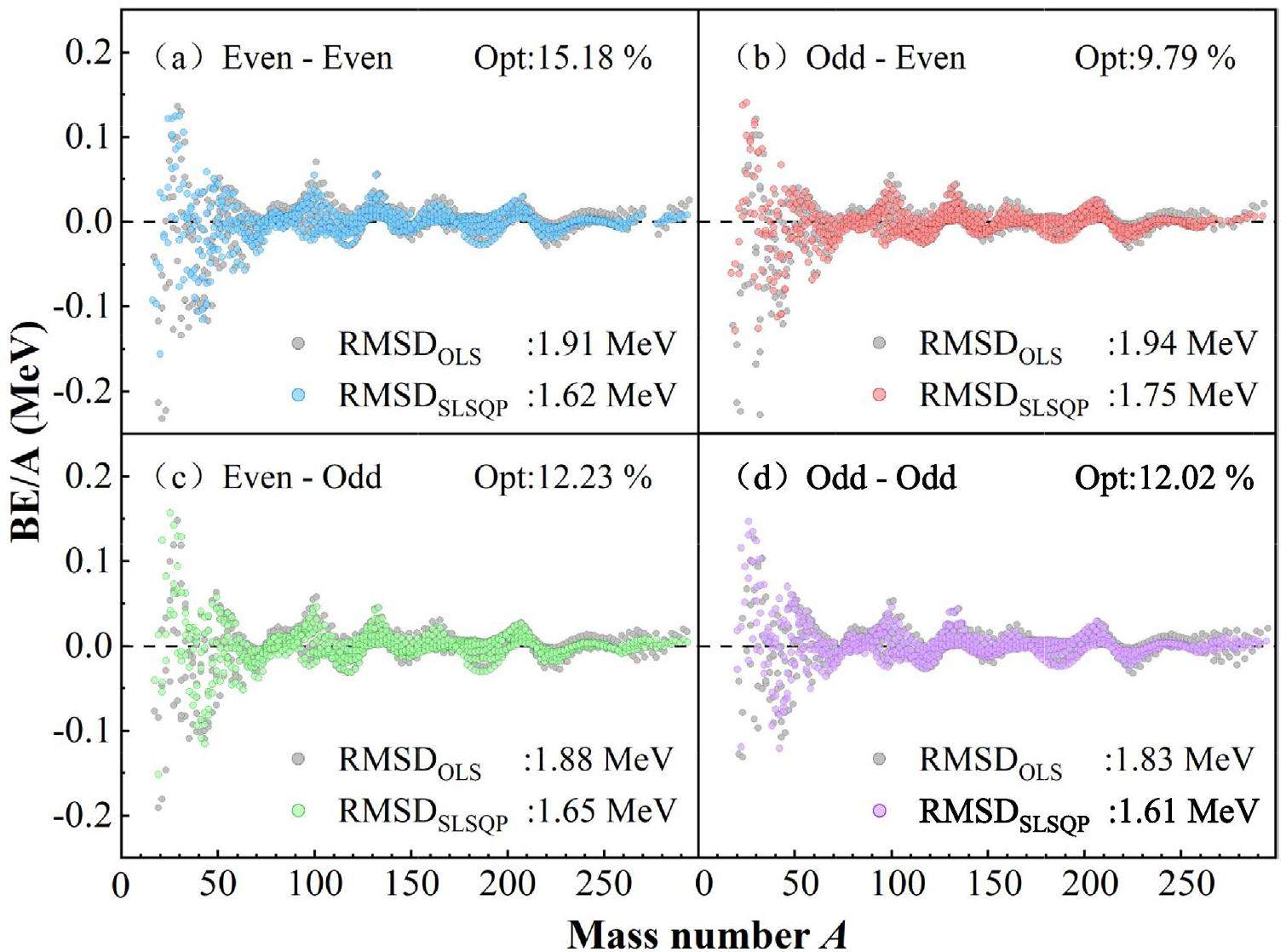
Figure 3 shows the performance of the SLSQP algorithm with regard to even-even, odd-odd, and odd-A nuclei. The optimization effect of the SLSQP algorithm on different types of nuclei exhibit significant differences. The improvement is most pronounced for even-even nuclei, whereas certain optimization results can also be attained for odd-A and odd-odd nuclei. Figure 3a shows that for even-even nuclei [48] (both Z and N are even), the SLSQP algorithm provides a significant reduction in RMSD [28] by 0.29 MeV, with a performance improvement of approximately 15.18%, achieving a more substantial optimization in the entire nuclei region compared with the theoretical value of the BW3 model with OLS coefficients. In Fig. 3b, for odd-Z and even-N nuclei, after the SLSQP optimization, the model RMSD is reduced by 0.19 MeV, with a performance improvement of approximately 9.79%. Similarly, in Fig. 3c, for even-Z and odd-N nuclei, the model RMSD is reduced by 0.23 MeV, with a performance improvement of approximately 12.23%. Notably, in the medium-nuclei region, the optimization results are closer to the experimental values. For odd-odd nuclei (both Z and N are odd), Fig. 3d shows that after SLSQP optimization, the model RMSD is reduced by 0.22 MeV and the performance is improved by approximately 12.02%. In particular, in the heavy-nuclei region, the optimization results are closer to the experimental values. These results further validate the effectiveness of the SLSQP algorithm for mass model optimization.

Fig. 3Full-screen View

(Color online) BW3 mass model performance on total nuclei with SLSQP/OLS coefficients

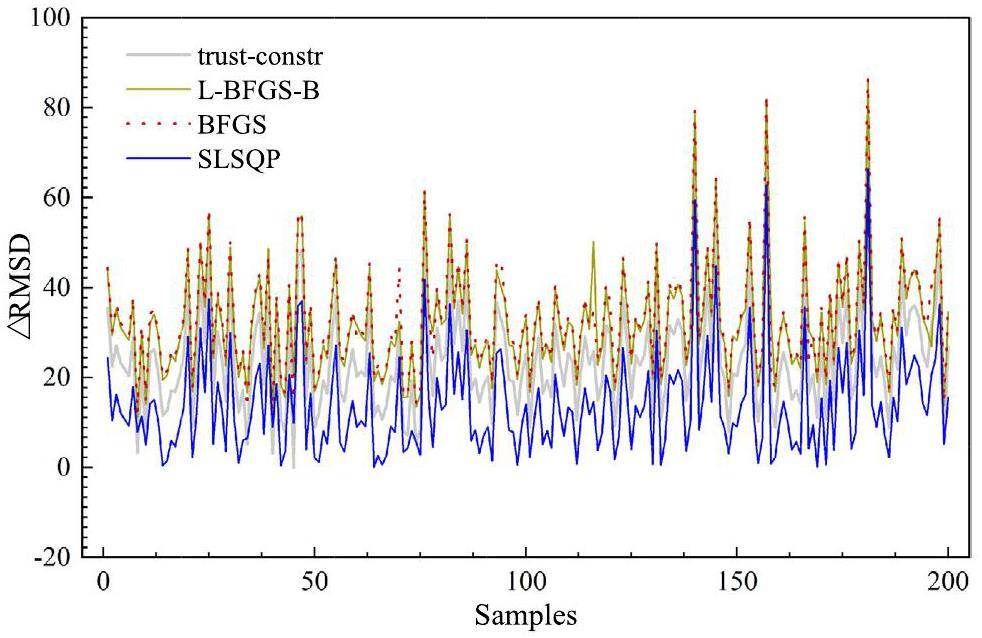
To test the generality of the SLSQP method, we devised 200 sample mass formulae by randomly selecting parameters from the F-parameters in the δE term of the E_isospin mass model. As mentioned previously, the E_isospin mass model consists of two parts: the E_LDM term, which contains nine M-parameters derived from the liquid drop model, and the δE term, which encompasses more than 100 F-parameters. If we set M = 4 in the E_isospin mass model, then 144 F-parameters are obtained. Subsequently, we compared the results with the nuclear mass dataset AME2020 and found that the RMSD was 1.268 MeV in this situation. Next, we tested the contributions of these F-parameters individually and identified 53 parameters that had obvious effects on the binding energy. Subsequently, we randomly selected 10 F-parameters from the 53 F-parameters and combined them with nine M-parameters to form a sample mass formula. Thus, we devised 200 sample mass formulas to test the proposed algorithms presented in this work. The SLSQP method outperformed the other algorithms in terms of both error and convergence speed.

As shown in Fig. 4, the SLSQP algorithm performs significantly better than the BFGS and L-BFGS-B algorithms. For example, at the 48th sample point, the $\text{Δ}RMSD$ of the SLSQP algorithm was 4 MeV, whereas those of BFGS and L-BFGS-B were 23.9 MeV and 23.0 MeV, respectively. At the 67th sample point, the $\text{Δ}RMSD$ of the SLSQP algorithm was 2.7 MeV, whereas those of BFGS and L-BFGS-B were 22.7 MeV and 21.8 MeV, respectively. However, the Trust-Constr algorithm exhibits a large error amplitude, which results in poor stability during parameter optimization. In terms of computational efficiency, compared with the SLSQP algorithm as a reference, the BFGS takes approximately 2.44 times longer, L-BFGS-B takes around 2.78 times longer, and the Trust-Constr takes a staggering 8.44 times longer. The SLSQP algorithm not only has good stability with small root mean square errors, but also high computational efficiency.

Fig. 4Full-screen View

(Color online) Finding 62 important parameters from the δE term of the E_isospin mass model, randomly selecting 10 items as a sample formula with E_LDM, and obtaining 200 samples of mass formulas. The $\text{Δ}RMSD$ is defined as (RMSD-RMSD_min)× 100, where RMSD_min is the minimum root mean square deviation optimized by the algorithm for 200 samples

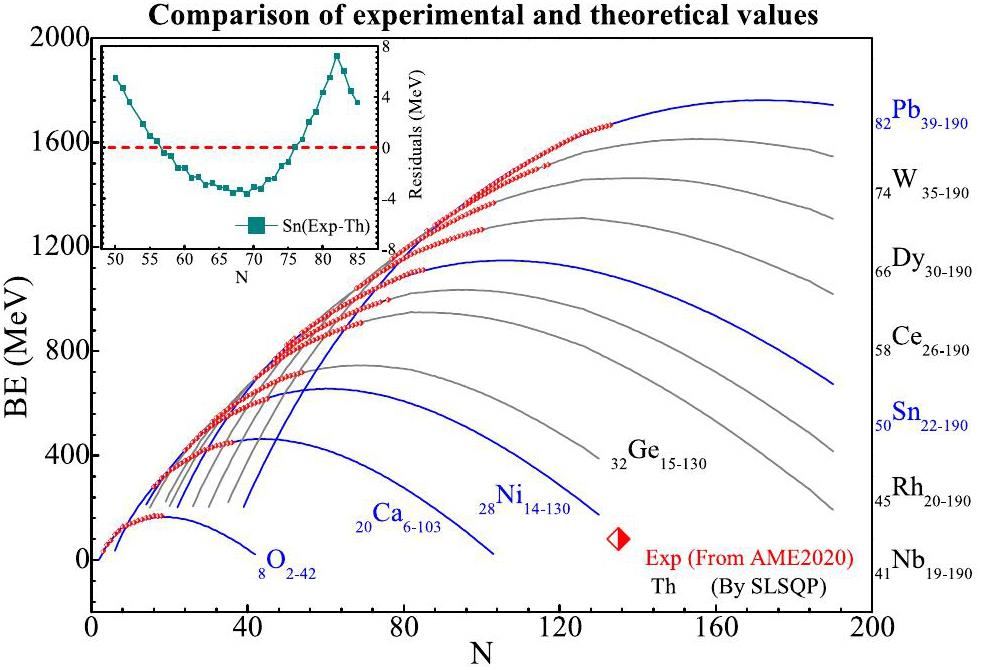
To verify the effectiveness of the SLSQP algorithm, the experimental and theoretical values were compared, as illustrated in Fig. 5. The experimental binding energy values were obtained from AME2020, whereas the theoretical values were obtained by optimizing the BW3 mass model using the SLSQP method. Among the experimental values, the maximum binding energy for the O isotopes is currently measured at ²⁴O₁₆, with a binding energy value of 168.95 MeV. Beyond this isotope, the binding energy decreases as N increases. The SLSQP-optimized theoretical model predicts the maximum point to be at ²⁶O₁₈ with a binding energy value of 168.95 MeV, followed by a similar decline in the binding energy with an increase in N. For the other isotope chains, the experimental binding energy values exhibit an overall increasing trend without reaching a maximum. By optimizing the BW3 nuclear mass model using the SLSQP method, the following maximum binding energy points are predicted for these isotope chains: ⁶⁴Ca=464.33 MeV, ⁸⁸Ni=656.72 MeV, ¹²³Nb=950.29 MeV, ¹⁴¹Rh=1035.66 MeV, ¹⁰⁰Ge=745.77 MeV, ¹⁵⁶Sn=1148.31 MeV, ¹⁸⁴Ce=1311.84 MeV, ²⁰⁶Dy=1463.63 MeV, ²³⁰W=1613.36 MeV, ²⁵²Pb=1761.89 MeV.

Fig. 5Full-screen View

(Color online) Experimental binding energy values from the AME2020 [6, 7], and the theoretical predicted value by the SLSQP method

Conclusions

In this study, we investigated an improved mass model with a higher-order symmetry energy term by employing several algorithms. The SLSQP algorithm demonstrated the best performance in terms of both root mean square errors and computational efficiency. This algorithm reduced the global RMSD from 1.863 MeV to 1.631 MeV (12.45% reduction). The odd (even) numbers of protons and neutrons are discussed, and the SLSQP algorithm reduced the local RMSD from 1.91 MeV to 1.62 MeV (15.18% optimization) when the nuclei have even numbers of both protons and neutrons. The local RMSD is reduced from 1.83 MeV to 1.61 MeV when the nuclei have odd numbers of protons and neutrons. With an odd (even) number of protons (neutrons), the local RMSD decreases from 1.94 MeV to 1.75 MeV (9.79% optimization). The local RMSD is reduced from 1.88 MeV to 1.65 MeV (12.23% optimization) when the number of protons is even and the number of neutron is odd. We tested these algorithms using 200 sample mass formulas derived from the E_isospin mass model. Each sample mass formula includes 19 free parameters, of which nine are M-parameters derived from the liquid drop model and 10 are F-parameters from the δE term of the E_isospin mass model. The SLSQP method provides better performance than the other algorithms in terms of errors and convergence speed. According to this study, the SLSQP algorithm is suitable for handling large-scale multiparameter optimization tasks in nuclear physics.