Introduction

The asymmetric fission mode in neutron-deficient ¹⁸⁰Hg was discovered in 2010 via β decay of ¹⁸⁰Tl [1]. For the fission of ¹⁸⁰Hg, its splitting into two ⁹⁰Zr fragments with magic N = 50 and semimagic Z = 40 is believed to dominate the fission process. However, unlike the initial theoretical prediction, ¹⁸⁰Hg has been observed to fission asymmetrically, with heavy and light fragment mass distributions centered around A=100 and 80 nucleons, respectively, [1, 2].

Much theoretical research attention has been drawn to the puzzling fission behavior of ¹⁸⁰Hg. For example, macroscopic-microscopic models [1, 3-6] and self-consistent microscopic approaches [7-9] have been used to analyze multidimensional potential energy surfaces (PESs). The presence of an asymmetric saddle point with a rather high ridge between the symmetric and asymmetric fission valleys is the main factor that determines the mass split in fission.

Calculations of fission-fragment yields have also been performed for ¹⁸⁰Hg using the Brownian Metropolis shape-motion treatment [3, 5, 10], Langevin equation [11], scission-point model [4, 12-14], and random neck rupture mechanism [15], based on the PESs or scission configurations. The results are in approximate agreement with the experimental data, with a deviation of ∼ four nucleons for the peak positions. Several attempts have also been made to describe the fragment mass distribution of ¹⁸⁰Hg in a fully microscopic manner, that is, the time-dependent generator coordinate method (TDGCM) based on covariant density functional theory (CDFT) [9]. The asymmetric peaks were reproduced very well, whereas a more asymmetric fission mode with A_H ~ 116 was predicted, which was not observed in the experimental measurements.

In the theoretical study of nuclear fission, PES is an important infrastructure that describes the evolution of nuclear energy with its shape variations on its way from the initial configuration towards scission. In nuclear physics, there are generally two approaches to generating a PES. The first method is based on the historical liquid drop model [16-22] to the well-known macroscopic-microscopic model using parametrization of the nuclear mean-field deformation [23-33]. The other is based on microscopic self-consistent methods [34-43] or the constrained relativistic mean-field method [9, 44-50].

In the macroscopic-microscopic method, a predefined class of nuclear shapes is defined uniquely in terms of selecting appropriate collective coordinates, and a relatively smooth potential energy surface can be obtained. However, owing to limitations in computing resources, the microscopic calculation of the PES can only be performed within a limited number of deformation degrees of freedom. In the microscopic self-consistent method, higher-order collective degrees of freedom are incorporated self-consistently based on the variational principle. In fission studies, the quadrupole and octupole deformation (moments) constraints are natural and most often used to calculate microscopic PES.

However, several studies have shown that because of the absence of hexadecapole deformation (q₄₀ or β₄), PES may exhibit discontinuities in large deformation scission regions [51-55]. Ref. [56] investigated the role of the hexadecapole deformation in the PES calculation of ²⁴⁰Pu by applying a disturbance to β₄. The results show that one can obtain a smooth 2-dimensional PES in (β₂, β₃) by parallel calculations with a suitable disturbance of the hexadecapole deformation.

But for asymmetric fission of ¹⁸⁰Hg, there have been no reports about the effect of q₄₀ or β₄ on the PES of ¹⁸⁰Hg. The self-consistent calculation in the quadrupole and octupole deformation spaces indicated that the PES of ¹⁸⁰Hg exhibits a different behavior from that of ²⁴⁰Pu or ²³⁶U with an increase in the quadrupole moment [7, 9]. Thus, it is interesting to examine the influence of the hexadecapolepole moment on the PES of ¹⁸⁰Hg under large deformations and analyze some properties of the scission configuration. In this study, we extend two-dimensional (q₂₀, q₃₀) constraint calculations to large deformation regions by adding q₄₀ constraint to the microscopic PES calculation of ¹⁸⁰Hg. The importance of q₄₀ in the self-consistent calculation of the PES for ¹⁸⁰Hg under large deformations was investigated. Moreover, the fission dynamics of ¹⁸⁰Hg, total kinetic energies, and fragment mass yield distributions based on TDGCM [57] are described and discussed.

Theoretical framework

To study the static fission properties, PES was determined using Skyrme density functional theory (DFT). The dynamic process was further investigated using the TDGCM framework. In this section, we briefly explain these two methods. A detailed description of Skyrme DFT can be found in Ref. [58], and the formulations of the TDGCM can be found in Refs. [57, 59-61].

Results and discussion

In the adiabatic approximation approach for fission dynamics, precise multidimensional PES is the first and essential step toward the dynamical description of fission. Figure 1 displays the PES contour of ¹⁸⁰Hg obtained by the HFB calculation in the collective space of (q₂₀, q₃₀), where q₂₀ ranges from - 20 b to 300 b and q₃₀ ranges from 0 b ^3/2 to 40 b^3/2 with a step of Δq₂₀ = 2 b and Δq₃₀ = 2 b^3/2. Overall, the PES pattern obtained in this work based on the DFT solver HFBTHO with the Skyrme SkM^* functional is similar to that obtained using the symmetry unrestricted DFT solver HFODD [7] with the same functional and that obtained using covariant density functional theory with the relativistic PC-PK1 functional [9]. The static fission path starts from a nearly spherical ground state (q₂₀ = 20 b, q₃₀ = 0 b^3/2), the reflection-symmetric fission path can be found for small quadruple deformations, and the reflection-asymmetric path branches away from the symmetric path for q₂₀ = 100 b. One can see that unlike the PES of actinide nuclei, there is no valley toward scission for ¹⁸⁰Hg, which undergoes a continuous uphill process until the mass asymmetric scission point with high q₃₀ asymmetry.

Fig. 1Full-screen View

(Color online) Potential energy surface of ¹⁸⁰Hg in the collective space of (q₂₀, q₃₀). The pink solid line and purple circle dots denote the static fission path and scission line respectively

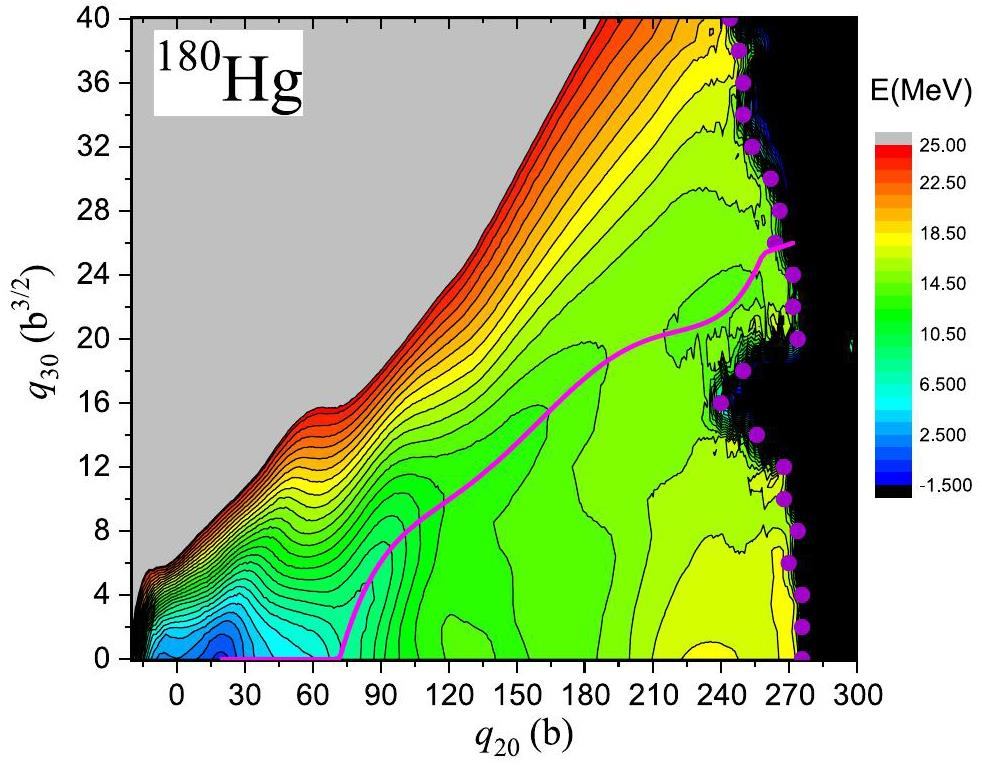
In the (q₂₀, q₃₀)-constrained PES calculations by DFT, other degrees of deformation are obtained based on the variational principle. In Refs. [56, 55], it has been learned that at a given q₂₀ and q₃₀, there are two minima with different values of q₄₀, and the minimum with a larger q₄₀ disappears when q₂₀ is large enough, which indicates the transition toward scission. Hexadecapole deformation is an important degree of freedom for the description of PES under large deformations. In particular, a disturbance of the hexadecapole deformation is required for a smooth and reasonable PES, as shown in Ref. [56]. Thus, in our work, at large quadrupole moments, that is, larger than $q_{20}\simeq 200$ b (${\beta }_2\simeq 3.2$), a further constraint on the hexadecapole moment q₄₀ is introduced. It is performed in a “perturbative” manner. A hexadecapole moment smaller than that obtained variationally is used as a further constraint in the first ten steps of DFT iterations, and it is then released to vary freely. Thus, a lower energy minimum with a smaller q₄₀ can be obtained. This treatment was used to calculate the PES in Fig. 1, and labeled “(B)” in Figs. 2 and 3. The calculation with the constraints q₂₀ and q₃₀ is labeled “(A)” in Figs. 2 and 3.

Fig. 2Full-screen View

(Color online) HFB energies along the symmetric-fission and asymmetric-fission pathways of ¹⁸⁰Hg as a function of q₂₀. The least-energy fission pathway (static fission path) is given as a blue curve. The symmetric-fission pathways are shown as the black or green curves, labeled as (A) or (B) respectively. These two curves are obtained with different treatment of q₄₀ (see text for details). The red line shows the transitional valley that bridges the asymmetric and symmetric paths

Fig. 3Full-screen View

(Color online) The hexadecapole moment (q₄₀), the particle number of neck (qN), and HFB energies as a function of q₂₀ are shown in panels (a), (b) and (c), respectively, for q₃₀ = 0 b^3/2 and 10 b^3/2

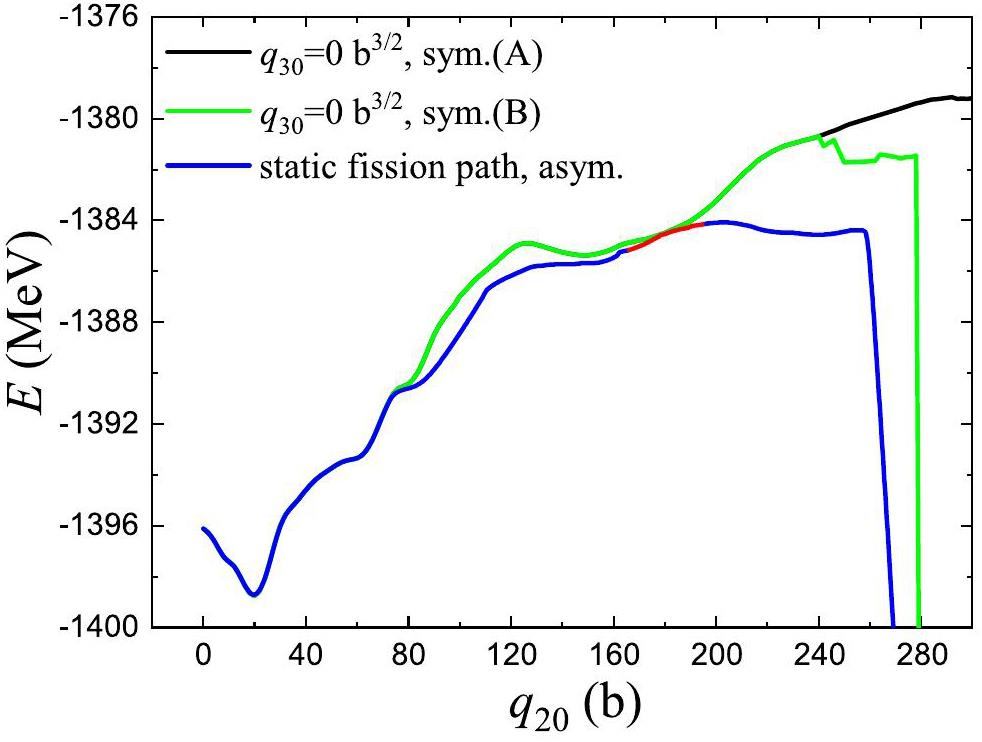
In Fig. 2, the energies of the static fission path as a function of quadruple moment q₂₀ are shown. The symmetric (q₃₀ = 0 b^3/2) and asymmetric fission paths in ¹⁸⁰Hg are given, respectively. It can be clearly observed that these energies increase with q₂₀ steadily. At approximately q₂₀ ~ 100 b, the asymmetric fission path starts to be favored in terms of energy compared to the symmetric fission path. The transitional valley that bridges the asymmetric and symmetric paths is shown in red in Fig. 2. Notably, this connection occurs at the deformation stage where the symmetric and asymmetric paths are nearly equivalent in energy. This characteristic of ¹⁸⁰Hg was verified in Ref. [68] using the HFB-Gogny D1S interaction. From Fig. 2, for case (A), one can see that the energy of ¹⁸⁰Hg increases continuously with q₂₀, and that it is difficult to rupture even at very large elongations, for example, $q_{20}\ge 300$ b (${\beta }_{20}\ge 4.8$). As seen in case (B), with the inclusion of the q₄₀ constraint, a gentle decent trend of energy occurs at q₂₀~240 b, and a sudden drop in energy occurs at q₂₀~280 b, indicating nuclear scission.

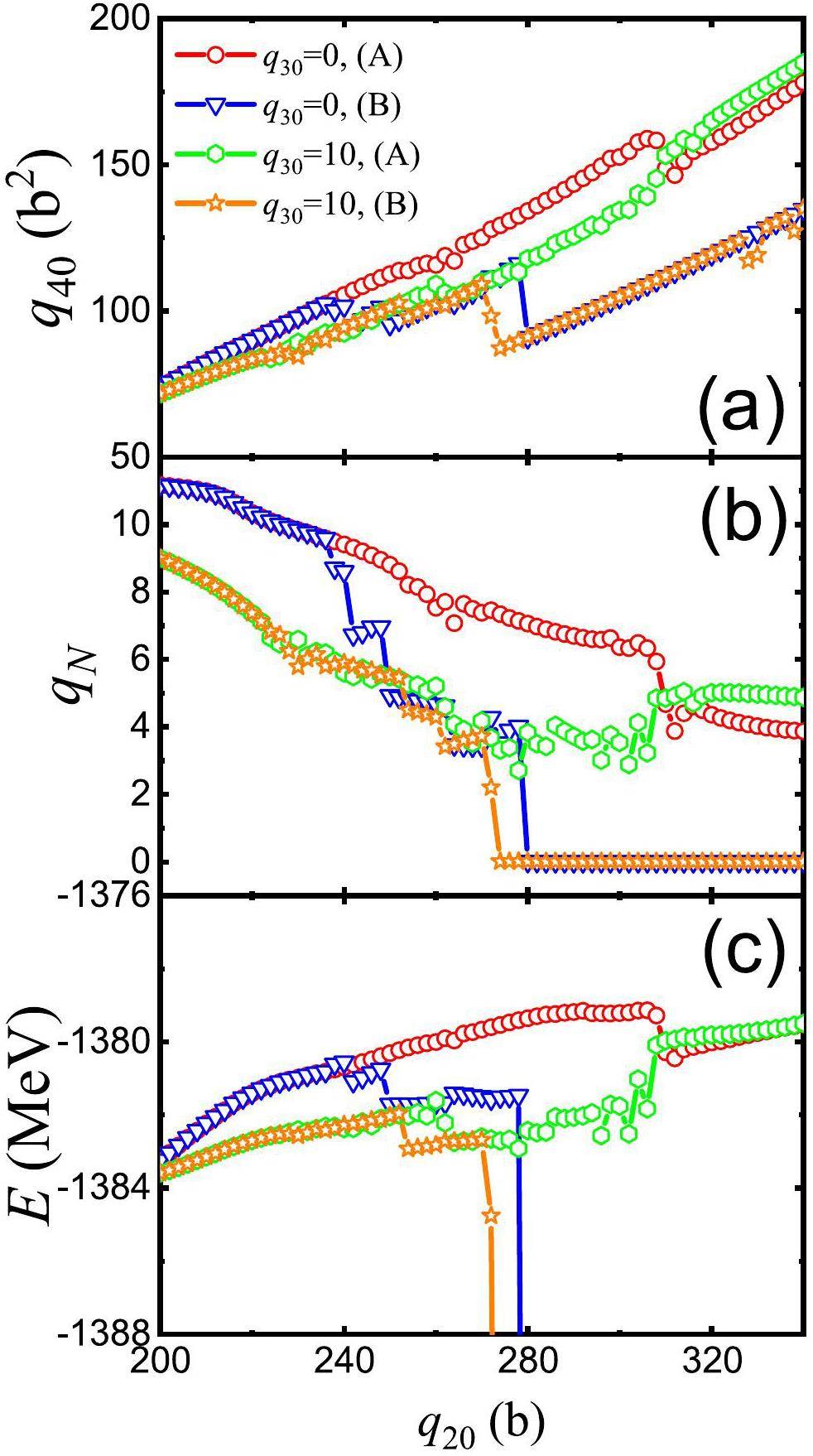
In Fig. 3, the hexadecapole moment (q₄₀), the average particle number around the neck (qN), and the HFB energies are given as functions of q₂₀ respectively, at a given q₃₀. To investigate the role of q₄₀, only the region with large q₂₀ is shown. From Fig. 3(a), it can be seen that q₄₀ increases nearly linearly until a very large q₂₀ value, especially for case (A), in which q₄₀ can become very large during elongation. After a “perturbative” constraint on q₄₀, as the case (B) in the figure, the q₄₀ value has sudden drop and then grow linearly. In studies of nuclear fission, qN is often adopted as an indicator of nuclear scission. For example, qN=4 was used for the determination of the scission line of ²⁴⁰Pu in Refs [40, 54, 69]. In Fig. 3(b), qN gradually decreases with q₂₀. However, in case (A), the reduction in qN becomes rather slow with an increase in q₂₀. In particular, at q₂₀~340 b (${\beta }_2\sim 5.4$), qN> 4 for q₃₀= 0 and 10 b^3/2, and the total energy increases continuously at a large q₂₀, as shown in Fig. 3(c)], respectively. After considering the q₄₀ constraint, as shown in case (B) in Fig. 3(b) and (c), both qN and the total energy exhibit a sudden drop at approximately q₂₀~280 b (${\beta }_2\sim 4.5$), indicating a nuclear rupture. It can be observed that when $q_N\le 4$, qN approaches zero with an increase in q₂₀.

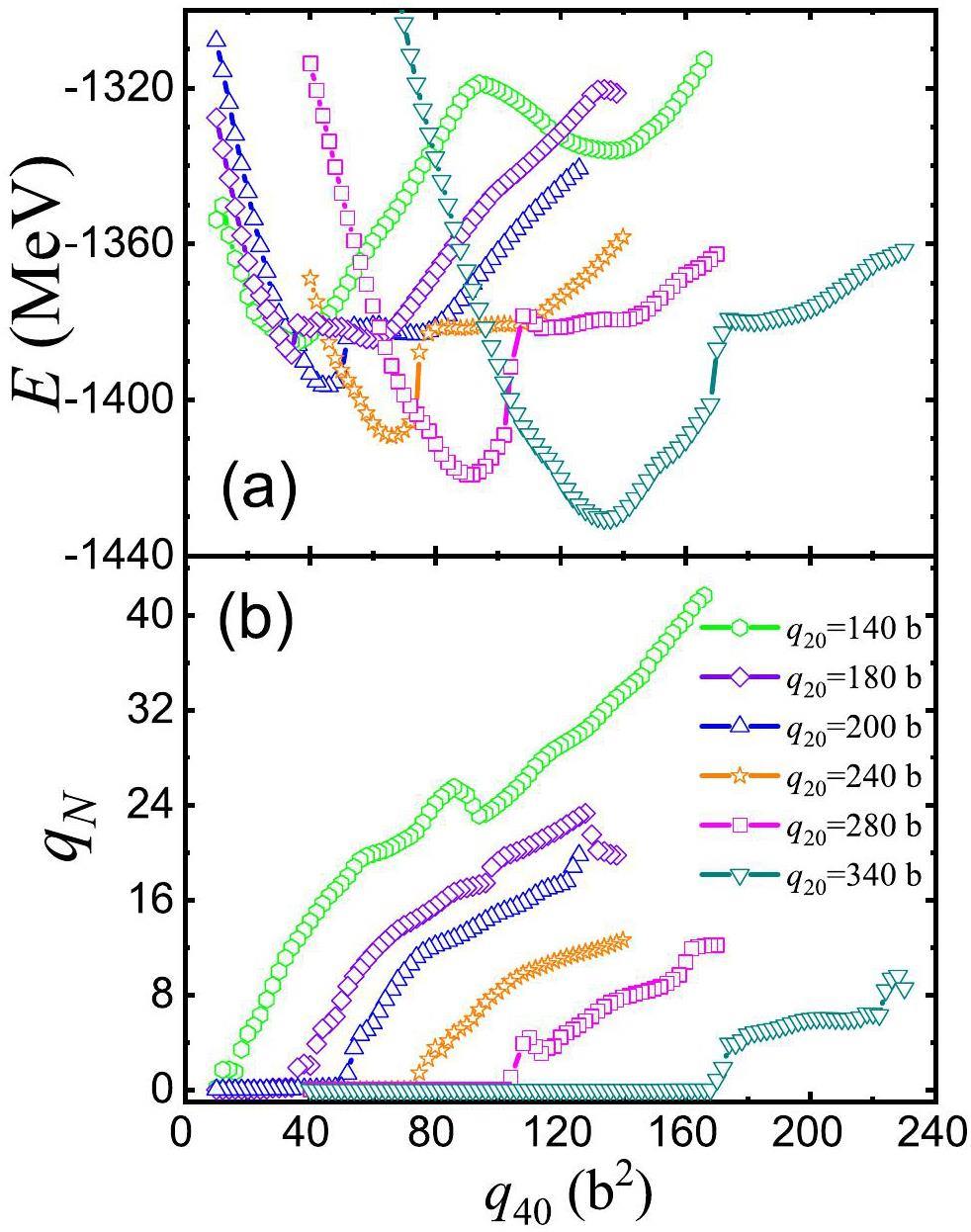
To investigate the role of q₄₀ on PES, the HFB energies and q_N against q₄₀ at given q₂₀ and q₃₀ are plotted in Fig. 4, which were obtained through exact constrained calculations of q₂₀, q₃₀ and q₄₀. In this figure, q₃₀ is constrained to 0 b ^3/2. The other q₃₀ values were also tested, and the results were similar to those in Fig. 4. In Fig. 4(a), one can see that there are two local minima along q₄₀ degrees of freedom, which correspond to distinct valleys on the multidimensional potential energy surface. In Ref. [56], a similar trend in ²⁴⁰Pu was found, and the minima related to the larger q₄₀ disappeared with increasing quadruple deformation (at roughly ${\beta }_2\sim 3.8$), leading to a natural transition to the minimum with a smaller q₄₀. This transition causes the discontinuity and sudden drop in energy in the two-dimensional PES of (q₂₀, q₃₀). However, for ¹⁸⁰Hg, there remains an extremely soft and relatively flat minimum with larger q₄₀ values, even at very large q₂₀ values, for example, at q₂₀ =340 b (${\beta }_2\sim 5.4$). In the PES calculation with only the (q₂₀, q₃₀) constraint, q₄₀ degrees of freedom are obtained by varying the total energies. As shown in Case (A) in Fig. 3, q₄₀ after the variation calculation grows steadily, even at a very large q₂₀, and no transition to the minimum with a smaller q₄₀ occurs. With only the (q₂₀, q₃₀) constraint, it is difficult to determine the proper scission configuration, at least for ¹⁸⁰Hg. After the “perturbative” inclusion of q₄₀ constraint, as in case (B) in Fig. 3, such a transition can occur at large q₂₀. In Fig. 4(b), it can be observed that qN increases with q₄₀. qN around the minimum with a larger q₄₀ is approximately larger than 4, and when q₂₀>200 b, its value around the minimum with a smaller q₄₀ is close to zero (numerically 10^-3-10^-4, effectively near zero). For $q_N\sim 0$, the nucleus is well separated into two fragments. From this calculation, one can learn that the introduction of q₄₀ constraint in the self-consistent PES calculation can ensure the continuity of the potential energy surface. q₄₀ is essential in DFT calculations for fission studies, particularly for the transition to scission.

Fig. 4Full-screen View

(Color online) Panels (a) and (b) show HFB energies as functions of q₂₀ under different treatments of the hexadecapole moment (q₄₀) for symmetric fission path (q₃₀= 0 b^3/2)

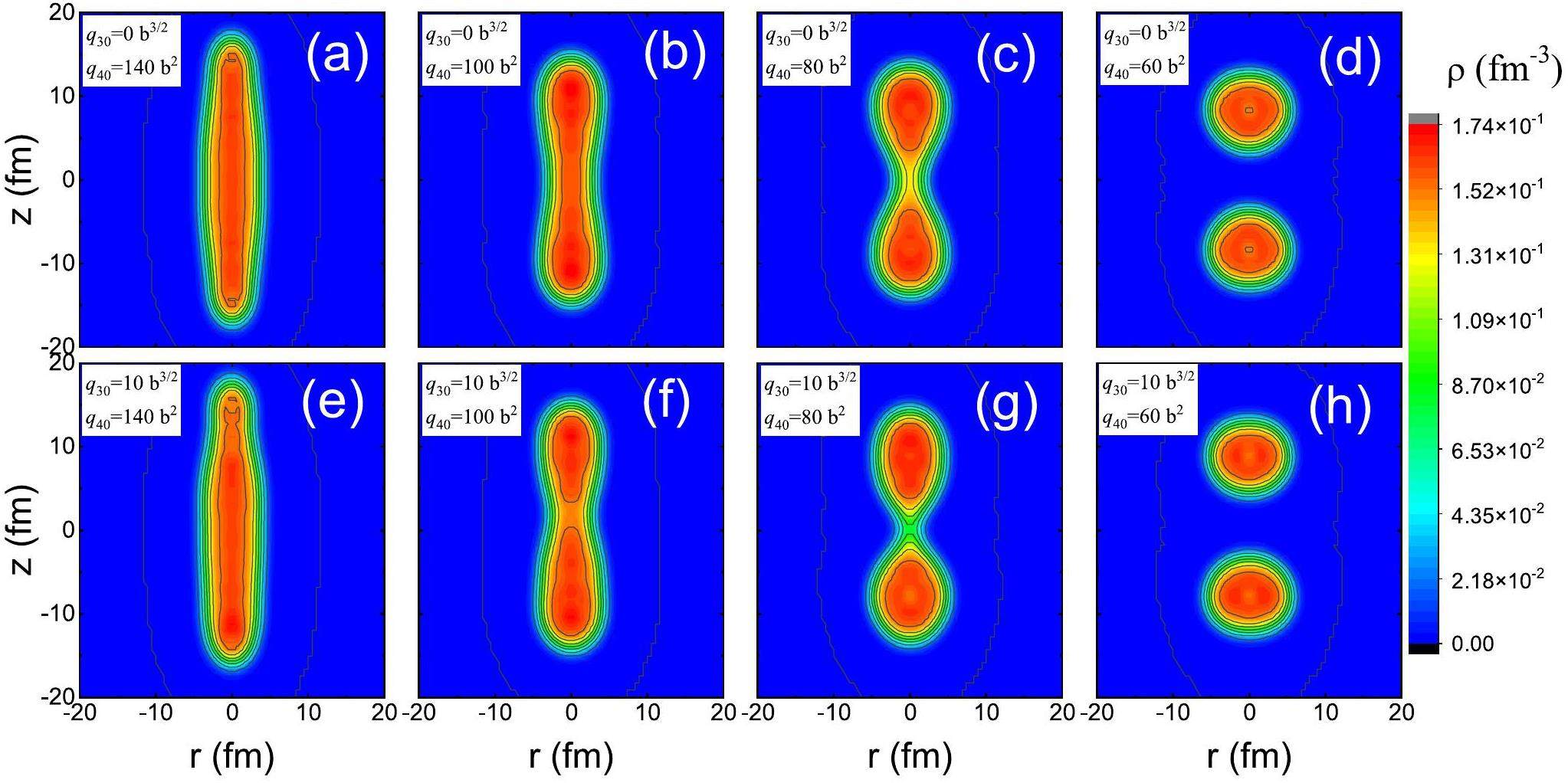
Several results of the (q₂₀, q₃₀, q₄₀) constrained calculations are shown in Fig. 5 for the density distribution profiles of ¹⁸⁰Hg. q₂₀ is constrained to 240 b, and q₄₀ changes from 140 b ² to 60 b² for q₃₀ = 0 b^3/2 and q₃₀ = 10 b^3/2 in the upper and lower panels, respectively. q₄₀ degrees of freedom influenced the formation of neck and scission configurations. From the figure, it can be seen that, with a large q₄₀, there is no neck in the nucleus, and the nucleus is stretched very long. For the calculation with only the (q₂₀, q₃₀) constraint, as in case (A) in Figs. 2 and 3, q₄₀ has a very large value with an increase in q₂₀ and thus, the nucleus cannot undergo scission. With a decrease in q₄₀, the neck structure of the nucleus appears and becomes well separated when q₄₀ has small values.

Fig. 5Full-screen View

(Color online) Density distributions of ¹⁸⁰Hg obtained with (q₂₀, q₃₀, q₄₀) constrained calculations. Results are obtained with different constrained q₄₀ for symmetric fission channel (q₂₀, q₃₀) = (240 b, 0 b^3/2) (upper panels) and for asymmetric fission channel (q₂₀, q₃₀) = (240 b, 10 b^3/2)(lower panels)

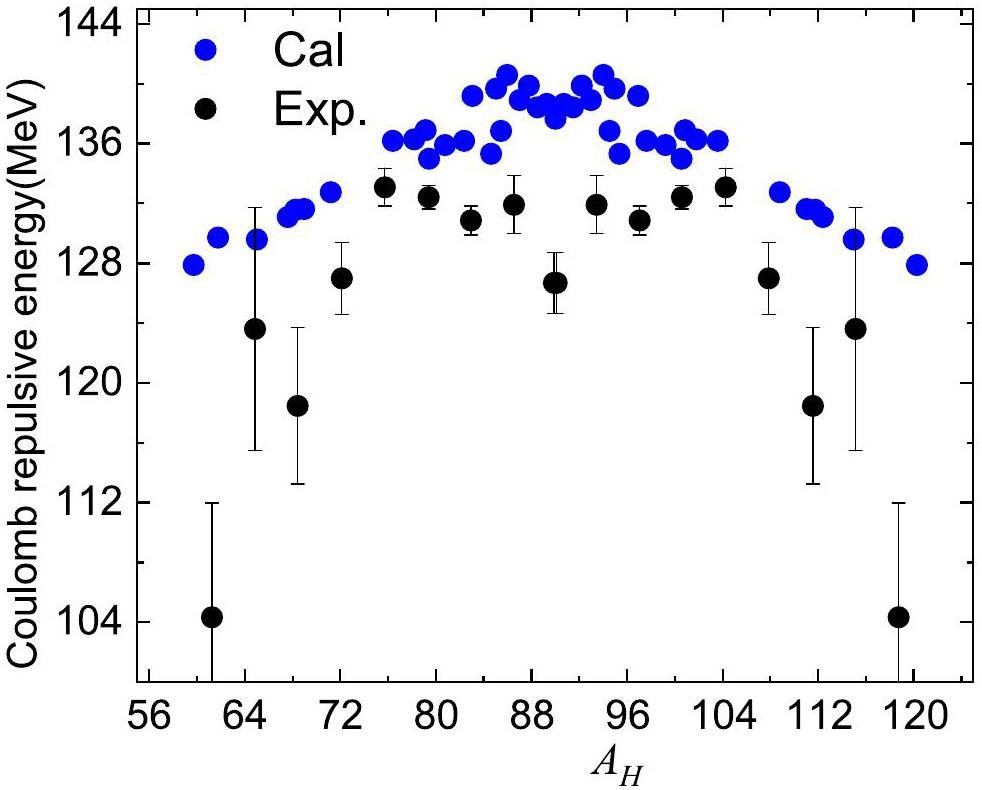
One of the most important quantities in induced fission is the total kinetic energy (TKE) carried out by the fission fragments. In this work, the total kinetic energy of the two separated fragments at scission point can be approximately estimated as the Coulomb repulsive interaction by using a simple formula $e^2{Z}_{\text{H}}{Z}_{\text{L}}/d_{\text{ch}}$, where e stands for the proton charge, Z_H and Z_L denote the charge numbers of the heavy and light fragments, respectively, and d_ch is the distance between the centers of charge of the two fragments at the scission point. Fig. 6 displays the distribution of the calculated Coulomb repulsive energy based on the scission line indicated by the purple circle in Fig. 1 and compared it with the measured TKE [2]. It can be seen that the calculated results reproduce the trend of the measured TKE quite well, especially a dip at A_H = 90 and peak at A_H = 94, although the calculated results are generally overestimated about several MeV compared to data, which might be caused by the neglect of the dissipation effect.

Fig. 6Full-screen View

(Color online) The calculated Coulomb repulsive energy of the nascent fission fragments for ¹⁸⁰Hg as functions of fragment mass, in comparison to the experimental data of the total kinetic energy [2]

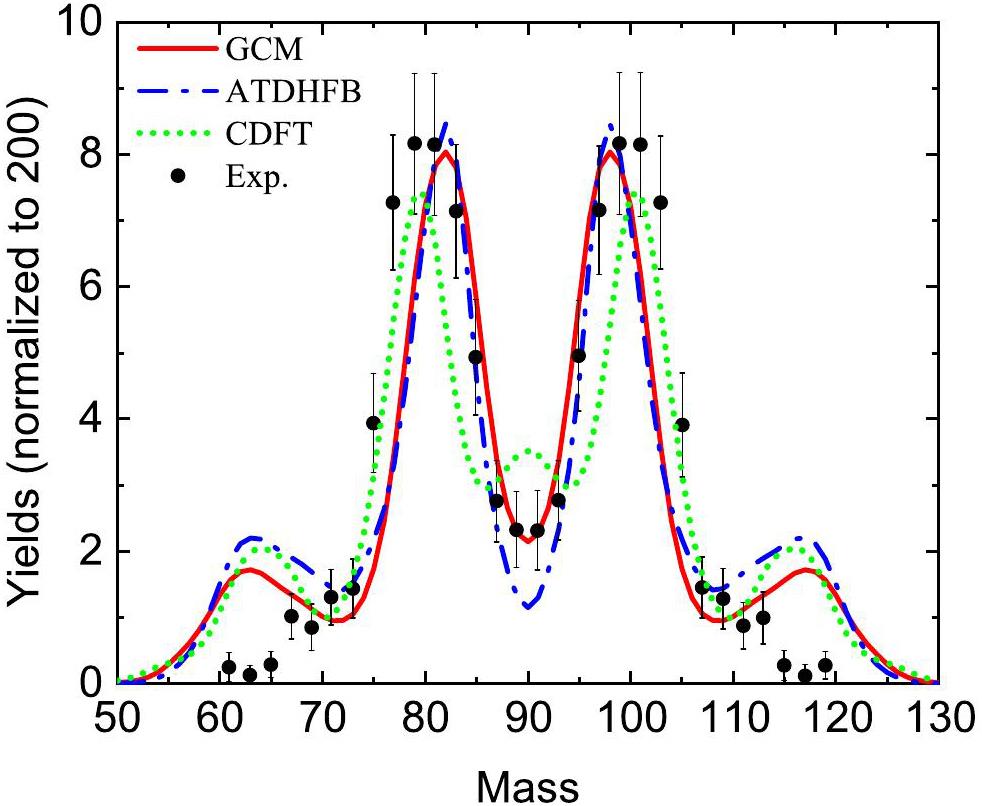
Finally, we performed TDGCM+GOA calculations to model the time evolution of the fission dynamics of ¹⁸⁰Hg. Figure 7 shows the calculated mass distributions of the fission fragments of ¹⁸⁰Hg compared with the experimental data [1, 2]. The theoretical results in the framework of covariant density functional theory (CDFT) using PES generated with the neck coordinate constraint qN from Ref. [9] are also given in the figure for comparison, denoted as “CDFT.” As one of the most important microscopic inputs of fission dynamic calculations, the mass tensor was calculated using the GCM or ATDHFB methods in the present work. The calculated mass distribution is generally similar when using the mass tensor by these two methods, and better agreement was obtained by using the GCM method for the height of asymmetric peaks and symmetric valleys. Overall, the calculations accurately reproduced the experimental data. The calculated peak position deviated by one unit from the experimental peak position. The results of CDFT show good asymmetric peak positions but overestimate the data and even predict a small peak for the symmetric valley. The deviation of the peak position from the data may have been caused by the mean-field potential. In the analysis of PES for ¹⁸⁰Hg in Ref. [7], it was found that the mass of the optimum fission fragment at the static scission point varies by two units when using either the Skyrme force or the Gogny force. In the dynamic calculation results, discrepancies were observed in the peak positions between the results based on skyrme-DFT and CDFT. The tail of fission fragment distribution is sensitive to the approximation of the mass tensor in dynamic calculations. The width of the distribution becomes slightly wider when the GCM mass tensor is used. Moreover, a more asymmetric fission mode with A_H ∼ 116–117 was predicted in both this work and the CDFT calculation. As explained in Ref. [9], this mode resulted from the use of the initial state with mixed angular momenta, whereas in the experiment, there were only certain values owing to the selection rule of electron capture of ¹⁸⁰Tl. In the current study, these discrepancies from the data still exist as the initial state with mixed angular momenta.

Fig. 7Full-screen View

(Color online) Mass distribution of the fission fragments of ¹⁸⁰Hg calculated by TDGCM method (lines), in comparison with the experimental data (circles) [1, 2]. The dash dot line and solid line stand for the calculation results with the ATDHFB mass tensor and GCM mass tensor respectively. The dotted line is the calculation result in the framework of CDFT with PC-PK1 functional with qN constraint from Ref. [9]

Summary

In this study, the static fission properties and fission dynamics of ¹⁸⁰Hg were investigated using Skyrme DFT and TDGCM, respectively. During the calculation of the multi-dimensional PES, it was found that the hexadecapole moment is crucial for obtaining a smooth PES and proper scission configurations; thus, it is essential for fission dynamic studies. For the calculation of PES with only the q₂₀ and q₃₀ constraints, nuclear rupture does not occur, even at a very large q₂₀. Through calculations with q₂₀, q₃₀ and q₄₀ constraints, it was found that a rather soft and flat minimum with a large hexadecapole moment still exists in the PES of ¹⁸⁰Hg even with a very elongated shape, which hinders the transition to the lower energy minimum with a smaller q₄₀. With the strategy of “perturbative” constraint of the collective freedom q₄₀, the transition to the minimum corresponding to the nuclear rupture could happen naturally, and thus reasonable scission configurations can be obtained. From these scission configurations, the estimated distribution of the TKE reproduced the trend of the experimental data.

Based on the static PES calculation, the asymmetric fission channel is favored in ¹⁸⁰Hg. Finally, the fission fragment yields were calculated using TDGCM. The calculated mass distributions also support asymmetric fission for ¹⁸⁰Hg. This calculation agrees well with the experimental data. Moreover, a more asymmetric peak with A_H ∼ 117 was predicted, which was also predicted by covariant DFT with the PC-PK1 parameter set [9].