Introduction

Nuclear reactions play a significant role in energy generation and the synthesis of elements in the universe [1]. H, He, and a small amount of Li were produced by primordial nucleosynthesis in the first few minutes after the Big Bang [2-4]. During the stellar burning phases, elements up to Fe are produced by a series of charged-particle-induced nuclear reactions [5, 6], and their reaction rates are commonly hindered by the small Coulomb barrier tunneling probability at astrophysical energies, which makes direct measurements at the Gamow window extremely challenging [7-10]. The activation method is an alternative approach to measure the cross-section by irradiating the target and determining the number of reaction product nuclei separately [11]. It involves the use of an accelerator mass spectrometer [12] for direct counting or a low background γ spectrometer for the decay γ-rays with a known branching ratio [13]. If the reaction product nuclei are radioactive and have a suitable half-life, the activation method with offline decay γ-ray detection provides a portable solution to avoid the difficulties encountered in online direct measurement.

A γ spectrometer with high detection efficiency and low background is essential for this purpose. A low background can be achieved by active and passive shielding of cosmic and laboratory γ-rays [14, 15]. A well-type HPGe detector has an almost 4π geometry when placing the radioactive sample in the well bottom, thus making it ideal for achieving high detection efficiency and energy resolution simultaneously [16, 17]. This is vital for the upcoming astrophysical reaction measurements of ${}^3\text{He}{\left(\alpha \mathrm{,}\gamma \right)}^7\text{Be}$ etc [17] at Jinping Underground Nuclear Astrophysics (JUNA) [19-24] via the activation method. However, the near 4π geometry of a well-type HPGe detector introduces a severe true coincidence summing (TCS) effect from cascade γ-rays [25, 26]; therefore, the measured γ spectrum must be deconvoluted for true full energy peak (FEP) statistics and intrinsic efficiency.

In this study, a low-background γ spectrometer called the Gamma spectrometer for Nuclear Activation Study (GNAS) was developed with a well-type HPGe detector and optimized multi-layer shielding with elaborately selected materials. A Monte Carlo simulation approach was applied to retrieve the intrinsic detection efficiency and correct for the TCS effect with a ¹³⁷Cs monoenergetic source and online-produced ^55,57,58Co sources. By simulating the HPGe detector response and comparing the simulated decay spectra with those measured from irradiated natural Fe samples, the intrinsic detection efficiency of the GNAS was obtained. An algorithm for the correction of the TCS effect was programmed using decay data from the ENSDF library and Nuclear Wallet Cards.

GNAS description

The GNAS is based on an ORTEC GWL series HPGe well-type detector with a low-background oxygen-free copper endcap and a high-purity aluminum well tube. The active volume of the germanium detector is 349 cm³, with a well 1.55 cm in diameter and 4.0 cm in depth. The detector is equipped with a low-background J-type cryostat and a remote preamplifier. Because it is near the 4π geometry for small radioactive samples, the detector has a high absolute counting efficiency for radiochemical analysis and low-level γ-ray spectroscopy.

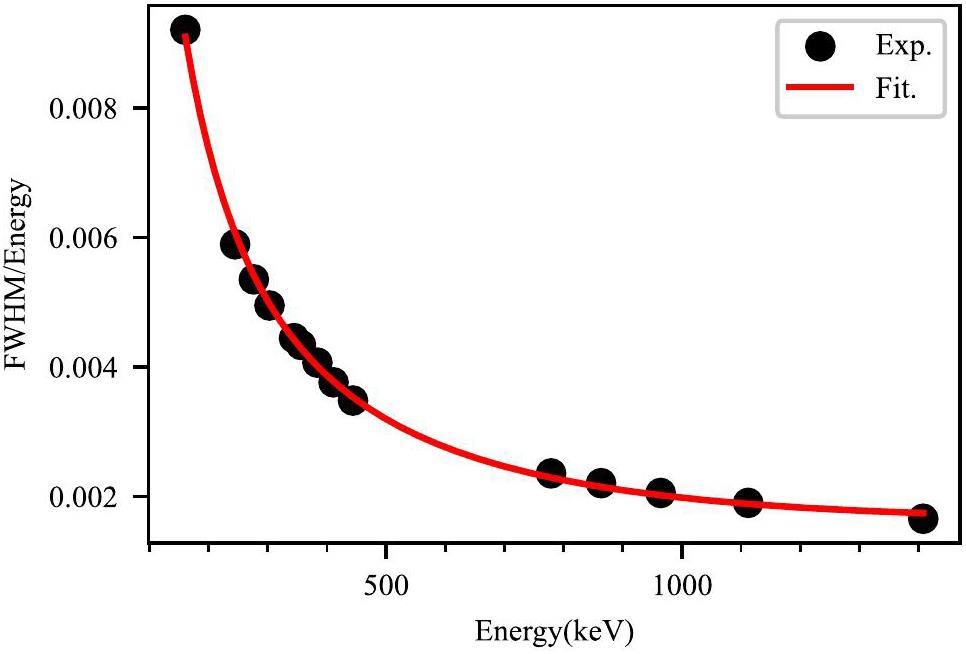
Figure 1 shows the energy resolution curve of the detector, defined as the ratio of the FWHM to γ energy, which was measured using a mixed γ radioactive source of ¹⁵²Eu and ¹³³Ba. The FWHM of the GNAS at 1408 KeV was 2.33 KeV, which is similar to that of other coaxial p-type HPGe detectors.

Fig. 1Full-screen View

(Color online) Energy resolution curve of the GNAS. The solid circles represent the experimental measurement, whereas the line is the fitting curve with a formula of $1.43/E+{4.35\times 10}^{-7}\cdot E+0.000113$ (E in keV)

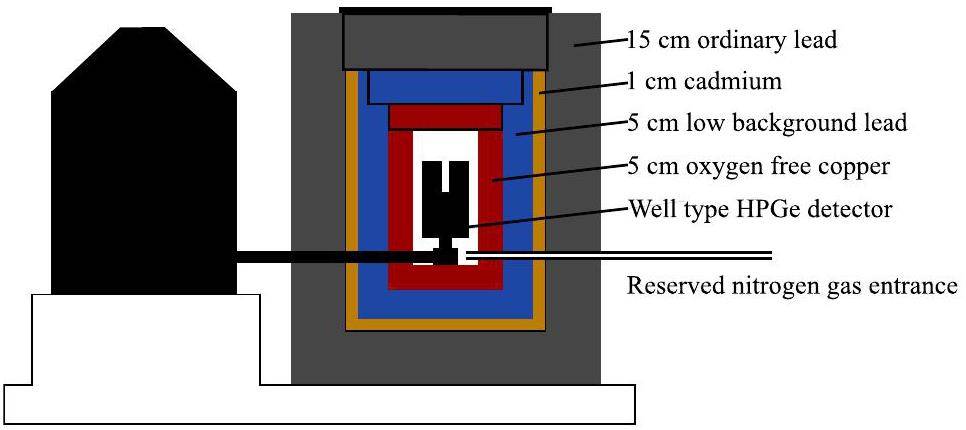
A schematic of the low-background γ spectrometer GNAS is shown in Fig. 2. The germanium detector is set in a chamber with a diameter of 12 cm and a height of 41 cm surrounded by 5 cm-thick high-purity oxygen-free copper. The copper layer is then enclosed by 5 cm-thick low background lead, 1 cm-thick cadmium, and 15 cm-thick ordinary lead. The cadmium layer is used to absorb the thermalized background neutrons [27]. The inner layer of the low-background lead and oxygen-free copper is used to shield the outside and secondary γ radiation from neutron absorption, respectively.

Fig. 2Full-screen View

(Color online) Schematic of the low-background γ spectrometer GNAS (not to scale)

The background γ counting rate spectra with and without shielding are shown in Fig. 3. With the multi-layer shielding structure of the GNAS, its background counting rate in the energy range 195–2910 KeV decreased from 185.74 counts per second (cps) to 0.89 cps, a reduction rate of approximately 99.5%.

Fig. 3Full-screen View

(Color online) GNAS background γ spectra with and without shielding

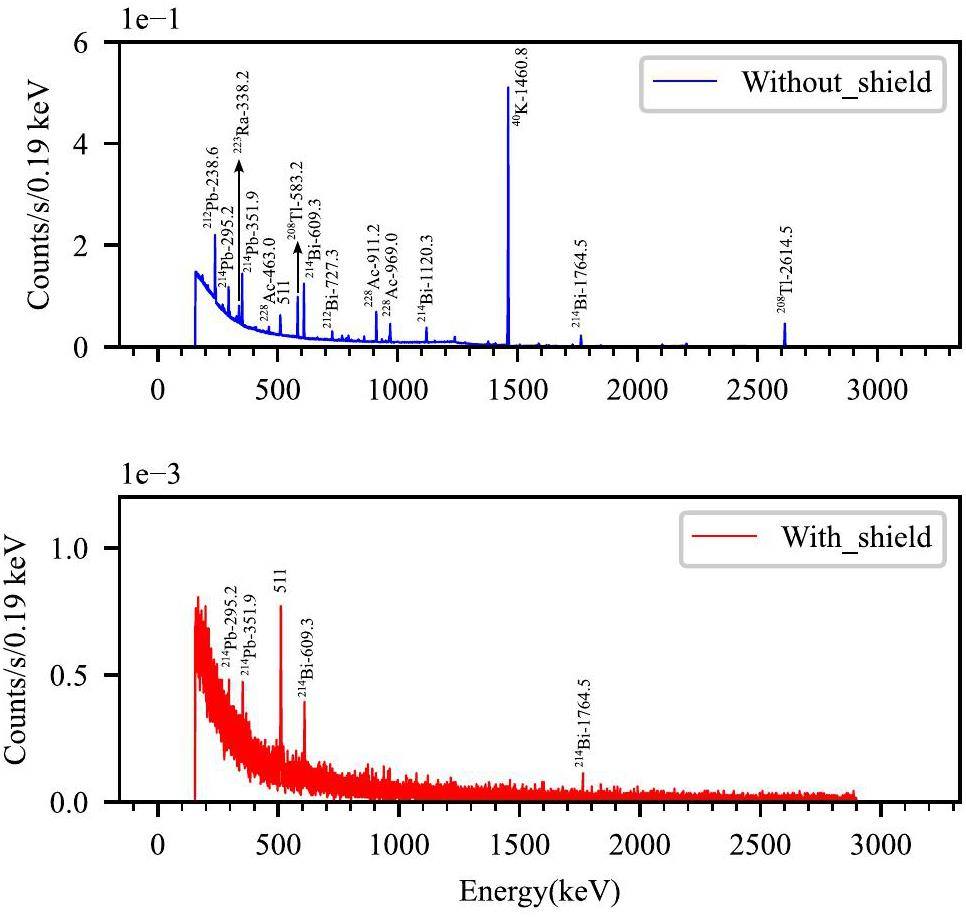
To measure offline the decay γ-rays from nuclear activation experiments, the energy range of interest for γ-rays typically does not exceed 3 MeV. In this energy range, the background γ spectrum is highly complex, as shown in Fig. 3. These γ-rays mainly originate from environmental radioactivity, including the natural radioactive series of ²³⁸U and ²³²Th, the single radionuclide ⁴⁰K, and the background neutron-induced series [28]. With the multi-layer shielding structure of the GNAS, most background γ lines were reduced to an unnoticeable level. The γ lines at 295.2 KeV and 351.9 KeV arose from ²¹⁴Pb, whereas those at 609.3 KeV and 1764.5 KeV arose from ²¹⁴Bi, which originated from shielding materials and radon in the air [28-30]. The γ line at 511 KeV originated from the annihilation of positrons produced mainly by the high-energy environmental γ-ray-induced pair production in the germanium crystal.

The peak counting rates of the background γ lines of ²¹⁴Pb and ²¹⁴Bi with and without the shielding are listed in Table 1.

It is planned that the GNAS will be used at JUNA for activation experiments; therefore, it will be necessary to introduce nitrogen gas into the HPGe detector room to remove the natural radon background.

The significant decrease in the background and the blind well design of HPGe enhanced the sensitivity of the GNAS. Several low-activity ⁷Be samples were prepared using the ${}^7\text{Li}{\left(\text{p}\mathrm{,}\text{n}\right)}^7\text{Be}$ reaction. The decay spectra of ⁷Be with different activities are shown in Fig. 4.

Fig. 4Full-screen View

(Color online) γ spectra from the decay of ⁷Be samples with different activities, 0.074 Bq in (a), and 0.044 Bq in (b). As an example of nuclear activation study, the ⁷Be activity was determined via GNAS measurement, as shown in (a), and via decay law evaluation, as shown in (b), when the remeasurement was performed

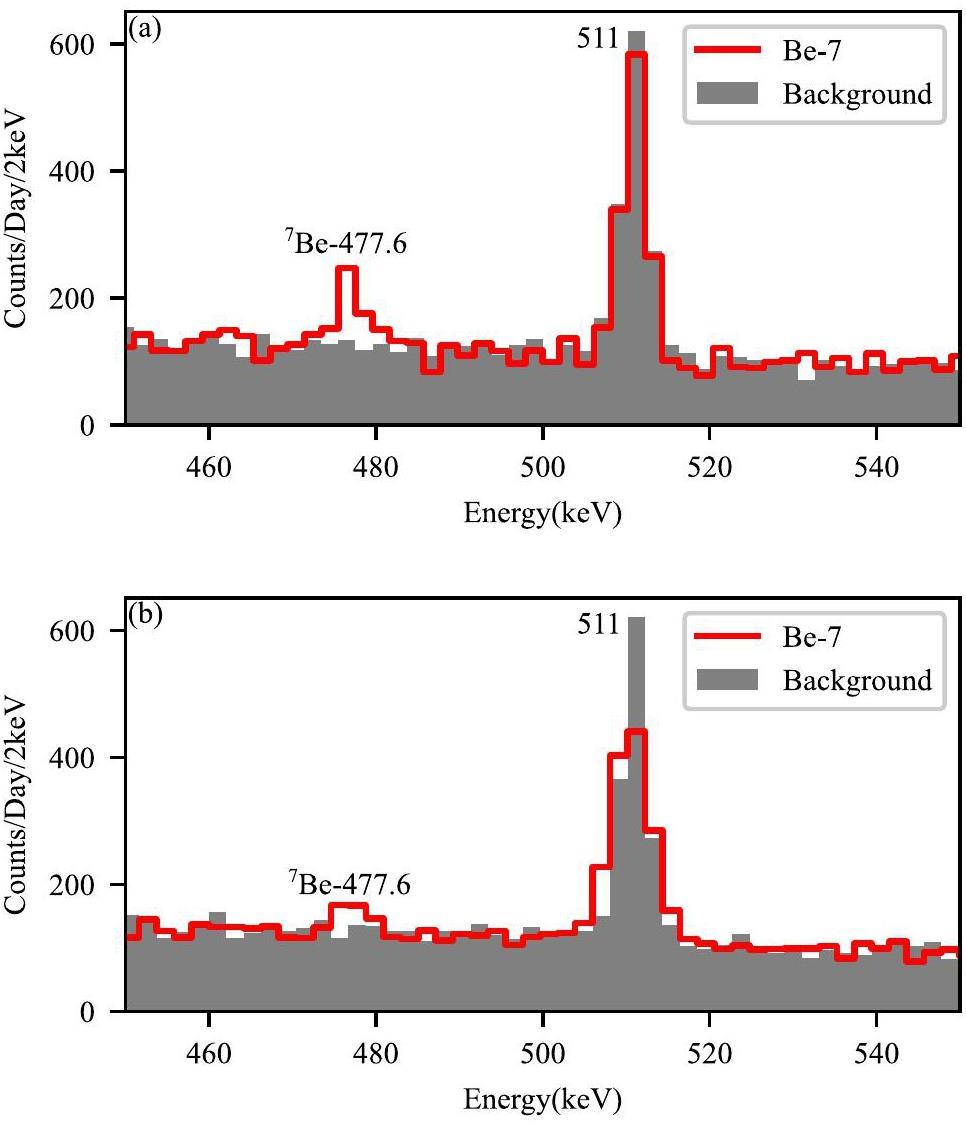
The counting rate of 477.6 keV γ-rays is 199(39) counts per day (cpd) in Fig. 4 and 94(47) cpd in Fig. 4b. For a sample with an activity as low as 0.044 Bq, which is less than 4.5 × 10^-3 s^-1 out of the emission rate of 477.6 KeV γ rays, the GNAS was still capable of distinguishing and evaluating its statistics, as shown in Fig. 4b.

True coincidence summing

The intrinsic FEP efficiency of a γ spectrometer is typically calculated using Eq. (1) and standard γ sources with known activities and γ branching ratios, $\begin{array}{l}\epsilon (E)=\frac{\lambda N(E)}{A(E)\cdot \eta (E)\cdot \left(1-{\text{e}}^{-\lambda t}\right)}\mathrm{,}\hfill \end{array}$ (1) where E is the energy of the decay γ, N(E) is the net area of the FEP, $A(E)$ is the activity of the source at the start of the measurement, η(E) is the branching ratio, λ is the decay constant, and t is the measurement time. Such a measurement should take place with the sources separated 20∼30 cm from the detector, which inevitably results in a low detection efficiency if a HPGe detector is used. However, the GNAS has high efficiency from the near 4π geometry; therefore, the TCS effect must be well resolved. When two or more γ-rays deposit their energies within the resolving time of the HPGe detector, the detector records them as one γ line with summed energy [26, 31]. This effect is particularly significant for cascade γ-rays emitted sequentially from the same nucleus. When TCS occurs, the FEP statistics are shifted, and the correction of TCS depends on the decay scheme of the individual radioactive nuclei. Even the γ spectra of most standard sources need to be deconvolved; therefore, an algorithm must be developed to determine the intrinsic detection efficiency of the GNAS and the correction for TCS.

For two cascade γ-rays, there are three types of TCS: (1) both γ-rays deposit their full energies in the active volume of the HPGe detector; (2) one γ-ray deposits its full energy, whereas the other deposits only part of its energy; and (3) both γ-rays deposit only part of their energies. The first two types of summing events can significantly deflect the FEP statistics in the γ spectrum, which is represented by N(E) in Eq. (1). The third type of summing event contributes only to the Compton plateau in the spectrum, which is not directly attributed to the statistics of the FEPs.

3.1

Correction for TCS

Numerical methods have been developed to correct for TCS effects in γ-ray spectroscopy [32-35]. In recent years, Monte Carlo simulations have been intensively used to determine the detection efficiency and TCS correction of various customized γ spectrometers [36-39]. The ideal method for determining the intrinsic FEP efficiency of the GNAS is through a set of weak monoenergetic γ-ray sources [40-42], which in turn helps to determine the dimensional parameters of the HPGe detector for the simulation. For this purpose, a right-sized ¹³⁷Cs source with an activity of only 601 Bq was fabricated. Because we did not have other weak monoenergetic γ-ray sources, several natural Fe targets were irradiated using a 4 MeV proton beam from the HI-13 tandem accelerator, and the activities of ⁵⁵Co, ⁵⁷Co, and ⁵⁸Co were subsequently calibrated using a standard γ spectrometer [43]. Based on these γ sources, we developed a Monte Carlo simulation method using the Geant4 toolkit.

The primary task of the simulation was to determine the dimensional parameters of the well-type HPGe detector, with which the intrinsic FEP efficiency ε_inc could be directly simulated at the user-set γ-ray energies. The next step was to simulate real radioactive decay to correct the TCS effect numerically.

With Geant4, decay data can be generated from the G4RadioactiveDecayPhysics module based on the ENSDF library and Nuclear Wallet Cards. The G4EmLowEPPhysics package is used to describe low-energy polarized X/γ-ray transport [44]. A ⁵⁵Co decay event at the bottom of the well and its interactions with the germanium crystal are schematically shown in Fig. 5. The emitted positron annihilated into two 511 keV γ-rays, whereas the ⁵⁵Fe daughter nucleus deexcited by single or cascaded γ lines. The energy deposited in the detector by each decay was treated as a single signal; therefore, these γ-rays may partly or totally sum into a single γ line.

Fig. 5Full-screen View

(Color online) Schematic description of a ⁵⁵Co decay event and its interactions with the germanium crystal (shielding layers are hidden; not to scale)

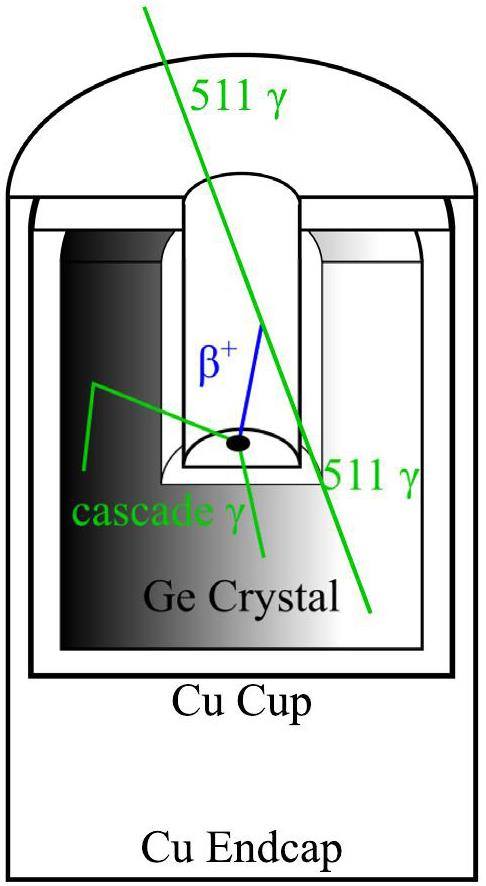
The HPGe dimensions provided by the manufacturer were optimized [40, 45] to reproduce the known activities of the ^55,57,58Co spectrum, as listed in Table 2.

Table 2Full-screen View

Manufacturer-provided and optimized HPGe dimensions

Detector parameters	Manufacturer	Optimized
Crystal diameter	79.3 mm	79.3 mm
Crystal length	77 mm	79.5 mm
Dead layer thickness	0.3 μm	0.6 μm
Endcap thickness	-	0.8 mm
Endcap-to-crystal distance	-	10.3 mm
Well tube thickness	1 mm	0.65 mm
Well tube inner diameter	15.5 mm	15.5 mm
Well tube active depth	40 mm	40 mm
Coaxial hole diameter	-	33.34 mm
Coaxial hole depth	-	50 mm

Show more

The dead layer and well tube thicknesses were found to significantly affect the efficiency in the low-energy region because of the absorption of γ lines. The dimensions of the crystals also affected the efficiency, owing to the solid angle and crystal thickness difference.

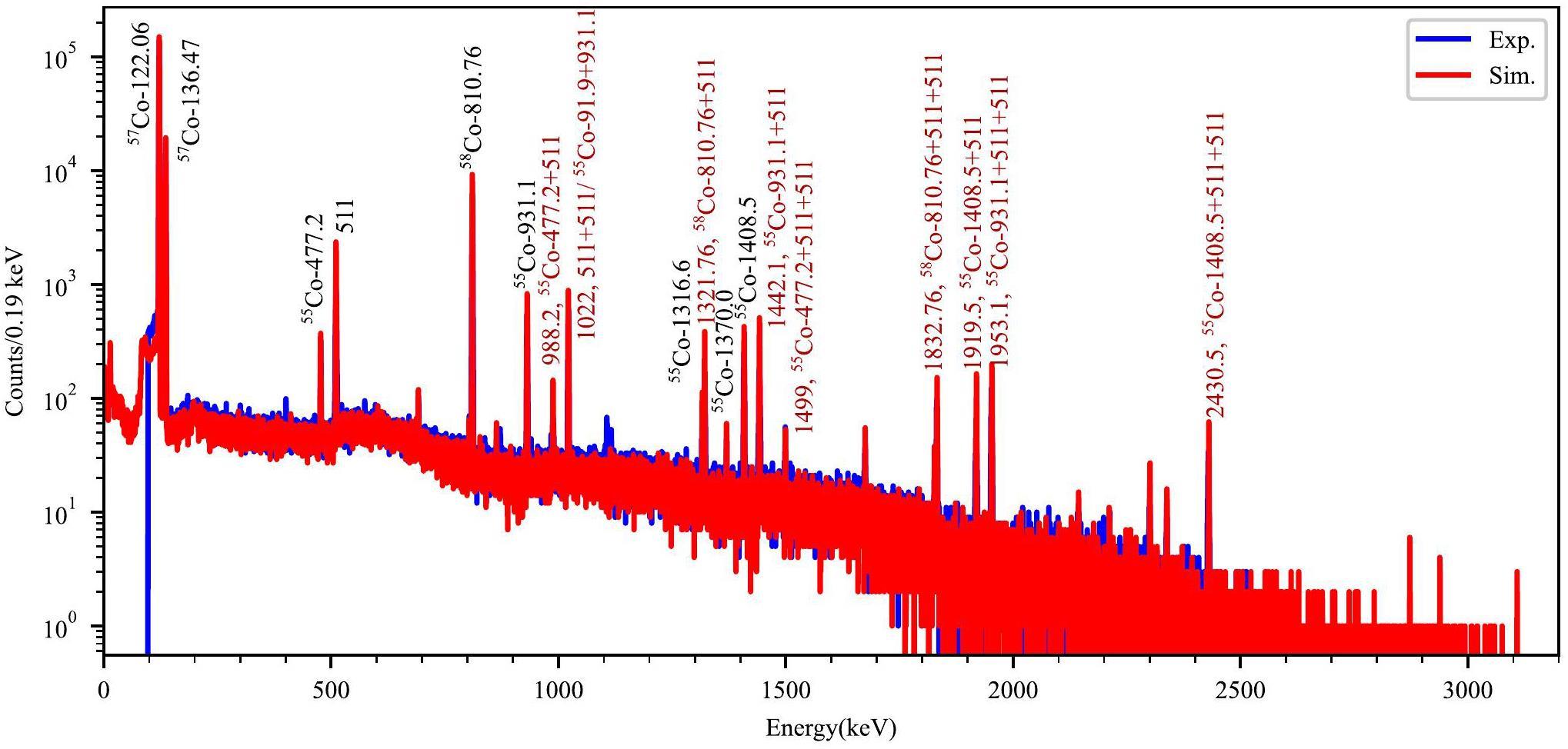
The dead layer and well tube thicknesses were preliminarily optimized to constrain the deviation between the simulated and experimental ¹³⁷Cs statistics to within 10%. Subsequently, most parameters were varied in small steps and eventually constrained by the experimental spectra of the ^55,57,58Co source to obtain the optimized values. For example, the simulated γ spectrum containing the calibrated ^55,57,58Co activities was compared with the measured spectrum, as shown in Fig. 6. All FEPs and summing peaks were accurately reproduced in the simulation. For instance, the 1321.76 keV and 1832.76 keV γ-ray peaks, which were the summing peaks of 810.76 keV and one or two 511 keV γ-rays from ⁵⁸Co, were well reproduced.

Fig. 6Full-screen View

(Color online) Simulated and measured spectra of an irradiated sample containing calibrated ⁵⁵Co, ⁵⁷Co, and ⁵⁸Co activities. Peaks from TCS are marked in red. All the FEPs and summing peaks are well reproduced in the simulation

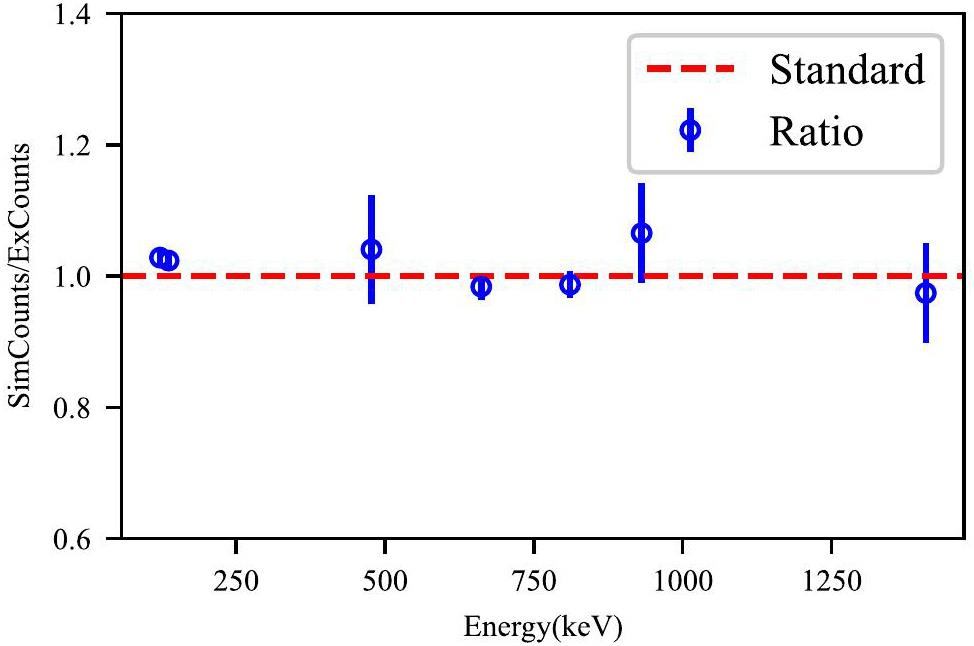
To evaluate the simulation uncertainty of the detector parameter optimization, the ratios of the simulated and experimental γ FEP areas for the ¹³⁷Cs and ^55,57,58Co sources are shown in Fig. 7. Most of the simulated FEP areas agreed with the experimental areas within a 5% margin of error. The γ lines with large deviations were mainly due to weak activities and uncertainties in the calibrated activity value. To reduce the uncertainty, a ⁶⁵Zn ($t_{1/2}=244.26\text{d}$) source with near 1115.6 keV monoenergetic γ radioactivity will be produced at the HI-13 tandem accelerator using the ${}^{65}\text{Cu}{\left(\text{p}\mathrm{,}\text{n}\right)}^{65}\text{Zn}$ reaction.

Fig. 7Full-screen View

(Color online) Ratio of the simulated and experimental γ FEP areas for the ¹³⁷Cs and ^55,57,58Co sources. The error bars are from the uncertainties of the relevant γ-ray FEP statistics and calibrated activity value

3.2

Intrinsic efficiency and TCS correction factor

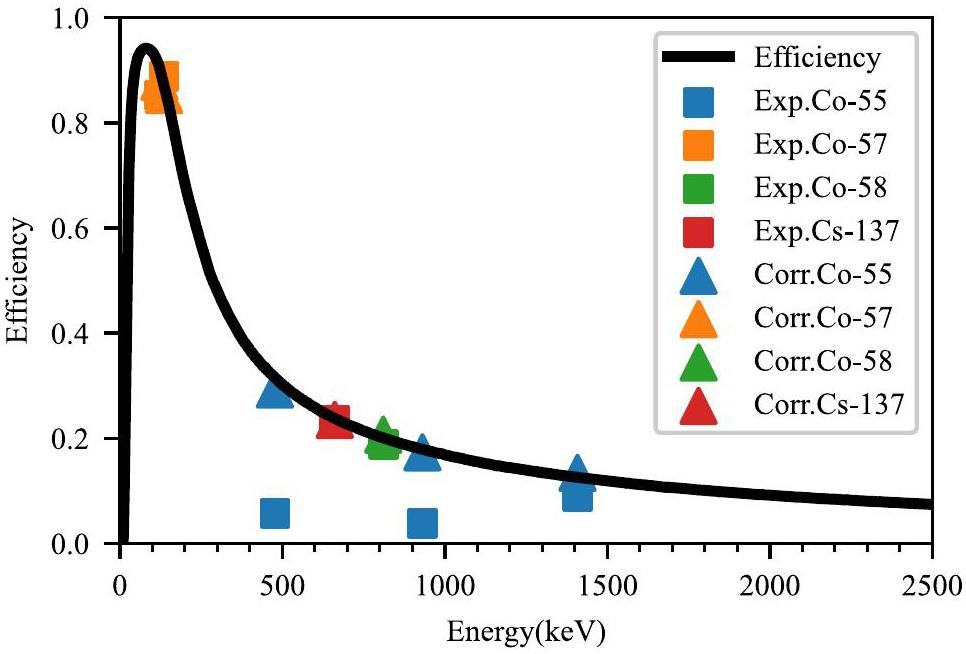
Using the optimized detector model, we calculated the intrinsic FEP efficiency of the GNAS using different energy steps of Geant4 simulations. The resulting efficiency curve is presented in Fig. 8. To illustrate the impact of TCS, the specific energy points from ¹³⁷Cs and ^55,57,58Co are marked. These points represent the efficiencies obtained directly from the measured FEP statistics according to Eq. 1 with and without correction for the TCS effect.

Fig. 8Full-screen View

(Color online) Intrinsic efficiency curve of the GNAS. Several energy points from ¹³⁷Cs and ^55,57,58Co with and without correction for TCS are marked. ⁵⁷Co can be regarded as a quasi-monoenergetic source without a γ cascade and 511 keV γ-rays from β⁺ decay, whereas ⁵⁵Co suffers heavy TCS owing to significant cascade γ-rays

If we define a TCS correction factor as the ratio of the intrinsic FEP efficiency ε_inc to that without correcting for TCS ε_nc, $\begin{array}{l}{F}_{\text{TCS}}=\frac{{\epsilon }_{\text{inc}}}{{\epsilon }_{\text{nc}}}\mathrm{,}\hfill \end{array}$ (2) where ε_inc can be simulated using the user-set γ-ray energy, and ε_nc can be calculated from the simulation spectra, such as that shown in Fig. 6.

Detailed data are presented in Table 3, which lists the measured and simulated uncorrected FEP efficiencies as well as the TCS correction factor and intrinsic FEP efficiencies after TCS corrections. For certain γ-ray peaks, such as the 477.2 keV and 931.1 keV lines from ⁵⁵Co, the TCS effect was particularly pronounced because of the cascade γ decay and high efficiency of the detector.

Table 3Full-screen View

Measured (ε_exp) and simulated (ε_sim) uncorrected FEP efficiencies, TCS correction factor (F_TCS), and FEP efficiencies (ε_inc) after TCS corrections

Nuclide	Eγ (keV)	εexp	εsim	FTCS	εinc
137Cs	661.6	0.235(1)	0.235(1)	1	0.235(1)
55Co	477.2	0.057(3)	0.061(6)	5.1(5)	0.3153(6)
	931.1	0.039(2)	0.039(4)	4.5(5)	0.1788(4)
	1408.5	0.089(5)	0.083(8)	1.5(1)	0.1260(4)
57Co	122.1	0.852(10)	0.879(16)	1.03(2)	0.9063(10)
	136.5	0.889(11)	0.913(17)	0.96(2)	0.8745(9)
58Co	810.8	0.188(3)	0.182(5)	1.10(3)	0.2007(4)

Show more

For activation measurements in nuclear astrophysics at JUNA, when the produced radioactive nuclei decay through cascade γ-rays, TCS evidently deflects the real FEP statistics. With the newly developed Monte Carlo method, one can simulate the TCS correction factor by simply changing the decay nucleus together with the well-determined intrinsic detection efficiency curve of the GNAS.

Summary

A low-background γ spectrometer (GNAS) was installed for activation measurements within nuclear astrophysics. Using a multi-layer shielding structure, a background reduction of 99.5% was achieved, which enabled the detection edge of a low activity of 10^-2 Bq with a high-efficiency well-type HPGe. A Monte Carlo simulation approach using Geant4 was developed to address the TCS effect. The optimized detector model ensured a good agreement between the simulated and experimental spectra. The intrinsic efficiency curve was determined, and the algorithm for TCS correction was programed using decay data from the ENSDF library and Nuclear Wallet Cards. The GNAS fulfills the requirements of the ongoing activation measurement of proton- and alpha-induced reactions in nuclear astrophysics on the ground and at the JUNA facility.