Atmospheric-pressure ion transfer in a gas flow device connected to the UniCell buffer gas cell for superheavy elements chemistry: simulation studies

NUCLEAR ELECTRONICS AND INSTRUMENTATION

Atmospheric-pressure ion transfer in a gas flow device connected to the UniCell buffer gas cell for superheavy elements chemistry: simulation studies

Yeqiang Wei，

Alexander Yakushev，

Jochen Ballof，

Jörg Krier，

Christoph E. Düllmann

Nuclear Science and Techniques

Vol.36, No.10

Article number 187

Published in print Oct 2025

Available online 19 Jul 2025

DOI：10.1007/s41365-025-01772-7

CSTR：32136.14.NST.2025.10187

11400

Man-made superheavy elements (SHE) are produced as energetic recoils in complete fusion reactions and need to be thermalized in a gas-filled chamber for chemical studies. The ever-shorter half-lives and decreasing production rates of the elements beyond Fl (atomic number Z = 114) – the heaviest element chemically studied today – require the development of novel techniques for quantitative thermalization and fast extraction efficiently. The Universal high-density gas stopping Cell (UniCell), currently under construction, was proposed to achieve this. Within this work, we propose an Ion Transfer by Gas Flow (ITGF) device, which serves as a UniCell ejector to interface with a gas chromatography detector array for chemical studies. Detailed parameter optimizations, using gas dynamics and Monte Carlo ion-trajectory simulations, promise fast (within a few ms) and highly efficient (up to 100%) ion extraction across a wide mass range. These ions can then be transmitted quantitatively through the ITGF into the high-pressure environment needed for further chemical studies.

Superheavy elementsBuffer gas cellIon funnelFast extractionAtmospheric-PressureChemical studies

Introduction

Superheavy elements with an atomic number Z higher than 103 follow the actinide series in the periodic table. Investigations of these elements are crucial in the field of nuclear physics and chemistry [1], e.g., to elucidate the influence of relativistic effects on their chemical properties. Due to the low production rates and short nuclear lifetimes of superheavy elements, our knowledge of their properties is limited. Nonetheless, the quest for discovery and understanding of these elusive elements remains a fascinating and challenging area of current research [2]. However, the inability of existing chemistry-setups to efficiently capture and study shorter-lived isotopes limits further progress in SHE research. Addressing this bottleneck is essential for advancing our understanding of SHE chemistry and physics. In typical SHE study setups, the products of complete fusion reactions are either directly implanted into a detector installed at the focal plane of a physical recoil separator (see, e.g., [3] for a current setup at the TASCA separator at GSI) for radioactive decay measurements or are extracted through a vacuum window into a gas stopping cell, where they are decelerated in a series of collisions with the buffer gas atoms. There are two main classes of such setups: Buffer Gas Cells (BGC) [4] and Recoil Transfer Chambers (RTC) [5], differentiated by the presence or absence of guiding electrical fields.

Chemical studies of superheavy elements [6] often probe the interaction strength of a single atom or molecule with a solid, ideally well-defined surface. To meet strict efficiency requirements, detector arrays like the Cryo-Online Multidetector for Physics and Chemistry of Transactinides (COMPACT) [7, 8] have been developed. These arrays feature detector diodes coated with materials such as gold or silicon dioxide. Two detector arrays are connected together to form a gas-tight enclosure, which is at the same time a chromatography channel for introducing superheavy elements with a carrier gas. For chemical studies, a relatively fast and efficient stopping and extraction of energetic residues from heavy-ion fusion reactions into the aforementioned chemistry setup was typically achieved using RTCs, which rely solely on gas flow extraction. RTCs have been widely used in experiments with elements up to ¹¹⁴Fl [9] and provide high efficiency for chemically non-reactive volatile species [10]. However, it usually takes almost one second to extract 50% of the recoils, even in advanced RTCs [11]. This extraction time significantly exceeds the half-lives [12] of all known isotopes of elements beyond ¹¹⁵Mc and also of the most accessible Mc isotope, ²⁸⁸Mc, and thus prohibits their efficient chemical study. Decades ago, the Ion-Guide Isotope Separation On-Line (IGISOL) technique demonstrated that the swift transport of ions of any element can be achieved by preserving the recoil ion charge and manipulating it with electric fields [13, 14]. A variety of BGCs have since been developed [15] to enable fast and efficient extraction of ions. Different kinds of BGCs find many applications for the thermalization of fast multi-charged ions and their extraction as secondary ion beams [16-21], as well as for studies of the heaviest elements [22-24]. First on-line chemistry studies with accelerator-produced radionuclides extracted from a BGC have recently demonstrated the feasibility of this approach [25]. The achieved extraction time of 55(4) ms would be fast enough for efficient studies of ¹¹⁵Mc, ¹¹⁶Lv, and ¹¹⁷Ts with currently known isotopes. For each of these elements, at least one isotope with a half-life of at least around 50 ms is known. In offline studies, the extraction efficiency was 35(3)% [26] due to the rather low maximum gas pressure of this BGC, which provided insufficient stopping power to thermalize ions across the whole kinetic energy range behind the entrance vacuum window. To overcome the limited stopping power and provide even faster extraction times, a novel concept of high-pressure Universal high-density gas stopping Cell (UniCell) was proposed by Varentsov and Yakushev in Ref. [27]. Therein, initial simulation studies suggested that extraction times as short as 2 ms could be achieved. The article also included a concept of an interface (RF-ejector) to guide ions emerging from UniCell to a downstream COMPACT detection setup at ambient pressure by means of an electric field. However, computational simulations of the RF-ejector have not yet been reported.

In this paper, we expand on the previous work. Besides further detailed optimizations on UniCell, we explored solutions, complementary to the RF-driven ejector interface, which might electromagnetically interfere with the detector setup. Notably, we suggest the Ion Transfer by Gas Flow (ITGF) device. Its carefully designed geometry prevents ions, even in the absence of electric fields, from encountering the wall and aims at unity efficiency while retaining fast extraction time. Together with the optimized UniCell, this approach represents a significant step toward overcoming the current limitations in SHE research. In Sect. 2, we present gas-dynamic and Monte-Carlo ion trajectory simulations to optimize the UniCell setup for efficient ion extraction and define the source of ions for the subsequent ITGF simulations, which are provided in Sect. 3. In Sect. 4, conclusions and an outlook are given.

UniCell

2.1

UniCell setup

The UniCell setup and working principle were first presented in Ref. [27]. For the convenience of the reader, a brief summary is provided within this section, along with the implemented modifications and the geometry used in simulations. An overview of the setup is sketched in Fig. 1. The main components of UniCell include a direct current (DC) cage and an atmospheric pressure ion funnel, to which a DC gradient and a specific radio-frequency (RF) signal at first appearance are applied. The sophisticated ion funnel, which poses the biggest engineering challenge, has meanwhile been built and undergoes electrical testing. The remainder of the setup is under construction. Energetic ions enter the DC cage through a vacuum window and are thermalized in helium gas at ambient temperature and pressure. The DC gradient guides the ions through the DC cage and funnel. Subsequently, they enter the ITGF and reach the defined COMPACT detector. The DC cage consists of 7 cylindrical electrodes, each with a length of 8 mm and an inner radius of 35 mm. Considering the distance between neighboring ring electrodes of 2 mm, the total length of the DC cage is 70 mm. The ion funnel was fabricated from 352 stacked zirconia sheets with a thickness of w = s = 0.1 mm (see Fig. 2) each. On every second plate, a 10 μm-thick gold ring, produced by the sintering of gold nanoparticles and surrounding the circular opening in the center, serves as an electrode. The intermediate zirconia sheets ensure electrical insulation. A circular cut-out in the center gradually decreases from a maximum diameter of d_max = 70 mm to a minimum of d_min = 0.3 mm. The thin window is mounted on a supporting grid and connected to the ground. The potential of the grid electrode behind the window (see Fig. 2) is the same as that of the first electrode in the DC cage; both are set to a high voltage (e.g., V_dc = 1010.5 V) for the case when the DC gradient is equal to 100 V cm^-1. The schematic of the electronic layout and of the supply of the cage and the funnel by DC and RF power are shown in Fig. 2.

Fig. 1

(Color online) The schematic of the UniCell setup for the study of chemical properties of superheavy elements. Isotopes of interest are separated in a physical recoil separator and enter the UniCell through the thin window and grid electrode (A). A direct-current cage (B) and a direct-current + radiofrequency-based funnel (C) form the core components of the UniCell. Ions emerging from UniCell enter the Ion Transfer by Gas Flow (ITGF) device, which is connected to the entrance of, e.g., a miniCOMPACT detector array (D). P₁ = 1 bar and T = 300 K are the background gas pressure and temperature in the UniCell, and P₂ is the gas pressure in the ITGF

Fig. 2

The schematic of the electronic layout of the UniCell

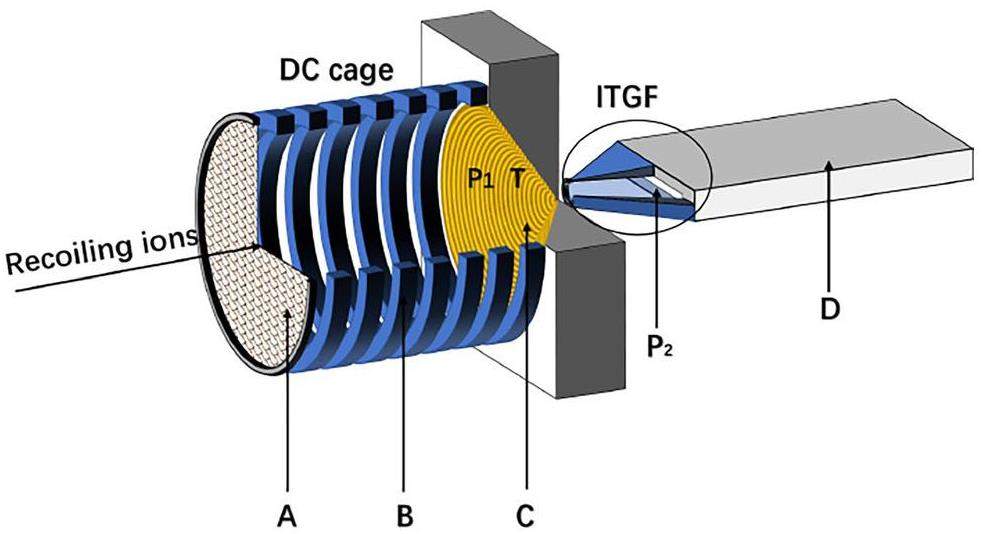
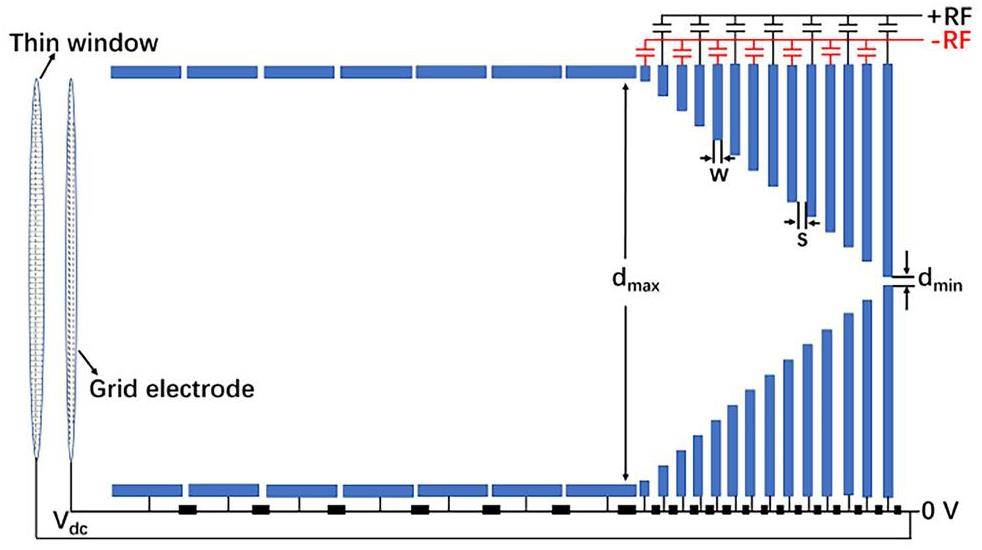
To prevent ions from striking the funnel surface, a 180° phase-shifted RF signal is applied between adjacent electrodes. The resulting electric force F_RF [15] in the vicinity of the electrodes repels ions and is given by $F_{RF} = m K^{2} \frac{V_{pp}^{2}}{4 r^{3}},$ (1) here, m is the mass of the ion, V_pp the RF peak-to-peak voltage, r half of the electrode spacing, and K the ion mobility, which can be conveniently expressed via its temperature and pressure dependence as $K = K_{0} \frac{T}{T_{0}} \frac{P_{0}}{P},$ (2) with $K_{0} = \frac{3 q}{16 N} \sqrt{\frac{2 π}{μ k_{b} T_{0}}} \frac{1}{Ω},$ (3) where K₀ is the reduced ion mobility, T₀=273.15 K, P₀=1.01325 bar, q the ion charge, N the buffer gas number density, μ the reduced mass of the ion and buffer gas, $k_{b}$ the Boltzmann constant, T the buffer gas temperature, P the buffer gas pressure and Ω the collision cross-section between the ion and the buffer gas molecules. According to Eqs. (1) and (2), the ion mobility scales with the inverse of the gas pressure, and the repelling force scales with the inverse square of the gas pressure. Relatively high values of the DC gradient are required for short extraction times from a high-pressure BGC. The DC ion driving force has to be compensated by a strong repelling RF force F_RF. Thus, the construction of highly effective RF-repelling electrode structures is required and poses an engineering challenge. A high RF peak-to-peak voltage V_pp and narrow electrode spacing are required to create a sufficiently strong repelling force. According to Eq. (1), reducing the electrode spacing distance of 1 mm, which is common for many BGCs, by a factor of 10 increases the repelling force F_RF by a factor of 10³. In addition, the breakdown voltage needs to be considered for elevated V_pp values. Preliminary investigations by Verentsov and Yakushev [27] suggest that an RF peak-to-peak voltage of 200 V is sufficient and well below the breakdown limit of the envisaged configuration. An electrode distance of 0.1 mm was proposed to obtain a sufficient repulsive force, thereby significantly increasing the extraction efficiency of the ions of interest [27]. This promising configuration of the high-density gas cell with a dense electrode spacing of 0.1 mm was chosen for the fabrication of the first prototype of the ceramic RF funnel (Fig. 3).

Fig. 3

(Color online) First prototype of the UniCell RF funnel was produced at the Functional Materials Center of the Łukasiewicz Instytut Mikroelektroniki i Fotoniki, Poland

2.2

Ion stopping range

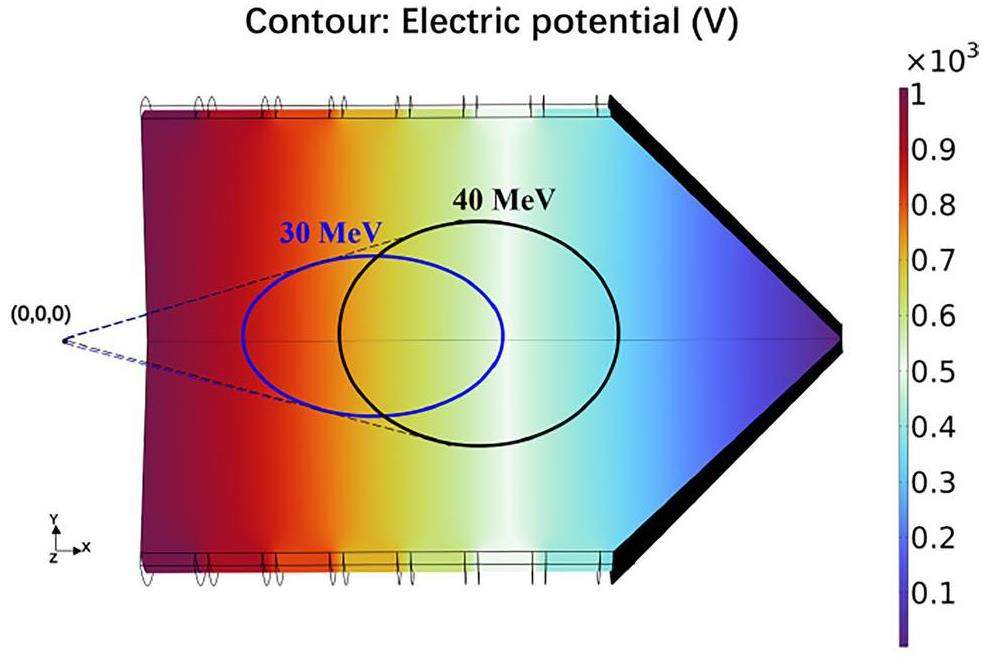
Ions are thermalized by collisions with the buffer gas within the DC cage after travelling through a thin window. SRIM [28] was used to estimate their stopping range. In this work, we estimated the stopping range of the ions of ²⁹³Lv and ²⁹³Ts; their kinetic energy after production by the ⁴⁸Ca-induced fusion reactions [29] and their separation in a gas-filled recoil separator ranges between 30 MeV and 40 MeV. In simulations with SRIM, the atomic number is limited to 92 (i.e., uranium). To assess the range of the heavier ions of interest, we used uranium with a mass of 293 in the SRIM simulation and applied the energy conversion outlined in Ref. [30]. The window material was selected to be Mylar with a thickness of 3.5 μm. Reference [31] shows an estimation of the ion stopping range simulated by SRIM. Within this work, the primary focus is on the effectiveness of the DC cage’s longitudinal length in stopping recoil ions. Ions from the TASCA separator have the highest probability to originate from the central axis, while the exact radial image size depends on the separator settings. Therefore, the ion stopping range simulations are based on all ions emerging from a point source (coordinate zero, cf. Fig. 4). In our case, simulations for 30 - 40 MeV ions traveling through a thin window predict stopping within the DC cage, with their final depth distribution also following a Gaussian shape. Through simulations, for 30 MeV ions, the ions’ longitudinal (x-axis) stopping range within 5σ (standard deviation) is calculated to be between +8.75 mm and +34.35 mm, and the lateral projected range along the y-axis is between -9.81 mm and +9.69 mm, as illustrated in Fig. 4 (blue circle). For 40 MeV ions, the ions’ longitudinal (x-axis) stopping range within 5σ is in the range from +21.45 mm to +46.35 mm, and the lateral range along the y-axis is in the range from -10.82 mm to +10.98 mm, as shown in Fig. 4 (black circle). The simulation results confirm that the envisaged length of the DC cage (70 mm) is expected to be sufficient to thermalize all ions of interest.

Fig. 4

(Color online) Simulated electric potential distribution and simulated stopping range for recoiling ions emerging from the indicated coordinate origin (0, 0, 0) with an energy of 30 MeV (blue oval) and 40 MeV (black oval)

2.3

Extraction efficiency for UniCell

COMSOL Multiphysics version 6.1 [32] is a commercial finite element package that allows users to build complex models in an advanced graphical user interface. Further advantages of COMSOL are its ability to couple different physical effects in the same model and the comprehensive built-in library of meshing tools, numerical solvers and post-processing tools. It includes the AC/DC Module and the Particle Tracing Module, where the “Electrostatics” and “Laminar Flow” interfaces are used to evaluate the electric potential distribution and gas dynamics within the UniCell. The electrical potential distribution obtained in our simulation is shown in Fig. 4. For the average DC field strength of 100 V cm^-1, the potential difference between adjacent electrodes was 100 V in the DC cage and 2 V in the funnel. At a mean flow rate of 10 mbar L s^-1, the maximum gas flow velocity, which occurs near the nozzle, was calculated to be about 227 m/s. As will be discussed in the following Sect. 3, the gas flow velocity in other locations in UniCell is negligible compared to the ion velocity resulting from electric forces. Thus, the simulation is based on the precondition that the buffer gas within the UniCell volume is considered stationary.

The trajectory simulation of ions with 40 MeV initial energy moving in the DC + RF field was performed using SIMION 8.2.0.11 [33], where the final positions obtained from the SRIM simulation were used as the initial positions for SIMION simulations. The size of the grid elements used in our model is 0.01 mm, which is sufficiently small for the electrodes. The following parameters were commonly used for all simulations: helium gas pressure P₁=1 bar, gas cell temperature T=300 K, ion mass M=293 u, and RF frequency f = 5 MHz. The mutual Coulomb repulsion among ions is neglected due to the low production rate of superheavy elements and byproducts entering UniCell, which leads to negligible ion density. The statistical diffusion simulation (SDS) model was used to efficiently simulate the high-pressure atmosphere. The SDS model utilizes a combination of a viscous Stokes’ law drag force and a superimposed diffusion effect [34]. The reduced ion mobility in helium was assumed to be K₀=17.37 cm²V^-1s^-1 [35].

Simulations were performed within a range of the DC field strengths between 30 V cm^-1 and 260 V cm^-1. Ions are typically extracted from BGCs in a charge state of 1+ or 2+ [36]. In each simulation, the trajectories of 100 ions were calculated after convergence studies. It was found that beyond the number of 100 simulated ions, a further increase in ion number does not significantly affect the averaged simulation observables. The fractions of all ions injected into the UniCell and the ITGF, passing through the device without wall encounters and emerging from its outlet, are given as extraction efficiency. The detailed ion trajectories are shown in Fig. S1 in the Supplementary Material. As shown in Fig. 5, when the RF voltage V_pp = 200 V, the extraction time gradually decreases with increasing DC field strength. While a short extraction time is desired, ion losses occur at elevated fields above ≈ 100 V cm^-1. However, quantitative extraction is predicted to be independent of the ion charge state at lower field strengths. If a charge state higher than 1+ can be retained, field strengths up to ≈ 200 V cm^-1 can be applied without significant loss. At the optimum DC field strength of 100 V cm^-1, the corresponding mean extraction times of singly and doubly charged ions are 4.4 ms and 2.2 ms, respectively. The difference in extraction efficiency between singly and doubly charged ions, as shown in Fig. 5, can be attributed to the difference in the force exerted by the electric field. In particular, the RF-Force F_RF (Eq. (1)), preventing ions from striking the electrodes, scales quadratically with the ion charge. Thus, high extraction efficiencies for doubly charged ions can be achieved even at an elevated DC field strength and resulting higher ion velocities.

Fig. 5

Extraction time and efficiency as a function of DC field strength for singly and doubly charged ions. A peak-to-peak voltage of V_pp = 200 V was applied to the RF + DC funnel electrodes at an RF frequency of f = 5 MHz

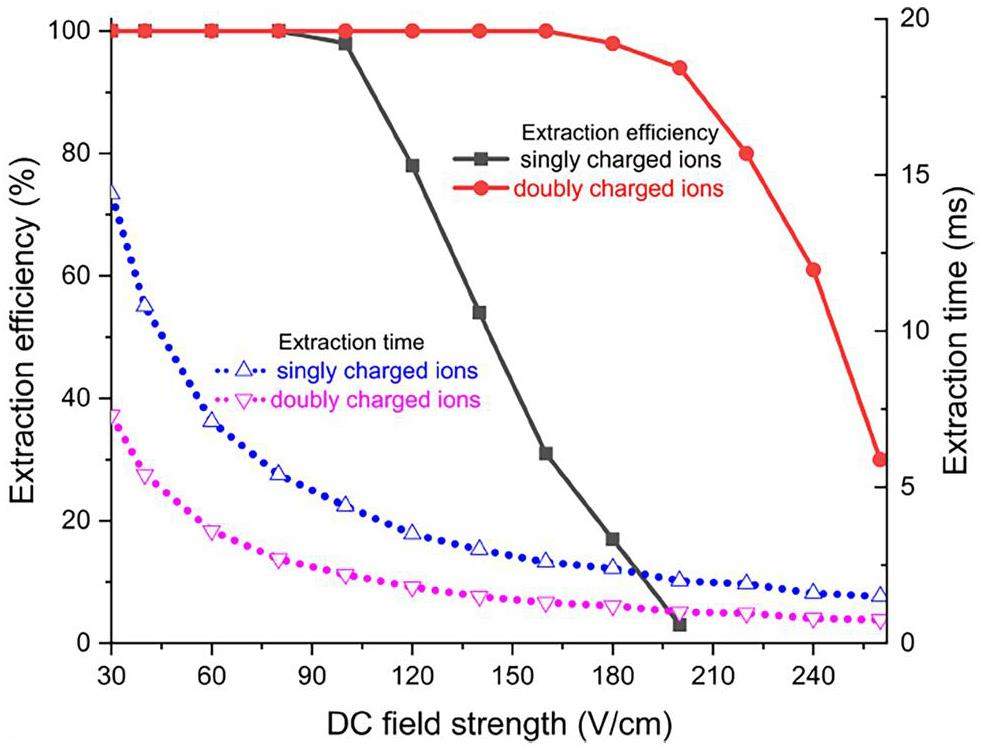
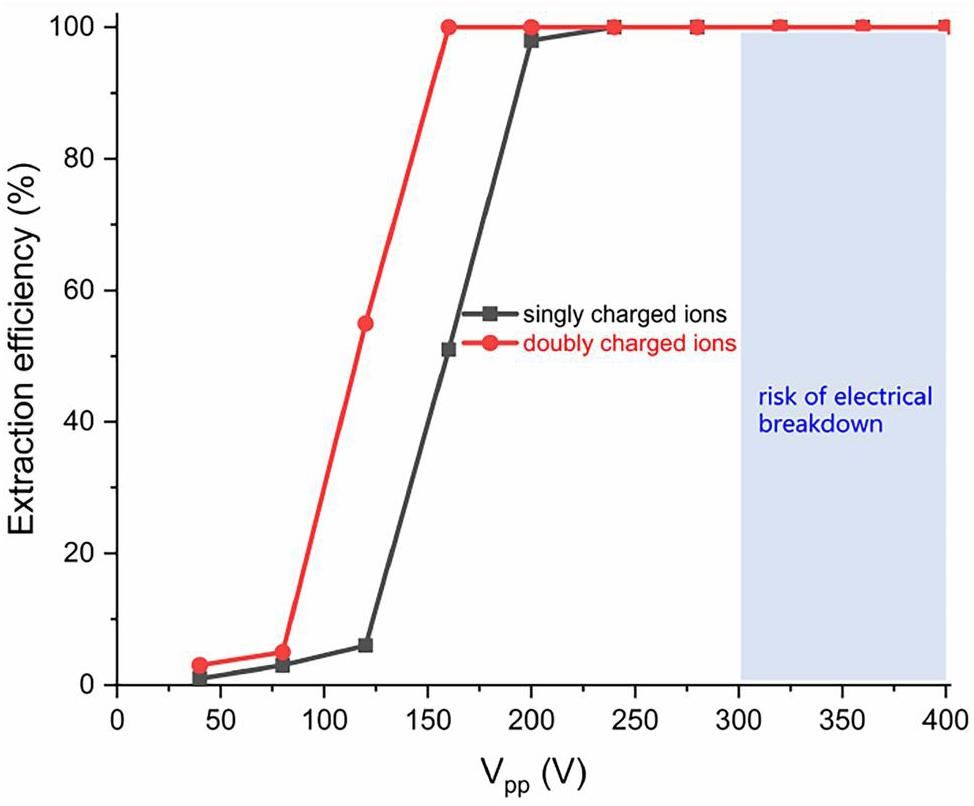
Figure 6 indicates that the extraction efficiency also depends on V_pp. When the DC field strength E=100 V cm^-1, the extraction efficiency increases with V_pp. Values of at least V_pp≈200 V result in a predicted extraction efficiency of ≈100% for singly charged ions, while the threshold V_pp is 160 V for doubly charged ions. We note here that the breakdown voltage between the neighboring electrodes has to be taken into account. The breakdown voltage for the UniCell funnel at the above-mentioned conditions should be higher than 300 V, which is the value of the breakdown voltage found for a gap distance of 0.13 mm, an RF frequency of 13 MHz, and a pressure of ≈ 1 bar [37]. As the breakdown voltage is expected to increase with decreasing frequency [38, 39], the desired voltage of V_pp = 200 V to reach quantitative extraction at our design frequency of 5 MHz is expected to be within a range that allows stable operation.

Fig. 6

Extraction efficiency as a function of V_pp for singly and doubly charged ions. A DC field strength of E = 100 V cm^-1 was applied to the RF + DC funnel electrodes at an RF frequency of f = 5 MHz

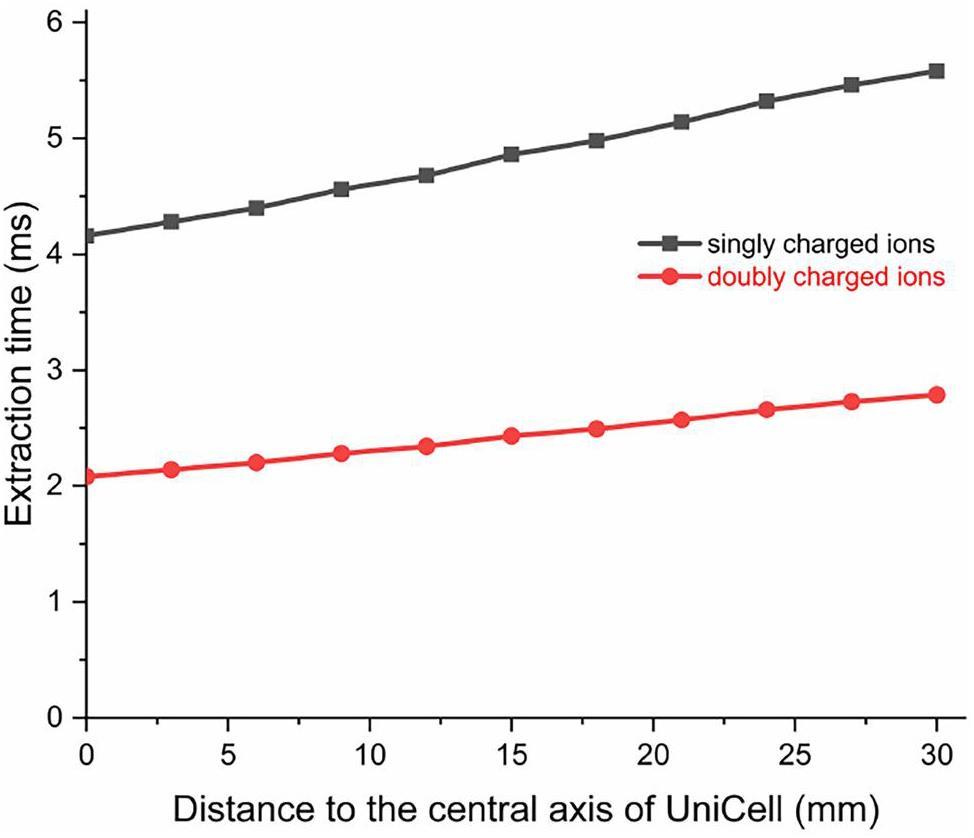
The trajectory analysis resulted in the extraction time distribution as a function of the radial stopping position given in Fig. 7 for the thermalized ions inside the DC cage. Extraction times between 2 ms and 6 ms were obtained. As expected, the flight times for thermalized singly charged ions are almost twice as long as those for doubly charged ions. When the initial positions of the thermalized ions are closer to the central axis of the UniCell, the extraction time is shorter. In addition, the difference between the SRIM simulation assuming a point source of ions and the realistic image size of the ions from the TASCA separator in the UniCell should be taken into account. The farther the initial positions of the thermalized ions are from the central axis of the UniCell, the longer the extraction time will be, with a maximum difference of approximately 1.5 ms for singly charged ions. If the ions are released from different locations within the DC-cage (such as the distance is close to the edge of the first electrode of the DC-cage), the ions can also be effectively transported at the current simulation settings (such as E = 100 V cm^-1 and V_pp = 200 V). The maximum extraction time is about 6 ms.

Fig. 7

Extraction time of ions with charge states of 1+ and 2+ as a function of distance to the central axis of UniCell. The voltage applied to the electrodes was adjusted to obtain a DC field strength of E = 100 V cm^-1 and a peak-to-peak voltage of V_pp = 200 V at an RF frequency of f = 5 MHz

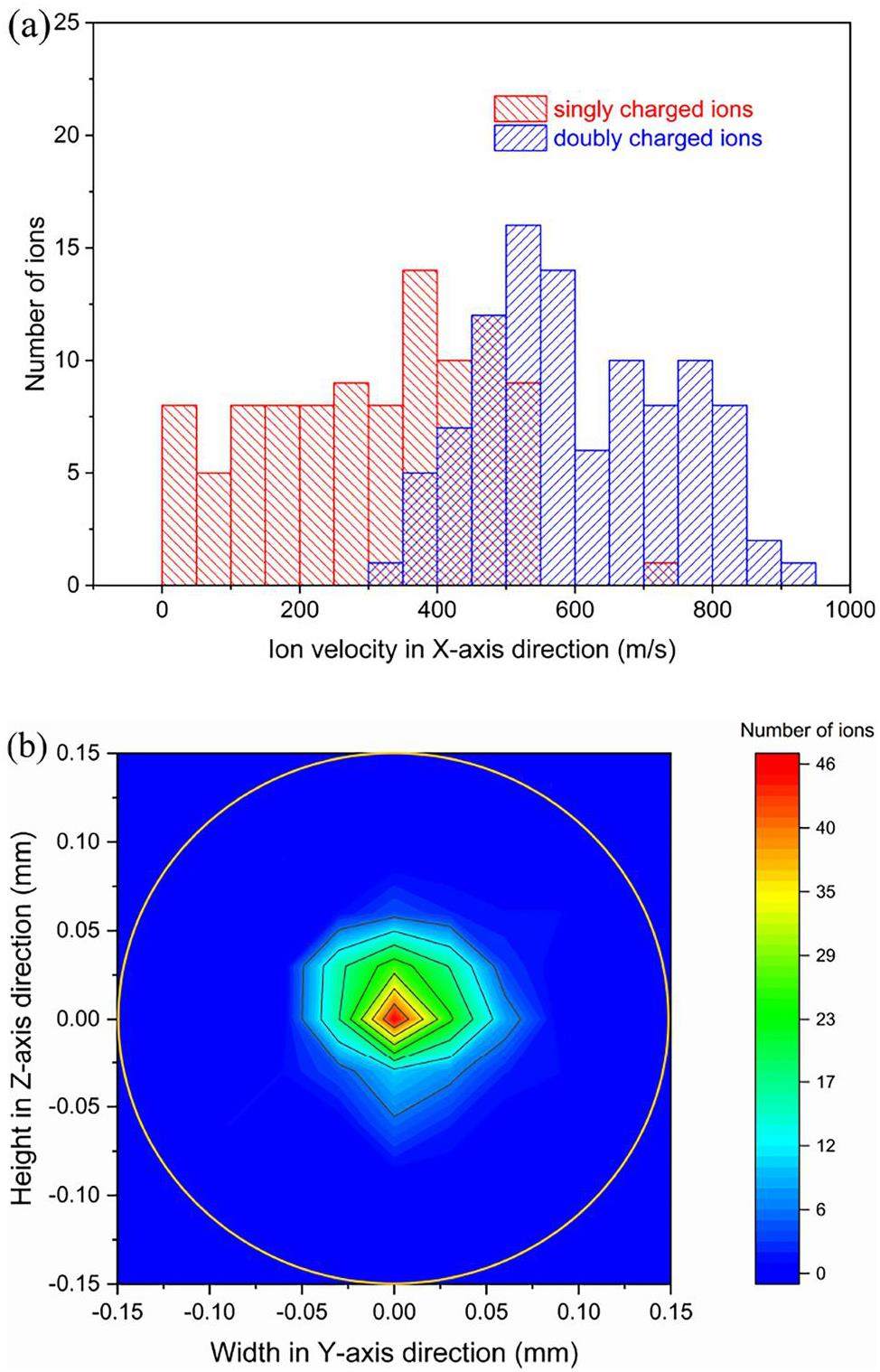
Through these optimizations, the following parameter values of UniCell were chosen for further studies on ion trajectories through the remaining setup: DC field strength E = 100 V cm^-1, RF voltage V_pp = 200 V, and RF frequency f = 5 MHz. When the ions arrive at the nozzle, they have rather broad velocity distributions with mean velocity values of about 330 m/s and 630 m/s for ions in the 1+ and 2+ charge states, respectively, as shown in Fig. 8a. Figure 8b shows that the positions of all ions near the nozzle are focused within a circle with a radius well below 0.15 mm. This resembles the size of the funnel exit opening. These velocities and positions are used as the initial conditions for subsequent simulations of the ions’ propagation through the ITGF.

Fig. 8

(Color online) The distribution of ion velocities (a) and (b) positions for all ions arriving at the recorder near the nozzle (Fig. S1 in the Supplementary Material). The orange circle shows the exit opening of the funnel. The voltage applied to the electrodes was adjusted to obtain a DC field strength of E = 100 V cm^-1 and a peak-to-peak voltage of V_pp= 200 V at an RF frequency of f = 5 MHz

Ion Transfer by Gas Flow (ITGF) device

3.1

ITGF geometry

To ensure fast and efficient ion transfer from UniCell to a gas chromatography detector array for chemical studies, an RF-driven ejector to mitigate diffusion losses was proposed by Varentsov and Yakushev [27], but no ion-transport simulations were performed. In the present work, we investigate if an adapted geometry can be found, that allows guiding ions solely by gas flow without the need of time-varying electric fields. It is desirable to reduce electromagnetic interference in the detector array, which was shown to render the registration of decay events difficult [25]. Here, the Ion Transfer by Gas Flow (ITGF) device is put forward (Fig. 9a), and the results of numerical studies are presented in this section. The entrance of the ITGF is coupled to the UniCell nozzle; the entrance has a circular shape with an inner radius of 1.38 mm, which accepts the full distribution of ions behind the nozzle (cf. Fig. 8b). The cross-section transforms smoothly towards the exit of the ITGF, into narrow elliptical slit with a cross-section of 10 mm × 0.6 mm. This matches the cross-section of the miniCOMPACT detector array [40, 41]. The geometry of the inner ITGF channel changes along the ITGF while the channel cross-section stays essentially constant (see the geometrical parameters in the Supplementary Materail). The ions are only dragged by gas flow through this ITGF. In chromatography applications, the resolution depends on the gas flow rate [42]. To enable experiments with low gas flow rates, where diffusion losses are inevitable unless the ions are confined by electric fields, a design with an additional supply of sheath gas and an RF electrode structure was studied. For the latter case, the width of the electrodes and the thickness of the insulators between electrodes were each taken to be 0.1 mm, similar to the UniCell structure, as shown in Fig. 9a.

Fig. 9

(Color online) The schematic of the ITGF setup without electrodes and with electrodes (a) and simulated gas flow distribution (b) in the nozzle connecting UniCell and ITGF at a helium flow rate of Q₁=10 mbar L s^-1

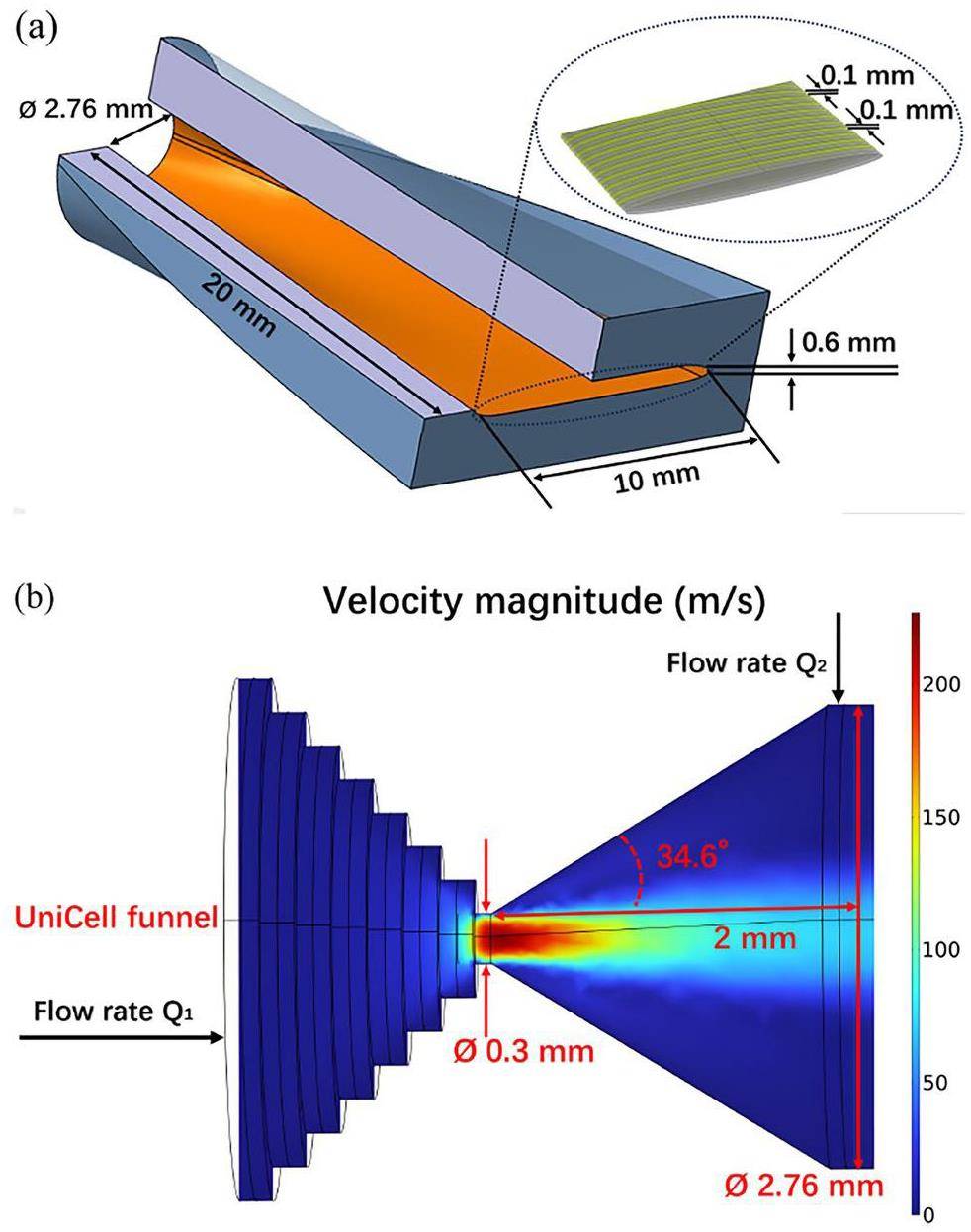
The ITGF interface is connected to the UniCell via a nozzle with a length of 2 mm. The half-angle of the diverting cone is chosen to be 34.6° in order to ensure a smooth connection (Fig. 9b). The maximum gas velocity at the nozzle exit is calculated to be 227 m/s^-1.

3.2

Extraction efficiency from the ITGF

3.2.1

Extraction efficiency with gas flow only

Considering the UniCell and ITGF filled with helium gas near ambient temperature and pressure, the mean free path is calculated to be about 0.12 μm. The Knudsen number in the nozzle is calculated to be less than 0.01. The Reynolds number at the nozzle is calculated to be about 233. Therefore, it is a laminar flow inside the ITGF, which is consistent with the situation in Ref. [27]. The ITGF geometry was modeled using COMSOL in 3D. The coupling of the two interfaces, “Laminar Flow” and “Particle Tracing for Fluid Flow,” was used not only for gas flow simulation in the ITGF but also for the simulation of ion trajectories dragged by the gas flow in the ITGF. Here, “Compressible Flow (Mach < 0.3)” was selected as the compressibility of the gas. The boundary condition of the wall was “freeze”, which means that ions colliding with the wall are considered lost. The gas flow Q₁ emerges from the UniCell. An additional sheath gas flow Q₂ (see Fig. 9b) can be applied between the UniCell and the ITGF (Supplementary Material Fig. S2). The additional gas can be: i) a non-reactive sheath gas like He or Ar, ii) a reactive gas like H₂ or O₂ to form a chemical compound with the extracted ions, or iii) a mixture of both.

The particle tracing for the fluid flow interface was used to simulate the trajectory of each ion in the field of a propagating background fluid. The ion motion is governed by a combination of the Stokes drag force and the Brownian force; the Stokes drag force F_D is proportional to the difference between fluid velocity u and ion velocity v and was implemented as $F_{D} = 6 π η \frac{r_{p}}{C_{c}} (u - v),$ (4) where η is the fluid viscosity and $r_{p}$ is the ion radius [43]. The Cunningham slip correction factor C_c [42] was estimated as $C_{c} = \frac{1.66 λ}{r_{p}},$ (5) where λ is the mean free path. The random movement of ions caused by consecutive collisions with the background gas atoms uniformly broadens the ion distribution in the fluid. Molecular diffusion was modeled, as described in Ref. [44], by application of the Brownian force $F_{B} = ς \sqrt{\frac{12 π k_{b} η T r_{p}}{C_{c} Δ t}},$ (6) where ς is a vector of independent, normally distributed random numbers with zero mean and unit standard deviation, and Δt is the size of the time step taken by the solver. The ions were initialized with velocities and positions obtained as output from UniCell simulations discussed in Sect. 2.3 (Fig. 8a and 8b). For each simulation run, the trajectories of 200 ions (M=293 u, 100 ions each with charge state 1+ and 2+, respectively) traveling down the ITGF were calculated.

The gas flow between UniCell and ITGF is restricted by the UniCell outlet orifice, so uniform pressure distributions are mostly obtained within the UniCell (P₁) and ITGF volumes (P₂). Within the ITGF, a lower pressure is maintained by a vacuum pump. The resulting flow rate (Q₁) varies with the differential pressure ( $P_{1} - P_{2}$ ). The simulations were conducted with pure helium gas at different flow rates (see Table 1). The detailed gas flow distribution obtained in the fluid dynamic simulation is shown in Fig. 2 of the supplement. The maximum gas velocity occurs in the UniCell nozzle. Its magnitude depends on the gas flow rate Q₁ and reaches 227 m/s at Q₁=10 mbar L s^-1. The gas velocity gradually decreases axially along the ITGF center and towards the ITGF surface. The central gas velocity at the ITGF outlet is calculated to be about 6 m/s. Table 1 also lists parameters obtained in mixed gas flow simulations with Q₂=10 mbar L s^-1, unaffected by the additional sheath gas flow Q₂. The maximum velocity near the nozzle remains unchanged (227 m/s). However, the central gas velocity inside the ITGF is accordingly two times larger and reaches a value of about 12 m/s at the outlet. Even at relatively high gas flow rates in the UniCell, the transport efficiency through the ITGF by the gas flow alone is rather moderate and reaches only 68% at a gas flow rate of Q₁=20. At this gas flow rate, the ITGF transport time is only 0.3 ms. If the mixed gas flow regime is applied, the higher total gas flow rate inside the ITGF results in increased efficiency values of up to 90% at Q₁=Q₂=20 mbar L s^-1. This means that the extraction efficiency can be significantly improved by higher gas flow rates. The ion loss inside the ITGF occurs due to the diffusion of ions within the background gas, which eventually collide with the ITGF wall. Higher flow rates through the ITGF result in shorter sojourn times, thereby reducing the probability of collision with the wall. If an RF field is applied on the ITGF wall, one can expect increasing extraction efficiency values also for lower gas flow rates.

Key parameters of the ITGF depending on the gas flow rate Q₁ and Q₂: V_max indicates the maximum gas flow velocity in the UniCell nozzle, V_end is the central gas velocity at the outlet of the ITGF, t is the time ions spend inside the ITGF, P₁ = 1 bar and P₂ correspond to the pressures in the UniCell and ITGF, respectively

Flow rate Q1 (mbar L s-1)	Flow rate Q2 (mbar L s-1)	Vmax (m/s)	Vend (m/s)	t (ms)	P2 (bar)	Extraction efficiency (%)
2	0	48	1	29	0.99	2%
6	0	136	2.8	4.5	0.98	15%
10	0	227	6	1.3	0.95	34%
10	10	227	12	0.7	0.95	38%
15	0	350	19	0.5	0.88	56%
20	0	502	35	0.3	0.76	68%
20	10	502	45	0.25	0.76	80%
20	20	502	52	0.2	0.76	90%

3.2.2

Extraction efficiency with gas flow and electrical fields

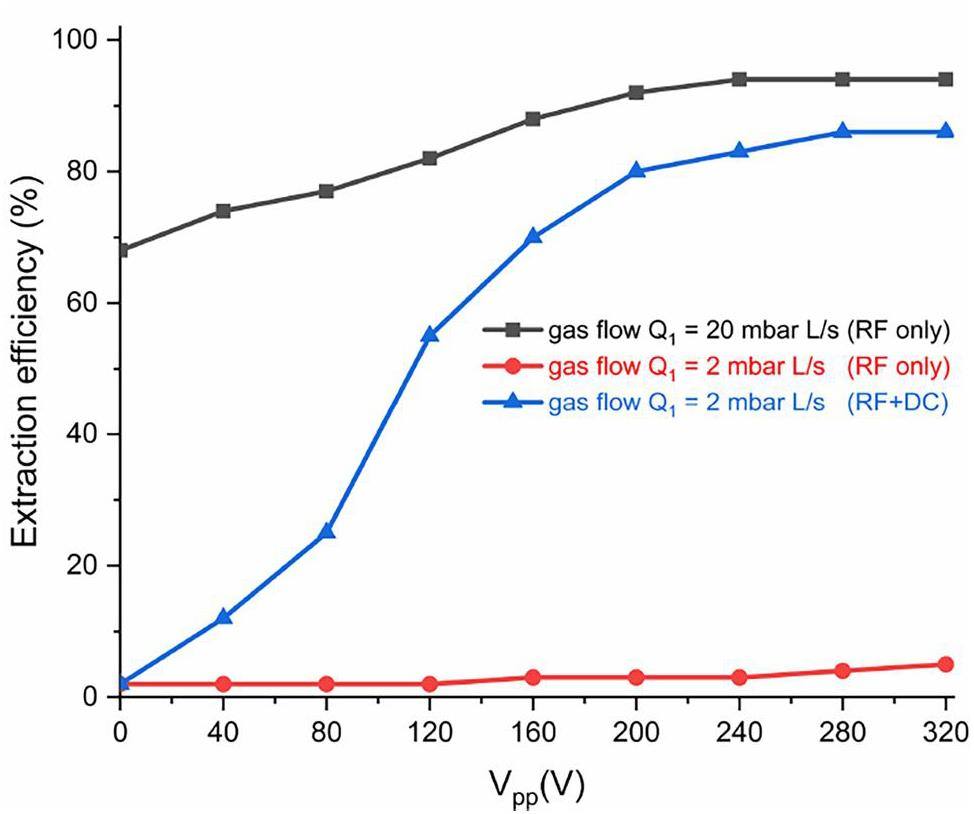
To further increase the ITGF extraction efficiency, the application of an RF signal with f = 5 MHz and V_pp up to 320 V to the ITGF electrode structure was considered, which is expected to reduce diffusion losses. However, at very low flow rates (e.g., Q₁=2 mbar L s^-1), the extraction efficiency of the ITGF still does not exceed a few percent. A significantly larger extraction efficiency was obtained by a combination of the RF field and a DC gradient. If the DC field strength of E = 100 V cm^-1 is additionally applied to the ITGF electrodes, the extraction efficiency increases to 84%. At sufficiently large flow rates (e.g., Q₁=20 mbar L s^-1), the RF-only configuration with V_pp = 240 V can reach 94% extraction efficiency (see Fig. 10). Thus, when the gas flow is not sufficient for effective ion transport, implementing an RF field with a DC field allows for increased extraction efficiency.

Fig. 10

Extraction efficiency from the ITGF as a function of V_pp on the ITGF at different gas flow rates

3.2.3

Extraction efficiency with gas flow using diffusion loss evaluation

To assess the accuracy of the COMSOL simulation, the time-dependent diffusion displacement and subsequent losses were estimated. The mean squared lateral diffusional displacement $〈 {(Δ Y)}^{2} 〉$ of ions after time t is given by $〈 {(Δ Y)}^{2} 〉 = 2 D t,$ (7) where the diffusion coefficient can be expressed via the ion mobility K as $D = \frac{K k_{b} T}{e} .$ (8) Diffusion losses were estimated by evaluating the expected displacement for single ions in the ITGF outlet region, which is the most critical for the diffusion losses. Ions with diffusion displacement larger than the half-width of the outlet slit (R=0.3 mm) are considered lost. The distribution of particles after time t is obtained as $P (x, t) = \frac{1}{\sqrt{4 π D t}} e^{- \frac{x^{2}}{4 D t}},$ (9) and the fraction of particles with diffusion displacement smaller than R is given by $ε_{diff} = \int_{- R}^{R} P (x, t) d x = erf (\frac{R}{2 \sqrt{D t}}),$ (10) As listed in Table 1, the ITGF transport time decreases with increasing flow rate. At the flow rate of 2 mbar L s^-1, the lateral RMS diffusion displacement $\sqrt{〈 {(Δ Y)}^{2} 〉}$ was calculated to be 1.7 mm. Therefore, the extraction efficiency is estimated to be ε_diff=14%. At a greater flow rate of 20 mbar L s^-1, the ITGF transport time is only 0.3 ms, and thus, the RMS diffusion displacement is calculated to be only about 0.20 mm. Therefore, the corresponding extraction efficiency is significantly larger, approximately ε_diff=87%. Despite not exactly reproducing the efficiencies obtained by COMSOL, the first-order analytical approximation is qualitatively in agreement and suggests the validity of the simulations.

Conclusions and outlook

In this paper, we have introduced an ITGF device, which was designed to enable swift and efficient ion transfer of superheavy elements from the UniCell BGC to a detector array. Our numerical studies predict almost quantitative extraction and the total time (UniCell extraction time + ITGF transport time) to be well below the lifetimes of known isotopes of the elements of interest, ¹¹⁶Lv and ¹¹⁷Ts. Through our detailed simulations, the optimum DC field strength of the UniCell was found to be 100 V cm^-1 at an RF peak-to-peak voltage of V_pp = 200 V at a frequency of 5 MHz. A flow rate of more than 20 mbar L s^-1 required to ensure an extraction efficiency of 90% for an ITGF connected with UniCell. If lower flow rates are required by the experiment, the application of RF and DC fields in the ITGF should be considered. The UniCell and ITGF are currently under construction at GSI. The next step is the offline commissioning at GSI. This is foreseen to include: 1) application test of an RF peak-to-peak voltage of V_pp = 200 V at a frequency of 5 MHz, and 2) evaluation of the effectiveness of the repulsive force of the funnel-shaped RF electric field at a 100 V cm^-1 DC electric field strength. Special attention will be given to the supply of purified gas and the characterization of efficiency degradation by gas impurities. The optimum operating parameter values obtained within this work serve for the detailed planning of the layout of the UniCell + ITGF setup and will be used as initial parameters in the upcoming commissioning. In the following project phase, a vacuum interface will be developed which will allow coupling UniCell to devices that e.g., allow mass measurements. We are confident that this setup will contribute to enhancing the performance of existing gas stopping setups and facilitate the development of new systems.

References

Ch.E. Düllmann, R.D. Herzberg, W. Nazarewicz, et al.,

Foreword

. Nucl. Phys. A 944, 1-2 (2015). https://doi.org/10.1016/j.nuclphysa.2015.11.004