Introduction

High-energy heavy-ion collisions provide a unique way to understand the origin of the universe. However, their processes cannot be directly observed in experiments. We can only study the collision process indirectly by analyzing the properties of the final particles produced in the collisions. The pseudo-rapidity distribution of charged particles is one of the important experimental observables. The study of this observable could lead to a better understanding of the properties of the particles produced in the collisions, the particle production mechanism and so on. There have been numerous works in previous studies using different models, such as HIJING [1], AMPT [2-4], EPOS-LHC [5], a multi-source thermal model [6, 7], a new revised Landau hydrodynamics model [8], a 1 + 1 dimensional hydrodynamics model [9, 10], a dynamical initial state model coupled to (3 + 1)D viscous relativistic hydrodynamics [11] and so on, to analyze the existing experimental data of pseudo-rapidity distributions of the charged particles [12-30]. Although these models are based on different physical ideas, valuable physical information on the collision process has been extracted and learned.

Recently, a fireball model based on Tsallis thermodynamics was utilized to analyze the pseudo-rapidity distribution of charged particles measured in high-energy heavy-ion collisions [31-33]. In our previous works [32, 33], we used the fireball model to study the pseudo-rapidity distributions of the charged particles produced in p+p($\overline{\text{p}}$) collisions for energies ranging from $\sqrt{s_{\text{NN}}}$ = 23.6 GeV to 13 TeV and A+A collisions at the RHIC and LHC, and extended the fireball model to the asymmetric collision systems, i.e., d+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV and p+Pb collisions at $\sqrt{s_{\text{NN}}}=5.02$ TeV, by considering the asymmetric collision geometry configuration. In this paper, we utilize recently published data from the PHINEX Collaboration [30] at RHIC to systematically study the pseudo-rapidity distributions of the charged particles produced in asymmetric collision systems, including p+Al, p+Au and ³He+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV. We also predict the total multiplicities of the charged particles from the fireball model and study their centrality dependence. Further, we analyze the centrality and system size dependencies of the fireball model parameters obtained from the pseudo-rapidity distributions of the charged particles.

The paper is organized as follows. In Sect. 2, the fireball model with Tsallis thermodynamics is briefly introduced. In Sect. 3, the fitting results of the fireball model and the total charged particle multiplicities extracted from the fireball model are shown. The dependences of the model parameters on the centrality and size of the collision systems are also presented. A brief conclusion is drawn in Sect. 4.

Theoretical descriptions

In the self-consistent Tsallis thermodynamics, the Tsallis distribution is proposed as a generalization of the Boltzmann–Gibbs distribution [34]. To describe the transverse momentum spectrum of particles, the Tsallis distribution is written as [31-33] $\begin{array}{c}\frac{{\text{d}}^{2}N}{2\pi p_{\text{T}}\text{d}{p}_{\text{T}}\text{d}y}=gV\frac{m_{\text{T}}\cosh y}{{\left(2\pi \right)}^3}\\ \times {\left[1+\left(q-1\right)\frac{m_{\text{T}}\cosh y-\mu }{T}\right]}^{-\frac{q}{q-1}},\end{array}$ (1) where g is the particle state degeneracy, V is the volume, $m_{\text{T}}=\sqrt{m_0^2+p_{\text{T}}^2}$ is the transverse mass and m₀ is the particle rest mass, y is the rapidity, q is the entropic factor, which measures the non-additivity of the entropy [34, 35], μ is the chemical potential and T is the temperature. The Boltzmann distribution is recovered when q=1. We take μ=0 because the multiplicities of π⁺ and π^- are equal and they are the majority of particles produced in the collision systems considered. For the middle rapidity $y\approx 0$, Eq. (1) can be rewritten as $\frac{{\text{d}}^{2}N}{2\pi p_{\text{T}}\text{d}{p}_{\text{T}}\text{d}y}=gV\frac{m_{\text{T}}}{{\left(2\pi \right)}^3}{\left[1+\left(q-1\right)\frac{m_{\text{T}}}{T}\right]}^{-\frac{q}{q-1}}\mathrm{.}$ (2) The parameters q and T are extracted from the experimental transverse momentum spectrum of the particles.

In the fireball model with Tsallis thermodynamics [31-33], the particles measured in the experiment were produced by fireballs following the Tsallis distribution Eq. (1). The density distribution of these fireballs in the rapidity space is $\nu \left(y_{\text{f}}\right)$, where y_f is the rapidity of the fireball. Therefore the transverse momentum spectrum of particles can be written as $\begin{array}{c}\frac{{\text{d}}^{2}N}{2\pi p_{\text{T}}\text{d}{p}_{\text{T}}\text{d}y}=\frac{N}{A}{\displaystyle {\int }_{-\infty }^{\infty }}\nu \left(y_{\text{f}}\right)\frac{m_{\text{T}}\cosh \left(y-y_{\text{f}}\right)}{{\left(2\pi \right)}^3}\\ \times {\left[1+\left(q-1\right)\frac{m_{\text{T}}\cosh \left(y-y_{\text{f}}\right)}{T}\right]}^{-\frac{q}{q-1}}\text{d}{y}_{\text{f}}\mathrm{,}\end{array}$ (3) where N is the total particle multiplicity and A is the normalization constant such that ${\displaystyle {\int }_{-\infty }^{\infty }}{\displaystyle {\int }_0^{\infty }}\frac{{\text{d}}^{2}N}{p_{\text{T}}\text{d}{p}_{\text{T}}\text{d}y}{p}_{\text{T}}\text{d}{p}_{\text{T}}\text{d}y=N\mathrm{.}$ (4) Sometimes, the experimental data are measured in the pseudo-rapidity η space. To describe the experimental data $\frac{dN}{d\eta }$, we substitute the relation between rapidity and pseudo-rapidity [36] $\frac{\text{d}y}{\text{d}\eta }\left(\eta \mathrm{,}{p}_{\text{T}}\right)=\sqrt{1-\frac{m_0^2}{m_{\text{T}}^2{{\displaystyle \cosh }}^{2}y}}$ (5) into Eq. (3) and integrate the transverse momentum in the equation to obtain [32, 33] $\begin{array}{c}\frac{\text{d}N}{\text{d}\eta }=\frac{N}{A}{\displaystyle {\int }_{-\infty }^{\infty }}\text{d}{y}_{\text{f}}{\displaystyle {\int }_0^{\infty }}\text{d}{p}_{\text{T}}{p}_{\text{T}}\sqrt{1-\frac{m_0^2}{m_{\text{T}}^2{{\displaystyle \cosh }}^{2}y}}\\ \times \nu \left(y_{\text{f}}\right)\frac{m_{\text{T}}\cosh \left(y-y_{\text{f}}\right)}{{\left(2\pi \right)}^2}\times {\left[1+\left(q-1\right)\frac{m_{\text{T}}\cosh \left(y-y_{\text{f}}\right)}{T}\right]}^{-\frac{q}{q-1}},\end{array}$ (6) where $y=\frac{1}{2}\ln \left[\frac{\sqrt{p_{\text{T}}^2{{\displaystyle \cosh }}^2\eta +m_0^2}+p_{\text{T}}\sinh \eta }{\sqrt{p_{\text{T}}^2{{\displaystyle \cosh }}^2\eta +m_0^2}-p_{\text{T}}\sinh \eta }\right]\mathrm{.}$ (7) Because of the term of $\sqrt{1-\frac{m_0^2}{m_{\text{T}}^2{{\displaystyle \cosh }}^{2}y}}$, Eq. (6) cannot be analytically integrated over p_T and it is done numerically.

In this paper the asymmetric collision systems are studied, and the distribution $\nu \left(y_{\text{f}}\right)$ is assumed to be the sum of two asymmetric q-Gaussian functions [33], $\begin{array}{c}\nu \left(y_{\text{f}}\right)=\frac{1}{\sqrt{2\pi }{\sigma }_a}{\left[1+\left(q^{\prime }-1\right)\frac{{\left(y_{\text{f}}-y_{0a}\right)}^2}{2{\sigma }_a^2}\right]}^{-\frac{1}{q^{\prime }-1}}\\ +\frac{x}{\sqrt{2\pi }{\sigma }_A}{\left[1+\left(q^{\prime }-1\right)\frac{{\left(y_{\text{f}}+y_{0A}\right)}^2}{2{\sigma }_A^2}\right]}^{-\frac{1}{q^{\prime }-1}},\end{array}$ (8) where $y_{0a\left(A\right)}$ and σ_a(A) are the centroid position and width of the fireball distribution in the direction of the light (heavy) nucleus beam, respectively. The normalization of Eq. (8) is handled by the normalization constant A in Eq. (3). x is the parameter to characterize the extent of asymmetry, which was first proposed in our previous work [33]. In this work, we take q’=q as in [31-33]. A representative figure of Eq. (8) is shown in the Appendix 5 with the parameters obtained for the p+Al collisions at 0-5% centrality and $\sqrt{s_{\text{NN}}}=200$ GeV.

Results and discussion

Because the data of the transverse momentum spectra of the charged particles produced in p+Al, p+Au and ³He+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV have not been released yet, the data of the transverse momentum spectra of π⁰ produced from these collisions are obtained from [37] in this study. Using Eq. (2) by taking g=1 and V as a free parameter, the parameters T and q for the Tsallis distribution are extracted and listed in Table 2 in the Appendix 6. A representative figure of the transverse momentum spectra of π⁰ for p+Al collisions at $\sqrt{s_{\text{NN}}}=200$ GeV is shown in Appendix 7. It is worth noting that the transverse momentum spectrum of π⁰ is very similar to that of π^± at $\sqrt{s_{\text{NN}}}=200$ GeV for a given collision centrality, and the temperature parameter T extracted from π⁰ should reasonably characterize the property of the collision system. We take the parameters T and q from the closest centrality when the centrality of the particle transverse momentum spectrum and centrality of the charged particle pseudo-rapidity distribution are not the same. These two parameters and the fireball model with Tsallis thermodynamics, Eqs. (6) and (8), are then utilized to study the pseudo-rapidity distribution of the charged particles produced in the collisions. The corresponding values of x in Eq. (8) are also listed in Table 3 in the Appendix 2.

In Figs. 1, 2, and 3, the results of the pseudo-rapidity distributions of the charged particles from the fireball model with Tsallis thermodynamics for different centrality bins in p+Al, p+Au and ³He+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV are shown. The fireball model effectively describes the experimental data within the errors. Notably, the data quality of the pseudo-rapidity distributions of the charged particles is not as good as that for the d+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV shown in [33], i.e., in terms of larger errors, a fewer number of data points as well as a lower pseudo-rapidity coverage, which leads to larger uncertainties to the fireball model parameters and affects our analyses of the fireball model parameters versus collision centrality and the collision system size to some extent later in the following. The pseudo-rapidity distribution of the charged particles for centrality 5–10% is lower than the case for centrality 10–20% in some pseudo-rapidity regions for the ³He+Au collisions, which is observed in Fig. 3. A larger x at centrality 5–10% compared with the others for the ³He+Au collisions is also observed in Table 3 in the Appendix 6. We emphasize that the same fitting protocol is applied for all the pseudo-rapidity distribution data of the charged particles. Because the collision system is asymmetric, the pseudo-rapidity distribution of the charged particles has significant forward/backward asymmetry. Fewer particles are produced in the direction of the light nucleus (p, ³He) beam compared to the heavy nucleus (Al, Au) beam. As the d+Au collision system at $\sqrt{s_{\text{NN}}}=200$ GeV and the p+Pb collision system at $\sqrt{s_{\text{NN}}}=5.02$ TeV we studied in [33], the pseudo-rapidity distributions of the charged particles produced by these collision systems also become more symmetric from the central to peripheral collisions. This is because the peripheral collisions for asymmetric collision systems are more similar to the symmetric p+p collisions according to collision geometry.

Fig. 1Full-screen View

(Color online) The pseudo-rapidity distributions of the charged particles produced in p+Al collisions at $\sqrt{s_{\text{NN}}}=200$ GeV for different centralities. The symbols are experimental data taken from [30]. The curves are the results from Eqs. (6) and (8).

Fig. 2Full-screen View

(Color online) Same as Fig. 1, but for p+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV.

Fig. 3Full-screen View

(Color online) Same as Fig. 1, but for ³He+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV.

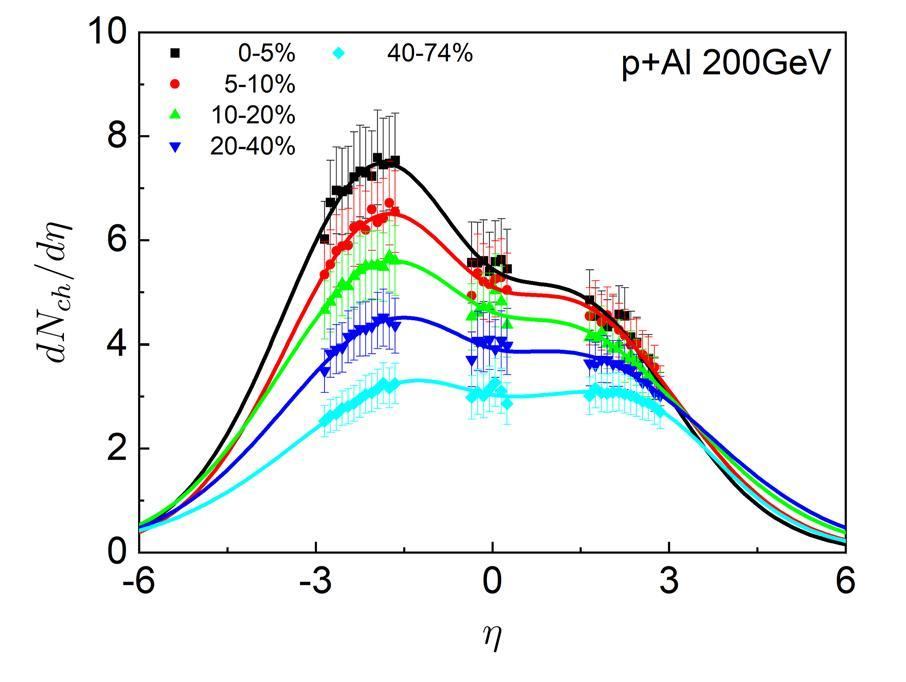
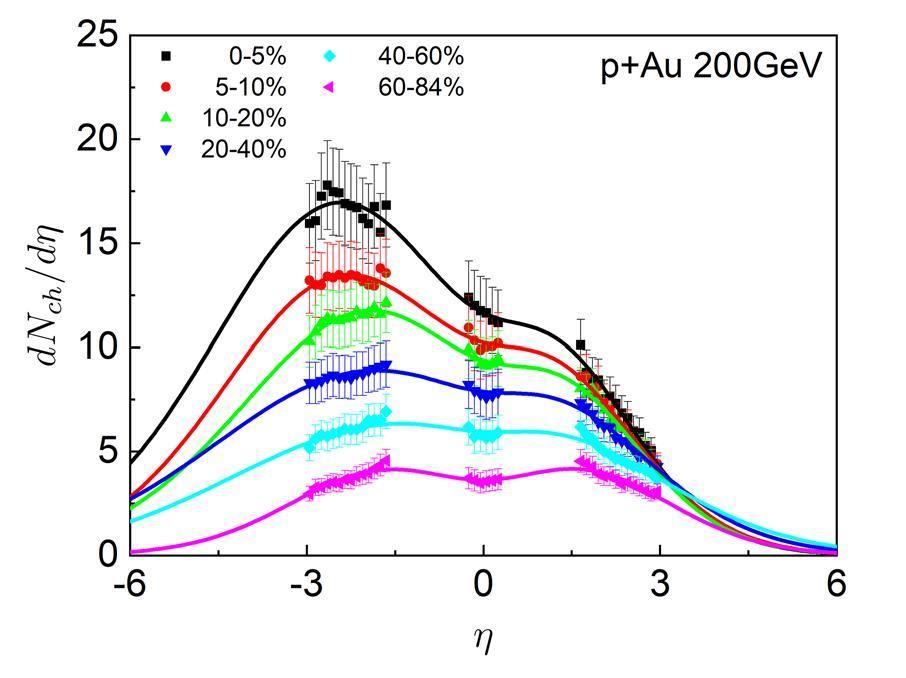
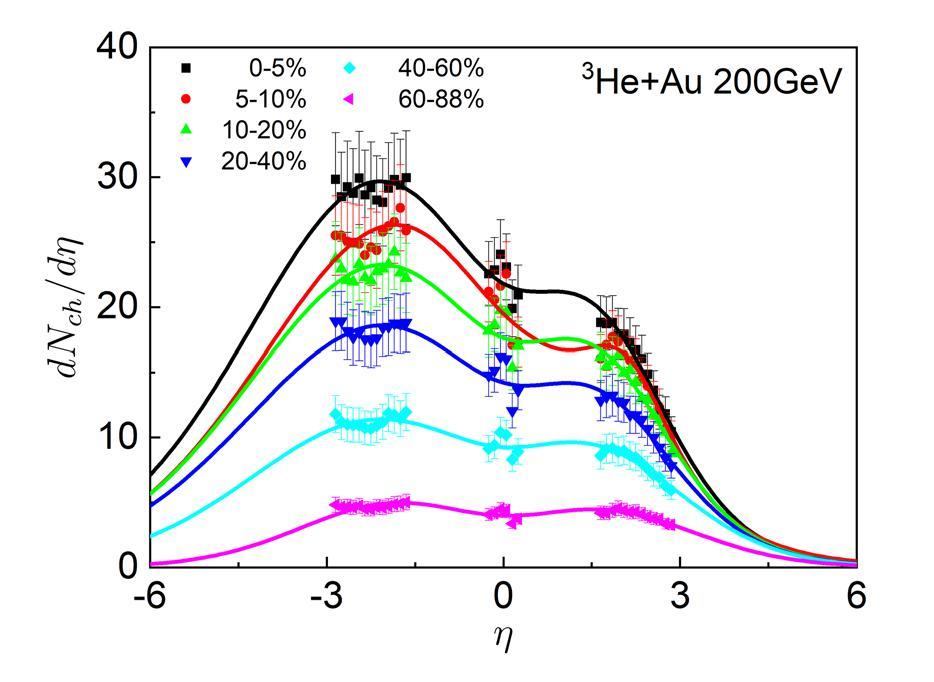
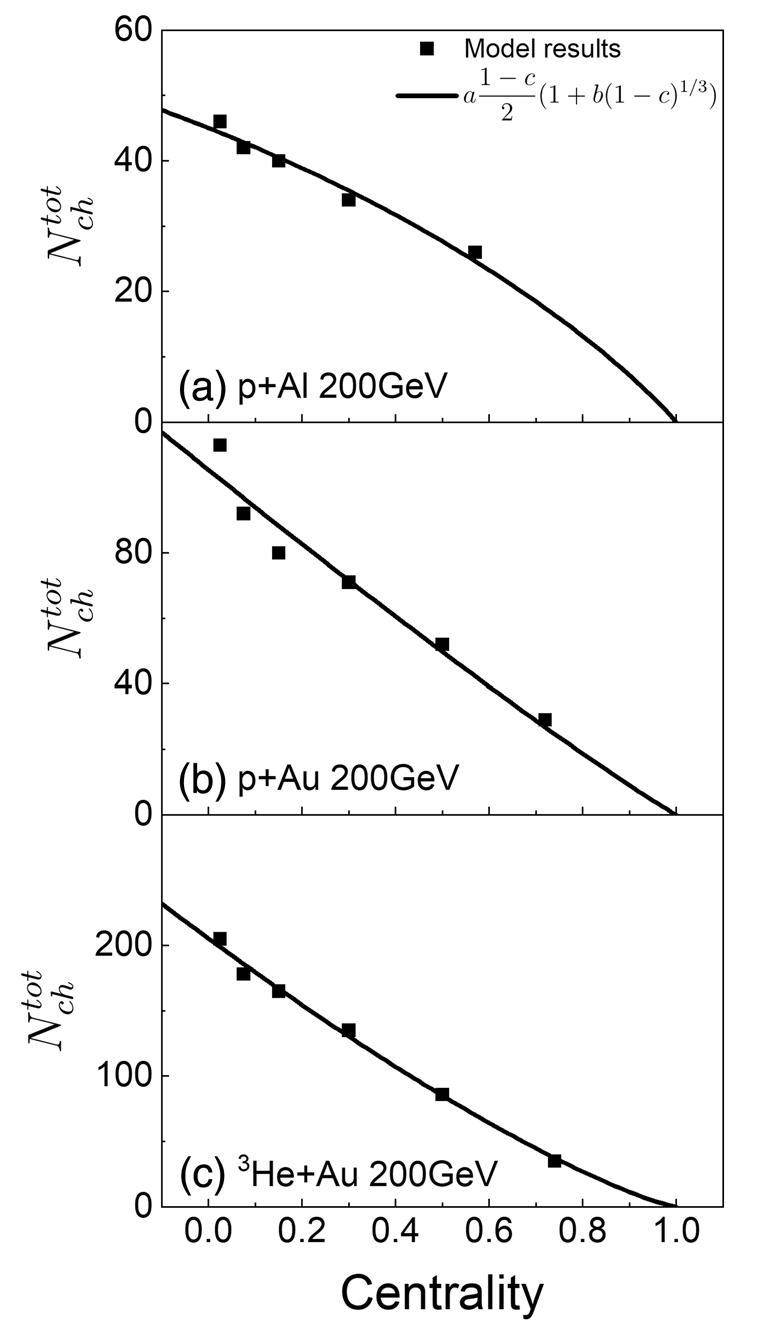
We then evaluate the centrality dependence of the total multiplicities of the charged particles produced in these collision systems. Integrating Eq. (6) over the $\eta \in [-\mathrm{10,10}]$ we obtain the total multiplicity of the charged particles for each centrality from the fireball model. Because the corresponding experimental data are not yet available, we only analyze the results extracted from the fireball model and treat them as predictions. Figure 4 shows the total multiplicities of the charged particles calculated from the fireball model versus the collision centrality c. c=0 represents the most central collisions and c=1 represents the most peripheral collisions. It can be observed that the fitting function taken from [14] can effectively describe the centrality dependence of the total multiplicities of the charged particles. As the centrality changes from the central to peripheral collisions, fewer charged particles are produced.

Fig. 4Full-screen View

Total charged particle multiplicities produced in the p+Al, p+Au and ³He+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV versus the collision centrality c. The squares are the fireball model results. The lines are the fitting results. The fitting function is from [14] and specified in the legend.

We also analyze both the centrality and system size dependence of the parameters (y_0a, y_0A, σa and σA) of the fireball model. In Fig. 5 the dependence of the fireball model parameters on the collision centrality in the p+Al, p+Au and ³He+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV are shown. Inspired by the linear relation of the centrality dependence of the fireball model parameters for d+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV and p+Pb collisions at $\sqrt{s_{\text{NN}}}=5.02$ TeV shown in Fig. 12 of our previous work [33], the linear fittings are performed to guide the eyes in Fig. 5 and the fitting functions are listed in Table 1. The negative and positive slopes of the linear fittings for the fireball model parameters (y_0a, y_0A and σA) versus centrality are similar to those of the d+Au and p+Pb collisions in [33]. In the following discussion, the results for d+Au and p+Pb are obtained from [33]. It can be observed that the slopes of the linear fittings for parameter y_0a versus centrality are positive and the corresponding slopes of the linear fittings for parameter y_0A versus centrality are negative for the p+Al, p+Au and d+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV. However, the slopes of the linear fittings for parameters (y_0a, y_0A) reverse the signs respectively for the ³He+Au collision at $\sqrt{s_{\text{NN}}}=200$ GeV compared to the above mentioned cases. The slopes of the linear fittings for parameters (y_0a, y_0A) are positive for p+Pb at $\sqrt{s_{\text{NN}}}=5.02$ TeV. It can also be observed that there is a universal trend with increasing centrality for parameter σ_a(A) except the lightest collision system p+Al, i.e., σa increases with increasing centrality in the direction of the light nucleus beam and σA decreases with increasing centrality in the direction of the heavy nucleus beam. In the p+Al collision system, σa and σA have opposite trends with increasing centrality to their counterparts in the other collision systems. These different patterns indicate the complex dynamics in the asymmetric collisions relevant to the combinations of the projectile and target as well as the collision energy, which needs more investigations.

Fig. 5Full-screen View

(Color online) Centrality dependence of model parameters y_0a, y_0A, σa and σA in p+Al, p+Au and ³He+Au collision at $\sqrt{s_{\text{NN}}}=200$ GeV. The lines are the linear fit results to guide the eyes.

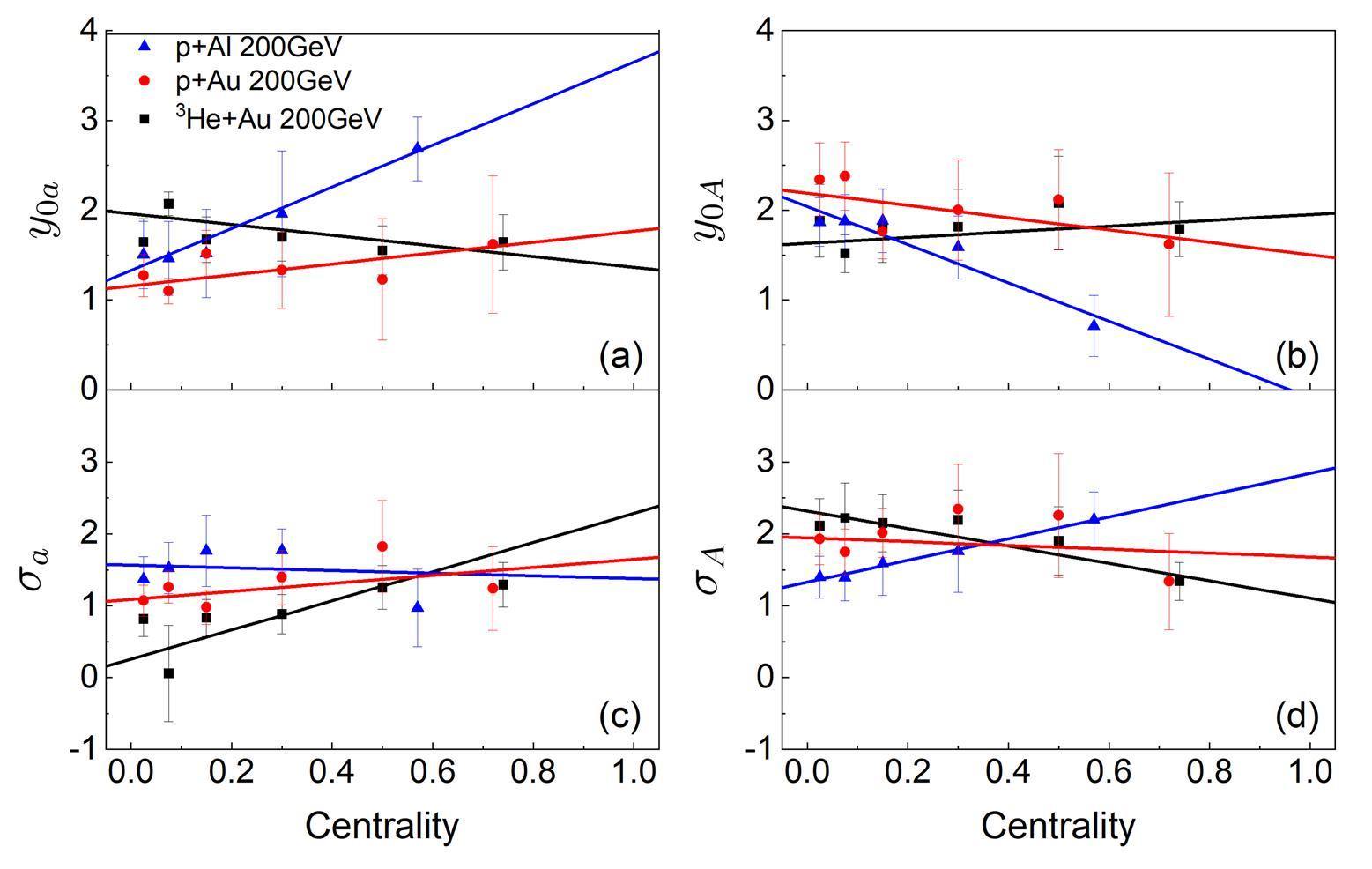
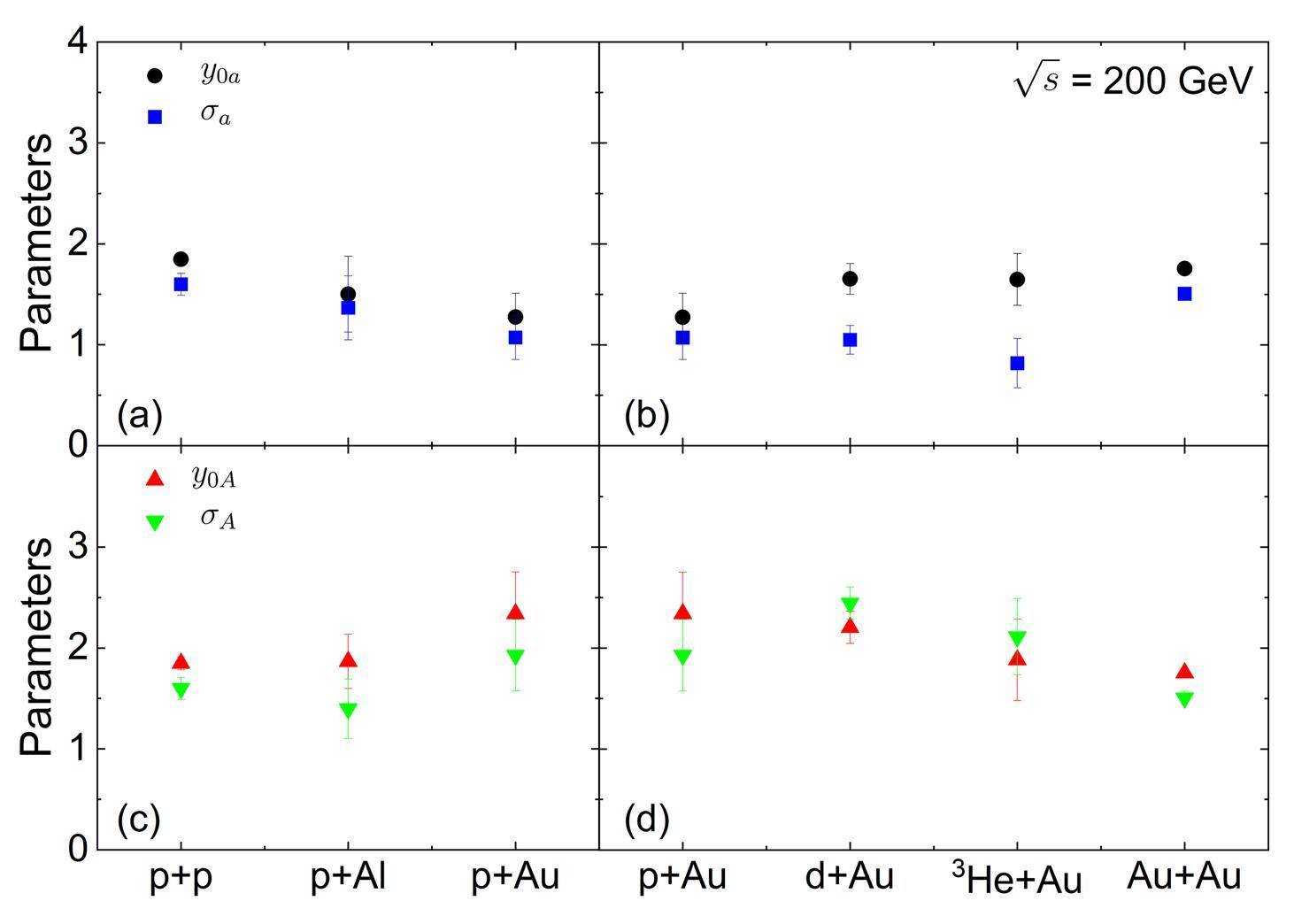
Figure 6 shows the collision system size dependence of the fireball model parameters at $\sqrt{s_{\text{NN}}}=200$ GeV. For collision systems other than p+p, the parameters of the most central collisions are considered. In the p+p and Au+Au collisions, the parameters $y_{0a}=y_{0A}=y_0$, σa=σA=σ, where y₀ and σ are the rapidity centroid and width of fireball distribution in the symmetric collision system, as detailed in [33]. It can be deduced that when the light nucleus is p, y_0a decreases as the size of the heavy nucleus increases, whereas y_0A shows the opposite trend. This indicates that a larger heavy nucleus has stronger stopping power for p. When the heavy nucleus is Au, y_0a increases as the size of the light nucleus increases, whereas y_0A shows the opposite trend. This means that a larger light nucleus is more difficult to stop by Au but has a stronger stopping power for Au. For parameters σa and σA, no conclusive patterns are observed. We expect that more discussions can be added when the data quality of the pseudo-rapidity distributions of the charged particles is improved by experimentalists. These phenomena manifest the complex dynamics in the asymmetric collisions.

Fig. 6Full-screen View

(Color online) Collision system size dependence of model parameters y_0a, y_0A, σa, σA for p+p, p+Al (0-5%), p+Au (0-5%), d+Au (0-20%), ³He+Au (0-5%) and Au+Au (0-6%) collisions at $\sqrt{s_{\text{NN}}}=200$ GeV. The parameters for the p+p, d+Au and Au+Au collisions are taken from [33].

Summary

In this paper, we studied the pseudo-rapidity distributions of the charged particles produced in p + Al, p + Au, and ³He + Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV using the fireball model with Tsallis thermodynamics. The model can well fit the experimental data from the asymmetric collisions. We also extracted the total multiplicities of the charged particles from the fireball model as predictions and analyzed their dependence on collision centrality. Notably, the data quality of the pseudo-rapidity distributions of the charged particles produced in the p + Al, p + Au, and ³He + Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV affected our results to some extent. Combining our previous results of d+Au collisions at $\sqrt{s_{\text{NN}}}=200$ GeV and p+Pb collision at $\sqrt{s_{\text{NN}}}=5.02$ TeV, we analyzed the centrality and system size dependence of the fireball model parameters (y_0a, y_0A, σa and σA). Interesting patterns were revealed, which indicated the complex dynamics in the asymmetric collisions. Our results confirmed the conclusion made previously in [33] that the fireball model with Tsallis thermodynamics as a universal framework could also describe the pseudo-rapidity distribution of charged particles produced in asymmetric collision systems.