Introduction
The recent isobar data [1, 2] stimulated a wide interest from the relativistic heavy ion community in the physics of nuclear structures of isobars (nuclei with equal number of nucleons but different numbers of protons and neutrons) [3-12]. The isobar collisions of
Much progress has been made in quantitatively assessing the differences in size and shape of isobars by using relativistic isobar collisions [5, 7-9, 12, 22-26]. These differences can place stringent constraints on key parameters in theoretical modeling of nuclear interactions, which is the backbone of all theoretical calculations of nuclear structure including DFT. One of such parameters is the slope parameter
We use the Optical Glauber model and Monte Carlo Glauber model [38-40] to investigate the effect of nuclear deformations and initial fluctuations on the relative differences
The rest of the paper is organized as follows. Section 2 gives a brief description of the models and the nuclear density profiles used in this work. Section 3 discusses the effects of nuclear deformation and initial fluctuations on
Glauber model and isobar nuclear densities
Particle production in relativistic heavy ion collisions is usually parameterized by the two-component model,
The elliptic flow (v2), triangular flow (v3) are the Fourier coefficients of the azimuthal angle (ϕ) distribution
For spherical nucleus-nucleus collisions, the multiplicity and eccentricities can be calculated analytically in the Optical Glauber model for a given impact parameter b. For deformed nucleus-nucleus collisions, we calculate the ratio observables at a given shape orientation with a specific Euler rotation and then take the average over all orientations
The event-by-event fluctuations are not included in the Optical Glauber model [39], and such an effect is crucial for the anisotropic flow observables, especially the odd-order ones. We, therefore, use the Monte Carlo Glauber model to include the fluctuation effect, where the finite number of nucleons (96 for the Ru and Zr isobars) are sampled in each colliding nucleus. The event-by-event fluctuations depend on the number of nucleons in the colliding nuclei, so these effects are expected to be larger in the isobar collisions than in Au+Au collisions. After sampling the nucleons with the appropriate nuclear density, the multiplicity is calculated based on Eq. (3), and the eccentricity is calculated from the transverse position of those finite participating nucleons. Here the participants and binary collisions are determined from nucleon-nucleon interactions which happens when the distance between the two nucleons, each from the incoming and outgoing nuclei, is less than
The density profiles of 96Ru and 96Zr nuclei are required in the Glauber simulations. In this study, the parameters for the Woods-Saxon density distributions of 96Ru and 96Zr are taken from Ref. [22, 45] (see Tab. 1), which are extracted from the isobar densities obtained by DFT calculations with the symmetry energy
| 96Ru | 96Zr | ||||||
|---|---|---|---|---|---|---|---|
| ρ0 | R | a | β2 | ρ0 | R | a | β3 |
| 0.159 | 5.093 | 0.487 | 0.00 | 0.163 | 5.022 | 0.538 | 0.00 |
| 0.159 | 5.093 | 0.471 | 0.16 | 0.163 | 5.021 | 0.517 | 0.20 |
Centrality is determined by the multiplicity distributions in the Monte Carlo Glauber model, similar to what was done in heavy ion experiments [1]. For the optical Glauber model and optical Trento model in spherical nucleus-nucleus collisions, the centrality is related to the differential cross-section in impact parameter [39]. In this study, we use the 16 equal-size centrality bins from 0-80% centrality range. The results obtained with the fixed impact parameter corresponding to the centre of each centrality bin are used to mimic the observables in such a centrality bin. The impact parameters for 96Ru and 96Zr are listed in Tab. 2. The impact parameters are larger in
| Centrality (%) | 2.5 | 7.5 | 12.5 | 17.5 | 22.5 | 27.5 | 32.5 | 37.5 | 42.5 | 47.5 | 52.5 | 57.5 | 62.5 | 67.5 | 72.5 | 77.5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bRu (fm) | 1.865 | 3.230 | 4.170 | 4.933 | 5.594 | 6.184 | 6.723 | 7.222 | 7.688 | 8.128 | 8.545 | 8.943 | 9.323 | 9.689 | 10.042 | 10.384 |
| bZr (fm) | 1.903 | 3.296 | 4.255 | 5.035 | 5.709 | 6.312 | 6.862 | 7.370 | 7.846 | 8.295 | 8.721 | 9.127 | 9.515 | 9.888 | 10.249 | 10.600 |
In order to achieve high precision of calculations in our study, the GPU parallel computing technology [46] is used in our Glauber model simulations.
Results and discussions
The
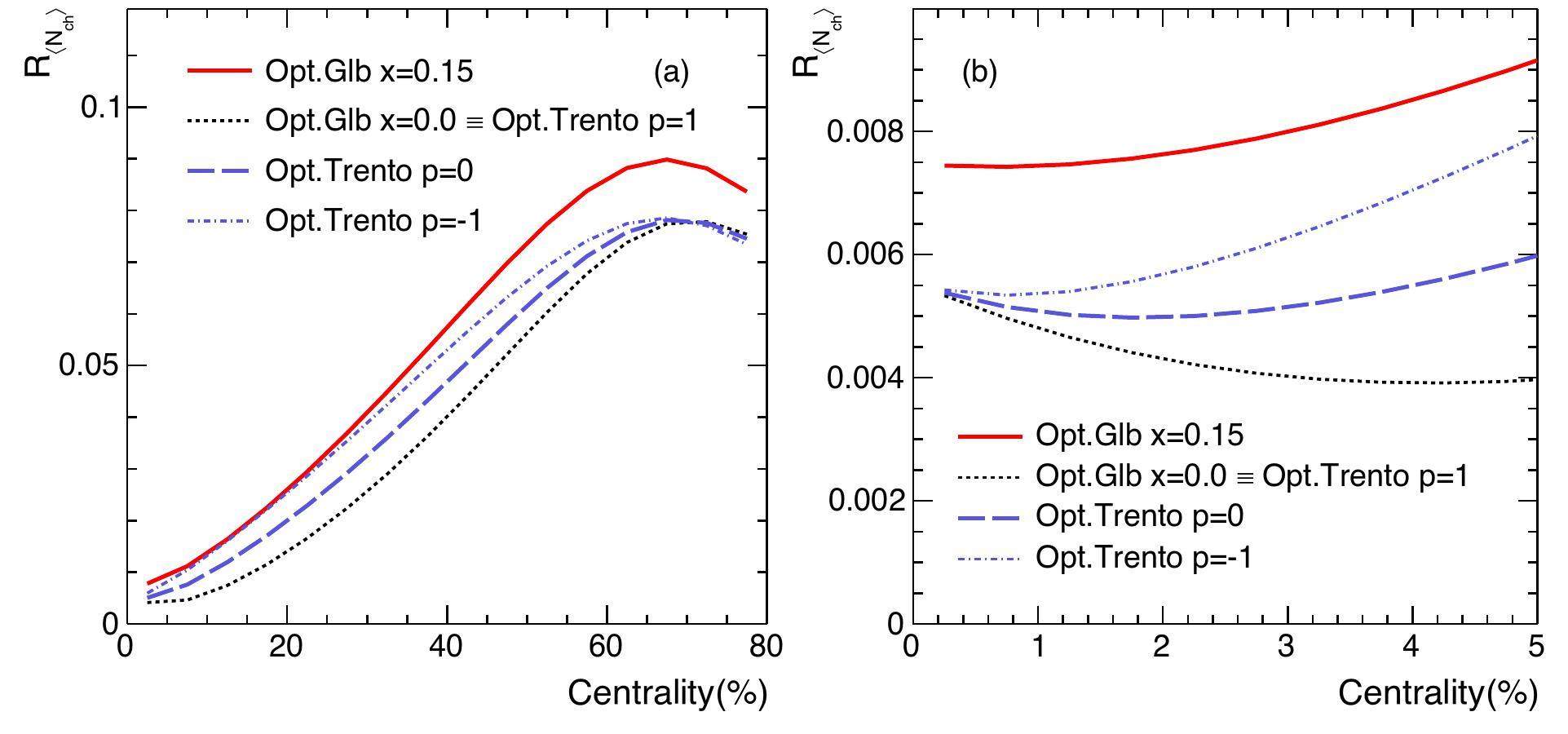
The parameters x and p are usually constrained by the individual multiplicity distributions (in this case, of isobar collisions or their mean). The
To study effects from event-by-event fluctuations, we present the
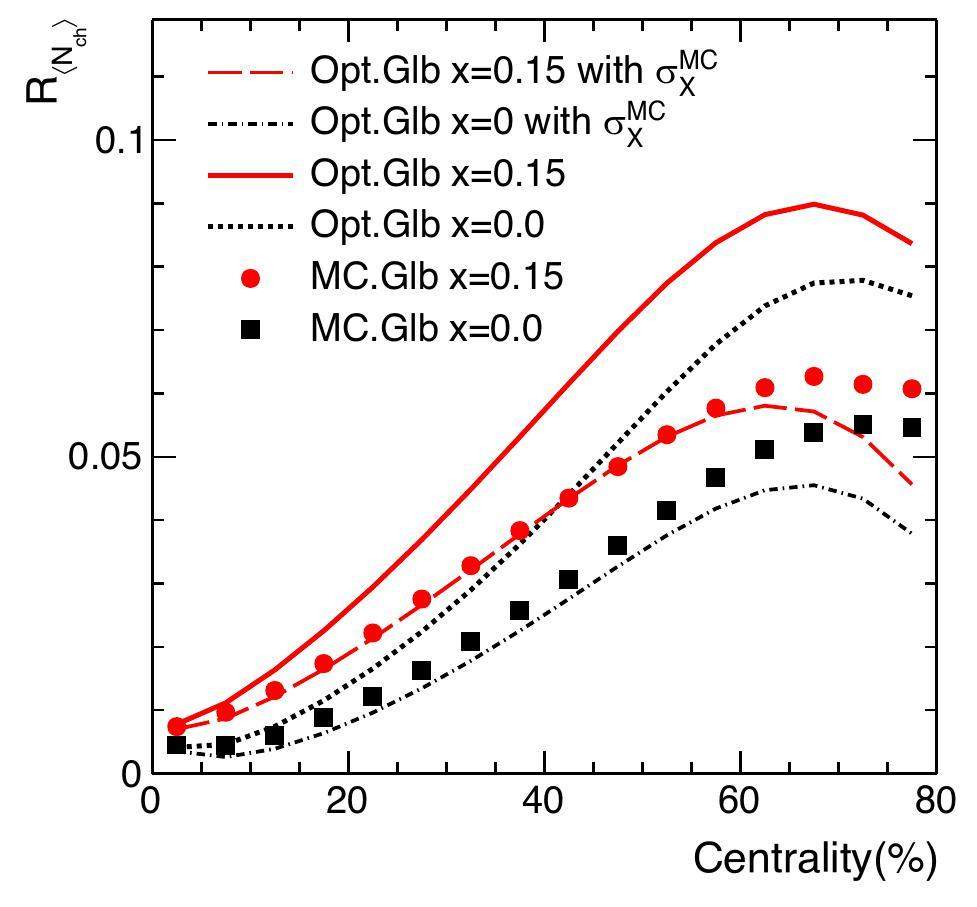
The
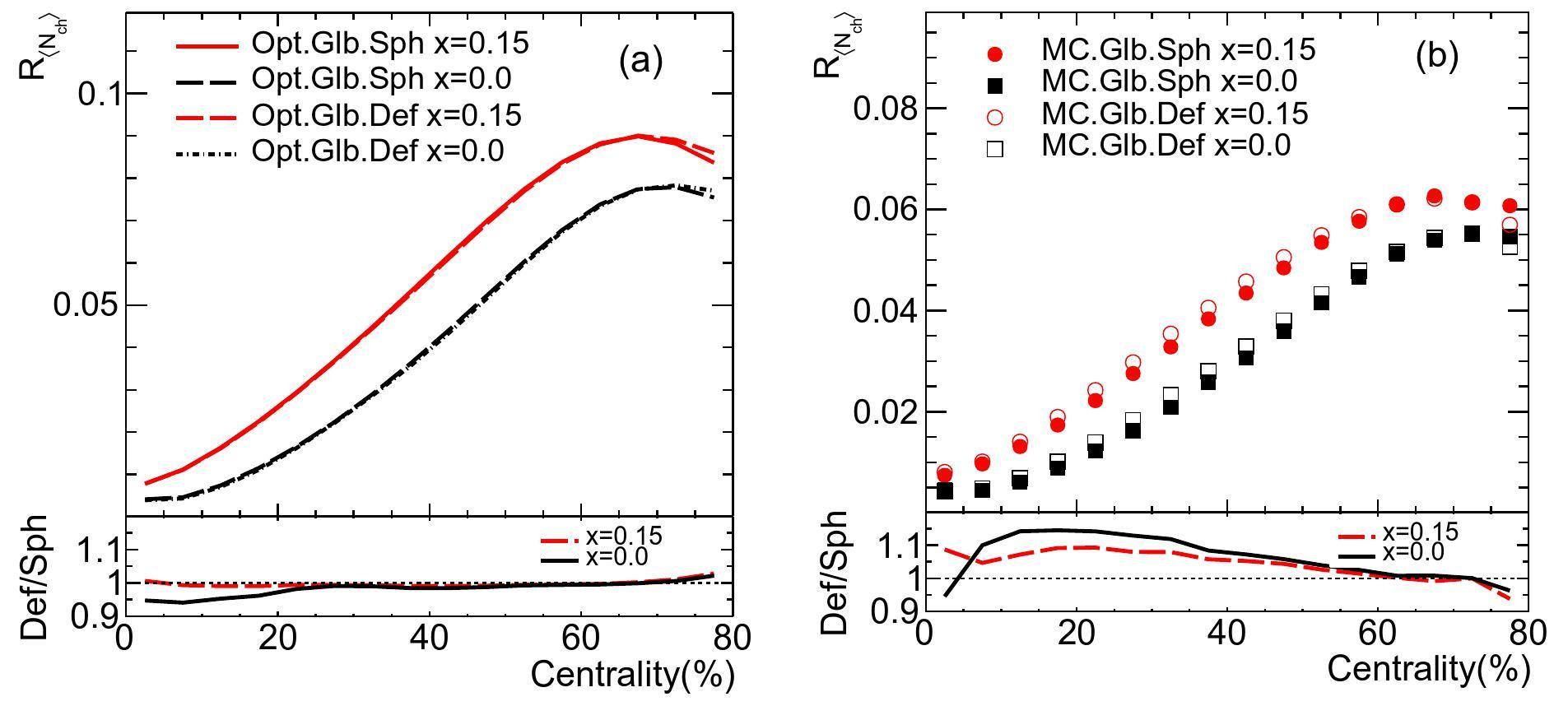
This is not the case for the anisotropic flow observables, where previous studies suggest that both nuclear deformation and event-by-event fluctuations are important [39, 49, 50]. Apart from nuclear deformation, most of the anisotropic flow produced in the most central heavy-ion collisions is due to the position fluctuations of nucleons in the colliding nuclei. In this paper, we study the effect of nuclear deformations and initial fluctuations on geometry eccentricities
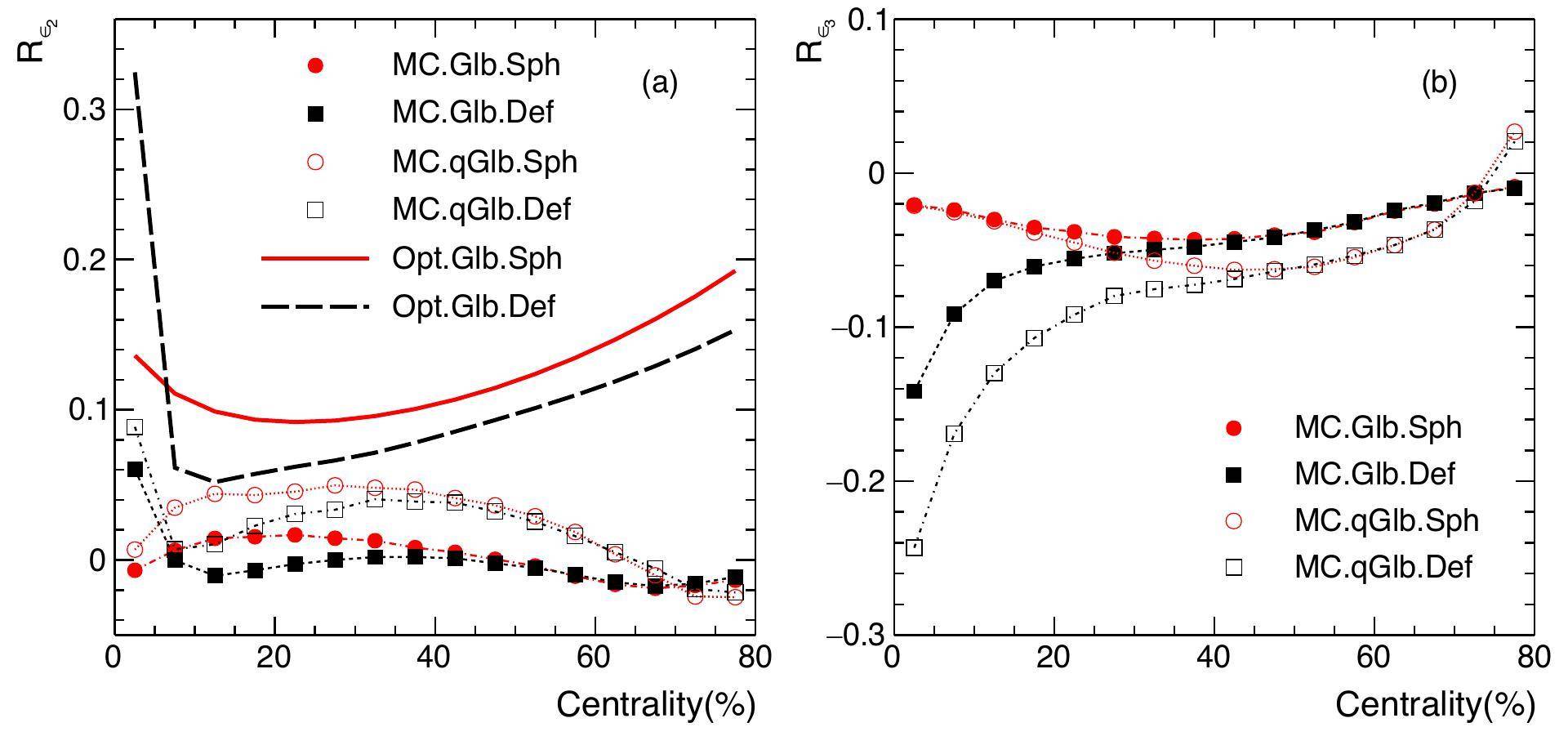
The magnitudes of
In the Monte Carlo Glauber simulation, the participating nucleons are usually treated as point-like particles as we did in the simulations above. However, nucleons have substructures [51-53]. More substructure constituents are expected to suppress the fluctuations. We use the quark participant assumption as it was done in Ref. [51], increasing the density by three times and decreasing the inelastic cross-section by a factor of 9. The results are also shown in Fig. 4. The Monte Carlo Glauber simulations under quark participant scenario significantly increase the
There are more sources of initial fluctuations in heavy ion collisions, for example, the correlations between the quarks in a nucleon, as well as the correlations between the nucleons in the colliding nuclei. We find that the minimum distance between two nucleons in simulations, as one of the sources of nucleon-nucleon correlations, does not change our results. We note that the final-state effects, which are not the focus of the present study, are also important for the accurate extraction of the symmetry energy slope parameter. We postpone such investigation to a future work.
Summary
In this work, the effects of nuclear deformations and initial fluctuations on the ratio observables in relativistic isobar collisions are studied using the Optical Glauber and Monte Carlo Glauber models. The GPU parallel computing technology is used in our calculations to achieve high precision, especially for the deformed colliding nucleus. Our main findings are as follow.
•
• Initial fluctuations affect the total cross section and thus the
• Because of the constraints of the total volumes and the measured RMS radii of the isobar nuclei, their deformations are found to have negligible effects on
• The
Our results indicate unique (in)sensitivities of the ratio observables of
Search for the chiral magnetic effect with isobar collisions at sNN=200 GeV by the STAR Collaboration at the BNL Relativistic Heavy Ion Collider
. Phys. Rev. C 105, 014901 (2022). arXiv:2109.00131, https://doi.org/10.1103/PhysRevC.105.014901Methods for a blind analysis of isobar data collected by the STAR collaboration
. Nucl. Sci. Tech. 32, 48 (2021). arXiv:1911.00596, https://doi.org/10.1007/s41365-021-00878-yImportance of isobar density distributions on the chiral magnetic effect search
. Phys. Rev. Lett. 121, 022301 (2018). arXiv:1710.03086, https://doi.org/10.1103/PhysRevLett.121.022301Multiphase transport model predictions of isobaric collisions with nuclear structure from density functional theory
. Phys. Rev. C98, 054907 (2018). arXiv:1808.06711, https://doi.org/10.1103/PhysRevC.98.054907Probing the neutron skin with ultrarelativistic isobaric collisions
. Phys. Rev. Lett. 125, 222301 (2020). arXiv:1910.06170, https://doi.org/10.1103/PhysRevLett.125.222301Evidence of Quadrupole and Octupole Deformations in 96Zr+96Zr and 96Ru+96Ru Collisions at Ultrarelativistic Energies
. Phys. Rev. Lett. 128, 022301 (2022). arXiv:2109.01631, https://doi.org/10.1103/PhysRevLett.128.022301Inferring nuclear structure from heavy isobar collisions using Trajectum
. SciPost Phys. 15, 041 (2023). arXiv:2112.13771, https://doi.org/10.21468/SciPostPhys.15.2.041Separating the Impact of Nuclear Skin and Nuclear Deformation in High-Energy Isobar Collisions
. Phys. Rev. Lett. 131, 022301 (2023). arXiv:2206.10449, https://doi.org/10.1103/PhysRevLett.131.022301Ratios of collective flow observables in high-energy isobar collisions are insensitive to final-state interactions
. Phys. Rev. C 106, L031901 (2022). arXiv:2206.01943, https://doi.org/10.1103/PhysRevC.106.L031901Impact of nuclear structure on longitudinal flow decorrelations in high-energy isobar collisions
. Phys. Lett. B 845, 138177 (2023). arXiv:2208.05416, https://doi.org/10.1016/j.physletb.2023.138177Vorticity in isobar collisions of 4496Ru+4496Ru and 4096Zr+4096Zr at sNN = 200 GeV
. Eur. Phys. J. A 59, 33 (2023). https://doi.org/10.1140/epja/s10050-023-00932-wExamination of nucleon distribution with Bayesian imaging for isobar collisions
. Phys. Rev. C 107, 064909 (2023). arXiv:2301.03910, https://doi.org/10.1103/PhysRevC.107.064909The Effects of topological charge change in heavy ion collisions: ’Event by event P and CP violation’
. Nucl. Phys. A 803, 227-253 (2008). arXiv:0711.0950, https://doi.org/10.1016/j.nuclphysa.2008.02.298Testing the Chiral Magnetic Effect with Central U+U collisions
. Phys. Rev. Lett. 105, 172301 (2010). arXiv:1006.1020, https://doi.org/10.1103/PhysRevLett.105.172301Test the chiral magnetic effect with isobaric collisions
. Phys. Rev. C 94, 041901 (2016). arXiv:1607.04697, https://doi.org/10.1103/PhysRevC.94.041901Search for the chiral magnetic effect in heavy ion collisions
. Nucl. Sci. Tech. 29, 179 (2018). https://doi.org/10.1007/s41365-018-0520-zA Skyrme parametrization from subnuclear to neutron star densities
. Nucl. Phys. A 627, 710-746 (1997). https://doi.org/10.1016/S0375-9474(97)00596-4Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XI. Stabilizing neutron stars against a ferromagnetic collapse
. Phys. Rev. C 80, 065804 (2009). arXiv:0911.3346, https://doi.org/10.1103/PhysRevC.80.065804Nuclear Zemach moments and finite-size corrections to allowed β decay
. Phys. Rev. C 94, 034314 (2016). arXiv:1607.02149, https://doi.org/10.1103/PhysRevC.94.034314Extended Skyrme interactions for nuclear matter, finite nuclei and neutron stars
. Phys. Rev. C 94, 064326 (2016). arXiv:1510.06459, https://doi.org/10.1103/PhysRevC.94.064326Determine the neutron skin type by relativistic isobaric collisions
. Phys. Lett. B 819, 136453 (2021). arXiv:2103.05595, https://doi.org/10.1016/j.physletb.2021.136453Measuring neutron skin by grazing isobaric collisions
. Phys. Rev. C 105, L011901 (2022). arXiv:2105.04052, https://doi.org/10.1103/PhysRevC.105.L011901Probing nuclear structure with mean transverse momentum in relativistic isobar collisions
. Phys. Rev. C 108, L011902 (2023). arXiv:2111.14812, https://doi.org/10.1103/PhysRevC.108.L011902Constraints on Neutron Skin Thickness and Nuclear Deformations Using Relativistic Heavy-ion Collisions from STAR
. Acta Phys. Polon. Supp. 16, 30 (2023). arXiv:2208.06149, https://doi.org/10.5506/APhysPolBSupp.16.1-A30Probing neutron-skin thickness with free spectator neutrons in ultracentral high-energy isobaric collisions
. Phys. Lett. B 834, 137441 (2022). arXiv:2203.09924, https://doi.org/10.1016/j.physletb.2022.137441Methods for systematic study of nuclear structure in high-energy collisions
. Eur. Phys. J. A 59, 110 (2023). arXiv:2302.14026, https://doi.org/10.1140/epja/s10050-023-01021-8Nuclear matter symmetry energy and the neutron skin thickness of heavy nuclei
. Phys. Rev. C 72, 064309 (2005). arXiv:nucl-th/0509009, https://doi.org/10.1103/PhysRevC.72.064309Constraints on the symmetry energy and neutron skins from experiments and theory
. Phys. Rev. C 86, 015803 (2012). arXiv:1204.0466, https://doi.org/10.1103/PhysRevC.86.015803Constraints on the skewness coefficient of symmetric nuclear matter within the nonlinear relativistic mean field model
. Nucl. Sci. Tech. 28, 185 (2017). arXiv:1402.4242, https://doi.org/10.1007/s41365-017-0329-1Determination of the neutron skin thickness from interaction cross section and charge-changing cross section for B, C, N, O, F isotopes
. Nucl. Sci. Tech. 27, 71 (2016). https://doi.org/10.1007/s41365-016-0064-zInvestigation of the symmetry energy of nuclear matter using isospin-dependent quantum molecular dynamics
. Nucl. Sci. Tech. 31, 61 (2020). https://doi.org/10.1007/s41365-020-00766-xProgress in Constraining Nuclear Symmetry Energy Using Neutron Star Observables Since GW170817
. Universe 7, 182 (2021). arXiv:2105.04629, https://doi.org/10.3390/universe7060182Decoding the nuclear symmetry energy event-by-event in heavy-ion collisions with machine learning
. Phys. Lett. B 835, 137508 (2022). arXiv:2208.10681, https://doi.org/10.1016/j.physletb.2022.137508Determination of neutron-skin thickness using configurational information entropy
. Nucl. Sci. Tech. 33, 6 (2022). arXiv:2201.01442, https://doi.org/10.1007/s41365-022-00997-0Constraining nuclear symmetry energy with the charge radii of mirror-pair nuclei
. Nucl. Sci. Tech. 34, 119 (2023). arXiv:2303.14667, https://doi.org/10.1007/s41365-023-01269-1Nuclear ground-state masses and deformations: FRDM(2012)
. Atom. Data Nucl. Data Tabl. 109-110, 1-204 (2016). arXiv:1508.06294, https://doi.org/10.1016/j.adt.2015.10.002Nuclear mass table in deformed relativistic Hartree–Bogoliubov theory in continuum, I: Even–even nuclei
. Atom. Data Nucl. Data Tabl. 144, 101488 (2022). arXiv:2201.03216, https://doi.org/10.1016/j.adt.2022.101488Anisotropic transverse flow and the quark hadron phase transition
. Phys. Rev. C 62, 054909 (2000). arXiv:hep-ph/0006129, https://doi.org/10.1103/PhysRevC.62.054909Glauber modeling in high energy nuclear collisions
. Ann. Rev. Nucl. Part. Sci. 57, 205-243 (2007). arXiv:nucl-ex/0701025, https://doi.org/10.1146/annurev.nucl.57.090506.123020Improved Monte Carlo Glauber predictions at present and future nuclear colliders
. Phys. Rev. C 97, 054910 (2018). [Erratum: Phys.Rev.C 99, 019901 (2019)]. arXiv:1710.07098, https://doi.org/10.1103/PhysRevC.97.054910Alternative ansatz to wounded nucleon and binary collision scaling in high-energy nuclear collisions
. Phys. Rev. C 92, 011901 (2015). arXiv:1412.4708, https://doi.org/10.1103/PhysRevC.92.011901Applying Bayesian parameter estimation to relativistic heavy-ion collisions: simultaneous characterization of the initial state and quark-gluon plasma medium
. Phys. Rev. C 94, 024907 (2016). arXiv:1605.03954, https://doi.org/10.1103/PhysRevC.94.024907Methods for analyzing anisotropic flow in relativistic nuclear collisions
. Phys. Rev. C 58, 1671-1678 (1998). arXiv:nucl-ex/9805001, https://doi.org/10.1103/PhysRevC.58.1671Linear and cubic response to the initial eccentricity in heavy-ion collisions
. Phys. Rev. C 93, 014909 (2016). arXiv:1511.03896, https://doi.org/10.1103/PhysRevC.93.014909Probing the nuclear deformation with three-particle asymmetric cumulant in RHIC isobar runs
. Phys. Lett. B 839, 137838 (2023). arXiv:2204.02387, https://doi.org/10.1016/j.physletb.2023.137838ZMCintegral: a Package for Multi-Dimensional Monte Carlo Integration on Multi-GPUs
. Comput. Phys. Commun. 248, 106962 (2020). arXiv:1902.07916, https://doi.org/10.1016/j.cpc.2019.106962Tables of E2 Transition Probabilities from the first 2+ States in Even-Even Nuclei
. Atom. Data Nucl. Data Tabl. 107, 1-139 (2016). [Erratum: Atom.Data Nucl.Data Tabl. 114, 371–374 (2017)]. arXiv:1312.5975, https://doi.org/10.1016/j.adt.2015.10.001REDUCED ELECTRIC-OCTUPOLE TRANSITION PROBABILITIES, B (E 3;01+ 31-)—AN UPDATE
. Atom. Data Nucl. Data Tabl. 80, 35-82 (2002). https://doi.org/10.1006/adnd.2001.0871Collision geometry fluctuations and triangular flow in heavy-ion collisions
. Phys. Rev. C 81, 054905 (2010). [Erratum: Phys.Rev.C 82, 039903 (2010)]. arXiv:1003.0194, https://doi.org/10.1103/PhysRevC.82.039903Elliptic and triangular flow in event-by-event (3+1)D viscous hydrodynamics
. Phys. Rev. Lett. 106, 042301 (2011). arXiv:1009.3244, https://doi.org/10.1103/PhysRevLett.106.042301Nucleon participants or quark participants
? Phys. Rev. C 67, 064905 (2003). arXiv:nucl-th/0302071, https://doi.org/10.1103/PhysRevC.67.064905Glauber modeling of high-energy nuclear collisions at the subnucleon level
. Phys. Rev. C 94, 024914 (2016). arXiv:1603.07375, https://doi.org/10.1103/PhysRevC.94.024914Symmetric cumulants as a probe of the proton substructure at LHC energies
. Phys. Lett. B 778, 128-136 (2018). arXiv:1707.05592, https://doi.org/10.1016/j.physletb.2018.01.011The authors declare that they have no competing interests.


