Introduction
The Coherent Elastic Neutrino-Nucleus Scattering (CEνNS) process has garnered considerable attention since it was first detected in 2017 by the COHERENT collaboration [1]. Owing to the coherent enhancement of the cross-section (2–3 orders of magnitude higher than any other neutrino matter interaction process with neutrino energies below 100 MeV) and nearly pure electromagnetic-weak dynamics (the cross-section is easy to calculate), the CEνNS process serves as a valuable probe and novel neutrino detection method. As a probe with precise cross-section measurement, it examines the Standard Model at low momentum transfer, aids the understanding of core-collapsed supernova bursts [2, 3], helps to determine the neutron radius of a nucleus [4], and clarifies neutrino fog in WIMP dark matter searches, such as CDEX and PandaX experiments [5, 6]. As a new neutrino detection method, it offers a flavor-independent approach for searching sterile neutrinos because it is insensitive to neutrino flavors but sensitive to all flavors of neutrinos [7], sensitive detection of solar and supernova neutrinos, and threshold-free method to measure the reactor neutrino spectrum below the 1.8 MeV Inverse Beta Decay (IBD) threshold, which would be highly valuable for reactor oscillation experiments such as JUNO [8]. However, the typical observable ionization energy of a recoiled nucleus is only approximately 1 keV electron equivalent (keVee), making signal detection highly challenging. Various technologies have been proposed for detecting CEνNS signals. For instance, the RELICS project plans to utilize liquid-xenon detectors [9], whereas the RECODE experiment opts for HPGe detectors [10].
To precisely measure the cross-section of the CEνNS process and advance detector technology based on CEνNS, we propose the CLOVERS (Coherent eLastic neutrinO(V)-nucleus scattERing at the China Spallation Neutron Source (CSNS)) experiment [11, 12]. Cryogenic pure CsI (pCsI) detectors are adopted because of their large cross section, proportional to the square of the neutron number in the nucleus [13], and high light yield, reaching 33.5 photo-electrons (PE)/keVee coupled to photomultiplier tube (PMT) [14] and 43.0PE/keVee coupled to Si photomultiplier (SiPM) [15]. To better understand and enhance the performance of the cryogenic pCsI detector, a detailed characterization and optimization was conducted. In this study, the light yield, energy resolution, and scintillation decay time of pCsI crystals at 77 K were characterized. Moreover, the influence of temperature, crystal shape, and crystal surface treatment on light yield was investigated. A world-leading energy resolution for scintillator detectors was achieved, and a direction for optimizing future CLOVERS 10 kg pCsI detectors was identified.
Experimental setup
The experimental setup used in this study is illustrated in Fig. 1. The pCsI crystals obtained from HAMAMATSU BEIJING has two different shapes: 2 cm×2 cm×2 cm cubes and Φ2.5×2 cm3 cylinders. The light output surfaces of all the crystals were polished, whereas the remaining surfaces were ground or polished, depending on the specific crystal. The arithmetic mean roughness values (Ra) of the surfaces were approximately 40 for polished surfaces and 800 for ground surfaces.
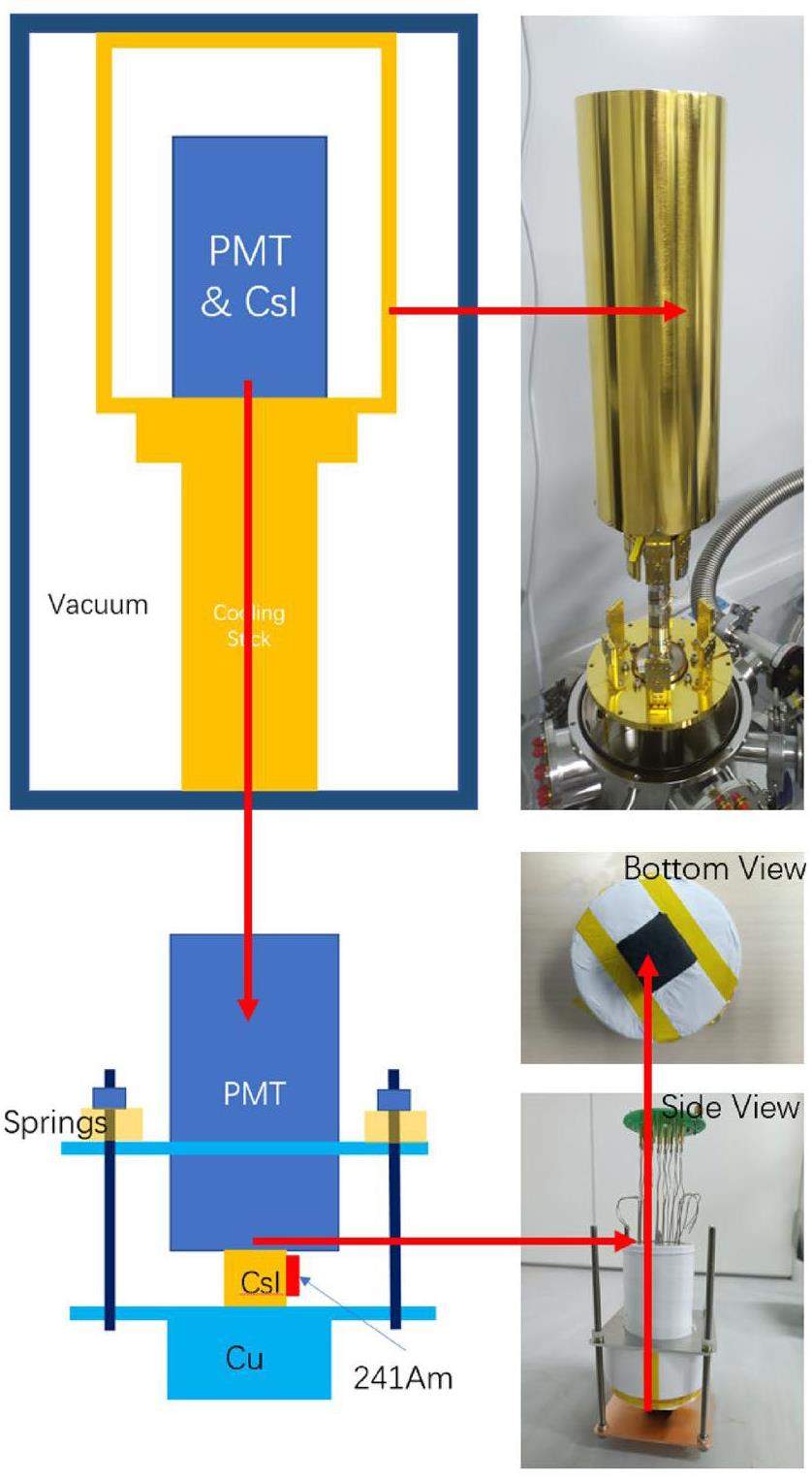
An 241Am radioactive source was affixed to the side surface of the crystal. Signals generated by 10–26 keV X-rays and 59.54 keV gamma rays were used to characterize and optimize the detector. The crystal was directly coupled to the quartz window of a 3-in HAMAMATSU R11065 because the commonly used optical coupling grease or silicon rubber deforms at low temperatures and deteriorates the light-coupling effect. To minimize light leakage, the side and bottom surfaces of the crystal, as well as the remaining area of the PMT window, were enveloped in four layers of Luxiumsolutions BC-642 Teflon reflection material. Outside the Teflon-type, the crystal was warped with black masking tape to protect the Teflon layers from stretching. Springs were employed to press the PMT window against the light output surface of the crystal, ensuring adequate optical contact between the PMT and the crystal as well as thermal contact between the crystal and the copper base coupled to the cooling platform using cryogenic vacuum silicone thermal grease outside the black masking tape.
The cryogenic system comprised a custom vacuum chamber, Agilent TPS-mini molecular pump, CryoPride KDC6000V helium compressor and CryoPride KDE401SA refrigerating machine capable of achieving a vacuum pressure below 1×10-6 Pa and temperature as low as 3 K. Temperature control and monitoring were performed using a Lake Shore Model 325.
The R11065 PMT was powered by a CAEN NDT1470 HV module with a high negative voltage of 1500 V. The PMT signal was read using a CAEN DT5751 digitizer with 1 GHz sampling rate, 500 MHz bandwidth, 1 Vpp dynamic range, and 10 bit resolution. The working mode of the DT5751 was set to a self-trigger, and the trigger threshold was set to 30 ADC counts. The original waveform data were directly recorded in the CERN ROOT format using a modified WaveDump software [16, 17].
Data analysis
A typical signal waveform induced by 59.54 keV gamma from 241Am in pCsI at 77 K is shown in Fig. 2. Each waveform consists of 8000 samples, corresponding to a duration of 8000, given the 1 GHz sampling rate of DT5751.
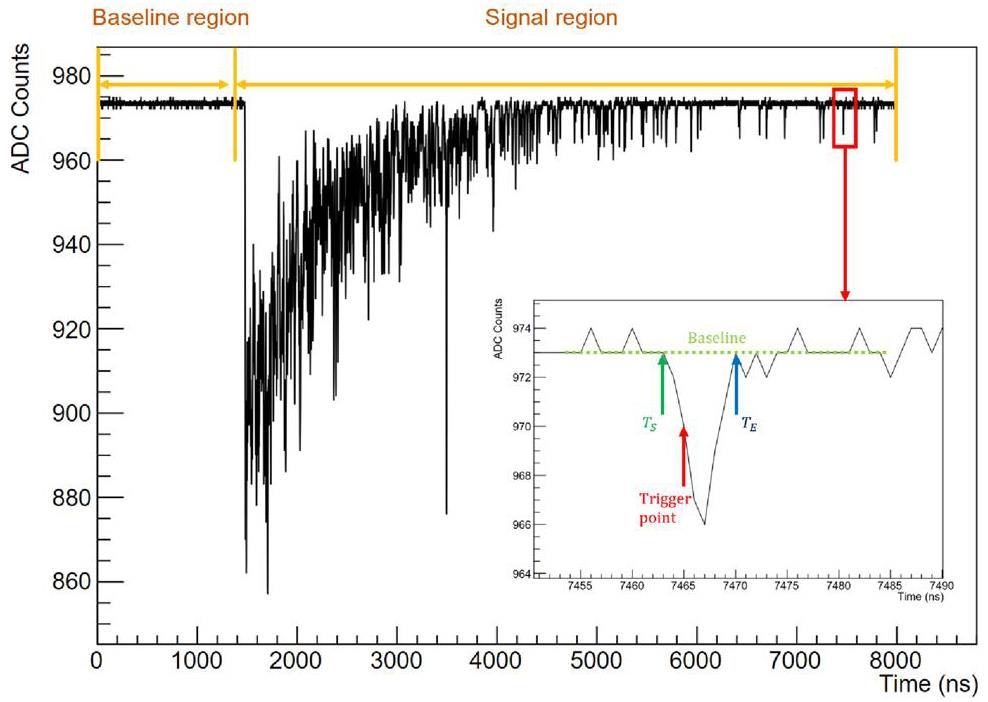
To analyze the waveforms, a toolkit based on C++ and CERN ROOT was developed [18] by implementing the following algorithm:
1. The waveform is divided into two regions: the baseline (BL) region covering samples 0–1399 and the signal (SG) region covering samples 1400–7999.
2. In the BL region, the mean value (μBL) and standard deviation (σBL) of the baseline for each waveform are decided.
3. Next, the baseline of the waveform is adjusted to 0, and the waveform is inverted.
4. A peak-searching algorithm to identify all peaks in the SG region is applied. A peak is identified when a sample deviates from 0 by at least 5σBL. This sample is defined as the trigger point. The start (TS) and end (TE) of each peak are defined by the first sample falling back to 0 backwards and forwards from the trigger point, as illustrated in the subplot of Fig. 2.
5. The integral of the ADC numbers of each peak is recorded in a C++ std::vector named PeakQ for each event. The total charge, that is, the sum of all elements in PeakQ, is stored as a C++ float variable named TotalQ for each event. These variables are utilized to derive the results in subsequent analyses.
Characterization of pCsI detector at 77 K
Using the setup and analysis methods described in Sect. 2 and Sect. 3, the light yield, energy resolution and scintillation decay time of pCsI detector at 77 K were measured. The crystal used in this characterization was a 2 cm×2 cm×2 cm cube, with all polished surfaces.
Single PE calibration of the PMT
Single-photoelectron (SPE) calibration was necessary to determine the light yield of the pCsI detector. The online SPE calibration was performed by populating a histogram (Fig. 3 with the PeakQ values of peaks with TS between 7000 and 7999 for all events in dataset. As depicted in Fig. 2, within the 7000-7999 ns range, the pulses are sparse, with each likely corresponding to an SPE. The subplot shows a typical SPE signal. Given the small contributions of multi-PE events, the histogram in Fig. 3 is fitted using a simplified SPE model, similar to the one described in Ref. [19].
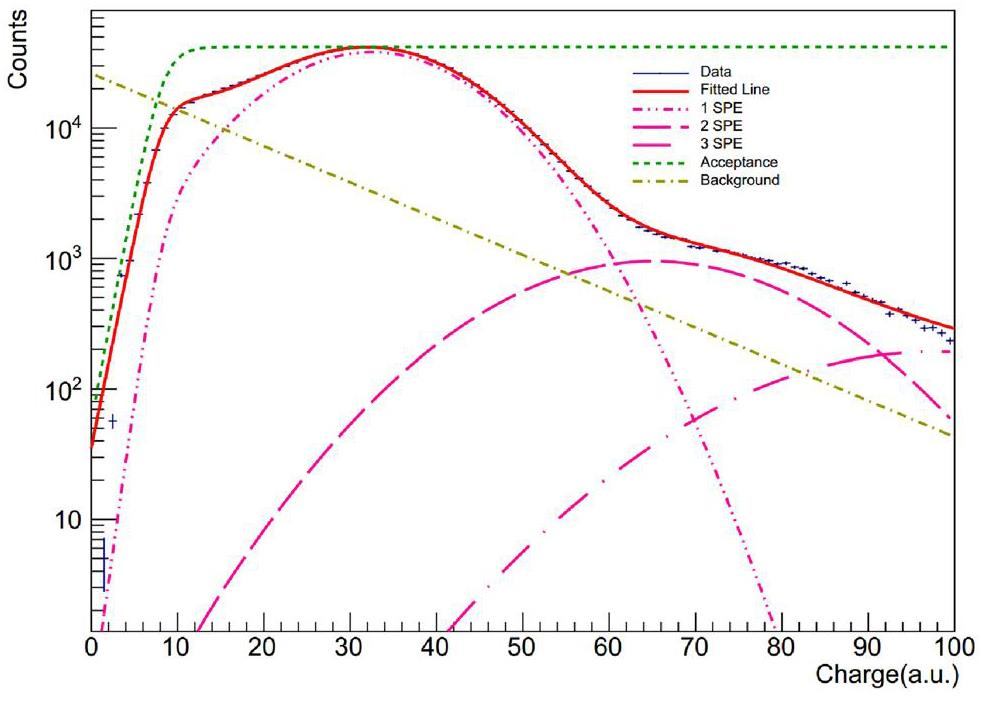
The fitted curves are shown in Fig. 3. The fitted results are as follows: Qspe=32.50(3) and σspe = 10.37(3) in units of ADC count ·ns.
Light yield and energy resolution of pCsI
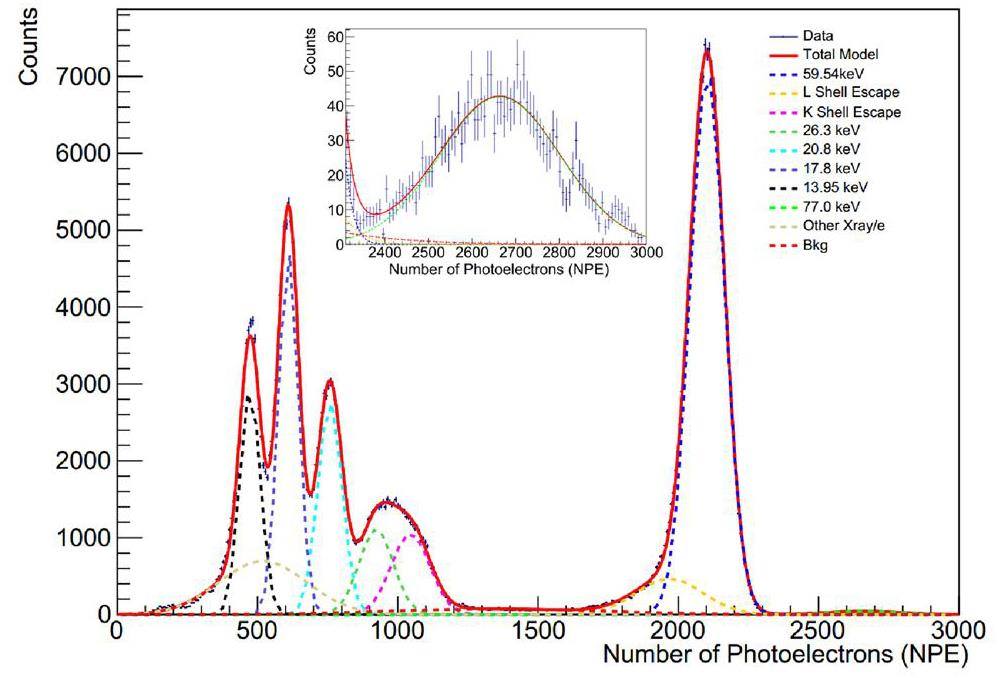
The recorded energy spectrum of 241Am measured in terms of the number of photoelectrons (NPE) generated during each event is shown in Fig. 4 with the fitting results listed in Table 1 The NPE is computed using the following formula:
| Type | Energy (keVee) | μnpe | σnpe | LY (NPE/keVee) | FHWM (%) |
|---|---|---|---|---|---|
| γ | 59.54 | 2103.4 | 61.46 | 35.3 | 6.9 |
| L shell excape | 55.43* | 1968.4 | 119.2 | 35.5 | 14.3 |
| K shell excape | 29.5* | 1045.6 | 68.7 | 35.4 | 15.5 |
| γ | 26.3 | 922.8 | 61.2 | 35.1 | 15.6 |
| X-ray | 20.8† | 758.3 | 43.1 | 36.5 | 13.4 |
| X-ray | 17.8† | 610.2 | 35.5 | 34.3 | 13.7 |
| X-ray | 13.95† | 473.5 | 36.7 | 33.9 | 18.2 |
| Coincidence | 77.3 | 2664.0 | 137.7 | 34.5 | 12.2 |
The spectrum undergoes a global fit by employing ten unconstrained Gaussian functions to accommodate the various components. The 59.54 keV and 26.3 keV gamma peaks originate from intrinsic gamma rays emitted during 241Am decay. The K-shell escape and L Shell escape peaks are unique to CsI detectors because of the delayed release or escape of X-rays or Auger electrons after a 59.54 keV gamma ejects a K- or L-shell electron into Cs or I atoms. The 13.95, 17.8, and 20.8 keV X-rays originated from the activated states of 237Np, a decay product of 241Am. These peaks are merged because of nearby X-rays rather than monotonous X-rays. The 77 keV peak arises from the coincidence of the 59.54 keV gamma-rays and X-rays. The Bkg component accounts for events from an environmentally radioactive background. In addition, another X-ray/e component addresses the complex X-ray and electron spectra below 25 keV, requiring more than three Gaussian functions to achieve fitting convergence. However, using a single Gaussian function to describe other X-ray/e spectra remains oversimplified, resulting in an overall χ2/ndf value of 4.0. However, when the χ2/ndf calculation is constrained to the range NPE∈ [600, 3000], the value improves to 1.8. We did not pursue a more refined model for the Other X-ray/e components because their influence on the fitting of the peaks, which are used to determine the light yield, should be minimal because of the significant prominence of the peaks as long as the fitting converges.
The fitted curves and their components are shown in Fig. 4, with fitting results listed in Table 1. The detector light yield (LY) at various energy points is calculated as:
The light yield results obtained at various energy points were fitted using a zero-order polynomial function to determine the mean light yield and the associated uncertainties. The fitted results are shown in Fig. 5. The error bars in the graph represent the standard deviation of the Gaussian function fitted at different energy points divided by the energy (σnpe/Energy). The final mean light yield of the pCsI detector at 77 K is 35.20.6PE/keVee, which is slightly higher than the assumed value used in the CLOVERS sensitivity estimation, 33.50.7PE/keVee, as reported in Ref. [14], where the CsI crystal was also coupled to an R11065 PMT.
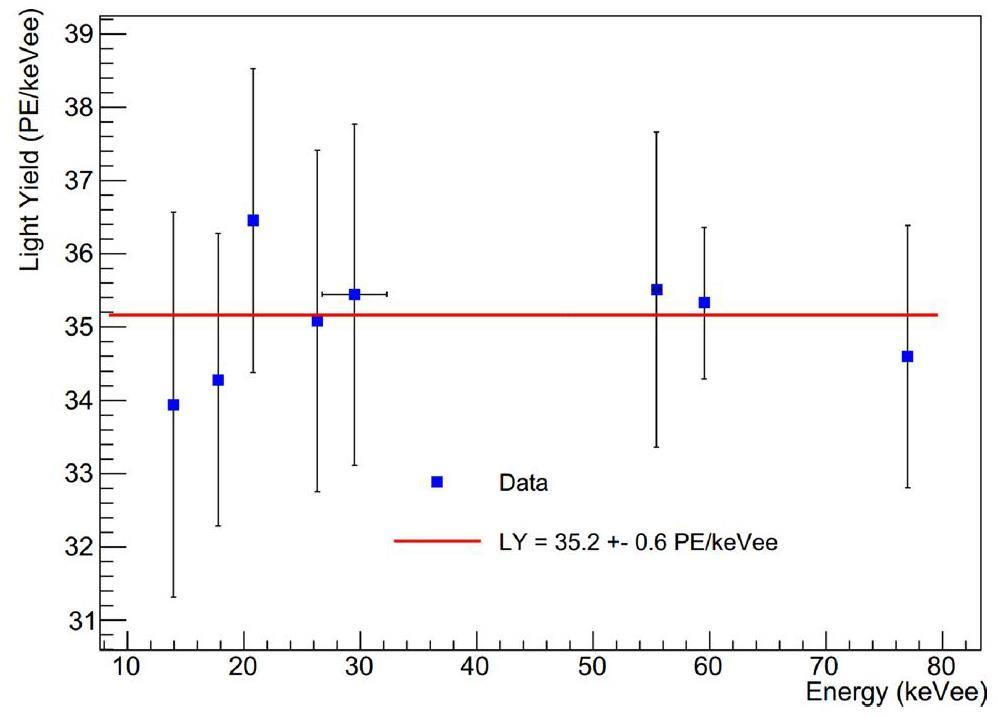
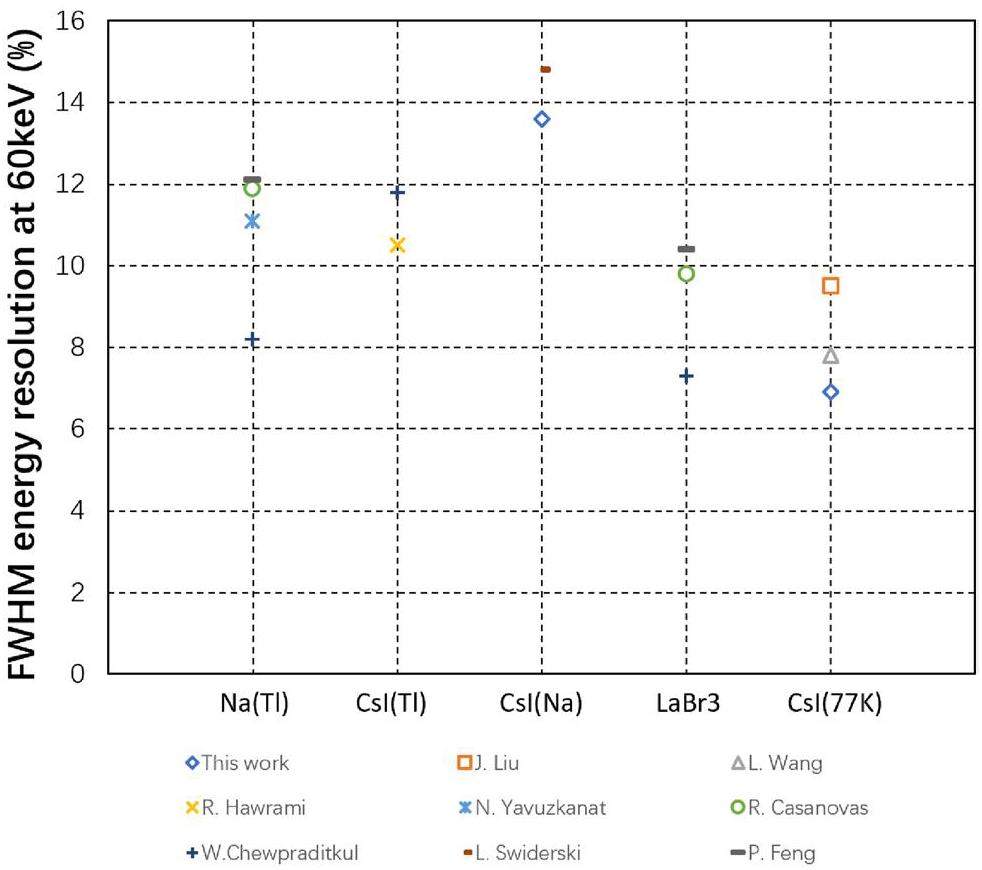
The most remarkable achievement of this study is the world-leading energy resolution achieved by scintillator detectors. Given that the 59.54 keV gamma peak is monotonic (unlike the X-rays, K/L Shell escape, and coincidence peaks) and is less influenced by nearby peaks (unlike the 26.3 keV gamma peak, which is strongly affected by nearby X-rays and K shell escape peaks), its resolution is chosen to represent the overall resolution of this study. The full width at half maximum (FWHM) energy resolution of this pCsI detector at 77 K at 59.54 keV reached 6.9%, surpassing the reported 9.5% in Ref. [14], 8.8% in Ref. [21] and 7.8% in Refs. [22], making it the best among all the reported resolutions of cryogenic pCsI detectors. This resolution even outperforms that of the brightest inorganic scintillators typically used at room temperature, such as NaI(Tl), CsI(Na), CsI(Tl) or LaBr3. A summary of the comparison is presented in Fig. 6.
Scintllation decay time of pCsI
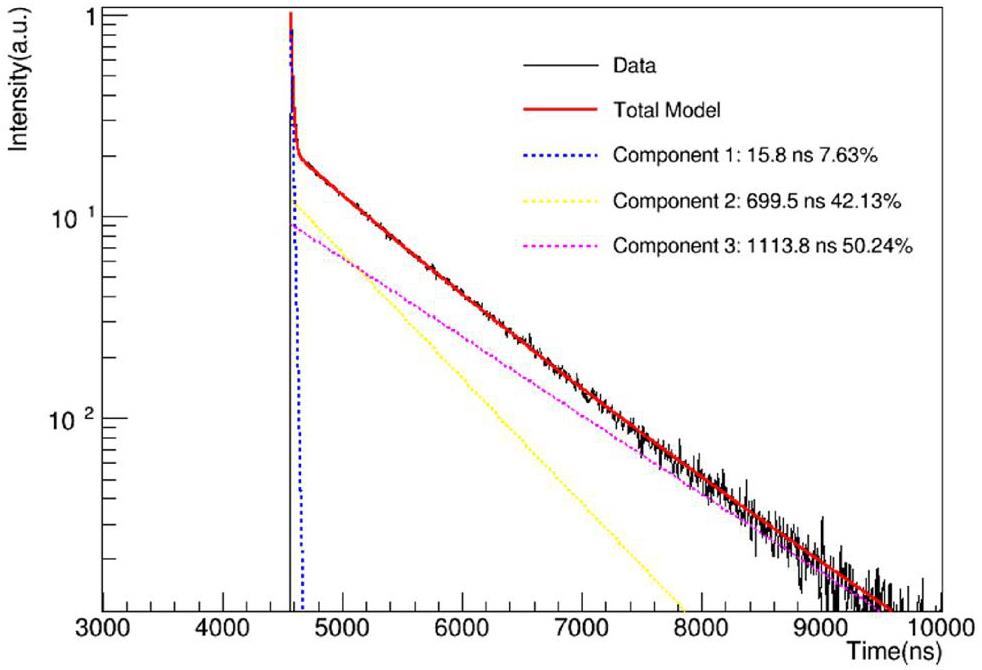
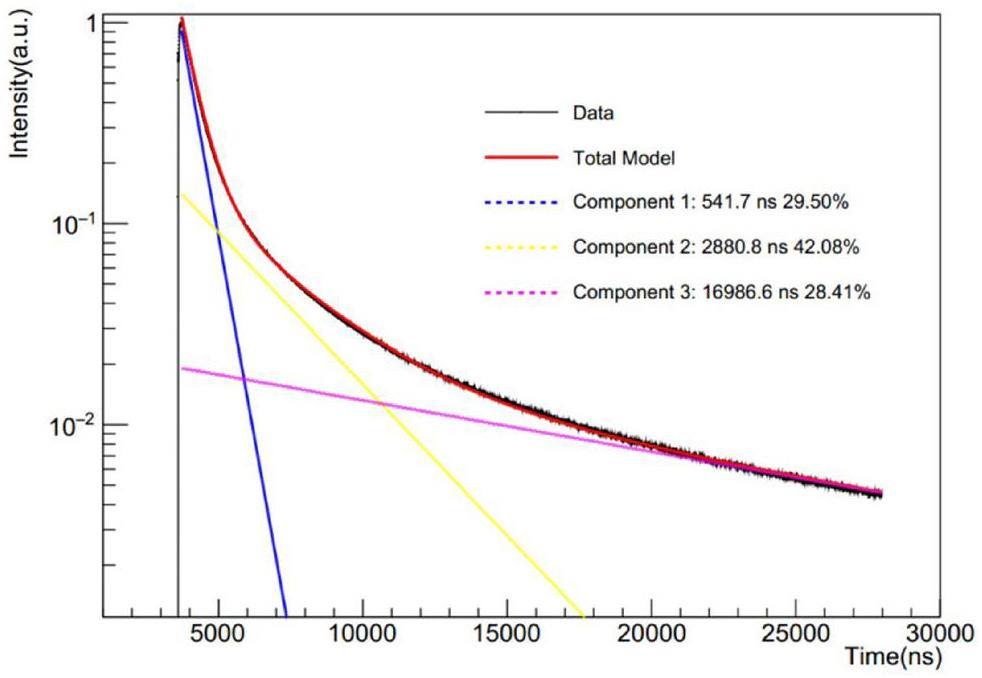
The scintillation decay time of the pCsI detector at 77 K was determined by fitting the accumulated and normalized waveforms to three exponential components. The waveforms and fitted results are shown in Fig. 7. The decay time of the slowest component of pCsI at 77 K is approximately 1 μs, which is considerably faster than that of the CsI(Na) crystal, which is approximately 17 μs, as shown in Fig. 8. These results are consistent with those in previous studies [29-32]. The considerably shorter decay time of pCsI significantly reduces the afterglow background induced by environmental radioactive events, which contaminates approximately 30% of all events in the COHERENT CsI(Na) experiment [19].
Optimization of cryogenic pCsI detector
To optimize the performance of the cryogenic pCsI detector, investigations were conducted to assess the influence of the temperature, surface treatment, and crystal shape on the light yield.
Influence of temperature on the light yield
The relative light yields of the pCsI detector at different temperatures are shown in Fig. 9, alongside results from V. Mikhailik [33], C. Amsler [29], X. Zhang [34] and W.K.Kim [32]. The results of this study and those of Mikhailik are normalized to the maximum value for each dataset. However, Amsler and Zhang and W.K. Kim do not include data points below 77 K; therefore, their light yields are normalized to the values in this study at 77 K based on their results at the same temperature. All results show good agreement in the overall trend, with slight differences, possibly owing to variations in the PMT setup and crystal used.
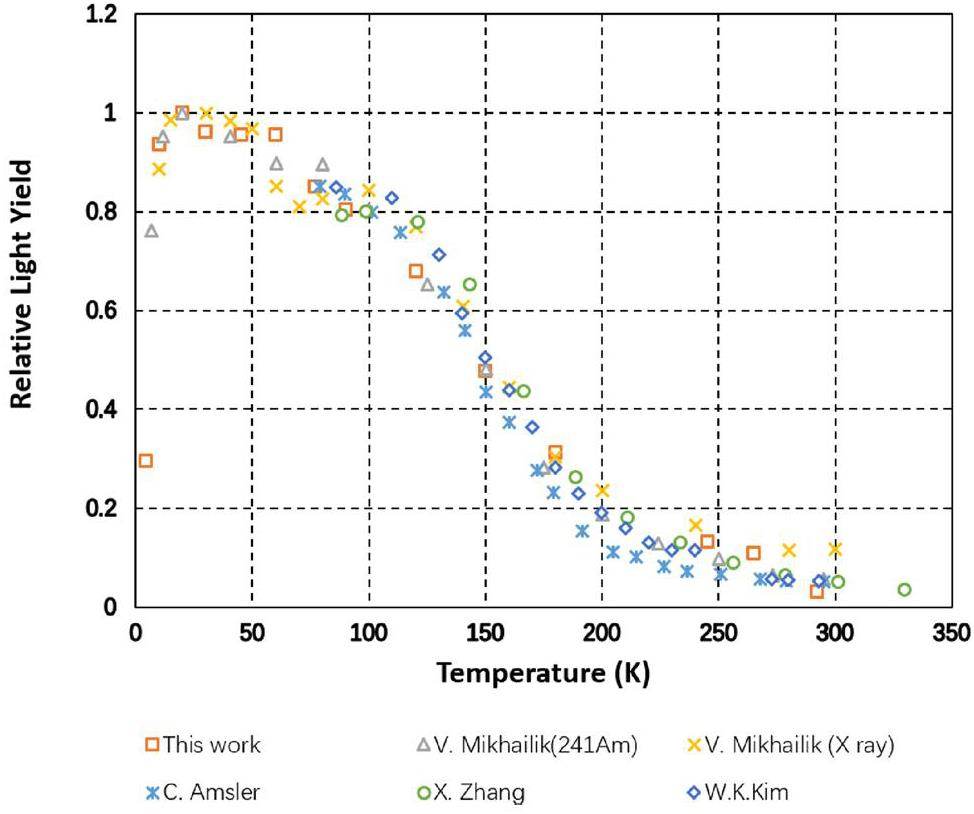
The light yield increases rapidly as the temperature decreases from room temperature to approximately 100 K. Subsequently, it reached a plateau between 70 K and 100 K, followed by a slight increase at approximately 60 K. The maximum light yield was attained at approximately 20 K, after which it decreased rapidly as the temperature decreased, which is consistent with both our results and those of Mikhailik. Although there is a 20% increase in light yield from 77 K to 20 K, cooling down to 20 K is considerably more challenging than cooling to 77 K, which can be easily achieved with liquid nitrogen, is inexpensive, and safer than liquid hydrogen, which must be obtained to 20 K.
Because the light yield remains relatively stable between 70 K and 100 K, another potential approach is to place pCsI in an 87 K liquid argon environment and utilize liquid argon as an active veto system to reject the background introduced by external particles such as neutrons or gamma rays.
Influence of surface treatment on the light yield
In addition to temperature, another factor that could influence the light yield is the surface treatment of the crystal, which affects the light-collection efficiency of the detector system, as mentioned in Ref. [35]. [36] and Ref. [37]. To optimize the surface treatment (ground or polished), four comparison experiments were conducted.
Experiment A compared the light yields of two cubic crystals subjected to different surface treatments. One crystal had all its surfaces polished, whereas the other had a surface ground, except for the light output surface. The ratio between the light yield of the ground and polished crystals, Rly, is defined as follows:

Experiment B was identical to Experiment A except that the crystals were cylindrical rather than cubic.
Experiments A and B compared the different crystals. To eliminate differences between crystals, Experiments C and D were conducted. In Experiment C, a cubic crystal was initially ground and then polished, and the light yields were measured before and after polishing. Experiment D was identical to Experiment C, except that a different ground crystal was used. Experiments C and D were conducted at the room temperature.
In addition to these four experiments with pCsI crystals, similar experiments were conducted for CsI(Na) and CsI(Tl) crystals using the same procedure as in Experiments C and D, respectively. The measured Rly from the experiments are listed in Table 2.
| Experiment | pCsI(A) | pCsI(B) | pCsI(C) | pCsI(D) | CsI(Na) | CsI(Tl) |
|---|---|---|---|---|---|---|
| Rly(293K) | 0.68 | 0.62 | 0.63 | 0.68 | 0.94 | 1.0 |
| Rly(77K) | 0.70 | 0.68 | - | - | - | - |
As shown in Table 2, the light yields of the ground crystals are consistent at approximately 60–70% of the polished crystals, regardless of the temperature, crystal shape, or individual crystals. However, the ratio of CsI(Na) to CsI(Tl) are almost 1. We hypothesize that UV light (310 nm at room temperature [38, 39] and 340 nm at 77 K [38]) emitted by pCsI is more likely to be absorbed by microstructures on the ground surface. In contrast, light with longer wavelengths emitted by CsI(Na) (420 nm [40, 41]) and CsI(Tl) (550 nm [42, 43]) is less susceptible to absorption by these microstructures. Although this hypothesis requires further verification, the results suggest that for future 10 kg pCsI detectors in the CLOVERS experiment, all crystal surfaces should be polished to achieve higher light yields.
Influence of crystal shape on the light yield
The crystal shape may also influence the light yield, as reported in Ref. [44] and Ref. [45]. The light yields of cubic and cylindrical crystals were compared for both the ground and polished crystals. The results are presented in Table 3. The light yields and energy resolutions of the cubic crystals are slightly higher than those of the cylindrical crystals under both ground and polished conditions; however, the difference is not significant. Therefore, in future CLOVERS experiments, the choice of the crystal shape may depend on the shape of the photon detector to balance the light collection efficiency and detector mass. For instance, the crystal should be cuboidal for SiPMs with square cathode regions and cylindrical for PMTs with circular cathode regions.
| Crystal | LY(PE/keVee) | FWHM(%) |
|---|---|---|
| Cubic (polished) | 35.2 | 6.9 |
| Cubic (ground) | 24.8 | 7.8 |
| Cylindrical (polished) | 33.9 | 7.1 |
| Cylindrical (ground) | 22.3 | 7.9 |
Summary
We measured the light yield, energy resolution, and scintillation decay time of pCsI detectors at 77 K coupled with PMT HAMAMASTU R11065. We achieved a light yield of 35.2PE/keVee, surpassing the assumed value for CLOVERS sensitivity estimation, and an unprecedented energy resolution of 6.9% FWHM at 59.54 keV, which is the best ever for cryogenic pCsI detectors and world-leading scintillation detectors. The improved light yield and resolution enhanced the sensitivity of CEvNS detection. The shorter scintillation decay time of pCsI at 77 K compared with that of CsI(Na) at room temperature also implies that it is much less likely for afterglow photons from a previous environmental radioactive event to fake a real CEνNS signal, suppressing this kind of background significantly.
To optimize the future CLOVERS 10 kg pCsI detector, we investigated the effects of temperature, surface treatment, and crystal shape. Although the light yield peaks at approximately 20 K, cooling a 10 kg material to 20 K was challenging. As the light yield remained stable between 70 and 100 K, placing pCsI in liquid argon at 87 K may be a more viable option, utilizing liquid argon as an active veto system to mitigate the outer background.
Surface treatment significantly affected the light yield, with ground crystals yielding only 60–70% polished crystals. However, the crystal shape had a minimal influence on the light yield. These findings suggest that for future CLOVERS 10 kg pCsI detectors, crystals should be polished, and their shape should match the cathode area of the photon detectors to maximize light yield and utilize the entire sensitive area of the photon detector.
Observation of coherent elastic neutrino-nucleus scattering
. Science 357, 1123-1126 (2017). https://doi.org/10.1126/science.aao0990Core-collapse supernovae, neutrinos, and gravitational waves
. Nuclear Physics B-Proceedings Supplements 235, 381-387 (2013). https://doi.org/10.1007/978-3-319-99747-6Neutrino signature of supernova hydrodynamical instabilities in three dimensions
. Phys. Rev. Lett. 111,Neutron radius determination of 133Cs and its impact on the interpretation of CEvNS-CsI measurement
. Arxiv. arXiv:2403.03566Introduction to the CDEX experiment
. Front. Phys. (Beijing) 8, 412-437 (2013)., https://doi.org/10.1007/s11467-013-0349-1PandaX: A Liquid Xenon Dark Matter Experiment at CJPL
. Sci. China Phys. Mech. Astron. 57, 1476-1494 (2014). arXiv:1405.2882, https://doi.org/10.1007/s11433-014-5521-2Coherent effects of a weak neutral current
. Phys. Rev. D 9, 1389 (1974).Neutrino Physics with JUNO
. J. Phys. G 43,RELICS: a REactor neutrino LIquid xenon Coherent elastic Scattering experiment
. Arxiv. arXiv:2405.05554Recode program for reactor neutrino cevns detection with ppc germanium detector
. 2024, p. 296. https://doi.org/10.22323/1.441.0296CEνNS Experiment Proposal at CSNS
. Phys. Sci. Forum 8, 19 (2023)., https://doi.org/10.3390/psf2023008019Study of accelerator neutrino detection at a spallation source
. Chinese Phys. C 40,Principles and applications of a neutral-current detector for neutrino physics and astronomy
. Phys. Rev. D 30, 2295 (1984). https://doi.org/10.1103/PhysRevD.30.2295Light yield of cold undoped CsI crystal down to 13 keV and the application of such crystals in neutrino detection
. Eur. Phys. J. C 80, 1146 (2020)., https://doi.org/10.1140/epjc/s10052-020-08712-2First operation of undoped CsI directly coupled with SiPMs at 77 K
. Eur. Phys. J. C 82, 344 (2022). arXiv:2201.00483, https://doi.org/10.1140/epjc/s10052-022-10289-xCAEN, Caen wavedump software webpage
(2024)., https://www.caen.it/products/caen-wavedump/, accessedModifed wavedump program by ucas
(2024)., https://gitee.com/schg_ucas/WaveDump_UCAS, accessedWaveform analysis program
(2024)., https://gitee.com/schg_ucas/wave-ana, accessedNuDat 3.0
, (2024)., https://www.nndc.bnl.gov/nudat3/, accessedPerformance of a liquid nitrogen cryostat setup for the study of nuclear recoils in undoped CsI crystals
. Nucl. Instrum. Meth. A 1063,Reactor neutrino physics potentials of cryogenic pure-CsI crystal
. Eur. Phys. J. C 84, 440 (2024)., https://doi.org/10.1140/epjc/s10052-024-12800-yGrowth and evaluation of improved csi: Tl and nai: Tl scintillators
. Crystals 12, 1517 (2022). https://doi.org/10.3390/cryst12111517Investigation of the gamma-ray efficiency for various scintillation detector systems
. Revista mexicana de fisica, https://doi.org/10.31349/revmexfis.68.04120Energy and resolution calibration of NaI(Tl) and LaBr3(Ce) scintillators and validation of an egs5 monte carlo user code for efficiency calculations
. Nucl. Instrum. Methods Phys. Res., Sect. A 675, 78-83 (2012). https://doi.org/10.1016/j.nima.2012.02.006Light yield non-proportionality and intrinsic energy resolution of doped csi scintillators
. Nukleonika 53, 51-56 (2008). https://doi.org/10.1016/j.proeng.2012.02.010Scintillators for high temperature plasma diagnostics
. 2015. https://doi.org/10.22323/1.240.0162The energy response of labr3(ce), labr3(ce, sr), and nai (tl) crystals for gecam
. Nucl. Sci. Tech. 35, 1-13 (2024). https://doi.org/10.1007/s41365-024-01383-8Temperature dependence of pure CsI: Scintillation light yield and decay time
. Nucluear Instrum. Meth. A 480, 494-500 (2002). https://doi.org/10.1016/S0168-9002(01)01239-6The luminescence characteristics of csi (na) crystal under α and x/γ excitation
. J. Appl. Phys., https://doi.org/10.1063/1.4773528Fast light of csi (na) crystals
. Chinese Phys. C 35, 1130 (2011). https://doi.org/10.1088/1674-1137/35/12/009Scintillation characteristics of an undoped CsI crystal at low-temperature for dark matter search
. Arxiv. arXiv:2312.07957Luminescence and scintillation properties of csi: A potential cryogenic scintillator
. Phys. Status Solidi B 252, 804-810 (2015). https://doi.org/10.1002/pssb.201451464The low temperature performance of csi (na) crystals for wimps direct searches
. Radiation Detection Technology and Methods 2, 15 (2018). https://doi.org/10.1007/s41605-018-0039-1Simulations of light collection in long tapered csi (tl) scintillators using real crystal surface data and comparisons to measurement
. Nucl. Instrum. Methods Phys. Res., Sect. A 1003,Study of light collection as a function of scintillator surface roughness
. Radiat. Meas. 45, 383-385 (2010). https://doi.org/10.1016/j.radmeas.2010.01.027Simulation of light transport in scintillators based on 3d characterization of crystal surfaces
. Phys. Med. Biol. 58, 2185 (2013). https://doi.org/10.1088/0031-9155/58/7/2185Readout techniques and radiation damage of undoped cesium iodide
. IEEE Trans. Nucl. Sci. 37, 492-499 (1990). https://doi.org/10.1109/23.106667Luminescence and decay time properties of pure csi crystals
. J. Inorg. Mater. 32, 169-174 (2017). https://doi.org/10.15541/jim20160304Scaling-induced enhancement of x-ray luminescence in csi (na) crystals
. Appl. Phys. Lett. 10, (1063/1),Luminescence of csi and csi: Na films under led and x-ray excitation
. Coatings 9, 751 (2019). https://doi.org/10.3390/coatings9110751Effect of humidity exposure on microstructure and photoluminescence properties of polycrystalline csi (tl) screens
. Crystals 13, 1355 (2023). https://doi.org/10.3390/cryst13091355Influence of the humid air on the structure and fluorescent property of csi: Tl thin film
. J. Mater. Sci. Mater. Electron. 30, 7691-7694 (2019). https://doi.org/10.1007/s10854-019-01084-8Impact of geometry on light collection efficiency of scintillation detectors for cryogenic rare event searches
. Nucl. Instrum. Methods Phys. Res., Sect. B 336, 26-30 (2014). https://doi.org/10.1016/j.nimb.2014.06.015Geometry dependence of the light collection efficiency of bgo crystal scintillators read out by avalanche photo diodes
. Nucl. Instrum. Methods Phys. Res., Sect. A 715, 105-111 (2013). https://doi.org/10.1016/j.nima.2013.03.022The authors declare that they have no competing interests.


