Graphite crystal atomic modelling

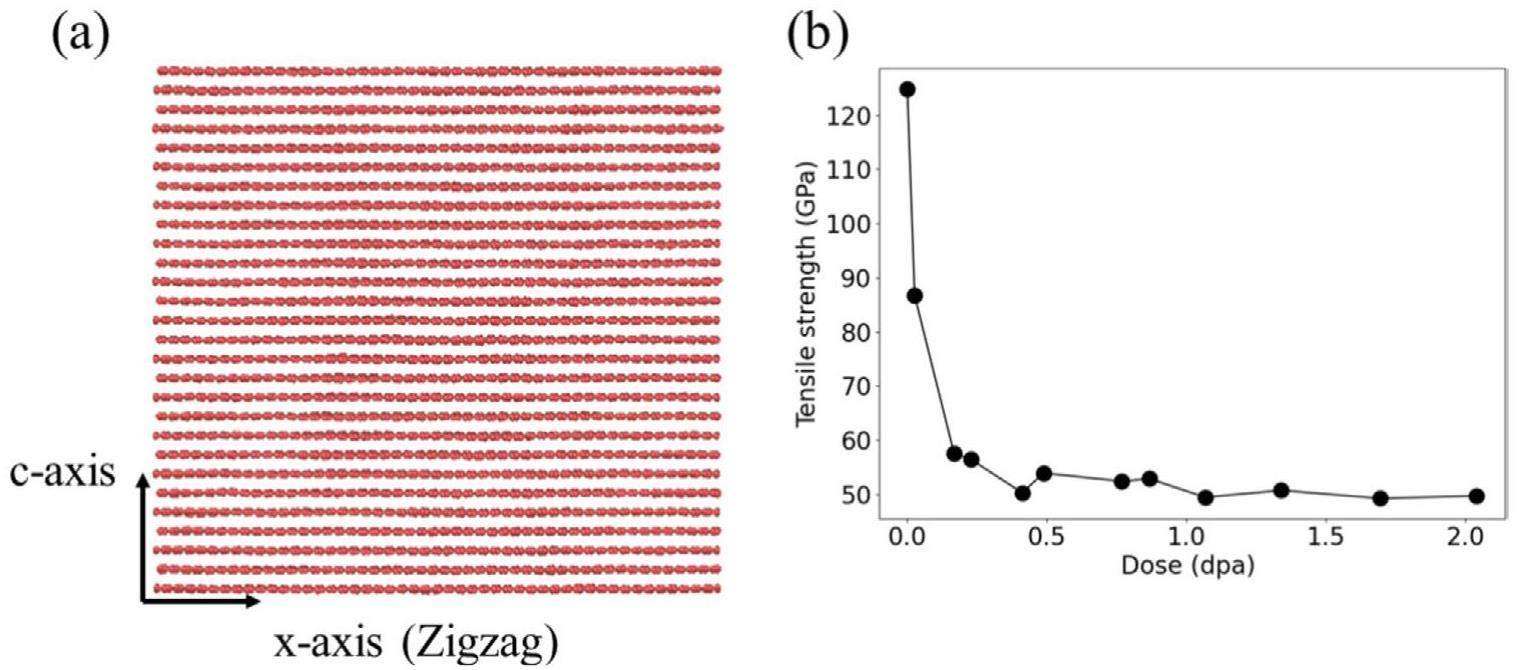
A graphite crystal supercell has been considered here with size of 10 nm × 9.9 nm × 9.5 nm, as in previous works [22, 23, 28], to investigate the microstructural evolution of irradiation defects under applied loading. The supercell consisted of 28 graphite sheets is shown in Fig. 1(a) by using OVITO [37]. These graphite sheets are stacked in the Bernal structure (AB stacking). To balance computational speed and accuracy, the adaptive intermolecular reactive empirical bond order (AIREBO) potential [38] has been employed to describe the interaction between carbon atoms. The AIREBO potential has been used extensively to evaluate the irradiated structures and properties of graphite crystal [22-24, 28, 39]. The ZBL pair potential [40] has been used to describe atomic close-range collisions and the Fermi-type scaling functions [29] has been used to achieve smooth switching between ZBL pair potential and the AIREBO potential. All the aforementioned potentials and MD simulations were performed in the large-scale atomic/molecular massively parallel simulator (LAMMPS) code [41]. These MD simulations were performed at 1073 K (800 ℃) chosen based on the temperature conditions inside a Molten Salt Reactor (MSR).

Fig. 1Full-screen View

(Color online) (a)Graphite crystal supercell model; (b) Average tensile strength of irradiated crystal models under NPT ensemble along the x(a)-axis

Irradiated graphite crystal modeling

In this work, irradiation defects are generated by PKA cascades. To create different damage states, a series of impulsing cascades [21] was performed one after the other in the crystal model, until the model was completely amorphous. Multiple PKAs were set with random positions at each impulsing cascade to accelerate the amorphization process. This approach produced a high damage ratio ranging from 0.001 to 0.005 dpa/ps. Considering the limited model size and the PKA energy limit that causes saturation displacement damage [30], the energies of PKAs were set at values below 11 keV with an average value of 8 keV. PKA cascades were performed in the microcanonical (NVE) ensemble. After each irradiation process, the canonical (NVT) ensemble was used to relax the irradiated crystal model, heated by irradiation, to 1073 K and stabilize the potential energy. The NVT relaxation process ensured that irradiation defects were in a stable state, ensuring that the applied loading becomes the primary factor affecting subsequent defect migration process. To analyze displacement damage dose, a neighbor list and initial coordinate reference points were generated for every atom before each irradiation event. Each atomic displacement was determined by checking the displacement distance and IDs in each neighbor list [23, 25] with a cutoff distance of 1.9 Å [25]. If an atom moved more than the cutoff based on thermal diffusion and its original neighbor list changed, the atom was considered it have been knocked out of its equilibrium position.

Microstructural evolution method for crystal creep

Considering that graphite sheets can withstand larger external loads during the loading process, this study investigated the irradiation process and the evolution of damage structures after irradiation when graphite crystal was subjected to tensile loads along the x(a)-axis. However, it is difficult to evaluate an actual engineering creep rate using molecular dynamics method within picoseconds duration. To observe noticeable creep behavior and gain insight into atomic-scale mechanisms, high tensile loads are often applied [34]. These values of different applied tensile loads are referenced to the minimum tensile strength of these irradiated crystal models along the x(a)-axis of these models. Uniaxial tension was conducted at 1073 K using the isothermal-isobaric (NPT) ensemble and periodic boundary conditions to estimate the tensile strength. All tensile strength values and implementation details are shown in Supplementary material S1. By averaging ten independent amorphization processes, the effects of random amorphization can partly be generalized. After the damage dose exceeds 1 dpa, the change in strength becomes less noticeable. The minimum tensile strength remains around 50 GPa, as shown in Fig. 1(b). Therefore, in this study a series of tensile loads was applied to the crystal model within the tensile strength range at values of 1 GPa, 5 GPa, 10 GPa, 20 GPa, 30 GPa, and 40 GPa. Although loads greater than 20 GPa did not reach the minimum tensile strength, they surpassed the elastic region of the stress-strain curve. The higher loads become more similar to shock loads that can induce high-rate plastic strains [27]. The comparison between low and high stress loading can be conducted to reveal the underlying deformation mechanisms of dislocation pinning-unpinning and crystallite yielding [14, 26]. The NPT ensemble has been utilized to apply these applied loads, which can evaluate Poisson's effect and apply stable tensile stress load.

Evaluation methods of irradiation behavior and creep behavior

Threshold displacement energy (E_d) is usually employed to represent the irradiation performance of nuclear graphite [25, 30]. To quantify the effect of the applied tensile loading on the E_d, this study evaluated the average number of defects formed by PKA energies ranging from 10 to 60 eV. One hundred atoms were randomly assigned in the crystal model, ensuring that the distance between any two atoms was greater than 15 Å, which exceeds the maximum PKA displacement observed in previous studies [25, 30]. These atoms are assigned a random velocity distribution, and each energy value is tested ten times with randomly replaced atoms. Consequently, defect formation resulting from each energy value can be evaluated 1000 times. Additionally, to quantify the degree of amorphization caused by irradiation and migration behavior of irradiation defects under applied loading, the proportion of graphitized region (G) and mean square displacement (MSD) were utilized to describe the structure and diffusive properties of defects. G is defined as the ratio of graphitized atomic structures to the total number of atoms in crystal model, which characterizes the extent of irradiation-induced damage to graphitized structures. MSD is defined as the expectation of the square of the displacement value of a group of atoms at a certain moment with respect to the origin moment [34]. $\text{MSD}=\langle {\left|r\left(t\right)-r\left(0\right)\right|}^2\rangle \mathrm{,}$ (1) where $r(t)$ and $r(0)$ denote the positions of a group of atoms at moment t and at the initial moment, and $\langle \rangle$ denotes the expectation of calculating all values. MSD can be used to characterize the motion of atoms under different applied loads and thus to determine the diffusion properties and their qualitative influence on the creep properties.

Irradiation behavior of graphite crystal under applied tensile loading

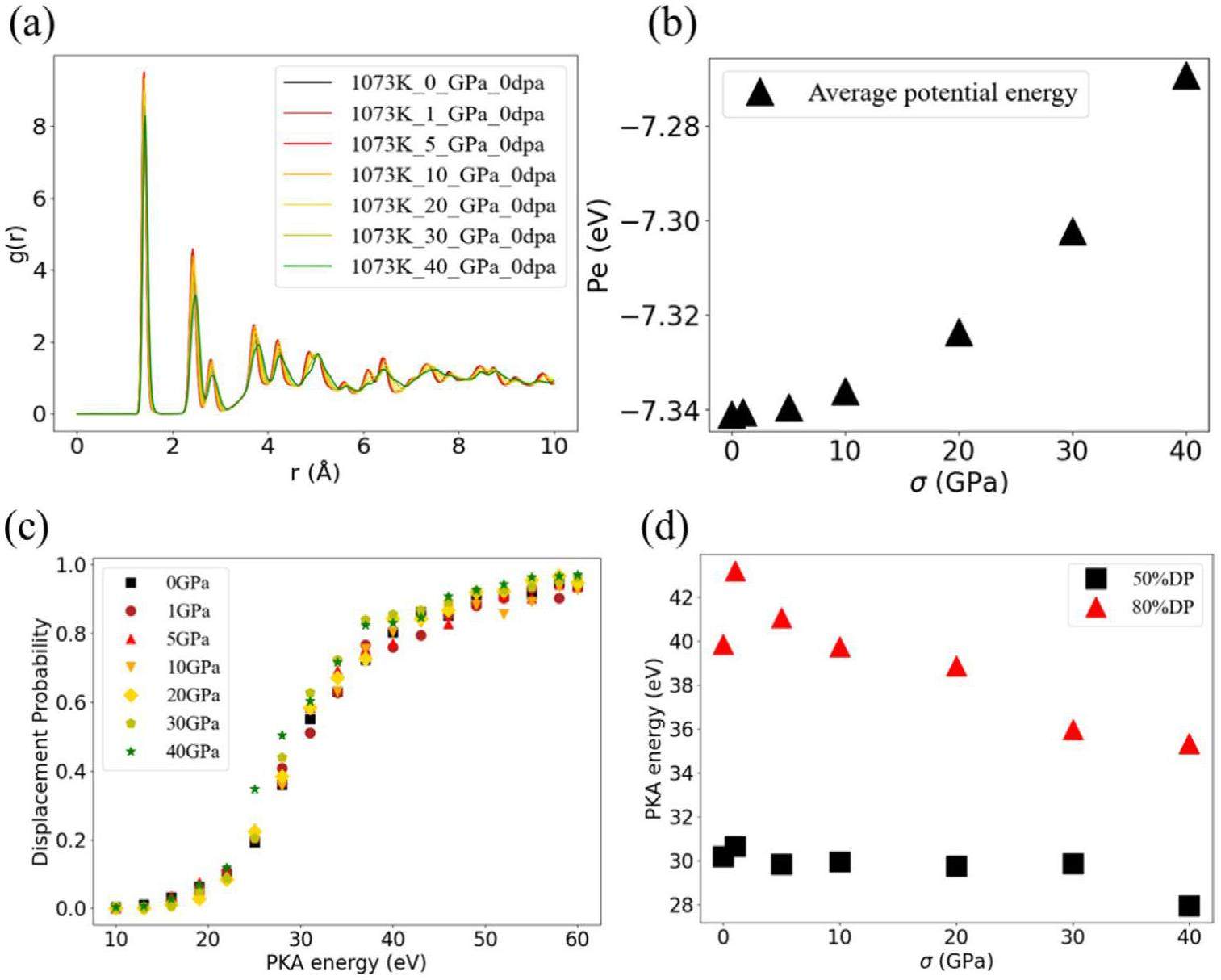
The irradiation behavior of perfect graphite crystal was discussed first. Before each irradiation process, the applied tensile loading was implemented for 300 ps along the x(a)-axis to ensure the stability of the potential energy of the graphite crystal model. Figure 2(a) shows the radial distribution function (RDF) of the graphite crystal model under different applied loads. The RDF is commonly used to describe the atomic density around a central atom and can be employed, similar to characterization methods such as X-ray diffraction, to represent lattice parameters and the degree of order in a crystal structure. The right shift of the RDF peaks in Fig. 2(a) illustrates an increase in atomic distance due to the applied loading. The additional increase based on equilibrium distance can increase the atomic potential energy of the loaded crystal model. Figure 2(b) shows that the average atomic potential energy increases with increasing applied load. Specifically, a load of 40 GPa increases the potential energy by 0.07 eV/atom compared to the state without applied loading. The average atomic potential energy serves as the well depth of potential in which an atom is influenced by its surrounding atoms, to some extent indicating the stability of the structure. Therefore, these changes in crystal structure and atomic potential energy can affect the irradiation performance of graphite crystal, such as threshold displacement energy (E_d) [10]. The E_d reflects the ability of a material to resist irradiation damage, and materials with lower E_d are more likely to experience displacement damage under irradiation. Figure 2(c) shows that as the applied tensile load increases, the displacement probability (probability of lattice atoms leaving equilibrium positions due to irradiation) of lattice atoms in the graphite crystal model decreases at 1 GPa and then continues to increase. The change in PKA energy for 50% displacement-probability and 80% displacement-probability with the applied tensile load (Fig. 2(d)) also shows that the E_d can increase at the initial time and decrease at higher applied tensile loads, which is consistent with the decrease of threshold displacement energy at higher applied strain [10]. Therefore, based on the above results, smaller applied tensile loads of σ< 1 GPa can increase the difficulty of point defect unpinning caused by irradiation in graphite sheets. However, based on like Kelly et al.'s theory, as the applied load continues to increase, unpinning caused by irradiation becomes increasingly likely to occur.

Fig. 2Full-screen View

(Color online) (a) RDF of the graphite crystal model under different applied tensile loads; (b) Average atomic potential distribution of the graphite crystal model under different applied loads along the x(a)-direction; (c) Displacement probability distribution under different applied tensile loads; (d) 50% displacement probability (50%DP) and 80% displacement probability (80%DP) distributions

To observe the effect of the changes in crystal structure and threshold displacement energy on PKA irradiation process as well as point defect evolution, a primary damage with insignificant amorphization was first implemented. A PKA with energy of 4 keV was set at the same position for different applied load conditions to observe the irradiation process. Additionally, eight PKAs with energy of 4 keV were placed near the center of the model to study the interactions between PKAs and point defects under applied load. The diagrams of these two PKA processes are shown in Fig. 3(a).

Fig. 3Full-screen View

(Color online) (a) Diagram of PKA cascade; Morphology and point defect distribution of irradiated crystal under different applied tensile loads: (b) Single PKA and (c) Eight PKAs

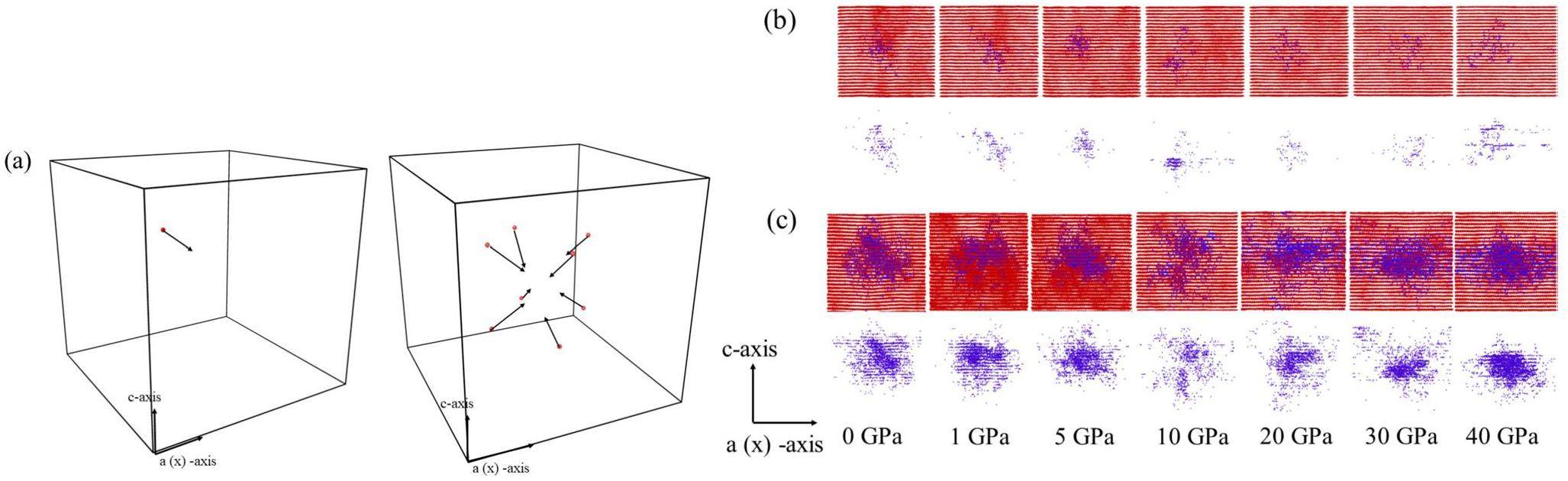
PKA irradiation process and point defect evolution showed significant differences under different applied loads. In Fig. 3(b), the distribution of point defects along the initial incident direction of the PKA is prominent at lower applied loads, but as the applied tensile load increases, the path of the PKA and the distribution of point defects gradually change. One notable phenomenon is the significant limitation of the movement distance of the PKA along the initial incident direction under high applied loads. The PKA in Fig. 3(b) can move further distance along the initial incident direction at lower applied loads, causing the point defect clusters to be preferentially oriented in this direction. However, as the applied tensile load increases, an obstruction along the initial incident direction becomes apparent, leading to a deflection in the path of the PKA and the orientation of the point defect clusters. Ultimately, this results in a more apparent preferred orientation of the point defect clusters along the basal plane, increasing the probability of incident particles causing interlayer pinning and unpinning.

Figure 3(c) indicates that the applied tensile loading can also influence the interaction of PKAs and point defects. The distribution of point defects is more concentrated at lower applied loads under the same PKA irradiation case. Then, the reduced threshold displacement energy and increased atomic potential energy may weaken the interaction between PKA and lattice atoms. As a result, high applied tensile loads might cause an increase in mean PKA displacement relative to the simulation without applied stress [21, 24], resulting in a more dispersed distribution of point defects. As the applied tensile load increases, the mean PKA displacement also increases from 35 Å to 39 Å (From 1 GPa to 10 GPa). At higher applied loads of σ> 10 GPa, hindrance along the initial incident direction restricts the displacement of both PKAs and point defects along the c-axis, leading to a more concentrated distribution of point defect clusters along the a-axis. As a result, higher tensile loads along the a-axis of the crystal model increased the interlayer displacement of incident particles, thereby increasing the probability of unpinning of interlayer dislocations. However, this phenomenon has not been considered in previous theories [5, 14, 26], which may further accelerate irradiation creep rate based on pinning and unpinning theory [14].

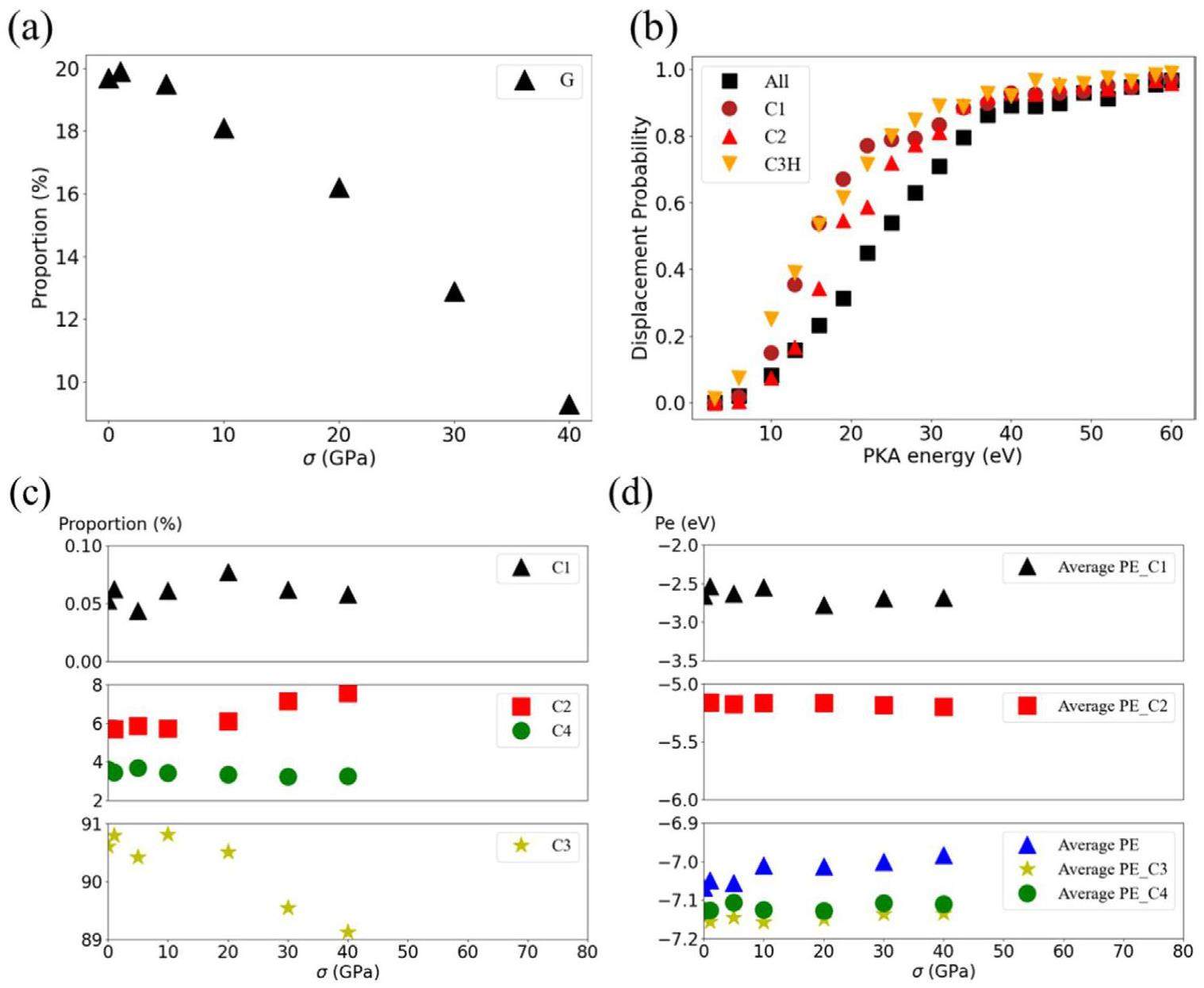
At higher damage doses with significant amorphization, the applied tensile loading also resulted in different damage states compared to the state without applied loading. These random PKA irradiation settings keep the same conditions (same position, velocity direction, and PKA energy) for each applied tensile loading condition. Figure 4(a) illustrates a marked reduction in the proportion of graphitized region (G) under higher tensile loads of σ> 10 GPa, which is consistent with a significant reduction in the threshold displacement energy at loads greater than 10 GPa. In this study, carbon atomic type and potential energy analysis were used as another perspective to investigate the structural changes and mechanisms that occur during irradiation-induced amorphization and loading. During the irradiation process with significant amorphization, the sp²-hybridized atoms located in crystal sheets are converted to other types [23, 42, 43]. The changes of atomic type and potential energy shown in Fig. 4(c, d) indicate that high applied tensile loads can cause more onefold (C1) and twofold (C2) coordinated atoms with higher potential energy, as well as threefold coordinated atoms with higher potential energy (C3H, referring to sp²-hybridized atoms with potential energy higher than those of undistorted carbon lattice planes). Meanwhile, the proportion and average potential energy of threefold (C3) and fourfold (C4) coordinated atoms also increase with increasing tensile load, thus increasing the average atomic potential energy of the irradiated crystal model. Moreover, these atoms with higher potential energy exhibit lower threshold displacement energy as demonstrated in previous studies [25, 42] and shown in Fig. 4(b). Consequently, they are more susceptible to displacement by irradiation, potentially leading to enhanced diffusion [44] and an accelerated irradiation creep under applied loading.

Fig. 4Full-screen View

(Color online) (a) Proportion of graphitized region (G) under different applied tensile loads; (b) Displacement probability distribution of the atoms with lower potential energy at 0.17 dpa and 0 GPa; (c) Proportion of atomic types under different applied tensile loads; (d) Change of average potential energy under different applied tensile loads

Creep behavior of irradiated crystal under applied tensile loading

To investigate the creep behavior of irradiated crystal, different applied tensile loads were applied along the x(a)-axis. The strain curves over time under various applied loads and damage doses are shown in Supplementary material S2. The steady state creep rate (SSCR) [45] along to the x(a)-axis in Fig. 5(a, b) is fitted using the strain curves from the last 100 ps. However, the tensile loading of 40 GPa is approaching the minimum tensile strength, which results in an excessively rapid strain rate in the crystal model. Therafore, at 40 GPa only some converged results are shown here. The resulting creep curves illustrate that even if the applied load exceeds 30% of the tensile strength of perfect crystal, the perfect crystal does not show significant creep behavior at 1073 K. However, when the complete crystal structure is damaged by irradiation, Fig. 5(b) show that the crystal model exhibits creep behavior under high applied load of σ > 10 GPa at 0.03 dpa. Furthermore, the primary creep and SSCR increase with the increase of damage dose and applied load.

Fig. 5Full-screen View

(Color online) (a, b) SSCR changes with different damage doses and applied loads; (c) Stress exponent (n) changes with different damage doses; (d) Average stress exponent changes with different damage doses

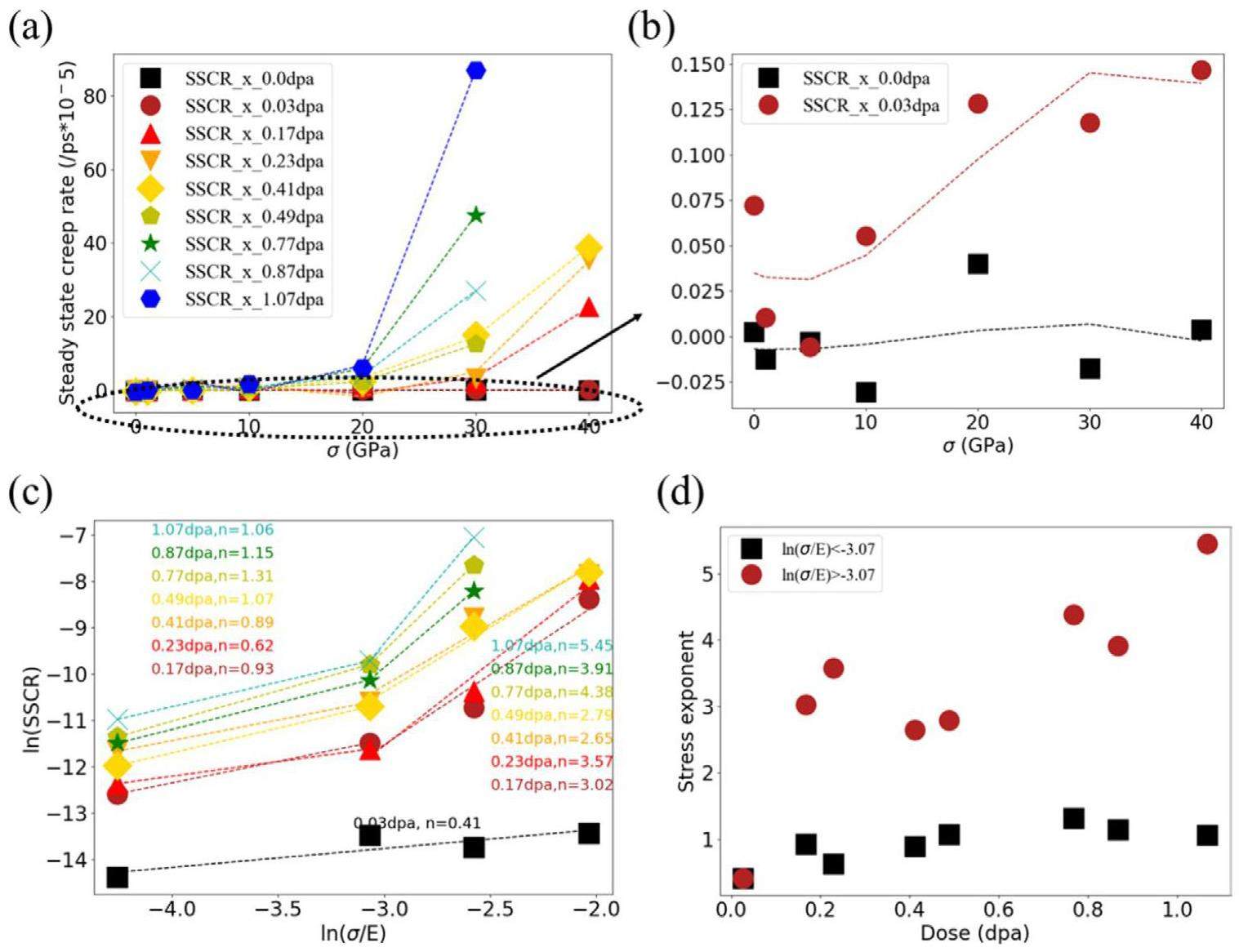
Meanwhile, the effect of damage dose and applied loading is observed to differ in various states, as shown in Fig. 5(a, b). At the applied loads of σ< 10 GPa and damage doses (< 0.17 dpa and G > 30%), the tensile loading only changes the dimensional changes produced by irradiation and does not cause significant creep behavior. Then a slight creep phenomenon occurs as the applied load increases. However, at higher damage dose, creep behavior becomes more pronounced with increasing applied load. The steady state creep rate in Fig. 5(a) shows that the applied tensile loading significantly influences the creep behavior at higher damage dose, which can be related to the decreasing tensile strength due to irradiation. The study by Sarkar et al. also indicates that irradiation creep behavior is sensitive to irradiation dose [12]. Their rate theory shows that [12] ${\dot{ϵ}}_{\text{Φ}}\propto {\sigma }^n\mathrm{,}$ (2) where ${\dot{ϵ}}_{\text{Φ}}$ is the rate of change of irradiation creep with dose, and n is the stress exponent. According to the analysis conducted by Sarkar et al., higher irradiation doses are associated with higher stress exponents, even at lower temperatures, which results in Fig. 5(c, d). As depicted in Fig. 5(c), at the lower damage state of 0.03 dpa (G > 70%), the stress exponent remains low under different loads. However, as the level of irradiation damage increases, distinct creep characteristics are observed under low and high stress loading conditions. Additionally, it is noting that under higher damage state with more amorphous regions (> 0.23 dpa, i.e. G < 10%), a low dose irradiation can cause irradiation strengthening and decrease the creep trend of irradiated crystals. Figure 5(a-d) demonstrates that the creep strain and SSCR decrease after a low dose irradiation but increase after a higher dose irradiation. And the phenomenon did not occur at lower damage doses, which is consist with the mean tensile strength change of irradiated crystal models in Fig. 1(b).

Analysis of creep mechanism

The significant difference in the stress exponent observed in Fig. 5(c, d) under different damage states and loads indicates that the creep mechanism may differ. To understand the creep mechanism of irradiated graphite crystal, MSD analysis and visual atomic structure analysis were used to reveal the diffusion properties of defects and structure changes in each damage state. Figure 6(a) and Fig. 7(a) indicate that perfect crystal sheets are more prone to slip, and the applied tensile loading increases the trend of interformational sliding. Figure 6(a) shows that under the influence of applied tensile loading, there is a significant displacement of crystal atoms along the a-axis, while there is no noticeable migration along to the z(c)-axis. By combining the MSD analysis in Fig. 6(a) and visual structural analysis in Fig. 7(a), it can be deduced that the significant migration phenomenon along the a-axis is a consequence of the overall slip of graphite sheets. But the sliding did not cause significant creep strain. At the damage dose of 0.03 dpa (G > 70%), interstitials and vacancies are the primary types of irradiation defects and strongly restrict the interformational sliding, as illustrated in Fig. 7(a). As a result, significant diffusion cannot be observed at lower applied loads, as shown in Fig. 6(b). However, with the increase of the applied load, a slight diffusion effect occurs along the x(a)-axis. Furthermore, compression in the z(c)-axis can be observed, and whereas the atomic displacement in the y(a)-axis increases with the applied load.

Fig. 6Full-screen View

(Color online) The overall and axial atomic diffusion MSD analysis of irradiated crystal models under different applied tensile loads and damage doses

Fig. 7Full-screen View

(Color online) Visual structural analysis of irradiated crystal under different applied tensile loads

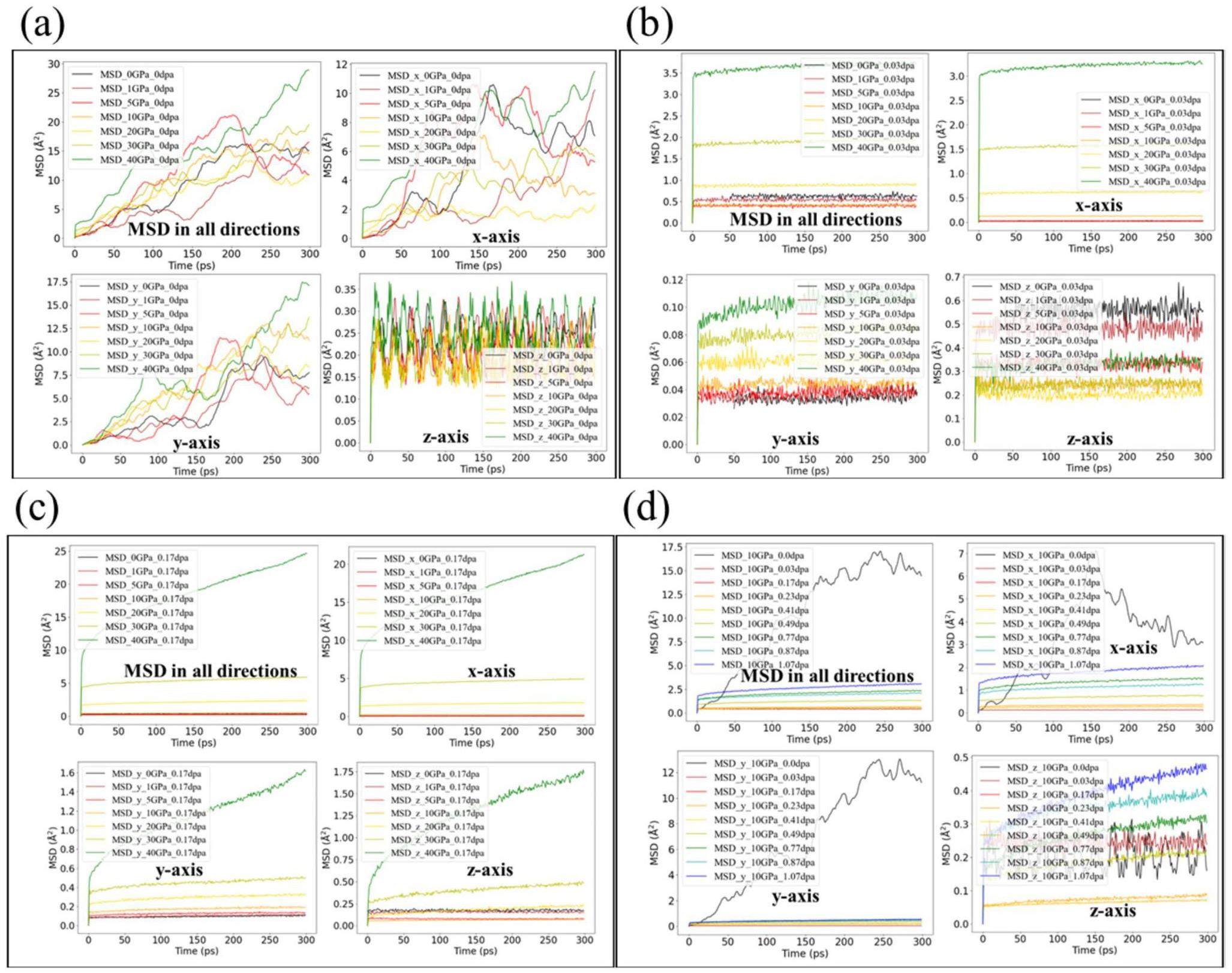
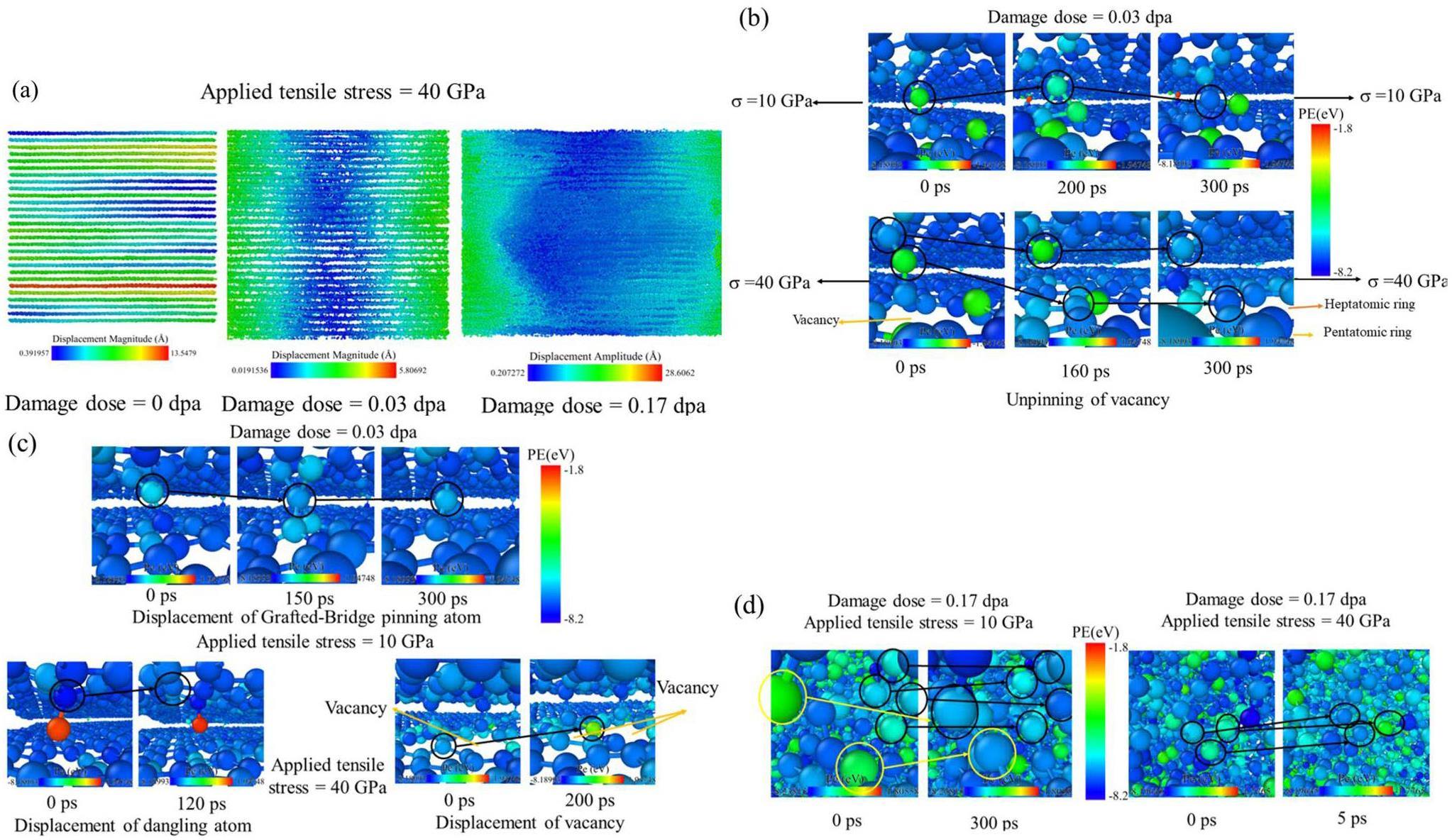
Figure 5(b) shows that lower applied tensile loads of σ< 10 GPa did not lead to the significant creep behavior at 0.03 dpa. However, the MSD analysis in Fig. 6(b) reveals the occurrence of defect migration even under lower tensile loads, particularly evident in the y-axis direction. This indicates that these defects, such as interstitial atoms, undergo migration. The type of damage state aligns with the dislocation pinning-unpinning model proposed by Kelly et al., thus providing verification of the structural mechanism of their model. Visual structural analysis also confirms the specific patterns of dislocation pinning-unpinning (Pinning refers to the connection of interstitial atoms entering the interlayer with vacancy dislocation defects in the upper and lower graphite sheets, thereby fixing and anchoring the dislocations, hence referred to as pinning atoms by Kelly et al. [14]. At an applied load of 10 GPa, the main mode of migration for these pinning atoms in the basal plane occurs through a defect type conversion of interstitials, which requires less activation energy. Figure 7(b) shows that an interstitial atom of Wallace combines with a sp-hybridized atom on the edge of the vacancy to form a new defect under the action of 10 GPa applied tensile loading. Additionally, Fig. 7(c) shows the migration of a Grafted-Bridge atom by bonding and breaking bonds with surrounding sp²-hybrid atoms. In this migration mode, the conversion of intermediates is involved, which limits the migration distance and results in insignificant diffusion and creep. However, considering the irradiation behavior described in Sect. 3.1, the effects of irradiation under applied loading may accelerate the unpinning of such interlayer pinning structures, thereby contributing to an increasing defect migration rate and creep strain.

High applied loads can directly break the bond between interstitial atoms and the basal plane. Figure 7(b) shows the unpinning process of the same interstitial atom of Wallace at 40 GPa, as compared to the process at 10 GPa. The bond between the interstitial atom of Wallace and upper basal plane is broken by the high applied loading, leading to the backward movement of the pinning and the forward movement of vacancy. In this way, these defects can move larger distances, thus causing a more pronounced diffusion phenomenon, as shown in Fig. 6(b). Figure 7(c) also shows that the dangling atoms can jump and migrate directly, and vacancies can migrate by breaking the bonds of the edges under an applied load of 40 GPa. Since these defects migrate in the basal plane, which may cause diffusion phenomenon in the y-axis as well. By directly breaking and migrating bonds in this manner, the migration rate of defect structures and the creep rate increase rapidly, which explains the significant differences in the stress exponent at high stress levels (ln(σ/E) > 3.07) observed in Fig. 5(d). Simultaneously, the rapid bond-breaking migration facilitated by pinning structures leads to the rapid migration of the entire basal plane and irradiation structure under external loading, resulting in plastic deformation and ultimately crystal yield. In contrast, for intact graphite sheets, the strong interlayer sliding allows the graphite sheets to bear the main load, making them prone to brittle fracture. This may explain the occurrence of “nanoscale kink band mediated plasticity” observed by Thomas et al. during the micro-pillar compression of irradiated graphite [27].

In the damage state where amorphous regions are clearly present, the layered structure for the dislocation pinning-unpinnin mode gradually disappear, giving way to the amorphous structure which becomes the main type of irradiation defects. A higher stress exponent indicates that an atomic diffusion mechanism can be dominant [12, 14], which is supported by MSD analysis in Fig. 6(c, d) and visual structural analysis in Fig. 7(d). Both the creep and diffusion rate increase significantly with the applied tensile load and damage dose. Furthermore, the diffusion phenomenon along the c-axis can also be observed, as shown in Fig. 6(c, d). Figure 7(d) show the specific atomic diffusion modes within the amorphous region. The visual structural analysis in Fig. 7(d) indicate that triangular defects, quadrilateral defects and other types of defects with higher potential energy are more susceptible to conversion by the applied tensile loading. Figure 7(d) show that the threefold coordinated atom of the triangular defect undergoes conversion to a twofold coordinated atom at 40 GPa. These atoms can quickly migrate over short distances by breaking their existing bonds and forming new ones with the surrounding atoms. Furthermore, due to the absence of hindrance from graphite layered structure, atoms can also migrate rapidly along the z(c)-axis, resulting in diffusion phenomena along the z(c)-axis.

Analysis of creep behavior

The analysis of stress exponent in Fig. 5(c, d) reveals applied tensile loads and damage dose can cause differences in creep behavior. Moreover, the structure analysis in previous section indicates that the defect migration mechanism at different damage structures and applied tensile loads may be the main reason for the great difference in stress exponent. Therefore, with reference to [12], the empirical relationship between the applied tensile load and SSCR along to the x(a)-axis can be describe as: ${\dot{ϵ}}_{\text{Φ}}=C{\sigma }^n\mathrm{,}$ (3) where stress exponent n is a function related to damage structure and applied load, and C is a function that may be to temperature and other variables [12]. In this work, the graphitized component proportion (G) can be used as a parameter to describe the relationship between irradiated damage structure and stress exponent. Figure 8(a) shows that $n=\exp (aG+b)$ (4) where the coefficients a and b are related to applied load. The parameter G serves as a general structure descriptor that specifically characterizes the structure of irradiation-induced amorphization. Previous work by Kelly et al. has established a correlation between creep behavior and dislocation-pinning structure [14]. However, the migratory behavior of amorphous structures cannot be adequately explained by the pinning-unpinning mechanism.

Fig. 8Full-screen View

(Color online) (a) Change of stress exponent (ln(n)) with graphitized component proportion (G); (b-c) Change of atomic diffusion coefficient (ln(D)) with applied tensile load and damage dose; (d) Change of steady state creep rate (ln(SSCR)) with atomic diffusion coefficient (ln(D))

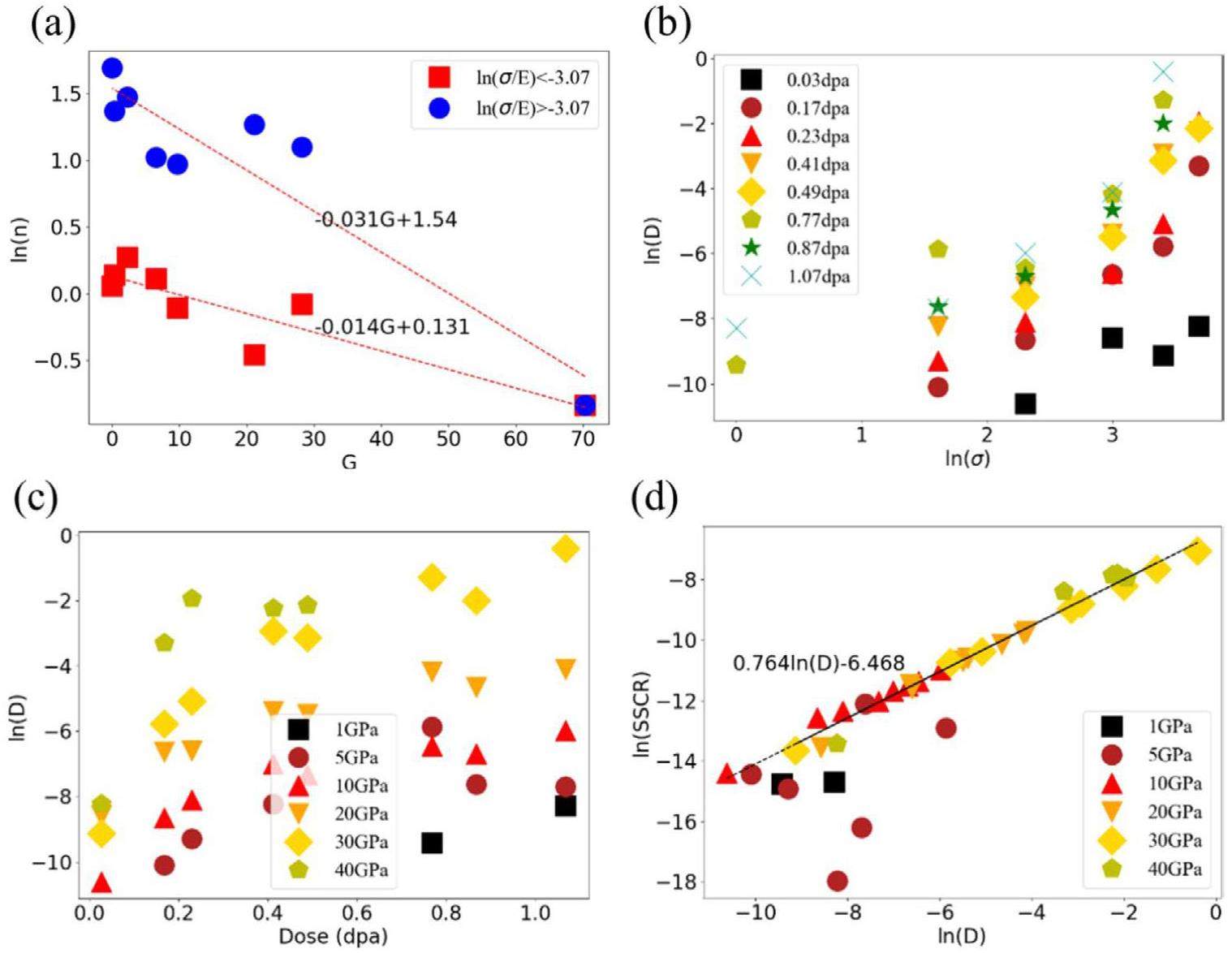
In addition, applied tensile loading and damage structures also influence the relationship between diffusion behavior and creep behavior. Figure 8(b, c) show that $\ln D\propto \text{Φ}\ln \sigma$ (5) here D is the atomic diffusion coefficient and Φ is a variable related to G in this work. Moreover, a linear relationship between lnD and ln SSCR in Fig. 8(d) can be obtained at applied load ≥ 5 GPa, which indicates the creep behavior is dominated by diffusion properties under higher applied loads. The difference under lower applied loads can be related to defect migration mechanism, such as conversion of intermediate. The effect of atomic structure conversion on creep and diffusion behavior under lower applied load requires further research.