Material

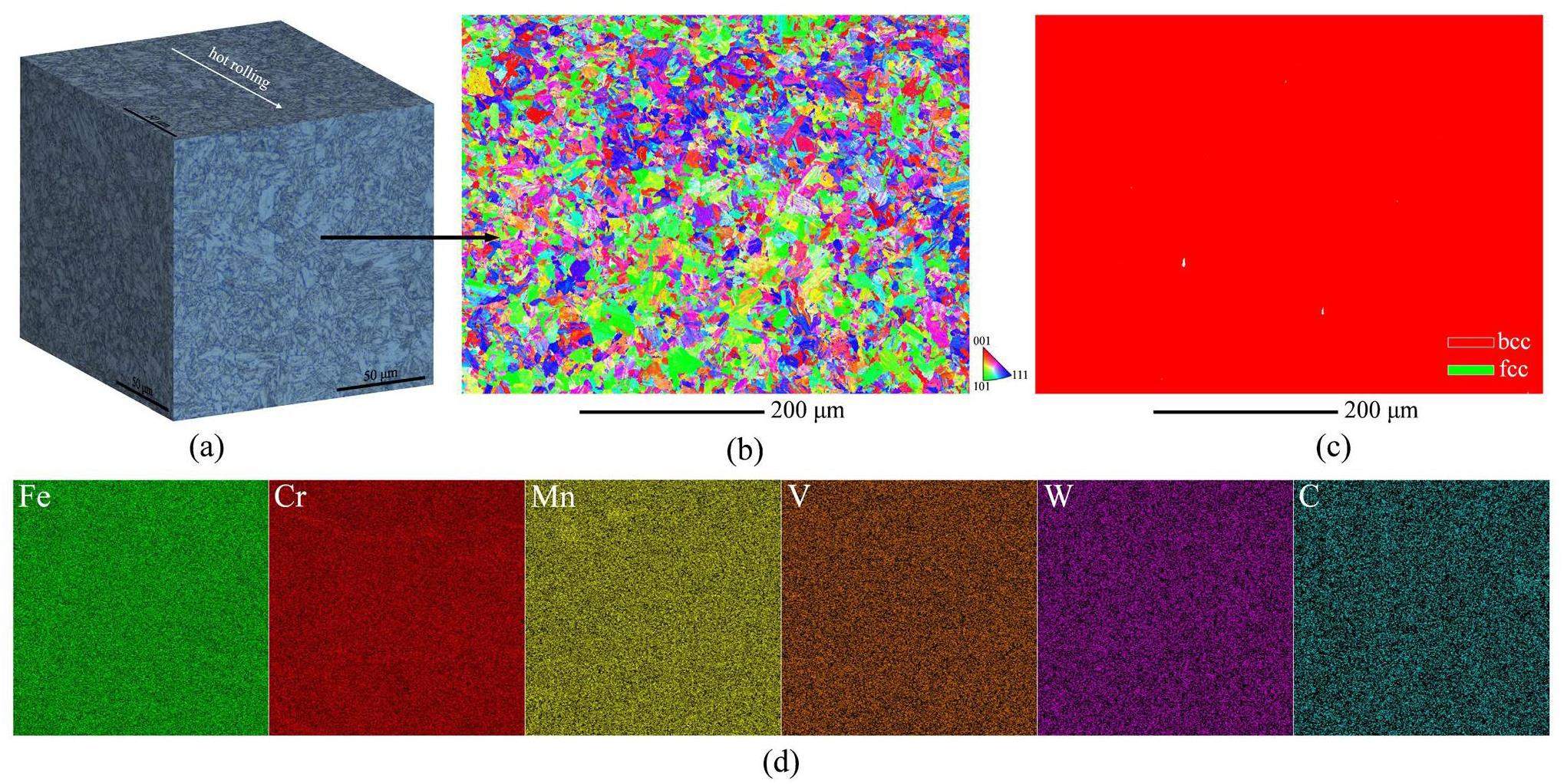
The CLF-1 steel used in this study was produced using a vacuum induction method. The studied steel was manufactured from a 5-t ingot. The measured chemical composition of the steel was 8.49 Cr-1.50 W-0.22 V-0.09 Ta-0.50 Mn-0.13 C-Fe in wt%. Finally, the steel was supplied as plates that were hot-rolled to a thickness of 30 mm. The as-received (AR) steel was heat-treated via normalization and tempering (NT). The normalization process was performed at 980 ℃ for 3.6 ks, and the cooling method was water cooling; subsequently, the tempering process was performed at 740 ℃ for 7.2 ks, the cooling method was air cooling. The microstructure revealed equiaxed grains, and the prior austenite grain size was approximately 14 μm (Fig. 1(a, b)). The studied steel had an all martensitic structure, as depicted in Fig. 1(a–c). The elemental distributions are presented in Fig. 1(d).

Fig. 1Full-screen View

(Color online) (a) Photomicrograph, (b) SEM/EBSD images, (c) phase mapping, and (d) corresponding EDX mapping of CLF-1 steel

Uniaxial tensile test

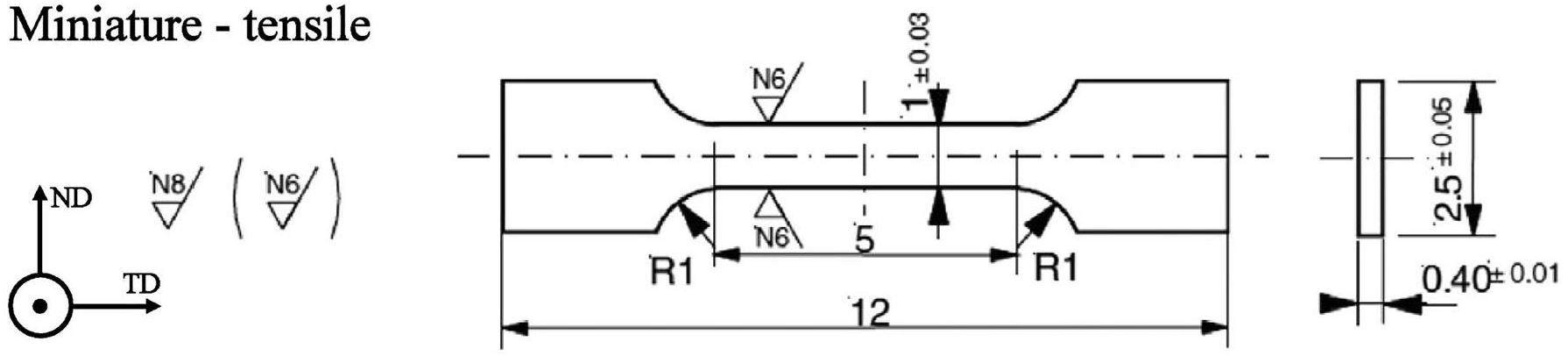
Typically, tensile tests of irradiated specimens use small tensile specimens. For further comparison with the tensile test data of irradiated specimens, miniature flat tensile specimens, which were consistent with “small tensile materials” in the SINQ Target Irradiation Program (STIP) [35-39], were fabricated from plate as shown in Fig. 2. The specimens had a geometry of 5.0 mm gauge length, 0.40 mm thickness, and 1.00 mm width. Before the tensile tests, the dimensions of each specimen were measured precisely.

Fig. 2Full-screen View

Dimensions of miniature flat tensile specimens of RAFM steel CLF-1. (in mm)

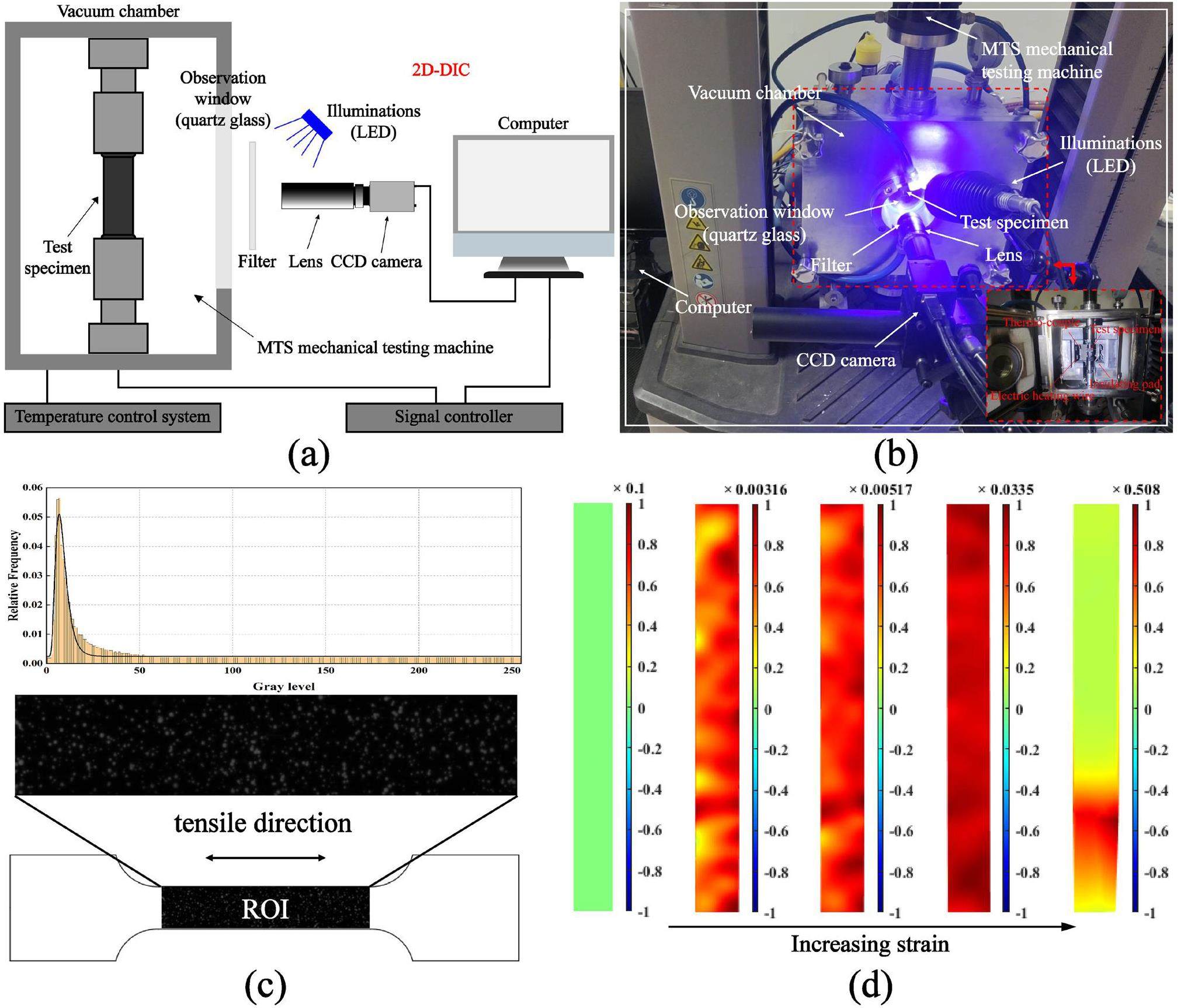
Uniaxial tensile tests were performed on an MTS mechanical testing machine with a capacity of 10-kN force, which was equipped with a video extensometer. The experiments were conducted in a vacuum, the strain rate was set to 1×10^-3 s^-1, and the test temperature range was 25–650 ℃. Before the tensile test, the specimens were maintained at a set temperature for 3.6 ks. The accuracy of the force measurements was within ±0.1%. DIC [40, 41] was used to measure the full-field displacement (or full-field strain). The DIC system, as depicted in Fig. 3(a, b), consisted of one LED light and one FLIR camera with a resolution of 0.006 mm/pixel equipped with a lens (Schneider-KREUZNACH). The speckles shown in Fig. 3(c) were formed using spray painting [42]. The image-acquisition rate was 1 Hz. A schematic of the full-field strain in the form of a contour plot during tensile testing is shown in Fig. 3(d). The strain (eyy) discussed in this paper was along the tensile direction. Experiments were performed twice at each temperature to ensure reproducibility.

Fig. 3Full-screen View

(Color online) (a) Diagram of the DIC system, (b) experimental platform of the DIC system, (c)speckle pattern after spraying, (d) full-field strain distribution

Strain error evaluation

The specimen surface under zero-strain conditions was photographed twice to evaluate the errors. Ideally, displacement should be null under zero-strain conditions. However, inevitable micro-movements of the experimental components would result in micro-displacement during an actual experiment. The micro-strain generated by this micro-displacement is considered an error. This error consists of systematic and random errors. "Accuracy" reflects systematic errors, whereas "precision" reflects random errors [43]. The mean absolute error (MAER) and standard deviation of error (SDER) are computed using Eqs. (1) and (2) [44] to represent systematic and random errors, respectively. $MAER=\frac{1}{N}{\displaystyle \sum _{m=1}^N}\left(\frac{1}{3}{\displaystyle \sum _{n=1}^3}\left|{ϵ}_{n\mathrm{,}m}\right|\right)$ (1) $SDER=\sqrt{\frac{1}{N}{\displaystyle \sum _{m=1}^N}{\left(\frac{1}{3}{\displaystyle \sum _{n=1}^3}\left|{ϵ}_{n\mathrm{,}m}\right|-MAER\right)}^2}$ (2) where ϵ, n, m, and N represent the strain, three strain components, measurement point, and number of measurement points, respectively. The MAER and SDER were 75.983 micro-strain and 67.719, respectively, which was lower than 150 micro-strain [45]. Because the algorithm causes a relatively large strain error at the edge of the region of interest (ROI), this study used a cropped edge approach to further reduce the error. Thus, the SDER should be lower than 67.179 micro-strain. This demonstrates that the DIC system used in this study has high measurement accuracy and precision.

Tensile property

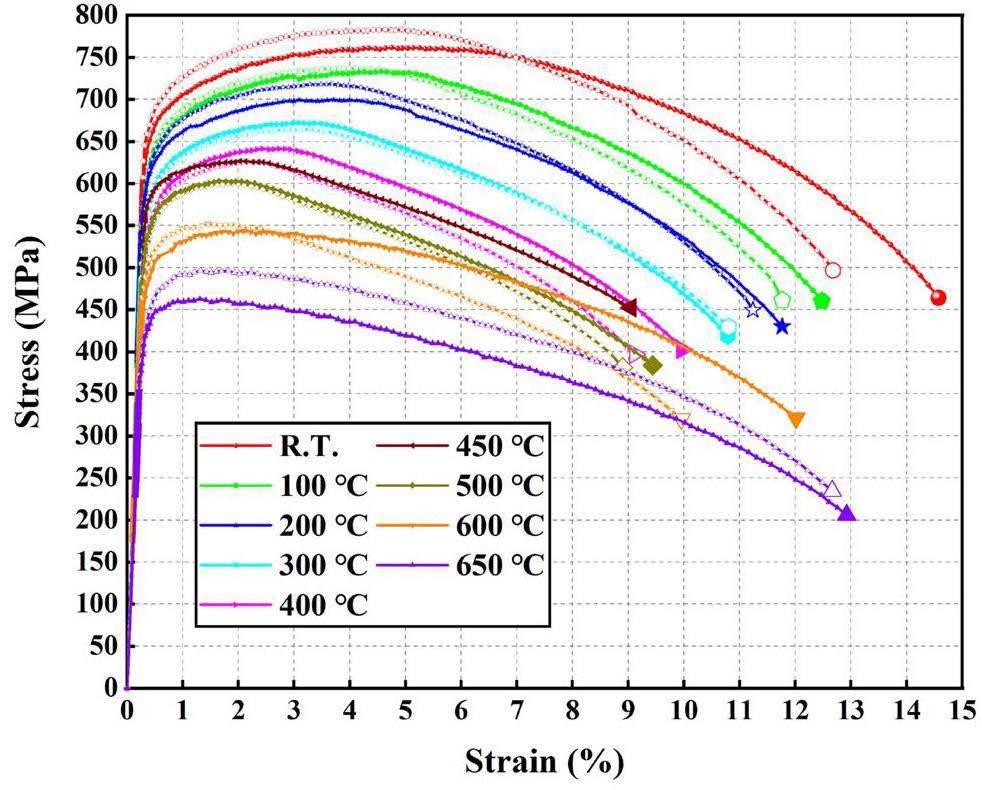
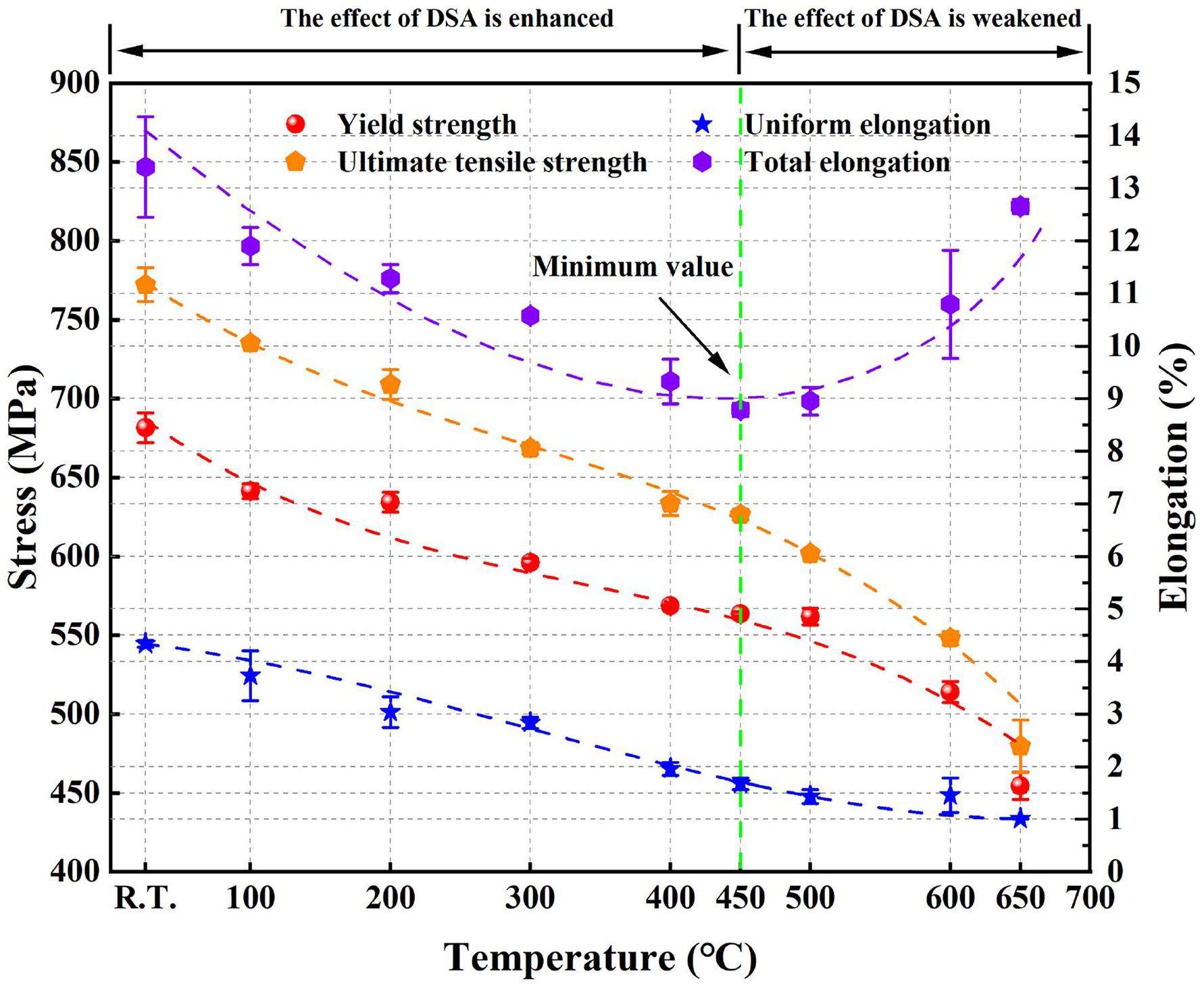
The engineering stress–strain curves in the uniaxial tensile tests are shown in Fig. 4. The documentation revealed a narrow scattering in the repeated uniaxial tensile tests. The ultimate tensile strength (UTS), 0.2% yield strength (YS), uniform elongation (UE), and total elongation (TE) of the studied steel at 25–650 ℃ are shown in Fig. 5. As the test temperature increased, the UTS, YS, and UE decreased, whereas the trend of the TE was different. The TE curve reached its lowest level when the temperature was approximately 450 ℃. This trend was consistent with other previous findings [46-48]. Notably, the YS and UTS changed with increasing temperature and had plateaus, whereas the TE changed with increasing temperature to a minimum value. This phenomenon was attributed to dynamic strain aging (DSA) [49-51]. DSA, which can be attributed to the interaction between mobile dislocations and diffusing solute atoms [50, 52], depends on the temperature and strain rate during uniaxial tensile tests, which control the diffusion of solute atoms and mobile dislocations, respectively. At 200–450 ℃, the reduction in the YS and UTS with increasing test temperature was retarded, namely, the above-mentioned plateaus, which could be attributed to DSA-induced hardening. The reason for the existence of the minimum TE was DSA-induced embrittlement.

Fig. 4Full-screen View

(Color online) Engineering stress-strain curves in uniaxial tensile tests of CLF-1 steel measured at different tensile test temperatures

Fig. 5Full-screen View

(Color online) YS, UTS, UE, and TE of the studied steel at different test temperatures

Strain distribution evolution during deformation

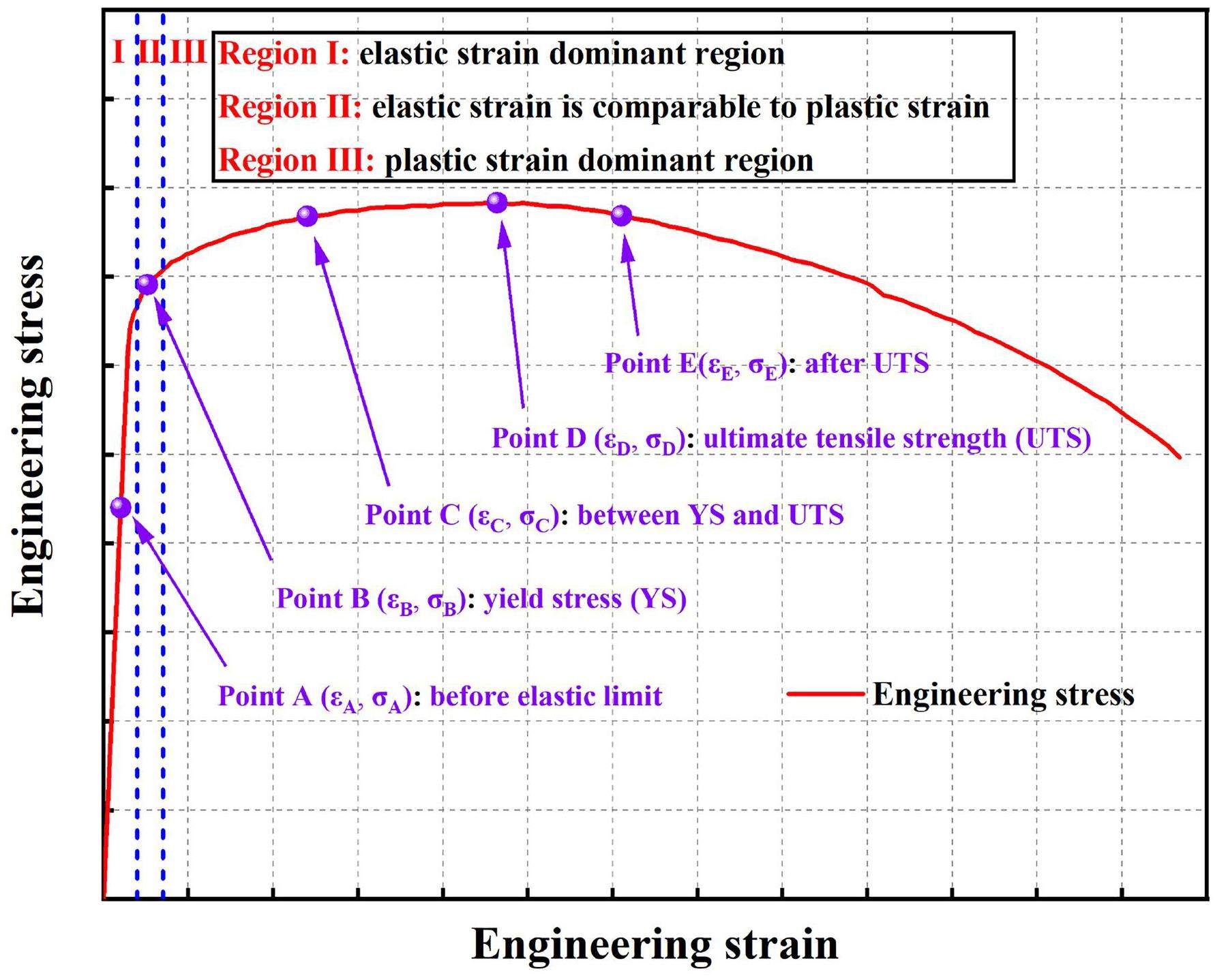
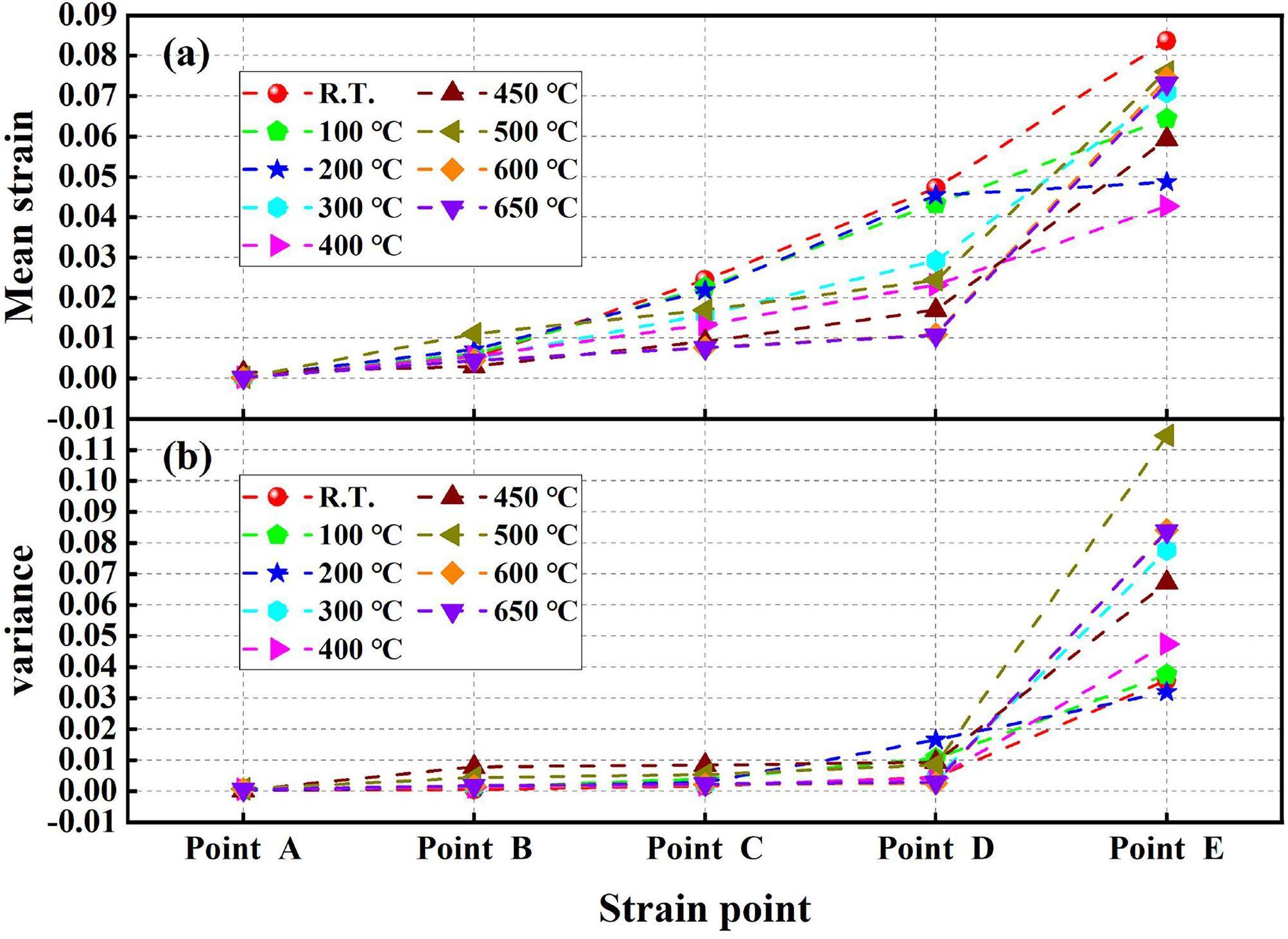
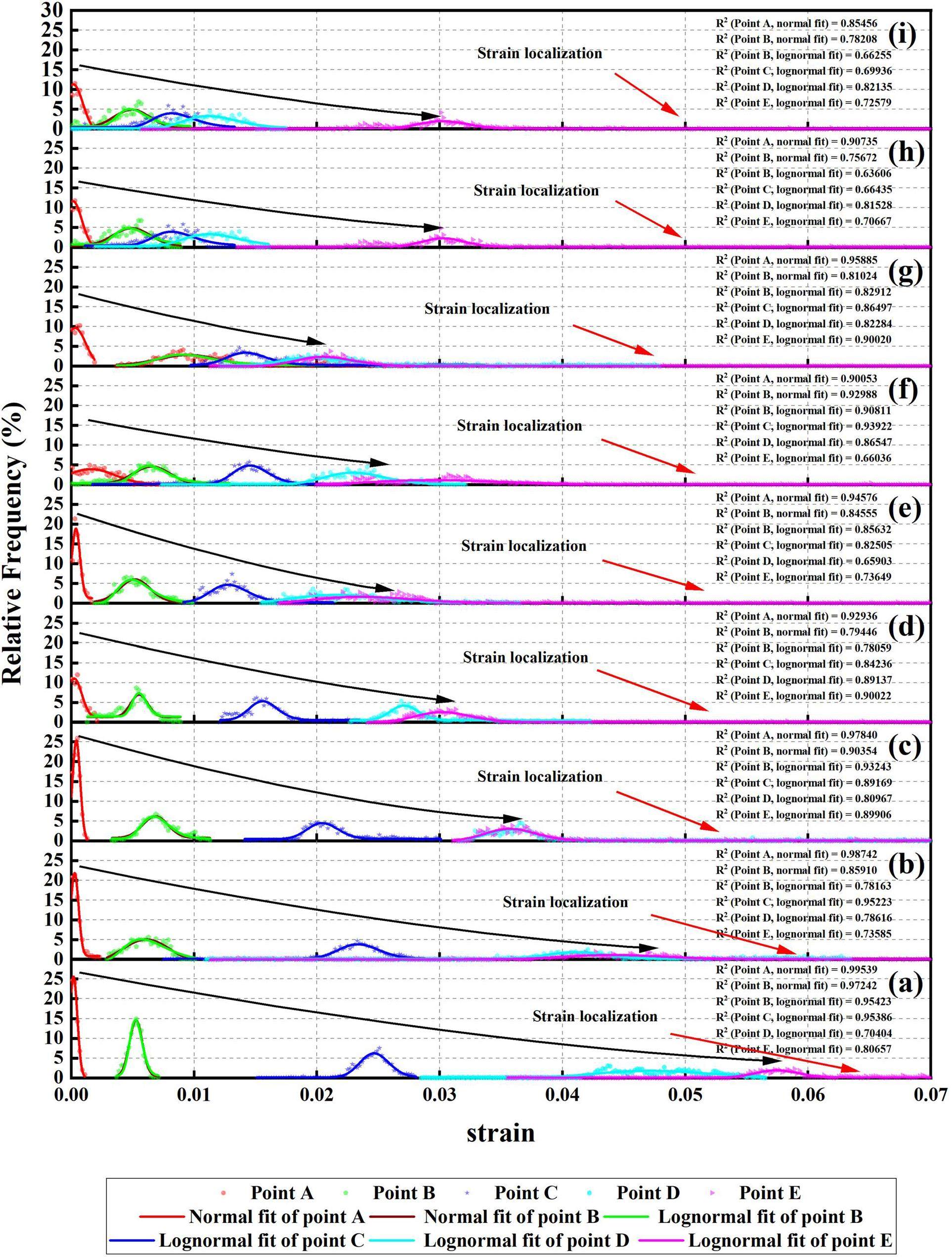
A schematic of the engineering stress–strain curve is shown in Fig. 6. The curve was divided into three regions: the elastic-dominant region (region 1), elastic–plastic transition region (region 2), and plastic-dominant region (region 3). The statistics of the normalized strain (eyy) distribution at points A, B, C, D, and E are shown in Fig. 7. Points A, B, C, D, and E were before the elastic limit, near the YS, between the YS and UTS, and after the UTS, respectively. The normalized methods were the strain at each point divided by the maximum strain, and the count at each strain interval divided by the total count. The mean strain (eyy) values and variances at the different strain points are shown in Figs. 6 and 7 at different test temperatures are presented in Fig. 8. The mean strain (eyy) gradually increased as the tensile tests progressed, as shown in Fig. 8(a), which was consistent with common sense. The variance also increased gradually as the tensile tests progressed, particularly after reaching the UTS, as depicted in Fig. 8(b), which indicated that the strain localization was enhanced as the tensile test progressed. Additionally, the strain localization was also reflected in the strain distribution statistics, which are elaborated on in the next section.

Fig. 6Full-screen View

(Color online) Different regions of the engineering stress–strain curve. Region 1: elastic strain dominant region, region 2: elastic strain comparable to the plastic strain region, region 3: plastic strain dominant region

Fig. 7Full-screen View

(Color online) Normalized strain (eyy) distribution at different test temperatures at (a) Point A (before the elastic limit), (b) Point B (near the YS), (c) Point B (near the YS), (d) Point C (between the YS and UTS), (e) Point D (at the UTS), and (f) Point E (after the UTS), respectively

Fig. 8Full-screen View

(Color online) (a) Mean strain (eyy) value and (b) strain (eyy) variance at points A, B, C, D, and E at different test temperatures

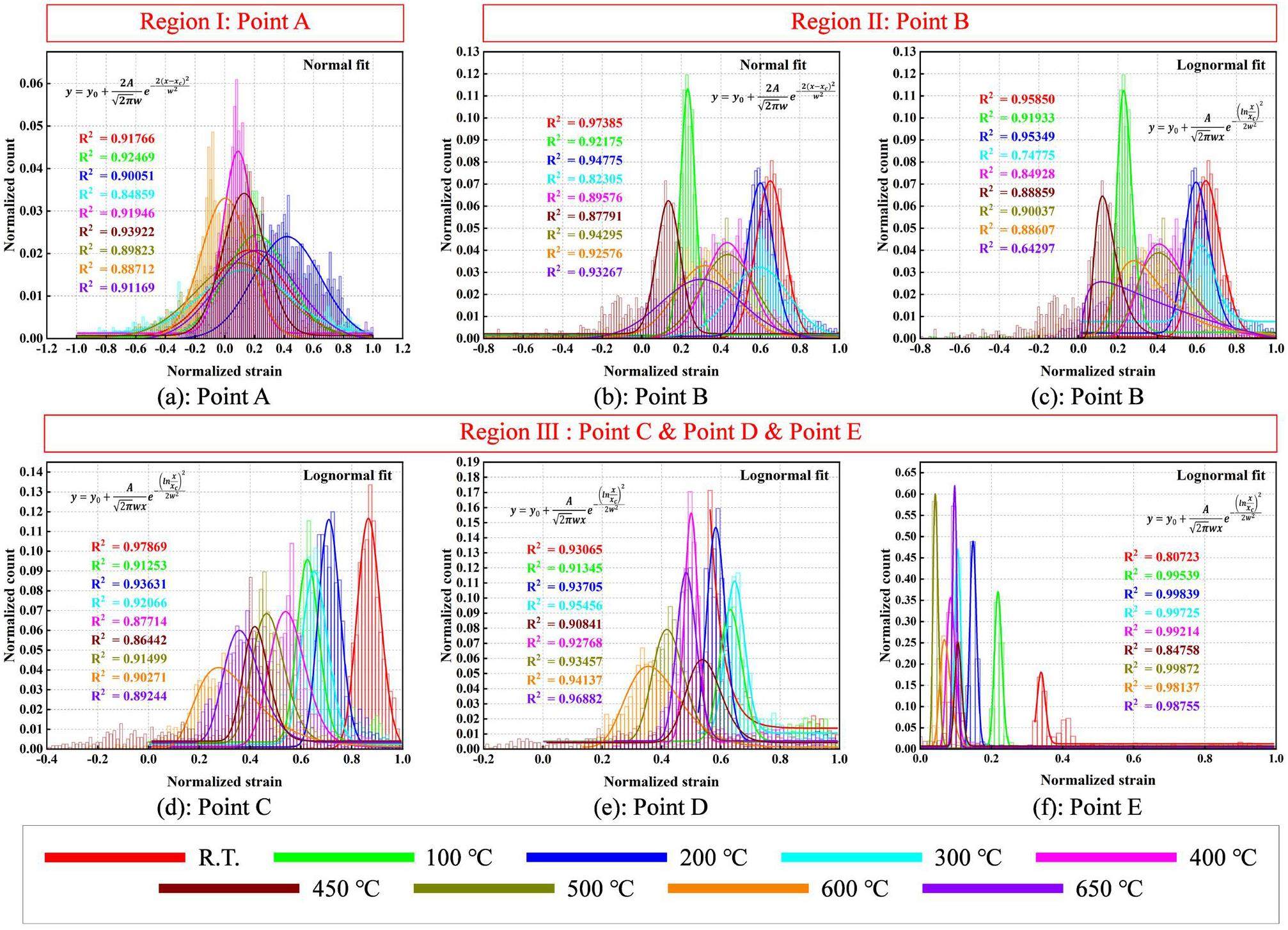
It is widely known that the total strain (ϵ^total) consists of elastic strain (ϵ^elastic) and plastic strain (ϵ^plastic), ϵ^total= ϵ^elastic + ϵ^plastic. In this study, the total strain (ϵ^total) was incorporated into the elastic strain (ϵ^elastic) and plastic strain (ϵ^plastic). We observed that the strain distribution followed a normal distribution in region 1, when the strain distribution followed a lognormal distribution in region 3. However, the strain distribution conformed to both the normal and lognormal distributions in region 2. The normal distribution and lognormal distribution are represented by Eqs. (3) and (4), respectively. $y=y_0+\frac{2A}{\sqrt{2\pi }w}{e}^{-\frac{2{\left(x-x_{\text{c}}\right)}^2}{w^2}}$ (3) $y=y_0+\frac{A}{\sqrt{2\pi }wx}{e}^{-\frac{{\left(\ln \frac{x}{x_{\text{c}}}\right)}^2}{2w^2}}$ (4) where y represents the probability density, w represents the standard deviation, x_c represents the mean value, x represents the median of each strain interval, and y₀ and A represent the fitting parameters. Most of the coefficients of determination were greater than 0.850, as shown in Fig. 7(a–f), representing a good fit. Additionally, this meant that the strain distribution region studied in this study was larger than the MSRW of the studied steel and had statistical significance.

These findings held true for all the test temperatures in this study. To the best of our knowledge, this is the first study to report the statistics of the strain distribution during deformation at different temperatures. At point A, as shown in Fig. 6, the deformation could be considered purely elastic. Thus, the elastic strain obeyed a normal distribution [53] as shown in Fig. 7. At point B, which was in the elastic–plastic transition region, the numerical value of the plastic strain was comparable to the numerical value of the elastic strain. The strain distribution could be fitted using both normal and lognormal distributions owing to the strong interaction between the elastic strain and the occurrence of plastic strain, as depicted in Fig. 7(b,c). Here, the strain accumulation process changed from following additive to following multiplicative. At point C, the numerical value of the elastic strain could not be compared with the numerical value of the plastic strain, that is, the plastic strain dominated; therefore, the strain distribution obeyed a lognormal distribution, as depicted in Fig. 7(d). This was also why previous studies [30, 54] reported that the total strain conforms to a lognormal distribution during deformation. Additionally, the long “tail” in Fig. 7(d–f) corresponds to strong strain localization, which could be used to predict damage initiation [55, 56]. At points D and E, the strain distribution obeyed a lognormal distribution because the plastic strain dominated, as depicted in Fig. 7(e, f).

Strain (eyy) maps at points A, B, C, D, and E are shown in Fig. 9. Strain (eyy) maps were cropped to eliminate the edge effect produced during the calculation. Typically, an uneven strain distribution occurs primarily during plastic deformation. However, a significantly uneven strain distribution appeared in the elastic stage (Point A), as shown in Fig. 9. This phenomenon can be attributed to the difference in the soft- and hard-phase deformations of the studied steel, as reported by Li et al. [57]. Significant strain concentration was observed, and strain-concentrated regions were approximately oriented at ±45° along the tensile direction at point B and point C, as shown in Fig. 9. This may be because shear stress had the maximum value at ±45° along the tensile direction. It was consistent with the results reported by Lindfeldt et al. [58], Gong et.al. [59], Wu et al. [60], and Tanaka et al. [54]. However, the strain-concentrated regions were not strictly at ±45 along the tensile direction. The reason for this phenomenon may be the effects of the microstructure, such as the grain boundaries [61-65] and grain orientation [66, 67], which require further exploration. The alternating distributions of the high- and low-strain-concentrated regions in Fig. 9 were caused by the coordinated deformation of the microstructure during the initial stage of plastic deformation. Meanwhile, the strain in each region increased steadily, and the strain-concentrated regions did not expand significantly during uniform plastic deformation compared with those during elastic deformation. This can be attributed to strain-concentrated regions driving the entire uniform plastic deformation of the other regions. Necking occurred in the local strain-concentrated regions during non-uniform plastic deformation at points D and E. The strain was concentrated in the necking region, and the strain in the remaining parts gradually reduced until deformation stopped.

Fig. 9Full-screen View

(Color online) Equivalent strain (eyy) maps from the uniaxial tensile tests using the DIC image of the ROI at different temperatures and stresses. (a) R.T., (b) 100 ℃, (c) 200 ℃ (d) 300 ℃, (e) 400 ℃, (f) 450 ℃, (g) 500 ℃, (h) 600 ℃, and (i) 650 ℃

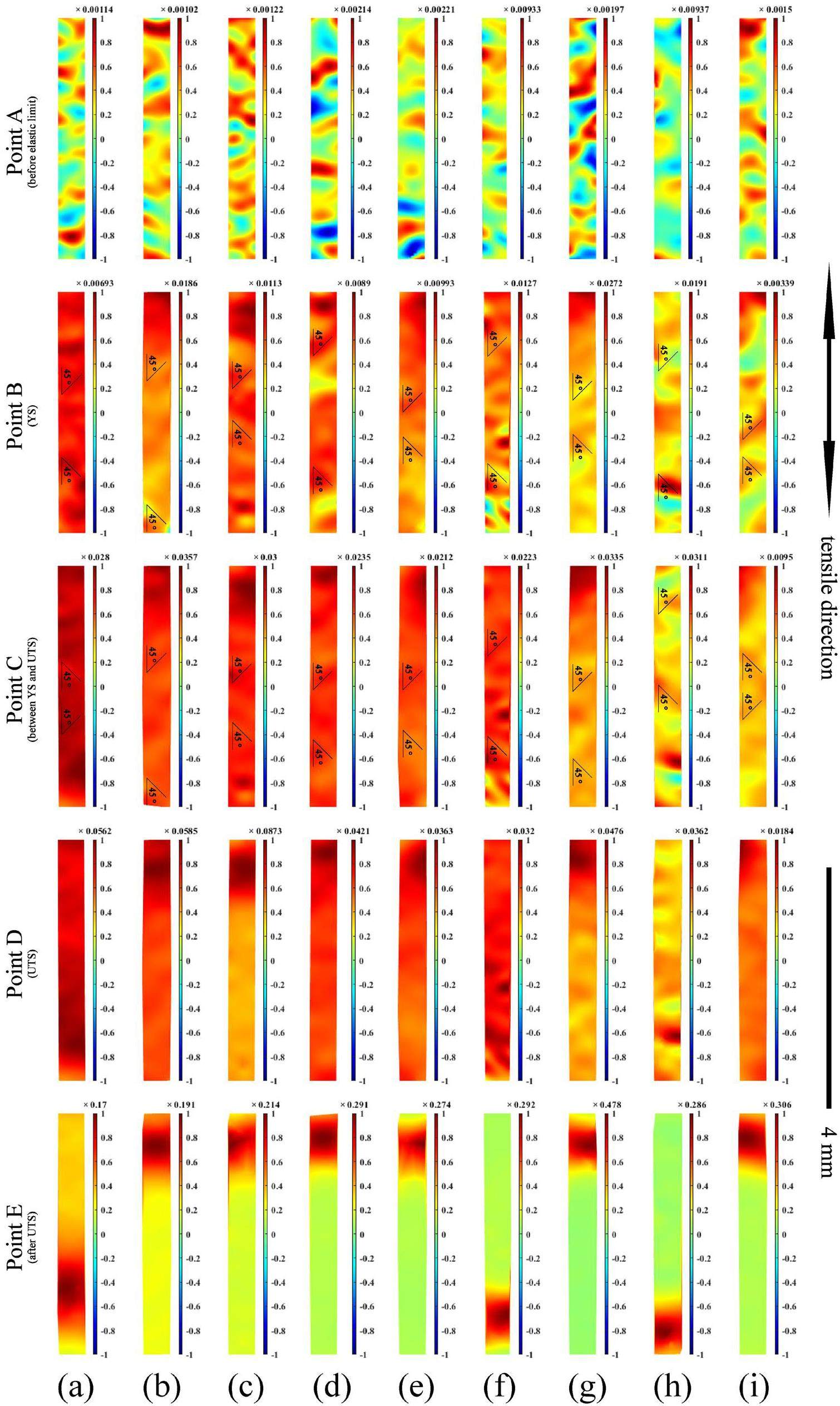
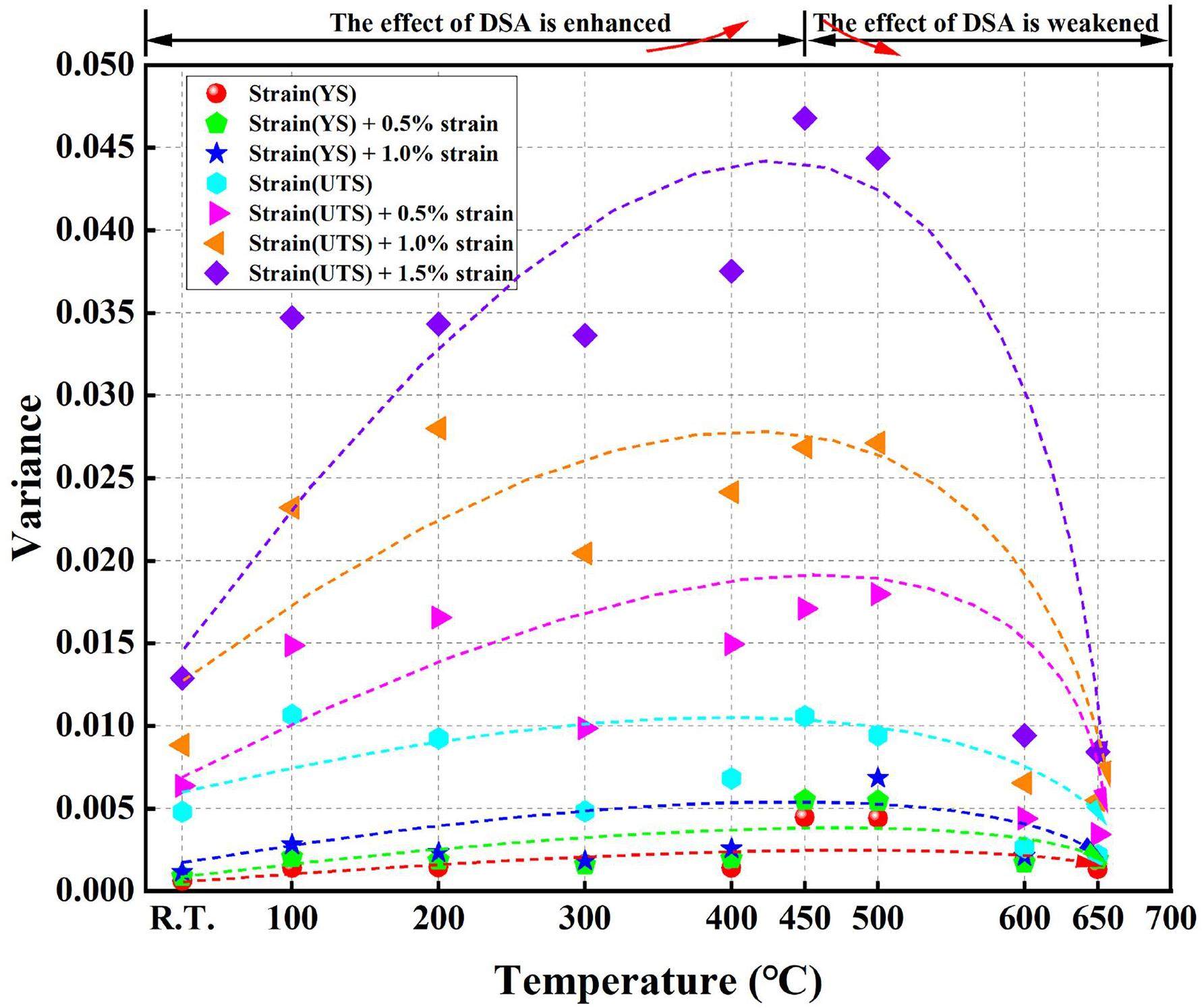
The strain (eyy) distributions at points A, B, C, D, and E at different test temperatures are shown in Fig. 10. The strain (eyy) distribution shifted to the right, the peak value of the strain value of the strain distribution gradually decreased, and the distribution gradually widened with the progress of the tensile tests at all test temperatures, as shown in Fig. 8(a, b). The strain variances in the eight deformation states at 25–650 ℃ are shown in Fig. 11. To the best of our knowledge, the variance and strain localization were positively correlated; that is, the greater the variance, the stronger the strain localization. The strain variance first increased and then decreased with increasing test temperature, reaching a maximum value of approximately 450 ℃ in all deformation states, as shown in Fig. 11. Interestingly, the analysis in Sect. 3.1. A has shown that the decline rate of the YS and UTS increased, and the TE reached the lowest value at approximately 450 ℃ with increasing test temperature owing to the effect of DSA as depicted in Fig. 5. With increasing test temperature, the variance increased; that is, the strain localization was enhanced, whereas the temperature was lower than 450 ℃, possibly because the effect of DSA was enhanced with increasing test temperature. The interaction between the solute atoms and dislocations was enhanced. In contrast, with increasing test temperature, the variance decreased when the temperature was higher than 450 ℃, possibly because the effect of DSA weakened with increasing temperature. The interaction between the solute atoms and dislocations was weakened. We believe that this discovery has general applicability to polycrystalline materials.

Fig. 10Full-screen View

(Color online) Normalized strain (eyy) distribution at different deformations and temperatures. (a) R.T., (b) 100 ℃, (c) 200 ℃ (d) 300 ℃, (e) 400 ℃, (f) 450 ℃, (g) 500 ℃, (h) 600 ℃, (i) 650 ℃

Fig. 11Full-screen View

(Color online) Relationship between variance of the fitted curves and test temperature