Cavity Phase upon Beam Arrival

For a given cavity, the relationship between the set phase φ_set and the phase of the cavity when the beam arrives φ_in is given by: ${\phi }_{\text{in}}-{\phi }_{\text{RF}-\text{ref}}={\phi }_{\text{set}}+{\phi }_{\text{offset}}-n\times 360°\mathrm{,}$ (1) where φ_RF-ref is the phase of the radiofrequency (RF) reference line when the beam arrives at the cavity and φ_offset is the phase offset caused by the low-level RF system.

The phase-setting problem involves finding the correct φ_set for each cavity such that the corresponding φ_in is equal to the value in the beam dynamics design. As shown in Eq. (1), for a given target φ_in, setting φ_set requires knowledge of φ_offset and φ_RF-ref.

φ_RF-ref is highly sensitive to differences in the upstream beam conditions between runs. Therefore, phase-setting is not a one-off problem that can be solved by reusing φ_set once a successful run is achieved. At the start of each new run, φ_set for each cavity must be correctly reset according to the unique beam conditions.

φ_offset is often assumed to be a fixed parameter in the absence of hardware changes. Under this assumption, φ_offset must only be measured once per hardware setup; however, it is currently unfeasible to directly measure it electronically. In practice, φ_offset experiences small drifts during day-to-day operation, particularly in older facilities. Such time drifts introduce additional errors in future phase-settings after φ_offset is calibrated. As an ongoing research subject, where recent advances include time-drift-aware optimization techniques based on machine learning [23, 24], this problem is beyond the scope of this study. Time drifts are ignored in φ_offset in the following sections.

The description above uses φ_in, the cavity phase when the beam reaches the entrance of the cavity, which can be taken as the upstream end of the cavity fringe fields. φ_in is selected rather than the synchronous phase φ_s because the former is unambiguous. Although φ_s is part of the standard description in the basic treatment of beam acceleration and longitudinal dynamics, it has different possible definitions once the constant-velocity assumption no longer holds within the cavity, and such an ideal assumption operates poorly in hadron linacs, particularly in the low-β section. To avoid obtaining the details for defining φ_s, only the calculation of φ_in is discussed. Such a treatment does not affect the utility of the results because regardless of the definition of φ_s, given the incoming beam energy and cavity field distribution, φ_s can always be calculated from φ_in. Considering the existence of such a conversion, only φ_in is used in this study.

Relevant Parameters and Uncertainties

Given a new superconducting linac, typical knowledge about the relevant parameters of cavities and BPMs in CMs is shown in Table 1. BPMs are standard diagnostic devices that can return both the transverse position and arrival phase of a beam up to a fixed phase offset relative to the RF reference line [25]. The BPM parameters are crucial because phase-setting is typically resolved with the aid of measurements from BPMs installed along the entire linac [26].

The phase offsets of the cavities and BPMs are completely unknown, whereas uncertainties over the longitudinal positions of the cavities and BPMs, caused by structural displacements in the CM during cool-down, are estimated assuming that intra-CM position monitors are absent. These values are close to the typical tolerances for the longitudinal displacements [27, 28] or cavity phases [29] in CMs. Note that these two tolerances can be approximately converted by simply exchanging mm with °. Suppose that the beam velocity is in the β=0.1 regime, where the cavity frequency is typically ≈ 100 MHz. A longitudinal displacement of 1 mm then approximately corresponds to a phase error of 1.2° because $\frac{{10}^{-3}\text{ m}}{0.1\times 3\times {10}^8\text{ m/s}}\times {10}^8\text{ Hz}\times 360°=1.2°.$ (2) If the frequency jumps in the higher-β structures downstream are accounted for, this relationship continues to hold up to factors of two to three, which is sufficient to corroborate the uncertainties in the longitudinal positions listed in Table 1.

The cavity voltage coefficients provide the ratio between the set and the true voltages, which is typically in the neighborhood of unity. These coefficients are also required to set up the beam acceleration correctly, but they are fixed parameters that can be obtained from one conventional phase scan and thus are significantly less challenging than phase-setting.

Cavity Phase Scan

A widely used technique for resolving the phase-setting problem is the cavity phase scan [14], where φ_set corresponding to the desired φ_in is found without explicit knowledge of φ_RF-ref and φ_offset. This can be achieved by scanning the operating phases of the cavities, recording the phases of the beam upon reaching the downstream BPMs, and obtaining a sine-like curve that represents the cavity-BPM phase relationship, often referred to as the signature of the phase scan. Next, in a procedure that is often referred to as signature matching, mathematical modeling is employed to determine the cavity voltage and φ_in [15], and occasionally the incoming beam energy, under the criterion that the modeled curve fits the phase scan results by matching the phase scan signature. If the information from a single phase scan is insufficient, the scan is repeated at different cavity voltages to obtain better fitting results.

In the two-BPM version of the cavity phase scan [14, 30], the only requisite knowledge is the relative distance between the two BPMs downstream of the cavity, where the relative phase difference upon beam arrival is used to obtain the cavity-BPM phase relationship. The exact position of the cavities, z_cav, is not required in the calculations, which can avoid the problem of displacements within CMs due to cool-down.

A cavity phase scan is performed sequentially through the linac, cavity by cavity. Hence, the larger the number of cavities, the longer the process. Even in linacs where automatic phase-setting is implemented, a cavity phase scan is often an indispensable step in the calibration stage.

Automatic Phase-Setting

As phase scans are time-consuming, many linac facilities, notably SNS and FRIB, have developed methods to tune-up the linac without phase scans, which can reduce the tune-up time by two orders of magnitude, from ~10 h to ~10 min [18, 31]. In these methods, a beam-based TOF calibration experiment [32] involving a phase scan alongside additional BPM measurements is first conducted to calculate φ_offset. Once all φ_offset are known, they can be employed to accurately calculate φ_RF-ref in each cavity, thereby achieving an automatic phase-setting in each subsequent tune-up. Both the calibration and automatic phase-settings require good knowledge of the cavity positions provided by alignment surveys.

Table 2 presents a comparison of different solutions that employ BPM phase information for the phase-setting problem. The proposed method is listed in the rightmost columm, where both the cavity and BPM positions are obtained via TOF alignment. A method that simultaneously performs the alignment and phase calibration is introduced in the following section.

Linac Setup

To apply the TOF alignment and calibration method, the linac setup must fulfill two requirements [33]. First, there must be a pair of BPMs not far downstream of every cavity such that it is possible to conduct a conventional phase scan. As conventional phase scans are compulsory in modern hadron linacs, this requirement is always satisfied. Second, there must be an energy measurement device downstream of the last cavity, normally in high-energy beam transport (HEBT), which follows the superconducting section. In this study, it was assumed that the energy measurement was performed via TOF on a pair of BPMs dedicated to this purpose. This is the most common and practical setup used for accelerated hadron beams. This method still applies if the energy is measured using other means.

All the quantities listed in Table 1 were determined via TOF experiments and subsequent data analysis. Once obtained, they do not need to be measured again unless the linac hardware changes.

It is noteworthy that this TOF alignment and calibration method is applicable only to hadron linacs. As electrons are highly relativistic, each superconducting cavity can create only minuscule velocity changes, and the resulting differences in TOF measurements are far below the noise level of the phase monitors.

Calibration Experiment

The calibration experiment comprised two steps. The first step was a forward phase scan that moved forward through the entire linac and performed a phase scan on each cavity. Conversely, the second step was a backward voltage scan that conducted a voltage scan on each cavity from the exit to the entrance.

Data Analysis

The measurement results from the calibration experiment were analyzed in several steps, with each step depending on the analysis in the previous steps. The analysis provides the relative positions and relative phase offsets between all the cavities and BPMs in the linac. Section 3.4 addresses whether absolute positions and phase offsets are required and how the calibration results can be utilized to achieve automatic phase-setting.

3.3.3

Cavity Positions

Once φ_in and the voltage coefficient for a cavity are known, the distance between the cavity and the BPM unit downstream can be obtained by following the same principle as in Sect. 3.3.1. However, this situation is more complex because the TOF within the cavity must be considered.

Based on the calibration setup illustrated in Fig. 1: ${\phi }^{\prime }=\phi -{\phi }_{\text{out}}+{\phi }_{\text{in}}-n\times 360°\mathrm{,}$ (7) where φ is the phase reading of the BPM; and φ_in and φ_out are the phases at the cavity entrance and exit, respectively. The cavity entrance and exit were chosen such that the cavity fields were effectively zero at these positions. With φ_in the cavity voltage coefficient known from the previous step and the incoming beam energy known from TOF measurements, φ_out can be calculated using beam simulations with the cavity field map.

Fig. 1Full-screen View

(Color online) Schematic of the cavity position calibration

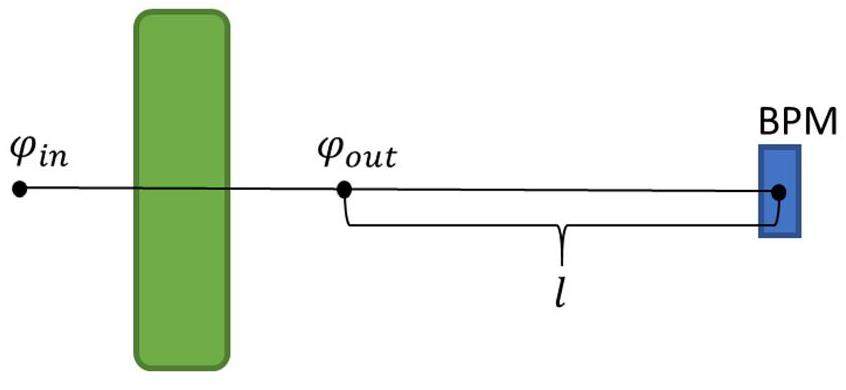
After leaving the electromagnetic field of the cavity, the particles drift uniformly until they reach the BPM, exhibiting a relationship similar to Eq. (6). Therefore, plotting the scatter graph of $t_{\text{TOF}}-{\phi }^{\prime }$ and conducting linear fitting enables the determination of the slope as $lf/l_{\text{TOF}}\times 360°$. A simple conversion yields length l.

3.3.4

Lattice Model

The position calculations in Sect. 3.3.1 and 3.3.3 enable the construction of a lattice model by following the steps illustrated in Fig. 2. Starting with a designated reference BPM, the positions of the downstream BPMs relative to the reference BPM can be determnined. Next, the relative positions of each cavity and its adjacent downstream BPM provide the locations of the respective cavities. Finally, if required, the calibrated BPMs can serve as TOF devices (as discussed at the end of Sect. 3.3.1) to determine the positions of elements upstream of the reference BPM.

Fig. 2Full-screen View

(Color online) Schematic of the position alignment of the entire linac: (a) original setup; (b) alignment of BPMs; (c) alignment of cavities; and (d) if applicable, the use of aligned BPMs for TOF measurements to align elements further upstream

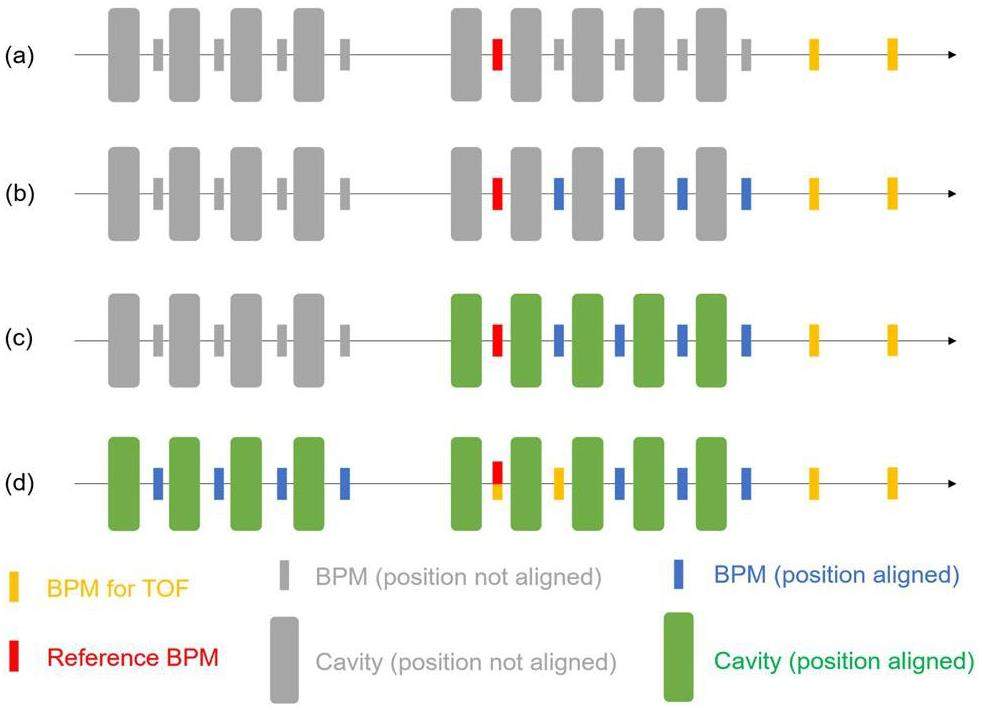
Assuming that calibrated BPMs were not used as TOF devices more than once, the uncertainties of all BPM positions relative to the reference BPM can be given directly by the calculations in Sect. 3.3.1. As each cavity position is obtained from the sum of two quantities, the uncertainties of the cavity positions ${\sigma }_{\text{ref}-\text{to}-\text{cavity}}$ are generally larger: ${\sigma }_{\text{ref}-\text{to}-\text{cavity}}^2={\sigma }_{\text{ref}-\text{to}-\text{BPM}}^2+{\sigma }_{\text{BPM}-\text{to}-\text{cavity}}^2,$ (8) where ${\sigma }_{\text{ref}-\text{to}-\text{BPM}}$ is the uncertainty of the position of the BPM unit upstream of the cavity and ${\sigma }_{\text{BPM}-\text{to}-\text{cavity}}$ is the uncertainty of the BPM-to-cavity distance.

Reference Point and Automatic Phase-Setting

The TOF experiment and data analysis provided the relative phase offsets and positions of all the cavities and BPMs of the linac. The absolute position of such a section is still unknown and determines the absolute phase offset of each element with the RF reference line.

In hadron linacs, the cavities with phases that must be set are commonly preceded by a radiofrequency quadrupole (RFQ). The beam is bunched out of the RFQ, and its energy does not change during medium-energy beam transport (MEBT), which connects the RFQ to the first cavity. Depending on whether the normally conducting structure upstream can vary its outgoing beam energy, there are two solutions to this problem to implement automatic phase-setting.

CAFe II Accelerator

The China Accelerator Facility for Superheavy Elements (CAFe II), is a superconducting heavy-ion linac located at the Institute of Modern Physics (IMP). In a modification of the CiADS demonstration facility [35], the main mission of CAFe II is the synthesis of superheavy elements. CAFe II can accelerate heavy-ion beams with charge-to-mass ratios from approximately 1/3 to 4-6.5 MeV/u. Designed for continuous-wave (CW) operation, the average particle current of the beam ranges from 1 to 10 uA.

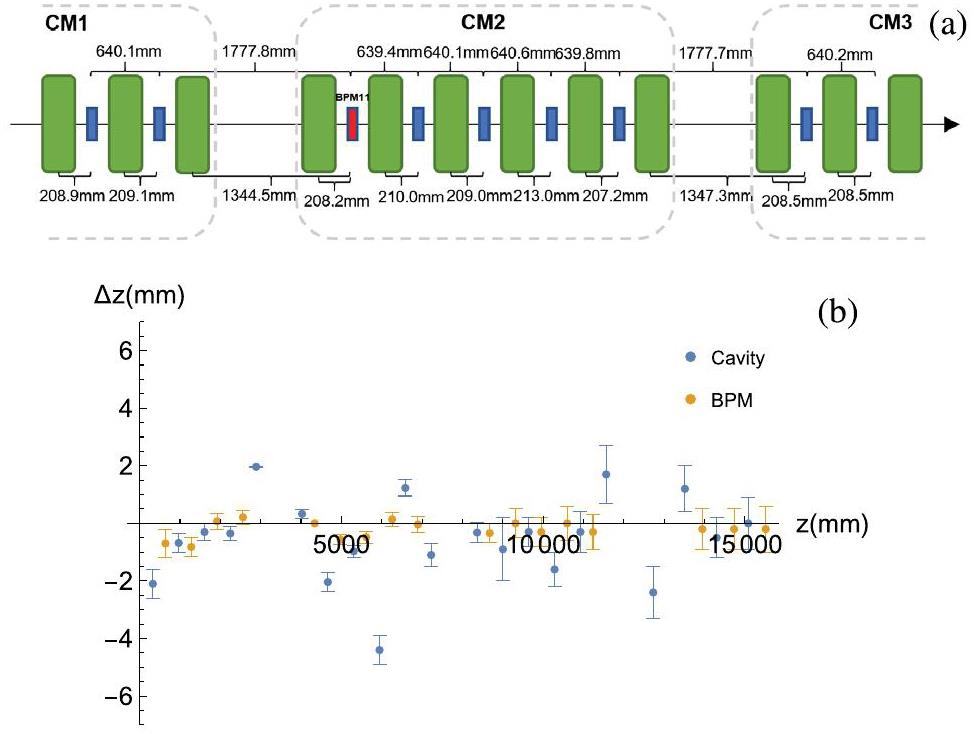
The superconducting section of CAFe II consists of four CMs. Within each CM, there is a BPM between each pair of adjacent cavities. The first three CMs contain six cavities and five BPMs, whereas the last CM contains five cavities and four BPMs. A schematic of CAFe II is shown in Fig. 3; the cavity and BPM names are listed in Table 3. Cavities are named by both the CM to which they belong and their position within it; for example, CM1-3 denotes the third cavity in the first CM.

Fig. 3Full-screen View

(Color online) Schematic of CAFe II

TOF Alignment and Calibration Experiment

The TOF alignment and calibration experiment at CAFe II followed the procedure detailed in Sect. 3.2. After the forward phase scan, a 0.3 mA proton beam was accelerated by 22 superconducting cavities from 1.36 MeV at the RFQ exit to 17.78 MeV at the end of the superconducting linac. BPM25 and BPM26 after CM4, at the end of the linac, were used as energy measurement devices. These two BPMs were connected to an oscilloscope instead of an electronic system, which allowed observation of the waveform when the beam passed through them. With errors caused by cable transmission calibrated and corrected in advance, manually aligning the two waveforms of BPM25 and BPM26 provided the absolute TOF of the beam from BPM25 to BPM26.

TOF energy measurements from BPM25 and BPM26 were then used to calibrate the distances between the 19 pairs of BPMs, as well as the distances between each BPM and the preceding cavity. As discussed in Sect. 3.4, because the CAFe II superconducting section is directly downstream of the RFQ, the calibration ultimately provides the relative positions of all the cavities and BPMs, as well as their relative phase offsets.

It is also necessary to discuss the experimental details of BPMs. To perform the data analysis, the frequency of the BPM unit must be known, as shown in Eq. (6). At a frequency of 162.5 MHz, which is the working frequency of CAFe II, the phase readings of BPMs were susceptible to interference from the electromagnetic field in the cavity. To mitigate this interference, the BPM readings were measured at the experimental second harmonic frequency of 325 MHz. To minimize errors owing to beam fluctuations, 50 samples of BPM readings were conducted and the median value was selected. In the case of excessive variance, the dataset was excluded. The findings of the calibration experiment are presented subsequently.

Alignment and Calibration Results

The alignment and calibration results were obtained based on the data analysis scheme described in Sect. 3.3. First, the spacing between the BPMs was calculated. Figure 4a shows a scatter plot of $t_{\text{TOF}}-\text{Δ}\phi$ for BPM11 and BPM12 at various energies. As the range of BPM readings was between 0-360° [36, 37], making the range $\text{Δ}\phi \pm 360°$, direct linear fitting was not feasible. Therefore, Δφ was adjusted by appropriate increments or decrements of 360° such that all data points could be fitted to a straight line. The slope and error of the fitting shown in Fig. 4b were determined as 122.01±0.04. By multiplying the slope by $l_{\text{TOF}}/\left(f\times 360°\right)$, the distance between BPM11 and BPM12 was 639.4±0.2 mm.

Fig. 4Full-screen View

(Color online) Scatter plot of the raw data (a) and straight line fitting (b) of $t_{\text{TOF}}-\text{Δ}\phi$ for BPM11 and BPM12 at various energies, along with a histogram (c) of the standard deviations of all measured Δφ

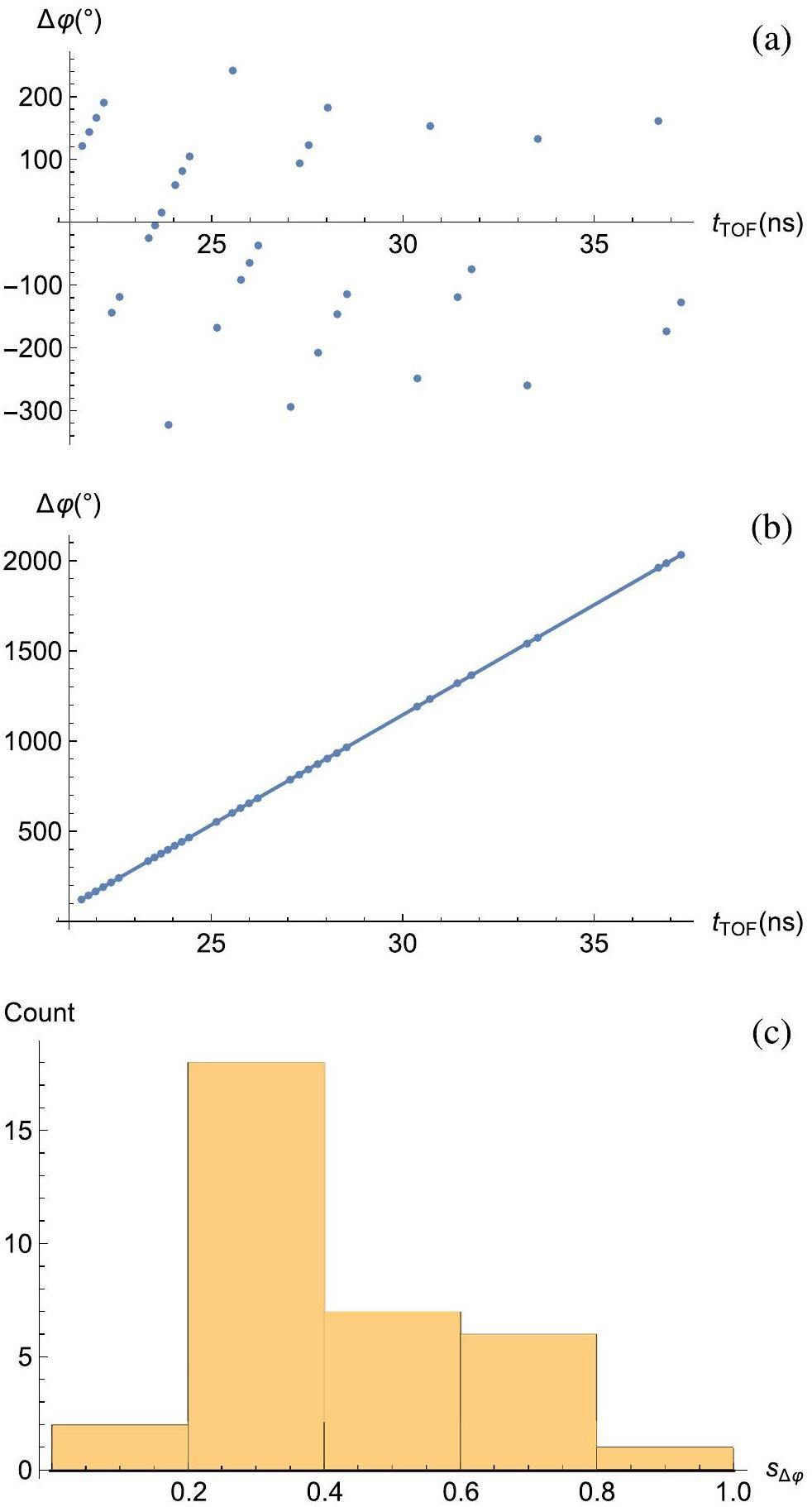
Next, the data in the forward phase scan were analyzed using the relative BPM positions. The electromagnetic field distributions of the HWR010 and HWR019 cavities were obtained using CST Studio software [38], and the particle transmission through the cavity was performed using TraceWin software [39], which provided the beam simulation code. The cavity voltage coefficient and φ_in in each cavity were determined as in the conventional phase scans.

These results enabled the distance between each cavity and the downstream BPM to be determined. Figure 5 shows a scatter plot of $t_{\text{TOF}}-{\phi }^{\prime }$ for CM2-1 and BPM11. The determined values of the fitted slope and error were 19.68 ± 0.15. By multiplying the slope by $l_{\text{TOF}}/\left(f\times 360°\right)$, a distance of 103.2 ± 0.8 mm between the CM2-1 cavity exit and BPM11 was obtained. When the spacing between BPMs and the distance between the cavity and BPM are known, the respective positions can be determined.

Fig. 5Full-screen View

(Color online) Scatter plot and straight line fitting graph of $t_{\text{TOF}}-{\phi }^{\prime }$ for CM2-1 and BPM11

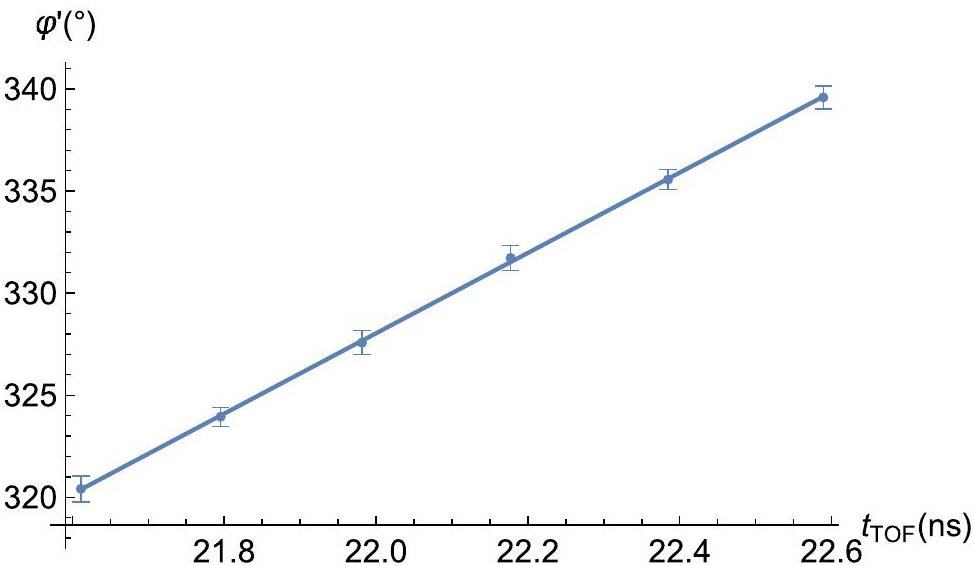
Figure 6 shows the TOF-aligned positions of one section of the CAFe II linac as well as the differences between TOF-aligned positions and their respective values in the original lattice design of CAFe II for all cavities and BPMs. Almost all the differences in position were smaller than the typical displacements within CMs discussed in Sect. 2.2, which shows that TOF alignment results are consistent with the lattice design.

Fig. 6Full-screen View

(Color online) Distances obtained from TOF alignment among various elements along part of the linac a). BPM 11 is red to emphasize that it serves as the reference for TOF position alignment. Supposing BPM 11 is located at the design location (yellow dot located at approximately z=4200 on the x-axis), the difference between the TOF-aligned position and respective value in the lattice design for each BPM and cavity (b)

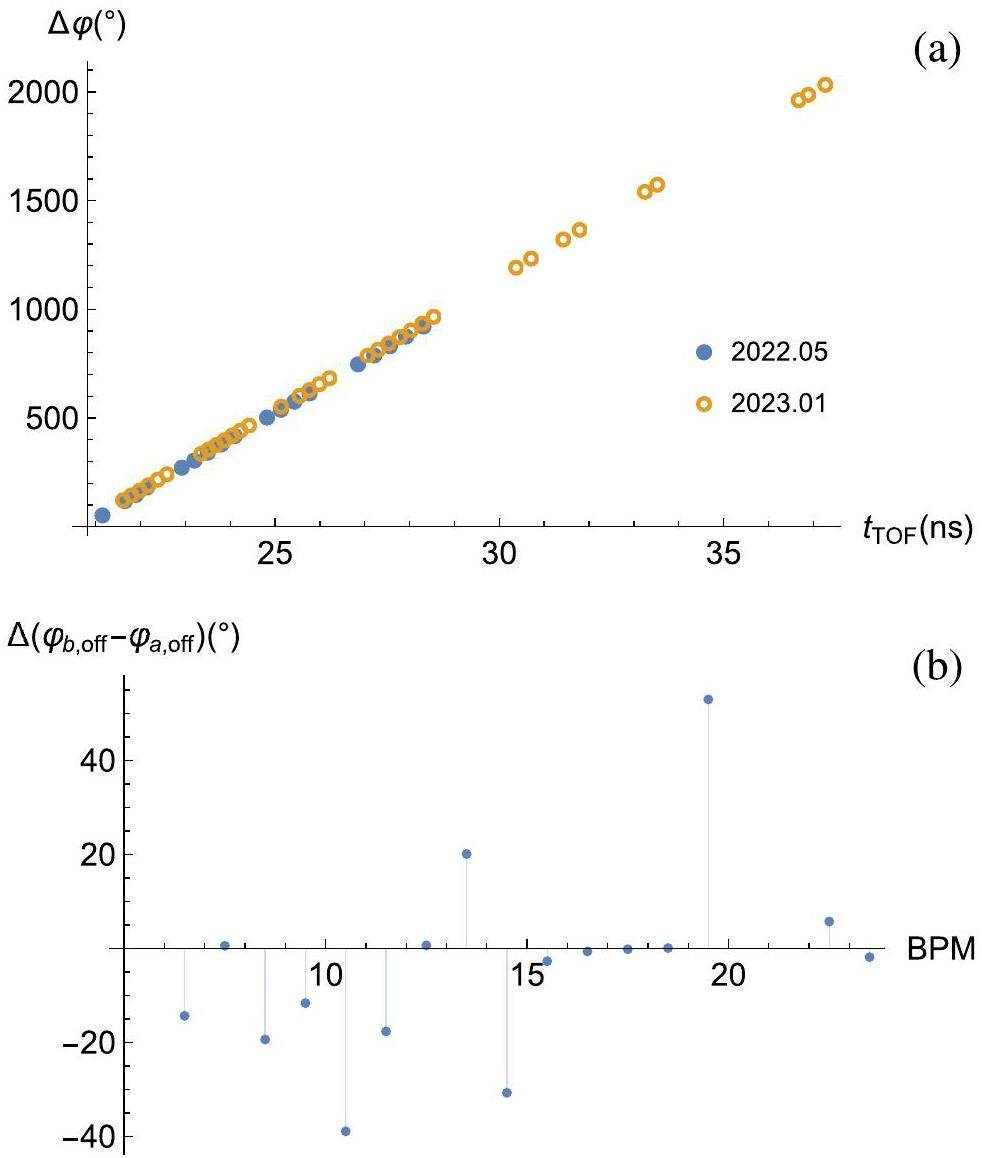
Eight months before this experiment, a TOF experiment that calibrated only BPMs was also conducted. Figure 7 illustrates the differences between the results of the two calibration experiments. While there were modifications in the low-level RF system between 2022.05 and 2023.01, which caused changes in some relative phase offsets, the relative phase offsets between BPMs unaffected by such modifications remained almost unchanged. These results corroborate the proposition that as long as the positions of the cavities and BPMs are fixed and the RF circuit structure remains unchanged, the phase offsets obtained from the calibration experiment remain constant.

Fig. 7Full-screen View

(Color online) (a) $t_{\text{TOF}}-\text{Δ}\phi$ for BPM11 and BPM12 at various energies, measured at 2022.05 and 2023.01, respectively. Error values are similar to those plotted in Fig. 4c. (b) difference in relative phase offsets between the calibration experiments at 2022.05 and 2023.01, for each pair of adjacent BPMs along CAFe II (with the exception of pairs that included BPM 22, which was not functional)

Automatic Phase-Setting

To demonstrate automatic phase-setting and verify the calibration results, several new lattice designs were created and the predicted final energies were compared the with TOF energy measurements.

In each lattice design, z_cav from the alignment results enabled φ_RF-ref and φ_in to be calculated via simulations. These two phases, combined with the phase calibration results φ_offset (which were constant as long as the low-level circuits remained unchanged), allowed φ_set to be calculated using Eq. (1). Similar to the previous data analysis, all simulations were performed using TraceWin. Calculating φ_set for a CAFe II lattice design required only several minutes, which was a significant time saving compared to that required for the phase scan. Hence, this method can significantly expedite beam tune-up.

Furthermore, any design calculation is expected to have the same level of accuracy, regardless of the beam intensity. However, this is not the case for cavity phase scans, which suffer from larger errors owing to weaker BPM signals when the beam intensity is low. Such errors would pose significant problems for cavity phase scans in the tune-up of heavy-ion beams, which typically have low intensities compared to protons. With automatic phase-setting, low-intensity beams can achieve a highly accurate phase-setting as long as the TOF alignment and phase calibration experiments are performed using a high-intensity beam, which is the case for CAFe II.

To examine the accuracy of the phase calculations, a new set of lattice settings were constructed by introducing random variations in the cavity voltage and synchronous phase based on the original lattice. Owing to a malfunction in BPM21, the new lattice terminated at CM3-6 with a designed exit energy of 9.289 MeV. The operational phase of the cavity was calculated by using a previously described method. Subsequently, the TOF of the beam at the CM3-6 exit was measured as 14.65 ns, corresponding to an energy of 9.285 MeV, which closely matched the design value.

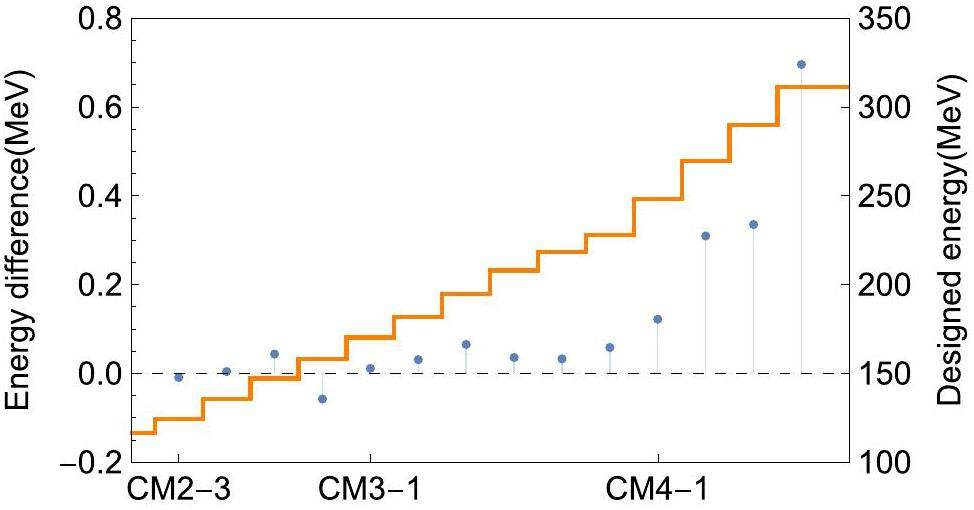
Next, the case in which φ_RF-ref changes in the first cavity was tested. This occurs when the particle type is changed to a particle other than a proton or when there are changes in the RFQ exit energy or the initial phase of the RFQ. To resolve this issue, a phase scan of CM1-1 was performed and the technique discussed in Sect. 3.4 was applied. Figure 8 shows the results for a beam tune-up using ⁵⁴Cr¹⁷⁺, where the predicted output energy at each cavity closely agreed with the direct TOF energy measurements. These results confirmed the accuracy of the calibration results and validated the effectiveness of the automatic phase-setting.

Fig. 8Full-screen View

(Color online) Designed energy (orange line) of the ⁵⁴Cr¹⁷⁺ beam at the cavity exit along the CAFe II linac, as well as the difference (blue dots) between the measured and design energy values