Impact parameter manipulation in exclusive photoproduction in Electron-Ion Collisions

ACCELERATOR, RAY TECHNOLOGY AND APPLICATIONS

Impact parameter manipulation in exclusive photoproduction in Electron-Ion Collisions

Xin Wu，

Xin-Bai Li，

Ze-Bo Tang，

Kai-Yang Wang，

Wang-Mei Zha

Nuclear Science and Techniques

Vol.36, No.9

Article number 157

Published in print Sep 2025

Available online 27 Jun 2025

DOI：10.1007/s41365-025-01704-5

CSTR：32136.14.NST.2025.09157

9800

In the context of future electron-ion collision experiments, particularly the Electron-Ion Collider (EIC) and the Electron-Ion Collider in China (EicC), investigating exclusive photoproduction processes is of paramount importance. These processes offer a distinctive opportunity to probe the gluon structure of nuclei across a broad range of Bjorkenx, thereby enabling measurements of nuclear shadowing and facilitating the search for gluon saturation and color glass condensates. This study explores the potential of utilizing neutron tagging via the Coulomb excitation of nuclei to precisely determine the impact parameter for exclusive photoproduction in electron-ion collisions. By developing the Equivalent Photon Approximation for fast electrons, this study incorporates a coordinate-space-dependent photon flux distribution to elucidate the relationship between the photon transverse momentum distribution and the collision impact parameter. Furthermore, the differential cross section for Coulomb excitation of nuclei is derived by leveraging the spatial information from the photon flux. Our calculations demonstrate that neutron tagging can significantly alter the impact parameter distributions, thereby providing a robust method for impact parameter manipulation in electron-ion collisions. This study provides valuable insights and strategies for exploring the impact parameter dependence of exclusive photoproduction, offering novel insights for experimental design and data analysis. Ultimately, it enhances our understanding of the gluon distribution within the nucleus.

Electron-Ion collisionsExclusive photoproductionCoulomb dissociationGluon tomography

Introduction

Electron-ion collisions present an unparalleled opportunity for investigating the internal structures of nucleons and nuclei [1], particularly the distribution of gluons across different momentum scales. Upcoming facilities, including the Electron-Ion Collider (EIC) [2] in the United States and the Electron-Ion Collider in China (EicC) [3], are specifically designed to probe these structures over a broad range of photon virtuality (Q²) and Bjorken-x, thereby enabling the study of phenomena such as nuclear shadowing and gluon saturation. The deployment of high-energy electron beams in interactions with protons and heavy ions facilitate precise measurements of the spatial and momentum distributions of gluons within the target [4], which is crucial for advancing our understanding of quantum chromodynamics (QCD) in dense nuclear environments.

Exclusive photoproduction is a key process for probing the gluon distribution within nuclei. In this process, a virtual photon emitted by an electron coherently interacts with the target, producing a vector meson while leaving the target intact. This interaction serves as a direct probe of the gluon density, as the cross-section is sensitive to the gluon distribution within the target. Specifically, in coherent photoproduction, the virtual photon fluctuates into a quark-antiquark pair, which subsequently scatters elastically from the target through the exchange of a color-neutral object, typically a Pomeron, at high energies [5]. Such studies are essential in understanding phenomena such as gluon shadowing, where gluon densities in nuclei are suppressed compared with those in free protons, and in providing compelling evidence for gluon saturation and the formation of color glass condensates [6-9].

To gain insights into the spatial distribution and fluctuations of gluons, measurements of the differential cross section $d σ / d t$ are of paramount importance [10]. Momentum transfer t is directly related to to the transverse distance between the interacting particles, thereby yielding essential information on the spatial distribution of gluons within the nucleus. In relativistic heavy-ion collisions, significant progress has been made in probing this distribution via $d σ / d t$ measurements [11]. Early studies conducted by the STAR experiment at the Relativistic Heavy Ion collider (RHIC) utilized ρ meson photoproduction to reconstruct the spatial distribution of gluons via an inverse Fourier transform of the $d σ / d t$ distribution [12]. Further advancements were achieved by the ALICE experiment at the Large Hadron Collider (LHC), which measured $d σ / d t$ while accounting for the transverse momentum of the photons [13]. This approach introduced interference effects that facilitated a more detailed analysis of gluon spatial distributions. More recently, STAR [14] reported measurements of ρ meson photoproduction that exploited the linear polarization of photons, which introduced an additional dimension to the analysis, thereby enhancing the sensitivity to spatial anisotropy and gluon density fluctuations within the nucleus.

The accurate determination of the t distribution also necessitates a comprehensive understanding of the transverse momentum distribution of the photons involved in photoproduction. As this transverse momentum distribution cannot be directly measured, it is typically approximated using the Equivalent Photon Approximation (EPA) [15], which inherently involves integration over the impact parameter. However, recent theoretical and experimental studies on photon-photon collisions in heavy ion collisions have demonstrated that the photon transverse momentum distribution is highly dependent on the collision impact parameter [16-21]. This dependence necessitates a detailed investigation of the parameter dependence of exclusive photoproduction processes. In both electron-ion collisions and ultra-peripheral heavy-ion collisions (UPCs), conventional methods, such as using charged-particle multiplicity to determine the impact parameter, are not feasible. Recent measurements by the STAR [18], ALICE [22, 23], and CMS [9, 19] experiments have successfully utilized neutron emission from the Coulomb excitation of nuclei to effectively control the “collision centrality” in UPCs. This progress motivates the adoption of a similar technique for regulating the impact parameter in electron-ion collisions specifically by tagging neutrons from Coulomb excitation to determine the interaction centrality, that is, the impact parameter.

Determining the probability of Coulomb dissociation (CD) as a function of the impact parameter in UPCs necessitates the calculation of the photon flux in spatial coordinates. In UPCs, the spatial distribution of the photon flux is typically computed using EPA, which assumes a straight-line trajectory for the ions involved. This assumption is valid when the motion of colliding ions is not significantly influenced by the electromagnetic field over the collision duration. However, in electron-ion collisions at an EIC, the photon flux induced by the electron cannot be described by the conventional EPA, as the straight-line approximation breaks down owing to the substantial deflection of the electron under the electromagnetic field of the heavy ion. Consequently, a precise derivation of the spatial distribution of the photon flux induced by the electron is essential to accurately calculate the CD probability as a function of the impact parameter in electron-ion collisions.

This study aims to address these challenges by extending the conventional EPA framework to incorporate the unique dynamics of electron-induced photon flux in electron-ion collisions. By developing a spatially dependent photon flux distribution, we aim to establish a more precise relationship between the transverse momentum distribution of photons and the impact parameters of the collisions. Within this refined framework, we propose to study the impact parameter manipulation in exclusive photoproduction processes in electron-ion collisions by tagging neutrons from Coulomb excitation. By achieving impact parameter control via neutron tagging, this study introduces a new methodology for probing the spatial and momentum structures of gluons in nuclei, thereby contributing to the experimental design and data analysis strategies for future electron-ion collision experiments.

Methodology

2.1

Kinematics of Electron-Proton/Nucleus Scattering

To derive the photon flux, we begin by analyzing the kinematics of lowest-order of electron-proton (e + p) scattering, as illustrated in Fig. 1. Although our primary interest lies in electron-nucleus (e + A) collisions, the photon flux generated by the electron is essentially the same in both e + p and e + A interactions. Therefore, to ensure both simplicity and generality in the derivation, we perform the analysis within the context of e + p-scattering.

Fig. 1

(Color online) Feynman-like diagram for electron-proton scattering. p and

p^{'}

are the four-momenta of the electron before and after scattering, respectively. Furthermore, q and P represent is the four-momentum of the photon and proton, respectively

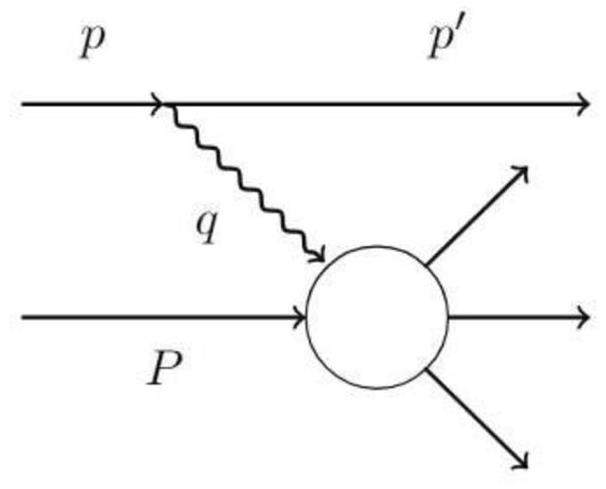
Let the z-axis be the direction of motion of the incident electron. The four vector of the incident electron p and that of the scattering electron $p^{'}$ are given by $p = (E_{e},0,0, p_{z})$ (1) and $p^{'} = ({E^{'}}_{e}, p_{x}, p_{y}, {p^{'}}_{z}) .$ (2) The four-momentum q of the emitted photons is $q = (ω, - p_{x}, - p_{y}, p_{γ}) .$ (3) The four-momentum conservation is as follows: $p_{z} = {p^{'}}_{z} + p_{γ},$ (4) $E_{e} = {E^{'}}_{e} + ω,$ (5) $E_{e}^{2} = p_{z}^{2} + m_{e}^{2},$ (6) $p_{T}^{2} = {E^{'}}_{e}^{2} - {p^{'}}_{z}^{2} - m_{e}^{2} = {(E_{e} - ω)}^{2} - {(p_{z} - p_{γ})}^{2} - m_{e}^{2},$ (7) where Ee and ${E^{'}}_{e}$ are the energies of the incident and scattering electrons, respectively; me is the mass of the electron; pz and ${p^{'}}_{z}$ are the z-components of the momentum of the incident and scattering electrons, respectively; ω and p_T are the energy and transverse momentum of the virtual photon. The momentum of the virtual photon is $p_{γ} = p_{z} - \sqrt{{(E_{e} - ω)}^{2} - p_{T}^{2} - m_{e}^{2}} .$ (8) The virtuality of the photon is expressed as $q^{2} = ω^{2} - p_{T}^{2} - p_{γ}^{2}$ (9) $= ω^{2} - p_{T}^{2} - {(p_{z} - \sqrt{{(E_{e} - ω)}^{2} - p_{T}^{2} - m_{e}^{2}})}^{2} .$ (10) The virtuality of the photon reaches its minimum and maximum values in two distinct scenarios: when the electron’s direction remains unchanged after scattering, and when the electron’s direction is reversed following scattering. Then, $q_{min}^{2}$ and $q_{max}^{2}$ can be written as $\begin{matrix} q_{min}^{2} = 2 E_{e} ω - 2 E_{e}^{2} + 2 m_{e}^{2} + \\ 2 \sqrt{(E_{e}^{2} - m_{e}^{2}) [{(E_{e} - ω)}^{2} - m_{e}^{2}]}, \\ q_{max}^{2} = ω^{2} - {[\sqrt{E_{e}^{2} - m_{e}^{2}} + \sqrt{{(E_{e} - ω)}^{2} - m_{e}^{2}}]}^{2} . \end{matrix}$ (11) The maximum photon energy is $E_{e} - m$ , which consequently results in $q_{max}^{2} |_{ω = E_{e} - m} = q_{min}^{2} |_{ω = E_{e} - m} = 2 m_{e}^{2} - 2 E_{e} m,$ (12) This indicates that the photon flux is zero at ω=ω_max, which is consistent with our expectations. For $Q^{2} = - q^{2} ≪ ω^{2}$ , the $Q_{min}^{2}$ and $Q_{max}^{2}$ are expressed as $Q_{min}^{2} = \frac{m_{e}^{2} ω^{2}}{E_{e} (E_{e} - ω)},$ (13) $Q_{max}^{2} = 4 E_{e} (E_{e} - ω) .$ (14)

2.2

Photon Flux Derivation

Considering the lowest order of QED, the cross-section for the process shown in Fig. 1 is given by [24] $d σ_{e p} = σ_{γ} (ω) d n,$ (15) $σ_{γ} (ω)$ is the absorption cross section for photons with frequency ω, and dn is the equivalent photon number. Let the amplitude for virtual photon absorption be represented as $M^{μ}$ On averaging over the initial spin states and summing across the final states, the cross section for electron-proton scattering is given by $\begin{matrix} d σ_{ep} = \frac{4 π α}{(- q^{2})} M^{* ν} M^{μ} ρ^{μ ν} \\ \times \frac{{(2 π)}^{4} δ (p + P - p^{'} - k) d Γ}{4 \sqrt{{(p P)}^{2} - p^{2} P^{2}}} \frac{d^{3} p^{'}}{2 E_{e}^{'} {(2 π)}^{3}}, \end{matrix}$ (16) where, Γ is the phase space volume and $ρ^{μ ν}$ is the density matrix of the virtual photon produced by an electron that is given by $\begin{matrix} ρ^{μ ν} = \frac{1}{2 (- q^{2})} Tr [(p + m_{e}) γ^{μ} (p^{'} + m_{e}) γ^{ν}] \\ = - (g^{μ ν} - \frac{q^{μ} q^{ν}}{q^{2}}) - \frac{{(2 p - q)}^{μ} {(2 p - q)}^{ν}}{q^{2}} . \end{matrix}$ (17) For a nucleus with a defined charge distribution, rather than a point-like particle, Eq. 17 can be extended to the following: $\begin{matrix} ρ^{μ ν} = \frac{1}{2 (- q^{2})} Tr [(p^{'} + m) γ^{μ} (p^{'} + m) γ^{ν}] \\ = - (g^{μ ν} - \frac{q^{μ} q^{ν}}{q^{2}}) C (Q^{2}) \end{matrix}$ (18) $- \frac{{(2 p - q)}^{μ} {(2 p - q)}^{ν}}{q^{2}} D (Q^{2}),$ (19) where, $C (Q^{2}) = F_{M}^{2} (Q^{2})$ and $D (Q^{2}) = \frac{4 m^{2} F_{E}^{2} + Q^{2} F_{M}^{2}}{4 m^{2} + Q^{2}}$ and $F_{M}^{2}$ and $F_{E}^{2}$ are the magnetic and electric form factors of the nucleus, respectively. After integration over the phase-space volume, the cross section can be expressed as $\begin{matrix} d σ = \frac{α}{4 π^{2} | q^{2} |} {[\frac{{(q P)}^{2} - q^{2} P^{2}}{{(p P)}^{2} - p^{2} P^{2}}]}^{1 / 2} \\ \times (2 ρ^{+ +} σ_{T} + ρ^{00} σ_{S}) \frac{d^{3} p^{'}}{{E^{'}}_{e}}, \end{matrix}$ (20) σT and σS are the cross-sections for transverse and scalar photon absorption, respectively, and σS is negligible. The coefficients ρab are the elements of the density matrix in the $γ p$ -helicity basis, written as $2 ρ^{+ +} = \frac{{(2 p P - q P)}^{2}}{{(q P)}^{2} - q^{2} P^{2}} + 1 + \frac{4 m_{e}^{2}}{q^{2}}, ρ^{00} = 2 ρ^{+ +} - \frac{4 m_{e}^{2}}{q^{2}} - 2.$ (21) In the remaining frame of the proton, that is, the target frame, the following relationship holds. $\begin{array}{l} ω = \frac{q P}{m_{p}}, E_{e} = \frac{p P}{m_{p}}, \\ \frac{d^{3} p^{'}}{{E^{'}}_{e}} = \frac{d ω d (- q^{2}) d φ}{2 \sqrt{E_{e}^{2} - m_{e}^{2}}} . \end{array}$ (22) Let $Q^{2} = - q^{2}$ , where the equivalent photon number is: $\begin{matrix} \frac{d^{2} n}{d Q^{2} d ω} = \frac{α}{2 π Q^{2} E_{e} (E_{e} - m_{e})} ρ^{+ +} \sqrt{ω^{2} + Q^{2}} \\ = \frac{α}{4 π Q^{2} E_{e} (E_{e} - m_{e})} \\ \times [\frac{{(2 E_{e} - ω)}^{2}}{ω^{2} + Q^{2}} + 1 - \frac{4 m_{e}^{2}}{Q^{2}}] \sqrt{ω^{2} + Q^{2}} . \end{matrix}$ (23) Here, $\frac{d^{2} n}{d Q^{2} d ω}$ can be converted into $\frac{d^{2} n}{d p_{T} d ω}$ by applying a variable change. $\begin{matrix} d Q^{2} d ω = | \begin{matrix} \frac{\partial Q^{2}}{\partial p_{T}} & \frac{\partial Q^{2}}{\partial ω} \\ \frac{\partial ω}{\partial p_{T}} & \frac{\partial ω}{\partial ω} \end{matrix} | d p_{T} d ω \\ = \frac{2 p_{z} p_{T}}{\sqrt{{(E_{e} - ω)}^{2} - p_{T}^{2} - m_{e}^{2}}} d p_{T} d ω, \end{matrix}$ (24) $\frac{d^{2} n}{d p_{T} d ω} = \frac{2 p_{z} p_{T}}{\sqrt{{(E_{e} - ω)}^{2} - p_{T}^{2} - m_{e}^{2}}} \frac{d^{2} n}{d Q^{2} d ω} .$ (25) The photon density matrix can be treated as the square of the photon wave function. Therefore, the equivalent photon number in the coordinate space can be obtained by performing a representation transformation in Eq. 25: $\frac{d^{3} n}{d^{2} r d ω} = \frac{α}{ω π^{2}} {(\int_{0}^{p_{T_{max}}} \sqrt{\frac{p_{T} π ω}{2 α} \frac{d^{2} n}{d p_{T} d ω}} J_{1} (p_{T} \cdot r))}^{2},$ (26) $p_{T_{max}}$ is determined using Q², Ee and ω. Hereafter, we refer to the method for obtaining the photon flux in this manner as the lowest-order QED approach.

For photoproduction in relativistic heavy-ion collisions, the photon flux is typically estimated using the conventional EPA, which was independently derived by Williams [25] and Weizsäcker [26] in the 1930s. In their derivation, they assumed that the charged particles moved along straight-line trajectories and obtained the spatial distribution of the electromagnetic field by solving the vector potential wave equation. The spatial distribution of the equivalent photon number was subsequently derived based on the relationship between the energy flux density and equivalent photon number. This approach provides an effective way to describe the photon flux distribution, which can be expressed as $\begin{array}{l} n (ω, {\vec{x}}_{⊥}) = \frac{1}{π ω} {| {\vec{E}}_{⊥} (ω, {\vec{x}}_{⊥}) |}^{2} \\ = \frac{4 Z^{2} α}{ω} {| \int \frac{d^{2} {\vec{k}}_{⊥}}{{(2 π)}^{2}} {\vec{k}}_{⊥} \frac{F ({\vec{k}}_{⊥}^{2} + {(\frac{ω}{γ})}^{2})}{{\vec{k}}_{⊥}^{2} + {(\frac{ω}{γ})}^{2}} e^{i {\vec{x}}_{⊥} \cdot {\vec{k}}_{⊥}} |}^{2} \\ = \frac{Z^{2} α}{π^{2} ω} {| \int_{0}^{\infty} d k_{⊥} k_{⊥}^{2} \frac{F (k_{⊥}^{2} + {(\frac{ω}{γ})}^{2})}{k_{⊥}^{2} + {(\frac{ω}{γ})}^{2}} J_{1} (x_{⊥} k_{⊥}) |}^{2}, \end{array}$ (27) where Z denotes the charge number of the charged particle, γ represents the Lorentz factor of the charged particle, ω is the photon energy. For a point-like particle, the photon flux is $n_{pt} (ω, x_{⊥}) = \frac{Z^{2} α_{Q E D} ω}{π^{2} γ^{2}} {[K_{1} (\frac{ω x_{⊥}}{γ})]}^{2} .$ (28)

2.3

Coulomb Dissociation in Electron-Ion Collisions

Analogous to the Coulomb excitation process in relativistic heavy-ion collisions, Coulomb excitation in electron-ion collisions can be factorized into two distinct components: the emission of virtual photons by electrons and the corresponding photon absorption cross-section of the nucleus. The virtual photons emitted by electrons can be estimated using the framework described in the previous subsection.

The lowest-order probability that a nucleus is excited to a state that subsequently emits at least one neutron (denoted as Xn) can be expressed as [27] $m_{X n} (b) = \int d ω n (ω, b) σ_{X n, γ A \to A^{*}} (ω),$ (29) where $n (ω, b)$ represents the photon flux at a given impact parameter b and $σ_{X n, γ A \to A^{*}} (ω)$ is the photoexcitation cross section for an incident photon with energy ω obtained from experimental data [28-32].

Notably, under specific conditions, such as very small impact parameters and extremely high beam energies, the value of mXn could exceed 1, implying that the excitation probability would lose its probabilistic interpretation. Although such conditions are improbable in current or near-future facilities, it is beneficial to address this scenario for the sake of completeness. To maintain a valid probabilistic interpretation, $m_{X n} (b)$ is treated as the mean number of photons absorbed by the nucleus and we assume that the photon multiplicity follows a Poisson distribution [33, 34]. In this context, the probability of absorbing zero photons (i.e., zero neutron emission) is given by $P^{(0)} (b) = e^{- m_{X n} (b)},$ (30) whereas, the probability of exactly absorbing N photons is: $P^{(N)} (b) = \frac{m_{X n}^{N} (b)}{N!} e^{- m_{X n} (b)} .$ (31) The normalized probability density for the absorption of one photon with energy E₁ can be expressed as $p^{(1)} (E_{1}, b) = \frac{n (E_{1}, b) σ_{γ A \to A^{*} (E_{1})}}{m_{X n} (b)},$ (32) and the probability density for absorbing N photons with energies $E_{1}, E_{2}, \dots, E_{N}$ is: $p^{(N)} (E_{1}, E_{2}, \dots, E_{N}, b) = \frac{\prod_{i = 1}^{N} n (E_{i}, b) σ_{γ A \to A^{*} (E_{i})}}{m_{X n} (b)} .$ (33) For a specific electromagnetic dissociation channel involving the emission of i neutrons, the probability density of an N-photon absorption process can be evaluated as $\begin{matrix} P_{i}^{(N)} (b) = \int \dots \int d E_{1} \dots d E_{N} \\ \times P^{(N)} (b) p^{(N)} (E_{1}, \dots, E_{N}, b) f_{i} (E_{1}, \dots, E_{N}), \end{matrix}$ (34) where, $f_{i} (E_{1}, \dots, E_{N})$ represents the branching ratio of a specific channel with i emitted neutrons. We assume that simultaneous absorption of multiple photons is allowed, leading to a simplified form of the branching ratio, $f_{i} (E_{1}, \dots, E_{N}) = f_{i} (\sum_{k = 1}^{N} E_{k})$ . The values of fi for different neutron emission channels were extracted from the $n_{O}^{O} n$ model, as described in Ref. [35].

Finally, the total probability of emission of i neutrons is given by $P_{in} (b) = \sum_{k = 1}^{\infty} P_{i}^{(k)} (b) .$ (35)

2.4

Vector Meson Photoproduction in Electron-Ion Collisions

The vector meson photoproduction in electron-ion collisions can be estimated in a manner similar to Coulomb excitation calculations. The primary difference lies in replacing the photon absorption cross section of the nucleus with the $γ A \to V A$ cross section. Specifically, the scattering amplitude $Γ_{γ A \to V A}$ , including the shadowing effect, can be derived using the Glauber model [36] combined with the vector meson dominance (VMD) approach [37]: $\begin{matrix} Γ_{γ A \to V A} ({\vec{x}}_{⊥}) = \frac{f_{γ N \to V N} (0)}{σ_{V N}} \\ \times 2 [1 - exp (- \frac{σ_{V N}}{2} T^{'} ({\vec{x}}_{⊥}))], \end{matrix}$ (36) where, $f_{γ N \to V N} (0)$ is the forward scattering amplitude for $γ + N \to V + N$ and $σ_{V N}$ represents the total vector mesonucleon ( $V N$ ) cross-section. The modified nuclear thickness function $T^{'} ({\vec{x}}_{⊥})$ that considers the coherence length effect is given by $T^{'} ({\vec{x}}_{⊥}) = \int_{- \infty}^{+ \infty} ρ (\sqrt{{\vec{x}}_{⊥}^{2} + z^{2}}) e^{i q_{L} z} d z, q_{L} = \frac{M_{V} e^{y}}{2 γ_{c}},$ (37) where, q_L denotes the longitudinal momentum transfer required to produce a real vector meson, MV is the vector meson mass, and γc is the Lorentz factor of the nucleus.

Considering the impact of the photon’s virtuality on the photon-nucleon scattering cross-section, the equivalent vector meson flux is introduced as $\frac{d^{2} V}{d ω d Q^{2}} = {(\frac{M_{V}^{2}}{M_{V}^{2} + Q^{2}})}^{n} \frac{d^{2} n}{d ω d Q^{2}},$ (38) where ${(\frac{M_{V}^{2}}{M_{V}^{2} + Q^{2}})}^{n}$ represents the suppression factor associated with the transition amplitude from the virtual photon fluctuation to the corresponding vector meson, and n is determined by fitting the experimental data [38, 39]. The equivalent vector meson flux in the coordinate space $\frac{d^{3} n}{d^{2} r d ω}$ can be obtained using the method outlined in the previous section.

The amplitude distribution for the vector meson photoproduction process is given by $A (b, {\vec{x}}_{⊥}) = Γ_{γ A \to V A} ({\vec{r}}_{1}) \sqrt{n (ω, {\vec{r}}_{2})},$ (39) where ${\vec{r}}_{2} - {\vec{r}}_{1} = \vec{b}$ and $\frac{\vec{b}}{2} + {\vec{r}}_{1} = {\vec{x}}_{⊥}$ . The production amplitude in momentum space can be obtained by applying a Fourier transformation to the amplitude in the coordinate representation: $\vec{A} ({\vec{p}}_{⊥}, b) = \frac{1}{2 π} \int d^{2} x_{⊥} \vec{A} ({\vec{x}}_{⊥}, b) e^{i {\vec{p}}_{⊥} \cdot {\vec{x}}_{⊥}} .$ (40) From Eq. 40, the differential cross section $\frac{d σ}{d t}$ can be calculated.

Finally, the photoproduction cross section in conjunction with the Coulomb excitation of the nucleus can be estimated as follows: $\begin{matrix} \frac{d σ_{e A \to e A^{*} + X n}}{d Y} = \int d^{2} {\vec{x}}_{⊥} \int ω {| A (b, {\vec{x}}_{⊥}) |}^{2} \\ \times P_{in} (b) 2 π b d b, \end{matrix}$ (41) where Y is the rapidity of the photoproduced vector meson and $ω = \frac{1}{2} M_{V} e^{Y}$ , where $P_{in} (b)$ represents the probability of emitting i neutrons, which accounts for the Coulomb excitation contribution.

RESULTS

In ultraperipheral heavy-ion collisions, the photon flux is typically calculated using the classical EPA approach, as given by Eq. 27. This model assumes that the charged particles involved move along straight-line trajectories. However, concerns have been raised regarding the validity of this assumption, particularly at the energies probed at RHIC and LHC. To examine the applicability of the classical EPA model, we compared it with the QED approach, which does not rely on the straight-line trajectory assumption. Figure 2 presents the photon flux distribution induced by a Au nucleus with an energy of 100 GeV per nucleon, calculated using both the classical EPA and QED models, along with the ratio of the QED results to the classical EPA results. The figure indicates that both models predict a maximum photon flux at the radius of the Au nucleus, and a subsequent decrease as the photon energy ω increases. Furthermore, the ratio between the QED and classical EPA results remains close to unity, indicating that the classical EPA model provides an accurate approximation of the photon flux for UPCs and is effectively equivalent to the QED-derived expression under these assumptions.

Fig. 2

(Color online) Comparison of the photon flux distribution induced by a Au nucleus with E=100 GeV per nucleon, as calculated using the conventional EPA model (panel a) and the QED derivation (panel b), as well as the ratio of the QED results to the classical EPA results (panel c)

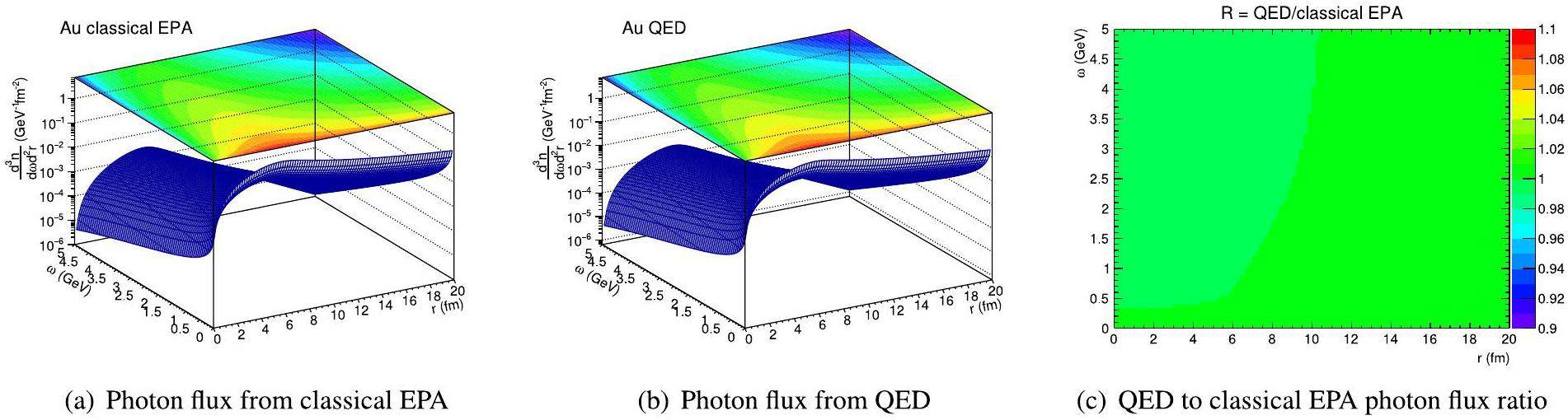
However, the use of Eq. 27 becomes problematic in the context of electron-ion collisions. This is primarily because the energy of an electron is significantly lower than that of a heavy ion, which renders the straight-line approximation invalid. Furthermore, direct application of Eq. 27 does not constrain the photon energy from exceeding the energy of the charged particle, which is physically incorrect. To illustrate this limitation, we compare the photon flux distributions calculated using the classical EPA and QED models for an electron with an energy of 5 GeV. Figure 3 presents the 2D photon flux distribution and the ratio of the QED to classical EPA results. The comparison clearly demonstrates a substantial difference between the two models, with the QED-derived flux showing distinct fluctuations and tending towards zero as the photon energy approaches the electron energy. This behavior underscores the inadequacy of the classical EPA model in describing the photon flux for electron-ion collisions.

Fig. 3

(Color online) Comparison of the photon flux distribution induced by an electron with E=5 GeV, as calculated using the conventional EPA model (panel a) and the QED derivation (panel b), along with the ratio of the QED results to the classical EPA results (panel c)

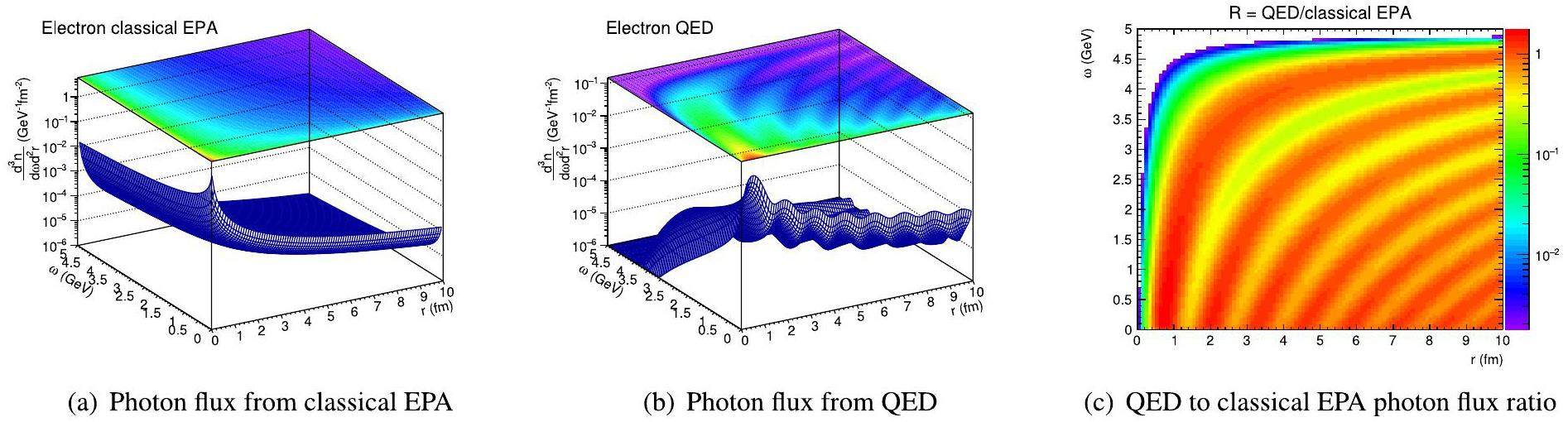
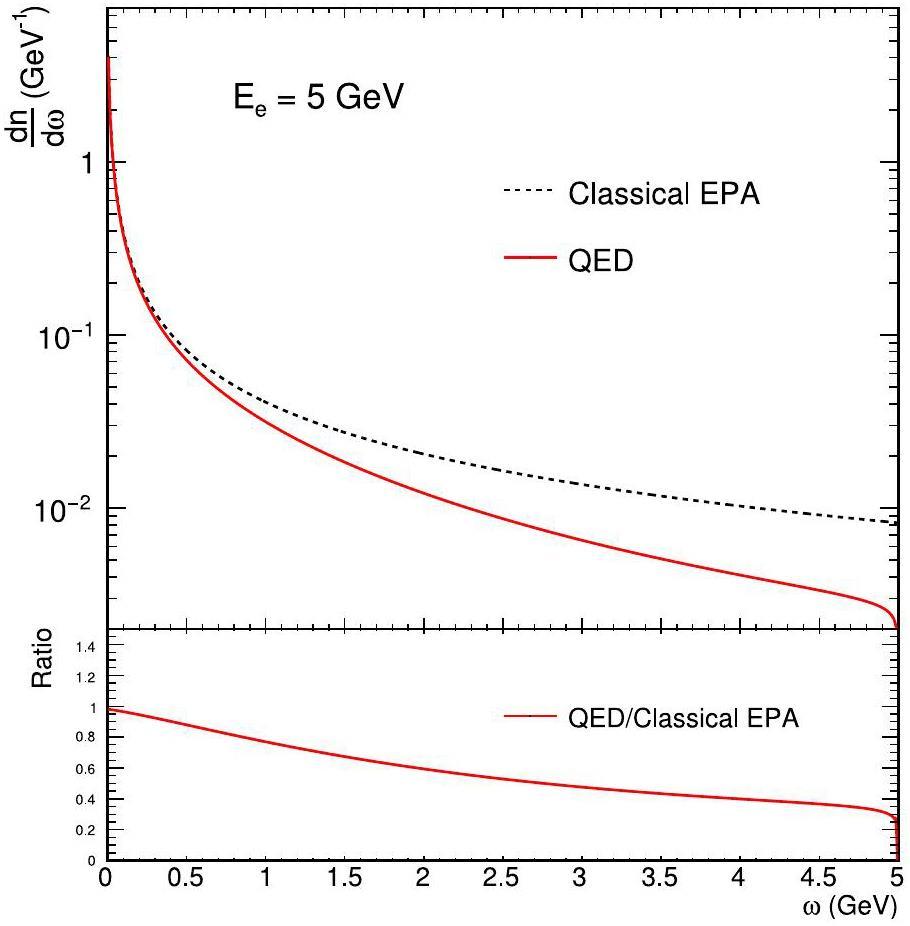
Figure 4 provides a further comparison of the photon energy distributions obtained using the classical EPA and QED models. The photon flux calculated using the QED model closely follows the classical EPA prediction at low photon energies but rapidly approaches zero as the photon energy approaches the total energy of the electron. In contrast, the photon flux calculated using the classical EPA model decreases smoothly without reaching zero. This discrepancy further underscores the limitations of the classical EPA model for electron-ion collisions and demonstrates that the photon flux distribution derived from the QED model is more suitable for accurately describing these processes. Consequently, the QED approach offers a more reliable framework for calculating the impact parameter dependence of photoproduction processes in electron-ion collisions.

Fig. 4

(Color online) Upper panel: The

\frac{d n}{d ω}

distribution calculated from the classical EPA model (black line) and the QED model (red line). Lower panel: The ratio of the QED results to the classical EPA results

The lowest-order QED-derived photon flux enables accurate evaluation of the Coulomb excitation of a nucleus during electron-ion collisions. As an illustrative example, we consider e + Au collisions at the EIC energies, specifically at 18 × 100 GeV per nucleon. The corresponding $P_{in} (b)$ -distribution, representing the dissociation probability as a function of the impact parameter, is shown in Fig. 5. The dissociation probability, characterized by neutron emission, exhibits a rapid decrease with increasing impact parameter. Notably, the probability distribution exhibits an oscillatory pattern, which can be attributed to the wave nature of the photons emitted by the electrons, resulting in interference effects. Dissociation processes involving a higher number of emitted neutrons are more probable at smaller impact parameters, indicating stronger electromagnetic interactions in more central collisions. This characteristic offers a practical method for determining the impact parameter in electron-ion interactions by counting the number of emitted neutrons detected using a zero-degree calorimeter (ZDC). The rapidity distribution of the emitted neutrons was studied at the EIC energy using a DPMJET generator [40], providing valuable insights for designing the ZDC for the EIC. The correlation between neutron emission and the impact parameter enables the categorization of the collision events based on their geometric overlap, facilitating a more precise study of photonuclear interaction dynamics in electron-ion collisions.

Fig. 5

(Color online) Nucleus break-up probability of Au-197 as a function of impact parameter in e+Au collision at EIC energy (18×100 GeV) for different number of neutron emission. Black line: “0n” mode. Red line: “1n” mode. Blue line: “>1n” mode

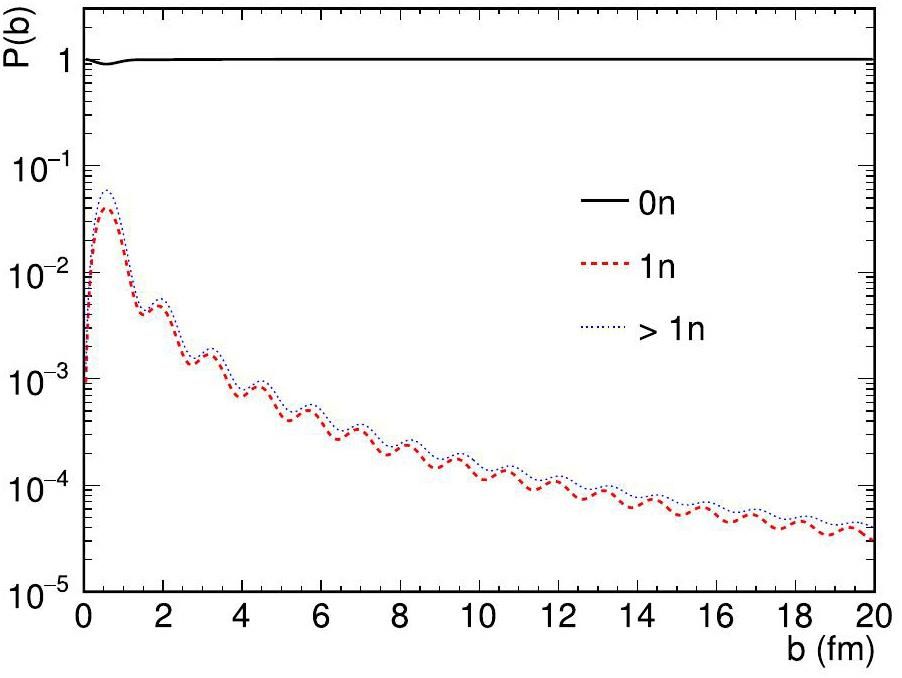
Furthermore, the different photoproduction processes, even those with the same neutron tagging, exhibit variations in impact parameter distributions. This is because the photon energies involved in different processes vary, thereby impacting the spatial distribution of photons relative to electrons. Unlike hadronic heavy-ion collisions, where centrality is defined by a fixed impact parameter range, the impact parameter determination in electron-ion collisions via neutron tagging depends on the specific photoproduction process under consideration. Therefore, this must be evaluated on a case-by-case basis. To illustrate this, we present calculations for coherent ρ⁰ and J/ψ photoproduction accompanied by different neutron tagging at the EIC and EicC energies.

Figure 6 presents the $d σ / d b$ distributions for coherent ρ⁰ photoproduction at the EIC and EicC energies, with different line types and colors representing distinct neutron emission modes. The average impact parameter for the “0n” mode is significantly larger than that for the “1n” and “>1n” (at least two neutrons) modes. This is because neutron excitation requires additional photons, which reduces the average impact parameter. The distinct variation in the impact parameters across neutron emission modes demonstrates the feasibility of determining the impact parameter of electron-ion collisions by tagging neutrons from Coulomb excitation. Furthermore, the cross section exhibits fluctuations with respect to the impact parameter, a phenomenon that arises from the oscillatory behavior of the J₁ Bessel function in the coordinate distribution of the photon flux, as described by Eq. 26. A comparison of the results at the EIC and EicC energies indicates that variations in the center-of-mass collision energy have negligible effect on the average impact parameter, indicating that the proposed method is effective across different collision energy regimes.

Fig. 6

(Color online) The

\frac{d σ}{d b}

for ρ⁰ photoproduction at EIC (a) and EicC (b) energy. Black line: “0n” mode. Red line: “1n” mode. Blue line: “>1n” mode. The results of “1n” and “>1n” have been multiplied by 100

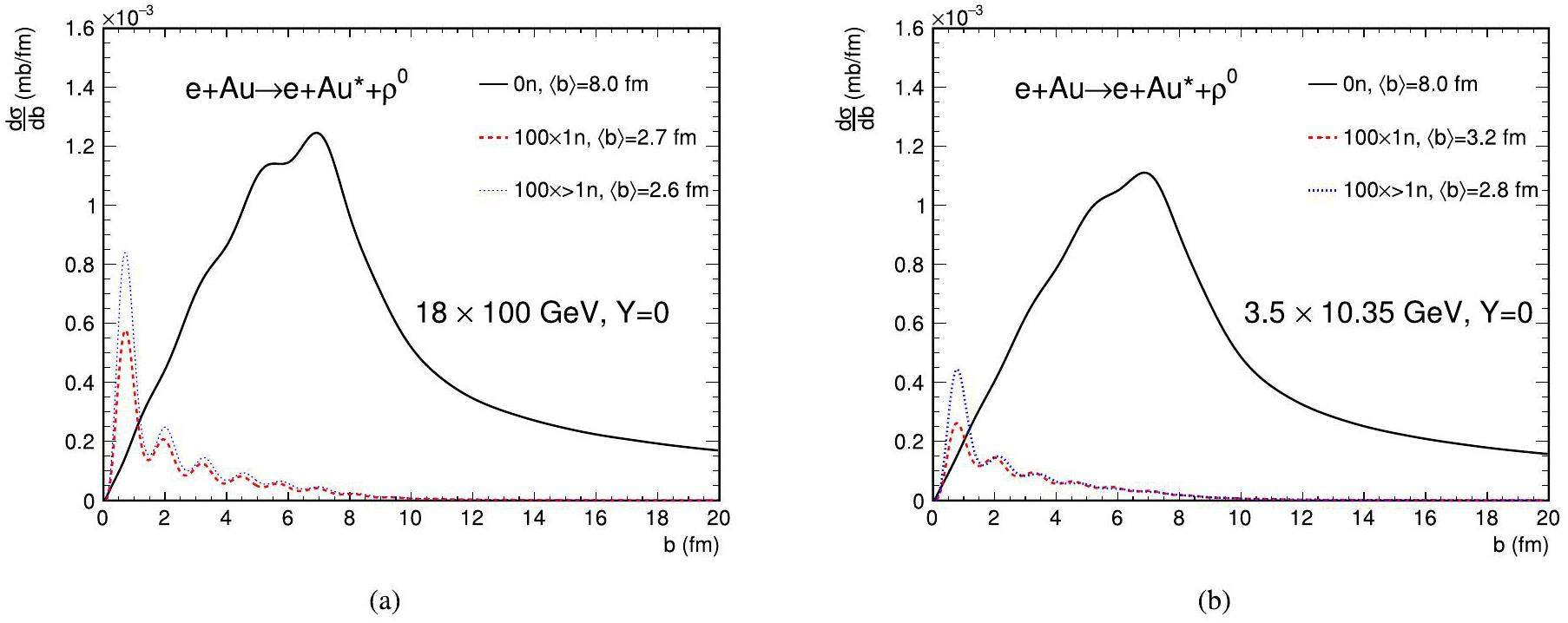
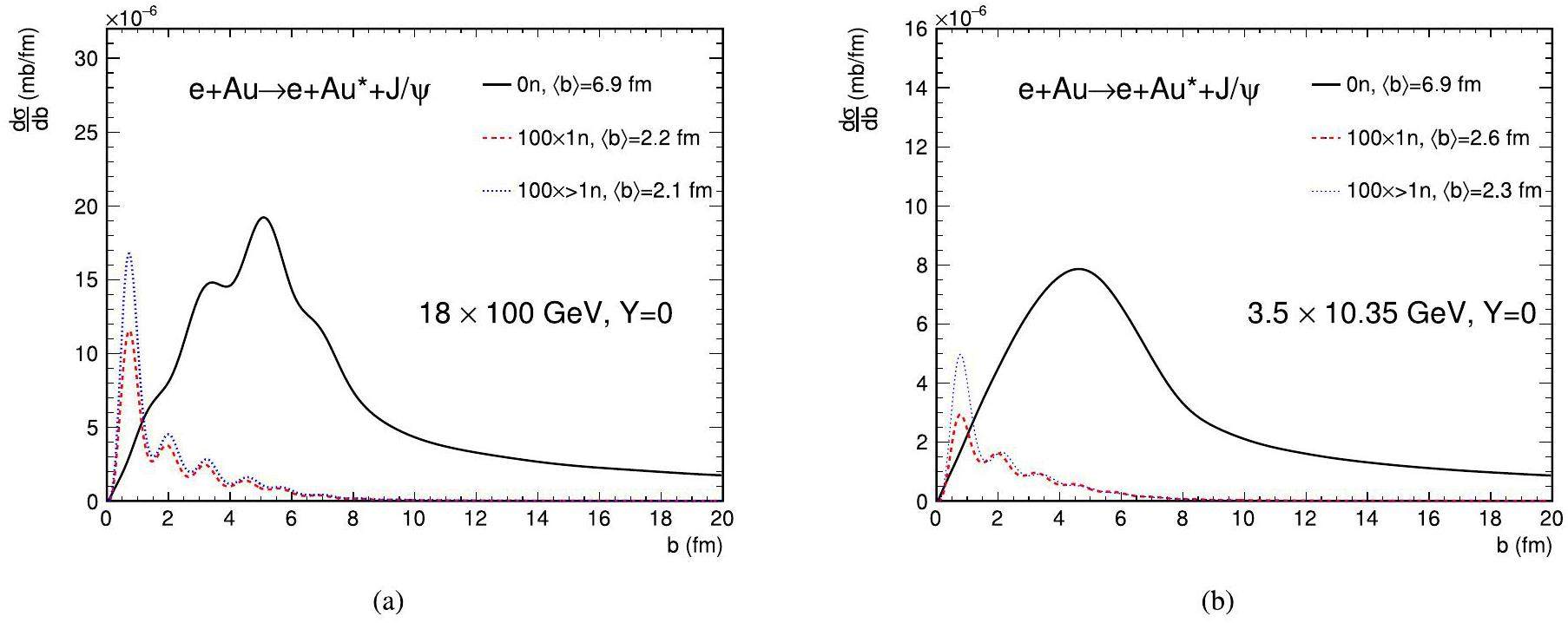
Figure 7 illustrates the $d σ / d b$ distributions for coherent J/ψ photoproduction at EIC and EicC energies. Similar to the ρ⁰ case, the average impact parameter for the 0n mode is much larger than those for the other neutron emission modes. In addition, the average impact parameter $〈 b 〉$ for J/ψ is typically smaller than that for ρ⁰ in the corresponding neutron emission modes. This behavior can be attributed to the larger mass of J/ψ compared with ρ⁰, which corresponds to a higher photon energy. In addition, this results in a larger cross-sectional ratio σ_>1n/σ_0n of J/ψ than for rho⁰. Consequently, the photon is closer to the electron, resulting in a reduced average impact parameter. The sensitive dependence of the average impact parameter on neutron emission via Coulomb excitation observed across different vector mesons further underscores the effectiveness of this method for determining the impact parameter in experimental electron-ion collisions.

Fig. 7

(Color online) The

\frac{d σ}{d b}

for J/ψ photoproduction at EIC (a) and EicC (b) energy. Black line: “0n” mode. Red line: “1n” mode. Blue line: “>1n” mode. The results of “1n” and “>1n” have been multiplied by 100

summary

We investigated the feasibility of employing neutron tagging, resulting from the Coulomb excitation of nuclei, as a precise method to ascertain the impact parameters of exclusive photoproduction events in electron-ion collisions. By developing an equivalent photon approximation for electrons, this study integrated a photon flux distribution in coordinate space, thereby validating the relationship between the distribution of the photon’s transverse momentum and the impact parameters of the collisions. The differential cross-section for the Coulomb excitation of nuclei was calculated by leveraging the spatial data of the photon flux. Our calculations indicate that the presence or absence of neutron excitation in the photoproduction process can markedly shift the distributions of impact parameters, thereby offering a reliable technique for controlling the impact parameter in electron-ion collision experiments. This study provides essential methodologies and insights for examining the dependence of exclusive photoproduction processes on impact parameters, yielding novel perspectives for the design of experiments and data analysis.

References

Z. Ji et al.,

Lambda polarization at the Electron-ion collider in China

. Nucl. Sci. Tech. 34, 155 (2023). https://doi.org/10.1007/s41365-023-01317-w