Theoretical analysis

In the ADL, particles are focused through the contraction and expansion of the flow field, causing them to deviate from gas streamlines owing to their inertia. The focusing effect is determined primarily by the Stokes number (St), which characterizes the degree of deviation. St is a dimensionless number in fluid mechanics defined as the ratio of the stopping distance of the particles to the characteristic size of an obstacle: $St=\frac{\tau u}{d_{\text{f}}}\mathrm{,}$ (1) where τ denotes the relaxation time of the particles, u is the average flow velocity at the entrance of the lens, and d_f is the orifice diameter of the lens.

Figure 1 shows the focusing principle of a single lens in the ADL. The single lens comprises a tube with a diameter D and an orifice plate with a diameter d_f. The aerosol enters the lens from the left side in the laminar-flow state. After passing through the lens, the particles at a specific initial radial position (r) deviate from the gas streamline owing to inertial effects. When $St\ll 1$, the drag force governs the movement of the particles, causing them to move along the gas streamline without focusing. When $St\gg 1$, the inertia governs the movement of the particles, causing them to diverge away from the axis. When $St\approx 1$, both the inertia and drag force are equivalent; thus, the particles are focused by the lens. Ideally, the particles move exactly along the axis, and the corresponding Stokes number is the optimum Stokes number [35, 40].

Fig. 1Full-screen View

Focusing principle of a single lens in the ADL. The red and green lines represent the inlet and outlet, respectively. The solid blue line represents the gas streamline and the three black dashed lines represent the trajectories of particles with different Stokes numbers

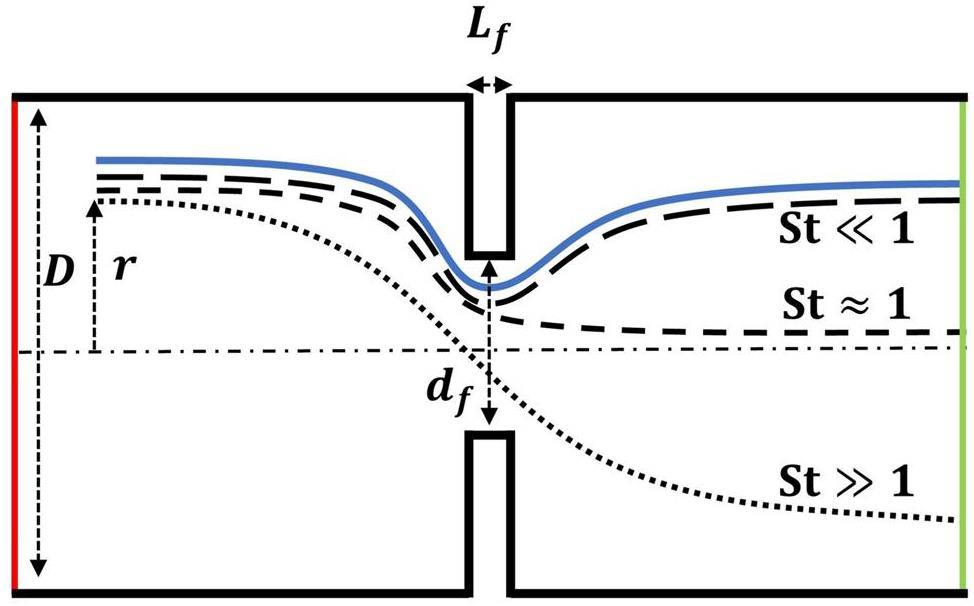
The particle diameter in SPI typically ranges from a few nanometers to a few micrometers, whereas the mean free path of gas molecules ranges from tens of micrometers to hundreds of micrometers in an ADL. According to the definition of the Knudsen number of particles (Kn_p, which is the ratio of the mean free path to the particle radius), Kn_p is considerably greater than one. Therefore, the Stokes number is defined using the Epstein flow model in the free molecular-flow regime [48]: $St=\frac{1}{\left(1+\frac{\pi \alpha }{8}\right)\sqrt{2\pi {\gamma }^3}}\frac{\dot{m}{\rho }_{\text{p}}{d}_{\text{p}}{c}^3}{P_1{}^2{d}_{\text{f}}^3}\mathrm{,}$ (2) where α is the momentum-adjustment coefficient that describes the ratio of possible collisions between the gas molecules and particles, γ is the specific heat of the gas, $\dot{m}$ is the gas-mass flowrate, ρ_p is the mass density of the particles, d_p is the particle diameter, c is the speed of sound in the gas upstream of the lens, P₁ is the pressure upstream of the lens, and d_f is the orifice diameter of the lens. Given the flow-field parameters and St_o, the required d_f and P₁ values for focusing on a particular particle can be calculated using Eq. 2.

St_o is affected by different geometric parameters and operating conditions [35, 39, 40], including the tube-constriction ratio (β, defined as d_f/D), ratio of the lens thickness to the lens orifice diameter (L_f/d_f), Reynolds number (Re), Mach number (Ma), gas-mass flowrate, and initial radial position of the particles (r). To simplify the design method of the ADL, we first conduct a mathematical analysis of the main parameters that affect St_o based on previous research and make reasonable assumptions. Subsequently, we establish a functional relationship between St_o and its influencing parameters through numerical simulations.

For a specific carrier gas, the relationship between St_o and its influencing parameters can be expressed as: $S{t}_{\text{o}}=f_1\left(\frac{d_{\text{f}}}{D}\mathrm{,}Re\mathrm{,}Ma\mathrm{,}\dot{m}\mathrm{,}\frac{L_{\text{f}}}{d_{\text{f}}}\mathrm{,}r\right)\mathrm{.}$ (3) Because of the viscous effect of the fluid, the flow velocity near the wall is low. For the same lens cross section, the local St value varies at different radial positions, resulting in different focusing effects. Because the particles significantly approach the axis after passing through the first lens, we assume that the particles are released from a radial position of 0.15 times the diameter of the tube (D). Moreover, L_f/d_f has a minor impact on the focusing effect [35] and the actual thickness of the lens is small (typically 0.1–0.3 mm); therefore, the influence of L_f/d_f on St_o can be neglected. Therefore, the relationship between St_o and its influencing parameters can be expressed as: $S{t}_{\text{o}}=f_2\left(\frac{d_{\text{f}}}{D}\mathrm{,}Re\mathrm{,}Ma\mathrm{,}\dot{m}\right)\mathrm{.}$ (4) If $\dot{m}$ and d_f are given, the average velocity of the carrier gas at the orifice is $u=\frac{\dot{m}}{{\rho }_1\frac{\pi d_{\text{f}}^2}{4}}=\frac{4\dot{m}}{\pi {\rho }_1{d}_{\text{f}}^2}\mathrm{,}$ (5) where ρ₁ denotes the carrier-gas density upstream of the lens.

Equation 5 is then substituted into the definition of the Reynolds number, and Re based on the orifice diameter is $Re=\frac{{\rho }_{1}u{d}_{\text{f}}}{\mu }=\frac{4\dot{m}}{\pi \mu d_{\text{f}}}\mathrm{,}$ (6) where μ denotes the gas viscosity determined by the gas temperature.

Equation 5 is substituted into the definition of the Mach number, and Ma based on the orifice diameter is $Ma=\frac{u}{c}=\frac{\frac{4\dot{m}}{\pi {\rho }_1{d}_{\text{f}}{}^2}}{\sqrt{\frac{\gamma R_{\text{c}}{T}_1}{M}}}\mathrm{.}$ (7) Equation 6 and Eq. 7 share the same parameters; therefore, Eq. 8 can be derived by dividing Eq. 6 by Eq. 7: $\frac{Re}{Ma}=P_1{d}_{\text{f}}\frac{1}{\mu }\sqrt{\frac{\gamma M}{R_{\text{c}}{T}_1}}\mathrm{,}$ (8) where γ, M, R_c, and T₁ are the specific heat, molar mass, universal gas constant, and temperature of the upstream gas, respectively. Because of the small temperature change in the laminar flow at low flow velocities, the viscosity of the gas before and after the orifice plate remains nearly constant. Therefore, we assume that only d_f and P₁ are the variables on the right-hand side of Eq. 8. Thus, Eq. 4 can be transformed as follows: $S{t}_{\text{o}}=f_3\left(\frac{d_{\text{f}}}{D}\mathrm{,}{d}_{\text{f}}\mathrm{,}{P}_1\mathrm{,}\dot{m}\right)\mathrm{.}$ (9) In addition, the mass flowrate through the lens orifice can be expressed as [49] $\dot{m}=\frac{\pi d_{\text{f}}^2}{4}\frac{C_{\text{d}}Y}{\sqrt{1-{\beta }^4}}{P}_1\sqrt{\frac{2M}{R{T}_1}\frac{\text{Δ}P}{P_1}}\mathrm{,}$ (10) where C_d is the flow coefficient related to the particle Reynolds number (Re_p), Y is the expansion factor, and $\text{Δ}P=P_1-P_2$ is the pressure decrease across the orifice. P₂ is the pressure downstream of the lens (i.e., back pressure).

Based on Eq. 10, P₁ is mainly determined by $\dot{m}$, d_f, and P₂. Then, Eq. 9 can be expressed as $S{t}_o=f_4\left(\frac{d_{\text{f}}}{D}\mathrm{,}{d}_{\text{f}}\mathrm{,}{P}_2\mathrm{,}\dot{m}\right)\mathrm{.}$ (11) Finally, when d_f/D is less than 0.2, the effect of d_f/D on the focusing can be neglected [35]. Therefore, the design of an aerodynamic lens must only ensure that D is at least five times the maximum orifice diameter. Thus, Eq. 11 can be simplified to $S{t}_{\text{o}}=f_5\left(d_{\text{f}}\mathrm{,}{P}_2\mathrm{,}\dot{m}\right)\mathrm{.}$ (12)

Numerical simulation

Owing to the large number of influencing parameters, an effective ADL design is difficult to achieve based solely on experimental experience. The design process of an ADL typically requires both iterative optimization and experimental measurements. Numerical simulations allow for the design and rapid iteration of the ADL on computers. Various internal-flow parameters of the ADL can be easily obtained through simulations. The computational fluid dynamics software FLUENT is adopted to calculate the flow field and predict the motion of the particles. The volume fraction of the particles is much smaller than that of the fluid in the ADL. We assume that the particles do not affect the flow field and that no interaction force exists between the particles. In addition, the particles are assumed to be spherical; thus, the lift force is neglected. We first calculate the flow field by solving the steady-state Navier–Stokes equations. The particles are then introduced into the flow field to obtain the trajectories and velocities using the Lagrangian method.

The geometry of the ADL is axisymmetric; thus, a 2D axisymmetric model is used. The Navier–Stokes equations are solved using the finite-volume method. The SIMPLEC algorithm is selected as the pressure–velocity coupling method. The flow properties are typically characterized by three dimensionless numbers: the Reynolds, Mach, and Knudsen (Kn) numbers. Because Re is generally less than 100 in the ADL, the viscous model is set as laminar. The flow inside the ADL is limited to a subsonic condition. Because Ma > 0.3 at the accelerating nozzle, the flow is assumed to be compressible. The mean free path of the gas in an ADL is several tens of micrometers, whereas the diameter of the lens is approximately 1 mm; hence, Kn < 0.1. The flow is assumed to be in the continuum- or slip-flow region. In the vacuum chamber, the gas is in the free molecular-flow region, and the particles are hardly affected by the gas. We assume that the simulation can still predict the particle motion after they leave the ADL.

A quadrilateral mesh is used for the simulations. The cell size near the orifices ranges from 4 to 10 μm, and is 100 μm in the spacers. The numbers of mesh cells for a single lens and the ADL are approximately 70,000 and 370,000, respectively, with a growth rate of 1.1 and an average element quality greater than 0.95. The boundary conditions are defined in Sect. 3. For all simulations, when the continuity residual is less than 1 × 10^-10 and the relative error of the inlet and outlet mass flowrate is less than 0.01%, the calculation is considered convergent.

A discrete phase model is used to introduce particles into the calculated flow field, and user-defined functions are used to describe the forces applied to the particles. In the ADL, particles are mainly subjected to drag and Brownian forces, as follows: $\frac{\text{d}{\overrightarrow{u}}_{\text{p}}}{\text{d}t}={\overrightarrow{F}}_{\text{drag}}+{\overrightarrow{F}}_{\text{bi}}\mathrm{,}$ (13) where ${\overrightarrow{u}}_{\text{p}}$ is the velocity vector of the particles, ${\overrightarrow{F}}_{\text{drag}}$ and ${\overrightarrow{F}}_{\text{bi}}$ are the drag and Brownian forces per unit mass, respectively.

Because the mean free path is much larger than the particle radius (i.e., $K{n}_{\text{p}}\ll 1$), the Cunningham slip correction is considered. Thus, the corrected Stokes law for the drag force on the particles is given by [50] $F_{\text{drag}}=\frac{3\pi \mu d_{\text{p}}\left(u_{\text{f}}-u_{\text{p}}\right)}{m_{\text{p}}{C}_{\text{c}}}\mathrm{,}$ (14) where μ denotes the dynamic viscosity of the gas, d_p is the particle diameter, u_f is the flow velocity, u_p is the particle velocity, and m_p is the particle mass. C_c denotes the slip correction factor given by [51]: $C_{\text{c}}=1+K{n}_{\text{p}}\left[1.257+0.4\exp \left(\frac{-1.1}{K{n}_{\text{p}}}\right)\right]\mathrm{.}$ (15) The Brownian force per unit mass in direction i at each time step (Δt) is represented as [52, 53] $F_{\text{bi}}=G_i\sqrt{\frac{216vk{T}_1}{\pi {\rho }_1{d}_{\text{p}}{}^5{\left(\frac{{\rho }_{\text{p}}}{{\rho }_1}\right)}^2{C}_{\text{c}}\text{Δ}t}}\mathrm{,}$ (16) where Gi is a Gaussian random number with zero mean and unit variance, v is the kinematic viscosity, k is the Boltzmann constant, and ρ₁ is the gas density.

The focusing effect of the ADL is determined by a combination of aerodynamic focusing and diffusion broadening caused by Brownian motion [39]. When studying the parameters that influence St_o in a single lens, only the drag force is considered. When evaluating the performance of the ADL, both the drag and Brownian forces are considered to approach a more realistic state. The particle trajectories are calculated from the injection location until they reach the exit or wall.

Optimization of the design method

For a single lens, when the mass flowrate and downstream pressure are given, the optimal upstream gas pressure (P_focusing) and d_f required to focus the particles can be calculated using Eq. 17. The pressure decrease of a gas passing through a single lens can be calculated using Eq. 10. By repeating this process, all the diameters and pressures of the multistage lens stack can be obtained sequentially. $P_{\text{focusing}}={\left[\frac{1}{\left(1+\frac{\pi \alpha }{8}\right)\sqrt{2\pi {\gamma }^3}}\frac{\dot{m}{\rho }_{\text{p}}{d}_{\text{p}}{c}^3}{S{t}_{\text{o}}\left(d_{\text{f}}\right)d_{\text{f}}^3}\right]}^{\frac{1}{2}}$ (17) The mass flow of the gas is conserved in the ADL, whereas the pressure decreases as the gas passes through each lens. Thus, the pressure downstream of each lens (i.e., P₂) varies. If an ADL is designed based on Eq. 17 and Eq. 10, multiple St_o functional relationships corresponding to different downstream pressures at the same flow rate are required. To simplify this problem, the effect of P₂ on St_o is ignored when the pressure decrease is small. Alternatively, we can linearly combine the St_o functional relationships corresponding to the two different downstream pressures under the same flow rate, as shown in Eq. 18–20: $S{t}_{\text{o}\mathrm{,}L}=f_L\left(d_{\text{f}}\right)\mathrm{,}$ (18) $S{t}_{\text{o}\mathrm{,}H}=f_H\left(d_{\text{f}}\right)\mathrm{,}$ (19) $\begin{array}{ll}S{t}_{\text{o}\mathrm{,}{P}_2}\hfill & =f\left(d_{\text{f}}\mathrm{,}{P}_2\right)\hfill \\ \hfill & =\frac{P_2-P_{\mathrm{2,}L}}{P_{\mathrm{2,}H}-P_{\mathrm{2,}L}}S{t}_{\text{o}\mathrm{,}H}+\frac{P_{\mathrm{2,}H}-P_2}{P_{\mathrm{2,}H}-P_{\mathrm{2,}L}}S{t}_{\text{o}\mathrm{,}L}\mathrm{,}\hfill \end{array}$ (20) where $S{t}_{\text{o}\mathrm{,}L}$ and $S{t}_{\text{o}\mathrm{,}H}$ are the optimum Stokes numbers at lower and higher downstream pressures, respectively. $S{t}_{\text{o}\mathrm{,}{P}_2}$ is a binary function of St_o with respect to d_f and P₂ at a given mass flowrate.

Based on the above analysis, the design process of ADL becomes simple and efficient when a functional relationship (or two) of St_o is given. The optimized method is as follows.

First, the particle diameter of each lens is set based on the particle-size range. When large particles pass through the front lens and are focused near the axis, they are less likely to diverge when passing through the rear lens. Therefore, the front lenses are used to focus the large particles, whereas the rear lenses are used to focus the small particles.

Second, the initial parameters are set and the diameter and pressure decrease of each lens are calculated using Eq. 17 and Eq. 10. The initial parameters are the pressure before the accelerating nozzle, tube diameter (D), and gas mass flowrate. The relationship between St_o and d_f for specific $\dot{m}$ and P₂ in Eq. 17 can be obtained by conducting several single-lens simulations (see Sect. 3). The St_o relationship varies for different gases. D is set to at least five times the diameter of the maximum lens orifice.

Third, the accelerating nozzle is designed based on the pressure before it. Because of the significant pressure decrease before and after passing through the acceleration nozzle, the gas exceeds the sonic speed [54, 55]. The nozzle diameter (d_n) is calculated as follows [56]: $\dot{m}=\frac{\pi d_{\text{n}}{}^2}{4}\frac{C_{\text{d}}{Y}_{\text{c}}}{\sqrt{1-{\beta }^4}}{P}_1\sqrt{\frac{2M}{R{T}_1}{x}_{\text{c}}}\mathrm{,}$ (21) where Y_c is the expansion coefficient of the critical state and x_c is determined by the specific heat ratio.

Finally, the spacer lengths (L) are calculated by using the overall simulations of the ADL. After passing through the lens, the flow forms a recirculation zone. Subsequently, the flow returns to the horizontal laminar-flow state after a particular distance (redevelopment length). Before entering the next lens, the flow starts to curve toward the centerline, resulting in the approach length. To provide sufficient space for periodic contraction and expansion, spacers are used to separate lenses that have lengths greater than the sum of the redevelopment and approach lengths. By presetting a sufficiently long length for each spacer, the redevelopment and approach lengths can be calculated through an overall simulation of the ADL. The spacer lengths for the final ADL can be determined based on the simulation results. Note that small changes in L have little effect on the pressure inside the ADL, because the flow resistance is mainly determined by the lens orifice. In addition to the simulation method, L can be estimated using empirical formulas [39].

Experimental setup

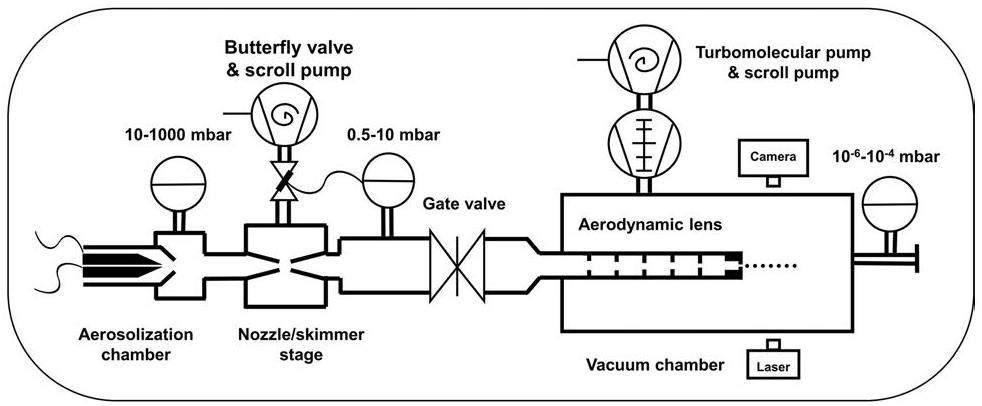
An aerosol sample-delivery system was established to validate the simulation and test the new ADL, as shown in Fig. 2. It consists of an atomization device, a nozzle/skimmer stage, an aerodynamic lens, and other auxiliary devices. Briefly, a solution containing the particles of interest was atomized using the GDVN [21] in the aerosolization chamber. The particles were then introduced into the ADL through a nozzle/skimmer stage placed 1–2 mm apart. The excess carrier gas was extracted to control the pressure in the relaxation chamber. The particles were focused by the ADL and a particle beam was generated in the downstream vacuum chamber (10^-6–10^-3 mbar). The particle beam was illuminated by a continuous laser (650 nm, 50 mW), and the scattered light was collected using an ultra-long working-distance objective lens (ULWZ-200M, OptoSigma, France; N.A. 0.014–0.08) and a complementary metal-oxide semiconductor camera (CS165MU1/M, Thorlabs, USA). The particle-beam diameter (full width at half maximum) in the experiment was determined by measuring the projection of the beam along the laser-propagation axis. Downstream of the accelerating nozzle, the point with the smallest beam width was defined as the focal point.

Fig. 2Full-screen View

Experimental setup of the aerosol sample-delivery system. The system was mainly composed of an atomization device, a nozzle/skimmer stage, and an aerodynamic lens, from left to right

Simulation results of the single lens

Single-lens simulations with different orifice diameters are performed to verify the theoretical analysis described in Sect. 2. As shown in Fig. 1, the red and green lines represent the inlet and outlet of the computational domain of the single lens, respectively. The solid black line on the exterior represents a wall. Mass-flow conservation is used as the inlet condition, and pressure is used as the outlet condition, according to the specific conditions shown in Fig. 3 and Fig. 4. A polystyrene (PS) sphere with a density of 1050 kg/m³ is injected from an initial position and experienced only a drag force. To avoid the impact of a non-fully developed flow at the entrance, the initial injection position is located 10 mm downstream of the lens inlet and $0.15D$ from the axis. After passing through the lens orifice, if the radial position of a particle is less than 1 μm and the particle moves parallel to the axis, the single lens is considered to be in its optimal operating state. The corresponding St_o value is obtained using Eq. 2.

Fig. 3Full-screen View

Relationship between St_o and d_f with different mass flowrates obtained by single-lens simulations when the downstream pressure is (a) 300 Pa for nitrogen, (b) 500 Pa for nitrogen, and (c) 1500 Pa for helium

Fig. 4Full-screen View

Relationship between St_o and d_f with different downstream pressures obtained by single-lens simulations when the carrier gas is (a) 0.01 standard liters per minute (SLM) nitrogen and (b) 0.01 SLM helium

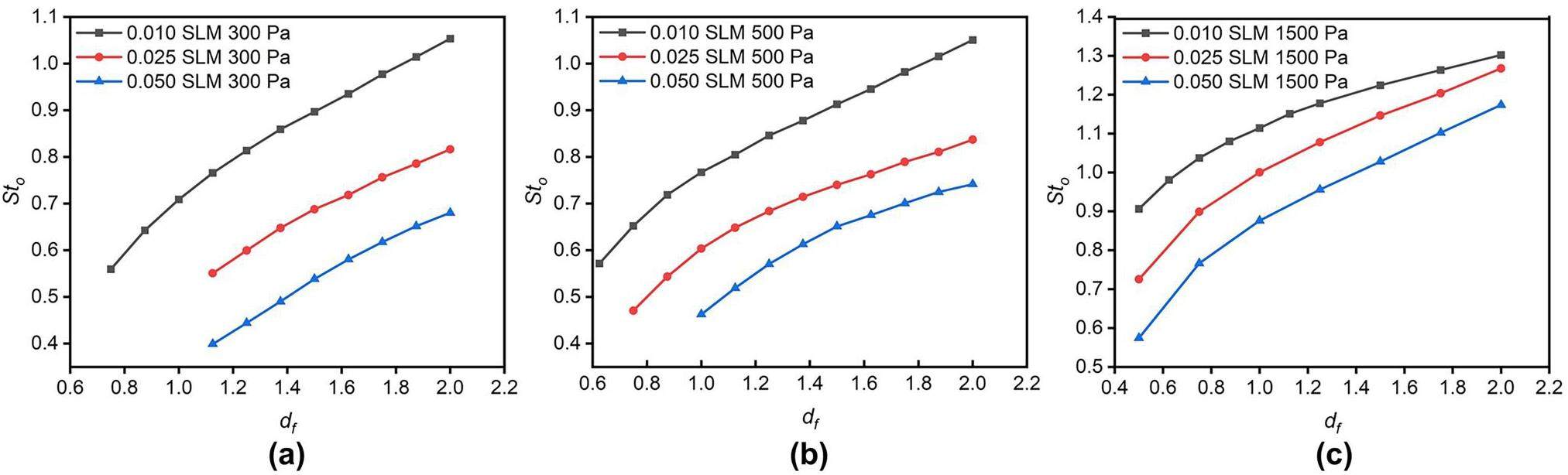
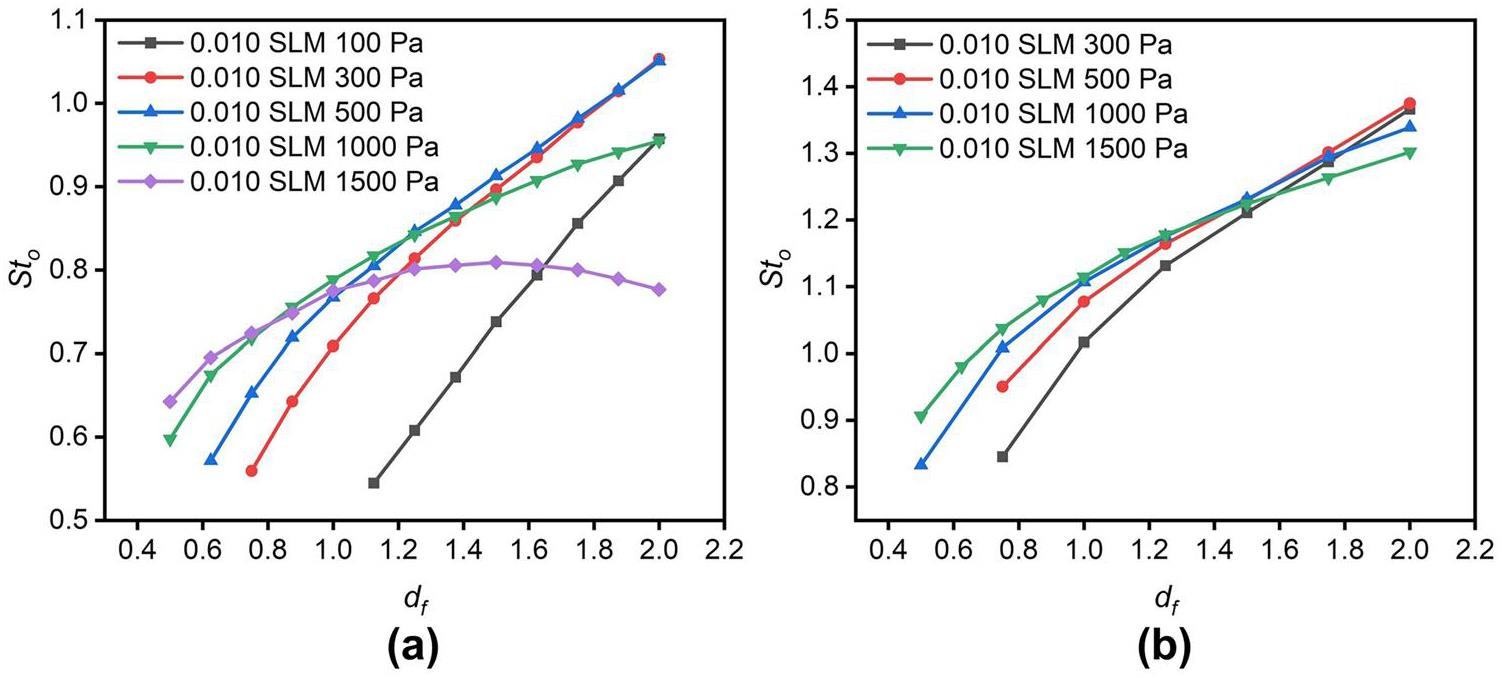
Figure 3 shows the relationship between St_o and d_f under the same downstream pressure but different mass flowrates using single-lens simulations. St_o increases with increasing d_f under the same downstream pressure and mass flowrate. This is attributed to the fact that the velocities of the gas and particles decrease near the lens orifice with an increase in d_f. Thus, the particles cannot easily deviate from the streamlines. Thus, the lens is suitable for focusing larger particles corresponding to a larger St_o. In addition, under the same d_f and downstream pressure, as the mass flowrate increases, St_o decreases. This is attributed to the fact that when the flow rate increases, the radial velocity of the gas at the orifice also increases, causing the particles to deviate from the gas streamlines more easily. Thus, the lens is more suitable for focusing smaller particles corresponding to a smaller St_o. In addition to the differences in St_o values, helium and nitrogen exhibit similar patterns.

Figure 4 shows the relationship between St_o and d_f with the same mass flowrate but different downstream pressures based on single-lens simulations. Under the same mass flow rate, the derivative of St_o with respect to d_f decreases as the downstream pressure increases (i.e., the growth rate of St_o decreases). When the downstream pressure is sufficiently high, St_o decreases with increasing d_f, as shown by the curve corresponding to 1500 Pa in Fig. 4a. If the two curves intersect, lenses with different downstream pressures have the same St_o value at the intersection point. Eq. 17 indicates that for lenses with the same geometry and flow rate, different particles can be focused by adjusting the pressure. This explains that particles of different sizes can be focused by adjusting the pressure and flow rate while maintaining a fixed geometry for the Uppsala injector [57].

As depicted in Fig. 3 and Fig. 4, St_o typically deviates significantly from 1 due to the influence of various parameters. Each point in the figures represents a simulation conducted under specific conditions. Multiple simulations under the same $\dot{m}$ and P₂ values but different df values form a curve that represents the relationship between St_o and d_f under specific $\dot{m}$ and P₂ values. The maximum value of d_f must be less than $D/5$, and the minimum value of d_f must maintain a subsonic flow. Thus, the maximum focusing range of the particle size under specific conditions can be obtained. In addition, St_o is different for different gases, even if d_f, P₂, and $\dot{m}$ are identical. However, a functional relationship always exists between St_o and d_f under specific $\dot{m}$ and P₂ values. We use the power function (not the only choice) to fit the relationships as follows: $S{t}_{\text{o}}\left(d_{\text{f}}\right)=a{d}_{\text{f}}^b+c\mathrm{.}$ (22) For example, by fitting the data shown in Fig. 4a (0.01 SLM, 300 Pa), we can obtain the functional relationship of St_o with respect to d_f: $S{t}_{\text{o}}\left(d_{\text{f}}\right)=-37.88d_{\text{f}}^{-0.01183}+\mathrm{41.8,}$ (23) where the sum of squares due to the error is 0.0002, and the coefficient of determination is 0.9992.

Design results of the aerodynamic lens

In the SPI experiments, the size of the particles of interest transitioned from larger viruses to smaller proteins. To achieve the high-resolution imaging of small particles, the particle-beam width must be further reduced and the background scattering noise must be minimized [13]. Based on the requirements of SPI, we designed a new ADL to focus 30–500 nm particles. The optimized design method was used in this process, and Eq. 23 was employed as the functional relationship for St_o. PS spheres with a mass density of 1050 kg/m³ were used in the design, as it is comparable to the density of biological materials. Nitrogen was used as the carrier gas to ensure compatibility with both GDVN and commercial electrospray (TSI-3482). The designed mass flowrate of the carrier gas was 0.01 SLM to minimize background scattering. The designed pressure before the accelerating nozzle was 300 Pa and the tube diameter was 10 mm. Table 1 lists the designed particle diameter and optimal Stokes number of each lens, as well as the pressure before and after each lens. The pressure before the first lens was 483 Pa (i.e., the inlet pressure of the ADL).

With the inlet pressure and diameter of each orifice already obtained, the redevelopment and approach lengths can be calculated through an overall simulation of ADL, where a sufficiently long length is preset for each spacer. The final spacer lengths for the ADL were then determined based on the simulation results. As shown in Fig. S1 in the Supplementary Material, each L value was preset to 25 mm. For the spacer between the third and fourth lenses, the redevelopment length was 9 mm, and the approach length was 3.8 mm. Therefore, L (18 mm, red line) was determined to be greater than the total length (12.8 mm). Figure 5 shows the final geometric parameters of the ADL. D was approximately six times the diameter of the largest lens orifice.

Fig. 5Full-screen View

Schematic of the aerodynamic lens (not to scale). The orifice plates of the lenses are 0.2 mm thick. The dimensions are in mm

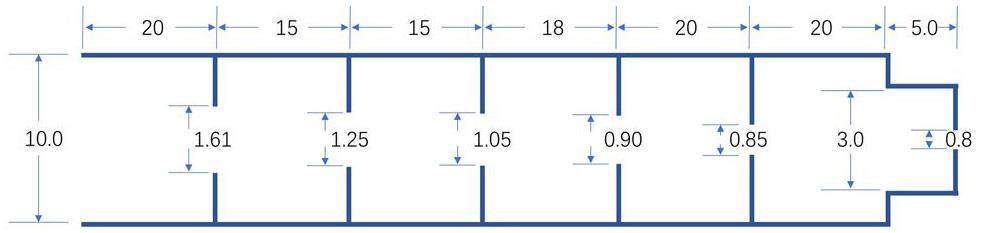
Simulations of the new ADL were performed to predict the behavior of particles. As shown in Fig. 6a, the inlet is defined as the starting plane of the ADL, and the outlet is defined as the boundary of a rectangular area (45 mm × 45 mm) added downstream of the ADL exit. A mass-flow conservation of 2.08 × 10^-7 kg/s (0.01 SLM) is used as the inlet condition, and a pressure of 1 Pa is used as the outlet condition. As shown in Fig. S2 in the Supplementary Material, after 16,000 iterations, the continuity residual is 6 × 10^-11. The absolute error of the inlet and outlet mass-flow rates is 1 × 10^-13 kg/s (i.e., the relative error is 0.005%). The static pressure at the monitoring point upstream of the accelerator nozzle remains almost constant. Therefore, the simulation of the new ADL is considered to be convergent.

Fig. 6Full-screen View

(Color online) (a) Simulated flow streamlines of the ADL. The red line represents the inlet, and the green line represents the outlet. The color scale corresponds to the flow speed. (b) Simulated static pressure and flow velocities along the axis of the ADL

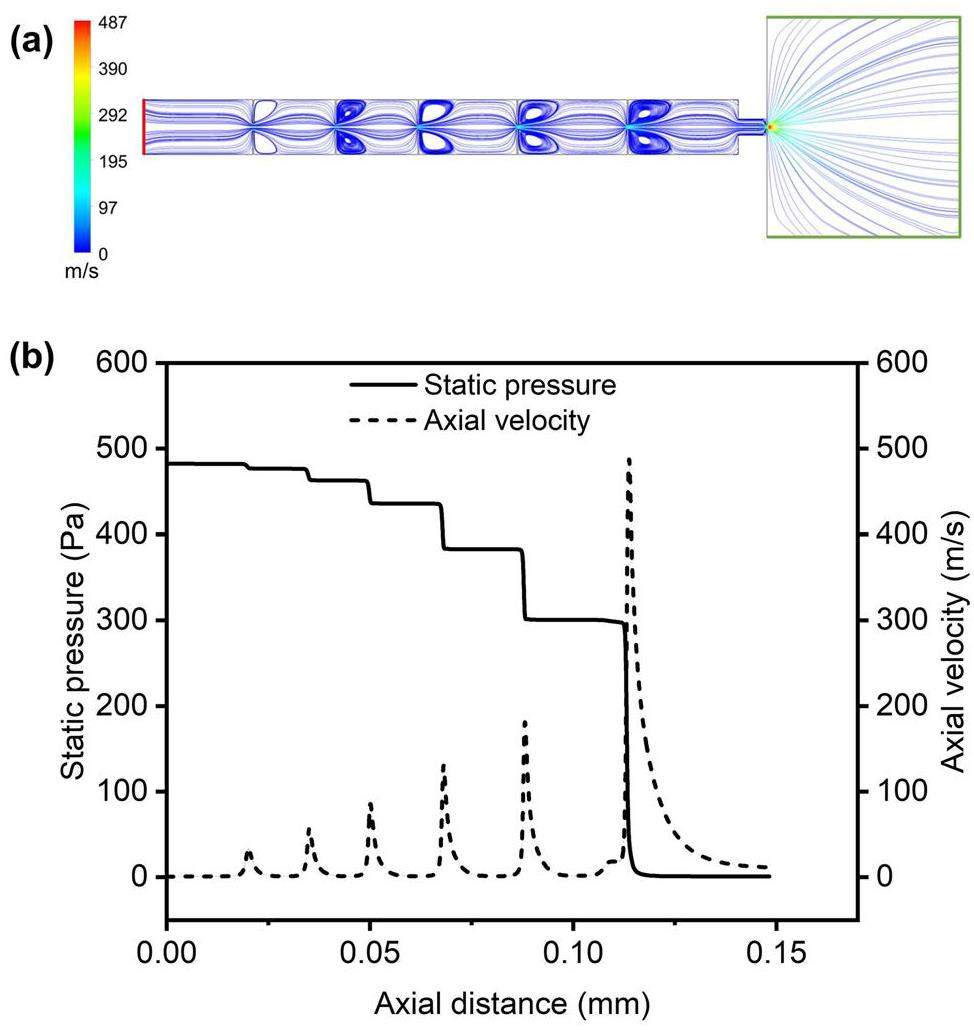
Figure 6a shows the simulated flow streamlines in the ADL. The gas contracts rapidly before the lens and expands slowly beyond the lens. The distance between the lenses enables the full development of the flow field, exhibiting a laminar-flow state. Figure 6b shows the simulated static pressure and velocity profiles along the axis. The pressure decreases after the gas passes through the lens. After passing through the five lenses, the pressure decreases by approximately 183 Pa, which is consistent with the designed pressure decrease in Table 1. As the lens diameter decreases, the gas velocity increases. Owing to the significant pressure decrease, supersonic expansion occurs downstream of the acceleration nozzle.

The trajectories of the particles were obtained by injecting 1000 particles with the same diameter at a cross section located 10 mm downstream of the inlet. They are uniformly distributed in this cross section. The initial particle velocity is zero. The particle time-step is limited to a fifth of the particle-relaxation time. The particle beam width (D₉₀) in the simulation is defined as the beam diameter containing 90% of the total particles. They are subjected to both drag and Brownian forces.

Figure 7 shows the simulated trajectories of PS spheres passing through the ADL. For clarity, only the trajectories of 10 particles are displayed. Owing to the periodic asymmetrical contraction and expansion of the flow field, the particles gradually gathered towards the axis. Larger particles are focused by the front lens, whereas smaller particles are focused by the back lens. The maximum value of the color scale represents the maximum velocity that the particles can reach. As the particle diameter increases, the maximum velocity decreases. This can be explained by the fact that drag forces are less capable of accelerating larger particles with greater inertia under the same flow field.

Fig. 7Full-screen View

(Color online) Simulated trajectories of PS particles through the ADL with diameters of (a) 30 nm, (b) 50 nm, (c) 100 nm, and (d) 500 nm. The color scale corresponds to the velocity magnitude of the particles

Furthermore, the particle-transmission rate is an important parameter for evaluating the performance of aerosol injectors. Based on the 1000 particles injected into the new ADL shown in Fig. 7, 30-nm PS spheres had a transmission rate of 90% through the ADL, whereas the transmission rate of the PS spheres larger than 100 nm was close to 100%. The main cause of particle loss is Brownian diffusion, which results in the loss of small particles on the wall. However, studies have shown that for an entire aerosol injector, the main particle loss occurs at the nozzle/skimmer stage rather than at the ADL [58]. Efforts should be made to improve the particle-transmission rate in the nozzle/skimmer stage.

The actual Stokes numbers obtained from the overall ADL simulation are listed in Table 2, where the number following St denotes the particle diameter. The Stokes numbers marked with asterisks correspond to the St_o value derived from the relationship in Table 1. These data are in good agreement, indicating that the design process is effective. St_o decreases with decreasing particle size, which is consistent with the analysis shown in Fig. 3. As the lens number increases, the Stokes numbers of all the particles increases. The Stokes numbers with asterisks form a dividing line that separates Table 2 into two regions. In the region below the dividing line, St is less than St_o when the particles pass through the lenses, indicating that the particles either follow the streamline or experience slight focusing. By contrast, in the region above the dividing line, St is greater than St_o when the particles pass through the lenses. These particles have already been focused by previous lenses and are close to the axis where the radial flow velocity is low; therefore, they are not significantly defocused. These analyses align with the particle trajectories shown in Fig. 7.

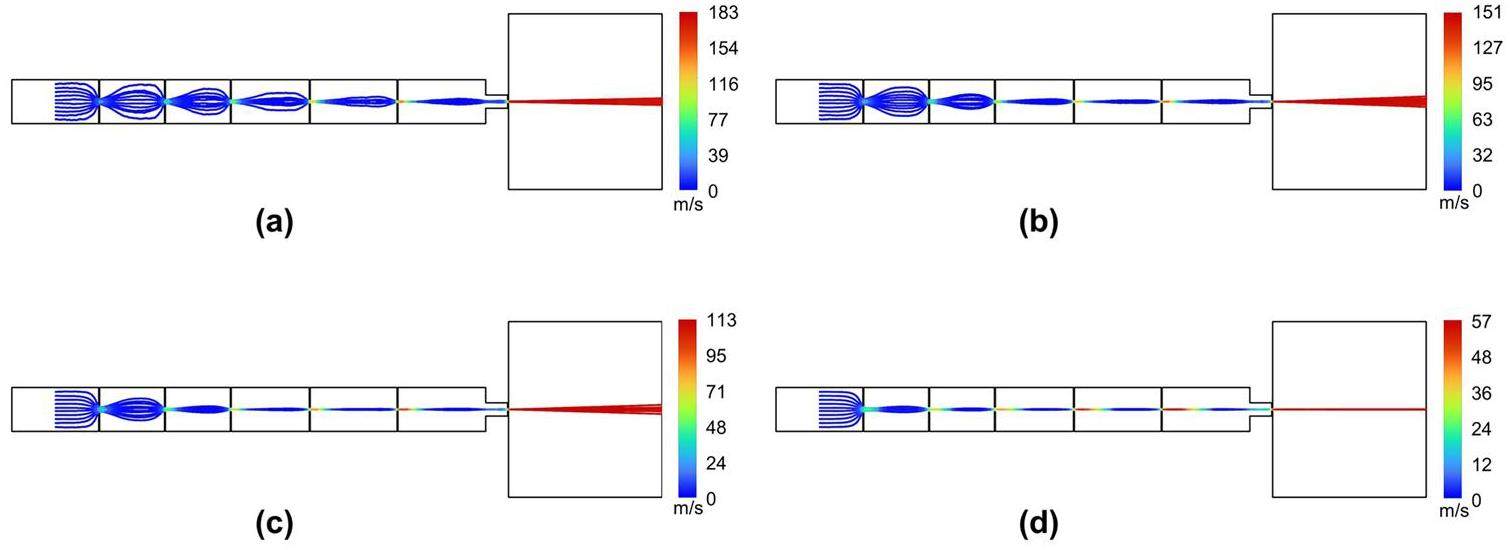
Figure 8 shows the simulated evolution of the beam width with the downstream distance from the ADL exit. The minimum beam width of the particles decreases with increasing particle diameter. Because of the influence of Brownian motion, the ADL has poor focusing effects on smaller particles. For example, the minimum beam width is 28.0 μm for 30-nm particles, and 8.4 μm for 500-nm particles. In addition, as the particle size increases, the focal point gradually moves away from the nozzle exit with a small divergence angle. The particle-beam focus position ranges from 0.8 to 2 mm in the simulation.

Fig. 8Full-screen View

Simulated particle-beam evolution curves for PS spheres with different diameters. All the lines are the result of fitting. As the particle diameter increases, the particle-beam focus moves further away from the ADL exit

Experimental results

The new ADL was commissioned using the PS spheres. During the commissioning, the inlet pressure of the ADL was set to 483 Pa. Figure 9a–c show that PS spheres formed long and straight beams in a vacuum after passing through the ADL. The particle beams were illuminated by a laser. The beams became dim at both ends owing to a decrease in laser-spot intensity. The irregular bright spots on the left side were a part of the ADL accelerator nozzle. Figure 9d–f show the comparison between the experimental-beam width measured at 483 Pa (red circles) and the corresponding simulated-beam width (black dots). The experimental-beam width curves were fitted with standard errors using repeated measurements. Based on the experimental data, the beam width initially decreased and then increased, forming a focus approximately 1.5–2 mm from the ADL exit. For all tests, the particle-beam width at the focus was less than 20 μm. Among them, the 50-nm particles had the smallest beam width (14.3 μm) and the largest divergence angle (0.99°). Compared with the Uppsala injector, which can focus 70-nm PS spheres to 18 μm with a divergence angle of 1.9° and gas-flow rate of approximately 0.03 SLM [57], the new ADL generated a smaller beam width on smaller particles with a lower flow rate (0.01 SLM). A smaller beam width can increase the sample density, which helps improve the hit rate. For particles larger than 100 nm, we could not directly compare our ADL with the Uppsala injector owing to the different flow rates and particle sizes [57], although our ADL generally demonstrated a comparable performance.

Fig. 9Full-screen View

PS-sphere beams formed in a vacuum with diameters of (a) 50 nm, (b) 100 nm, and (c) 300 nm. The inlet pressure is 483 Pa. The scale bar is 300 μm. Experimental and simulated particle-beam evolution curves for PS spheres with diameters of (d) 50 nm, (e) 100 nm, and (f) 300 nm. The error bars represent the standard error. All the lines are the result of fitting

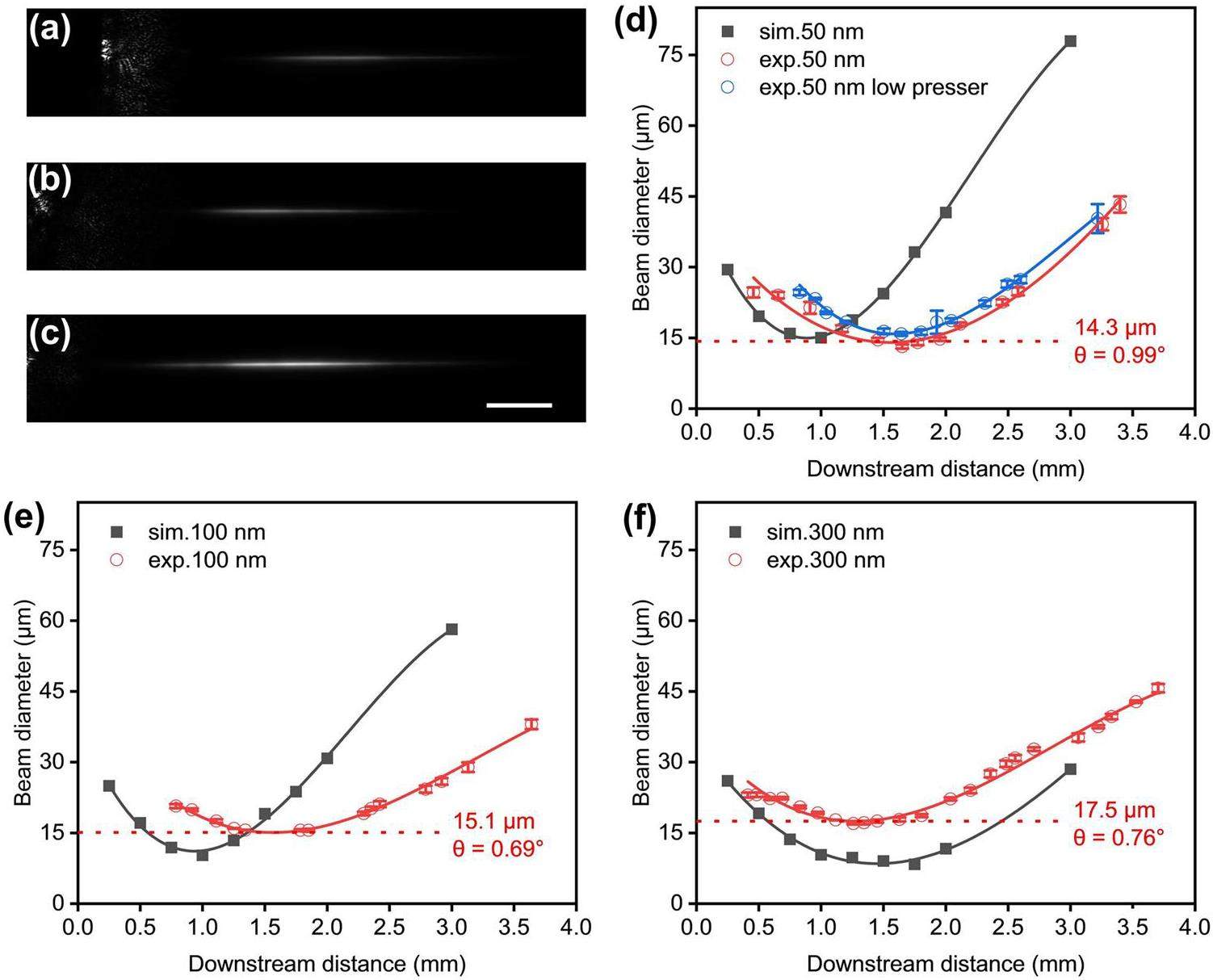
Moreover, we tested a beam width of 50-nm particles at a lower inlet pressure of 367 Pa (blue circles in Fig. 9d). The beam width at the focus was 15.9 μm, which was 11% larger than the beam width under the designed pressure (483 Pa). However, according to the simulation estimates, using a lower inlet pressure resulted in an approximately 30% reduction in the flow rate compared to the designed pressure. Adjusting the inlet pressure may further reduce the flow rate without significantly increasing the beam width or expanding the particle-diameter range that can be focused by the ADL.

For the larger divergence angles for small particles, the experiments and simulations are consistent; however, some deviations are observed for the smallest beam width. As shown in Fig. 9d–f, the experimental and simulated results for small particles are in good agreement; however, the simulation underestimates the beam width for large particles. For example, the minimum beam width measured in the experiment for 300 nm particles was twice that of the simulation prediction. Several possible reasons exist for the deviations between the simulation and experiment. Our design may amplify the simulation error of large particles. In our design, when large particles pass through the front lens, they are focused near the axis. Even if the actual value of St is large at the rear lens, the particles will not be significantly defocused when passing through the lens. For example, although the Stokes number of the 500-nm PS particles in the fifth lens is large (see Table 2), the particles are not significantly defocused (see Fig. 7d). However, simulation errors are inevitable. If the true radial position of the particle is farther from the axis than numerically predicted, this deviation is amplified by the multiple lenses behind it. In contrast, small particles are slightly focused by the front lens owing to their small St value (e.g., 30-nm particles in Fig. 7a). They are then effectively focused by the rear lens, and the deviation is not amplified. Consequently, the simulation underestimates the beam width of large particles rather than that of small particles, which agrees with the observed phenomenon. However, we considered not only the drag force, but also the Brownian force in the overall simulation of the ADL. However, using the Brownian-motion model under low-pressure conditions (a few hundred Pascals) may result in an increased error. The combination of these two factors can lead to deviations between the simulations and experiments. In addition, the electrostatic forces between the particles can lead to mismatches between the current numerical and experimental results. The charging of PS particles in an aerosol beam atomized by a GDVN was observed [59]. If the particles are very close to each other, the repulsion between particles with the same charge may widen the particle beam.