The pocket-type DDFP and the α-decay half-life calculations

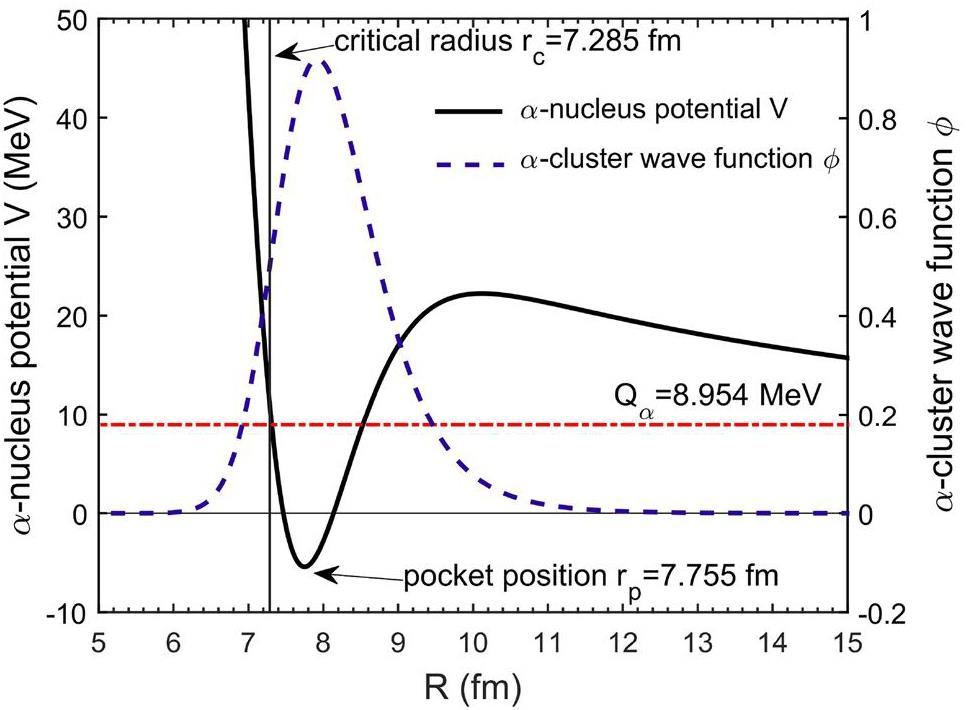
As mentioned in Sect. 1, α-clustering primarily occurs at the surface of heavy nuclei where the nucleon density is below the Mott density. This is illustrated by the pocket-type DDFP, as depicted in Fig. 1. A pocket-like geometry is formed in the surface region beyond the critical radius r_c which corresponds to the Mott density. This feature enables the formation of a quasi-bound state for the α-daughter system, and the α cluster is located at the pocket center. Conversely, within the internal region (R<r_c), Pauli repulsion suppresses the α correlation, preventing the formation of the α-cluster state. Consequently, the strongly repulsive core in the α-nucleus potential effectively inhibits the α cluster, as illustrated by the amplitude of the α-cluster wave function. The first classical turning point is close to the critical radius r_c. This classical turning point marks the boundary of the classical forbidden region, within which the amplitude of the α-cluster wave function undergoes rapidly reduction. A comparable reduction in α-clustering is expected when the medium density surpasses the Mott density; specifically, when the cluster moves into the interior of the daughter nucleus, crossing the critical radius. Therefore, the positions of the first classical turning point and the critical radius are expected to be close to each other. Our calculations indicate that the average distance between these two positions was 0.085 fm for the 129 α emitters studied, reinforcing the universality of this phenomenon.

Fig. 1Full-screen View

(Color online) Pocket-type dynamical double-folding potential (black solid curve) and the corresponding α-cluster wave function (blue dashed curve) as a function of internuclear distance R for the ${}^{208}\text{Pb}+\alpha$ system (ground-state to ground-state α decay in ${}^{212}\text{Po}$). The horizontal red dotted-dashed line denotes the α decay energy Qα. The pocket position r_p referring to the minimum of the potential is marked. The vertical black thin line denotes the critical radius r_c indicating the Mott density at the nuclear surface

Utilizing this pocket-type DDFP model, we investigated the ground state-to-ground state α transitions in even-even nuclei ranging from Nd to Cf. To calculate the decay half-lives using Eq. (9), the Pα factor is required as a theoretical input. Because the Pα factor is strongly correlated with the shell structure, a precise description of Pα during the shell evolution is crucial for reliable half-life calculations. However, a direct evaluation of the exact Pα within a microscopic formalism is challenging because of the complexity of many-body problems. Alternatively, the value of Pα can be estimated phenomenologically from well-established Pα systematics derived from experimental half-lives $P_{\alpha }^{\text{exp}\text{.}}=\frac{\hslash \text{ln}2}{T_{1/2}^{\text{expt}\text{.}}\text{Γ}}\mathrm{.}$ (10) For instance, a simple formula that depends on the valence nucleon number of the α emitter provides a reasonably accurate description of Pα as demonstrated in previous systematic calculations [34-38]. Figure 2(a) shows the $P_{\alpha }^{\text{exp}\text{.}}$ factors extracted from the experimental half-lives using Eq. (10) as a function of the valence neutron number with respect to its nearest neutron magic number, N₀. As shown, $P_{\alpha }^{\text{exp}\text{.}}$ factor generally decreases with increasing valence neutron number until the next shell closure. This dispersion exhibits a linear correlation with the valence neutron number. Based on these systematics, we employed an N-dependent formula for the Pα factor as the theoretical input in the half-life calculations: $P_{\alpha }=-0.0015\left(N-N_0\right)+\mathrm{0.0692,}$ (11) with N₀=82 for nuclei with 82<N≤126 and N₀=126 for nuclei with N>126, as denoted by the red line in Fig. 2(a). This input Pα formula is different from that used in our previous work, which was based on a Heaviside step function formalism [21]. This is because the previous approach was intended to describe the abrupt change in Pα near the shell closure. The present valence-nucleon-dependent formula is more appropriate for describing the systematic behavior of Pα factor in both the closed-shell and open-shell regions.

Fig. 2Full-screen View

(a) (Color online) Extracted α preformation factor $P_{\alpha }^{\text{exp}\text{.}}$ (black circles) as a function of the number of valence neutrons $N-N_0$, with N₀ being the neutron magic number. The Pα generally decreases with increasing the number of valence neutrons, which can be approximated by a linear fit (red line). (b) The logarithmic deviation between the theoretical and experimental α-decay half-lives as a function of the neutron number of the parent nucleus. The dashed-dotted lines mark the range from -0.5 to 0.5. The blue dashed boxes mark the data points of ${}^{194}\text{Pb}$, ${}^{\mathrm{214,216,218}}\text{U}$, and ${}^{228}\text{Pu}$ which deviate relatively far from the experimental data

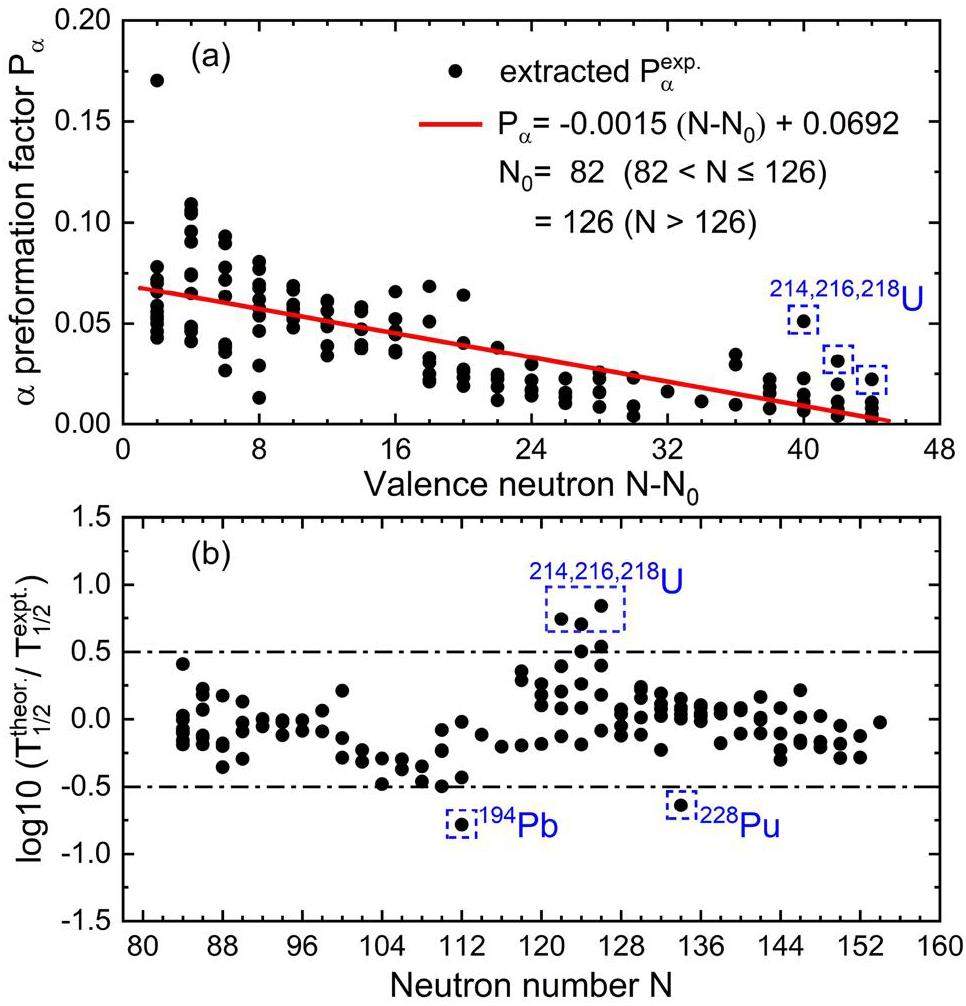
In Fig. 2(b), the deviations between the theoretical and experimental half-lives are plotted (denoted by black circles) on a logarithmic scale as a function of the neutron number of the parent nucleus. The agreement between the theoretical and experimental results was systematically evaluated using the average deviation, defined as $\sigma =\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\left|{{\displaystyle \log }}_{10}{T}_{1/\mathrm{2,}i}^{\text{theor}\text{.}}-{{\displaystyle \log }}_{10}{T}_{1/\mathrm{2,}i}^{\text{expt}\text{.}}\right|}$. We obtained $\sigma =0.1820$ for the 129 even-even nuclei investigated in this study. This result corresponds to an average factor $S{=10}^{\sigma }=1.521$ between the theoretical and experimental half-lives, which is slightly larger than S=1.475 obtained from our previous calculation [21]. Relatively large deviations were observed for the isotopes ${}^{\mathrm{214,216,218}}\text{U}$, as shown in Fig. 2. These deviations are primarily due to the limitation of the N-dependent formula for Pα [Eq. (11)], which cannot adequately describe the Pα behavior during the proton shell evolution [34, 35]. The input Pα for uranium isotopes that lie farther from the proton shell at Z=82 is underestimated compared with that of the extracted $P_{\alpha }^{\text{exp}\text{.}}$, as illustrated in Fig. 2(a). Hence, a more refined Pα that considers both the neutron and proton shell evolution would likely improve the agreement in the half-life calculations. Furthermore, large deviations were observed for ¹⁹⁴Pb and ²²⁸Pu. The deviation in ¹⁹⁴Pb is likely due to its extremely small α-branching ratio $[(7.3\pm 2.9)\times {10}^{-6}\%]$ with relatively large uncertainty [39], while the deviation in ²²⁸Pu stems primarily from the uncertainty in the measured half-life, which is ${1.1}_{-0.5}^{+2.0}\text{s}$ [40]. Nevertheless, as an extended calculation of our previous study [21], the present result further validate the reliability and accuracy of the pocket-type DDFP in describing the α-decay half-lives.

In addition to the ground-state-to-ground-state α decay discussed above, testing the performance of the proposed model in estimating the α-decay half-lives between the excited states would be valuable. For instance, we calculated the half-life of the favored α transition from the first isomeric state of ¹³⁹Po $\left(I^{\pi }{=13/2}^{+}\right)$ to that of ¹⁸⁹Pb $\left(I^{\pi }{=13/2}^{+}\right)$. The theoretical result is $T_{1/2}^{\text{theor}\text{.}}=9.53\times {10}^{-2}\text{s}$ with Pα estimated using Eq. (11). This value is in close agreement with that reported in previous theoretical studies [41, 42]. Our result is smaller than the experimentally measured half-life $T_{1/2}^{\text{expt}\text{.}}=2.47\times {10}^{-1}\text{s}$ by a factor of 2.6, which is acceptable particularly considering that Pα of odd-A nuclei are usually smaller than that of even-even nuclei due to the Pauli blocking from the unpaired nucleon [42, 43].

Nuclear charge radii estimated by the pocket-type DDFP model

Within the double-folding framework, the density distribution of the daughter nucleus is involved in constructing the α-nucleus potential. Consequently, deducing the nuclear charge radius of the daughter nucleus from its density distribution is feasible once the α-nucleus potential is determined using experimental decay data. For instance, in Ref. [22, 23], the charge radii of the daughter nuclei were determined using both the experimental half-lives and decay energies within the framework of a generalized density-dependent cluster model (GDDCM). In an extention of this approach, Ref. [24] improved the GDDCM (labeled GDDCM*) by considering the neutron skin structure, differences between proton and neutron density distributions, and a more refined α preformation factor. This modification provides a better description for the charge radii. To a certain extent, the accuracy of the deduced charge radii serves as an additional test of the effectiveness of the model in describing α-nucleus interactions.

As described in Sect. 2, the diffuseness parameter a in the density distribution of the daughter nucleus is determined by ensuring that the pocket-type DDFP, within the TPA framework, can support a bound state with its eigenvalue matching the experimental α-decay energy. Therefore, the pocket potential embodies both α-decay dynamics and information from the decay energy. This is linked to the density distribution and the surface diffuseness property a of the daughter nucleus through a double-folding procedure. Once the value of a is determined in the calculation, we obtain not only the α-nucleus potential for half-life calculations, but also the density distribution of daughter nuclei. Therefore, the RMS charge radius of the daughter nucleus can be calculated as follows: $R_{\text{ch}\text{.}}\equiv {\langle r^2\rangle }^{1/2}={\left[\frac{{\displaystyle \int }{\rho }_1\left(r\right)r^4\text{d}r}{{\displaystyle \int }{\rho }_1\left(r\right)r^2\text{d}r}\right]}^{1/2}\mathrm{.}$ (12) This strategy is notably simpler than previous cluster models, which require the experimental decay energy, half-life, and the introduction of an empirical Pα factor.

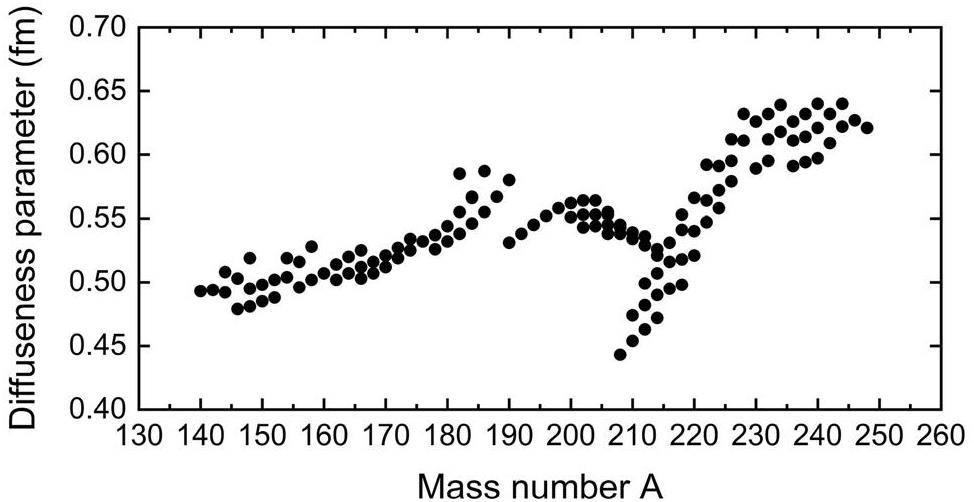
The diffuseness parameters determined using the double-folding procedure are shown in Fig. 3. The diffuseness parameters of the daughter nuclei generally fluctuate around the average value of $\overline{a}=0.545\text{fm}$. A clear shell effect can be observed around A=208, corresponding to a neutron number approaching the N=126 shell closure.

Fig. 3Full-screen View

(Color online) The diffuseness parameters a of the daughter nuclei, determined from the the calculations of pocket-type potentials, are plotted as a function of its mass number. The diffuseness parameters range from 0.44 fm to 0.64 fm for nuclei with A=140-248

In Fig. 4, we present the calculated charge radii of the daughter nuclei with Z=58-96 and the corresponding experimental values obtained from Ref. [44, 45]. The empirical relationship between the charge radius and the mass number is indicated by the gray line for reference. $R_{\text{ch}\text{.}}=\left(r_1+r_2{A}^{-2/3}+r_3{A}^{-4/3}\right)\times A^{1/3}\mathrm{,}$ (13) where, the parameters $r_1=0.9071(13)\text{fm}$, $r_2=1.105(25)\text{fm}$, and $r_3=-0.548(34)\text{fm}$ [44]. As shown, our results align with the trend of the experimental data as well as that indicated by the empirical formula. The standard deviation of the discrepancy between the theoretical and experimental values is evaluated as ${\sigma }_{\text{ch}\text{.}}={\left[{\displaystyle {\sum }_{i=1}^{84}{\left(R_{\text{ch}\mathrm{.,}i}^{\text{theor}\text{.}}-R_{\text{ch}\mathrm{.,}i}^{\text{expt}\text{.}}\right)}^2/84}\right]}^{1/2}$ yielding a value ${\sigma }_{\text{ch}\text{.}}=0.0420\text{fm}$, which was comparable to the empirical results calculated using Eq. (13). However, a notable discrepancy is observed at A=208-214, where the calculated radii indicate an abrupt decrease, whereas the corresponding experimental radii vary more smoothly. This abrupt variation is related to the N=126 shell effect, which significantly affects the neutron density distribution in the daughter nucleus [46]. The resulting variation in the neutron distribution, in turn, affects the proton distribution, which is reflected in a less pronounced kink appearing in the variation of the experimental charge radii at the neutron magic number (see Fig. 1 in Ref. [47] and Fig. 3 in Ref. [44]). However, the present DDFP formalism does not treat the proton and neutron distributions separately because it employs only one set of parameters, R_1/2 and a. The N=126 shell effect from the decay energy is incorporated into the parameters shared by both the proton and neutron density distributions [21]. This results in the magnification of the shell effect for the proton distributions, thereby impacting the charge radii. Therefore, a separate treatment for both the proton and neutron density profiles, considering the neutron skin structure, is expected to reduce this discrepancy and provide a more accurate description of both the charge radii and α-decay half-lives [48, 49].

Fig. 4Full-screen View

(Color online) Theoretical charge radii calculated using Eq. (12) (open circles) compared with experimental data (dark squares) as a function of mass number. The grey line represents the empirical relationship between nuclear radius and mass number [Eq. (13)]. Arrows indicate the shell closure at N=126 for isotopic chains of Pb, Po, Ra, and Th, where a sudden drop in calculated radii occurs due to the shell effect

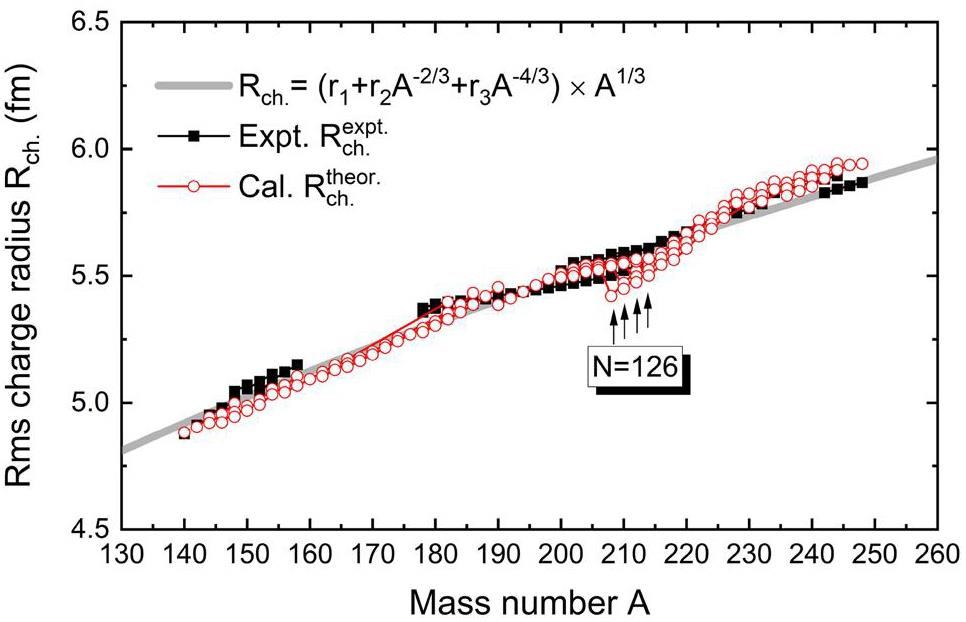
In addition, the charge radii of the pocket-type DDFP and previous GDDCMs can be quantitatively compared [22, 24]. Table 1 lists the standard deviations σ_ch. of the nuclear charge radii for these models compared with the experimental data from [44, 45]. Notably, although the DDFP relies solely on the experimental decay energy and reduces one free parameter by avoiding the input of empirical Pα, it yields a more accurate description for the charge radii. Specifically, the standard deviation is reduced by 67.3% compared to GDDCM and by 53.3% compared to GDDCM*. This significant improvement underscores the significance of the α-clustering features in the mechanism of α decay, particularly the medium effect and the strong Pauli repulsion, which make the pocket-type DDFP a more realistic description of the involved α-nucleus interaction.

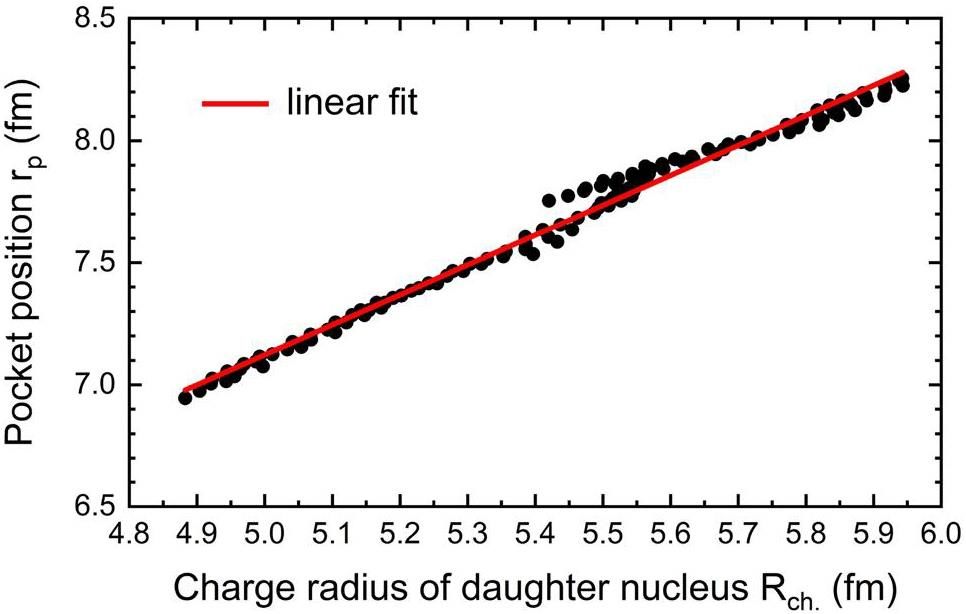
Having determined the charge radii, it is instructive to investigate the correlation between the charge radii of the daughter nuclei and the pocket positions r_p of the α-nucleus potentials (see Figs. 1 for ²¹²Po). As seen in Fig. 5, the pocket position is linearly correlated with the charge radius of the daughter nucleus with a correlation coefficient of 0.9885. This finding was expected, because both quantities are related to the spatial extent of the density distribution of the daughter nucleus. The pocket position corresponds to the region where the α cluster is most likely to form, and is located at the nuclear surface with a nucleon density below 1/5 of the saturation density. If the daughter nucleus had a broader density distribution, the pocket position would shift away from the core region, which would yield a larger charge radius. Therefore, the correlation between these quantities embodies the α-clustering feature of the pocket-type potential.

Fig. 5Full-screen View

(Color online) Positions of the pocket structures in the α-nucleus potentials as functions of the theoretical charge radii of daughter nuclei. These two quantities show an evident linear correlation with the correlation coefficient up to 0.9885, which emphasizes the α-clustering feature of the α-nucleus potential

In addition to the α-decay models, theoretical approaches based on mean-field models have proven to be very effective in describing nuclear structural properties, including nuclear charge radii [40, 50-57]. For instance, the deformed relativistic Hartree–Bogoliubov method accurately reproduced the charge radii of 369 even-even nuclei with Z=8-96 achieving a standard deviation ${\sigma }_{\text{ch}\text{.}}=0.032\text{fm}$ [46], which was significantly more accurate than the results presented in Table 1. This higher accuracy is expected because mean-field models typically have more fitting parameters than α-decay models. For instance, the present calculation uses only three free parameters (r₀, a, and $F_{\text{ex}}$) to achieve reasonable descriptions of both α-decay half-life and the nuclear charge radius. The calculation was simpler and the accuracy was acceptable as a comparative reference. Specifically, the present pocket-type DDFP approach offers a more accessible means of calculation, provided the experimental decay energy data are available.